Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Two regions of microphase separation in ion-containing polymer solutions
Artem M.
Rumyantsev
 and
Elena Yu.
Kramarenko
and
Elena Yu.
Kramarenko
 *
*
Physics Department, Lomonosov Moscow State University, 119991 Moscow, Russian Federation. E-mail: kram@polly.phys.msu.ru
First published on 4th September 2017
Abstract
The phenomenon of spinodal decomposition in weakly charged polyelectrolyte solutions is studied theoretically within the random phase approximation. A novel feature of the theoretical approach is that it accounts for the effects of ionic association, i.e. ion pair and multiplet formation between counterions and ions in polymer chains, as well as the dependence of local dielectric permittivity on the polymer volume fraction Φ. The main focus is on the spinodal instability of polyelectrolyte solutions towards microscopic phase separation. It has been shown that increasing the binding energy of ions decreases the classical microphase separation region (possible at low polymer concentrations) due to the effective neutralization of the chains. A qualitatively new type of microphase separation is found in the presence of a dielectric mismatch between polymer and solvent. This new branch of microphase separation is realized at high polymer concentrations where ion association processes are the most pronounced. Typical microstructures are shown to have a period of a few nanometers like in ionomers. The driving force for the microphase formation of a new type is more favourable ion association in polymer-rich domains where ionomer-type behavior takes place. Effective attraction due to ion association promotes microscopic as well as macroscopic phase separation, even under good solvent conditions for uncharged monomer units of polymer chains. Polyelectrolyte-type behavior at low Φ and ionomer-type behavior at high Φ result in the presence of two critical points on the phase diagrams of polyelectrolyte solutions as well as two separate regions of possible microscopic structuring. Our predictions on the new type of microphase separation are supported by experimental data on polymer solutions, membranes and gels.
1 Introduction
Microphase separation in semidilute polyelectrolyte solutions under moderately poor solvent conditions is a unique effect possible owing to three features inherent to these systems simultaneously: (I) connectivity of units of one type into long polymer chains; (II) the presence of non-neutralized electric charges interacting via long-range Coulomb forces; (III) short-range attractive interactions acting between monomers.Short-range attraction of monomer units (III) is the driving force for the occurrence of inhomogeneities. Their growth is accompanied by an increase in the excess Coulomb energy of regions enriched with polymer since counterions prefer to be homogeneously distributed throughout the solution in order to attain maximal translational entropy. Electrostatics (II) stabilize the finite size of inhomogeneities. Macroscopic phase separation is unfavourable because it is accompanied by the trapping of counterions within precipitate in order to provide electroneutrality. So precipitation causes a high loss in the translational entropy of counterions, and the formation of microphase separated structures turns out to be thermodynamically more favourable. At that, connectivity of monomer units (I) plays a crucial role in the formation of nanodomains. It results in the low entropy of polymer units unable to move independently, so that entropy loss caused by non-uniform polymer distribution in microphase separated solution is very low, much lower than that of separated units. Indeed, in a solution with nanodomain structure the distribution of low-molecular weight counterions is much more homogeneous than that of a polyelectrolyte.
The possibility of microphase separation in the solution of a weakly charged polyelectrolyte under poor solvent conditions was theoretically demonstrated in a weak segregation limit by means of the random phase approximation (RPA).1,2 Under an appropriate solvent quality, the homogeneous solution is unstable against fluctuations with the finite wave vectors while stable against macrophase separation. This results in the formation of nano-sized domains with characteristic length D = 2π/|q0|, and q0 is the limiting wave vector providing the lowest spinodal towards microphase separation. This effect takes place in solutions with a low polymer volume fraction Φ, Φ < ΦL. The spinodal towards microphase separation disappears in the so-called Lifshitz point {ΦL;χL} where the corresponding microstructure period diverges, D → ∞. It is clear that the Lifshitz point belongs to the spinodal of macrophase separation. In a salt-free solution microphase separation was experimentally detected in polyelectrolyte gels3,4 by means of small angle neutron scattering (SANS). The static structure factor revealed a maximum at wave vector values corresponding to the structure period D of about tens of nanometers.
The theoretical approach proposed in ref. 1 and 2 was later generalized to the cases of polyelectrolyte gels in poor solvent5–7 and solutions of polyelectrolytes with associating groups (stickers)8 where microphase separation was shown to take place as well. Ref. 9 is devoted to the effect of counterion solubility on microphase separation in polyelectrolyte solutions. In ref. 10 the modified free energy of the solution containing Flory–Huggins contribution was expanded to the fourth order terms in the vicinity of the critical point. This allowed the prediction of the stability region of different microstructures, such as disordered, body-centred-cubic (bcc), triangular and lamellar, and the plotting of the phase diagram of the solution.
Necklace-type conformations of a single linear polyelectrolyte in poor solvent can also be comprehended as microphase separation within a separate molecule.11 In fact, all three features (I)–(III) are proper to this system, but in the absence of any of them necklace conformations are impossible. Without condition (III), a polyelectrolyte in a good solvent adopts the usual extended conformation. Excluding feature (II) one gets a neutral polymer in poor solvent which forms a uniform spherical globule.12 Finally, the lack of connectivity property (I) leads to the problem of instability of a liquid droplet under charging, that separates into several smaller electrostatically repelling droplets moving away from each other at infinite distances.13 After the prediction of the necklace-type conformations via scaling arguments, a similar result was obtained in ref. 14 in the framework of a variational approach that conceptually resembles RPA for solutions. The instability of rodlike single chain conformations towards perturbations with finite wave length along the backbone resulting in the necklace formation was demonstrated.
To the best of our knowledge, in all theoretical works devoted to the investigation of microphase separation in weakly charged polyelectrolyte solutions/gels within the weak segregation limit, the effects of ion association enhanced by dielectric mismatch between the polymer and solvent were up to now entirely neglected. However, it is well known that the process of ion pairs and multiplet formation is of great importance in polyelectrolyte systems, especially in the case of low polar solvents and high polymer volume fractions.15,16 The mixed polyelectrolyte/ionomer behavior of polymer gels in organic solvents (e.g. methanol) under ionization17–19 as well as counterion specificity in polyelectrolyte gel swelling and solution behavior16,19–22 are striking manifestations of ion association processes. The formation of ion pairs and multiplets was observed in computer simulations23,24 and confirmed experimentally in luminescence25,26 and conductivity17,27,28 studies. Finally, theoretical approaches show that a considerable fraction of counterions binds with charges in chains even in semidilute solutions and swollen gels.20,29–31 For polyelectrolyte solutions, theoretical binodals and spinodals towards macrophase separation that account for ion condensation were constructed in ref. 29, 30 and 32.
The theoretical comprehension of the experimental results on polyelectrolyte gels and solutions revealed that the effect of dielectric mismatch between the solvent and polymer resulting in the dependence of the local medium dielectric constant on the polymer volume fraction plays a crucial role in ion association processes and, hence, the resulting system behavior. Since pure polymer is much less polar than solvent, dense chain conformations favour ion binding providing extra energy gain in the Coulomb interaction of closely-spaced charges. This is supported by the fact that the majority of counterions in ionomer melts are not free. Thus, a proper account for the influence of counterion condensation on microphase separation in polyelectrolyte solutions requires scrupulous consideration of the dielectric mismatch effect as well.
Besides, ionomers can also undergo microphase separation. However, the driving force for microstructuring in one-component ionomer melts more likely coincides with that in block-copolymers33,34 and differs from that in weakly charged polyelectrolytes: it is the connectivity of several types of different immiscible blocks into a single chain. In the event of ionomers these blocks are neutral and ionic ones. Theoretical estimations of domain dimensions in one-component ionomer melts carried out in the strong segregation limit approximately coincide with experimental data.35–38
In the present paper we consider the instability of polyelectrolyte solutions towards microphase separation with a glance to the effects of ion association and dielectric mismatch. Our theory unifies the cases of polyelectrolyte and ionomer regimes of solution behavior and predicts microphase separation in both of them. Spinodals of the solution are calculated within the RPA. The RPA can be correctly applied only to weakly fluctuating systems because it is one-loop approximation. Since fluctuations in concentrated polymer solutions, Φ ∼ 1, are very weak, the RPA is a suitable tool to study them. The only inaccuracy may exist in the region of low polymer volume fractions, Φ ≪ 1, where the solution is semidilute and the fluctuations are so high that they cannot be treated within the RPA.39,40
The paper is organized as follows. In Section 2 the theoretical model is outlined. Analytical expressions defining solution spinodals towards macro- and micro-phase separation, corresponding microstructure periods and equations determining Lifshitz points are obtained in Section 3. Section 4 showing the plots of spinodals towards micro- and macrophase separation is divided into seven parts, A–G. In the first one (A) we consider the case of ion association disregarding dielectric mismatch. Section B demonstrates that nonzero dielectric mismatch may lead to the formation of a new region of microphase separation. In Section C binodals of the solution are calculated and plotted, which allows the investigation of thermodynamical stability of the microstructures. Analysis of the monomer–monomer structure factor of homogeneous solution in the vicinity of the new critical point is performed in Section D. Section E is devoted to the influence of counterion type on microphase separation. In Section F we discuss how the functional dependence type for the solution dielectric constant on the polymer volume fraction, ε(Φ), influences our findings. Finally, Section G is devoted to the data on experimental observations of microphase separation in the new region. The essential results are briefly summarized in Section 5.
2 Theoretical model
Let us consider a solution of linear flexible polymer chains each consisting of N monomeric units with the characteristic size a. The chains contain a small fraction of groups that can dissociate in the solution with the release of low-molecular-weight counterions. Let us denote as fN the average number of these groups in the chain, f ≪ 1 for weakly charged polyelectrolytes. The counterions and the ions in the polymer chains are assumed to be monovalent. We consider the case of a salt-free solution, thus, the only mobile ions in the solution are counterions and their number per chain is equal to the number of charged groups in the chain.We suppose that the counterions can associate into ion pairs with the oppositely charged ions in chains. In turn, ion pairs are able to join into multiplets. Though computer simulations demonstrate that the structure and dimensions of ionic associates depend on the charge location both within the counterion and polymer chain, these microscopic details can be hardly included in the theoretical model.24,41 For simplicity, each multiplet is assumed to consist of two ion pairs. These processes of ion association can be described as reversible reactions
| 2A+ + 2C− ⇄ 2A+C− ⇄ (A+C−)2. | (1) |
To investigate the stability of the system with respect to microphase separation one has to write down the free energy of the inhomogeneous state of the system as a functional of smoothed densities. It can be written in the following form:
| F = F0 + FL + Fc + Fel-st + Fagg | (2) |
The first term in this expression accounts for the non-electrostatic interactions of the monomer units of the chains as well as the free energies of the translational motion of the chains and solvent molecules in the solution. Let ϕ(r) be the volume fraction of the monomer units of the polymer at the point r, then
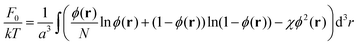 | (3) |
The next term in eqn (2) stands for the specific polymer contribution to the free energy connected with entropic loss from the inhomogeneous distribution of polymer concentration in the system. If the characteristic scale of inhomogeneities in the system is much larger than the size of the monomer units a, then this contribution can be written as follows:12,43
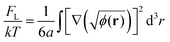 | (4) |
The third term in the total free energy corresponds to the ideal-gas translational entropy of counterions
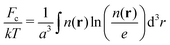 | (5) |
The next contribution in eqn (2) is the free energy of electrostatic interactions:
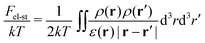 | (6) |
Here ρ(r) is the volume charge density at position r
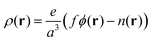 | (7) |
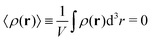 | (8) |
Finally, the last term in eqn (2) is the contribution to free energy due to the formation of ion pairs and multiplets consisting of counterions and ions in polymer chains. This contribution, taking into account not only energy gain due to ion association but also its combinatorics and concomitant translational entropy loss, has the following form:29,44,45
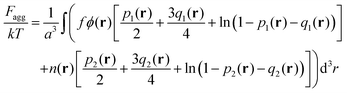 | (9) |
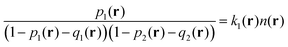 | (10) |
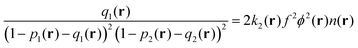 | (11) |
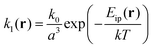 | (12) |
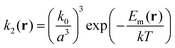 | (13) |
It should be mentioned that in our consideration we neglect the contribution to free energy caused by correlations between non-neutralized charges in polymer chains and oppositely charged free counterions, which can be written in the form proposed by Borue and Erukhimovich in ref. 1. This contribution is known to be smaller than the free energy of translational motion of mobile counterions46 when electrostatic interactions are weak, i.e. the translational entropy of counterions dominates over the Coulomb attraction of opposite charges. In the case of strong electrostatic interactions, charge correlations accounted for through ion pair and multiplet formation dominate in the system.
We do not account explicitly for dipole–dipole interactions between ion pairs as well as ion–dipole interactions47,48 because the number of ion pairs in a weakly charged system (f ≪ 1) at low polymer volume fractions is low. In highly concentrated solutions ion association is strong and the majority of ion pairs is involved in multiplets, so that multiplet formation effectively accounts for the interactions of dipoles. Whether polymer solution is sol or gel is also disregarded.8 According to Stockmayer, solution gelation takes place at Nfq = 2,29 however it influences the kinetics of solution decomposition rather than the equilibrium thermodynamics we deal with.
One can easily find that in the homogeneous solution without fluctuations the volume fractions of the polymer and counterions are equal to the averages, 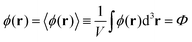 and
and 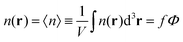 . Owing to the local electroneutrality, one can find p1 = p2 ≡ p and q1 = q2 ≡ q for the case of uniform distribution of polymer and counterion density in the system. In order to investigate solution behavior, it is necessary to calculate its binodal and spinodals toward micro- and macrophase separation.
. Owing to the local electroneutrality, one can find p1 = p2 ≡ p and q1 = q2 ≡ q for the case of uniform distribution of polymer and counterion density in the system. In order to investigate solution behavior, it is necessary to calculate its binodal and spinodals toward micro- and macrophase separation.
3 Spinodals of the solution
To study the stability of the solution towards spinodal decomposition, the free energy functional is expanded in the powers of fluctuations of volume fractions of polymer and counterions about their averaged values:| δϕ(r) = ϕ(r) − Φ = ϕ1(r) | (14) |
| δn(r) = n(r) − fΦ = ϕ2(r) | (15) |
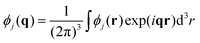 | (16) |
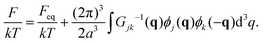 | (17) |
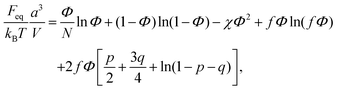 | (18) |
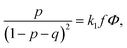 | (19) |
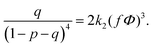 | (20) |
The components of the matrix G−1 are the following:
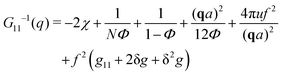 | (21) |
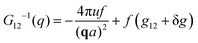 | (22) |
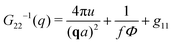 | (23) |
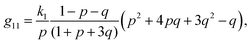 | (24) |
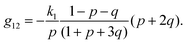 | (25) |
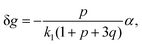 | (26) |
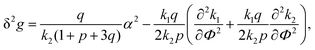 | (27) |
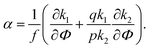 | (28) |
| G11−1G22−1 = (G12−1)2. | (29) |
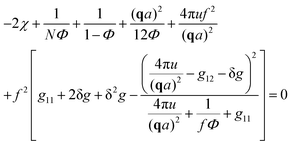 | (30) |
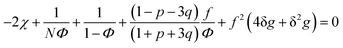 | (31) |
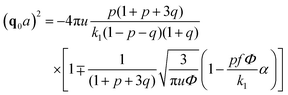 | (32) |
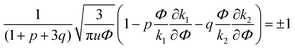 | (33) |
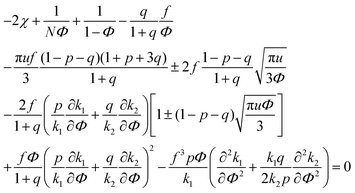 | (34) |
A spinodal with a plus sign corresponds to the first branch of microphase separation at low polymer volume fractions, 0 ≤ Φ ≤ ΦL+. On the contrary, the second branch of microphase separation given by eqn (34) with a minus sign defines the second branch of microphase separation which takes place at a high polymer volume fraction ΦL− ≤ Φ ≤ 1, if it exists. Indeed, at any reasonable ε(Φ) dependence ΦL+ < ΦL− if the second Lifshitz point ΦL− exists. The first one, ΦL+, always exists. In eqn (34), when defining the spinodals of microphase separation, as well as in eqn (30)–(33), the values of the ion pair and multiplet fractions are defined by laws of mass action (19) and (20) since we consider the stability of the homogeneous solution.
4 Results and discussion
A Effect of ion association in the absence of dielectric mismatch
We start considering the case of no dielectric mismatch assuming ε(Φ) = ε0 in order to reveal the effect of ion association on the spinodals of the solution and possible microphase separation in it. If the dependence of the media dielectric constant on the polymer volume fraction is disregarded, one can easily find that δg = δ2g = α = 0 and the association constants are independent of Φ, ∂k1/∂Φ = ∂k2/∂Φ = 0. Thus, eqn (33) defining Lifshitz points has the only root corresponding to the plus sign in the right-hand side of it. This root ΦL+ and the corresponding ion pair and multiplet fractions pL+ and qL+ are given by the system of three equations, namely, eqn (19), (20) and equation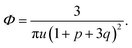 | (35) |
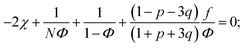 | (36) |
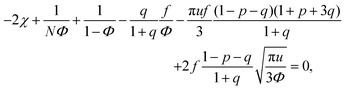 | (37) |
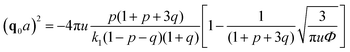 | (38) |
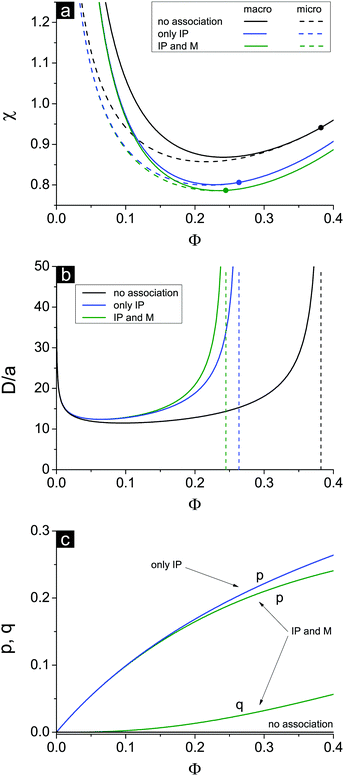
If one entirely ignores ion association, i.e. assumes p = q = 0, the well-known result for the Lifshitz point ΦL+ = 3/πu can be obtained. Accounting for only ion pairing, p ≠ 0 and q = 0, results in a shift of the Lifshitz point toward lower values: ΦL+ = 3/πu(1 + p)2. Additional accounting for multiplet formation, both p ≠ 0 and q ≠ 0, leads to additional diminution of ΦL+, see eqn (35). Thus, increasing ion association causes a decrease of the region of microphase separation. It results in the downwards shift of both spinodals (36) and (37) as well, as shown in Fig. 1a. This conclusion is rather natural. Indeed, it is known that the ionization of the neutral polymer broadens the region of its solution stability and may lead to the unique effect of microphase separation. Our results shows that the reverse process of ion association changes back the behavior of the system: it gradually starts to resemble a neutral solution rather than that of a polyelectrolyte, in accordance with ref. 9. One can also find that the microstructure period D/a grows if ion association is allowed, see Fig. 1b. This is due to a higher degree of polymer charge neutralization and, hence, lower excess Coulomb energy in the microphase separated structure, which grows with both an increasing polymer ionization degree and increasing structure period.
B Effect of dielectric mismatch
In the previous consideration it was demonstrated that only one Lifshitz point and only one branch of microphase separation exist in the event of no dielectric mismatch. To investigate the number of Lifshitz points in the common case, we substitute eqn (12) and (13) along with the corresponding dependencies of energy gains in both association stages on polymer volume fraction Φ in eqn (33). Since k2 = km1, we get the following equation defining Lifshitz points: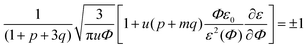 | (39) |
Note that the existence and position of the second Lifshitz point ΦL+ depend not only on the value of pure solvent and polymer dielectric constants, ε0 and εp, but also on the intermediate values of function ε(Φ) in the whole range of polymer volume fractions 0 ≤ Φ ≤ 1. In earlier publications we adopted linear dependence ε(Φ) = ε0(1 − δε·Φ),15,18,19,49,50 and here we follow this assumption. In order to show that even considerable deviations from the linear dependence do not strongly affect the main findings of our investigation, in the very end of this paper we will consider other dependencies ε(Φ) as well.
In the case of linear ε(Φ) dependence and m ≥ 1 it can be rigorously proven that the second Lifshitz point, if it exists, is more than the first one, ΦL+ < ΦL−. The relation m ≥ 1 means that the energy gain of multiplet formation exceeds or equals that of ion pairing, |Eip| ≤ |Em|. Since a multiplet in the framework of our model consists of two ion pairs which attract each other owing to dipole–dipole interactions providing extra energy gain, condition m ≥ 1 should be fulfilled despite a possible perturbation of the optimal distance between the counterion and the ion in the chain within the multiplet. In fact, it is natural to expect that the optimal distance and mutual spatial location of an ion and a counterion take place in an ion pair where sterical restrictions are minimal. Multiplets in real systems usually contain more than 4 charges, which additionally justifies the assumption m ≥ 1. Thus, under these conditions the square brackets in eqn (39) as a function of Φ show a strictly decreasing behavior because ∂ε/∂Φ = −δε, ε(Φ) monotonically decreases, while Φ, u and p + mq monotonically increase. Growth of the last term is clear after the representation p + mq = (p + q) + (m − 1)q since p + q is the fraction of associated ions in either the ion pairs or multiplets. Both p + q and q monotonously grow with increasing Φ despite the fact that p(Φ) can be non-monotonous and reaches maximal values at intermediate Φ before the ion pairs massively join into multiplets,29,32 see Fig. 2c. Since the term before the square brackets in eqn (39) is always positive, one can conclude that ΦL+ < ΦL−.
Spinodals of the solution toward macro- and microphase separation accounting for dielectric mismatch and linear ε(Φ) approximation are plotted in Fig. 2, and the values of the parameters are the same as in Fig. 1. The curve corresponding to the case of no dielectric mismatch δε = 0 is added for comparison and coincides with that in Fig. 1.
First, the increasing dielectric mismatch δε causes a downwards shift of the spinodal in the range of high Φ and emergence of the new (second) critical point in this region. This result is supported by the calculation of binodals of this system revealing two critical points as well.29 The inflection point on the spinodal is located between two critical points. The spinodal corresponding to the rather high δε lies in the region of good solvent, χ < 1/2, at high Φ, as one can see in Fig. 2a in the curve for δε = 0.7. Polyelectrolyte insolubility is caused by the fact that ionic dissociation can be unfavourable if the dielectric constant of the polymer media is rather low and energy loss under dissociation is too high. Experimental investigations on polyelectrolyte gels revealed that these gels can be collapsed even in the solvent which is a good solvent or a Θ-solvent for its non-ionized neutral chains.19
Second, accounting for dielectric mismatch results in the shift of the first Lifshitz point ΦL+ toward zero, so that the first branch of microphase separation becomes narrower, see Fig. 2a.
Third, a high enough dielectric mismatch results in the appearance of the second branch of microphase separation in the region of high polymer volume fractions, Φ > ΦL−. Favourable ion pairing and multiplet formation in the domains with high polymer volume fraction are the driving force for microphase separation: association constants k1 and k2 strongly depend on Φ at high Φ. At that, some fraction of counterions bind with charges on the chains and the rest are still able to move freely. Fractions of charges involved in ion pairs, p, and multiplets, q, are shown in Fig. 2c. At high Φ values and high enough dielectric contrast δε the majority of counterions are bound providing the ionomer solution structure, whereas the fraction of free counterions, 1 − p − q, doesn't exceed 10–20%. Both p and q are defined by solution concentration Φ and independent of the solvent quality χ.
A typical structure period corresponding to the second branch of microphase separation equals several nanometers, D/a ∼ 10, see Fig. 2b. At Φ → 1 the structure period is finite, and its value corresponds to that observed in ionomers. However, in the framework of our theory microphase separation in polymer melts with a low content of solvent is caused by solvent redistribution owing to dielectric mismatch. On the contrary, at Φ → 0 on the first branch of microphase separation the microstructure period diverges.
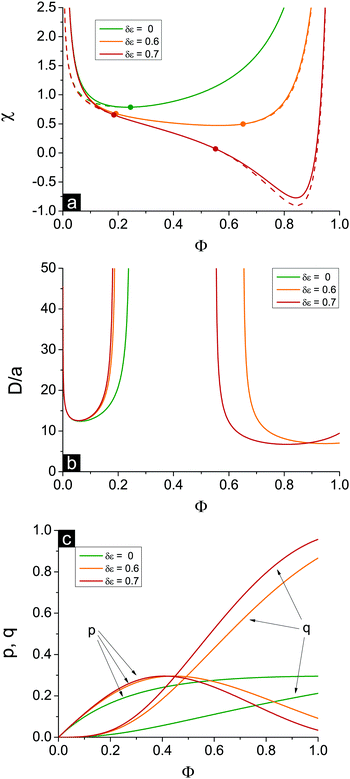
The appearance of the second branch of microphase separation is possible when the polymer polarity is rather low. It corresponds to high enough dielectric mismatch δε values. One can see in Fig. 2a that decreasing δε caused a decrease of the second branch of microphase separation. It entirely disappears at some δεcr when ΦL− = 1 and does not exist at δε < δεcr. The dependence of this critical value of δεcr on the solvent polarity u0 is shown in Fig. 3, and the inset demonstrates the corresponding value of up. Decreasing solvent polarity (i.e. increasing u0) requires a decrease of polymer polarity (increase in up) in order to provide a remarkable difference between polymer and solvent media, which is the driving force for strong ion association in polymer-rich regions and resulting microphase separation. On the other hand, diminution of the solvent dielectric constant requires a lower relative difference of media polarity. Indeed, dielectric mismatch δε = 1 − εp/ε0 = 1 − u0/up goes down at high u0 because a moderate amount of low-polar solvent in polymer-rich regions does not considerably hinder the formation of ion pairs and multiplets. Finally, one can find that the increasing degree of polymer ionization causes a slight decrease of δεcr and ucrp, compare the curves for f = 0.05 and f = 0.1 in Fig. 3. Therefore, a higher degree of polyelectrolyte ionization f promotes an expansion of the second branch of microphase separation at a fixed δε, because the total number of ion pairs and multiplets per chain increases and a higher concentration of charges in the solution additionally promotes ion condensation providing lower entropy losses of ions involved in ion associates.
Notwithstanding that the second branch of microphase separation predominantly lies in the region of good solvent χ < 1/2, all three conditions (I)–(III) necessary for microphase separation are fulfilled. Connectivity of units (I) is evident. Long-range electrostatic interactions (II) are provided by the counterions and charges on the chains that are not bound, and their fraction 1 − p − q is nonzero even in rather concentrated solution. Finally, short-range attraction of polymer chains (III) in good/Θ-solvent is induced not by conventional volume interactions but rather by Φ-dependent energy gain in ion association. Emergence of domains enriched with polymer strongly encourages ion pairing and multiplet formation, so that the entropy losses caused by non-uniform polymer density distribution are outbalanced by the energy of Coulomb interactions of bound ions in these domains. It is important to stress that this mechanism provoking homogeneous solution instability takes place only at nonzero high enough δε. Otherwise, at least in the framework of our theoretical model, ion association leads to neither emergence of the second critical point at high Φ nor appearance of the second branch of microphase separation because it does not induce effective polymer–polymer attraction. Curve δε = 0 corresponding to zero dielectric mismatch is shown in Fig. 2.
C Solution binodals and thermodynamically equilibrium microphase separation
Microphase separated structures occur to be thermodynamically equilibrium in the region where the spinodal of microphase separation is lower than the binodal of macrophase separation of the solution. The binodal of macrophase separation is given by the equality of osmotic pressures Π and chemical potentials μ of the phases: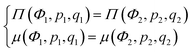 | (40) |
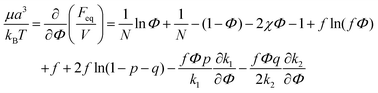 | (41) |
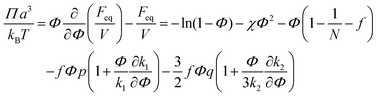 | (42) |
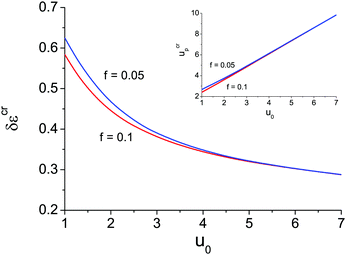
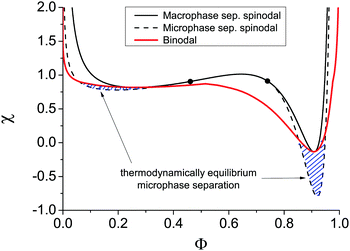
The binodal and spinodal of macrophase separation as well as the spinodal of microphase separation at u0 = 1, dielectric mismatch δε = 0.8, m = 3 and linear ε(Φ) dependence are plotted in Fig. 4. It is seen that regions of thermodynamically equilibrium microphase separation exist in both semidilute and concentrated polymer solutions.
It is also worth noting that the binodal of macrophase separation in Fig. 4 has three local extrema points: two minima correspond to critical points and a maximum being the triple point of the solution. This result derived for the first time in the framework of our model in ref. 29 was later confirmed in theoretical calculations combining the Flory–Huggins approach with liquid-state theory methods and generalized to the case of polymer blends.51 Spinodals of the solution of polymer in ionic liquid were also theoretically shown to reveal the second critical point and triple point only when the dielectric contrast between the solution components is high enough.52
D Solution structure factor
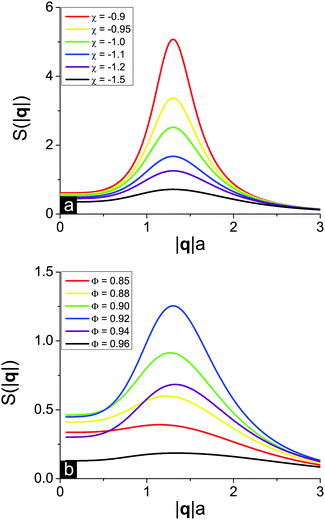
In order to get detailed information about the structure of the solution when it is close to the microphase separation conditions, it is useful to calculate and plot the solution structure factor S(|q|) which can be experimentally measured by scattering techniques. At f = 0.1, u0 = 1, N = 1000, δε = 0.8 and m = 3 the solution critical point toward microphase separation of a new type has coordinates Φcr = 0.92 and χcr = −0.80. Below the critical point, i.e. at χ < χcr, the solution remains homogeneous but the monomer–monomer structure factor S(|q|) should reveal a maximum at finite wavelength owing to the strong concentration fluctuations.We plot two series of curves demonstrating the effects of the solvent quality (Fig. 5a) and polymer volume fraction in the solution (Fig. 5b) on the solution structure factor S(|q|), which was calculated from eqn (30) defining the inverse function S−1(|q|). Solvent deterioration corresponding to increasing χ leads to peak growth, while the position of the finite wavelength peak remains unchanged, see Fig. 5a. As soon as the spinodal line is reached, the S(|q|) function diverges. At that the solution critical point towards microphase separation lies in the region of good solvent since χ < 0. A change of solvent quality can be experimentally achieved by solution cooling or heating,3 depending on the polymer and solvent type.
The influence of the polymer concentration, that can be altered in experiment by the addition of low-molecular-weight solvent, on the structure factor S(|q|) is twofold (Fig. 5b). First, the more the difference between the polymer volume fraction Φ and the critical point coordinate Φcr, the lower and broader the S(|q|) peak. Second, a decrease of the polymer volume fraction causes a very weak shift of the peak position towards lower wavelengths. This result coincides with the dependence of the microphase separated structure period D on the polymer volume fraction Φ in the region of the microphase separation of the new type, ΦL− < Φ < 1 (see Fig. 2b), where D is almost a constant function of Φ except for the narrow vicinity of the second Lifshitz point ΦL− according to the structure period divergence, D → ∞.
Matching our theoretical predictions on S(|q|) with real experimental data on polyelectrolyte solutions using SAXS and SANS is rather complicated since the majority of experimental works deal with dilute and semidilute rather than very concentrated solutions.40 Nevertheless, the structure of very concentrated aqueous salt-free solutions of poly(sodium styrene sulfonate) (NaPSS) was studied independently by two groups,53–55 and they came to similar findings. As soon as the volume fraction of polyelectrolyte exceeds 40–60 vol%, discontinuous transition in the solution takes place. It is accompanied with an abrupt shift of the scattering peak position to |q| ≈ 3.5 Å−1, i.e. 2π/|q| = 1.8 nm, which then remains almost unchanged under further solvent removal.53,55 At that, there exists a region of very high polymer volume fractions (below ≈ 80 vol%) where the system is still solution rather than hydrated amorphous NaPSS powder,55 so that our thermodynamical theory is applicable. Theoretical predictions shown in Fig. 5 on both a very slight shift of the S(|q|) peak position toward higher q values with the growth of polymer concentration Φ53,55 and a maximal peak height to width ratio realized at intermediate Φ values53 are supported by experimental results. This concentration range where the S(|q|) peak position is virtually independent of q is usually considered as a separate regime of polyelectrolyte solution behavior called the hydrated melt of swollen regime, and our theory apparently describes it.
Though in initial theoretical considerations we assumed the polyelectrolyte to be weakly charged, f ≪ 1, the proposed approach can be applied to the case of very concentrated solutions of highly charged polyelectrolytes. Indeed, the dielectric constant of hydrated bulk is low, so that ionic association is strong and the concentration of free counterions increases with f very slow. E.g. at parameter values corresponding to Fig. 4 and 5 quarter of the counterions are free for f = 0.1 while only 5% are free for f = 1, i.e. a ten times growth of ionic group content results in only a twofold increase of the free counterions number.
It also has to be mentioned that experimental dependencies of scattering intensity reveal a large peak near q = 0 which is caused by large-scale inhomogeneities with long relaxation times (slow modes).40 Since our theory is purely thermodynamical, this peak is not shown in Fig. 5.
E Counterion specificity in microphase separation
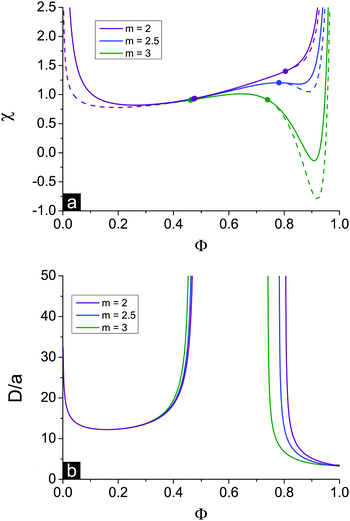
The existence and width of microphase separation regions and the position of Lifshitz points depend on the different system parameters. Decreasing polymer polarity up (i.e. increasing dielectric mismatch δε at a fixed u0) and/or decreasing solvent polarity u0 at a fixed polymer polarity up and/or increasing the fraction of charged units f favour ion pairing and multiplet formation, so that both Lifshitz points ΦL+ and ΦL− shift left. At that, the first branch of microphase separation becomes narrower while the second branch gets wider.Increasing the ratio between energy gains in multiplet formation and ion pairing, m = Em/Eip, has a similar effect on the solution spinodals, see Fig. 6. The shift of the first Lifshitz point ΦL+ is rather small because in the region of low Φ ion association is hindered and does not strongly affect system behaviour. In the region of low Φ spinodals of both microphase and macrophase separation are weakly affected by the value of m. On the contrary, at a high content of polymer, ion binding starts to play a crucial role, and the shift of the second Lifshitz point is much higher. Different values of m can be treated as the values corresponding to different counterions. It is known that energy gain in ion association depends strongly on the dimensions of counterion and charge distribution. E.g. a small counterion with symmetric charge distribution and a bulky counterion with charge located at its interface reveal approx. equal energy gain in ion pair Eip, but the energy gain in the course of multiplet formation in the second case is much lower because of a high sterical repulsion.24 Thus, ion association with these counterions can be described in terms of different m values.
F Effect of functional form of ε(Φ) dependence
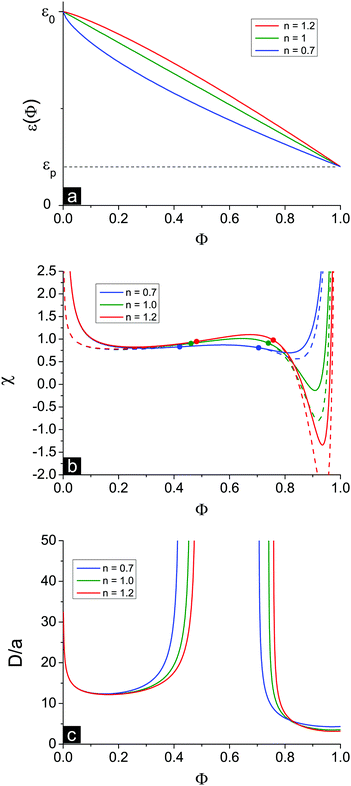
In the above consideration we adopted a linear approximation of the ε(Φ) dependence. In fact, the real dependence can deviate from this law. To investigate the effect of the ε(Φ) functional form, we use the following generalized dependence ε(Φ) = ε0(1 − δε·Φn). Dielectric constants of pure solvent ε(Φ = 0) = ε0 and pure polymer ε(Φ = 1) = εp are fixed at a fixed δε and do not depend on n. The value of n defines the shape of the dependence: n = 1 results in the linear approximation, while n > 1 and n < 1 correspond to convex and concave ε(Φ) functions, respectively, see Fig. 7a.The behavior of the dielectric constant as a function of Φ is most important in the region of high Φ where ion association processes are strong. At n = 0.7 the values of the derivative ∂ε/∂Φ are relatively high at low Φ and small at high Φ, and vice versa at n = 1.2, see Fig. 7b. Therefore, in accordance with eqn (39) the volume fraction ΦL+ is the largest at high n. Similarly, higher n values provide a larger shift of the second Lifshitz point towards high Φ. However, the principal result of our consideration is almost independent of the shape of ε(Φ), i.e. n value: microphase separation is possible not only in the region of low Φ but also at high Φ. Thus, the second branch of microphase separation is the common result irrespective of the particular assumptions used in the theoretical model.
Experimental results on mixtures of low-molecular-weight liquids demonstrate that deviations from the linear law for ε(Φ) are usually moderate,57 though theoretical models57 predict that dependence ε(Φ) should be influenced by molecule dimensions and geometry. For instance, in mixtures of water (ε = 78) with methanol (ε = 32) at T = 293.15 K the dielectric constant of the mixture ε(ΦCH3OH) is slightly lower than the linear approximation,56,58i.e. ε(ΦCH3OH) is concave, but it fits quite well with the generalized power law. The n value is only slightly lower than unity, n ≈ 0.81, and lies within the range considered in Fig. 7.
Here it is suitable to point out that the theoretical predictions about the second branch of microphase separation and the position of the Lifshitz points are justified owing to the applicability of the random phase approximation to the concentrated polymer solutions. RPA underestimates fluctuations in the region of semidilute solution, Φ ≪ 1, so that in this narrow range of concentrations some inaccuracy in spinodal equations should take place. However, this fact does not influence the main results of the developed theory.
G Experimental confirmation of the microphase separation induced by ion association
A direct confirmation of our theoretical results on the possibility of the new type of microphase separation is the microphase separated structures observed in water swollen perfluorosulfonated ionomer (PFSI) membranes containing 13% of ionic groups, either in the form of acid or neutralized with Li+ counterions.59 Depending on the temperature, these membranes absorb different amount of water. At low (room) temperature membrane swelling is weak, so that it contains only 33 vol% of water. Under these conditions both SANS and SAXS spectra of the membrane reveal a maximum at a finite wave vector |q| = 0.13 Å−1 (D = 4.8 nm) called the ionomer peak.59 Moreover, scattering intensity I(|q|) demonstrates ∼|q|−4 asymptotic behavior at high |q| indicating the formation of a microphase separated two phase structure according to the Porod law.60,61 Moderate temperature growth providing extra water absorption by a weakly swollen membrane causes its reorganization with inter-cluster distance D growth and solvent redistribution rather than its affine swelling.59Experimental observations of microphase separation in the region Φ < ΦL+, i.e. its first branch, were for the first time achieved in the case of polyelectrolyte gels which were immersed in moderately poor solvent and remained swollen.3,4 The second branch of microphase separation, Φ > ΦL−, corresponds to a rather dense system, so that microphase separation induced by ion association might have a place in collapsed rather than swollen polyelectrolyte gels.
Ref. 62–64 were devoted to the study of inhomogeneities in collapsed gels of poly(acrylamide-co-diallyldimethylammonium bromide) immersed in water/ethanol mixtures. In the solution containing 60% of ethanol and 40% of water this gel demonstrated a collapse not affected by kinetic aspects. Though it is known that kinetically frozen structures appear within these gels in pure ethanol, in a 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 water/methanol mixture the gel volume was controlled by thermodynamics since both preliminary dried gel and preliminary swollen in pure water gel reached the same swelling ratio being immersed in this mixture. The gel was collapsed, with a low content of solvent within it (∼50%), and a high value of the small angle neutron scattering exponent μ = 3.5 for scattering intensity I(|q|) ≈ |q|−μ in the range 0.1 nm−1 < |q|< 0.47 nm−1 was found. This μ value is close to 4, which corresponds to the formation of microphase separated structures within the gel according to the Porod law,60,61 and these structures are under thermodynamical rather than kinetic control.62–64
60 water/methanol mixture the gel volume was controlled by thermodynamics since both preliminary dried gel and preliminary swollen in pure water gel reached the same swelling ratio being immersed in this mixture. The gel was collapsed, with a low content of solvent within it (∼50%), and a high value of the small angle neutron scattering exponent μ = 3.5 for scattering intensity I(|q|) ≈ |q|−μ in the range 0.1 nm−1 < |q|< 0.47 nm−1 was found. This μ value is close to 4, which corresponds to the formation of microphase separated structures within the gel according to the Porod law,60,61 and these structures are under thermodynamical rather than kinetic control.62–64
These experimental results coincide well with our theoretical analysis. Assume a = 0.7 nm, which is of the order of persistent length for many carbon-chain polymers, and find that u0 = 1 corresponds to pure water since the Bjerrum length in water lb = 0.7 nm, while low polar organic solvents provide higher u0. Thus, the dielectric constant of a 40% water and 60% ethanol mixture εmix ≈ 47, i.e. u0 ≈ 1.7, while that of pure polyacrylamide is much lower, εPAM ≈ 5. Since experimentally investigated gels contained a low fraction of ionic groups, their dielectric constant in dried state should be slightly higher. Thus, dielectric constant values of solvent and polymer ensure a high dielectric mismatch δε ≈ (0.8–0.9) which provides the existence of microphase separation, in accordance with theoretical predictions. The spatial scale of experimentally detected inhomogeneities of 2–10 nm also accords well with theory, see any plot for the microphase separated structure period in Sections B, E and F. The existence of microphase separation only in the case of concentrated solutions/collapsed gels with a volume fraction of polymer higher than ∼50% was also confirmed experimentally: microphase separated structures in the gel at lower than 60% content of ethanol in the mixture were not found except in the case of the gel that was still highly swollen, that corresponds to the first branch of microphase separation Φ < ΦL+.62–64 On the other hand, much higher than 60% content of ethanol caused the formation of kinetically frozen domains.
Thus, experimental observation of microphase separation happened to be a complicated experimental task since it is difficult to reach the required conditions, namely, dense collapsed polymer gel in low polar solvent still being under thermodynamical control. Moreover, the content of ionic units should also be appropriate. In ref. 62–64 microphase separation was detected only in gels with 10% content of diallyldimethylammonium bromide units, while lower contents, 5% and 2%, broke the effect. These data are also supported by theoretical analysis: decreasing the fraction of ionic groups f weakens the effective short-range attraction of monomers (condition (III) for microphase separation) caused by ion pairing and multiplet formation and results in the shift of the second Lifshitz point ΦL− to still higher polymer volume fractions.
Finally, agreement between our predictions and experimental data53–55 on the highly concentrated solution structure factor S(|q|) discussed in Section D is another justification of the developed theory.
5 Conclusion
In this paper we theoretically analyse instability of weakly charged polyelectrolyte solutions with respect to macro- and microphase separation. Spinodals are calculated within the RPA and account for possible reversible association of counterions and ions in polymer chains into ion pairs and multiplets. Furthermore, the dielectric permittivity and, hence, association constants describing ion binding are supposed to depend on the local volume fraction of the polymer being less polar than pure solvent. This approach allowed us to describe not only polyelectrolyte-type behavior typical for semidilute solutions but also ionomer-type behavior realized in concentrated solutions of low-polar ion-containing polymers.Possible switching between polyelectrolyte-type and ionomer-type behavior of polyelectrolyte solutions with increasing polymer concentration results in the presence of not only two critical points on the phase diagrams but also two regions of microphase separation. The first critical point as well as the first region of microphase separation found by Borue and Erukhimovich1 and later by Joanny and Leibler2 correspond to the classical phase behavior of semidilute polyelectrolyte solutions studied previously within the Flory–Huggins approach supplemented by counterion translational entropy and electrostatic interactions with a disregard of any ion pairing. We demonstrate that indeed ion association processes are weakly expressed in semidilute polyelectrolyte solutions in polar solvents. As expected, minor ion pairing leading to partial chain neutralization only slightly shifts the spinodals as well as binodals of macroscopic phase separation into the region of better solvent conditions and simultaneously diminishes the region of microphase separation stabilized by translational entropy of counterions and electrostatic interactions.
On the contrary, ion association plays a crucial role in concentrated polymer solutions where the medium dielectric constant ε is low. The appearance of the second critical point on the phase diagram of polyelectrolyte solutions as a manifestation of the avalanche-type ion association with increasing polymer concentration Φ has been previously predicted in ref. 29 while the second branch of microphase separation is found for the first time in this work. The driving force for phase separation is the progressive energy gain from ion pair and multiplet formation with increasing Φ which causes effective attraction between monomer units of polymer chains destabilizing the homogeneous concentrated solution even in good solvents. It is translational entropy of mobile counterions that favours formation of microstructures instead of macrophases. Indeed, there is a higher energy gain from ion association in polymer-rich domains while free counterions distribute more or less homogeneously throughout the solution, with microscopically modulated density. In such a way counterions gain more entropy of translational motion in comparison with the macroscopically separated case when they are forced to stay in one of the phases in order to fulfil the condition of macroscopic phase electroneutrality.
The second branch of microphase separation is shown to appear when the dielectric mismatch between polymer and solvent is rather high. At the same time, at decreasing solvent polarity and/or increasing fraction of ion-containing groups in polymer chains the critical dielectric mismatch, below which microphase separation disappears, decreases. It is revealed that not only the value of dielectric mismatch but also the functional form of ε(Φ) dependence somewhat affects the position of the solution critical points and microstructuring region width. However, in real polymer–solvent mixtures one could expect deviations of ε(Φ) dependence from the linear one to be moderate, so that the principal findings of this work remain valid.
Calculated binodals of polyelectrolyte solutions demonstrated the possible thermodynamic stability of microscopically segregated regions not only in semidilute polyelectrolyte-type but also concentrated ionomer-type solutions. The experimentally found microphase separated structures in water swollen Nafion Li+ membranes containing 67 vol% of polymer59 as well as inhomogeneities in polyelectrolyte gels collapsed in 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 water/ethanol mixtures62–64 should be considered as a confirmation of our theoretical predictions, although the detection of nanostructures in concentrated ion-containing solutions is a challenging future task.
60 water/ethanol mixtures62–64 should be considered as a confirmation of our theoretical predictions, although the detection of nanostructures in concentrated ion-containing solutions is a challenging future task.
Conflicts of interest
There are no conflicts to declare.References
- V. Y. Borue and I. Y. Erukhimovich, Macromolecules, 1988, 21, 3240–3249 CrossRef.
- J. F. Joanny and L. Leibler, J. Phys., 1990, 51, 454–557 Search PubMed.
- M. Shibayama, T. Tanaka and C. C. Han, J. Chem. Phys., 1992, 97, 6842–6854 CrossRef CAS.
- F. Schosseler, F. Ilmain and S. J. Candau, Macromolecules, 1991, 24, 225–234 CrossRef CAS.
- K. Zeldovich, E. Dormidontova, A. R. Khokhlov and T. Vilgis, J. Phys. II, 1997, 7, 627–635 CrossRef CAS.
- P. K. Jha, F. J. Solis, J. J. de Pablo and M. Olvera de la Cruz, Macromolecules, 2009, 42, 6284–6289 CrossRef CAS.
- K.-A. Wu, P. K. Jha and M. Olvera de la Cruz, Macromolecules, 2010, 43, 9160–9167 CrossRef CAS.
- A. N. Kudlay, I. Y. Erukhimovich and A. R. Khokhlov, Macromolecules, 2000, 33, 5644–5654 CrossRef CAS.
- A. Alexander-Katz and L. Leibler, Soft Matter, 2009, 5, 2198–2207 RSC.
- E. E. Dormidontova, I. Y. Erukhimovich and A. R. Khokhlov, Macromol. Theory Simul., 1994, 3, 661–675 CrossRef CAS.
- A. V. Dobrynin, M. Rubinstein and S. P. Obukhov, Macromolecules, 1996, 29, 2974–2979 CrossRef CAS.
- I. M. Lifshitz, A. Y. Grosberg and A. R. Khokhlov, Rev. Mod. Phys., 1978, 50, 683–713 CrossRef CAS.
- L. Rayleigh, Philos. Mag., 1882, 14, 184–186 CrossRef.
- F. J. Solis and M. Olvera de la Cruz, Macromolecules, 1998, 31, 5502–5506 CrossRef CAS.
- A. R. Khokhlov and E. Y. Kramarenko, Macromol. Theory Simul., 1994, 3, 45–49 CrossRef CAS.
- D. Kawaguchi and M. Satoh, Macromolecules, 1999, 32, 7828–7835 CrossRef CAS.
- O. E. Philippova, N. L. Sitnikova, G. B. Demidovich and A. R. Khokhlov, Macromolecules, 1996, 29, 4642–4645 CrossRef CAS.
- A. R. Khokhlov and E. Y. Kramarenko, Macromolecules, 1996, 29, 681–685 CrossRef CAS.
- O. E. Philippova, A. M. Rumyantsev, E. Y. Kramarenko and A. R. Khokhlov, Macromolecules, 2013, 46, 9359–9367 CrossRef CAS.
- A. M. Rumyantsev, A. Pan, R. S. Ghosh, P. De and E. Y. Kramarenko, Macromolecules, 2016, 49, 6630–6643 CrossRef CAS.
- N. Malikova, A.-L. Rollet, S. Čebašek, M. Tomšič and V. Vlachy, Phys. Chem. Chem. Phys., 2015, 17, 5650–5658 RSC.
- H. Mori, M. Wakagawa, S. Kuroki and M. Satoh, Colloid Polym. Sci., 2015, 293, 1023–1033 CAS.
- R. G. Winkler, M. Gold and P. Reineker, Phys. Rev. Lett., 1998, 80, 3731–3734 CrossRef CAS.
- A. A. Gavrilov, A. V. Chertovich and E. Y. Kramarenko, Macromolecules, 2016, 49, 1103–1110 CrossRef CAS.
- V. A. Smirnov, O. E. Philippova, G. A. Sukhadolski and A. R. Khokhlov, Macromolecules, 1998, 31, 1162–1167 CrossRef CAS.
- V. A. Smirnov, G. A. Sukhadolski, O. E. Philippova and A. R. Khokhlov, J. Phys. Chem. B, 1999, 103, 7621–7626 CrossRef CAS.
- E. V. Volkov, O. E. Filippova and A. R. Khokhlov, Colloid J., 2004, 66, 663–668 CrossRef CAS.
- E. V. Volkov, O. E. Filippova and A. R. Khokhlov, Colloid J., 2004, 66, 669–672 CrossRef CAS.
- E. Y. Kramarenko, I. Y. Erukhimovich and A. R. Khokhlov, Macromol. Theory Simul., 2002, 11, 462–471 CrossRef CAS.
- A. V. Ermoshkin and M. Olvera de la Cruz, Macromolecules, 2003, 36, 7824–7832 CrossRef CAS.
- J. Hua, M. K. Mitra and M. Muthukumar, J. Chem. Phys., 2012, 136, 134901 CrossRef PubMed.
- E. Y. Kramarenko, I. Y. Erukhimovich and A. R. Khokhlov, Polym. Sci., Ser. A, 2004, 46, 1570–1582 CAS.
- C. E. Sing, J. W. Zwanikken and M. Olvera de la Cruz, Nat. Mater., 2014, 13, 694–698 CrossRef CAS PubMed.
- C. E. Sing, J. W. Zwanikken and M. Olvera de la Cruz, J. Chem. Phys., 2015, 142, 034902 CrossRef PubMed.
- A. Eisenberg, Macromolecules, 1970, 3, 147–154 CrossRef CAS.
- A. Eisenberg, B. Hird and R. B. Moore, Macromolecules, 1990, 23, 4098–4107 CrossRef CAS.
- I. A. Nyrkova, A. R. Khokhlov and M. Doi, Macromolecules, 1993, 26, 3601–3610 CrossRef CAS.
- A. N. Semenov, I. A. Nyrkova and A. R. Khokhlov, Macromolecules, 1995, 28, 7491–7500 CrossRef CAS.
- M. Muthukumar, J. Chem. Phys., 1996, 105, 5183 CrossRef CAS.
- M. Muthukumar, Polym. Sci., Ser. A, 2016, 58, 852–863 CrossRef CAS.
- L. M. Hall, M. J. Stevens and A. L. Frischknecht, Phys. Rev. Lett., 2011, 106, 127801 CrossRef PubMed.
- P. J. de Gennes, Scaling Concepts in Polymer Physics, Cornell University, Ithaca, 1979 Search PubMed.
- A. Y. Grosberg and A. R. Khokhlov, Statistical Physics of Macromolecules, AIP Press, New York, 1994 Search PubMed.
- I. Y. Erukhimovich, Sov. Phys. - JETP, 1995, 81, 553–566 Search PubMed.
- A. N. Semenov and M. Rubinstein, Macromolecules, 1998, 31, 1373–1385 CrossRef CAS.
- A. R. Khokhlov, S. G. Starodubtzev and V. V. Vasilevskaya, Adv. Polym. Sci., 1993, 109, 123–171 CrossRef CAS.
- T. B. Liverpool and K. K. Müller-Nedeboch, J. Phys.: Condens. Matter, 2006, 18, L135 CrossRef CAS.
- R. Kumar, B. Sumpter and M. Muthukumar, Macromolecules, 2014, 47, 6491–6502 CrossRef CAS.
- E. Y. Kramarenko, A. R. Khokhlov and K. Yoshikawa, Macromol. Theory Simul., 2000, 9, 249–256 CrossRef CAS.
- S. B. Moldakarimov, E. Y. Kramarenko, A. R. Khokhlov and S. E. Kudaibergenov, Macromol. Theory Simul., 2001, 10, 780–788 CrossRef CAS.
- H. K. Kwon, J. W. Zwanikken, K. R. Shull and M. Olvera de la Cruz, Macromolecules, 2015, 48, 6008–6015 CrossRef CAS.
- I. Nakamura, Macromolecules, 2016, 49, 690–699 CrossRef CAS.
- K. Nishida, K. Kaji and T. Kanaya, J. Chem. Phys., 2001, 114, 8671–8677 CrossRef CAS.
- K. Nishida, K. Kaji and T. Kanaya, J. Chem. Phys., 2001, 115, 8217–8220 CrossRef CAS.
- P. Lorchat, I. Konko, J. Combet, J. Jestin, A. Johner, A. Laschewski, S. Obukhov and M. Rawiso, EPL, 2014, 106, 28003 CrossRef.
- Landolt-Börnstein – Group IV Physical Chemistry, ed. M. D. Lechner, Springer, Berlin Heidelberg, 2008, vol. 17 Search PubMed.
- J. A. Reynolds and J. M. Hough, Proc. Phys. Soc., London, Sect. B, 1957, 70, 769–775 CrossRef.
- U. Böhme and U. Scheler, J. Colloid Interface Sci., 2007, 309, 231–235 CrossRef PubMed.
- G. Gebel, Polymer, 2000, 41, 5829–5838 CrossRef CAS.
- G. Porod, Kolloid Z. Z. Polym., 1951, 124, 83–114 CrossRef CAS.
- G. Porod, Kolloid Z. Z. Polym., 1952, 125, 109–122 Search PubMed.
- A. R. Khokhlov, E. E. Makhaeva, O. E. Philippova and S. G. Starodubtzev, Macromol. Symp., 1994, 87, 69–91 CrossRef CAS.
- O. E. Philippova, T. G. Pieper, N. L. Sitnikova, S. G. Starodoubtsev, A. R. Khokhlov and H. G. Kilian, Macromolecules, 1995, 28, 3925–3929 CrossRef CAS.
- A. R. Khokhlov, O. E. Philippova, N. L. Sitnikova and S. G. Starodubtsev, Faraday Discuss., 1995, 101, 125–131 RSC.
| This journal is © The Royal Society of Chemistry 2017 |