Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On the apparent yield stress in non-Brownian magnetorheological fluids
Daniel
Vågberg
 and
Brian P.
Tighe
and
Brian P.
Tighe
 *
*
Delft University of Technology, Process & Energy Laboratory, Leeghwaterstraat 39, 2628 CB Delft, The Netherlands. E-mail: b.p.tighe@tudelft.nl
First published on 14th September 2017
Abstract
We use simulations to probe the flow properties of dense two-dimensional magnetorheological fluids. Prior results from both experiments and simulations report that the shear stress σ scales with strain rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) as σ ∼
as σ ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 1−Δ, with values of the exponent ranging between 2/3 < Δ ≤ 1. However it remains unclear what properties of the system select the value of Δ, and in particular under what conditions the system displays a yield stress (Δ = 1). To address these questions, we perform simulations of a minimalistic model system in which particles interact via long ranged magnetic dipole forces, finite ranged elastic repulsion, and viscous damping. We find a surprising dependence of the apparent exponent Δ on the form of the viscous force law. For experimentally relevant values of the volume fraction ϕ and the dimensionless Mason number Mn (which quantifies the competition between viscous and magnetic stresses), models using a Stokes-like drag force show Δ ≈ 0.75 and no apparent yield stress. When dissipation occurs at the contact, however, a clear yield stress plateau is evident in the steady state flow curves. In either case, increasing ϕ towards the jamming transition suffices to induce a yield stress. We relate these qualitatively distinct flow curves to clustering mechanisms at the particle scale. For Stokes-like drag, the system builds up anisotropic, chain-like clusters as Mn tends to zero (vanishing strain rate and/or high field strength). For contact damping, by contrast, there is a second clustering mechanism due to inelastic collisions.
1−Δ, with values of the exponent ranging between 2/3 < Δ ≤ 1. However it remains unclear what properties of the system select the value of Δ, and in particular under what conditions the system displays a yield stress (Δ = 1). To address these questions, we perform simulations of a minimalistic model system in which particles interact via long ranged magnetic dipole forces, finite ranged elastic repulsion, and viscous damping. We find a surprising dependence of the apparent exponent Δ on the form of the viscous force law. For experimentally relevant values of the volume fraction ϕ and the dimensionless Mason number Mn (which quantifies the competition between viscous and magnetic stresses), models using a Stokes-like drag force show Δ ≈ 0.75 and no apparent yield stress. When dissipation occurs at the contact, however, a clear yield stress plateau is evident in the steady state flow curves. In either case, increasing ϕ towards the jamming transition suffices to induce a yield stress. We relate these qualitatively distinct flow curves to clustering mechanisms at the particle scale. For Stokes-like drag, the system builds up anisotropic, chain-like clusters as Mn tends to zero (vanishing strain rate and/or high field strength). For contact damping, by contrast, there is a second clustering mechanism due to inelastic collisions.
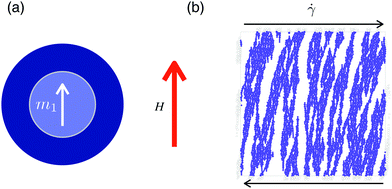
Magnetorheological (MR) fluids consist of magnetizable particles suspended in a viscous carrier fluid. An external magnetic field H induces magnetic moments in the particles, which rearrange into chain-like structures, as illustrated in Fig. 1. Chain formation dramatically enhances the stress σ needed to maintain a strain rate
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , and by varying H it is possible to tune the viscosity of the suspension, with applications to damping and switching. An excellent introduction to the fundamental physics and engineering applications of MR fluids can be found in recent review articles by Vicente et al.1 and Ghaffari et al.2 and references therein.
, and by varying H it is possible to tune the viscosity of the suspension, with applications to damping and switching. An excellent introduction to the fundamental physics and engineering applications of MR fluids can be found in recent review articles by Vicente et al.1 and Ghaffari et al.2 and references therein.
Here we numerically study non-Brownian MR fluids in steady shear flow. Steady state rheology is commonly characterized in terms of the enhancement of the shear viscosity η = σ/![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) over its value η0 at zero field. The ratio η/η0 is governed by the dimensionless Mason number Mn ∝
over its value η0 at zero field. The ratio η/η0 is governed by the dimensionless Mason number Mn ∝ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) /H2 (discussed in detail below), which quantifies the relative strengths of viscous and magnetic stresses in the system; magnetic interactions dominate when Mn tends to zero. In practice, the empirical fitting function
/H2 (discussed in detail below), which quantifies the relative strengths of viscous and magnetic stresses in the system; magnetic interactions dominate when Mn tends to zero. In practice, the empirical fitting function
 | (1) |
The value Δ = 1 is an important reference case, as eqn (1) is then equivalent to the flow curve of a Bingham plastic
σ(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) = σy + A ) = σy + A![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . . | (2) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ) in the limit
) in the limit ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) → 0 (henceforth “the yield stress”). Experiments are of course performed at small but finite strain rates, hence in practice the yield stress is also identified with an apparent plateau in the flow curve at the lowest accessible rates; i.e. one assumes the plateau persists to asymptotically low strain rates. If instead Δ < 1, then the system has no yield stress and the stress vanishes slowly with the strain rate, σ ∼
→ 0 (henceforth “the yield stress”). Experiments are of course performed at small but finite strain rates, hence in practice the yield stress is also identified with an apparent plateau in the flow curve at the lowest accessible rates; i.e. one assumes the plateau persists to asymptotically low strain rates. If instead Δ < 1, then the system has no yield stress and the stress vanishes slowly with the strain rate, σ ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 1−Δ as
1−Δ as ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) → 0. Competing theoretical descriptions predict exponents Δ = 14–8 and Δ = 2/3;9 for a discussion of the different models see ref. 2, 10 and 11. Numerous experimental and numerical studies have measured Δ values throughout this range in a number of magnetorheological (and electrorheological) systems under varying conditions; a summary of their results is given in Table 1. Thermal motion has been shown to give Δ < 1 both in experiment8 and simulation.12 However there is no effective way to predict a priori whether a given non-Brownian MR fluid will display a yield stress.
→ 0. Competing theoretical descriptions predict exponents Δ = 14–8 and Δ = 2/3;9 for a discussion of the different models see ref. 2, 10 and 11. Numerous experimental and numerical studies have measured Δ values throughout this range in a number of magnetorheological (and electrorheological) systems under varying conditions; a summary of their results is given in Table 1. Thermal motion has been shown to give Δ < 1 both in experiment8 and simulation.12 However there is no effective way to predict a priori whether a given non-Brownian MR fluid will display a yield stress.
| Authors | Type | Δ |
|---|---|---|
| Marshall et al.4 | Experiment ER-fluid | 1 |
| Halsey et al.9 | Experiment ER-fluid | 0.68–0.93 |
| Felt et al.32 | Experiment MR-fluid | 0.74–0.83 |
| Martin et al.33 | Experiment ER-fluid | 0.67 |
| de Gans et al.8 | Experiment inverse MR-fluid | 0.8–0.9 |
| de Gans et al.34 | Experiment inverse MR-fluid | 0.94 ± 0.02 |
| Volkova et al.35 |
Experiment
(a) MR-fluid (b) inverse MR-fluid |
(a) 0.86–0.97
(b) 0.74–0.87 |
| Sherman et al.36 | Experiment MR-fluid | 1 |
| Bonnecaze and Brady37 | Simulation 2D | 1 |
| Melrose38 | Simulation 3D | 0.8 ± 0.05 |
In the present work we address the presence or absence of a yield stress in a simple model system, which we choose to facilitate direct comparison with the extensive literature on rheology close to the jamming transition.13–23 The model is minimalist: our goal is to capture bulk phenomenology qualitatively, but not necessarily to reproduce experimental results quantitatively. The canonical model for rheology near jamming consists of packings of viscous soft spheres, also known as Durian's “bubble model.”13 Particles in the bubble model are athermal and typically have a polydisperse (here bidisperse) size distribution to frustrate crystallization.15,24 They interact via purely repulsive spring-like forces and one of two types of damping, detailed below. There is no Coulomb friction. As long simulation times are required to achieve acceptable steady state averages at low strain rates, we restrict our focus to systems in two spatial dimensions to reduce computational expense.
In order to introduce magnetostatic interactions to the bubble model, we treat particles as composites with a magnetizable core and elastic shell structure, as seen in Fig. 1a. Similar core–shell structures have been used in experiment to change the surface properties of particles and to lower the effective density of the particles in order to avoid sedimentation.25–29 The core–shell structure is also suitable to model the recent experiments of Cox et al.,30 which bridge the gap between conventional magnetic suspensions and amorphous magnetic solids.
There are two standard types of damping in the bubble model, and we consider both. The first, which we denote reservoir damping (RD) in accord with the terminology of ref. 31, is a Stokesian drag with respect to the carrier fluid. The second, contact damping (CD), is applied to the relative velocity of particles in contact. The absence of Coulomb friction gives us a cleaner system that helps us to understand the underlying physics. We will ultimately argue that contact damping provides insight into the case of frictional contacts.
Our main finding is that the form of the viscous force law has a dramatic influence on the viscosity enhancement in the magnetically dominated regime, as characterized by the exponent Δ. For reservoir damping we find no evidence of a yield stress over a wide range in ϕ and for Mason numbers as low as 10−6; instead the exponent Δ ≈ 0.75 gives an excellent description of the rheology. In sharp contrast, for contact damping there is a clear nonzero yield stress in the same range of Mason numbers, and so Δ = 1. We relate this difference to clusters that form in the CD model at intermediate Mn due to inelastic collisions between particles, an effect that is absent in the RD model.
We further investigate the role of finite size effects and volume fraction, both of which we find to promote the emergence of a yield stress.
1 Model
The system comprises N spherical particles confined to a plane. The particle distribution is a 50–50 bidisperse mixture with size ratio 1.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The bi-disperse size distribution inhibits crystallization, which can strongly influence material properties.24,39 Each particle consists of an elastic non-magnetic outer layer and a hard inner core of a magnetically soft permeable material (Fig. 1a). The diameter of the core is di/2, where di is the diameter of particle i. The mass of each particle mi is directly proportional to its volume Vi such that mi = Viρ, where ρ = 1 is the density of the material. For simplicity we assume the density is constant throughout the particle. We assume the particles are large enough so that thermal motion can be neglected and that there is no static friction.
1. The bi-disperse size distribution inhibits crystallization, which can strongly influence material properties.24,39 Each particle consists of an elastic non-magnetic outer layer and a hard inner core of a magnetically soft permeable material (Fig. 1a). The diameter of the core is di/2, where di is the diameter of particle i. The mass of each particle mi is directly proportional to its volume Vi such that mi = Viρ, where ρ = 1 is the density of the material. For simplicity we assume the density is constant throughout the particle. We assume the particles are large enough so that thermal motion can be neglected and that there is no static friction.
The motion of each particle is governed by
 | (3) |
All systems are periodic in the ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) and ŷ directions (see Fig. 1b). In order to impose a uniform shear rate
and ŷ directions (see Fig. 1b). In order to impose a uniform shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) in the
in the ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) direction while maintaining periodicity, we employ Lees–Edwards “sliding brick” boundary conditions.40 Periodic images of the unit cell in the transverse direction are uniformly translated along
direction while maintaining periodicity, we employ Lees–Edwards “sliding brick” boundary conditions.40 Periodic images of the unit cell in the transverse direction are uniformly translated along ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) with a velocity ±
with a velocity ±![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) L, where L is the side length of the square simulation box. The equations of motions were integrated using a velocity-Verlet scheme modified to better handle dissipative forces.41 The simulation is controlled by varying three parameters: the shear rate
L, where L is the side length of the square simulation box. The equations of motions were integrated using a velocity-Verlet scheme modified to better handle dissipative forces.41 The simulation is controlled by varying three parameters: the shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , the external magnetic field H = Hŷ transverse to the flow direction, and the packing fraction
, the external magnetic field H = Hŷ transverse to the flow direction, and the packing fraction
 | (4) |
1.1 Interaction forces
Overlapping particles repel elastically (Fig. 2a). The elastic contact forces are given by the potential | (5) |
The potential (5) produces an elastic force
 | (6) |
 | (7) |
For the dissipative force fdi we use a viscous force proportional to the velocity difference between the particle velocity vi and a reference velocity. We compare two different viscous dissipations (Fig. 2b and c), by changing the definition of the reference velocity. With the first viscous force law, which we denote reservoir dissipation (RD), the particle loses energy when moving relative to the carrier fluid. We select the reference as vRD = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) yi
yi![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) , the affine shear velocity. This gives
, the affine shear velocity. This gives
| fRDi = −kd(vi − vRD), | (8) |
| fCDij = −kd(vi − vj). | (9) |
To obtain the full dissipative force on particle i one must sum over all particles j in contact with i. The RD model is commonly used in the MR fluid literature,39,43 though more detailed particle–fluid interaction models are possible.44
We use kd = 1 for both the RD and CD dissipation. For RD this ensures the dynamics is overdamped for the studied parameter ranges. While the CD-dissipation is overdamped for contacting particles, it is highly sensitive to the average contact number and free particles do not dissipate energy. This mainly affects the behavior of dilute systems at high shear rates, which is not the limit we focus on here.
The RD and CD force laws can be seen as two limiting cases: RD only considers the particle–carrier fluid interaction, while CD only considers the particle–particle interaction. The two force laws have been studied in detail for dense suspensions in the absence of dipole-interactions.31,41,45 In experimental systems both solvent and particle interactions affect the dissipation and a combination of CD- and RD-dissipation are usually needed to describe the behavior. Simulations are advantageous, in that they allow us to study these effects separately.
The magnetic interaction is modeled using point dipoles positioned at the center of each particle – see Fig. 2d. The dipole moments are induced in the particle core by the external field H. The magnetic flux density B at a distance r from a dipole m is given by
 | (10) |
| Um(rij) = −mj·Bi, | (11) |
| fmij = −∇Um(rij). | (12) |
Inserting (10) and (11) into (12) and evaluating gives the force from dipole i acting on dipole j,
 | (13) |
The magnitude and direction of the induced dipole-moments are given by
| mi = VciM = Vci(3βH), | (14) |
 | (15) |
1.2 Stresses
The shear stress σ is a sum of four contributing terms| σ = σe + σm + σd + σk. | (16) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) → 0.
→ 0.
The first three stress terms are calculated by substituting f0 with the corresponding force from eqn (3) in the expression
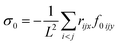 | (17) |
 | (18) |
1.3 Dimensionless numbers
Much of the observed rheology of MR-fluids can be described using four dimensionless numbers: the Mason number (Mn), the Peclet number (Pe), lambda (λ), and the volume fraction ϕ. The first three characterize the relative strengths of magnetic, viscous, and thermal forces. As we consider non-Brownian particles, the Peclet number (viscous versus thermal forces) and Lambda (magnetic versus thermal forces) play no role in the present results. We are left with the volume fraction and the Mason number, which vanishes when magnetic interactions dominate.There is some flexibility when selecting the reference forces used to define the Mason number, which has led to competing conventions in the literature.46 We use microscopic properties to define Mn. Assume there are two particles of the smaller species with diameter d (core diameter d/2) placed at a distance d such that their surfaces just touch. The dipole force between these two particles when their dipole moments are aligned is 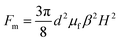 . For reservoir damping the typical viscous force is Fd = dkd
. For reservoir damping the typical viscous force is Fd = dkd![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , while for contact damping there is an additional dependence on the mean number of contacts per particle, Z, such that Fd = Zdkd
, while for contact damping there is an additional dependence on the mean number of contacts per particle, Z, such that Fd = Zdkd![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) . The Mason number Mn ≡ Fd/Fm is therefore
. The Mason number Mn ≡ Fd/Fm is therefore
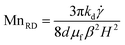 | (19) |
| MnCD = ZMnRD | (20) |
We report shear stresses in the dimensionless form
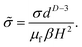 | (21) |
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) (Mn;ϕ), as opposed to plotting the viscosity enhancement η/η0. A yield stress is then clearly signaled by a plateau in
(Mn;ϕ), as opposed to plotting the viscosity enhancement η/η0. A yield stress is then clearly signaled by a plateau in ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) at low Mn. When there is no yield stress, the stress vanishes as
at low Mn. When there is no yield stress, the stress vanishes as ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ∼ Mn1−Δ.
∼ Mn1−Δ.
1.4 Simulation
The length of each simulation in total strain γ varies from γ = 50 at![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 0.05 down to γ = 4 at
= 0.05 down to γ = 4 at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 10−8. Simulations are started at high shear rates, and lower shear rate simulations are initialized using starting configurations obtained from the previous higher shear rate. In order to avoid transient effects the first 20% of each run is discarded before calculating time-averaged quantities. For N ≥ 1024 we perform one simulation for each parameter value, while for N = 256 and N = 64 two, respectively five, independent runs are performed to improve statistics. We study the parameter range 0.1 ≤ ϕ ≤ 0.86, 10−8 ≤
= 10−8. Simulations are started at high shear rates, and lower shear rate simulations are initialized using starting configurations obtained from the previous higher shear rate. In order to avoid transient effects the first 20% of each run is discarded before calculating time-averaged quantities. For N ≥ 1024 we perform one simulation for each parameter value, while for N = 256 and N = 64 two, respectively five, independent runs are performed to improve statistics. We study the parameter range 0.1 ≤ ϕ ≤ 0.86, 10−8 ≤ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ≤ 10−1, 10−4 ≤ H ≤ 10−1 and 64 ≤ N ≤ 16
≤ 10−1, 10−4 ≤ H ≤ 10−1 and 64 ≤ N ≤ 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384, which allows us to probe Mason numbers in a window spanning 12 orders of magnitude for N = 256 and 10 orders of magnitude for N = 4096. Consequently, we cover a larger parameter space than any of the works referenced in Table 1.
384, which allows us to probe Mason numbers in a window spanning 12 orders of magnitude for N = 256 and 10 orders of magnitude for N = 4096. Consequently, we cover a larger parameter space than any of the works referenced in Table 1.
For this work we are especially interested in the behavior at low Mason numbers. At N = 4096 our lowest Mason number is Mn = 5 × 10−7, which is significantly lower than the lowest values accessed by any of the simulations in Table 1 and comparable to or slightly lower than the lowest values accessed in experiment.4,8,32,33
2 Bulk rheology
We start by considering the bulk rheological properties of the RD and CD models, with emphasis on the form of their steady state flow curves.
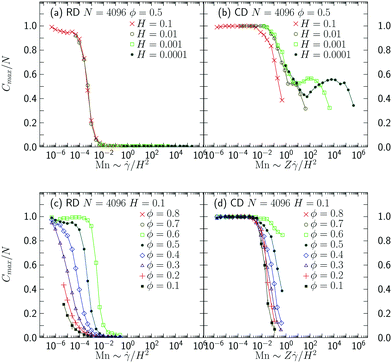
Fig. 3 compares the rheology of the RD and CD models and its dependence on ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and H at fixed ϕ = 0.5 and N = 4096. We first consider rheology of the RD model, shown in the left column of Fig. 3. From top to bottom we plot the same data set as dimensionful flow curves, dimensionless flow curves, and in terms of the viscosity enhancement, respectively. The dimensionless data displays excellent collapse to a master curve that exhibits two flow regimes: a Newtonian regime, σ ∼ Mn, at high Mason numbers, and a magnetically dominated regime at low Mason numbers. It is clear that the RD model does not exhibit a yield stress over the accessible range of Mn; instead we find Δ ≈ 0.75 in the magnetically-dominated regime. The corresponding panels for the CD model (Fig. 3, right column) display a striking difference. There are again two flow regimes, but in this case there is a more gradual crossover to a yield stress in the limit of low Mn, hence Δ = 1.
and H at fixed ϕ = 0.5 and N = 4096. We first consider rheology of the RD model, shown in the left column of Fig. 3. From top to bottom we plot the same data set as dimensionful flow curves, dimensionless flow curves, and in terms of the viscosity enhancement, respectively. The dimensionless data displays excellent collapse to a master curve that exhibits two flow regimes: a Newtonian regime, σ ∼ Mn, at high Mason numbers, and a magnetically dominated regime at low Mason numbers. It is clear that the RD model does not exhibit a yield stress over the accessible range of Mn; instead we find Δ ≈ 0.75 in the magnetically-dominated regime. The corresponding panels for the CD model (Fig. 3, right column) display a striking difference. There are again two flow regimes, but in this case there is a more gradual crossover to a yield stress in the limit of low Mn, hence Δ = 1.
It is natural to ask if the qualitative differences in the flow curves of Fig. 3 are due to finite size effects. To answer this question, we simulate steady state shear flow for a range of system sizes N = 64…16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 384. The corresponding flow curves for the RD and CD models are plotted in Fig. 4a and b, respectively; the legend in Fig. 4a applies to all panels in Fig. 4. In both cases, we obtain good data collapse over the entire sampled range of Mn, independent of N. We therefore conclude that differences between the RD and CD flow curves at ϕ = 0.5 are not due to finite size effects. Finite size effects at higher volume fractions close to the jamming transition (Fig. 4c and d) will be discussed in the Section 2.1.
384. The corresponding flow curves for the RD and CD models are plotted in Fig. 4a and b, respectively; the legend in Fig. 4a applies to all panels in Fig. 4. In both cases, we obtain good data collapse over the entire sampled range of Mn, independent of N. We therefore conclude that differences between the RD and CD flow curves at ϕ = 0.5 are not due to finite size effects. Finite size effects at higher volume fractions close to the jamming transition (Fig. 4c and d) will be discussed in the Section 2.1.
 | ||
Fig. 4 Finite size effects in the steady state shear stress ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) for varying Mason number Mn and particle number N. Data for the RD and CD models (left/right column) at packing fraction ϕ = 0.5 (a and b) and ϕ = 0.84 (c and d). Data for N = 4096 is identical to Fig. 3. for varying Mason number Mn and particle number N. Data for the RD and CD models (left/right column) at packing fraction ϕ = 0.5 (a and b) and ϕ = 0.84 (c and d). Data for N = 4096 is identical to Fig. 3. | ||
Boundary effects are closely related to finite size effects. They are also particularly relevant to experiments, of course, as shearing surfaces are necessary to sustain flow. To probe the influence of boundaries on the flow curve, we fix the positions of a thin layer of particles intersecting the line y = 0, i.e. in the center of the cell. This creates a rough wall, and the particles in the wall can anchor one end of a chain in place. The resulting RD flow curves are plotted in Fig. 5. One clearly sees that the system with a wall develops a plateau at low Mn that is absent in the wall-free case for the same system size. This effect is clearly not a material property, but should be borne in mind when interpreting experimental data.
In order to quantify stress fluctuations in flow, we have also sampled the cumulative distribution function (CDF) of shear stress in steady state. In Fig. 6a and b we plot the CDF for a range of strain rates, with the highest chosen to correspond roughly to the “elbow” in the RD flow curve. While the curves shift left with decreasing ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (as already apparent from the flow curve), their overall shape changes little, indicating that stress fluctuations are insensitive to the strain rate. In Fig. 6c and d we plot the CDF for low Mn and a range of system sizes N. There is a slow systematic increase of the median stress (CDF = 0.5) with N, which is too weak to be seen on the log–log plots of Fig. 4a and b. For small system sizes the flow regularly samples states with negative shear stress; however increasing the system size causes the CDF's to sharpen, reducing the fraction of negative stress states. For N = 4096 and Mn = 10−6 (Fig. 6c and d), the fraction sampled by the RD model is negligible, while in the CD model it is less than 0.1.
(as already apparent from the flow curve), their overall shape changes little, indicating that stress fluctuations are insensitive to the strain rate. In Fig. 6c and d we plot the CDF for low Mn and a range of system sizes N. There is a slow systematic increase of the median stress (CDF = 0.5) with N, which is too weak to be seen on the log–log plots of Fig. 4a and b. For small system sizes the flow regularly samples states with negative shear stress; however increasing the system size causes the CDF's to sharpen, reducing the fraction of negative stress states. For N = 4096 and Mn = 10−6 (Fig. 6c and d), the fraction sampled by the RD model is negligible, while in the CD model it is less than 0.1.
 | ||
Fig. 6 Stress statistics of the RD and CD models (left/right column). Cumulative distribution functions (CDF's) of ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) at H = 0.1, N = 256, and varying strain rate at H = 0.1, N = 256, and varying strain rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (a and b). CDF's of the steady state stress histogram for (a and b). CDF's of the steady state stress histogram for ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 10−7, H = 0.1, and varying N (c and d). Data for N = 4096 is identical to Fig. 3. = 10−7, H = 0.1, and varying N (c and d). Data for N = 4096 is identical to Fig. 3. | ||
Based on the above results, we conclude that the bulk flow curve of the RD model at ϕ = 0.5 has no apparent yield stress over the experimentally (and numerically) accessible range of Mason numbers. The CD model, by contrast, does have an apparent yield stress.
2.1 Towards jamming
We now consider the role of packing fraction ϕ in the bulk rheology. Intuitively, one expects the stress required to sustain steady flow to increase with ϕ. Moreover, soft sphere packings in the absence of an applied field (i.e. H = 0) are known to develop a yield stress at a critical volume fraction ϕc (the jamming point).14–16 The precise value of ϕc depends and particle size distribution24 as well as the protocol used to generate the packings.47 For sheared systems in the quasistatic limit and H = 0 both the CD and RD model have been shown to jam at the same packing fraction ϕc ≈ 0.8433.45,48It is therefore reasonable to ask what happens when the volume fraction is increased towards ϕc in the presence of a magnetic field H > 0. We start by looking at the RD model.
In the top row of Fig. 7, panels (a–e), we plot RD flow curves for ϕ = 0.4, 0.6, 0.7, 0.82, and 0.84 at varying strain rate and field strength. For ϕ ≤ 0.7 we do not observe a plateau, although fitting a power law ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) ∼ Mn1−Δ to the low Mn data reveals an effective exponent Δ approaching 1 as ϕ increases. For ϕ = 0.82 there is an unambiguous plateau at low Mn. Data above the plateau no longer collapse with Mn, which is an indication that critical effects near jamming have begun to play a significant role; at the same time, flow curves at ϕ = 0.82 and H = 0 do not show a yield stress.31 For ϕ = 0.84 the dynamics is completely dominated by the proximity to the jamming transition and data collapse with Mn is wholly absent. There are also strong finite size effects (as expected near a critical point), as seen in Fig. 4c, where the curves for varying N no longer collapse. The flow curves at high Mn are no longer Newtonian but shear thinning – also a signature of the approach to jamming. For comparison, in the bottom row of Fig. 7, panels (f–j), we plot flow curves for the CD model for the same volume fractions; in all cases there is a plateau at low Mn, and we observe identical trends regarding data collapse with Mn. And as with the RD flow curves in Fig. 4c, finite size effects are present in the CD flow curves of Fig. 4d.
∼ Mn1−Δ to the low Mn data reveals an effective exponent Δ approaching 1 as ϕ increases. For ϕ = 0.82 there is an unambiguous plateau at low Mn. Data above the plateau no longer collapse with Mn, which is an indication that critical effects near jamming have begun to play a significant role; at the same time, flow curves at ϕ = 0.82 and H = 0 do not show a yield stress.31 For ϕ = 0.84 the dynamics is completely dominated by the proximity to the jamming transition and data collapse with Mn is wholly absent. There are also strong finite size effects (as expected near a critical point), as seen in Fig. 4c, where the curves for varying N no longer collapse. The flow curves at high Mn are no longer Newtonian but shear thinning – also a signature of the approach to jamming. For comparison, in the bottom row of Fig. 7, panels (f–j), we plot flow curves for the CD model for the same volume fractions; in all cases there is a plateau at low Mn, and we observe identical trends regarding data collapse with Mn. And as with the RD flow curves in Fig. 4c, finite size effects are present in the CD flow curves of Fig. 4d.
 | ||
| Fig. 7 (top row) Flow curves at varying field strengths H for five packing fractions ϕ for system size N = 4096 in the RD model. (bottom row) Corresponding flow curves in the CD model. | ||
In order to compare stresses at low Mn directly, we plot the stress over a range of volume fractions for constant Mn = 2 × 10−6 in both drag models – see Fig. 8. The stresses display an approximately exponential growth with ϕ over a wide range of volume fractions, before increasing more rapidly close to jamming. To test whether the flow curve has approached a plateau, we numerically evaluate the logarithmic derivative q ≡ d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) /d
/d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) and plot the stress only when q < 0.2 (filled symbols). For comparison we also plot the unfiltered stress (open symbols). It is apparent that the CD model always reaches a plateau (apart from a small number of outliers), while the RD model only shows a clear plateau at sufficiently high volume fractions. The particular value of ϕ where the plateau appears has some dependence on system size (compare panels (a) and (b)). While the stress in the RD model always exceeds that in the CD model, the two curves grow closer with decreasing Mason number. This is suggestive of convergence to a common asymptote, and therefore indirect evidence that the RD flow curves display a plateau at asymptotically low strain rates.
and plot the stress only when q < 0.2 (filled symbols). For comparison we also plot the unfiltered stress (open symbols). It is apparent that the CD model always reaches a plateau (apart from a small number of outliers), while the RD model only shows a clear plateau at sufficiently high volume fractions. The particular value of ϕ where the plateau appears has some dependence on system size (compare panels (a) and (b)). While the stress in the RD model always exceeds that in the CD model, the two curves grow closer with decreasing Mason number. This is suggestive of convergence to a common asymptote, and therefore indirect evidence that the RD flow curves display a plateau at asymptotically low strain rates.
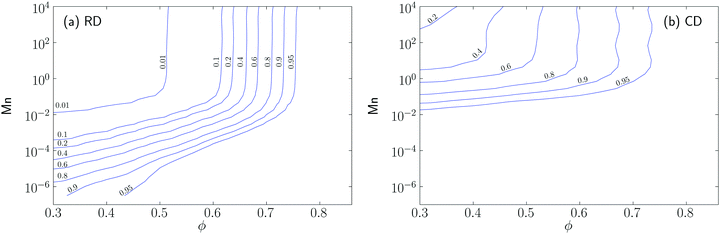
The data of Fig. 7 demonstrates that a plateau in the flow curve (i.e. an apparent yield stress) emerges in the RD model at sufficiently high volume fractions. We speculate that the plateau is present for all ϕ where the particles form a percolating cluster, which at lower ϕ values occurs for smaller Mason numbers than those accessed here. This hypothesis cannot be tested directly using present methods, but in the following section we provide supporting evidence based on the evolution of microstructural measures with Mn and ϕ.
3 Microscopic structure
What microscopic features of the system correlate with (changes in) the bulk rheology? To gain insight into the qualitative differences between the RD and CD models apparent in the flow curves, we now seek to characterize the microstructural evolution of MR fluids in steady shear flow as a function of the Mason number and volume fraction. Our goals are twofold. First, at sufficiently low Mason numbers one expects MR fluids to quasistatically sample states that minimize the sum of the elastic and magnetic potential energies, with viscous forces playing a negligible role. Hence we will seek evidence that our simulations are approaching, if not definitively reaching, this asymptotic regime. Second, the qualitatively different flow curves in the RD and CD models should be reflected in their microstructure. Therefore we seek evidence of qualitative differences, in general, and competing clustering mechanisms in particular.Snapshots of the system are presented in Fig. 9 for both the RD (top row) and CD (bottom row) model and several values of Mn (increasing from left to right). In the RD model there is an apparently homogeneous and isotropic microstructure in the Newtonian regime at high Mn. Chains gradually emerge as the Mason number is lowered and magnetic interactions increasingly dominate. The microstructural evolution in the CD model is comparatively complex. There is anisotropy even in the Newtonian regime. More strikingly, large clusters appear at intermediate Mn. These clusters are more compact than the chains that eventually form at low Mn, and which resemble those seen in the RD model. In the remainder of this section we quantify the above observations.
 | ||
Fig. 9 Particle configurations at varying Mason number Mn ∝ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) /H2 in the RD and CD models (top/bottom row). From left to right: /H2 in the RD and CD models (top/bottom row). From left to right: ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) /H2 = 10−5, 10−1, 10, 104. /H2 = 10−5, 10−1, 10, 104. | ||
3.1 Coordination
At asymptotically low Mason numbers, particles must follow quasistatic trajectories that track minima of the (magnetic and elastic) potential energy as parameterized by the strain coordinate; viscous dissipation can only play a subdominant role. Therefore the![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) → 0 (and hence Mn → 0 at fixed H and ϕ) limit of the flow curve σ(
→ 0 (and hence Mn → 0 at fixed H and ϕ) limit of the flow curve σ(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ;H,ϕ), i.e. the “true” yield stress, must be the same in both the RD and CD models. To obtain evidence of the approach to this asymptotic limit, we now study the evolution of the mean contact number Z at low Mn. Z plays an important role in determining whether a network (e.g. the contact network of a soft sphere packing) can elastically support a load. Here we present evidence that microstructure is indeed independent of the damping mechanism in the limit of vanishing strain rate.
;H,ϕ), i.e. the “true” yield stress, must be the same in both the RD and CD models. To obtain evidence of the approach to this asymptotic limit, we now study the evolution of the mean contact number Z at low Mn. Z plays an important role in determining whether a network (e.g. the contact network of a soft sphere packing) can elastically support a load. Here we present evidence that microstructure is indeed independent of the damping mechanism in the limit of vanishing strain rate.
In the absence of a magnetic field, a packing jams (develops a shear modulus and yield stress) when it satisfies Maxwell's49 counting argument Z ≥ Ziso = 2D + ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1/LD−1), where Z is the mean number of contacts per particle calculated after removing non-load bearing “rattlers” and D is the spatial dimension. The correction term accounts for boundary effects. For several reasons, one expects magnetic interactions to generate elastically rigid states with mean contact numbers Z < Ziso. First, magnetic interactions enhance boundary effects due to clusters' anisotropic shape.50–53 They also introduce long range, potentially tensile forces between particles. The connectivity of the contact network still provides a useful characterization of the flow, however, because the tail of the magnetic interaction potential falls off rapidly with distance, so that the strongest magnetic forces are between nearest neighbors. Finally, when chains are present at low Mason numbers, to minimize the potential energy the particles will arrange such that nearest neighbor magnetic forces are nearly always tensile. Tensile forces increase the likelihood of a structure containing states of self stress, which reduce the number of contacts needed to render a structure rigid. Maxwell's original counting argument can be extended to correctly count states of self stress as described by Calladine,54 a procedure which has also been adopted for studying dense sphere packings.55–57
(1/LD−1), where Z is the mean number of contacts per particle calculated after removing non-load bearing “rattlers” and D is the spatial dimension. The correction term accounts for boundary effects. For several reasons, one expects magnetic interactions to generate elastically rigid states with mean contact numbers Z < Ziso. First, magnetic interactions enhance boundary effects due to clusters' anisotropic shape.50–53 They also introduce long range, potentially tensile forces between particles. The connectivity of the contact network still provides a useful characterization of the flow, however, because the tail of the magnetic interaction potential falls off rapidly with distance, so that the strongest magnetic forces are between nearest neighbors. Finally, when chains are present at low Mason numbers, to minimize the potential energy the particles will arrange such that nearest neighbor magnetic forces are nearly always tensile. Tensile forces increase the likelihood of a structure containing states of self stress, which reduce the number of contacts needed to render a structure rigid. Maxwell's original counting argument can be extended to correctly count states of self stress as described by Calladine,54 a procedure which has also been adopted for studying dense sphere packings.55–57
We now empirically determine the scaling of Z(Mn) at low Mason number, including its asymptote Z0 as Mn tends to zero. The contact number is a “bare” Z with no correction for rattlers. Recalling that Ziso ≈ 4 in large systems with no magnetic interactions, in Fig. 10a (crosses) we plot 4 − Z as a function of Mason number the RD model with ϕ = 0.5 and N = 4096. While in the Newtonian regime at high Mason number the contact number is insensitive to Mn, the quantity 4 − Z decreases (Z increases) as chains form in the magnetically dominated regime. There is an apparent leveling off at the lowest simulated values of Mn, suggesting that Z asymptotes to a value below 4. In order to estimate this value, we plot Z0 − Z (Fig. 10b, circles) and adjust the value of Z0 to find the cleanest power law at low Mn. For Z0 = 3.78 we find a power law Z0 − Z ∼ Mna with exponent a ≈ 0.37. Interestingly, a similar scaling relation Ziso − Z ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 0.38 has been observed in hard sphere suspensions with no magnetic interactions.58 In Fig. 10b we plot the same quantities for the CD model, finding nearly identical values for the extrapolated asymptote Z0 = 3.78 and exponent a ≈ 0.41. We note that the small difference in the exponent a seems to be entirely due to the Z factor in the definitions of Mn, which differs between the RD and CD model. If we fit both data sets using the same definition of Mn the exponent a is the same for both models within statistical error. We have verified that both a and Z0 are independent of N for sufficiently large system sizes, and that their values vary little over a wide range of volume fractions (not shown). Between ϕ = 0.3 and 0.7 the value of Z0 trends from Z0 ≈ 3.78 to 3.85 and eventually approaches Z0 ≈ 4 as ϕ → ϕc for both RD and CD models.
0.38 has been observed in hard sphere suspensions with no magnetic interactions.58 In Fig. 10b we plot the same quantities for the CD model, finding nearly identical values for the extrapolated asymptote Z0 = 3.78 and exponent a ≈ 0.41. We note that the small difference in the exponent a seems to be entirely due to the Z factor in the definitions of Mn, which differs between the RD and CD model. If we fit both data sets using the same definition of Mn the exponent a is the same for both models within statistical error. We have verified that both a and Z0 are independent of N for sufficiently large system sizes, and that their values vary little over a wide range of volume fractions (not shown). Between ϕ = 0.3 and 0.7 the value of Z0 trends from Z0 ≈ 3.78 to 3.85 and eventually approaches Z0 ≈ 4 as ϕ → ϕc for both RD and CD models.
To further verify that the microstructure in both models is statistically indistinguishable in the zero Mason number limit, we now investigate the distribution of local contact numbers. In Fig. 10c we plot the fraction of contacts fz having z contacts, for z = 0…7, in both the RD and CD models. At large Mason numbers, fz differs strongly between the two models, both in its magnitude and its trend with Mn. However, at low Mn each fraction fz approaches a constant value. To within the accuracy of our measurements, the asymptotes of each fz are equal in the RD and CD models.
To summarize our results on contact number, we have seen that for two types of damping, the flow samples states with the same mean value Z0 of the contact number, as well as the same contact number frequencies {fz}z=0…7. This provides strong evidence that steady shear flows in the RD and CD models sample the same ensemble of states as Mn tends to zero. However it is also clear that the asymptotically low-Mn regime is at the limit of the lowest Mason numbers we can practically access numerically.
3.2 Cluster statistics
From the snapshots in Fig. 9 it is apparent that the build-up of clusters proceeds differently in the RD and CD models. Here we present evidence that, whereas clustering in the RD model is driven solely by magnetic interactions, inelastic collisions between particles provide a second, unrelated clustering mechanism in the CD model. Clustering due to inelastic collisions is well known in granular gases: particles exit a collision with a lower relative velocity, and hence tend to stay closer together.59,60 In the CD model, and unlike the RD model, dissipation indeed occurs via collisions. Moreover, due to the model's overdamped dynamics, particles remain in contact after colliding; i.e. their relative velocity is zero (see Fig. 11).We now seek to quantify the degree of clustering in the RD and CD models. If, as hypothesized above, inelastic clustering is present only in the CD model, one should find differences in, e.g., the time-averaged size Cmax of the largest cluster in the system. We consider a particle to belong to a connected cluster if it has a non-zero overlap with any other particle belonging to that cluster. In other words, any particle in a cluster can be reached from any other particle in the same cluster by “walking” along contacts, while particles outside the cluster cannot be reached in this way. A size Cmax = N indicates that every particle participates in one cluster. In the left panel of Fig. 12, we plot Cmax/N in the RD model as a function of Mason number. Note, first, that the data collapse with Mn. Second, there are no clusters of significant size at high values of Mn, when the rheology is Newtonian; however, there is a sharp rise in cluster size below Mn ∼ 10−3, coinciding with the magnetically-dominated regime in the flow curve (cf.Fig. 3). We conclude that “clusters” in the RD model correspond to chains supported by magnetic interactions.
As with the flow curves, the clustering data for the CD model (Fig. 12b) are comparatively complex. First, there is a degree of clustering even in the Newtonian regime. Second, the data do not collapse with Mason number. This clearly indicates the presence of a clustering mechanism independent of magnetic interactions, which we identify with inelastic collisions. Finally, for sufficiently low Mn all particles participate in a single cluster, as in the RD model.
C max also shows qualitatively different dependence on the volume fraction ϕ in the two models. In Fig. 12c and d we plot Cmax/N as a function of ϕ at high field strength H = 0.1. It is clear that the clustering in the RD model shows a much stronger ϕ dependence than in the CD model. This ϕ dependence is consistent with our previous observations that the Mn needed to reach the plateau in σ decreases as ϕ is lowered, and that this shift is stronger in the RD model. Here we also include data for ϕ = 0.1 and 0.2. At these low values of ϕ, the Mason number needed to reach the yield stress plateau is currently inaccessible in simulation. However there is an increase in Cmax at low Mn, suggesting that a plateau does emerge at lower Mn. Another way of visualizing the ϕ dependence over a wider range of Mn is shown in Fig. 13a and b, where we plot contours of Cmax/N over the same range of ϕ and Mn for the RD and CD model, respectively. Differences are most easily seen by considering, e.g., the Cmax/N = 0.9 contour. In the CD model this contour is nearly independent of ϕ, up to some maximum ϕ close to ϕc. This suggests that large clusters appear in the CD model at a characteristic Mason number that is independent of ϕ. In the RD model, by contrast, the value of Mn where clusters appear is an increasing function of ϕ.
In the snapshots of Fig. 9, it is also evident that the orientation of the emergent chains differs between RD and CD flows. To characterize chain orientation, we study θH, defined as the average contact angle measured counter-clockwise relative the magnetic field axis (the ŷ-axis),
 | (22) |
The sum runs over all bonds with a positive overlap. θ(u,v) is the angle between the vectors u and v measured counterclockwise from v such that −π/2 < θ(u,v) < π/2, giving 0 < θH < π/2. In Fig. 14 we plot sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2θH as a function of Mn for three values of ϕ. Chains emerge in both models for sufficiently low Mn, indicated by sin
2θH as a function of Mn for three values of ϕ. Chains emerge in both models for sufficiently low Mn, indicated by sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2θH ≈ 0. Likewise, at high Mn there is a positive bias, indicating that contacts tend to be rotated in a positive sense with respect to H – as one would expect for collisions due to rapid shear flow. The height of the plateau at high Mn shows stronger ϕ-dependence in the RD model than in the CD model.
2θH ≈ 0. Likewise, at high Mn there is a positive bias, indicating that contacts tend to be rotated in a positive sense with respect to H – as one would expect for collisions due to rapid shear flow. The height of the plateau at high Mn shows stronger ϕ-dependence in the RD model than in the CD model.
 | ||
| Fig. 14 Comparison of the average bond angle θH as a function of Mn for the RD and CD model. The panels correspond to three different values of ϕ. | ||
There is a dramatic difference in how the two models cross over between the plateaus at high and low Mn. Whereas sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2θH has a sigmoidal shape in the CD model, in the RD model the curve overshoots its low-Mn asymptote. In this intermediate range of Mn, the two models approach their asymptotic values from opposite “directions”: chains in the CD model are rotated counter-clockwise with respect to H, while chains in the RD model have a clockwise rotation.
2θH has a sigmoidal shape in the CD model, in the RD model the curve overshoots its low-Mn asymptote. In this intermediate range of Mn, the two models approach their asymptotic values from opposite “directions”: chains in the CD model are rotated counter-clockwise with respect to H, while chains in the RD model have a clockwise rotation.
One expects the clusters promoted by inelastic collisions to have a different character from the chain-like structures formed due to magnetic interactions – they should be comparatively compact and isotropic (see Fig. 9). We find the clearest signature of this difference is found by plotting mean number of triangles Δs formed by small particles in contact. For a given cluster size, one expects Δs to be larger for a compact cluster than for an anisotropic, chain-like structure. Δs is plotted in Fig. 15 as a function of Mason number. While Δs increases monotonically with decreasing Mn in the RD model, its evolution is non-monotonic in the CD model. There is a peak at intermediate Mn, which we associate with the more compact collisional clusters, followed by a decrease as those clusters are converted to chains.
 | ||
| Fig. 15 The average number of small triangles per particle vs. Mason number for the RD and CD model. | ||
The data for cluster size, contact angle, and mean triangle number suggest the following picture. In the RD model chain-like clusters build up monotonically as Mn is lowered. In the CD model, in contrast, isotropic clusters form “earlier” (at higher Mn) due to inelastic collisions. As Mn is further lowered and magnetic interactions grow dominant, these compact clusters are reshaped into chains. All relevant observables approach the same asymptotic value in the two models, but they may do so from opposite sides (e.g. θH an Δs). This provides some insight into how the two models' flow curves can display qualitative differences even as they approach the same asymptote. It also provides indirect support of the hypothesis suggested in the previous section, namely that flow curves approach a finite yield stress plateau at inaccessible values of Mn. Of course one might instead infer that the common asymptote of the RD nor CD flow curves is at zero stress, i.e. that neither has a true yield stress. However this interpretation is disfavored by Occam's Razor, as all simulated values of ϕ show a plateau in the CD flow curve.
We recall that one popular framework for modeling the dynamic yield stress in MR and electrorheological (ER) fluids views σy as the average energy density resulting from of a competition between slow elastic deformation of chains, on the one hand, and a rupture and subsequent re-orientation process on the other.61 It is clear from the snapshots of Fig. 9 that this picture is schematic at best for the range of volume fractions considered here, as one cannot unambiguously identify individual chains. Nevertheless, our data for contact orientation indicate the post-rupture re-orientation process must proceed qualitatively differently in the RD and CD models. Indeed, a “dangling” chain segment in the CD model can re-orient to align with the field without dissipating energy by rotating as a rigid body. The same chain segment in the RD model will re-orient comparatively slowly due to drag with the carrier fluid. Consistent with these considerations, we observe that shear stresses in the RD model exceed those in the CD model in the range of Mason numbers where there average contact angles differ.
4 Conclusions
We have studied the steady state rheology of MR fluids interacting via magnetic, elastic, and two distinct viscous forces. While the results and equations in this paper are presented in the context of MR fluids, the model and the findings are more general and we expect that they can be generalized to electrorheological fluids or other similar dipolar systems.Performing numerical simulations that meet or exceed the lowest values of the Mason number accessed experimentally, we have shown that for moderate volume fractions only systems with contact damping (CD) show a clear plateau in their flow curve. Systems with reservoir damping (RD), by contrast, appear to follow a power law σ ∼ ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) 1−Δ with Δ < 1 – which, if extrapolated to zero strain rate, would imply the absence of a dynamic yield stress. We have argued, instead, that viscous forces must play a subdominant role at asymptotically low
1−Δ with Δ < 1 – which, if extrapolated to zero strain rate, would imply the absence of a dynamic yield stress. We have argued, instead, that viscous forces must play a subdominant role at asymptotically low ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , and hence either both models possess a yield stress or neither does. The fact that both models display a plateau in their flow curves at sufficiently high volume fractions strongly suggests it is the former: both models possess a dynamic yield stress, with the plateau in the RD flow curve appearing outside the accessible window of Mn for moderate ϕ. This interpretation is supported by statistical measures of the microstructure, which approach the same asymptote in each model – albeit at the edge of our numerically accessible window in Mn. Cluster statistics suggest that the difference in bulk rheology is related to cluster formation due to inelastic collisions in the CD model, which are absent in RD systems. Despite this conclusion, the clear qualitative difference between the RD and CD flow curves evidenced in our simulations is significant for at least two reasons. First, it persists over a wide interval in Mn including, as previously noted, the lowest values of Mn accessed experimentally. Second, the difference is clearest for moderate values of ϕ far below the jamming transition, which are typical of the MR fluids used in applications.
, and hence either both models possess a yield stress or neither does. The fact that both models display a plateau in their flow curves at sufficiently high volume fractions strongly suggests it is the former: both models possess a dynamic yield stress, with the plateau in the RD flow curve appearing outside the accessible window of Mn for moderate ϕ. This interpretation is supported by statistical measures of the microstructure, which approach the same asymptote in each model – albeit at the edge of our numerically accessible window in Mn. Cluster statistics suggest that the difference in bulk rheology is related to cluster formation due to inelastic collisions in the CD model, which are absent in RD systems. Despite this conclusion, the clear qualitative difference between the RD and CD flow curves evidenced in our simulations is significant for at least two reasons. First, it persists over a wide interval in Mn including, as previously noted, the lowest values of Mn accessed experimentally. Second, the difference is clearest for moderate values of ϕ far below the jamming transition, which are typical of the MR fluids used in applications.
The viscous, elastic, and magnetic force laws we have chosen are particularly simple. An advantage of this simplicity is that they capture essential features of a wide range of MR fluids, as well as inverse MR fluids and ER fluids. We note encouragingly that our CD flow curves can be fit using the Casson model, as recently suggested by Ruiz et al., with fit parameters within the range of experimentally determined values.3 (Neither the Casson nor the Bingham model can describe our RD flow curves, as both models assume there is a yield stress.) More detailed force laws, with additional free parameters and/or more complex micromechanical models, could likely reproduce the flow curve of individual systems more accurately. On the other hand, our results demonstrate that such a flow curve will be non-universal and therefore narrowly applicable.
One can of course ask when a system behaves more like the RD model, and when it flows like the CD model. It seems likely that MR fluids contain a combination of drag with respect to the carrier fluid and dissipation due to contacts. The relative strength of these dissipative interactions should vary with the viscosity of the carrier fluid and the roughness of the particles (for solid suspensions) or the choice of surfactant (in ferrofluid emulsions). Our simulations omit Coulomb friction, though it presumably also plays a role in the laboratory. Insofar as friction renders collisions between particles inelastic, we expect that shear flows in the CD model more closely resemble systems with friction.
Our work raises several (computationally expensive) questions that might profitably be addressed in future work. One, of course, is whether the speculated crossover to a plateau is in fact seen in RD flow curves at volume fractions around 0.5 or lower. We have focused on higher ϕ values in part to make the connection to jamming, but also because a yield stress, if present, should be more readily apparent. In practice, ϕ values around 0.1 are common in experiments and applications. In this dilute limit, chains form, break, and re-form slowly. Hence transients are long and it becomes necessary to simulate for comparatively (and impractically) long total strains.
A second important question concerns the role of dimensionality. Inelastic collisions are also present in the CD model (and absent in RD) in higher dimensions, which would suggest that differences in their flow curves could indeed persist. However there may also be qualitative differences in the clusters and chains that appear in 2D versus 3D. Simulations are needed to determine details such as the apparent value of Δ and the Mn-interval over which effects are observed.
Third, one can ask about the origins of the exponent Δ ≈ 0.75 in the RD flow curves. We note that the critical exponent β in directed percolation (DP), which characterizes the mass of the percolating cluster, has a value β ≈ 0.276 in 1 + 1 dimensions.62 It is tempting to think there might be a connection to 1 − Δ in MR flows, with the applied field defining the time-like dimension. However such a connection is purely speculative.
Conflicts of interest
There are no conflicts of interest to declare.Appendix: simulation details
Dipole moments
There are many effects to consider when modeling the dipole moments d induced by the external field H. For simplicity we assume our materials are ideal so that we do not need to consider saturation effects at high field strengths. We also assume the magnitude and direction of the induced dipole-moments are given by| B = μf(H + M), | (23) |
| mi = VciM = Vci(3βH), | (24) |
where Vci is the core-volume of particle i, and
 | (25) |
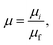 | (26) |
When there are multiple particles the fields from the induced dipoles interact, giving a total dipole moment of
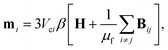 | (27) |
Long range interactions
The dipole–dipole potential between two particles decays as 1/r3. The interaction is therefore long-ranged in 3D and decays too slowly to be easily truncated in 2D, and care must be taken to correctly include the influence of distant particles. There are several methods to do this, of which the lattice-based Ewald summation64 and cutoff-based reaction field methods65 are the most common – see e.g.ref. 66 and 67 for comparisons of different methods. We use a cutoff-based method because it is more computationally efficient (computational complexity O(N)) and easier to generalize when changing the geometry of the simulation cell and applying external deformations such as shearing.While cutoff-based methods are commonly used to simulate MR systems, the long range correction terms used (if any) are rarely published. We therefore include the correction terms employed here. We consider only dipole–dipole interactions; free point charges are not treated. The expressions stated in this Appendix are for 2D systems.
We introduce a cutoff distance rc and evaluate all pair interactions at close distances rij < rc directly. Evaluating each pair interaction at longer distances quickly becomes computationally expensive. Instead we assume the space outside the sphere given by rc is filled with a uniformly polarized continuous phase. It is then possible to analytically integrate over the continuous phase to obtain the long range correction.
For each observable ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) dependent on the dipole potential, it is necessary to calculate a correction term
dependent on the dipole potential, it is necessary to calculate a correction term  by integrating the corresponding observable density function
by integrating the corresponding observable density function  over r > rc. The observable for a single particle i is then given by
over r > rc. The observable for a single particle i is then given by
 | (28) |
We now show how this is applied to the dipole–dipole potential energy. The magnetic flux density Bj from a dipole mj at a distance r is given by
 | (29) |
![[m with combining tilde]](https://www.rsc.org/images/entities/b_char_006d_0303.gif) . There are several ways to approximate
. There are several ways to approximate ![[m with combining tilde]](https://www.rsc.org/images/entities/b_char_006d_0303.gif) ; we use
; we use | (30) |
![[m with combining tilde]](https://www.rsc.org/images/entities/b_char_006d_0303.gif) . Here we have introduced a weight factor w(ri) used to taper the interaction as the cut off distance rc is approached. This prevents discontinuous jumps in measured quantities when particles move in or out of the cutoff sphere. We use a simple linear taper function
. Here we have introduced a weight factor w(ri) used to taper the interaction as the cut off distance rc is approached. This prevents discontinuous jumps in measured quantities when particles move in or out of the cutoff sphere. We use a simple linear taper function | (31) |
![[m with combining tilde]](https://www.rsc.org/images/entities/b_char_006d_0303.gif) i into (29) and integrating over all r > rc yields the correction term
i into (29) and integrating over all r > rc yields the correction term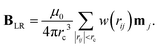 | (32) |
| ULR = −mi·BLR. | (33) |
 .
.
It is straight forward to repeat the above procedure for other observables. For the force one obtains
| fLR = 0, | (34) |
 | (35) |
 | (36) |
σxy![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) LR = −cpLR LR = −cpLR | (37) |
 | (38) |
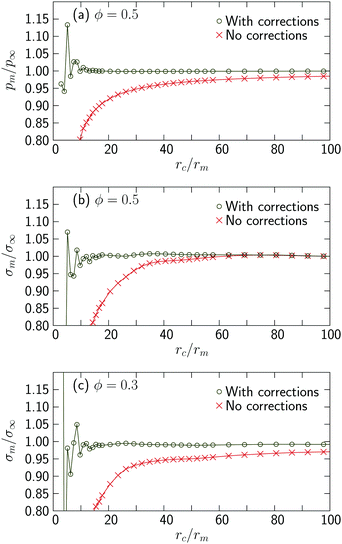
Fig. 16 shows the effect of the above mentioned correction terms. In our simulations we use rc = 15rm for ϕ > 0.3 and rc = 60rm for dilute systems with 0.1 < ϕ ≤ 0.3. Here rm is the radius of the magnetic core of the larger particles.
In general the need for corrections is lower for isotropic packings, i.e. packings with high Mn or high ϕ, and their contribution is often insignificant at the rc we use. At the other end in dilute low Mn packings the corrections play an important role as they can reduce the rc needed during simulation. In Fig. 17 we see the flow curve ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) vs. Mn for ϕ = 0.5 with and without corrections. It is clear from the figure that the corrections are only important at the lowest Mn. The use of the stress correction term shifts the onset of the yield stress plateau to higher Mn, making the plateau easier to observe. However our main conclusions are not sensitive to the use of the correction term; most significantly, our observations regarding the presence or absence of a yield stress plateau at low Mn are also supported by looking at the raw stress without the correction term.
vs. Mn for ϕ = 0.5 with and without corrections. It is clear from the figure that the corrections are only important at the lowest Mn. The use of the stress correction term shifts the onset of the yield stress plateau to higher Mn, making the plateau easier to observe. However our main conclusions are not sensitive to the use of the correction term; most significantly, our observations regarding the presence or absence of a yield stress plateau at low Mn are also supported by looking at the raw stress without the correction term.
Acknowledgements
This work was sponsored by NWO Exacte Wetenschappen (Physical Sciences) for the use of supercomputer facilities, with financial support from the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (Netherlands Organization for Scientific Research, NWO). For the final stages of the work D. V. also received support from the European Research Council under the European Unions Seventh Framework Programme (FP7/2007-2013)/ERC Grant Agreement No. 306845. D. V. acknowledges simulating discussions with H. P. Svea.References
- J. de Vicente, D. J. Klingenberg and R. Hidalgo-Alvarez, Soft Matter, 2011, 7, 3701–3710 RSC.
- A. Ghaffari, S. H. Hashemabadi and M. Ashtiani, J. Intell. Mater. Syst. Struct., 2015, 26, 881–904 CrossRef CAS.
- J. A. Ruiz-López, R. Hidalgo-Alvarez and J. de Vicente, Smart Mater. Struct., 2017, 26, 054001 CrossRef.
- L. Marshall, C. F. Zukoski and J. W. Goodwin, J. Chem. Soc., Faraday Trans. 1, 1989, 85, 2785–2795 RSC.
- D. J. Klingenberg and C. F. Zukoski IV, Langmuir, 1990, 6, 15–24 CrossRef CAS.
- J. E. Martin and R. A. Anderson, J. Chem. Phys., 1996, 104, 4814–4827 CrossRef CAS.
- J. de Vicente, M. T. López-López, J. D. Durán and F. González-Caballero, Rheol. Acta, 2004, 44, 94–103 CrossRef.
- B.-J. de Gans, H. Hoekstra and J. Mellema, Faraday Discuss., 1999, 112, 209–224 RSC.
- T. C. Halsey, J. E. Martin and D. Adolf, Phys. Rev. Lett., 1992, 68, 1519–1522 CrossRef CAS PubMed.
- G. Bossis, O. Volkova, S. Lacis and A. Meunier, Ferrofluids, Springer, 2002, pp. 202–230 Search PubMed.
- J. A. Ruiz-López, J. C. Fernández-Toledano, D. J. Klingenberg, R. Hidalgo-Alvarez and J. de Vicente, J. Rheol., 2016, 60, 61–74 CrossRef.
- Y. Baxter-Drayton and J. F. Brady, J. Rheol., 1996, 40, 1027–1056 CrossRef CAS.
- D. Durian, Phys. Rev. Lett., 1995, 75, 4780 CrossRef CAS PubMed.
- A. J. Liu and S. R. Nagel, Nature, 1998, 396, 21–22 CrossRef CAS.
- C. S. O'Hern, L. E. Silbert, A. J. Liu and S. R. Nagel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 68, 011306 CrossRef PubMed.
- P. Olsson and S. Teitel, Phys. Rev. Lett., 2007, 99, 178001 CrossRef PubMed.
- C. Heussinger and J.-L. Barrat, Phys. Rev. Lett., 2009, 102, 218303 CrossRef PubMed.
- T. Hatano, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79, 050301 CrossRef PubMed.
- B. P. Tighe, E. Woldhuis, J. J. C. Remmers, W. van Saarloos and M. van Hecke, Phys. Rev. Lett., 2010, 105, 088303 CrossRef PubMed.
- B. P. Tighe, Phys. Rev. Lett., 2011, 107, 158303 CrossRef PubMed.
- A. Ikeda, L. Berthier and P. Sollich, Phys. Rev. Lett., 2012, 109, 018301 CrossRef PubMed.
- J. Boschan, D. Vågberg, E. Somfai and B. P. Tighe, Soft Matter, 2016, 12, 5450–5460 RSC.
- K. Baumgarten, D. Vågberg and B. P. Tighe, Phys. Rev. Lett., 2017, 118, 098001 CrossRef PubMed.
- D. Koeze, D. Vågberg, B. Tjoa and B. Tighe, EPL, 2016, 113, 54001 CrossRef.
- J. You, B. Park, H. Choi, S. Choi and M. Jhon, Int. J. Mod. Phys. B, 2007, 21, 4996–5002 CrossRef CAS.
- H. Choi, B. Park, M. Cho and J. You, J. Magn. Magn. Mater., 2007, 310, 2835–2837 CrossRef CAS.
- S. Ko, J. Lim, B. Park, M. Yang and H. Choi, J. Appl. Phys., 2009, 105, 07E703 CrossRef.
- F. F. Fang, H. J. Choi and W. Choi, Colloid Polym. Sci., 2010, 288, 359–363 CAS.
- F. F. Fang, H. J. Choi and Y. Seo, ACS Appl. Mater. Interfaces, 2009, 2, 54–60 Search PubMed.
- M. Cox, D. Wang, J. Barés and R. P. Behringer, EPL, 2016, 115, 64003 CrossRef.
- D. Vågberg, P. Olsson and S. Teitel, Phys. Rev. Lett., 2014, 112, 208303 CrossRef.
- D. W. Felt, M. Hagenbuchle, J. Liu and J. Richard, J. Intell. Mater. Syst. Struct., 1996, 7, 589–593 CrossRef CAS.
- J. E. Martin, J. Odinek and T. C. Halsey, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 3263 CrossRef CAS.
- B. De Gans, N. Duin, D. Van den Ende and J. Mellema, J. Chem. Phys., 2000, 113, 2032–2042 CrossRef CAS.
- O. Volkova, G. Bossis, M. Guyot, V. Bashtovoi and A. Reks, J. Rheol., 2000, 144, 91–104 CrossRef.
- S. G. Sherman, A. C. Becnel and N. M. Wereley, J. Magn. Magn. Mater., 2015, 380, 98–104 CrossRef CAS.
- R. Bonnecaze and J. Brady, J. Chem. Phys., 1992, 96, 2183–2202 CrossRef CAS.
- J. Melrose, Mol. Phys., 1992, 76, 635–660 CrossRef CAS.
- D. Kittipoomwong, D. J. Klingenberg and J. C. Ulicny, J. Rheol., 2005, 49, 1521–1538 CrossRef CAS.
- D. Evans and G. P. Morris, Statistical Mechanics of Nonequilibrium Liquids, Academic, London, 1990 Search PubMed.
- D. Vågberg, P. Olsson and S. Teitel, Phys. Rev. E, 2017, 95, 052903 CrossRef PubMed.
- J. P. Segovia-Gutiérrez, J. de Vicente, R. Hidalgo-Alvarez and A. M. Puertas, Soft Matter, 2013, 9, 6970–6977 RSC.
- J. C. Fernández-Toledano, J. Rodrguez-López, K. Shahrivar, R. Hidalgo-Álvarez, L. Elvira, F. Montero de Espinosa and J. de Vicente, J. Rheol., 2014, 58, 1507–1534 CrossRef.
- H. G. Lagger, T. Breinlinger, J. G. Korvink, M. Moseler, A. Di Renzo, F. Di Maio and C. Bierwisch, J. Non-Newtonian Fluid Mech., 2015, 218, 16–26 CrossRef CAS.
- D. Vågberg, P. Olsson and S. Teitel, Phys. Rev. Lett., 2014, 113, 148002 CrossRef PubMed.
- D. J. Klingenberg, J. C. Ulicny and M. A. Golden, J. Rheol., 2007, 51, 883–893 CrossRef CAS.
- D. Vågberg, P. Olsson and S. Teitel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 031307 CrossRef PubMed.
- P. Olsson and S. Teitel, Phys. Rev. Lett., 2012, 109, 108001 CrossRef PubMed.
- J. C. Maxwell, London, Edinburgh Dublin Philos. Mag. J. Sci., 1864, 27, 294–299 Search PubMed.
- B. P. Tighe and T. J. H. Vlugt, J. Stat. Mech.: Theory Exp., 2011, P04002 Search PubMed.
- C. P. Goodrich, A. J. Liu and S. R. Nagel, Phys. Rev. Lett., 2012, 109, 095704 CrossRef PubMed.
- S. Dagois-Bohy, B. P. Tighe, J. Simon, S. Henkes and M. van Hecke, Phys. Rev. Lett., 2012, 109, 095703 CrossRef PubMed.
- C. P. Goodrich, S. Dagois-Bohy, B. P. Tighe, M. van Hecke, A. J. Liu and S. R. Nagel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 022138 CrossRef PubMed.
- C. Calladine, Int. J. Solids Struct., 1978, 14, 161–172 CrossRef.
- G. Lois, J. Blawzdziewicz and C. S. O'Hern, Phys. Rev. Lett., 2008, 100, 028001 CrossRef PubMed.
- M. Wyart, L. E. Silbert, S. R. Nagel and T. A. Witten, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 051306 CrossRef PubMed.
- D. Head, Eur. Phys. J. E: Soft Matter Biol. Phys., 2007, 22, 151–155 CrossRef CAS PubMed.
- E. Lerner, G. Düring and M. Wyart, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 4798–4803 CrossRef CAS PubMed.
- I. Goldhirsch and G. Zanetti, Phys. Rev. Lett., 1993, 70, 1619 CrossRef CAS PubMed.
- S. McNamara and W. Young, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1996, 53, 5089 CrossRef CAS.
- R. Bonnecaze and J. Brady, J. Rheol., 1992, 36, 73–115 CrossRef CAS.
- J. W. Essam, A. J. Guttmann and K. De'Bell, J. Phys. A: Math. Gen., 1988, 21, 3815 CrossRef.
- F. J. Vesely, J. Comput. Phys., 1977, 24, 361–371 CrossRef CAS.
- P. P. Ewald, Ann. Phys., 1921, 369, 253–287 CrossRef.
- J. Barker and R. Watts, Mol. Phys., 1973, 26, 789–792 CrossRef CAS.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, 1989 Search PubMed.
- C. J. Fennell and J. D. Gezelter, J. Chem. Phys., 2006, 124, 234104 CrossRef PubMed.
Footnote |
| † Note that there exist other empirical flow curves that match the asymptotic scaling of eqn (1) when Δ = 0; in fact we find that the Casson equation3 provides a better fit to data in the crossover region of Fig. 3b, d and f. Nevertheless, as our focus is on asymptotic scaling, we restrict our discussion to eqn (1) for simplicity. |
| This journal is © The Royal Society of Chemistry 2017 |


![[f with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0066_20d1.gif)
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif)