Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Polymer conformation during flow in porous media†
Durgesh
Kawale
 abc,
Gelmer
Bouwman
b,
Shaurya
Sachdev
b,
Pacelli L. J.
Zitha
a,
Michiel T.
Kreutzer
b,
William R.
Rossen
a and
Pouyan E.
Boukany
abc,
Gelmer
Bouwman
b,
Shaurya
Sachdev
b,
Pacelli L. J.
Zitha
a,
Michiel T.
Kreutzer
b,
William R.
Rossen
a and
Pouyan E.
Boukany
 *b
*b
aDepartment of Geosciences and Engineering, Delft University of Technology, Delft, The Netherlands. E-mail: D.Kawale@tudelft.nl
bDepartment of Chemical Engineering, Delft University of Technology, Delft, The Netherlands. E-mail: P.E.Boukany@tudelft.nl
cDutch Polymer Institute (DPI), P.O. Box 902, 9600 AX, Eindhoven, The Netherlands
First published on 24th October 2017
Abstract
Molecular conformations of individual polymers during flow through porous media are directly observed by single-DNA imaging in microfluidics. As the Weissenberg number increases during flow (Wi > 1), we observe two types of elastic instabilities: (a) stationary dead-zone and (b) time-dependant dead-zone washing. When stretched polymer chains enter a dead-zone, they first re-coil and, once inside the dead-zone, they rotate and re-stretch again. The probability distribution of DNA chains under the stretched condition inside the dead-zone is found to be heterogeneous with a broad distribution.
1 Introduction
The flow of polymer solutions through porous media plays a crucial role in various applications such as injection molding, textile coating, inkjet printing, turbulent drag reduction and enhanced oil recovery.1 As polymer solutions flow through a porous medium it shows several non-Newtonian behaviours such as a dramatic increase in pressure drop and flow instabilities at a high Weissenberg number, Wi > 1 (Wi = τ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) , where τ is the polymer relaxation time and
, where τ is the polymer relaxation time and ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is the deformation rate of the imposed flow).2–4 Often these non-Newtonian behaviours are characterized by flow visualization and by measuring the pressure drop, or the stresses due to flow. For instance, elastic instabilities are observed when the flow through porous media increases beyond Wi > 1.5–7 The corresponding molecular conformation beyond Wi > 1 is unknown for the flow of polymer solutions through porous media.
is the deformation rate of the imposed flow).2–4 Often these non-Newtonian behaviours are characterized by flow visualization and by measuring the pressure drop, or the stresses due to flow. For instance, elastic instabilities are observed when the flow through porous media increases beyond Wi > 1.5–7 The corresponding molecular conformation beyond Wi > 1 is unknown for the flow of polymer solutions through porous media.
Traditionally, flow through packed beds of spheres or particles was used to investigate the resistance to flow of polymeric fluids through porous media and determine the constitutive parameters that describe the rheological properties of polymeric fluids.8–10 When the Wi is larger than a critical value at a low Reynold number, Re, (Re = ρvl/η(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ), where ρ is the density, v is the velocity, l is a characteristic length scale and η is the viscosity) there is a sudden increase in the pressure drop across the porous medium.11–14 Direct visualization of flow in two-dimensional (2D) models of porous media (such as a periodic array of cylinder) was the first step towards understanding pore-scale flow phenomena related to polymer flows (from Boger fluids to shear-thinning systems) in porous media.5–7,15–19
), where ρ is the density, v is the velocity, l is a characteristic length scale and η is the viscosity) there is a sudden increase in the pressure drop across the porous medium.11–14 Direct visualization of flow in two-dimensional (2D) models of porous media (such as a periodic array of cylinder) was the first step towards understanding pore-scale flow phenomena related to polymer flows (from Boger fluids to shear-thinning systems) in porous media.5–7,15–19
In recent years, planar microfluidic devices have been widely used to investigate the strong viscoelastic features of polymer flow over a very wide range of Wi under non-inertial conditions (Re ≪ 1).20,21 By using microfluidic analogues of a porous medium, elastic instabilities were shown to cause the dramatic pressure drop increase during flow of Boger and shear-thinning fluids.6,7,22 In particular, Kawale et al.6 studied the flow of a shear-thinning system, hydrolyzed polyacrylamide with and without salt, through a microfluidic device containing a periodic array of obstacles. At very low flow rates (Wi ≪ 1, Re ≪ 1), as expected, creeping flow was obtained. As the flow rate was increased (Wi > 1, Re ≪ 1), the non-Newtonian effects emerged. Stationary dead zones (DZs) appeared to be pinned upstream of the obstacles. The local shear rate in a DZ is negligible compared to that outside of the DZ. As the flow rates increased further (Wi ≫ 1, Re < 1), the stationary DZ starts wobbling and washing away periodically. This time-dependant elastic instability, dead zone washing (DZW), was found to start when the viscoelastic Mach number, Ma ∼ 1 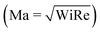 . DZW-like instabilities were also observed during flow of Boger fluids23,24 and worm-like micellar solutions25 around a single cylinder. Not only is the local velocity magnitude inside a DZ close to zero,6,24,25 but there is also a stagnation point at the upstream of the pillar where the local velocity magnitude is zero. The flow inside a DZ is a combination of steady shear flow and extensional flow.6 In a Wi < 1 steady shear flow, the polymer chains will be coiled.26 At the same time, the polymer chains in an extensional flow field can be stretched beyond Wi ∼ 0.5.27 Given a combination of steady shear and extensional flow inside a DZ, the corresponding dynamics of the polymer chain is unclear as the polymer chain approaches and enters a DZ.
. DZW-like instabilities were also observed during flow of Boger fluids23,24 and worm-like micellar solutions25 around a single cylinder. Not only is the local velocity magnitude inside a DZ close to zero,6,24,25 but there is also a stagnation point at the upstream of the pillar where the local velocity magnitude is zero. The flow inside a DZ is a combination of steady shear flow and extensional flow.6 In a Wi < 1 steady shear flow, the polymer chains will be coiled.26 At the same time, the polymer chains in an extensional flow field can be stretched beyond Wi ∼ 0.5.27 Given a combination of steady shear and extensional flow inside a DZ, the corresponding dynamics of the polymer chain is unclear as the polymer chain approaches and enters a DZ.
Rheo-optical methods have been used to complement bulk rheometric measurements with the aim of the direct measurement of stresses, deformations and alignment of polymer chains in the flow of viscoelastic fluids.21,28–30 Specifically, flow-induced birefringence (FIB) imaging has been employed to determine the localized deformation and alignment of worm-like micelles at high Wi during flow through a micro-channel, containing either a single cylinder or a periodic array of cylinders.31–33 Zhao et al.25 investigated vortex formation and growth in micellar solution flow around a cylinder with increasing Wi near the upstream stagnation point of the cylinder by using a combination of FIB imaging and particle image velocimetry (PIV). In such FIB measurements, the molecular parameters are extracted based on an ensemble average, which does not necessarily reflect the molecular individualism of the polymer during flow. Direct visualization of fluorescently labeled DNA provides a unique opportunity for polymer scientists to reveal polymer chain conformation and address molecular processes behind the macroscopic flow phenomena under strong flow conditions (Wi ≫ 1).27,34,35 For instance, Perkins et al.35 used these techniques to directly observe the tube-like motion of polymer molecules assumed in the reptation model for an entangled polymer solution.36,37 Fluorescent DNA molecules that act as molecular tracers have also often been employed to confirm various phenomena such as (1) coil–stretch (C–S) transition in extensional flows,27,38,39 (2) C–S transition with periodic tumbling in shear flows,26,40 (3) C–S transition in free surface flow,41–43 and (4) interfacial disentanglement of DNA chains as the cause for wall-slip in the presence of strong interaction between the adsorbed chains and the wall44,45 and transient stress overshoot in startup shear flows.46–48 All these studies successfully link polymer conformation to the macroscopic behaviour of flow.
To date, experimental studies on pressure driven flow of polymer solutions in microfluidic geometries consisting of contractions and obstacles are focussed on size-based separation of DNA chains.49–51 For instance, for a cylindrical obstacle, the diameter would be small (order of few tens of nanometers or about a micrometer) such that a DNA chain can ‘hook’ on the post. Understanding the hooking and unhooking process is crucial for separating DNA chains based on their size. Little attention was given to high-Wi number flows around larger diameter obstacles wherein the flow field becomes unstable. In the field of single-molecule sequencing, the flow of DNA across single/array of obstacles with an electric-field52 or pressure-drop49,51 is often studied with an intention of DNA chain stretching or size-based DNA chain separation. The length scales of obstacles in these studies are much smaller than the DNA chain length. During DNA flow due to an electric-field, the resulting local velocity-field is purely elongational near an insulating obstacle such as polydimethylsiloxane (PDMS).53 On the other hand, DNA flow due to pressure-gradient results in shear flow across the entire channel. In the current study, we will focus on polymer conformation in microfluidic geometries during elastic instabilities due to pressure-driven flow.
Corner vortex formation during polymeric flow through a planar, sharp or gradual contraction geometry is typically observed around Wi = ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1) −
(1) − ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (10).54,55 Hemminger et al.54 showed that for an entangled shear-thinning polymer solution, the DNA molecules located in the corner vortex disentangle from the molecules at the center of the channel. This observation is reminiscent of shear banding in entangled polymer solutions.56 Francois et al.57 studied drag enhancement during Boger fluid flow around a single cylindrical obstacle. They also observed shear-banding at Wi ∼ 1 near the vicinity of the obstacle. The DNA extension distribution in both shear-bands was positively skewed, with the mean extension in the high shear-rate band (closer to the obstacle) being twice that in the low shear-rate band (further away from the obstacle). As Wi increases in shear flow, the DNA extension distribution shifted from positively skewed to a broad probability distribution.26 Such a broad distribution of DNA extensions in a shear flow is caused by the tumbling motion of DNA chains. Liu and Steinberg58 studied DNA chain dynamics in elastic turbulence and found that the DNA extension distribution is negatively skewed with mean fractional extension reaching a value of 0.8 asymptotically. Such a high mean fractional extension has also been observed in an extensional flow field.27,59 In this paper, we report the molecular processes leading to DZ formation during flow of shear-thinning polymer solutions through a periodic array of obstacles. We probe conformation of single chains by visualizing fluorescently labelled DNA molecules in polyacrylamide (PAA) solutions with and without the addition of salt. In addition, we use a combination of pressure-drop measurement and streamline visualization to map elastic instabilities and the corresponding pressure losses.
(10).54,55 Hemminger et al.54 showed that for an entangled shear-thinning polymer solution, the DNA molecules located in the corner vortex disentangle from the molecules at the center of the channel. This observation is reminiscent of shear banding in entangled polymer solutions.56 Francois et al.57 studied drag enhancement during Boger fluid flow around a single cylindrical obstacle. They also observed shear-banding at Wi ∼ 1 near the vicinity of the obstacle. The DNA extension distribution in both shear-bands was positively skewed, with the mean extension in the high shear-rate band (closer to the obstacle) being twice that in the low shear-rate band (further away from the obstacle). As Wi increases in shear flow, the DNA extension distribution shifted from positively skewed to a broad probability distribution.26 Such a broad distribution of DNA extensions in a shear flow is caused by the tumbling motion of DNA chains. Liu and Steinberg58 studied DNA chain dynamics in elastic turbulence and found that the DNA extension distribution is negatively skewed with mean fractional extension reaching a value of 0.8 asymptotically. Such a high mean fractional extension has also been observed in an extensional flow field.27,59 In this paper, we report the molecular processes leading to DZ formation during flow of shear-thinning polymer solutions through a periodic array of obstacles. We probe conformation of single chains by visualizing fluorescently labelled DNA molecules in polyacrylamide (PAA) solutions with and without the addition of salt. In addition, we use a combination of pressure-drop measurement and streamline visualization to map elastic instabilities and the corresponding pressure losses.
2 Experimental details
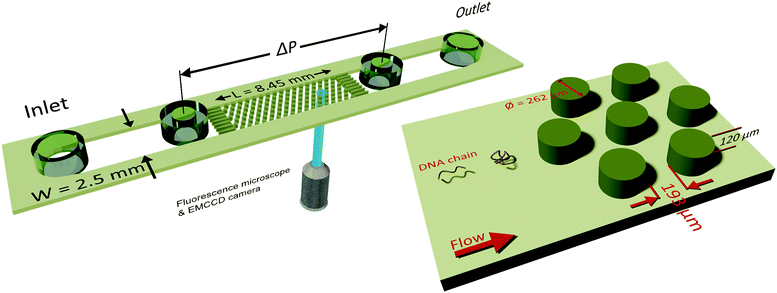
2.1 Microfluidic device and pressure measurements
A microfluidic device was combined with an inverted fluorescence microscope as shown in Fig. 1 to enable visualization of streamlines and single DNA molecules. The microfluidic device consisted of a periodic array of cylinders in a hexagonal layout. The cylinder diameter was 262 μm, with a spacing of 193 μm from the surrounding cylinders. The height of the cylinders was 120 μm. The cylinder diameter was chosen to maintain consistency with our previous study on elastic instabilities in porous media.6 Spacing between the pillars was indirectly determined as a conscious decision for maintaining a porosity of 0.7 to match our previous study with a hexagonal layout of cylinder placement. The microfluidic geometry was fabricated out of PDMS (Polydimethylsiloxane; Sylgard® 184, Dow Corning Corporation) using standard soft-lithography techniques.60 Pressure drop (ΔP) across the periodic array was measured via two pressure taps, to which two piezoresistive silicon pressure sensors (HSCMRNT005PGAA5, Honeywell Sensing and Control) were attached. Pressures were monitored using an in-house-developed LabVIEW data acquisition program sampling at 100 Hz. Pressure sensors were accurate to within 0.25% of the full-scale-span. After calibrating the sensors using a pressure pump (MFCS™, Fluigent GmbH) the instantaneous signal fluctuated with a standard deviation of 0.1 mbar around the mean value. The permeability of our microfluidic porous media was k = 6 × 10−11 m2 according to Darcy's law, k = (vηLPM/ΔP), where v is the superficial velocity; η is the viscosity; LPM = 8.5 × 10−3 m is the length of periodic array and ΔP is the pressure-drop across the periodic array of cylinders. To probe the flow behaviour of polymer solutions in porous media, we measured pressure drop for 600 s and simultaneously visualized the streamlines. The pressure drop measurements from the flow of polymer solutions were also used to calculate an apparent viscosity from Darcy's law. All experiments were performed at room temperature, T = (22 ± 2) °C.2.2 Polymer solutions
Polymer solutions used in the experiments were prepared by dissolving the required amount of polyacrylamide, PAA (Catalog No. 18522-100, Polyacrylamide/sodium acrylate – 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30, Molecular Weight, MW = 18 × 106 g mol−1, Polysciences, Inc.) in either brine or deionized (DI) water. Two PAA solutions at a concentration of C = 0.2 g L−1 in the presence or absence of salt were prepared. The first polymer solution was prepared by using deionized (DI) water as a solvent, whereas the second polymer solution was prepared using a 6 mM NaCl solution in DI water as the solvent. Adding salt fixes the ionic strength of the polymer solution, reduces the relaxation time and also suppresses the shear-thinning effect. We choose to limit salt concentration to 6 mM such that the shear rheology is still shear-thinning, since at higher salt concentrations the shear-viscosity became nearly independent of the shear-rate. In our earlier study, we found that the DZ forms in shear-thinning polymer solutions and that the DZ ceases to exist when shear-viscosity is independent of the shear-rate.6
30, Molecular Weight, MW = 18 × 106 g mol−1, Polysciences, Inc.) in either brine or deionized (DI) water. Two PAA solutions at a concentration of C = 0.2 g L−1 in the presence or absence of salt were prepared. The first polymer solution was prepared by using deionized (DI) water as a solvent, whereas the second polymer solution was prepared using a 6 mM NaCl solution in DI water as the solvent. Adding salt fixes the ionic strength of the polymer solution, reduces the relaxation time and also suppresses the shear-thinning effect. We choose to limit salt concentration to 6 mM such that the shear rheology is still shear-thinning, since at higher salt concentrations the shear-viscosity became nearly independent of the shear-rate. In our earlier study, we found that the DZ forms in shear-thinning polymer solutions and that the DZ ceases to exist when shear-viscosity is independent of the shear-rate.6
After adding the polymer granules to the solvent, the bottle was covered with an opaque material such as aluminium foil to minimize photo-degradation.61,62 The approximate radius of gyration for PAA in DI water was estimated from the scaling relation, Rg = 0.0749 × MW0.64 Å,57 as 330 nm. The critical overlap concentration for PAA in DI water was estimated as 200 μg mL−1 according to the formula, C* = (3·MW)/(4πNARg3). Here, C* is the overlap concentration; NA is Avogadro's number; and Rg is the radius of gyration. Therefore, our polymer solutions are close to the semi-dilute regime. The shear viscosity of our polymer solution was measured in a Couette geometry (cup ID = 28.92 mm, bob OD = 26.668 mm, gap = 1.626 mm) using a commercial rheometer, (MCR-302, Anton Paar GmBH) and is plotted in Fig. S1 (ESI†). Both the polymer solutions showed shear-thinning behaviour which is correlated with the DZ size.6 The relaxation time was estimated by fitting the shear rheology to the Carreau model,
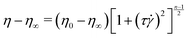 | (1) |
The Carreau model was fitted to the shear-viscosity experimental data by non-linear least-squares regression. Table 1 lists the fitting parameters of the Carreau model. The Weissenberg number, Wi, was then calculated as Wi = τ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) app, where
app, where ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) app = v/(D/2) is the apparent shear rate in the microfluidic geometry; D is the diameter of the cylinder. Note that the Wi number is calculated based on the relaxation time of PAA. All experiments were done at room temperature, T = (22 ± 2) °C.
app = v/(D/2) is the apparent shear rate in the microfluidic geometry; D is the diameter of the cylinder. Note that the Wi number is calculated based on the relaxation time of PAA. All experiments were done at room temperature, T = (22 ± 2) °C.
| Polymer & NaCl concentration | η 0 (Pa s) | η ∞ (Pa s) | n (−) | τ (s) |
|---|---|---|---|---|
| 0.2 g L−1 PAA, 0 mM NaCl | 2.71 | 0.001 | 0.24 | 88.17 |
| 0.2 g L−1 PAA, 6 mM NaCl | 0.01 | 0.001 | 0.70 | 0.48 |
2.3 Flow visualization
To push the working solutions through the microfluidic devices, a syringe pump (PHD2000, Havard Instruments) fitted with Hamilton Gastight syringes was used. The connection from the syringe to the microfluidic device was made by using a PTFE tubing (ID = 0.5 mm, OD = 1.6 mm). In order to visualize the streamlines, the polymer solutions were seeded with 1 μm-dyed-red aqueous fluorescent particles (emission 542 nm/excitation 612 nm wavelength, Catalog # R0100, Thermo Scientific™) at ∼0.1% (w/w) concentration. The entire microfluidic device assembly was installed on top of an inverted fluorescent microscope (Axiovert 100M, Carl Zeiss AG) fitted with a 10× (N.A. = 0.5) magnification objective and a high-speed camera (Phantom v9.1, Vision Research Inc.) to record videos. All streamlines were visualized near the exit of the periodic array of pillars within the microfluidic device, with the focal plane adjusted at the center along the vertical axis to minimize contribution from top/bottom wall effects.2.4 DNA visualization
To image polymer conformation during flow, we used fluorescently stained T4-DNA molecules (purchased from Nippon Gene Co. Ltd at a concentration of 440 μg mL−1 in 10 mM Tris (pH = 8.0) and 1 mM EDTA, 165![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 base-pairs). The contour length Lc of T4-DNA was 56 μm, which is close to the contour length of PAA (53 μm). YOYO-1 dye (Molecular Probes Inc.) was used to stain T4-DNA solution at a base-pair to dye ratio of 5
600 base-pairs). The contour length Lc of T4-DNA was 56 μm, which is close to the contour length of PAA (53 μm). YOYO-1 dye (Molecular Probes Inc.) was used to stain T4-DNA solution at a base-pair to dye ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Finally, in order to prevent photo-degradation, 20% (v/v) of β-mercaptanol was added to the T4-DNA solution. The resulting solution of stained DNA molecules in the buffer solution and β-mercaptanol was labelled as the DNA mother stock solution. For DNA-imaging, we dissolved 10 μL of the DNA mother stock solution in 5 mL of the polymer solutions. Eventually, the working polymer solutions for DNA visualization contain around 0.01 parts per million (PPM) of DNA molecules. DNA was imaged on an inverted fluorescence microscope (Zeiss AxioObserver-Z1, Carl Zeiss AG) fitted with an EMCCD camera (ANDOR ixon3, Andor Technology Ltd). The recorded DNA images had a resolution of 512 × 512 pixels (px) at the frame acquisition rate of 34 (fps). The frame acquisition rate could be increased up to 127 fps, with 4 × 4 image binning. These frame-acquisition rates are sufficiently high to capture DNA motion inside the DZ without blur for flow rates reported in the current study. We increased the frame acquisition rate upto the maximum achievable (127 fps) for flow rates between 5 μm min−1 and 50 μm min−1 to ensure motion blur does not introduce artefacts during DNA visualization experiments. DNA conformation near multiple pillars was imaged. We choose pillars close to the exit of the array of pillars.
1. Finally, in order to prevent photo-degradation, 20% (v/v) of β-mercaptanol was added to the T4-DNA solution. The resulting solution of stained DNA molecules in the buffer solution and β-mercaptanol was labelled as the DNA mother stock solution. For DNA-imaging, we dissolved 10 μL of the DNA mother stock solution in 5 mL of the polymer solutions. Eventually, the working polymer solutions for DNA visualization contain around 0.01 parts per million (PPM) of DNA molecules. DNA was imaged on an inverted fluorescence microscope (Zeiss AxioObserver-Z1, Carl Zeiss AG) fitted with an EMCCD camera (ANDOR ixon3, Andor Technology Ltd). The recorded DNA images had a resolution of 512 × 512 pixels (px) at the frame acquisition rate of 34 (fps). The frame acquisition rate could be increased up to 127 fps, with 4 × 4 image binning. These frame-acquisition rates are sufficiently high to capture DNA motion inside the DZ without blur for flow rates reported in the current study. We increased the frame acquisition rate upto the maximum achievable (127 fps) for flow rates between 5 μm min−1 and 50 μm min−1 to ensure motion blur does not introduce artefacts during DNA visualization experiments. DNA conformation near multiple pillars was imaged. We choose pillars close to the exit of the array of pillars.
DNA imaging was performed upstream of the pillar such that the conformation within a DZ can be captured. Using ImageJ, we extracted the end-to-end vector of the DNA chain, ![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) . The fluorescence microscopy technique employed in the current work visualizes along an xy-plane, where x is along the length and y is the along the width of the microfluidic device. The depth of the field is around 5–10 μm depending on the objective lenses. Therefore, the extracted end-to-end vector would be a projection of the true 3D DNA chain conformation on the xy-plane. The magnitude of this vector is termed as the DNA length, and its direction is the orientation angle, θ (see a schematic in Fig. S4, ESI†). Two objective lenses were used during imaging, namely 40× (N.A. = 1.3) or 63× (N.A. = 1.0) giving a single pixel resolution of 0.4 (μm per px) or 0.25 (μm per px) respectively. The corresponding field of view with the 40× objective was 205 × 205 μm2 and with the 63× objective it was 128 × 128 μm2. All the DNA lengths and orientation angles are plotted as a probability distribution, with a bin width of 5.5 μm and 18°, respectively.
. The fluorescence microscopy technique employed in the current work visualizes along an xy-plane, where x is along the length and y is the along the width of the microfluidic device. The depth of the field is around 5–10 μm depending on the objective lenses. Therefore, the extracted end-to-end vector would be a projection of the true 3D DNA chain conformation on the xy-plane. The magnitude of this vector is termed as the DNA length, and its direction is the orientation angle, θ (see a schematic in Fig. S4, ESI†). Two objective lenses were used during imaging, namely 40× (N.A. = 1.3) or 63× (N.A. = 1.0) giving a single pixel resolution of 0.4 (μm per px) or 0.25 (μm per px) respectively. The corresponding field of view with the 40× objective was 205 × 205 μm2 and with the 63× objective it was 128 × 128 μm2. All the DNA lengths and orientation angles are plotted as a probability distribution, with a bin width of 5.5 μm and 18°, respectively.
PAA molecules cannot be visualized natively, and hence we used T4-DNA molecules as a molecular probe. Using T4 or λ-DNA molecules as molecular probes in a solution of PAA or poly(ethylene oxide) (PEO) solutions has been fruitful in linking the molecular conformation with the macroscopic flow phenomena, such as (1) drag enhancement,63,64 (2) droplet pinch-off,42,43 (3) elastic turbulence,58,65 (4) impacting droplets,66 and (5) unstable polymeric flows in a straight channel due to an initial perturbation.67 In our working solutions for DNA visualization, we should note that the dispersed tracer T4-DNA chains can have higher relaxation time compared to the PAA solutions.63,68 We performed DNA-imaging at Wi < 1 and at Wi > 1 (see Fig. 2a and b). The coil–stretch transition is observed in the range of Wi = 0.5 to Wi = 1.10,34 We observe that the T4-DNA chains undergo C–S transition in the vicinity of the Wi number based on the relaxation time of (PAA) polymer solution.
This observation suggests that the T4-DNA chain behaves as a molecular tracer (or passive probe) of PAA chains. T4-DNA undergoes C–S transition when PAA chains are stretched (at Wi ∼ 1.0, as estimated based on the relaxation time of PAA chains). Similar observation was also made in previous studies wherein polymer solutions were seeded with fluorescently stained DNA molecules, for example, (1) PEO solutions with two types of DNA tracers flowed around an obstacle63 and (2) extensional flow of PAA solutions with a DNA tracer in a microfluidic T-junction.43 Both these studies also demonstrated that the onset of C–S transition for the tracer T4-DNA chain is similar to the Wi-number estimated from the relaxation time of PEO or PAA solutions. Therefore, the characteristic relaxation time of the background PAA or PEO solutions is the most relevant relaxation time-scale to identify polymer conformations during flow. In this work, the critical Wi is also estimated based on the characteristic relaxation time of PAA solutions. In addition, we also estimated the longest relaxation time of the T4-DNA tracer molecules in a viscoelastic solvent (PAA solution, at c = 0.2 g L−1) based on a scaling theory. We consider that the T4-DNA tracers are infinitely diluted in the PAA solution and that a T4-DNA chain does not interact with another T4-DNA chain and the PAA chains. Then, the longest relaxation time of the T4-DNA chain at infinite dilution τ0 can be estimated using the scaling law τ0 = 0.77η0,68 where η0 is the zero-shear viscosity in cP of the PAA solutions. At 0 mM NaCl, we calculate τ0 ∼ 2000 s and at 6 mM NaCl, we calculate τ0 ∼ 7.7 s. We should emphasize that this estimation is likely invalid for our semi-dilute solutions of PAA molecules with shear-thinning viscosity. For instance, it has been shown that convective constraint release can occur in entangled polymer solutions with shear-thinning rheology at high-Wi such that the effective relaxation time of polymer solutions can be reduced linearly with imposed shear rates.69,70 Investigation of DNA chain dynamics when it is added as a tracer in PAA solutions remains an important question. Future single-DNA studies that investigate relaxation response of DNA tracer molecules upon cessation of steady flow of polymer solutions at a very fast flow rate (high-Wi) will provide valuable information into the chain dynamics and applicability of theoretical ideas such as convective constraint release during fast flow.46
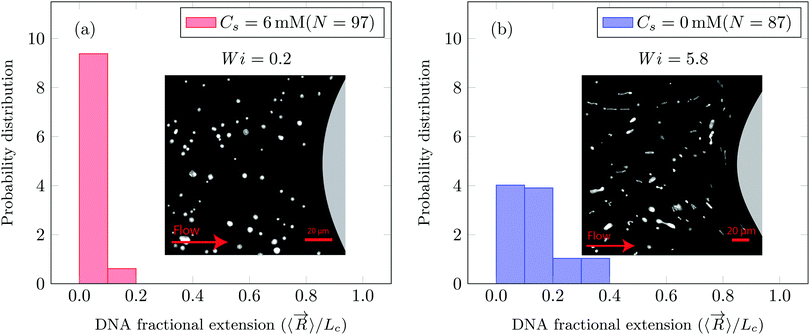
In this manuscript, we report the tracer DNA chain conformations in background ∼1c* PAA solution. In Fig. 2a we show that when Wi = 0.2 the DNA chains remain in the coiled conformation (mean fractional extension, μ = 0.06). Furthermore, we also observe that at Wi = 0.2, flow of saline polymer solution was uniform (referred to as creeping flow). In Fig. 2b we show that for Wi = 5.8 the DNA molecules began to stretch with a fractional extension of up to 0.4 (mean fractional extension, μ = 0.15). At Wi = 5.8, DZ formation was observed. DZ formation was the onset of non-Newtonian effects, which emerged at Wi ∼ 1. While the DNA-extension probability distribution shown in Fig. 2b for Wi = 5.8 in polymer solutions are prepared with DI water (Cs = 0 mM, where Cs is the NaCl concentration), we also note that the DNA begins to stretch at Wi > 1 in the presence of salt as shown later in the manuscript.
3 Results and discussion
3.1 Apparent viscosity and streamline visualization
The standard deviation of pressure drop fluctuations, std(ΔP) ∼ 0.1 mbar when DZ formation is observed during flow of PAA solutions with and without salt, and also for Newtonian fluid flow (Fig. S2a, ESI†). At a certain![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) app, the pressure fluctuations increased over those for Newtonian fluid, and simultaneously the flow-field transitioned to DZW. The onset apparent shear rate
app, the pressure fluctuations increased over those for Newtonian fluid, and simultaneously the flow-field transitioned to DZW. The onset apparent shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) onset was determined as the intersection of two curves: first one obtained by fitting a power-law in the DZW region and the second one obtained by fitting a power-law to the Newtonian fluid std(ΔP) as shown in Fig. S2a (ESI†). In the absence of salt, the onset apparent shear rate was
onset was determined as the intersection of two curves: first one obtained by fitting a power-law in the DZW region and the second one obtained by fitting a power-law to the Newtonian fluid std(ΔP) as shown in Fig. S2a (ESI†). In the absence of salt, the onset apparent shear rate was 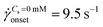 (Ma ∼ 1, Wi ∼ 842), whereas in the presence of 6 mM NaCl, the onset apparent shear rate was
(Ma ∼ 1, Wi ∼ 842), whereas in the presence of 6 mM NaCl, the onset apparent shear rate was 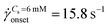 (Ma ∼ 1, Wi ∼ 8).
(Ma ∼ 1, Wi ∼ 8).
The apparent viscosity for salt-free polymer solutions is three times higher than that for saline polymer solutions at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) onset (Fig. S2b, ESI†). In the absence of salt, the apparent shear-viscosity is in the apparent shear-thinning region over
onset (Fig. S2b, ESI†). In the absence of salt, the apparent shear-viscosity is in the apparent shear-thinning region over ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) app= 0.1 to 300 s−1. However, in the case of saline polymer solutions, the apparent shear-viscosity is shear-thinning up to
app= 0.1 to 300 s−1. However, in the case of saline polymer solutions, the apparent shear-viscosity is shear-thinning up to ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) onset = 15.8 s−1, beyond which apparent shear-thickening is observed. Fig. S6 (ESI†) shows the ratio of the apparent viscosity to the steady shear viscosity at the apparent shear rate versus the Wi number. We can see that such a viscosity ratio shows a dramatic increase for both the polymer solutions. For Cs = 0 mM, this dramatic increase in the viscosity ratio occurs at Wi ∼ 1 whereas for Cs = 6 mM, it occurs at Wi ∼ 1000. This dramatic increase in the viscosity ratio appears to correlate with the onset of DZW-instability and consequently with the apparent shear-thickening region. An apparent shear-thickening region has been commonly observed for the flow of polymer solutions in porous media.5,6,71–74
onset = 15.8 s−1, beyond which apparent shear-thickening is observed. Fig. S6 (ESI†) shows the ratio of the apparent viscosity to the steady shear viscosity at the apparent shear rate versus the Wi number. We can see that such a viscosity ratio shows a dramatic increase for both the polymer solutions. For Cs = 0 mM, this dramatic increase in the viscosity ratio occurs at Wi ∼ 1 whereas for Cs = 6 mM, it occurs at Wi ∼ 1000. This dramatic increase in the viscosity ratio appears to correlate with the onset of DZW-instability and consequently with the apparent shear-thickening region. An apparent shear-thickening region has been commonly observed for the flow of polymer solutions in porous media.5,6,71–74
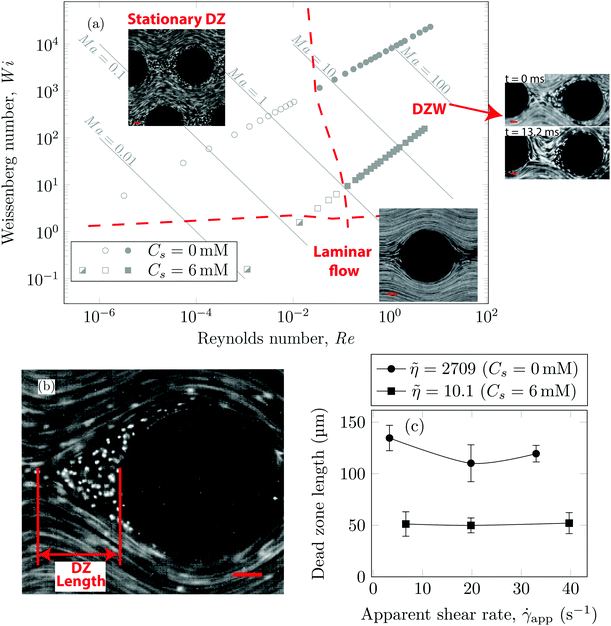
Using streamline visualization, we mapped how the flow-field changes with respect to the flow rate. In Fig. 3a we represent this on a Wi−Re flow space map. The DZ formation for flow of shear-thinning polymer solutions in a periodic array of pillars occurs at Ma ≤ 1.6 In the case of Boger fluid, no DZ formation was observed.6 However, for Boger fluid flow around a single cylinder, a DZ-like flow field was observed upstream of the cylinder at Ma ∼ 10.23,24 In our previous publication,6 we discussed the local flow field kinetics in DZ. For the specific experimental conditions of the current manuscript, the velocity field measurement using PIV can be found in Fig. S5 (ESI†). In Fig. S5a (ESI†) we show the specific streamlines for 0.2 g L−1 PAA in DI water and in Fig. Sb (ESI†) the corresponding velocity field calculated by Particle Image Velocimetry (PIV) is shown. Fig. S5c (ESI†) shows a zoomed-in image of the velocity field inside a DZ. The velocity inside the DZ is close to zero whereas the velocity outside the DZ is ∼3 × 10−4 m s−1. Downstream of the pillar, the velocity field converges at the tip of the DZ. Inside a DZ, the flow appears to be almost stationary. Close to the stagnation point upstream of the pillar, we can observe an extensional flow field. A detailed report on steady-state and unstable velocity fields of polymer solution flow through periodic arrays of cylinder has been reported earlier.75 In this work, we focus on the DZ formation in shear-thinning solutions. With increasing flow rate, the stationary DZs started wobbling in a direction perpendicular to the average flow direction and eventually got washed away. Dead zone washing (DZW) refers to this time-dependent instability and was observed at Ma > 1 for both polymer solutions as shown in Fig. 3a. We measured the DZ length, defined as the shortest distance between the tip of DZ and the pillar (see Fig. 3b for a schematic). Fig. 3c shows DZ length, lDZ, versus the apparent shear rate, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) app. For a given polymer system, lDZ is practically independent of
app. For a given polymer system, lDZ is practically independent of ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) app.
app.
3.2 DNA conformations
As the DNA chains approach the pillar, they undergo the coil–stretch transition. In our microfluidic device, the DNA chains undergo the coil–stretch transition at the upstream of every pillar. We choose to visualize the DNA chain near the exit of the array of pillars. Our choice was motivated based on our previous study in which we studied the dynamics of the DZW instability in a periodic array of pillars.6 We observed that the DZW washing frequency (which is the inverse of the time that a DZ takes to form, grow and wash) reaches a pseudo-steady state after roughly the 4th pillar column. Based on this, we decided to visualize DNA chain dynamics at a location where the DZ dynamics have certainly reached the pseudo-steady state. The prior deformation history of DNA chains near the exit of the pillared array (visualization region) is then assumed to have reached a certain pseudo-steady state similar to DZW washing frequency. Further research is necessary to understand the effect of DNA chain dynamics at varying deformation histories on a periodic array of pillars.The coil–stretch transition occurs in both the polymer solutions. In Fig. 4(a–c) we take the DNA conformation at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) app = 3.3 s−1, Cs = 0 mM as an example. Before entering a DZ, the DNA chain is stretched and oriented in the average flow direction (see Fig. 4a). This stretched conformation is likely because of the converging–diverging nature of flow in a staggered array of pillars. As the DNA chain moves closer to the pillar, it re-coils (see Fig. 4b). By comparing the position of the DNA-coiling region from the DNA-imaging experiments with the DZ size from the streamline visualization experiment, we note that the DNA re-coiling process occurs roughly at the tip of the DZ. After re-coiling, as the DNA chain traverses closer to the pillar, inside the DZ, it unravels to stretch and rotate in a direction perpendicular to the average flow direction (see Fig. 4c). Therefore, the DNA chains appear to align along the local flow-field upstream of the pillars inside the DZs (see Movies S1 and S2, ESI†). The large amplitude oscillatory extension experiments (LAOE) represent realistic flows better than the idealized stead-state or elongational flow fields that are typically used to characterize polymer rheology. The LAOE flow field can be obtained using the Stokes trap with a model predictive control,76 allowing for precise positioning and manipulating particles in flow. Recently, the Stokes trap was used to impose a LAOE flow and investigate single polymer dynamics. Polymer chain LAOE dynamics, under varying flow strength, like re-stretch-re-coil-re-stretch was studied to obtain single-molecule Lissajous plots showing molecular stretch–strain rate curves.77 In a followup study, the transient response during LAOE was investigated.78 Understanding these molecular processes is crucial for studying time-dependent flow of polymer solutions such as the instabilities reported in this study.
app = 3.3 s−1, Cs = 0 mM as an example. Before entering a DZ, the DNA chain is stretched and oriented in the average flow direction (see Fig. 4a). This stretched conformation is likely because of the converging–diverging nature of flow in a staggered array of pillars. As the DNA chain moves closer to the pillar, it re-coils (see Fig. 4b). By comparing the position of the DNA-coiling region from the DNA-imaging experiments with the DZ size from the streamline visualization experiment, we note that the DNA re-coiling process occurs roughly at the tip of the DZ. After re-coiling, as the DNA chain traverses closer to the pillar, inside the DZ, it unravels to stretch and rotate in a direction perpendicular to the average flow direction (see Fig. 4c). Therefore, the DNA chains appear to align along the local flow-field upstream of the pillars inside the DZs (see Movies S1 and S2, ESI†). The large amplitude oscillatory extension experiments (LAOE) represent realistic flows better than the idealized stead-state or elongational flow fields that are typically used to characterize polymer rheology. The LAOE flow field can be obtained using the Stokes trap with a model predictive control,76 allowing for precise positioning and manipulating particles in flow. Recently, the Stokes trap was used to impose a LAOE flow and investigate single polymer dynamics. Polymer chain LAOE dynamics, under varying flow strength, like re-stretch-re-coil-re-stretch was studied to obtain single-molecule Lissajous plots showing molecular stretch–strain rate curves.77 In a followup study, the transient response during LAOE was investigated.78 Understanding these molecular processes is crucial for studying time-dependent flow of polymer solutions such as the instabilities reported in this study.
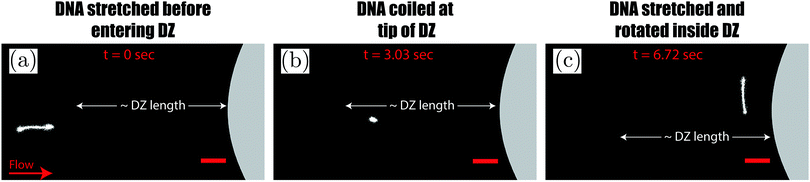 | ||
Fig. 4 Sequence of images showing (a) a stretched DNA chain approaching a pillar before entering the DZ, (b) a re-coiled DNA chain at roughly the tip of DZ and (c) a re-stretched DNA that is rotated inside the DZ. DZ length refers to the data shown in Fig. 3c. Cs = 0 mM, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) app = 3.3 s−1, Wi ∼ 291. Scale bar = 20 μm. app = 3.3 s−1, Wi ∼ 291. Scale bar = 20 μm. | ||
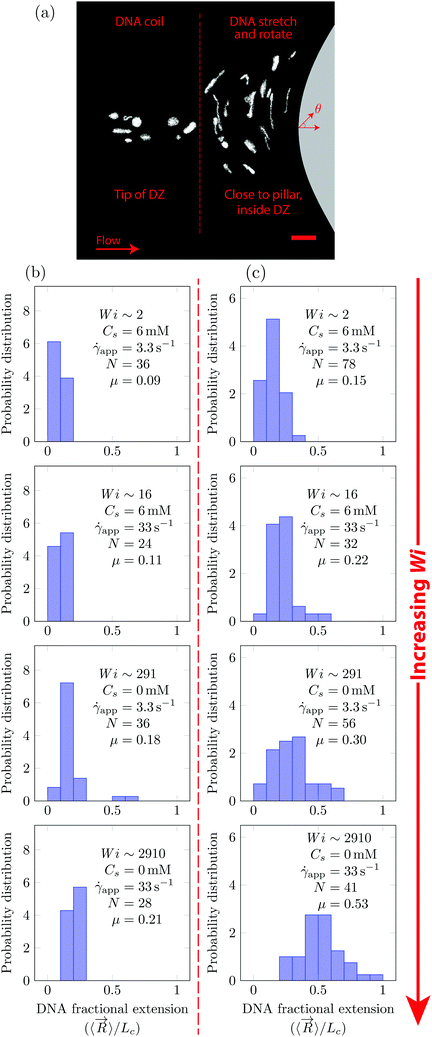
In Fig. 5, we quantify the DNA chain coil–stretch transition inside the DZ by measuring the probability distribution of DNA fractional extensions as the apparent Wi increases. In Fig. 5a, we superimpose the conformation of multiple DNA chains as they enter the DZ at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) app = 3.3 s−1, Wi = 291, Cs = 0 mM. The DNA chains at the tip of the DZ are in coiled conformation, whereas inside the DZ they are stretched and rotated by θ ∼ 90°. Fig. 5b shows the probability distribution of DNA fractional extension in the coiled-state (tip of DZ) for both salt-free and saline polymer solutions. The mean fractional extension μ varies from 0.09 to 0.21 as the apparent Wi number increases from 1.6 to 2910. On the other hand, Fig. 5c shows the probability distribution of DNA fractional extension in the stretched-state (inside DZ) for both salt-free and saline polymer solutions. As Wi increases, the probability distribution shifts to higher fractional extensions. The mean fractional extension μ increases from 0.15 to 0.53 as the Wi increases from 1.6 to 2910. The mean and skewness of the probability distribution are summarized in Table S1 (ESI†), whereas the probability distribution of the DNA orientation angle, θ, inside the DZ is shown in Fig. S3 (ESI†).
app = 3.3 s−1, Wi = 291, Cs = 0 mM. The DNA chains at the tip of the DZ are in coiled conformation, whereas inside the DZ they are stretched and rotated by θ ∼ 90°. Fig. 5b shows the probability distribution of DNA fractional extension in the coiled-state (tip of DZ) for both salt-free and saline polymer solutions. The mean fractional extension μ varies from 0.09 to 0.21 as the apparent Wi number increases from 1.6 to 2910. On the other hand, Fig. 5c shows the probability distribution of DNA fractional extension in the stretched-state (inside DZ) for both salt-free and saline polymer solutions. As Wi increases, the probability distribution shifts to higher fractional extensions. The mean fractional extension μ increases from 0.15 to 0.53 as the Wi increases from 1.6 to 2910. The mean and skewness of the probability distribution are summarized in Table S1 (ESI†), whereas the probability distribution of the DNA orientation angle, θ, inside the DZ is shown in Fig. S3 (ESI†).
The shape of distribution (for example uniform or positively/negatively skewed) of DNA fractional extensions depends on the flow-field and the Wi number. In steady-shear flow of dilute DNA solutions, Smith et al.26 found that as the Wi increases from ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1) to
(1) to ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (100), the distribution moves from positively skewed to uniform, respectively. Later, Teixeira et al.46 reported similar changes in the distribution shape in semi-dilute and entangled DNA solutions. François et al.63 studied the flow of Boger fluid around a single cylinder. Using DNA-imaging near the vicinity of cylinder (θ = 90° according to Fig. 5a) they showed that at Wi =
(100), the distribution moves from positively skewed to uniform, respectively. Later, Teixeira et al.46 reported similar changes in the distribution shape in semi-dilute and entangled DNA solutions. François et al.63 studied the flow of Boger fluid around a single cylinder. Using DNA-imaging near the vicinity of cylinder (θ = 90° according to Fig. 5a) they showed that at Wi = ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1), the DNA close to cylinder is stretched with μ = 0.33, with a positively skewed distribution. In Fig. 5b and c (Wi ∼ 2), we also find that the distribution is positively skewed (also see Table S1, ESI† for skewness values); however, the mean fractional extension, μ = 0.15. At Wi ∼ 2910, some polymer chains are fully stretched, however, the distribution of polymer conformations is still heterogeneous with the mean fractional extension of roughly half.
(1), the DNA close to cylinder is stretched with μ = 0.33, with a positively skewed distribution. In Fig. 5b and c (Wi ∼ 2), we also find that the distribution is positively skewed (also see Table S1, ESI† for skewness values); however, the mean fractional extension, μ = 0.15. At Wi ∼ 2910, some polymer chains are fully stretched, however, the distribution of polymer conformations is still heterogeneous with the mean fractional extension of roughly half.
Maximum polymer chain extension in an extension flow-field has been reported for dilute solutions27 and semi-dilute solutions.79 In semi-dilute solutions, a broader distribution of chain extensions is observed in transient extensional flow compared to dilute solutions.79 Intermolecular interactions between polymer chains in the semi-dilute region are suggested as a cause for the broad distribution of chain extensions. Upon reaching steady-state extension, the polymer chain fractional extension in dilute-solutions was found to be higher than that in semi-dilute solutions. A closer examination of the Wi number at which coil–stretch transition occurs in both dilute and semi-dilute solutions revealed that this Wi number depends on the concentration.79 Polymer chain extension in a random-flow has also been reported for dilute and semi-dilute solutions.58 A polymer chain's extension increases with the accumulated fluid strain at the stagnation point of the extension flow-field.27,79 In our microfluidic experiments, the flow field upstream of the pillar is a planar-extensional flow, similar to the flow in a microfluidic T-junction. The flow-field upstream of the pillar diverges which creates a region with an extensional flow-field.
The fact that we measured the DNA orientation angles of ∼90° within the DZ indicates that the DNA chains are aligned along the extensional flow component of the mixed flow-field upstream of the pillar. To study the effect of the local Weissenberg number, Wiloc, on the DNA fractional extension inside the DZ, we calculated the DNA velocity inside the DZ, vDNA. vDNA was calculated by averaging the velocity of 20 DNA chains by DNA tracking velocimetry (vDNA ∼ 19–575 μm s−1). In particular, we tracked the mid-point of the DNA end-to-end vector. The distance between the midpoint of a DNA in the coiled state (at the tip of DZ) to the midpoint of the same DNA when it reaches the stagnation point upstream the obstacle divided by the time this particular DNA chain takes is defined as the velocity of DNA chains vDNA. In this way, vDNA accounts for the transient residence time of DNA chains inside the DZ in the calculation of the Wiloc number. Additionally, we also used the DNA residence time in the DZ to calculate a local Deborah number, Deloc. The Deloc values are reported in Table S2 (ESI†). Note that the average velocity outside the DZ has a value of ∼430 μm s−1 at both salt concentrations. Then, Wiloc = τ·(vDNA/LDZ), where LDZ is the DZ length as shown in Fig. 3c. This Wiloc quantifies the transient time scale of flow inside the DZ. As the Wiloc increases from 0.72 ± 0.31 until 458.89 ± 178.13, the DNA fractional extension increases from 0.15 ± 0.07 to 0.53 ± 0.18 inside the DZ (see Table 2).
| DNA fractional extension (−) | Wiloc (−) | v DNA (μm s−1) |
|---|---|---|
| 0.15 ± 0.07 | 0.72 ± 0.31 | 78.48 ± 27.43 |
| 0.22 ± 0.10 | 4.78 ± 1.81 | 497.19 ± 174.17 |
| 0.30 ± 0.15 | 12.63 ± 3.62 | 19.28 ± 5.24 |
| 0.53 ± 0.18 | 458.89 ± 178.13 | 573.29 ± 202.09 |
4 Conclusions
We investigated the stationary dead-zone (DZ) and dead-zone washing (DZW) elastic instabilities of polymer solutions in porous media at the molecular scale. The DNA chain is coiled at the tip of the DZ. Close to the stagnation point upstream of the pillar inside the DZ, the DNA chain stretches and rotates in a direction perpendicular to the average flow direction. The mean fractional extension of the DNA chain at the DZ-tip is roughly the same in the DZ and the DZW instability for a given polymer solution. Inside the DZ, the DNA chains appear as if they are in a planar-extensional flow-field, with a positively skewed distribution of fractional extension. The fractional extension distribution for DNA chains inside the DZ shifts to higher extensions as the apparent Wi increases. The mean fractional extension in the DZ instability at a constant apparent shear-rate (3.3 s−1) is 0.3 and 0.15 for salt-free and saline polymer solutions, respectively. The difference is attributed to the higher local Weissenberg number inside DZ, as calculated by DNA tracking velocimetry.We believe that our developed microfluidics combined with single molecule experiments can provide a unique opportunity to study the dynamics of single chains in pore-scale flow features of various polymer solutions (ranging from dilute to well-entangled solutions with different architectures) in a realistic porous medium. These single molecule experiments allow us to develop a realistic theoretical picture of polymer solutions during flow in porous media.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Aswin Muralidharan for his help with the PIV calculations. This research forms part of the research programme of the Dutch Polymer Institute (DPI), project #736n. A part of this study was also supported by the European Research Council under the European Seventh Framework Programme (FP/2007-2013)/ERC Grant, agreement no. 337820 (to P. E. B. and S. S.).References
- J. Dealy and R. Larson, Structure and Rheology of Molten Polymers, Hanser Publications, 2006 Search PubMed.
- R. B. Bird, R. C. Armstrong and O. Hassager, Dynamics of polymeric liquids: fluid mechanics, A Wiley-Interscience Publication, John Wiley & Sons, 1987, vol. 1 Search PubMed.
- M. Rubinstein and R. H. Colby, Polymer Physics, Oxford University Press, 2003 Search PubMed.
- J. D. Ferry, Viscoelastic properties of polymers, John Wiley & Sons, 1980 Search PubMed.
- A. M. Howe, A. Clarke and D. Giernalczyk, Soft Matter, 2015, 11, 6419–6431 RSC.
- D. Kawale, E. Marques, P. L. J. Zitha, M. T. Kreutzer, W. R. Rossen and P. E. Boukany, Soft Matter, 2017, 13, 765–775 RSC.
- A. Machado, H. Bodiguel, J. Beaumont, G. Clisson and A. Colin, Biomicrofluidics, 2016, 10, 043507 CrossRef PubMed.
- C. Chmielewski and K. Jayaraman, J. Rheol., 1992, 36, 1105–1126 CrossRef CAS.
- D. F. James and A. J. Acosta, J. Fluid Mech., 1970, 42, 269–288 CrossRef.
- C. W. Macosko and R. G. Larson, Rheology: principles, measurements, and applications, VCH, New York, 1994 Search PubMed.
- J. G. Savins, Ind. Eng. Chem., 1969, 61, 18–47 CrossRef CAS.
- R. P. Chhabra, J. Comiti and I. Machač, Chem. Eng. Sci., 2001, 56, 1–27 CrossRef CAS.
- S. Flew and R. Sellin, J. Non-Newtonian Fluid Mech., 1993, 47, 169–210 CrossRef CAS.
- T. Sochi, J. Polym. Sci., Part B: Polym. Phys., 2010, 48, 2437–2767 CrossRef CAS.
- F. J. Galindo-Rosales, L. Campo-Deaño, F. Pinho, E. Van Bokhorst, P. Hamersma, M. Oliveira and M. Alves, Microfluid. Nanofluid., 2012, 12, 485–498 CrossRef CAS.
- M. Grilli, A. Vázquez-Quesada and M. Ellero, Phys. Rev. Lett., 2013, 110, 174501 CrossRef PubMed.
- B. Khomami and L. D. Moreno, Rheol. Acta, 1997, 36, 367–383 CrossRef CAS.
- C. Chmielewski and K. Jayaraman, J. Non-Newtonian Fluid Mech., 1993, 48, 285–301 CrossRef CAS.
- A. Clarke, A. M. Howe, J. Mitchell, J. Staniland, L. Hawkes and K. Leeper, Soft Matter, 2015, 11, 3536–3541 RSC.
- X. Hu, P. E. Boukany, O. L. Hemminger and L. J. Lee, Macromol. Mater. Eng., 2011, 296, 308–320 CrossRef CAS.
- L. Rems, D. Kawale, L. J. Lee and P. E. Boukany, Biomicrofluidics, 2016, 10, 043403 CrossRef PubMed.
- C. Scholz, F. Wirner, J. R. Gomez-Solano and C. Bechinger, EPL, 2014, 107, 54003 CrossRef.
- S. Kenney, K. Poper, G. Chapagain and G. F. Christopher, Rheol. Acta, 2013, 52, 485–497 CrossRef CAS.
- X. Shi, S. Kenney, G. Chapagain and G. F. Christopher, Rheol. Acta, 2015, 54, 805–815 CrossRef CAS.
- Y. Zhao, A. Q. Shen and S. J. Haward, Soft Matter, 2016, 12, 8666–8681 RSC.
- D. E. Smith, H. P. Babcock and S. Chu, Science, 1999, 283, 1724–1727 CrossRef CAS PubMed.
- T. T. Perkins, D. E. Smith and S. Chu, Science, 1997, 276, 2016–2021 CrossRef CAS PubMed.
- P. Van Puyvelde, C. Clasen, P. Moldenaers and J. Vermant, Rheology, 2010, 1, 359 Search PubMed.
- G. G. Fuller, Annu. Rev. Fluid Mech., 1990, 22, 387–417 CrossRef.
- A. B. Marciel and C. M. Schroeder, J. Polym. Sci., Part B: Polym. Phys., 2013, 51, 556–566 CrossRef CAS.
- G. R. Moss and J. P. Rothstein, J. Non-Newtonian Fluid Mech., 2010, 165, 1505–1515 CrossRef CAS.
- G. R. Moss and J. P. Rothstein, J. Non-Newtonian Fluid Mech., 2010, 165, 1–13 CrossRef CAS.
- C.-l. Sun and H.-Y. Huang, Biomicrofluidics, 2016, 10, 011903 Search PubMed.
- T. Perkins, S. Quake, D. Smith and S. Chu, Science, 1994, 264, 822–826 CAS.
- T. Perkins, D. Smith and S. Chu, Science, 1994, 264, 819–822 CAS.
- P. G. De Gennes, Scaling concepts in polymer physics, Cornell University Press, 1979 Search PubMed.
- M. Doi and S. Edwards, The Theory of Polymer Dynamics, Clarendon, 1986 Search PubMed.
- C. M. Schroeder, H. P. Babcock, E. S. Shaqfeh and S. Chu, Science, 2003, 301, 1515–1519 CrossRef CAS PubMed.
- C. M. Schroeder, E. S. Shaqfeh and S. Chu, Macromolecules, 2004, 37, 9242–9256 CrossRef CAS.
- C. M. Schroeder, R. E. Teixeira, E. S. Shaqfeh and S. Chu, Phys. Rev. Lett., 2005, 95, 018301 CrossRef PubMed.
- G. Juarez and P. E. Arratia, Soft Matter, 2011, 7, 9444–9452 RSC.
- F. Ingremeau and H. Kellay, Phys. Rev. X, 2013, 3, 041002 Search PubMed.
- S. Sachdev, A. Muralidharan and P. E. Boukany, Macromolecules, 2016, 49, 9578–9585 CrossRef CAS PubMed.
- P. E. Boukany, O. Hemminger, S.-Q. Wang and L. Lee, Phys. Rev. Lett., 2010, 105, 027802 CrossRef PubMed.
- O. Hemminger and P. E. Boukany, Biomicrofluidics, 2017, 11, 044118 CrossRef PubMed.
- R. E. Teixeira, A. K. Dambal, D. H. Richter, E. S. Shaqfeh and S. Chu, Macromolecules, 2007, 40, 2461–2476 CrossRef CAS.
- H. P. Babcock, D. E. Smith, J. S. Hur, E. S. Shaqfeh and S. Chu, Phys. Rev. Lett., 2000, 85, 2018 CrossRef CAS PubMed.
- J. S. Hur, E. S. Shaqfeh, H. P. Babcock, D. E. Smith and S. Chu, J. Rheol., 2001, 45, 421–450 CrossRef CAS.
- N. P. Teclemariam, V. A. Beck, E. S. Shaqfeh and S. J. Muller, Macromolecules, 2007, 40, 3848–3859 CrossRef CAS.
- K. D. Dorfman, S. B. King, D. W. Olson, J. D. Thomas and D. R. Tree, Chem. Rev., 2012, 113, 2584–2667 CrossRef PubMed.
- C. D. DeLong and D. A. Hoagland, Macromolecules, 2008, 41, 4887–4894 CrossRef CAS.
- K. D. Dorfman, Rev. Mod. Phys., 2010, 82, 2903 CrossRef CAS.
- G. C. Randall and P. S. Doyle, Macromolecules, 2005, 38, 2410–2418 CrossRef CAS.
- O. L. Hemminger, P. E. Boukany, S.-Q. Wang and L. Lee, J. Non-Newtonian Fluid Mech., 2010, 165, 1613–1624 CrossRef CAS.
- S. Gulati, S. J. Muller and D. Liepmann, Biomicrofluidics, 2015, 9, 054102 CrossRef PubMed.
- P. E. Boukany, S.-Q. Wang, S. Ravindranath and L. J. Lee, Soft Matter, 2015, 11, 8058–8068 RSC.
- J. Francois, D. Sarazin, T. Schwartz and G. Weill, Polymer, 1979, 20, 969–975 CrossRef CAS.
- Y. Liu and V. Steinberg, Macromol. Symp., 2014, 34–43 CrossRef.
- D. E. Smith and S. Chu, Science, 1998, 281, 1335–1340 CrossRef CAS PubMed.
- D. C. Duffy, J. C. McDonald, O. J. A. Schueller and G. M. Whitesides, Anal. Chem., 1998, 70, 4974–4984 CrossRef CAS PubMed.
- M. J. Caulfield, G. G. Qiao and D. H. Solomon, Chem. Rev., 2002, 102, 3067–3084 CrossRef CAS PubMed.
- S. Vijayalakshmi and G. Madras, J. Appl. Polym. Sci., 2006, 100, 3997–4003 CrossRef CAS.
- N. François, D. Lasne, Y. Amarouchene, B. Lounis and H. Kellay, Phys. Rev. Lett., 2008, 100, 018302 CrossRef PubMed.
- N. François, Y. Amarouchene, B. Lounis and H. Kellay, EPL, 2009, 86, 34002 CrossRef.
- S. Gerashchenko, C. Chevallard and V. Steinberg, EPL, 2005, 71, 221 CrossRef CAS.
- M. Smith and V. Bertola, Phys. Rev. Lett., 2010, 104, 154502 CrossRef CAS PubMed.
- D. Bonn, F. Ingremeau, Y. Amarouchene and H. Kellay, Phys. Rev. E, 2011, 84, 045301 CrossRef CAS PubMed.
- Y. Liu, Y. Jun and V. Steinberg, J. Rheol., 2009, 53, 1069–1085 CrossRef CAS.
- G. Marrucci, J. Non-Newtonian Fluid Mech., 1996, 62, 279–289 CrossRef CAS.
- P. E. Boukany and S.-Q. Wang, J. Rheol., 2009, 53, 1425–1435 CrossRef CAS.
- P. L. Zitha, G. Chauveteau and L. Léger, J. Colloid Interface Sci., 2001, 234, 269–283 CrossRef CAS PubMed.
- G. Chauveteau, M. Moan and A. Magueur, J. Non-Newtonian Fluid Mech., 1984, 16, 315–327 CrossRef CAS.
- F. Durst, R. Haas and B. Kaczmar, J. Appl. Polym. Sci., 1981, 26, 3125–3149 CrossRef CAS.
- R. Haas and F. Durst, Progress and Trends in Rheology, Springer, 1982, pp. 212–217 Search PubMed.
- S. De, J. van der Schaaf, N. Deen, J. Kuipers, E. Peters and J. Padding, arXiv preprint arXiv:1607.03672, 2016.
- A. Shenoy, C. V. Rao and C. M. Schroeder, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 3976–3981 CrossRef CAS PubMed.
- Y. Zhou and C. M. Schroeder, Phys. Rev. Fluids, 2016, 1, 053301 CrossRef.
- Y. Zhou and C. M. Schroeder, Macromolecules, 2016, 49, 8018–8030 CrossRef CAS.
- K.-W. Hsiao, C. Sasmal, J. Ravi Prakash and C. M. Schroeder, J. Rheol., 2017, 61, 151–167 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1–S6, Tables S1–S2, and two movies (Movies S1–S2). See DOI: 10.1039/c7sm00817a |
| This journal is © The Royal Society of Chemistry 2017 |

![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif)