Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Curvature variation controls particle aggregation on fluid vesicles†
Afshin
Vahid
 a,
Anđela
Šarić
a,
Anđela
Šarić
 b and
Timon
Idema
b and
Timon
Idema
 *a
*a
aDepartment of Bionanoscience, Kavli Institute of Nanoscience, Delft University of Technology, Van der Maasweg 9, 2629 HZ Delft, The Netherlands. E-mail: a.vahidbelarghou@tudelft.nl; t.idema@tudelft.nl
bDepartment of Physics and Astronomy, Institute for the Physics of Living Systems, University College London, Gower Street, London, WC1E 6BT, UK. E-mail: a.saric@ucl.ac.uk
First published on 15th June 2017
Abstract
Cellular membranes exhibit a large variety of shapes, strongly coupled to their function. Many biological processes involve dynamic reshaping of membranes, usually mediated by proteins. This interaction works both ways: while proteins influence the membrane shape, the membrane shape affects the interactions between the proteins. To study these membrane-mediated interactions on closed and anisotropically curved membranes, we use colloids adhered to ellipsoidal membrane vesicles as a model system. We find that two particles on a closed system always attract each other, and tend to align with the direction of largest curvature. Multiple particles form arcs, or, at large enough numbers, a complete ring surrounding the vesicle in its equatorial plane. The resulting vesicle shape resembles a snowman. Our results indicate that these physical interactions on membranes with anisotropic shapes can be exploited by cells to drive macromolecules to preferred regions of cellular or intracellular membranes, and utilized to initiate dynamic processes such as cell division. The same principle could be used to find the midplane of an artificial vesicle, as a first step towards dividing it into two equal parts.
1 Introduction
Cellular membranes are two-dimensional fluid interfaces that consist of a large variety of components. They form the boundary between the cell and the outside world, and, for eukaryotic cells, separate the inside of the cell into numerous compartments known as organelles. In order for biological processes like cell division, vesicular trafficking and endo/exocytosis to occur, cellular membranes have to reshape constantly. Consequently, membranes exhibit a variety of morphologies, from a simple spherical liposome to bewildering complex structures like interconnected tubular networks as found in mitochondria and the endoplasmic reticulum (ER), or connected stacks of perforated membrane sheets in the Golgi apparatus.1–4 There are different mechanisms by which membranes achieve these structures, the most important of which is through the interplay between membrane lipids and various proteins.5–7 A biological membrane is home to different types of proteins that are adhered to or embedded in it. These proteins deform the membrane and, consequently, they can either repel or attract each other.8–13 Spatial organization of such proteins in biological membranes is essential for stabilizing the membrane and for the dynamic behaviour of cellular organelles.14–17Recently, it has been experimentally18–20 and theoretically8,9,11,21–26 revealed that membrane-curving particles, like colloids or identical proteins, adhered to a membrane self-assembled into striking patterns. For instance it has been shown that colloids adhered to a spherical membrane form linear aggregations.18,24 In all of the studies to date, the global shape of the membrane is selected from one of three options: planar, spherical, or tubular. These global membrane shapes impose a homogeneous background curvature, which is considered to be conserved throughout the process under investigation. Outside factors changing the membrane have not yet been included in the study of membrane-mediated interactions. Membranes in cellular compartments such as in the ER and the Golgi complex are however dynamic entities and possess peculiar shapes forming regions with high local curvature and regions with less curvature.3 Forming and stabilizing such shape inhomogeneities are necessary for cellular functions like sensing and trafficking.27 It is therefore warranted to investigate how the interactions between membrane inclusions are affected by anisotropies in the membrane curvature.
Recently, studies have been performed to understand the role of non-uniform curvature in the interaction of single particles with a fluid membrane, both in the tension-dominated28 and bending-dominated29,30 regimes. In this study, through a numerical experiment, we investigate many body interactions between colloids adhered to a quasi-ellipsoidal membrane with a varying curvature. We also include all other factors from earlier studies such as surface tension, adhesion energy (required for colloids to adhere to the membrane) and constant volume effects. We use a dynamic triangulation network to model the membrane, and computationally minimize the total energy of the membrane via a Monte Carlo algorithm. Firstly, we show that the interaction between two colloids adhered to spherical vesicles is significantly affected by the vesicle curvature. Secondly, we demonstrate that linear aggregates of colloids exploit the curvature anisotropy and adjust their orientation to minimize the total energy on a quasi-ellipsoidal membrane. Using umbrella sampling, we further show that the total energy of the membrane favors two colloids to attract each other at the mid-plane of a prolate ellipsoid that is perpendicular to its major axis. Finally, we investigate how the various terms in the total energy of the membrane affect the strength of the interactions. Our results show that the variation in the membrane shape can play a crucial role in a variety of cellular functions that require macromolecular assembly or membrane remodeling.
2 Model
The conformation of a fluid membrane can be described as the shape minimizing the classical Helfrich energy functional:31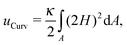 | (1) |
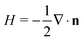 . In our computational scheme, we discretize the membrane by a triangulated network, whose triangles represent course-grained patches of the membrane.32,33 Using a discretized form of the Helfrich energy, we define the curvature energy as
. In our computational scheme, we discretize the membrane by a triangulated network, whose triangles represent course-grained patches of the membrane.32,33 Using a discretized form of the Helfrich energy, we define the curvature energy as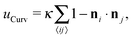 | (2) |
Having defined all the contributions to the total energy of the membrane (uTotal = uCurv + uA + uV + uAd + uEll), we perform Monte Carlo simulations to reach the equilibrium shape of an ellipsoid containing an arbitrary number of colloids. To do so, we implement the Metropolis algorithm, in which we have three types of moves: we can modify the position of a random bead of the membrane, impose a rearrangement in the connections of beads, or move the colloids around. The first two moves are energetically evaluated based on the total energy, while any changes in the position of colloids are only based on the adhesion energy. Our computer model is coarse-grained and cannot capture the fine corrugations of biological membranes that take place at small length-scales. The relative size of such corrugations is very small in comparison to that of colloids in this study.34 Therefore their effects will be much smaller than the elastic interactions caused by colloids.35
During the simulations, we keep the number of particles constant and set all the relevant parameters as: κ = 36kBT, ε = 8.5kBT, KA = 2 × 103kBT/σ2, KV = 250kBT/σ3 and KEll = 0.1kBT/σ2, where kBT is the thermal energy and σ is the diameter of the beads constructing the membrane. The values of κ and ε are chosen such that the colloids are partially wrapped and form linear patterns.24 For very low values of ε colloids would not bind to the membrane and for very high values they aggregate into tubes. The diameter of the colloids is set to σColl = 5σ.
3 Results and discussion
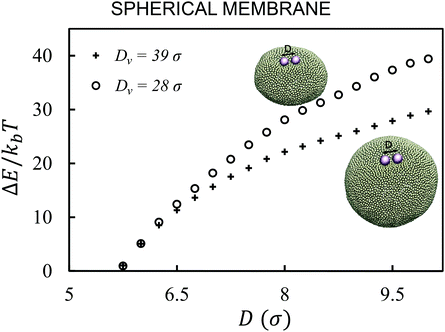
First, we analyze the interaction between two colloids adhered to the surface of two vesicles of different diameters. We keep the size of colloids and beads the same in both cases. We use umbrella sampling36 to calculate the excess energy of the membrane as a function of the distance between the colloids. In effect, we apply a harmonic potential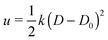 , as our biased potential, between the two colloids directed along the coordinate of interest in order to restrain the system to sample around each distance D0. Having performed the sampling process, we use the weighted histogram analysis method (WHAM) for obtaining the optimal estimate of the unbiased probability distribution, from which we can calculate the free energy of the system. The free energy is calculated with respect to the initial position of the colloids ΔE = E(at the coordinate of interest) − E(initial coordinate). As expected from earlier experimental and computational work,37 colloids in both vesicles attract each other. In contrast to the case studied in ref. 37, here the attraction is not solely because of the bending energy and closed nature of vesicles, but also due to maximizing the adhesion energy of the system. As illustrated in Fig. 1, the depth of the excess energy of the membrane with a smaller radius is significantly larger. In contrast, for the larger vesicle after a short distance colloids do not feel each other and the energy becomes flat. As the only difference between two test cases is the curvature, we conclude that this effect is due to vesicles being of different radii.
, as our biased potential, between the two colloids directed along the coordinate of interest in order to restrain the system to sample around each distance D0. Having performed the sampling process, we use the weighted histogram analysis method (WHAM) for obtaining the optimal estimate of the unbiased probability distribution, from which we can calculate the free energy of the system. The free energy is calculated with respect to the initial position of the colloids ΔE = E(at the coordinate of interest) − E(initial coordinate). As expected from earlier experimental and computational work,37 colloids in both vesicles attract each other. In contrast to the case studied in ref. 37, here the attraction is not solely because of the bending energy and closed nature of vesicles, but also due to maximizing the adhesion energy of the system. As illustrated in Fig. 1, the depth of the excess energy of the membrane with a smaller radius is significantly larger. In contrast, for the larger vesicle after a short distance colloids do not feel each other and the energy becomes flat. As the only difference between two test cases is the curvature, we conclude that this effect is due to vesicles being of different radii.
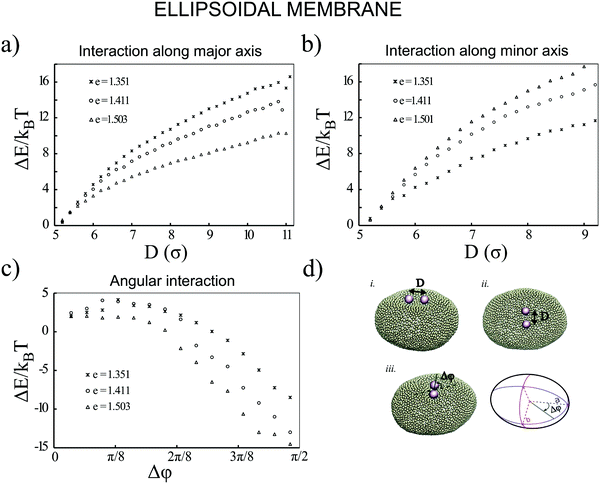
Next, we examine the interaction between two colloids on the surface of a quasi-ellipsoidal membrane. Following the recipe given in Section 2, we form an ellipsoidal membrane from spherical vesicles of size Dv = 28σ. We position the colloids symmetrically along the major axis of the ellipsoid (see Fig. 2d(i)). We repeat the sampling procedure for different aspect ratios, e = a/b, of the ellipsoid. Since the volume is conserved during the shape evolution, one can easily calculate the semi-minor axis, b, as 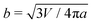 . As depicted in Fig. 2a, along the major axis colloids attract each other in order to minimize both the adhesion and curvature energies. Decreasing the asphericity of the ellipsoid (e → 1.0+) in this direction enhances the amount of available excess area, hence the strength of the attraction energy increases. Suppose that we have two ellipsoids with major axes a1 > a2 with the same excess area (dA). The ellipsoid with the larger major axis (a1) is more elongated and has a smaller cross section, hence the amount of initially given excess area (dA) available at the mid-plane between the colloids is less than that for the case we have the smaller axis a2. Therefore, the more elongated the vesicle (meaning that the more asphericity we have), the less available the initially-given excess area we have at the mid-plane.
. As depicted in Fig. 2a, along the major axis colloids attract each other in order to minimize both the adhesion and curvature energies. Decreasing the asphericity of the ellipsoid (e → 1.0+) in this direction enhances the amount of available excess area, hence the strength of the attraction energy increases. Suppose that we have two ellipsoids with major axes a1 > a2 with the same excess area (dA). The ellipsoid with the larger major axis (a1) is more elongated and has a smaller cross section, hence the amount of initially given excess area (dA) available at the mid-plane between the colloids is less than that for the case we have the smaller axis a2. Therefore, the more elongated the vesicle (meaning that the more asphericity we have), the less available the initially-given excess area we have at the mid-plane.
Similarly, particles that are situated along the semi-minor axis (as depicted in Fig. 2d(ii)) attract each other. There is, however, an important difference between the two directions. In contrast to the previous case, decreasing the asphericity of the ellipsoid makes the attraction force between colloids weaker. Since the number of membrane beads adhered to each colloid remains the same, this behavior cannot be explained by the adhesion energy of the membrane. To elucidate the reason that colloids select the direction along the minor axis to attract each other, we investigate the energy of a pair of colloids along a different coordinate. As shown in Fig. 2d(iii), we rotate a pair of colloids that are constrained at the fixed distance of 3σ to their center, along the angle spanning the space between the semi-major and -minor axes. As Fig. 2c depicts, the most energetically favorable configuration is when the colloids are aligned with the direction perpendicular to the major axis. This itself introduces a mechanism by which, without involving any other factors, two colloids find the mid-plane perpendicular to the symmetry axes of the ellipsoid, as it minimizes the total energy of the membrane. In contrast, in the case of having a perfect spherical membrane, it is not possible to predict the localization of colloidal aggregates as it will be randomly chosen. Increasing the major axis of the membrane (making e larger) drives the colloid reorientation more strongly. One should be careful about the values for the bending moduli and adhesion coefficients during the simulations, as it can cause an effect where colloids are arrested and prevented from diffusing on the surface of the membrane.24 In addition, a very high value of KEll, in addition to influencing the adhesion energy between the colloids and the membrane, would also pull two tubes out of the vesicle.
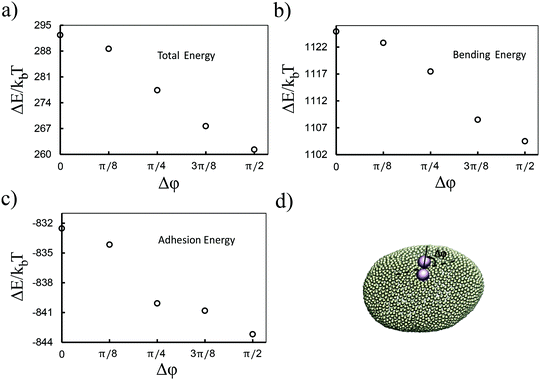
Although the above results quantitatively show different behaviors in two directions, the dominant contribution in the total energy of the membrane causing this effect is not yet clarified. In order to approximately determine this, we proceed as follows: we pick a vesicle with e = 1.351 and constrain the position of the colloids with a strong potential at a distance of 6σ from each other. Here, in contrast to earlier work, we do not use the sampling method. Instead we let the system explore possible configurations of the membrane after reaching equilibrium, and then take the average of the energies for all those configurations. As depicted in Fig. 3, both the adhesion energy and the curvature of the membrane decrease when the angle between the line connecting two colloids and the semi-major axis of the ellipsoid (Fig. 3d) approaches π/2. The bending energy, as quantified in Fig. 3b, has a larger contribution to the total energy than the adhesion energy (Fig. 3c).
Putting all the results together, we expect that when we have more than two colloids they will initially attract each other to form linear aggregates (to minimize the adhesion energy), and afterwards these aggregations change their orientation to align with the minor axes of the ellipsoid. This is indeed what we observe in our simulations. Fig. 4 depicts the equilibrium shape of the membrane for different numbers of colloids. In all the test cases colloids tend to form a ring-like structure in the mid-plane of the ellipsoid. With a sufficiently large number of colloids (Fig. 4c and d), they form a full ring in this plane (see also the supplemental movie SM1, ESI†). It is important to mention that these patterns are quite stable during the whole simulation. In contrast, in spherical vesicles there is no preferred direction for the aggregation of particles. Although colloids attract each other on a spherical membrane (Fig. 1), there is no preference for the direction of the attraction. This means that even in the case of forming a perfect ring on a vesicle, particles self-assemble in an arbitrary direction on the membrane. It has also been recently predicted that the particles adhered to a prolate vesicle can feel the curvature gradient and localize at the equatorial line of a vesicle.30
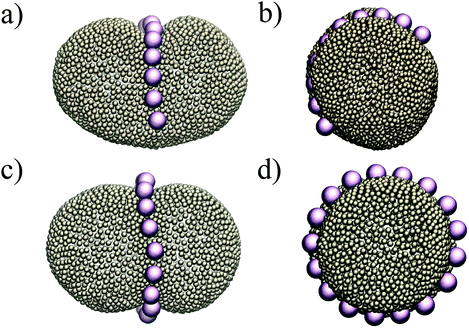 | ||
| Fig. 4 Colloids attract each other on ellipsoids, and in order to minimize the curvature energy, they form an arc (a and b) and a ring (c and d) at the mid-plane of the ellipsoid. | ||
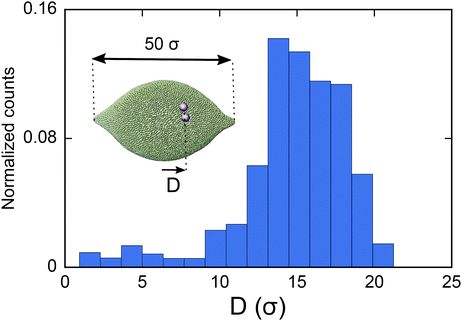
As the final experiment, we look at the movement of the particles on a vesicle containing regions with negative mean curvature. To create these vesicles, we first overstretch the springs and form two small negatively curved regions in a big vesicle (Dv = 40σ). Over-stretching the spring increases the tension in the membrane, making the role of tension more significant compared to the previous test cases. Having inserted a dimer in the system, we then look at the migration of the dimer. As shown in Fig. 5 in this case the dimer does not stay at the mid-plane of the vesicle. It instead spends much of its time during MC simulation in the areas that are closer to the negatively curved regions. Since the springs are overstretched, in the regions close to poles there is no excess area for the dimer to adhere to and therefore the dimer cannot explore that area (see also supplemental movies SM2–4, ESI†). This prediction is consistent with ref. 28 where the migration of a dimer in the tension dominant regime has been experimentally investigated.
The type of pattern formation we observe in our simulations is reminiscent of recruiting proteins by the membrane during different biological processes. It has been shown that, for example, dynamin proteins form a ring-like structure during exocytosis to facilitate membrane scission38 and that FtsZ proteins self-assemble into rings during the last step of bacterial cell division, namely cytokinesis.39 Because most of the proteins in biological cells are either anchored to or embedded in the membrane, their interaction is a response to the deformation of the membrane they themselves impose. As in our simulation the varying curvature is a determining factor that drives the pattern formation, we can relate our results to those membrane trafficking machinery functions. Although in this study we adjusted the included harmonic potential strength KEll such that it would not affect the interaction of the colloids with the membrane, it has been proven that during the cell division we have the same situation. Cytoplasmic dynein, as a multi-subunit molecular motor, generates the force that is exploited by the cell to direct the orientation of the division axis by mitotic spindles.40 Our results show that curvature inhomogeneity and anisotropy can at least facilitate the process of protein self-assembly in the mid-plane of the cell.
Although we have only investigated the interaction between identical isotropic inclusions, our results can explain the behavior of a system containing anisotropically shaped inclusions as well. Based on the local deformation of an ellipsoid, we expect that anisotropic inclusions adhered to a spherical membrane attract each other in the direction of negative curvature (with respect to the curvature of the membrane). This situation corresponds to having an isotropic inclusion embedded in a membrane with an anisotropic shape, which is the case we have studied here.
4 Conclusion
We studied the role of curvature heterogeneity and anisotropy in the interaction between colloids adhered to a membrane. First, we showed that the strength of the interaction between two colloids on the surface of a spherical vesicle is altered by changing the size of the vesicle. Next, we focused on such interactions on a membrane with an ellipsoidal shape. We revealed that the interaction on such an inhomogeneously shaped membrane depends on direction. For example, decreasing the asphericity of an ellipsoidal membrane makes the attraction between the colloids stronger along the semi-major axis and weaker in the semi-minor direction. Similarly, it has been previously shown in simulations that, on an elastic cylindrical membrane, colloids assemble perpendicularly to its major axis in the regime dominated by the bending energy.26,33 In the case of fluid membranes, through an analytical framework, it has also been shown that inclusions “embedded” in a tubular membrane can attract each other in a transversal direction.21 Simulating a vesicle containing many colloids, we showed how they form a ringlike structure around the mid-plane of the ellipsoid. While the cluster of colloids freely explores all the surface of a spherical membrane, a less curved area energetically is more favorable for colloids on an ellipsoid. Our results suggest that forming regions of different curvatures on membrane vesicles can control the pattern formation of inclusions, and this can be important from both nanotechnological application and biological points of view.Acknowledgements
This work was supported by the Netherlands Organisation for Scientific Research (NWO/OCW), as part of the Frontiers of Nanoscience program.References
- H. T. McMahon and E. Boucrot, J. Cell Sci., 2015, 128, 1065–1070 CrossRef CAS PubMed.
- M. Schmick and P. I. Bastiaens, Cell, 2014, 156, 1132–1138 CrossRef CAS PubMed.
- Y. Shibata, J. Hu, M. M. Kozlov and T. A. Rapoport, Annu. Rev. Cell Dev. Biol., 2009, 25, 329–354 CrossRef CAS PubMed.
- H. T. McMahon and J. L. Gallop, Nature, 2005, 438, 590–596 CrossRef CAS PubMed.
- S. Wang, H. Tukachinsky, F. B. Romano and T. A. Rapoport, eLife, 2016, 5, e18605 Search PubMed.
- L. Johannes, C. Wunder and P. Bassereau, Cold Spring Harbor Perspect. Biol., 2014, 6, a016741 CrossRef PubMed.
- G. Drin and B. Antonny, FEBS Lett., 2010, 584, 1840–1847 CrossRef CAS PubMed.
- B. J. Reynwar, G. Illya, V. A. Harmandaris, M. M. Müller, K. Kremer and M. Deserno, Nature, 2007, 447, 461–464 CrossRef CAS PubMed.
- P. G. Dommersnes and J.-B. Fournier, Biophys. J., 2002, 83, 2898–2905 CrossRef CAS PubMed.
- Y. Schweitzer and M. M. Kozlov, PLoS Comput. Biol., 2015, 11, e1004054 Search PubMed.
- K. Kim, J. Neu and G. Oster, EPL, 1999, 48, 99 CrossRef CAS.
- T. Weikl, M. Kozlov and W. Helfrich, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57, 6988 CrossRef CAS.
- M. Goulian, R. Bruinsma and P. Pincus, EPL, 1993, 22, 145 CrossRef CAS.
- D. Thalmeier, J. Halatek and E. Frey, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 548–553 CrossRef CAS PubMed.
- A. R. English and G. K. Voeltz, Cold Spring Harbor Perspect. Biol., 2013, 5, a013227 Search PubMed.
- M. Pannuzzo, A. Raudino, D. Milardi, C. La Rosa and M. Karttunen, Sci. Rep., 2013, 3, 2781 CrossRef PubMed.
- M. Ehrlich, W. Boll, A. van Oijen, R. Hariharan, K. Chandran, M. L. Nibert and T. Kirchhausen, Cell, 2004, 118, 591–605 CrossRef CAS PubMed.
- I. Koltover, J. O. Radler and C. R. Safinya, Phys. Rev. Lett., 1999, 82, 1991 CrossRef CAS.
- R. Sarfati and E. R. Dufresne, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2016, 94, 012604 CrossRef PubMed.
- B. J. Peter, H. M. Kent, I. G. Mills, Y. Vallis, P. J. G. Butler, P. R. Evans and H. T. McMahon, Science, 2004, 303, 495–499 CrossRef CAS PubMed.
- A. Vahid and T. Idema, Phys. Rev. Lett., 2016, 117, 138102 CrossRef PubMed.
- A. H. Bahrami, R. Lipowsky and T. R. Weikl, Phys. Rev. Lett., 2012, 109, 188102 CrossRef PubMed.
- M. Simunovic, A. Srivastava and G. A. Voth, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 20396–20401 CrossRef CAS PubMed.
- A. Šarić and A. Cacciuto, Phys. Rev. Lett., 2012, 108, 118101 CrossRef PubMed.
- A. Šarić and A. Cacciuto, Soft Matter, 2011, 7, 1874–1878 RSC.
- J. C. Pàmies and A. Cacciuto, Phys. Rev. Lett., 2011, 106, 045702 CrossRef PubMed.
- S. Aimon, A. Callan-Jones, A. Berthaud, M. Pinot, G. E. Toombes and P. Bassereau, Dev. Cell, 2014, 28, 212–218 CrossRef CAS PubMed.
- N. Li, N. Sharifi-Mood, F. Tu, D. Lee, R. Radhakrishnan, T. Baumgart and K. J. Stebe, Langmuir, 2016, 33, 600–610 CrossRef PubMed.
- J. Agudo-Canalejo and R. Lipowsky, Nano Lett., 2015, 15, 7168–7173 CrossRef CAS PubMed.
- J. Agudo-Canalejo and R. Lipowsky, Soft Matter, 2017, 13, 2155–2173 RSC.
- W. Helfrich, Z. Naturforsch., C: Biochem., Biophys., Biol., Virol., 1973, 28, 693–703 CAS.
- D. Nelson, T. Piran and S. Weinberg, Statistical mechanics of membranes and surfaces, World Scientific, 2004 Search PubMed.
- A. Šarić, J. C. Pàmies and A. Cacciuto, Phys. Rev. Lett., 2010, 104, 226101 CrossRef PubMed.
- S. Semrau, T. Idema, L. Holtzer, T. Schmidt and C. Storm, Phys. Rev. Lett., 2008, 100, 088101 CrossRef PubMed.
- H.-K. Lin, R. Zandi, U. Mohideen and L. P. Pryadko, Phys. Rev. Lett., 2011, 107, 228104 CrossRef PubMed.
- G. M. Torrie and J. P. Valleau, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- C. van der Wel, A. Vahid, A. Šarić, T. Idema, D. Heinrich and D. J. Kraft, Sci. Rep., 2016, 6, year Search PubMed.
- T. J. Pucadyil and S. L. Schmid, Cell, 2008, 135, 1263–1275 CrossRef CAS PubMed.
- R. Shlomovitz and N. Gov, Phys. Biol., 2009, 6, 046017 CrossRef CAS PubMed.
- A. Lesman, J. Notbohm, D. A. Tirrell and G. Ravichandran, J. Cell Biol., 2014, 205, 155–162 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sm00433h |
| This journal is © The Royal Society of Chemistry 2017 |