Dynamic pattern of wrinkles in a dielectric elastomer

Abstract

A membrane of a dielectric elastomer may undergo electromechanical phase transition from the flat to wrinkled state, when the applied voltage reaches a critical value. The wrinkled region is observed to expand at the expense of the flat region during the phase transition. In this paper, we report on a dynamic pattern of wrinkles in a circular membrane of a dielectric elastomer. During phase transition, both the flat and wrinkled regions move interchangeably in the membrane. The radial prestretch is found to significantly affect electromechanical phase transition. For example, a membrane with a small prestretch can exhibit a dynamic pattern of wrinkles, which is essentially related to snap-through instability. However, a membrane with a large prestretch undergoes continuous phase transition, without exhibiting a dynamic pattern. An analytical model is developed to interpret these experimental phenomena. Finite element simulations are performed to predict the wrinkle morphology, especially the coexistence of flat and wrinkled regions. Both the theoretical calculations and finite element simulations are qualitatively consistent with the experiments. Additionally, we observe another type of electromechanical behavior involving a dynamic pattern of wrinkles with different wavelengths. The membrane first undergoes continuous transition from the flat to wrinkled state, followed by discontinuous transition from one wrinkled state to another. These results may inspire new applications for dielectric elastomers such as on-demand patterning of wrinkles for microfluidics and stretchable electronics.

---

1. Introduction

Wrinkle patterns are a commonly observed phenomenon in nature. Studies on shark skin,¹ geckos’ feet,² and sandfish scales³ have revealed interesting details about the usefulness of hierarchical patterns. Surface instabilities have since been investigated in stimuli-responsive gels, elastomers, and multilayer systems for various applications such as tunable wetting,⁴ adhesion,⁵ anti-fouling,⁶ stretchable electronics,⁷etc.

This paper investigates voltage-induced wrinkling in a membrane of a dielectric elastomer, which consists of a thin layer of elastomer sandwiched between two compliant electrodes. When the two electrodes are connected to a power supply, the membrane of the elastomer is subjected to the voltage-induced Maxwell stress, resulting in its expansion in area and shrinkage in thickness. The attributes of this soft active material include large deformation, high energy density, fast response, quiet operation, and light weight.^8–10 Dielectric elastomers can function as artificial muscles to drive soft robots and devices.^11–13

A membrane of a dielectric elastomer may undergo electromechanical phase transition from the flat to wrinkled state, when the applied voltage reaches a critical value. A dielectric elastomer of equal-biaxial prestretches was found to form wrinkles locally with the flat and wrinkled regions coexistent on its surfaces.¹⁴ Keplinger et al. observed the propagation of wrinkles in a dielectric elastomer, where the flat area decreases, giving way to the wrinkled area.¹⁵ The propagation of wrinkles could be simulated by a meshfree method.¹⁶ Zhu et al. studied a clamped membrane of a dielectric elastomer, which is subjected to a vertical dead load and is clamped horizontally.¹⁷ It was found that the flat membrane could form wrinkles in two different ways. The first type of transition is discontinuous, accompanied by a sudden snap in the deformation. During this discontinuous transition, the flat and wrinkled states can coexist. The second transition is continuous, accompanied by a continuous change in the deformation. Recently, another phenomenon was reported as follows. The membrane first undergoes continuous transition from the flat to wrinkled state. Then the membrane also undergoes another discontinuous transition from a wrinkled state with a large wavelength to that with a small wavelength.¹⁸ Huang and Suo theoretically analyzed the transition from the flat to wrinkled state in a dielectric elastomer subjected to a uniaxial dead load.¹⁹ However, the wrinkled state is hardly observed experimentally since it cannot survive dielectric breakdown. Mao et al. studied nucleation and propagation of wrinkles in an inflated membrane of a dielectric elastomer mounted onto an air chamber.²⁰ It was found that the location and pattern of wrinkles largely depend on the initial air pressure and the applied step voltage. Lu and Suo studied electromechanical phase transition in a dielectric tube theoretically, and predicted the coexistence of tube regions with large and small diameters.²¹ Recently, Lu et al. experimentally verified this prediction. By harnessing this phase transition, the dielectric tube achieves a giant voltage-induced area strain of more than 2000%.²² In these previous works, when a dielectric elastomer undergoes phase transition, the region of larger deformation is popularly observed to propagate and increase, at the expense of the region of smaller deformation.^{15,17,18,20,22}

In this paper, we report on a dynamic pattern of wrinkles in a dielectric elastomer. Experiments are conducted in a simple structure – a circular membrane with the boundary fixed to a rigid frame (Fig. 1). The flat and wrinkled regions are observed to move interchangeably over the surfaces at the onset of phase transition (Fig. 2). An analytical model based on the theory of dielectric elastomers is utilized to interpret this phenomenon. A finite element model is developed to simulate the wrinkle morphology, which exhibits the coexistence of the flat and wrinkled regions. The effects of the radial prestretch on electromechanical phase transition are analyzed. Both the theoretical calculations and finite element simulations are qualitatively consistent with the experiments.

Fig. 1 A schematic of a membrane of a dielectric elastomer. (a) A circular membrane is stress free and has a radius B. The active part, which is smeared with the electrodes and functions as an actuator, has a radius A. (b) The membrane is subjected to a radial prestretch λ_pre, and then its boundary is fixed to a rigid frame. As a result, the membrane has a radius Bλ_pre, and the active part has a radius Aλ_pre. (c) When connected to a voltage, the active part expands in area, while the passive part decreases in area, and point R in the reference state moves to a position with radius r in the current state.

Fig. 2 The membrane with λ_pre = 3 and B/A = 2 exhibits a dynamic pattern at a fixed voltage, Φ = 7.38 kV. (a) The dynamic pattern starts, with wrinkles nucleating in the top right area. (b and c) The wrinkles in the top right area propagate to the left, while other wrinkles nucleate in the bottom right area. (d–f) The wrinkles in the bottom right area propagate to the left. (g and h) The wrinkled region propagates to the center, while the top area becomes flat. (i–k) The flat region at the top of the membrane propagates to the center. (l) The membrane suffers dielectric breakdown when the local electric field reaches the dielectric strength of the material.

This paper is organized as follows. The experimental observations of a dynamic pattern are discussed in Section 2. A theoretical model is developed in Section 3. Section 4 reports finite element simulations. Section 5 analyzes continuous transition from the flat to wrinkled state. Section 6 illustrates another type of discontinuous transition from one wrinkled state to another. All results are summarized in Section 7.

2. Dynamic pattern consisting of flat and wrinkled regions

Fig. 1 shows the schematic of a membrane of a dielectric elastomer. This structure has been popularly employed in the literature due to its simple design.^14,15 In the reference state (Fig. 1a), a circular membrane is subjected to no mechanical and electrical loads, and has a radius B and a thickness H. The active part, which is smeared with the electrodes and functions as an actuator, has a radius A. In the prestretched state (Fig. 1b), the membrane is subjected to a radial prestretch λ_pre, and then its boundary is fixed to a rigid frame. As a result, the membrane has a radius Bλ_pre, and the active part has a radius Aλ_pre. In the current state (Fig. 1c), when the active part is subjected to a voltage, it expands in area and reduces in thickness, and point R in the reference state moves to a position with radius r in the current state. In the experiments, we employ 3M VHB 4910 (with a thickness H = 1 mm) as the elastomer, and carbon grease as the compliant electrodes. We use a rigid frame with a radius Bλ_pre = 6 cm and radius ratio B/A = 2, but vary the prestretch λ_pre to test the behavior of the actuator. The voltage is programmed through LabVIEW (BNC-2120, NI), and is then amplified by using a high voltage amplifier (FR30P10, Glassman). We increase the voltage with a small ramp rate of 20 V s⁻¹ to minimize the viscoelastic effect of the elastomer. The frame is vertically placed, i.e., the in-plane directions of the membrane are aligned along the gravity. A camera is employed to capture the front view of the membrane.

In a membrane with λ_pre = 3 and B/A = 2, we observe a dynamic pattern (consisting of flat and wrinkled regions) upon loss of tension. When the voltage is small, the active part (covered with the electrodes) expands due to the voltage-induced Maxwell stresses, while the passive part (without the electrodes) decreases in area (Fig. 1c). As the voltage increases, wrinkles may nucleate in some regions due to local defects, but both the flat and wrinkled regions are stable on the surfaces. When the voltage further increases to a critical value, Φ = 7.38 kV, a dynamic pattern appears, with both the flat and wrinkled regions moving interchangeably on the surfaces. Movie 1 (ESI†) shows the experimental observations, in which we keep the voltage constant (Φ = 7.38 kV) at the onset of the dynamic pattern. Fig. 2 shows a sequence of still images of the membrane at this fixed voltage. At t = 0, the dynamic pattern starts when the membrane forms wrinkles in the top right area, as shown in Fig. 2a. In Fig. 2b and c, the wrinkles in the top right area propagate to the left, while other wrinkles nucleate in the bottom right area. In Fig. 2d–f, the wrinkles in the bottom right area propagate to the left. In Fig. 2g and h, the wrinkled region propagates to the center, while the top area becomes flat. In Fig. 2i–k, the flat region in the top middle area propagates to the center. In Fig. 2l, the membrane suffers dielectric breakdown when the local electric field reaches the dielectric strength of the material.

In previous works where a membrane of a dielectric elastomer was prestretched by clamps and dead loads in either direction, a vertically aligned wrinkling pattern was observed since the membrane suffered loss of tension horizontally.^17,18,23 The wrinkling pattern, in our current work, looks much more complex due to the concentric loading imposed on the active part of the membrane. In addition, voltage-induced wrinkling in a dielectric elastomer exhibits attributes different from wrinkling induced by other mechanisms. For example, for a membrane subjected to a uniaxial tensile force, wrinkles may first appear in the middle area (far from the boundaries), since they are induced by the compressive stress caused by the Poisson effect.²⁴ Different from this phenomenon, voltage-induced wrinkles first appear in the boundary (see Fig. 2), since they are induced by the compressive stresses applied by the passive part of membrane or the rigid frame.

In addition, this dynamic pattern, as shown in Movie 1 (ESI†) and Fig. 2, is distinctly different from the phenomena observed in previous works,^{15,17,18,20,22} where the wrinkled region usually enlarges at the expense of the flat region. Our current experiments show that both the flat and wrinkled regions not only coexist, but also move with the respective areas interchangeable with each other. We develop a model to interpret this dynamic pattern.

3. Theoretical model

The elastomer is taken to be incompressible, λ_rλ_θλ_h = 1, where λ_r, λ_θ, and λ_h are the stretches in the radial, hoop, and thickness directions, respectively. We employ a model of ideal dielectric elastomer, assuming that the electric displacement is linear in the electric field,²⁵i.e., D = εE, where ε is the permittivity of the dielectric elastomer. This assumption is consistent with experiments,²⁶ which show that VHB exhibits only a small change in permittivity (less than 5%) when subjected to large equal-biaxial stretches (say, 5 × 5).

When subjected to a voltage (Fig. 1c), the active part expands. Since the boundary of the membrane is fixed to a rigid frame, the passive part shrinks. The active part is subjected to a radial force and voltage, and thus undergoes homogeneous, equal-biaxial deformation with the same radial and hoop stretches λ_A. Its equation of state is^27,28

where s_A is the nominal radial stress applied by the passive part, ε is the permittivity of the dielectric elastomer, E is the true electric field, and W is the Helmholtz free energy density associated with the stretching of the elastomer. The first and second terms on the left hand side of (1) are the mechanical stress and the Maxwell stress (induced by the voltage), respectively, and the right hand side is the elastic restoring stress. Since we increase the voltage with a small ramp rate of 20 V s⁻¹ in the experiments, we assume that the elastomer has enough time for creep/relaxation, and we thus ignore the viscoelasticity of the elastomer in this current model.

The passive part (without the electrodes) undergoes inhomogeneous unequal-biaxial deformation.²⁸ As shown in Fig. 1, point R in the reference state reaches a position with radius r in the current state, and its radial and hoop stretches are defined as 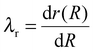and , respectively. For the passive part, we have the equilibrium equation

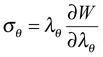where σ_r and σ_θ are the true stresses in the radial and the hoop directions, respectively. The material law gives , .²⁷ Based on the definition of λ_r and λ_θ, we haveBased on (2), we haveConsidering the strain-stiffening effect of the elastomer, we employ the Gent material model as follows:²⁹where μ is the small-strain shear modulus, and J_lim is the material parameter related to the stretch limit. Substituting (5) into (1), we obtain the governing equation which determines the state of the active part. Substituting (5) into (4), we obtain a set of ordinary differential equations, i.e.eqn (3) and (4), which define a boundary value problem for the passive part. Based on the no-slip displacement boundary condition, we have . 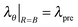We can solve eqn (3) and (4) for the radial stretch in the passive part at the junction with the active part by using the shooting method. Once the radial stretch and the hoop stretch (which is prescribed) at the inner boundary of the passive part are known, one can calculate the nominal radial stress at the inner boundary, i.e., . We can analyze the electromechanical behavior of the dielectric elastomer actuator and calculate the voltage–stretch/charge curves by solving eqn (1).

The dynamic pattern in wrinkles discussed earlier can be analyzed using the model as follows. Fig. 3a or b plots voltage (Φ) as a function of stretch (λ_A) or charge (Q), respectively, for a membrane with λ_pre = 3 and B/A = 2 with material parameters μ = 43 kPa, J_lim = 115, and ε = 4.12 × 10⁻¹¹ F m⁻¹. These parameters are obtained by fitting the experimentally recorded voltage–stretch curve for λ_pre = 3 and B/A = 2 and are employed for all calculations in this paper. As shown in Fig. 3a and b, when the deformation/charge is small, the voltage increases with the deformation/charge. As the active part expands in area, the passive part shrinks. As a result, the radial tensile stress s_A decreases as the voltage increases. At a certain level of voltage, s_A vanishes, causing the membrane to wrinkle and is represented by an open blue circle in Fig. 3. Loss of tension may cause the membrane to form wrinkles, due to its small bending rigidity. After the membrane forms wrinkles, we set s_A = 0. According to eqn (1), the state of the active part, after loss of tension, is governed by

When the membrane suffers loss of tension and forms wrinkles, the voltage–stretch/charge curve starts to go down (see Fig. 3c and d for enlarged regions in Fig. 3a and b, respectively). This observation can be interpreted as follows. The elastomer thins down appreciably after forming wrinkles, and the electric field in the layer is very high. As a result, the voltage needed to maintain the charge starts to decrease. Consequently, the voltage reaches a peak, which has long been identified as the onset of electromechanical instability.³⁰ Finally, the curve goes up again due to the strain-stiffening effect, when the stretch is close to the stretch limit.

Fig. 3 The calculation results for the membrane with λ_pre = 3 and B/A = 2. The material parameters are used as follows: μ = 43 kPa, J_lim = 115, and ε = 4.12 × 10⁻¹¹ F m⁻¹. (a) Voltage as a function of stretch. The curve consists of two branches. One goes up, corresponding to the flat states, and the other goes down and then up, corresponding to the wrinkled states. (b) Voltage as a function of charge. (c) Enlarged region in (a). (d) Enlarged region in (b). The open blue circle represents loss of tension, and the two solid black circles represent the flat and wrinkled states which can coexist. The transition voltage Φ* is such that the two shaded regions have equal areas.

The curve in Fig. 3a or b consists of two branches. One goes up, corresponding to the flat states, and the other goes down and then up, corresponding to the wrinkled states. The flat and wrinkled states can coexist over a range of charges at the voltage of transition, which is such that the two shaded regions in Fig. 3d have equal areas.^17–19,25 At this critical voltage for transition, any volume fraction of the flat/wrinkled regions can be possible, depending on the total charges on the electrodes. If one can control and increase the charges on the electrodes, the wrinkled area will propagate at the expense of the flat area. However, it is challenging to control the charges in the experiments, and the flat and wrinkled regions may move with their respective areas interchangeable with each other, as the charges on the electrodes vary. As shown in Fig. 3c and d, the flat state has a smaller stretch, while the wrinkled state has a larger stretch. As a result, this phase transition from the flat to wrinkled state is discontinuous, accompanied by a sudden snap in the deformation.

4. Finite element simulations

We next conducted finite element analysis to simulate the electromechanical behavior of a dielectric elastomer. Based on the nonlinear field theory of dielectric elastomers,³¹ the finite element method (FEM) is implemented in the commercial software ABAQUS via a user-subroutine (UMAT). Unlike the work of Zhao and Suo,³² we use the Gent model to account for the strain-stiffening effect of the elastomer,²⁹ which is significant to analyze electromechanical instability and phase transition in a dielectric elastomer. For more information about the method and code implementation, please refer to our previous work.³³

We simulate the membrane of a dielectric elastomer (Fig. 1) using Abaqus/Standard, at a low voltage ramp rate of 20 V s⁻¹ which is employed in the experiments. In order to eliminate the volumetric locking resulting from the incompressibility constraint, a hybrid-type C3D8H element is employed. Consistent with the theoretical modeling discussed above, we adopt an elastic model with the same material parameters (i.e., μ = 43 kPa, J_lim = 115, and ε = 4.12 × 10⁻¹¹ F m⁻¹) and configuration parameters (i.e., H = 1 mm, and Bλ_pre = 6 cm). In our simulations, a fixed boundary condition, u_x = u_y = u_z = 0, is applied for nodes on the boundary of R = B. The gravitational force is applied on the membrane placed in the vertical frame and parallel to the initial membrane plane, which is consistent with the experiment setup. The gravitational force introduces the inhomogeneity needed to trigger the instabilities. Mesh dependency has been investigated thoroughly via numerous FEM simulations in this work to justify the accuracy of the simulation results. These numerical tests have demonstrated that the mesh pattern has a marginal influence on the critical voltage and stretches of the instability; however, it affects the wrinkle patterns in the continuous/discontinuous wrinkle transition. To successfully trigger the wrinkling of the membrane and achieve comparable wrinkle patterns with experiments, it is greatly helpful to employ irregular mesh patterns. FEM simulation for post-instability stages such as wrinkle propagation requires a careful setup of the numerical stabilization technique in ABAQUS, while minimizing the side effects of using such a technique.

Movie 2 (ESI†) shows the simulation results of the membrane with λ_pre = 3 and B/A = 2. As we can see, the active part of the membrane first expands as the voltage ramps up. When the voltage reaches a critical value (Φ = 8.664 kV), wrinkles start to nucleate in the membrane, and then the flat and wrinkled regions coexist within a small voltage range between 8.664 kV and 9.006 kV. Fig. 4 shows the states of the membrane at four levels of voltage. Each left subfigure shows the pattern of the membrane with distribution of the radial stretch (in different colors). Each right subfigure shows the area ratio of the radial stretch, i.e., the ratio of the area with the specific radial stretch to the entire area of the active part (with electrodes). During discontinuous phase transition, the flat and wrinkled states can coexist. At Φ = 8.664 kV (Fig. 4a), the active part of the membrane is flat, with a radial stretch λ_r = 4.2. Due to the expansion of the active part, the passive part (without electrodes) shrinks and exhibits inhomogeneous deformation. At Φ = 8.728 kV or 8.747 kV (Fig. 4b or c), the flat region (in green) can coexist with the wrinkled region (in red), and the flat or wrinkled state has a radial stretch λ_r = 4.2 or 6, respectively. Comparing Fig. 4b and c, we can see that as the voltage increases, the wrinkled region increases at the expense of the flat region. At Φ = 9.006 kV (Fig. 4d), the entire membrane forms wrinkles, with a radial stretch λ_r = 6.3–6.5.

Fig. 4 Simulations of discontinuous phase transition in the membrane with λ_pre = 3 and B/A = 2. (Left) The pattern of the membrane with distribution of the radial stretch λ_r. (Right) The area ratio of the radial stretch, i.e., the ratio of the area with the specific radial stretch λ_r to the entire area of the active part with electrodes. (a–d) The membrane at Φ = 8.664 kV, 8.728 kV, 8.747 kV or 9.006 kV, respectively. During the discontinuous phase transition, the flat and wrinkled states can coexist.

During discontinuous phase transition, the flat and wrinkled states can coexist. Since the flat or wrinkled state is associated with two different stretches, this phase transition is accompanied by a sudden snap in the deformation. These FEM simulations are consistent with the calculations based on the theoretical modeling in Section 3 (see Fig. 3). In the experiments, the flat and wrinkled regions not only coexist, but also move with the respective areas interchangeable with each other. We cannot analyze this dynamic pattern using the FEM, since it is challenging to simulate the process at a fixed voltage but with varying controlled charges.

5. Continuous transition from the flat to wrinkled state

In a membrane with a larger radial prestretch, we observe continuous phase transition from the flat to wrinkled state. Movie 3 (ESI†) shows the electromechanical behavior of the membrane with λ_pre = 4.5 and B/A = 2. The membrane first expands when the voltage is small. When the voltage increases to a critical value (Φ = 6.26 kV), wrinkles nucleate at some points on the surfaces (Fig. 5a), and then the entire membrane forms wrinkles shortly in about 14 s (Fig. 5b). In contrast to discontinuous phase transition in Section 2, the membrane in Movie 3 (ESI†) does not exhibit a dynamic pattern, i.e., the flat and wrinkled regions do not move interchangeably on the surfaces. Instead, the entire membrane changes from the flat to wrinkled state rapidly.

Fig. 5 Continuous phase transition from the flat to wrinkled state in the membrane with λ_pre = 4.5 and B/A = 2. (a) Wrinkles nucleate on the surfaces at Φ = 6.26 kV. (b) The entire membrane forms wrinkles at Φ = 6.54 kV.

Fig. 6 shows the calculated voltage as a function of the stretch for a membrane with B/A = 2, at several levels of λ_pre with the same material parameters. When λ_pre is less than 3.2, the voltage–stretch curve has an “N” shape – going up, down, and up again. A membrane with a small prestretch will exhibit discontinuous phase transition, accompanied by snap-through instability. However, when λ_pre is more than 3.2, the voltage increases monotonically with the stretch, even after loss of tension represented by the open blue circle. Consequently, the membrane with λ_pre = 4.5 can avert snap-through instability and undergo continuous phase transition.

Fig. 6 Calculated voltage as a function of stretch for a membrane with B/A = 2, at several levels of radial prestretch λ_pre. When λ_pre is less than 3.2, the voltage–stretch curve has an “N” shape (going up, down, and up again), and the membrane undergoes discontinuous phase transition from the flat to wrinkled state. When λ_pre is more than 3.2, the voltage increases monotonically with the stretch, and the membrane undergoes continuous phase transition.

We have also employed finite element modeling to simulate the continuous transition observed in this experiment. Movie 4 (ESI†) shows the simulation results of the membrane with λ_pre = 4.5 and B/A = 2. The active part of the membrane first expands when the voltage is small. When the voltage reaches a critical value (Φ = 8.793 kV), the entire active part of the membrane forms wrinkles throughout its surfaces. Fig. 7 shows the states of the membrane at three levels of voltage. At Φ = 8.640 kV, the active part is flat, with a radial stretch λ_r = 6. At Φ = 8.793 kV, the entire active part forms wrinkles, with a radial stretch λ_r = 6.2. At Φ = 8.900 kV, the wrinkled part attains a larger radial stretch λ_r = 6.25. As we can see, this phase transition is accompanied by a continuous change in the deformation, different from discontinuous phase transition. These FEM simulations are qualitatively consistent with the calculations shown in Fig. 6 for λ_r = 4.5.

Fig. 7 Simulations of continuous phase transition in the membrane with λ_pre = 4.5 and B/A = 2. (Left) The pattern of the membrane with distribution of the radial stretch λ_r. (Right) The area ratio of the radial stretch. (a–c) The membrane at Φ = 8.640 kV, 8.793 kV, or 8.900 kV, respectively. The continuous phase transition is accompanied by a continuous change in the deformation.

6. Discontinuous transition from one wrinkled state to another

We also observe another electromechanical behavior that is different from the above two types of phase transition discussed in Sections 2 and 5. Movie 5 (ESI†) shows the progression of the state of the membrane with λ_pre = 4 and B/A = 2. As the voltage increases, the active part of the membrane expands as the passive part contracts. When the voltage reaches a critical value (Φ = 6.3 kV), the membrane suffers loss of tension, and wrinkles nucleate close to the periphery of the active part (Fig. 8a). In a short time span, the entire area forms wrinkles rapidly as shown in Fig. 8b and c. This observation indicates a type of continuous phase transition from the flat to wrinkled state. As the voltage further increases, there is a slight change in the wrinkle morphology (Fig. 8d). Once the voltage reaches another critical value (Φ = 7.0 kV), a small circular region in the middle right area becomes more transparent (Fig. 8e), due to much larger stretch, compared to other wrinkled regions. Then this region propagates to the bottom (Fig. 8f). Subsequently, the membrane exhibits a dynamic pattern (Fig. 8g–p). Wrinkles of smaller wavelengths can be observed in the right transparent region (say, Fig. 8l). As we can see, wrinkles of different wavelengths not only coexist but also move interchangeably on the surfaces. This dynamic pattern indicates a type of discontinuous phase transition from a wrinkled state of a larger wavelength to that of a smaller wavelength.

Fig. 8 The membrane with λ_pre = 4 and B/A = 2 undergoes continuous transition from the flat to wrinkled state, followed by discontinuous transition from one wrinkled state to another. (a) Wrinkles nucleate in regions close to the boundary at Φ = 6.3 kV. (b) Wrinkles propagate across the membrane. (c) The membrane is fully wrinkled at Φ = 6.54 kV. (d) As the voltage further increases, there is a slight change in the wrinkle morphology. (e) At Φ = 7.0 kV, a small circular region in the middle right area becomes more transparent. (f) This region propagates to the bottom. (g–p) The membrane exhibits a dynamic pattern, and wrinkles of different wavelengths not only coexist but also move interchangeably on the surfaces.

The experimental observations (Fig. 8) can be interpreted by using a schematic voltage–charge diagram, as shown in Fig. 9. As the voltage increases, the active part increases its area, and the charges on the membrane increase correspondingly. At a critical voltage indicated by the open circle, the membrane suffers loss of tension and undergoes continuous transition from the flat to wrinkled state, since the voltage monotonically increases with the charge. Experimentally, one can see that the entire membrane form wrinkles rapidly. As the voltage further increases to another critical voltage Φ* (such that the shaded regions are of equal area), the membrane undergoes discontinuous transition from a wrinkled state of a larger wavelength to that of a smaller wavelength. Experimentally, one can see that the membrane exhibits a dynamic pattern, and the wrinkles of different wavelengths move interchangeably on the surfaces.

Fig. 9 Schematic for continuous transition from the flat to wrinkled state, followed by discontinuous transition from one wrinkled to another wrinkled state.

In this paper, we report three types of phase transition in a circular membrane of a dielectric elastomer. Movie 1 (ESI†) and Fig. 2 show discontinuous transition from the flat to wrinkled state for a membrane with λ_pre = 3. Movie 3 (ESI†) and Fig. 5 show continuous transition from the flat to wrinkled state for a membrane with λ_pre = 4.5. Movie 5 (ESI†) and Fig. 8 show continuous transition from the flat to wrinkled state, followed by discontinuous transition from a wrinkled state of a larger wavelength to that of a smaller wavelength, for a membrane with λ_pre = 4. The above three types of phase transition are reminiscent of type I, II, and III transition, respectively, for a horizontally clamped membrane subjected to a vertical dead load.¹⁸ As shown in Fig. 12 of ref. 18, at any voltage ramp rate, a membrane with the same horizontal prestretch λ_2p undergoes type I, II or III phase transition when the vertical prestretch λ_1p is small, intermediate, or large, respectively. The critical vertical prestretch to separate the three types of transition depends on the voltage ramp rate.¹⁸ In this paper, a small ramp rate (20 V s⁻¹) is used to minimize the viscoelastic effect of the elastomer, and this circular membrane exhibits similar electromechanical behavior and undergoes three types of transition when the radial prestretch λ_pre = 3, 4, or 4.5, respectively. It should be noted that the third type of transition (as shown in Movie 5 (ESI†) and Fig. 8) cannot be predicted by using a theoretical model based on an elastic material (Fig. 6). As we know, in ref. 18, type III transition can be interpreted by using a viscoelastic material model. How viscoelasticity affects electromechanical phase transition (and dynamic patterns) in a circular membrane of a dielectric elastomer deserves further investigation.

Despite the similarity to a horizontally clamped membrane, this circular membrane exhibits a noticeable difference in electromechanical behavior, due to different boundary conditions. First, the wrinkled pattern becomes much more complex (the wrinkles in the horizontally clamped membrane are usually aligned vertically). What is more, the regions of smaller and larger stretches can move interchangeably on the surfaces when the membrane undergoes snap-through instability. This dynamic wrinkled pattern is especially distinct when the voltage is fixed at the critical value for phase transition (Movie 1 (ESI†) and Fig. 2). At this critical voltage, the ratio of the wrinkled to flat area depends on the total charges on the electrodes. In the current experiments, one cannot control the charges, and consequently the dynamic pattern of wrinkles looks random. Charge control can play a significant role in determining the electromechanical behavior of a dielectric elastomer actuator.^34–36 How to design boundary conditions of a dielectric elastomer and control its charges to achieve on-demand dynamic wrinkling patterns are interesting open questions, which can be utilized in antifouling technologies,³⁷ microfluidics,³⁸ and flexible electronics.³⁹ The experimental results along with the theoretical and finite element results advance our understanding of wrinkling behavior and phase transition in dielectric elastomers, which may pave the way for future applications utilizing these phenomena.

7. Concluding remarks

This paper investigates phase transition in a circular membrane of a dielectric elastomer. The radial prestretch is found to significantly affect its electromechanical behavior. The membrane with a small prestretch exhibits a dynamic pattern, and both the flat and wrinkled regions can move interchangeably on the surfaces at the onset of phase transition. This phase transition is discontinuous, accompanied by snap-through instability. On the other hand, the membrane with a large prestretch undergoes continuous transition from the flat to wrinkled state, averting snap-through instability. An analytical model is developed to interpret these experimental phenomena. Finite element simulations are performed to predict the wrinkle morphology, especially the coexistence of flat and wrinkled regions. Both the theoretical calculations and finite element simulations are qualitatively consistent with the experiments. Additionally, we report on another type of behavior, i.e., the membrane with an intermediate prestretch first undergoes continuous transition from the flat to wrinkled state, followed by discontinuous transition from a wrinkled state of a larger wavelength to that of a smaller wavelength. The membrane is observed to exhibit a dynamic pattern, in which wrinkles of different wavelengths move interchangeably on the surfaces. These results may inspire new applications for dielectric elastomers such as on-demand patterning of wrinkles for microfluidics and stretchable electronics.

Acknowledgements

H.G., U.G. and J.Z. thank MOE Tier 1, Singapore, for the support via grant numbers R-265-000-497-112 and R-265-000-558-112. Z.Q.Z. and C.C.F. acknowledge the support from A*STAR SERC (132 183 0025).

References

1. J. Oeffner and G. V Lauder, J. Exp. Biol., 2012, 215, 785–795.
2. K. Autumn, M. Sitti, Y. A. Liang, A. M. Peattie, W. R. Hansen, S. Sponberg, T. W. Kenny, R. Fearing, J. N. Israelachvili and R. J. Full, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12252–12256.
3. C. Greiner and M. Schäfer, Bioinspiration Biomimetics, 2015, 10, 044001.
4. J. Y. Chung, J. P. Youngblood and C. M. Stafford, Soft Matter, 2007, 3, 1163.
5. E. P. Chan, E. J. Smith, R. C. Hayward and A. J. Crosby, Adv. Mater., 2008, 20, 711–716.
6. K. Efimenko, J. Finlay, M. E. Callow, J. A. Callow and J. Genzer, ACS Appl. Mater. Interfaces, 2009, 1, 1031–1040.
7. D.-Y. Khang, H. Jiang, Y. Huang and J. A. Rogers, Science, 2006, 311, 208–212.
8. R. Pelrine, R. Kornbluh, Q. Pei and J. Joseph, Science, 2000, 287, 836–839.
9. F. Carpi, S. Bauer and D. De Rossi, Science, 2010, 330, 1759–1761.
10. S. Ashley, Sci. Am., 2003, 289, 52–59.
11. H. Godaba, J. Li, Y. Wang and J. Zhu, IEEE Robot. Autom. Lett., 2016, 1, 624–631.
12. Y. Wang and J. Zhu, Extreme Mechanics Letters, 2016, 6, 88–95.
13. J. Shintake, S. Rosset, B. Schubert, D. Floreano and H. Shea, Adv. Mater., 2015, 28, 231–238.
14. J.-S. Plante and S. Dubowsky, Int. J. Solids Struct., 2006, 43, 7727–7751.
15. C. Keplinger, M. Kaltenbrunner, N. Arnold and S. Bauer, Appl. Phys. Lett., 2008, 92, 192903.
16. J. Zhou, W. Hong, X. Zhao, Z. Zhang and Z. Suo, Int. J. Solids Struct., 2008, 45, 3739–3750.
17. J. Zhu, M. Kollosche, T. Lu, G. Kofod and Z. Suo, Soft Matter, 2012, 8, 8840–8846.
18. M. Kollosche, G. Kofod, Z. Suo and J. Zhu, J. Mech. Phys. Solids, 2015, 76, 47–64.
19. R. Huang and Z. Suo, Proc. R. Soc. A, 2011, 468, 1014–1040.
20. G. Mao, X. Huang, M. Diab, T. Li, S. Qu and W. Yang, Soft Matter, 2015, 11, 6569–6575.
21. T. Q. Lu and Z. G. Suo, Acta Mech. Sin., 2012, 28, 1106–1114.
22. T. Lu, L. An, J. Li, C. Yuan and T. J. Wang, J. Mech. Phys. Solids, 2015, 85, 160–175.
23. M. Kollosche, J. Zhu, Z. Suo and G. Kofod, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 051801.
24. E. Cerda and L. Mahadevan, Phys. Rev. Lett., 2003, 90, 074302.
25. X. Zhao, W. Hong and Z. Suo, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 134113.
26. G. Kofod, P. Sommer-Larsen, R. Kornbluh and R. Pelrine, J. Intell. Mater. Syst. Struct., 2003, 14, 787–793.
27. Z. Suo, Acta Mech. Solida Sin., 2010, 23, 549–578.
28. S. J. A. Koh, T. Li, J. Zhou, X. Zhao, W. Hong, J. Zhu and Z. Suo, J. Polym. Sci., Part B: Polym. Phys., 2011, 49, 504–515.
29. A. N. Gent, Rubber Chem. Technol., 1996, 69, 59–61.
30. X. Zhao and Z. Suo, Appl. Phys. Lett., 2007, 91, 061921.
31. Z. Suo, X. Zhao and W. H. Greene, J. Mech. Phys. Solids, 2008, 56, 467–486.
32. X. Zhao and Z. Suo, Appl. Phys. Lett., 2008, 93, 251902.
33. C. C. Foo and Z.-Q. Zhang, Int. J. Appl. Mech. Eng., 2015, 7, 1550069.
34. C. Keplinger, M. Kaltenbrunner, N. Arnold and S. Bauer, Proc. Natl. Acad. Sci. U.S. A., 2010, 107, 4505–4510.
35. B. Li, J. X. Zhou and H. L. Chen, Appl. Phys. Lett., 2011, 99, 244101.
36. T. Q. Lu, C. Keplinger, N. Arnold, S. Bauer and Z. Suo, Appl. Phys. Lett., 2014, 104, 022905.
37. A. K. Epstein, D. Hong, P. Kim and J. Aizenberg, New J. Phys., 2013, 15, 095018.
38. K. Efimenko, M. Rackaitis, E. Manias, A. Vaziri, L. Mahadevan and J. Genzer, Nat. Mater., 2005, 4, 293–297.
39. C. Yu, C. Masarapu, J. Rong, B. Wei and H. Jiang, Adv. Mater., 2009, 21, 4793–4797.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sm00198c

---