 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Front microrheology of the non-Newtonian behaviour of blood: scaling theory of erythrocyte aggregation by aging
C.
Trejo-Soto
ab,
E.
Costa-Miracle
 bcd,
I.
Rodriguez-Villarreal
b,
J.
Cid
e,
M.
Castro
f,
T.
Alarcon
bcdg and
A.
Hernandez-Machado
bcd,
I.
Rodriguez-Villarreal
b,
J.
Cid
e,
M.
Castro
f,
T.
Alarcon
bcdg and
A.
Hernandez-Machado
 *abdh
*abdh
aDepartament de Física de la Matèria Condensada, Facultat de Física, Universitat de Barcelona, Diagonal 645, E-08028 Barcelona, Spain. E-mail: a.hernandezmachado@gmail.com
bCentre de Recerca Matemàtica, Edifici C, Campus de Bellaterra, 08193 Bellaterra, Barcelona, Spain
cDepartament de Matemàtiques, Universitat Autònoma de Barcelona, 08193 Bellaterra, Barcelona, Spain
dBarcelona Graduate School of Mathematics (BGSMath), Barcelona, Spain
eServicio de Hemoterapia y Hemostasia, Hospital Clinic de Barcelona, Barcelona, Spain
fGISC and Grupo de Dinámica No Lineal (DNL), Escuela Técnica Superior de Ingeniería (ICAI), Universidad Pontificia Comillas, E-28015 Madrid, Spain
gICREA, Pg. Llus Companys 23, 08010 Barcelona, Spain
hInstitute of Nanoscience and Nanotechnology (IN2UB), Universitat de Barcelona, Barcelona, Spain
First published on 27th March 2017
Abstract
We introduce a new framework to study the non-Newtonian behaviour of fluids at the microscale based on the analysis of front advancement. We apply this methodology to study the non-linear rheology of blood in microchannels. We carry out experiments in which the non-linear viscosity of blood samples is quantified at different haematocrits and ages. Under these conditions, blood exhibits a power-law dependence on the shear rate. In order to analyse our experimental data, we put forward a scaling theory which allows us to define an adhesion scaling number. This theory yields a scaling behaviour of the viscosity expressed as a function of the adhesion capillary number. By applying this scaling theory to samples of different ages, we are able to quantify how the characteristic adhesion energy varies as time progresses. This connection between microscopic and mesoscopic properties allows us to estimate quantitatively the change in the cell–cell adhesion energies as the sample ages.
1 Introduction
The non-linear microrheology of several types of complex fluids has attracted a great deal of attention in recent times,1–3 particularly regarding the properties of a number of complex biological fluids.4–9 In spite of a wealth of studies regarding the physical characterisation of blood,10–13 the characterisation of its microrheological properties is a much more open field of study. The non-linear rheological properties of blood are mainly determined by the presence of red blood cells (RBCs) suspended in plasma.14–17 Some haematological pathologies have been associated with blood rheological properties such as viscosity, as for example the hyperviscosity syndrome, which is a set of symptoms triggered by an increase in blood viscosity,18 resulting in vascular occlusion,19 particularly in the microcirculation. These symptoms are observed in sickle cell anemia due to loss of deformability of red blood cells.20 It has been observed that severe malaria also produces the symptoms associated with hyperviscosity syndrome.21,22 Based on this concept, new avenues have opened for the diagnosis of haematological pathologies based on the analysis of the microrheological properties of blood.Advances in experimental approaches to the rheological properties of blood are starting to be complemented by quantitative modelling, both theoretical and computational. A number of studies have focused on the role of red blood cell (RBC) elasticity.23–30 Further to the role of RBC elasticity, Fedosov et al.14 analysed the role of RBC aggregation in blood rheology which has emerged as a fundamental ingredient to understand the non-Newtonian behaviour of blood. In this paper, we present the experimental results and develop a theoretical framework which allows us to further explore the role of RBC aggregation in the non-linear rheology of blood. We have carried out experiments at the microscale using a device aimed to track the dynamics of blood in microchannels. Working at that scale our setup has two main advantages. First, micro-fabrication allows for improved control of the fluid-flow conditions at a very low cost and using microliter-sized blood samples.31–33 Second, our microfluidic device allows us to directly track the advancement of the air–blood interface using an optical microscope.
Our main contribution is to develop a scaling theory of the non-linear viscosity which allows us to account for the effects of aging on the aggregation of RBCs. To this end, we define an adhesion scaling number and obtain a scaling behaviour whereby the viscosity exhibits a power-law dependence on the capillary number. The adhesion number represents how the characteristic energy of aggregation between RBCs varies as age progresses. This framework provides a new methodology to characterise the rheology of non-Newtonian fluids based on the dynamics of the fluid–air interface. We dub this new concept front microrheology. In order to achieve this, we characterise a hydrodynamic regime in which the fluid–air interface moves at constant velocity. This regime is different from the usual approach (Washburn regime) in which the front velocity is a decreasing function of time. The analysis presented in this paper is a generalisation to non-Newtonian fluids of the one presented in ref. 34. In particular, we define a new quantity associated with this non-Washburn regime, the front shear rate, which allows us to characterise the non-linear rheology of non-Newtonian fluids.
2 Experimental set-up and measurements
Our experimental setup (see Fig. 1) is designed such that we can characterise the non-linear rheology of blood through the advancement of the blood–air interface. The position of the advancing interface, h(t), is recorded by means of an inverted microscope Optika XDS-3 with an objective of magnitude 4×. The images are recorded using a high speed camera Photron Fastcam Viewer 3 with a capture frame rate between 60 and 125 frames per second. The position uncertainty is determined by the size of the pixel. In our case, it is δh = 7.2 μm over a 5 mm measured distance. A constant pressure drop is imposed by using a container located at a height H with respect to the position of the microchannel. This container is connected to the microsystem by a microtube of a biocompatible material with a uniform internal circular cross-section of radius r = 0.127 mm and length lt = 0.430 m. The microsystem is a rectangular microchannel of height b = 350 μm, width w = 1 mm, and length lc = 4 cm. The cross-section of our tube and the hydraulic diameter of the microchannel, Dh = 0.52 ± 0.02 mm, are both typical of large arterioles and venules. The typical magnitude of the flow rate, Q, in our experiments is Q = 6 μl min−1. This flow rate is of the same order of magnitude as the one measured in capillaries.35 Within this experimental set-up, the wall shear rate of the tube, defined as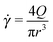 , varies within the range from 4.69 to 131.90 s−1. The microchannel is molded in a biocompatible hydrophobic silicone, PDMS (polydimethylsiloxane), on a glass substrate according to replica moulding and soft lithography microfabrication methods.34,36 The bottom surface of the microchannel is made of glass and the top and lateral surfaces are made of PDMS. In our experiments, we use human blood of varying ages (defined as the time elapsed since extraction) and haematocrits (the volume fraction occupied by the RBCs).
, varies within the range from 4.69 to 131.90 s−1. The microchannel is molded in a biocompatible hydrophobic silicone, PDMS (polydimethylsiloxane), on a glass substrate according to replica moulding and soft lithography microfabrication methods.34,36 The bottom surface of the microchannel is made of glass and the top and lateral surfaces are made of PDMS. In our experiments, we use human blood of varying ages (defined as the time elapsed since extraction) and haematocrits (the volume fraction occupied by the RBCs).
 | ||
| Fig. 1 Schematic representation of our experimental setup. An open reservoir at height H pumps fluid into the microchannel through a tube of radius r and length lt. | ||
Blood samples were obtained from anonymous donors randomly selected. Blood samples for our experiments were delivered by the blood bank of the Hematology Department of the Clinical Hospital of Barcelona, in 10 or 5 ml tubes with a heparin based anticoagulant. The use of these samples was authorised by the Bioethics Committee of the University of Barcelona. In order to preserve the state of the samples they were stored in a refrigerator at 4 °C. Before any intervention, the samples were placed under an extraction hood to acquire room temperature, between 21 ± 1 °C. For each blood sample, we performed 2 different measurements, on each occasion we carried out 5 repetitions at each different pressure value.
The results obtained using the setup shown in Fig. 1 are summarised in Fig. 2, where we show how the front velocity, ḣ, varies as the effective pressure changes. The effective pressure is defined as ρgH − PL, where ρ is the blood density and PL is the capillary pressure. We have calculated the capillary pressure based on the experimental determination of the contact angle, θ, from the images of the advancing front using the well-known formula:
 | (1) |
As shown in Fig. 2, the effective pressure exhibits a power-law dependence on ḣ, with the precise slope and location of the curve being dependent on the haematocrit and the age of the sample. Interestingly, for blood at 48% haematocrit, regardless of the age of the sample, our experiments display two regimes: one at low velocity with n ⋍ 0.70, and another at higher velocity with n ⋍ 1, in the same fashion as plasma alone (see Table 1). By contrast, blood with a reduced haematocrit (25%) has n ⋍ 1 in the whole range and regardless of the age of the sample. This suggests that aging effects may be strongly dependent on the haematocrit.
| Haematocrit | Exponent 1 (n−1) | Prefactor m |
|---|---|---|
| 48% 1d (low shear rate) | −0.29 | 0.01190 |
| 48% 5d (low shear rate) | −0.31 | 0.02030 |
| 48% 1d (high shear rate) | −0.12 | 0.00830 |
| 48% 5d (high shear rate) | −0.16 | 0.01096 |
| 38% 1d | −0.07 | 0.00315 |
| 38% 5d | −0.12 | 0.00407 |
| 25% 2d | −0.004 | 0.00265 |
| 25% 6d | −0.01 | 0.00256 |
| Plasma | 0 | 0.00152 |
3 Mathematical model
In order to rationalise the set of experiments presented above, we need to formulate a model which allows us to derive the expression of viscosity as a function of the setup parameters. In particular, we consider non-Newtonian fluids with power-law behaviour, i.e.η(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (z)) = m( (z)) = m(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) (z))n−1 (z))n−1 | (2) |
 is the shear rate, n is a constant which depends on the fluid and m depends on n. In the special case n = 1, the fluid is Newtonian and m is, directly, the viscosity of the fluid (so, only in that case, it has units of Pa s). Although power-law models are only accurate for intermediate shear rates,37Fig. 2 shows that it may accurately capture our working regime.
is the shear rate, n is a constant which depends on the fluid and m depends on n. In the special case n = 1, the fluid is Newtonian and m is, directly, the viscosity of the fluid (so, only in that case, it has units of Pa s). Although power-law models are only accurate for intermediate shear rates,37Fig. 2 shows that it may accurately capture our working regime.
Using eqn (2), we can use the Navier–Stokes equation to derive a non-Newtonian Darcy equation associated with the advancement of the fluid front:
 | (3) |
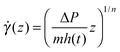 | (4) |
 | (5) |
 | (6) |
 | (7) |
 | (8) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) F(n), associated with the advancement of the front:
F(n), associated with the advancement of the front: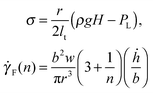 | (9) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) F, which we refer to as the front shear rate, is central to our analysis, as it allows a characterisation of the non-linear rheology in terms of the average front velocity, as opposed to the local definition of the shear rate, commonly used in other approaches. We can now define a viscosity associated with the dependence of the rescaled pressure, σ, on the shear rate: σ = η(
F, which we refer to as the front shear rate, is central to our analysis, as it allows a characterisation of the non-linear rheology in terms of the average front velocity, as opposed to the local definition of the shear rate, commonly used in other approaches. We can now define a viscosity associated with the dependence of the rescaled pressure, σ, on the shear rate: σ = η(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) F)
F)![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) F = m
F = m![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) nF, where η(
nF, where η(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) F) is given by:
F) is given by:η(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) F) = m F) = m![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) Fn−1 Fn−1 | (10) |
4 Results
4.1 Non-linear rheology
Following eqn (7) we determine under which experimental conditions we can consider that the advancement of the fluid front occurs at constant velocity. Such conditions are given in terms of the geometry of our setup and we make sure that they are fulfilled during our experiments. Furthermore, we can measure the velocity of the front as a function of the pressure drop. We then simply change the pressure drop by changing the height of the reservoir, H.In Fig. 3, we show how the blood viscosity varies as the shear rate, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) F(n), changes. These results are associated with the ones shown in Fig. 2. We observe that our experimental results fit within our power-law ansatz eqn (10). The values of the parameters m and n are given in Table 1. Although our results for the variation of viscosity as the front shear rate changes extend over one order of magnitude only, we note that our set-up allows for an extension of this range by merely changing the gap of the microchannel, b, as shown in eqn (9). The values obtained for viscosity, within the studied range of front shear rate, are very similar to those obtained by Cockelet et al.10
F(n), changes. These results are associated with the ones shown in Fig. 2. We observe that our experimental results fit within our power-law ansatz eqn (10). The values of the parameters m and n are given in Table 1. Although our results for the variation of viscosity as the front shear rate changes extend over one order of magnitude only, we note that our set-up allows for an extension of this range by merely changing the gap of the microchannel, b, as shown in eqn (9). The values obtained for viscosity, within the studied range of front shear rate, are very similar to those obtained by Cockelet et al.10
 | ||
Fig. 3 Plot showing how the viscosity of blood varies as a function of the front shear rate, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) F, for samples of different ages. We observe that as the sample ages, its viscosity increases. These results are associated with the experiments shown in Fig. 2. They have been obtained by using eqn (9) and (10). F, for samples of different ages. We observe that as the sample ages, its viscosity increases. These results are associated with the experiments shown in Fig. 2. They have been obtained by using eqn (9) and (10). | ||
4.2 Scaling theory of aging effects
We start our analysis by addressing the effects of aging on blood viscosity. Fig. 4(a) and (b) show that, as the sample ages, RBCs organise themselves into structures called rouleaux. Simulation results reported in ref. 14 have shown that the aggregation of RBCs into such structures affects the rheological properties of blood. Our experimental results (Fig. 4(a) and (b)) show that rouleaux appear due to aging of the samples, whereby we put forward that aging also affects blood viscosity.To analyse the effects of aging, we fix the value of the haematocrit and study the behaviour of the blood sample as it ages. We introduce a new, non-linear scaling parameter, the adhesion scaling number, A, which quantifies the effects of aging on RBC aggregation. This quantity is defined as:
 | (11) |
Our scaling ansatz claims that the viscosity, η, depends on the adhesion scaling number, A, alone:
 | (12) |
Fig. 5 shows the results for two different haematocrit values. These results show that our scaling ansatz can accurately account for the variation of viscosity with age. In particular, we observe that at lower values of the adhesion number, A, the effects of aging are more important than at higher values of A (see Fig. 5, 48% haematocrit sample). This behaviour is associated with the formation of rouleaux at low A (see Fig. 4(a) and (b)). We have also analysed a different sample with a lower haematocrit (see Fig. 5, 38% haematocrit sample), for which we only studied the larger A regime, in which we also find aging effects. The corresponding value of ka is very similar in both samples for the same range of values of the adhesion number A, which shows that our assumption that ka depends only on age and n holds (see Table 1).
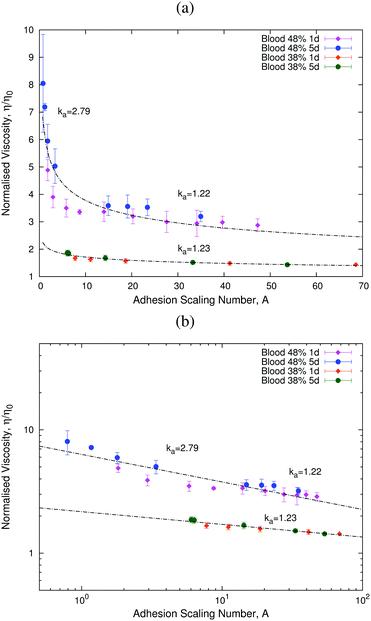 | ||
| Fig. 5 Plots showing how the normalised viscosity, η/η0, follows a universal curve as the adhesion scaling number (eqn (11)) changes. Panel (b) shows that this universal curve is well-described by a power-law in agreement with eqn (12). | ||
One could argue that the effects of varying the temperature could be important. We consider that changing the temperature would impact only the adhesion energy scale in eqn (10) and the viscosity of plasma, η0. However, since the estimated adhesion energy scale is 500 kBT, i.e. orders of magnitude higher than the thermal energy, we posit that the effects of temperature of RBC adhesion are likely to be negligible, and, therefore, the scaling behaviour described in this work should be robust to temperature changes. That is not to say that absolute values of viscosity will stay unchanged.
5 Discussion and conclusions
In this paper, we propose a new microrheological theory based on two fundamental points. First, we characterise a hydrodynamic regime in which the fluid–air interface moves at constant velocity. This regime is different from the usual approach in which the front velocity is a decreasing function of time. We then proceed to derive the appropriate physical description of the process within this regime. The former is achieved by using eqn (7). The usual set-up, from which Washburn's regime is obtained, involves neglecting the first term in the denominator, thus yielding a system where the front moves at a time-dependent speed. By contrast, our set-up operates within the regime where the first term in the denominator is the dominant one. By neglecting the part inducing time-dependence, we arrive at eqn (8) which allows us to define the new quantities associated with this particular regime: the front shear rate,![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) F, and the re-scaled pressure, σ. Finally, we define the viscosity as a function of the front shear rate as per eqn (10).
F, and the re-scaled pressure, σ. Finally, we define the viscosity as a function of the front shear rate as per eqn (10).
We have shown that variations in the non-linear viscosity of blood associated with aging can be explained by means of a scaling theory based on the introduction of an adhesion scaling number (eqn (11)). This quantity is defined as the ratio between the viscous energy and the aggregation energy. Our scaling theory allows us to quantify the increase in aggregation energy by aging with respect to its reference characteristic scale, E0, by providing an estimation of the fold increase in E0, ka. Note that further to its dependence on age, ka is also a function of the shear rate. This reflects the fact that, at low shear rates, RBC aggregates are more likely to form. We further show that the viscosity exhibits a power-law behaviour over almost two orders of magnitude as a function of the scaling parameter A. We observe that blood exhibits a non-Newtonian behaviour at large haematocrits, which, at the shear rate scales of our experiments, is associated with aggregation of RBCs. These results allow us to better characterise the non-linear microrheological behaviour of blood.
The strength of our approach comes from the use of a front microrheometer that allows us to extract bulk non-linear viscosities from the simple observation of a moving air–fluid interface. This framework allows us to develop a non-linear microrheometer.
Acknowledgements
C. T.-S. and A. H.-M. gratefully acknowledge partial financial support from MINECO (Spain) under projects FIS2013-47949-C01-01-P and FIS2016-78883-C2-1-P, and AGAUR project 2014SGR-878 and M. C. under projects FIS2013-47949-C01-02-P and FIS2016-78883-C2-2-P. E. C.-M., I. R.-V., and T. A. gratefully acknowledge the Spanish Ministry for Science and Innovation (MICINN) for funding under grants MTM2015-71509-C2-1-R and Generalitat de Catalunya for funding under grant 2014SGR1307. E. C.-M. and T. A. acknowledge support from the Ministry of Economy & Competitivity (MINECO) for funding awarded to the Barcelona Graduate School of Mathematics under the “Maria de Maeztu” programme, grant number MDM-2014-0445. E. C.-M. acknowledges funding from MINECO through the scholarship BES-2015-072365. C. T.-S. acknowledges CONICYT the Chilean Ministry of Education for funding PhD Fellowship, Becas Chile.References
- T. M. Squires and T. G. Mason, Annu. Rev. Fluid Mech., 2010, 42, 413–438 CrossRef.
- M. Aytouna, J. Paredes, N. Shahidzadeh-Bonn, S. Moulinet, C. Wagner, Y. Amarouchene, J. Eggers and D. Bonn, Phys. Rev. Lett., 2013, 110, 034501 CrossRef PubMed.
- A. V. Ivlev, V. Steinberg, R. Kompaneets, H. Hofner, I. Sidorenko and G. E. Morfill, Phys. Rev. Lett., 2007, 98, 145003 CrossRef CAS PubMed.
- M. L. Gardel and D. A. Weitz, Microscale Diagnostic Techniques, Springer, Berlin, 2005 Search PubMed.
- D. Weihs, T. G. Mason and M. A. Teitell, Biophys. J., 2006, 91, 4296–4305 CrossRef CAS PubMed.
- D. Wirtz, Annu. Rev. Biophys., 2009, 38, 301–326 CrossRef CAS PubMed.
- A. Lindner, Phys. Fluids, 2014, 26, 101307 Search PubMed.
- J. Gachelin, G. Mino, H. Berthet, A. Lindner, A. Rousselet and E. Clement, Phys. Rev. Lett., 2013, 110, 268103 Search PubMed.
- T. G. Mason, K. Ganesan, J. H. van Zanten, D. Wirtz and S. C. Kuo, Phys. Rev. Lett., 1997, 79, 3282 Search PubMed.
- G. R. Cockelet, E. W. Merrill, E. R. Gilliland, H. Shin, A. Britten and R. E. Wells, Trans. Soc. Rheol., 1963, 7, 303–317 Search PubMed.
- S. Chien, S. Usami and J. F. Bertles, J. Clin. Invest., 1970, 49, 623–634 Search PubMed.
- A. R. Pries, D. Neuhaus and P. Gaehtgens, Am. J. Physiol.: Heart Circ. Physiol., 1992, 263, H1770–H1778 CAS.
- G. B. Thurston and N. M. Henderson, Biorheology, 2006, 43, 729–746 Search PubMed.
- D. A. Fedosov, W. Pan, B. Caswell, G. Gompper and G. E. Karniadakis, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 11772–11777 CrossRef CAS PubMed.
- M. Brust, C. Schaefer, R. Doerr, L. Pan, M. Garcia, P. E. Arratia and C. Wagner, Phys. Rev. Lett., 2013, 110, 078305 CrossRef CAS PubMed.
- D. P. Monroe, J. Phys., 2013, 6, 18 Search PubMed.
- M. Thiebaud, Z. Shen, J. Harting and C. Misbah, Phys. Rev. Lett., 2014, 112, 238304 CrossRef PubMed.
- H. Kwaan and A. Bongu, Semin. Thromb. Hemostasis, 1999, 25, 199–208 CrossRef CAS PubMed.
- J. M. Higgins, D. T. Eddington, L. Mahadevan and S. N. Bhatia, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 20496 CrossRef CAS PubMed.
- D. K. Wood, A. Soriano, L. Mahadevan, J. M. Higgins and S. N. Bhatia, Sci. Transl. Med., 2012, 4, 123ra26 Search PubMed.
- V. Sitprija, M. Vongsthongsri, V. Poshyachinda and S. Arthachinta, Nephron, 1977, 18, 277–287 CrossRef CAS PubMed.
- J. P. Shelby, J. White, K. Ganesan and D. T. Chiu, Proc. Natl. Acad. Sci. U. S. A., 2007, 100, 14168 Search PubMed.
- Y. Park, C. A. Best, K. Badizadegan, R. R. Dasari, M. S. Feld, T. Kuriabova, M. L. H. A. J. Levine and G. Popescu, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 6731–6736 CrossRef CAS PubMed.
- Y. Park, C. A. Best, T. Auth, N. S. Gov, S. A. Safran, G. Popescu, S. Suresh and M. S. Feld, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 1289–1294 CrossRef CAS PubMed.
- B. Kaoui, G. Biros and C. Misbah, Phys. Rev. Lett., 2009, 103, 188101 CrossRef PubMed.
- H. Noguchi and G. Gomper, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 14159–14164 CrossRef CAS PubMed.
- J. L. McWhirter, H. Noguchi and G. Gomper, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 6039–6043 CrossRef CAS PubMed.
- G. R. Lazaro, A. Hernandez-Machado and I. Pagonabarraga, Soft Matter, 2014, 10, 7195 RSC.
- G. R. Lazaro, A. Hernandez-Machado and I. Pagonabarraga, Soft Matter, 2014, 10, 7207 RSC.
- T. Savin, M. M. Bandi and L. Mahadevan, Soft Matter, 2016, 12, 562–573 RSC.
- G. Whitesides, Nature, 2006, 442, 368–373 CrossRef CAS PubMed.
- P. Nghe, G. Degre, P. Tabeling and A. Ajdari, Appl. Phys. Lett., 2008, 93, 204102 CrossRef.
- P. Nghe, S. M. Fielding, P. Tabeling and A. Ajdari, Phys. Rev. Lett., 2010, 104, 248303 CrossRef CAS PubMed.
- C. Trejo-Soto, E. Costa-Miracle, I. Rodriguez-Villarreal, J. Cid, T. Alarcon and A. Hernandez-Machado, PLoS One, 2016, 11, e0153559 CAS.
- W. W. Nichols, M. F. ORourke and C. Vlachopoulos, McDonald's blood flow in arteries, Hodder Arnold, USA, 2011 Search PubMed.
- J. C. McDonald, D. C. Duffy, J. R. Anderson, D. T. Chiu, H. Wu, O. J. Schueller and G. M. Whitesides, Electrophoresis, 2000, 21, 27 CrossRef CAS PubMed.
- F. A. Morrison, Understanding rheology, Oxford University Press, USA, 2001 Search PubMed.
- G. Késmárky, P. Kenyeres, M. Rábai and K. Tóth, Clin. Hemorheol. Microcirc., 2008, 39, 243–246 Search PubMed.
| This journal is © The Royal Society of Chemistry 2017 |


