Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Universal wetting transition of an evaporating water droplet on hydrophobic micro- and nano-structures†
Adrien
Bussonnière
ab,
Masoud B.
Bigdeli
 a,
Di-Yen
Chueh
c,
Qingxia
Liu
b,
Peilin
Chen
c and
Peichun Amy
Tsai
a,
Di-Yen
Chueh
c,
Qingxia
Liu
b,
Peilin
Chen
c and
Peichun Amy
Tsai
 *a
*a
aDepartment of Mechanical Engineering, University of Alberta, Edmonton, AB T6G 1H9, Canada. E-mail: peichun.amy.tsai@ualberta.ca; Fax: +1 780-492-2200; Tel: +1 780-492-5425
bDepartment of Chemical and Materials Engineering, University of Alberta, Edmonton, AB T6G 1H9, Canada
cApplied Sciences, Academia Sinica, 128 Section 2, Academia Road, Nankang, Taipei 11529, Taiwan
First published on 22nd December 2016
Abstract
Water-repellent, rough surfaces have a remarkable and beneficial wetting property: when a water droplet comes in contact with a small fraction of the solid, both liquid–solid adhesion and hydrodynamic drag are reduced. As a prominent example from nature, the lotus leaf—comprised of a wax-like material with micro- and nano-scaled roughness—has recently inspired numerous syntheses of superhydrophobic substrates. Due to the diverse applications of superhydrophobicity, much research has been devoted to the fabrication and investigations of hydrophobic micro-structures using established micro-fabrication techniques. However, wetting transitions remain relatively little explored. During evaporation, a water droplet undergoes a wetting transition from a (low-frictional) partial to (adhesive) complete contact with the solid, destroying the superhydrophobicity and the self-cleaning properties of the slippery surface. Here, we experimentally examine the wetting transition of a drying droplet on hydrophobic nano-structures, a previously unexplored regime. In addition, using a theoretical analysis we found a universal criterion of this wetting transition that is characterized by a critical contact angle. Different from previous results showing different critical droplet sizes, our results show a universal, geometrically-dependent, critical contact angle, which agrees well with various data for both hydrophobic micro- and nano-structures.
1 Introduction
Because of their promising applications for micro- and nano-fluidic devices,1–5 condensation heat transfer systems,6,7 friction control,8–12 self-cleaning13,14 and icephobic functionality,15,16 there is currently significant interest in the wetting states on patterned hydrophobic substrates that form the so-called superhydrophobic surfaces.17,18 Despite these intriguing and useful applications, the large-scale implementation of superhydrophobic surfaces with robust non-wetting properties has remained challenging because an irreversible wetting transition can occur, destroying a gas-trapping state. For instance, various experiments, theoretical modeling, and numerical simulations have demonstrated that evaporation can naturally induce a wetting transition from an air-trapping Cassie–Baxter state (CB or the so-called “Fakir”)19,20 to a completely wetting Wenzel (W)21 state on superhydrophobic substrates.22–30Different techniques have been developed in response to prevent the transition to the complete wetting state. These methods vary from altering the geometrical and chemical properties of the surfaces31–37 to stimulating substrates with light, heat, electric potential or mechanical vibration.38–41 The fabrication of extremely robust superhydrophobic surfaces is still very active. An advantageous CB state, albeit metastable, may be achieved by tuning the aspect ratio and the packing density of the pillars.22,24 Hence, finer textures at the nano-scale may be favorable for durable superhydrophobicity. Insofar, only a few studies have been performed to elucidate the influence of the nano-textured surfaces on the wetting behavior of an evaporating droplet.31,36,42 This pioneering work used (hierarchical) nano-grass structures, and the critical conditions for the CB to Wenzel wetting transition using nano-structures have not been concluded.
In this paper, using both theory and experiment, we elucidate the evaporation dynamics, wetting state and transition of small droplets on regular nano-structures. Systematic measurements of the evaporation rate, droplet contact angle and radius, and critical transition points were conducted for various nano-patterns. Owing to the nano-structuring, for the first time, we were able to investigate extremely dilute structures and high aspect ratio pillars. Our results highlight the interplay between the geometrical properties and the universality of the critical contact angle at the CB to W wetting transition for both hydrophobic micro- and nano-structured substrates.
2 Experimental
2.1 Sample preparation
To prepare nano-patterned silicon (Si) molds, the surfaces of the (100)-oriented Si wafers were cleaned by sonication in acetone and ethanol at room temperature for 10 and 5 min, respectively. The Si substrates were then placed in the boiling Piranha solution [H2SO4/H2O2, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v)] and RCA solution [NH3/H2O2/H2O, 1
1 (v/v)] and RCA solution [NH3/H2O2/H2O, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 (v/v/v)] for 1 h each and then rinsed several times with deionized water. The cleaned Si wafers were spin-coated with a photoresist (TMHR ip3650, TOK) and then patterned using I-line projection photolithography (FPA-3000i5+ Stepper, Canon). The designed metal masks with 200 nm or 400 nm square array patterns and a periodicity P (ranging from 800 nm to 2 μm) were applied. After the development of the photoresist, Si micro/nanopillar arrays were formed through inductively coupled plasma dry etching (ICP; MESC Multiplex, STS) with 600 W power and 11.5 W bias power, when two working gases per duty cycle were used (25 sccm of SF6 for 7 s; 75 sccm of C4F8 for 7 s). The height of the Si micro/nanopillar arrays could be tuned by changing the etching time. The height of the nano-pillars, H, is 1 or 2 μm. The remaining photoresist was removed in boiling Piranha solution [H2SO4/H2O2, 4
5 (v/v/v)] for 1 h each and then rinsed several times with deionized water. The cleaned Si wafers were spin-coated with a photoresist (TMHR ip3650, TOK) and then patterned using I-line projection photolithography (FPA-3000i5+ Stepper, Canon). The designed metal masks with 200 nm or 400 nm square array patterns and a periodicity P (ranging from 800 nm to 2 μm) were applied. After the development of the photoresist, Si micro/nanopillar arrays were formed through inductively coupled plasma dry etching (ICP; MESC Multiplex, STS) with 600 W power and 11.5 W bias power, when two working gases per duty cycle were used (25 sccm of SF6 for 7 s; 75 sccm of C4F8 for 7 s). The height of the Si micro/nanopillar arrays could be tuned by changing the etching time. The height of the nano-pillars, H, is 1 or 2 μm. The remaining photoresist was removed in boiling Piranha solution [H2SO4/H2O2, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v)]. Finally, the nano-patterned Si wafers were diced, cleaned with Piranha, and hydrophobized using trichloro(1,1,2,2-perfluroocytl)-silane.
1 (v/v)]. Finally, the nano-patterned Si wafers were diced, cleaned with Piranha, and hydrophobized using trichloro(1,1,2,2-perfluroocytl)-silane.
The superhydrophobic surfaces consist of nano-scale cylindrical pillars in a square lattice. We investigated a variety of nano-textures, by varying the periodicity P (from 0.8 to 2 μm), the post diameter D (200 and 400 nm) and the pillar height H (1 and 2 μm) (see the SEM images in Fig. 1a and Fig. S1, (ESI†)). The original silica surfaces were coated with a hydrophobic layer using trichloro(1,1,2,2-perflurocytl)-silane, leading to a contact angle of 115° on the smooth surface. The nano-structures were characterised with two crucial geometrical parameters: surface roughness 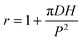 , the ratio of the actual to the apparent surface area, and the solid fraction
, the ratio of the actual to the apparent surface area, and the solid fraction 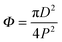 , corresponding to the packing fraction of the nano-pillars. In other words, r describes the relative change in the liquid/solid area compared to a flat surface in a Wenzel state;21Φ quantifies the percentage of the liquid–solid contact area in a Cassie–Baxter case.19 Our regular nano-patterned surfaces have a small packing fraction, 0.0079 ≤ Φ ≤ 0.20, and a wide range of roughness, 1.1 ≤ r ≤ 4.92.
, corresponding to the packing fraction of the nano-pillars. In other words, r describes the relative change in the liquid/solid area compared to a flat surface in a Wenzel state;21Φ quantifies the percentage of the liquid–solid contact area in a Cassie–Baxter case.19 Our regular nano-patterned surfaces have a small packing fraction, 0.0079 ≤ Φ ≤ 0.20, and a wide range of roughness, 1.1 ≤ r ≤ 4.92.
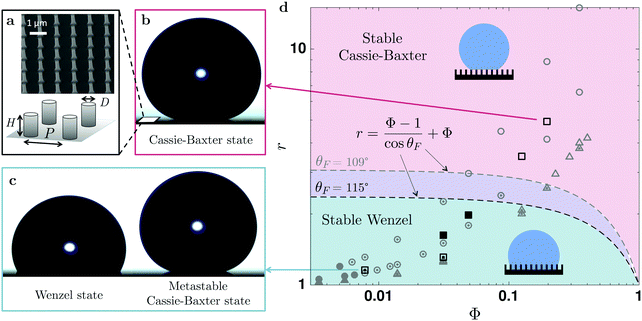 | ||
Fig. 1 Initial wetting state. (a) A scanning electron micrograph and a schematic representation of the hydrophobic nano-structures, whose geometric parameters are revealed by □,  , ■ in the phase space of surface roughness, r, and the packing fraction of nano-pillars, Φ, in (d). Using an energetic argument,44 the phase space shown in (d) can be divided in a stable Cassie–Baxter (CB) state domain (in red) and a stable Wenzel state region (in blue). The previous experimental data by Barbieri et al.,45 ( , ■ in the phase space of surface roughness, r, and the packing fraction of nano-pillars, Φ, in (d). Using an energetic argument,44 the phase space shown in (d) can be divided in a stable Cassie–Baxter (CB) state domain (in red) and a stable Wenzel state region (in blue). The previous experimental data by Barbieri et al.,45 ( , ,  , ,  ) and Jung et al.,23 ( ) and Jung et al.,23 ( , ,  , ,  ) using microstructures are also plotted for a comparison. Due to the different contact angles on the smooth surfaces (θF), the CB–W separation lines are depicted differently: the lower one for our data using nanostructures (θF = 115° − −) compared to the previous studies (θF = 109° ) using microstructures are also plotted for a comparison. Due to the different contact angles on the smooth surfaces (θF), the CB–W separation lines are depicted differently: the lower one for our data using nanostructures (θF = 115° − −) compared to the previous studies (θF = 109°  ). For high roughness surfaces, the initial drop shape always exhibits superhydrophobic states (denoted by the open symbols □, ). For high roughness surfaces, the initial drop shape always exhibits superhydrophobic states (denoted by the open symbols □,  , ,  ); for instance, the initial droplet shown in (b), with r = 4.92 and Φ = 0.20, has a contact angle higher than 165°, whereas at low roughness (e.g., in (c), r = 1.16 and Φ = 0.0079) a Wenzel state (denoted by the filled symbols, ●, ); for instance, the initial droplet shown in (b), with r = 4.92 and Φ = 0.20, has a contact angle higher than 165°, whereas at low roughness (e.g., in (c), r = 1.16 and Φ = 0.0079) a Wenzel state (denoted by the filled symbols, ●,  , ,  ) is more likely observed. However, by carefully depositing the drop, a metastable Cassie–Baxter state ( ) is more likely observed. However, by carefully depositing the drop, a metastable Cassie–Baxter state ( , ,  , ,  ) with a larger contact angle is also found (e.g., in (c), r = 1.16 and Φ = 0.0079). ) with a larger contact angle is also found (e.g., in (c), r = 1.16 and Φ = 0.0079). | ||
2.2 Experimental setup
Two synchronized cameras were used to record evaporation dynamics, one taking the side-view and the other top-view images at a rate of 0.5 frames per second. The side-view was magnified using a long-range microscope and the top-view using a fixed focal length lens mounted on an extension tube. Top-view visualisation was used to check drop sphericity. Drop shapes were first extracted from the side-view images using ImageJ software. The drop volume, contact angle, and base radius were measured using an axisymmetric drop shape analysis (ADSA)43 Matlab code by considering the gravity effect on the Laplace pressure. Instead of the spherical cap model, the ADSA method was used because non-spherical droplet shapes were observed, especially when the droplet size was comparable with the capillary length (see the ESI† for details). The experiments were conducted at 25 °C and 16% relative humidity (Ha).3 Results and discussion
3.1 Wetting state
Fig. 1 summaries the initial wetting state of a water droplet (of 10 μL) on various hydrophobic nano-structures. Snapshots in Fig. 1(b) and (c) reveal representative initial drop shapes for two nano-structures (r = 4.93 and r = 1.16, respectively). We observed two distinct wetting behaviours of the initial water droplet on various hydrophobic nano-structures, manifested by two different apparent contact angles, θapp. At contact angles θapp > 160°, the drop rests only on the top of the pillars, while air is trapped beneath. In this so-called Cassie–Baxter state,19 the droplet has hybrid inter-facial gas–liquid and liquid–solid contacts. By contrast, the liquid could completely wet the entire structure forming a smaller θapp ≈ 120°, in an impaled or Wenzel state,21 with solely homogeneous liquid–solid contact. This difference in apparent contact angles arises from the change in the solid–liquid contact area. For a CB drop, the contact angle depends on the solid fraction Φ and is defined by cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θCB = Φ(cos
θCB = Φ(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θF + 1) − 1, obtained with a surface energy argument.19 In contrast, in the Wenzel state the wet area is characterised by the surface roughness r, and thus the apparent contact angle is given by cos
θF + 1) − 1, obtained with a surface energy argument.19 In contrast, in the Wenzel state the wet area is characterised by the surface roughness r, and thus the apparent contact angle is given by cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θW = r
θW = r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θF, where θF is the contact angle measured on the flat surface of the same material.21
θF, where θF is the contact angle measured on the flat surface of the same material.21
The impaled (Wenzel) state makes the surface sticky by increasing the retention forces46via an increase of the contact angle hysteresis47,48 and contact radius, resulting in a loss of superhydrophobicity.49 The stability of the CB state can be predicted theoretically by comparing the two surface energies.44 The resulting criterion depends on the geometric parameters r and Φ in relation with θF, shown by the dashed line in Fig. 1. For given surface properties (θF), the Cassie–Baxter state will be favorable on patterned surfaces with a high roughness of 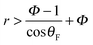 (i.e., the red area in Fig. 1d). This prediction agrees well with our observations; we always observed a Cassie–Baxter state of the initial drop for greater r (e.g., θapp ≳ 160° for r = 3.51 and r = 4.92). The Wenzel state is theoretically more favorable for low-roughness surfaces (the blue regime in Fig. 1d). Indeed, consistent with this prediction, we only observed an initial Wenzel drop in the intermediate range of roughness (e.g., r = 1.63 and r = 1.98).
(i.e., the red area in Fig. 1d). This prediction agrees well with our observations; we always observed a Cassie–Baxter state of the initial drop for greater r (e.g., θapp ≳ 160° for r = 3.51 and r = 4.92). The Wenzel state is theoretically more favorable for low-roughness surfaces (the blue regime in Fig. 1d). Indeed, consistent with this prediction, we only observed an initial Wenzel drop in the intermediate range of roughness (e.g., r = 1.63 and r = 1.98).
For even lower roughness (r = 1.16 and r = 1.31), corresponding to the stable Wenzel regime (marked in blue in Fig. 1d), if no precautions were taken during the drop deposition a Wenzel state was more likely to be observed. However, by using a needle and a slow approach we were able to deposit a Cassie–Baxter drop. This metastable CB state, also reported on other micro-structures,23,24,49 is unstable and undergoes a transition to the Wenzel state during the evaporation of a water droplet. Below, we focus on the results of such wetting transition and drop morphology during evaporation.
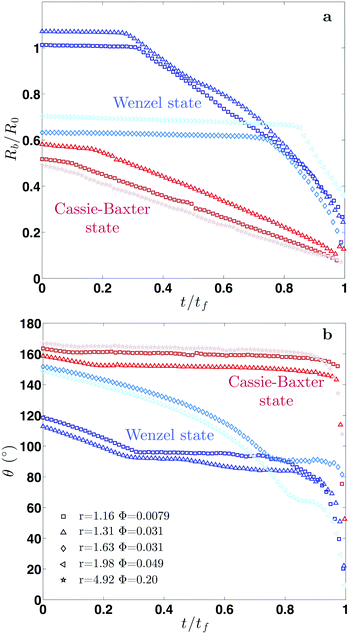
3.2 Evaporation dynamics
Fig. 2 shows our results for the contact radius and angle evolutions of evaporating water droplets on nano-structures, for the two different initial states: air-trapping CB and complete wetting Wenzel state (denoted in red and blue, respectively in Fig. 2). We found that drops exhibit similar behaviours regardless of the nano-structures and initial wetting states. In general, at the early stage the contact line is pinned, while the contact angle decreases due to the decreasing volume and hence the height during evaporation. Once the contact angle reaches the receding contact angle (≈155° for the Cassie–Baxter state and ≈90° for the Wenzel state), the contact radius starts decreasing, while maintaining a nearly constant contact angle. Finally, at the end of the evaporation, the contact radius and angle decrease simultaneously. These three sequential stages of evaporation dynamics are known as the constant contact radius (CCR), constant contact angle (CCA), and mixed mode (of CCR and CCA),50,51 which have been observed during drop evaporation on flat50,52 and micro-structured53–55 surfaces. A CB droplet evaporates mostly in the CCA mode due to the small contact angle hysteresis. Whereas, for impaled drops, the CCR mode is longer, lasting for almost the entire evaporation in the intermediate roughness range.A classical theory that models the evaporation rate of a sessile water drop is based on diffusive transport of saturated vapor along the top droplet surface to the ambient air56 (see the ESI†). We compare in Fig. 3 our experimental results using hydrophobic nano-structures with the theoretical prediction (dashed line) without the consideration of roughness r. The comparative quantity is a dimensionless mass flux rate, 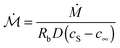 , derived from the vapor-diffusion model, where Rb is the base radius, D is the water vapor diffusion coefficient in air, cS is the saturated vapor concentration, and c∞ is the vapor concentration at infinity (see the ESI† for the details). Regardless of the nano-patterned surfaces, experimental data collapse, corroborating the theory that the evaporation rate only depends on the contact angle. Nevertheless, the classical theory based on a pure diffusion process slightly overestimates the evaporation rates measured on nano-patterned surfaces. This observation is in agreement with a recent study showing that drops evaporate more slowly on superhydrophobic surfaces.57 This discrepancy has been attributed to the evaporation cooling effect. At a high contact angle, the contact radius becomes small, limiting the heat flux between the substrate and drop. Consequently, the droplet becomes colder, which in turn results in a decrease of saturated vapor concentration and hence a slower evaporation. Based on the numerical simulation of the temperature field during the evaporation, a correction factor has been introduced in the classical theory of droplet evaporation to account for the drop cooling.58 Our experimental data show a better agreement with the latter model (see Fig. 3). For contact angles higher than 150°, we noticed that the discrepancy increases significantly, and the experiments show a lower evaporation rate. This discrepancy may be attributed to the assumption of a spherical drop used by the theory56,58 and the deviation of the drop shape from a spherical cap at such a high contact angle, observed in the experiments (see the ESI† note).
, derived from the vapor-diffusion model, where Rb is the base radius, D is the water vapor diffusion coefficient in air, cS is the saturated vapor concentration, and c∞ is the vapor concentration at infinity (see the ESI† for the details). Regardless of the nano-patterned surfaces, experimental data collapse, corroborating the theory that the evaporation rate only depends on the contact angle. Nevertheless, the classical theory based on a pure diffusion process slightly overestimates the evaporation rates measured on nano-patterned surfaces. This observation is in agreement with a recent study showing that drops evaporate more slowly on superhydrophobic surfaces.57 This discrepancy has been attributed to the evaporation cooling effect. At a high contact angle, the contact radius becomes small, limiting the heat flux between the substrate and drop. Consequently, the droplet becomes colder, which in turn results in a decrease of saturated vapor concentration and hence a slower evaporation. Based on the numerical simulation of the temperature field during the evaporation, a correction factor has been introduced in the classical theory of droplet evaporation to account for the drop cooling.58 Our experimental data show a better agreement with the latter model (see Fig. 3). For contact angles higher than 150°, we noticed that the discrepancy increases significantly, and the experiments show a lower evaporation rate. This discrepancy may be attributed to the assumption of a spherical drop used by the theory56,58 and the deviation of the drop shape from a spherical cap at such a high contact angle, observed in the experiments (see the ESI† note).
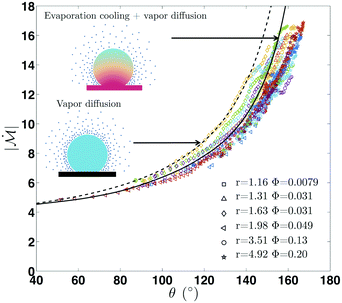 | ||
Fig. 3 Evaporation rate on hydrophobic nano-structures. Dimensionless outgoing mass flux rate, 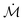 , as a function of the contact angle, for different surfaces (see the ESI†). In spite of the different patterned structures, all the experimental data collapse, indicating that the evaporation rate mainly depends on the contact angle. Comparison with a vapor diffusion model derived by Popov56 (dashed line) and an evaporation cooling correction58 (solid line) reveals that the low evaporation rate observed can be attributed to a cooling effect.58 , as a function of the contact angle, for different surfaces (see the ESI†). In spite of the different patterned structures, all the experimental data collapse, indicating that the evaporation rate mainly depends on the contact angle. Comparison with a vapor diffusion model derived by Popov56 (dashed line) and an evaporation cooling correction58 (solid line) reveals that the low evaporation rate observed can be attributed to a cooling effect.58 | ||
3.3 Cassie–Baxter to Wenzel wetting transition
For droplets initially in the CB state, sudden changes in the contact radius and contact angle are observed, while the droplet undergoes a transition to an impaled, i.e. complete wetting, state (see Fig. 4a). At this wetting transition, these changes arise due to liquid penetration into the nano-structures, thereby destroying superhydrophobicity. As a consequence, designing robust water repellant surfaces requires an insightful understanding of this wetting transition. A supporting movie illustrating the CB to W wetting transition corresponding to the data in Fig. 4 is provided (see the ESI† movie and info).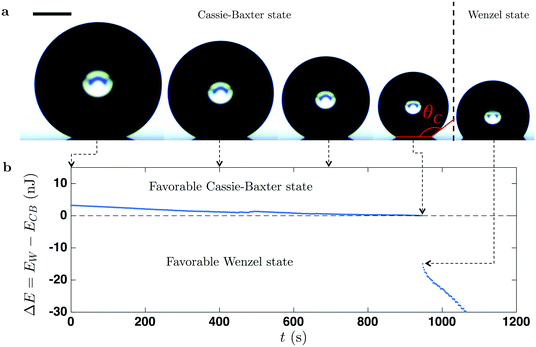 | ||
| Fig. 4 Wetting transition. (a) Successive snapshots of an evaporating, metastable Cassie–Baxter drop on a superhydrophobic surface of a low roughness (r = 1.16). After 945 s, sudden changes in the contact radius and angle are observed corresponding to the wetting transition from a composite wetting CB to an impaled state. The scale bar in (a) corresponds to 500 μm. By comparing the surface energies of each states (b) using eqn (6) and (7), the critical transition, denoted by θC, occurs when both states have the same energy, i.e., ΔE = EW − ECB = 0. Subsequently, the drop jumps to a Wenzel state that has a much lower surface energy. | ||
In previous studies, the transition is assumed to be triggered by the inter-pillar interface bending. As the drop evaporates, the Laplace pressure increases (as the drop curvature (∝1/R) increases), and this causes the bending of the air–liquid interface beneath the drop (between the solid pillars).22,24,59 By denoting the maximum interface bending as δ, local curvature between two pillars scales as δ/l2 with l being the inter-pillar spacing. Equating this curvature with the drop, one yields an estimation of the deformation δ ∼ l2/R. The transition may take place if the liquid touches the structure bottom (δ = H), or if the contact line starts to slide on pillar sides toward the bottom, i.e. if the local contact angle overcomes the advancing contact angle θa. Both scenarios lead to a critical drop radius: R* ∼ l2/H for the “touch-down” and R* ∼ l/|cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θa| for the sliding model. Following these models, by using nano-patterned surfaces, we may be able to lower these critical radii to ≈4 μm and hence should extend the range of the superhydrophobic state to extremely small drops. However, our experimental critical radii were found to be between 100 and 500 μm (see Fig. 4a), different from the predictions using the above models.
θa| for the sliding model. Following these models, by using nano-patterned surfaces, we may be able to lower these critical radii to ≈4 μm and hence should extend the range of the superhydrophobic state to extremely small drops. However, our experimental critical radii were found to be between 100 and 500 μm (see Fig. 4a), different from the predictions using the above models.
Based on the surface energy calculation26 as an alternative approach, we derived another criterion which is able to account for our own experimental results on nano-structures and the former results using micro-structures. We compared the surface energy of each (CB or Wenzel) state and accounted for the change in the contact angle during evaporation. According to this method, these surface energies at the Cassie–Baxter (CB) and Wenzel (W) states are expressed as:
ECB = Sb(γgsr + γ(1 − Φ(1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ))) + γSc, θ))) + γSc, | (1) |
EW = Sb(γgsr − γr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) + γSc, θ) + γSc, | (2) |
Fig. 4b shows the evolution over time of the difference between Wenzel and Cassie energies, ΔE = EW − ECB, for the surface with r = 1.16. At the beginning of the evaporation, the surface energy of a Cassie–Baxter drop is lower and thus stable; indeed, we observed a higher contact angle while the drop sits on the pillar top. During the evaporation, ECB decrease slightly faster than the Wenzel one, EW, resulting in a decrease of the energy difference. Subsequently, when the Cassie–Baxter and Wenzel states have the same energy (ΔE = EW − ECB = 0), the wetting transition takes place (e.g., after 945 s in Fig. 4b). The proposed model is able to predict the transition for hydrophobic nano-structures, while the two aforementioned models significantly under-predict the critical value, suggesting the universal character of this approach. To validate this universality, we compare our theoretical results with various experimental findings, using a variety of geometric parameters for micro-structures. To this end, we first derive a simple criterion based on the surface energy model. As shown in Fig. 4b, the wetting transition occurs at the critical contact angle θC when ΔE = 0, which can be expressed as: −r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θC = 1 − Φ(1 + cos
θC = 1 − Φ(1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θC) by setting EW = ECB. Consequently, the criterion for the CB to Wenzel transition is
θC) by setting EW = ECB. Consequently, the criterion for the CB to Wenzel transition is
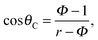 | (3) |
We now compare, in Fig. 5, this criterion with our experiments using nano-structures ( ) and ten other studies found in the literature using a wide variety of micro-patterned substrates. Regardless of the structure or the material, our critical condition is in good agreement with experimental data, demonstrating its universality. The surface energy calculation is a first-order approximation without considering the energy associated with the (pinned) contact line, and thus a small deviation of the various experimental data from the prediction exists. Several factors can also contribute to this discrepancy: imperfect (square or cylindrical) pillar shapes, pinned contact lines, small chemical contamination, different models used for calculating the contact angle, and the measurement uncertainty stems from the contact radius or/and droplet height. We carried out error analysis and noticed that a 10% measurement uncertainty in the contact radius and droplet height (of ≈20 μm) can contribute to a ≈8% error in the contact angle.
) and ten other studies found in the literature using a wide variety of micro-patterned substrates. Regardless of the structure or the material, our critical condition is in good agreement with experimental data, demonstrating its universality. The surface energy calculation is a first-order approximation without considering the energy associated with the (pinned) contact line, and thus a small deviation of the various experimental data from the prediction exists. Several factors can also contribute to this discrepancy: imperfect (square or cylindrical) pillar shapes, pinned contact lines, small chemical contamination, different models used for calculating the contact angle, and the measurement uncertainty stems from the contact radius or/and droplet height. We carried out error analysis and noticed that a 10% measurement uncertainty in the contact radius and droplet height (of ≈20 μm) can contribute to a ≈8% error in the contact angle.
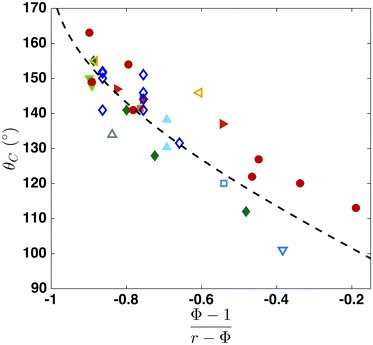 | ||
Fig. 5 Universal criterion of the critical contact angle at the Cassie–Baxter to Wenzel wetting transition. Comparison between the critical contact angle derived in this paper (dashed line) with our experimental data ( ) and the results reported by Blanco-Gomez et al.60 ( ) and the results reported by Blanco-Gomez et al.60 ( ), Chuang et al.61 ( ), Chuang et al.61 ( ), Dicuangco et al.28 ( ), Dicuangco et al.28 ( ), Dubov et al.25 ( ), Dubov et al.25 ( ), Jung et al.59 ( ), Jung et al.59 ( ), McHale et al.53 ( ), McHale et al.53 ( ), Tsai et al.26 ( ), Tsai et al.26 ( ), Wang et al.62 ( ), Wang et al.62 ( ), Xu et al.55 ( ), Xu et al.55 ( ) and Jung et al.23 ( ) and Jung et al.23 ( ). Our criterion is in good agreement with experimental data regardless of the patterns and hydrophobic materials, demonstrating the universality of the criterion for the critical CB to Wenzel wetting transition. ). Our criterion is in good agreement with experimental data regardless of the patterns and hydrophobic materials, demonstrating the universality of the criterion for the critical CB to Wenzel wetting transition. | ||
It is interesting to note that while previous models predicted a critical contact radius, our approach leads to a critical contact angle reflecting the difference in the underlying mechanism triggering the wetting transition. Some data using microstructures of P > 50 μm in Fig. 5 are consistent with the predictions by the touch-down/sliding criteria as well as our model, implying that both mechanisms may play a role in triggering the CB to W transition. However, for nanostructures and some microstructures of smaller P < 50 μm23,25,26 the touch-down/sliding model appears to underestimate the transition. We think that for smaller pillars, contact line pinning and imperfectly shaped pillars likely play a significant role, and these influences should be taken into account and remain an open question.
This new criterion, moreover, revises the way of maintaining a metastable CB state. Previous studies suggest that a reduction of the inter-pillar spacing would extend the CB state to small drops (via R* ∼ l2/H or l/|cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θa|); however, these predictions were not observed for nano-patterned pillars. In contrast, for extending the gas-trapping CB state, our new finding suggests a minimisation of θC, and hence |(Φ − 1)/(r − Φ)|, by exploiting eqn (3).
θa|); however, these predictions were not observed for nano-patterned pillars. In contrast, for extending the gas-trapping CB state, our new finding suggests a minimisation of θC, and hence |(Φ − 1)/(r − Φ)|, by exploiting eqn (3).
4 Conclusions
In summary, for the first time we carried out systematic sets of theoretical and experimental examinations of the dynamic wetting transition from a Cassie–Baxter to a Wenzel state during drop evaporation on nano-structured surfaces. Surprisingly, the downscaling of structures to the nanoscale does not sustain the stability of superhydrophobicity, which was expected by previous analyses. We extended a previous model using the surface energy to derive a new and universal criterion that is able to account for our experimental results (using nano-structures) and various data (with micro-structures) in the literature. From this unifying criterion, we see that the CB to Wenzel transition can occur even at a high contact angle (≈150°) for hydrophobic structures with both low roughness and solid fraction. In contrast, the transition to an impalement state is expected at a lower contact angle (≈100°) when the roughness and/or the solid fraction increases. Consequently, increasing roughness is a powerful way to extend the CB state of water drops on hydrophobic micro/nano-structures during evaporation.Appendix
The surface energy associated with the Cassie–Baxter state on a patterned surface can be expressed as: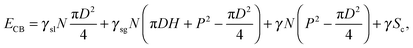 | (4) |
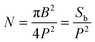 is the number of asperities under the drop, Sc is the surface of the spherical cap, Sb is the base surface and γsl, γsg and γ are the surface tension of the solid–liquid, solid–gas and liquid–gas interfaces, respectively. Using the definition of N, the surface energy for a Cassie–Baxter droplet on hydrophobic nano-structures, ECB, can be calculated using the roughness r and the solid fraction Φ:
is the number of asperities under the drop, Sc is the surface of the spherical cap, Sb is the base surface and γsl, γsg and γ are the surface tension of the solid–liquid, solid–gas and liquid–gas interfaces, respectively. Using the definition of N, the surface energy for a Cassie–Baxter droplet on hydrophobic nano-structures, ECB, can be calculated using the roughness r and the solid fraction Φ:| ECB = Sb(γslΦ + γsg(r − Φ) + γ(1 − Φ)) + γSc, | (5) |
| EW = Nγsl(πDH + P2) + γSc = Sbγslr + γSc. | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, by assuming (quasi-)force equilibrium in the horizontal direction during slow evaporation, and simply the surface energies for the two states in the following equations:
θ, by assuming (quasi-)force equilibrium in the horizontal direction during slow evaporation, and simply the surface energies for the two states in the following equations:ECB = Sb(γgsr + γ(1 − Φ(1 + cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ))) + γSc, θ))) + γSc, | (7) |
EW = Sb(γgsr − γr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) + γSc. θ) + γSc. | (8) |
References
- L. Ionov, N. Houbenov, A. Sidorenko, M. Stamm and S. Minko, Adv. Funct. Mater., 2006, 16, 1153–1160 CrossRef CAS.
- D. Byun, J. Kim, H. S. Ko and H. C. Park, Phys. Fluids, 2008, 20, 113601 CrossRef.
- P. Tsai, A. M. Peters, C. Pirat, M. Wessling, R. G. Lammertink and D. Lohse, Phys. Fluids, 2009, 21, 112002 CrossRef.
- L. Bocquet and P. Tabeling, Lab Chip, 2014, 14, 3143–3158 RSC.
- J. Lee, T. Laoui and R. Karnik, Nat. Nanotechnol., 2014, 9, 317–323 CrossRef CAS PubMed.
- J. Rafiee, X. Mi, H. Gullapalli, A. V. Thomas, F. Yavari, Y. Shi, P. M. Ajayan and N. A. Koratkar, Nat. Mater., 2012, 11, 217–222 CrossRef CAS PubMed.
- N. Miljkovic and E. N. Wang, MRS Bull., 2013, 38, 397–406 CrossRef CAS.
- C. H. Choi, U. Ulmanella, J. Kim, C. M. Ho and C. J. Kim, Phys. Fluids, 2006, 18, 087105 CrossRef.
- A. Steinberger, C. Cottin-Bizonne, P. Kleimann and E. Charlaix, Nat. Mater., 2007, 6, 665–668 CrossRef CAS PubMed.
- L. Bocquet and E. Lauga, Nat. Mater., 2011, 10, 334–337 CrossRef CAS PubMed.
- E. Karatay, A. S. Haase, C. W. Visser, C. Sun, D. Lohse, P. A. Tsai and R. G. Lammertink, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 8422–8426 CrossRef CAS PubMed.
- J. P. Rothstein, Annu. Rev. Fluid Mech., 2010, 42, 89–109 CrossRef.
- R. Blossey, Nat. Mater., 2003, 2, 301–306 CrossRef CAS PubMed.
- K. Liu and L. Jiang, Annu. Rev. Mater. Res., 2012, 42, 231–263 CrossRef CAS.
- P. Guo, Y. Zheng, M. Wen, C. Song, Y. Lin and L. Jiang, Adv. Mater., 2012, 24, 2642–2648 CrossRef CAS PubMed.
- V. Hejazi, K. Sobolev and M. Nosonovsky, Sci. Rep., 2013, 3, 2194 Search PubMed.
- J. Bico, U. Thiele and D. Quéré, Colloids Surf., A, 2002, 206, 41–46 CrossRef CAS.
- B. Bhushan and Y. C. Jung, Prog. Mater. Sci., 2011, 56, 1–108 CrossRef CAS.
- B. D. Cassie and S. Baxter, J. Chem. Soc., Faraday Trans., 1944, 40, 546–551 RSC.
- D. Quéré, Rep. Prog. Phys., 2005, 68, 2495–2532 CrossRef.
- R. N. Wenzel, Ind. Eng. Chem. Res., 1936, 28, 988–994 CrossRef CAS.
- S. Moulinet and D. Bartolo, Eur. Phys. J. E: Soft Matter Biol. Phys., 2007, 24, 251–260 CrossRef CAS PubMed.
- Y. C. Jung and B. Bhushan, J. Microsc., 2008, 229, 127–140 CrossRef CAS PubMed.
- M. Reyssat, J. M. Yeomans and D. Quéré, EPL, 2008, 81, 26006 CrossRef.
- A. Dubov, K. Perez Toralla, A. Letailleur, E. Barthel and J. Teisseire, J. Micromech. Microeng., 2013, 23, 125013 CrossRef.
- P. Tsai, R. G. H. Lammertink, M. Wessling and D. Lohse, Phys. Rev. Lett., 2010, 104, 2–3 CrossRef PubMed.
- H. C. Fernandes, M. H. Vainstein and C. Brito, Langmuir, 2015, 31, 7652–7659 CrossRef CAS PubMed.
- M. Dicuangco, S. Dash, J. A. Weibel and S. V. Garimella, Appl. Phys. Lett., 2014, 104, 201604 CrossRef.
- D. Murakami, H. Jinnai and A. Takahara, Langmuir, 2014, 30, 2061–2067 CrossRef CAS PubMed.
- P. Papadopoulos, L. Mammen, X. Deng, D. Vollmer and H. J. Butt, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 3254–3258 CrossRef CAS PubMed.
- U. Tuvshindorj, A. Yildirim, F. E. Ozturk and M. Bayindir, ACS Appl. Mater. Interfaces, 2014, 6, 9680–9688 CAS.
- G. Whyman and E. Bormashenko, Langmuir, 2011, 27, 8171–8176 CrossRef CAS PubMed.
- X. Liu, Q. Ye, X. Song, Y. Zhu, X. Cao, Y. Liang and F. Zhou, Soft Matter, 2011, 7, 515–523 RSC.
- K. C. Park, H. J. Choi, C. H. Chang, R. E. Cohen, G. H. McKinley and G. Barbastathis, ACS Nano, 2012, 6, 3789–3799 CrossRef CAS PubMed.
- L. Schneider, M. Laustsen, N. Mandsberg and R. Taboryski, Sci. Rep., 2016, 6, 21400 CrossRef CAS PubMed.
- C. H. Choi and C. J. Kim, Langmuir, 2009, 25, 7561–7567 CrossRef CAS PubMed.
- Y. Liu, Z. Lin, W. Lin, K. S. Moon and C. Wong, ACS Appl. Mater. Interfaces, 2012, 4, 3959–3964 CAS.
- W. Sun, S. Zhou, B. You and L. Wu, J. Mater. Chem. A, 2013, 1, 3146–3154 CAS.
- H. S. Lim, D. Kwak, D. Y. Lee, S. G. Lee and K. Cho, J. Am. Chem. Soc., 2007, 129, 4128–4129 CrossRef CAS PubMed.
- L. Xu, W. Chen, A. Mulchandani and Y. Yan, Angew. Chem., Int. Ed., 2005, 44, 6009–6012 CrossRef CAS PubMed.
- J. B. Boreyko and C. H. Chen, Phys. Rev. Lett., 2009, 103, 174502 CrossRef PubMed.
- B. Bhushan, K. Koch and Y. C. Jung, Soft Matter, 2008, 4, 1799–1804 RSC.
- O. Río and A. Neumann, J. Colloid Interface Sci., 1997, 196, 136–147 CrossRef PubMed.
- J. Bico, C. Tordeux and D. Quéré, EPL, 2001, 55, 214–220 CrossRef CAS.
- L. Barbieri, E. Wagner and P. Hoffmann, Langmuir, 2007, 23, 1723–1734 CrossRef CAS PubMed.
- C. G. L. Furmidge, J. Colloid Sci., 1962, 17, 309–324 CrossRef CAS.
- G. McHale, N. J. Shirtcliffe and M. I. Newton, Langmuir, 2004, 20, 10146–10149 CrossRef CAS PubMed.
- B. Bhushan, M. Nosonovsky and Y. C. Jung, J. R. Soc., Interface, 2007, 4, 643–648 CrossRef CAS PubMed.
- A. Lafuma and D. Quéré, Nat. Mater., 2003, 2, 457–460 CrossRef CAS PubMed.
- R. G. Picknett and R. Bexon, J. Colloid Interface Sci., 1977, 61, 336–350 CrossRef CAS.
- H. Y. Erbil, Adv. Colloid Interface Sci., 2012, 170, 67–86 CrossRef CAS PubMed.
- J. H. Kim, S. I. Ahn, J. H. Kim and W. C. Zin, Langmuir, 2007, 23, 6163–6169 CrossRef CAS PubMed.
- G. McHale, S. Aqil, N. J. Shirtcliffe, M. I. Newton and H. Y. Erbil, Langmuir, 2005, 21, 11053–11060 CrossRef CAS PubMed.
- K. R. Khedir, G. K. Kannarpady, H. Ishihara, J. Woo, S. Trigwell, C. Ryerson and A. S. Biris, J. Phys. Chem. C, 2011, 115, 13804–13812 CAS.
- W. Xu, R. Leeladhar, Y. T. Kang and C. H. Choi, Langmuir, 2013, 29, 6032–6041 CrossRef CAS PubMed.
- Y. O. Popov, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 1–17 Search PubMed.
- S. Dash and S. V. Garimella, Langmuir, 2013, 29, 10785–10795 CrossRef CAS PubMed.
- Z. Pan, J. Weibel and S. Garimella, Langmuir, 2014, 30, 9726–9730 CrossRef CAS PubMed.
- Y. C. Jung and B. Bhushan, Scr. Mater., 2007, 57, 1057–1060 CrossRef CAS.
- G. Blanco Gomez, A. Glidle, L. M. Flendrig and J. M. Cooper, Microelectron. Eng., 2009, 86, 1325–1328 CrossRef CAS.
- Y. C. Chuang, C. K. Chu, S. Y. Lin and L. J. Chen, Soft Matter, 2014, 10, 3394–3403 RSC.
- G. Wang, Z. H. Jia and H. N. Yang, Colloid Polym. Sci., 2016, 294, 851–858 CAS.
- P. G. de Gennes, Rev. Mod. Phys., 1985, 57, 827–863 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: SEM images of nanostructures, non-spherical drop shapes, evaporation flux, error analysis of contact angle, and supporting movie. See DOI: 10.1039/c6sm02287a |
| This journal is © The Royal Society of Chemistry 2017 |