Maximally dense random packings of cubes and cuboids via a novel inverse packing method

Abstract

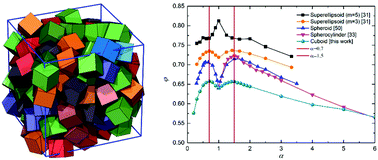
The packings of cubes and cuboids (i.e., “elongated” or “compressed” cubes) are ubiquitous in nature. The high symmetry and space-tiling nature of such particles make them easily packable in dense configurations with a high degree of orientational and translational order. In this paper, we devise a novel inverse packing method that enables one to generate dense hard-particle packings with a controllable degree of disorder/order quantified by predefined order metrics via stochastic Monte Carlo optimizations. We employ the inverse packing method to generate and investigate the maximally dense random packings (MDRPs) of hard cubes and cuboids with aspect ratio α, in which a series of newly introduced normalized local cubatic order parameters sensitive to the onset of any spatial order in packings of cubes and cuboids is minimized. The density of the MDRP of cubes is φ ≈ 0.637, which increases as the shape deviates from the cube limit (α = 1) and reaches the maximal values for cuboids with aspect ratios α = 0.7 or 1.5. These special α values associated with local density extrema are almost identical for those associated with the random packings of spherocylinders, spheroids and superellipsoids, suggesting a universal influence of shape elongation on random packing density. Our inverse packing method can be readily utilized to study the MDRPs of other hard particles and the normalized local cubatic order parameter introduced here is applicable to other shaped particles characterized by three principal axes.