Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A graph-based genetic algorithm and generative model/Monte Carlo tree search for the exploration of chemical space†
Jan H.
Jensen

Department of Chemistry, University of Copenhagen, Copenhagen, Denmark. E-mail: jhjensen@chem.ku.dk; Web: http://www.twitter.com/janhjensen
First published on 11th February 2019
Abstract
This paper presents a comparison of a graph-based genetic algorithm (GB-GA) and machine learning (ML) results for the optimization of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values with a constraint for synthetic accessibility and shows that the GA is as good as or better than the ML approaches for this particular property. The molecules found by the GB-GA bear little resemblance to the molecules used to construct the initial mating pool, indicating that the GB-GA approach can traverse a relatively large distance in chemical space using relatively few (50) generations. The paper also introduces a new non-ML graph-based generative model (GB-GM) that can be parameterized using very small data sets and combined with a Monte Carlo tree search (MCTS) algorithm. The results are comparable to previously published results (Sci. Technol. Adv. Mater., 2017, 18, 972–976) using a recurrent neural network (RNN) generative model, and the GB-GM-based method is several orders of magnitude faster. The MCTS results seem more dependent on the composition of the training set than the GA approach for this particular property. Our results suggest that the performance of new ML-based generative models should be compared to that of more traditional, and often simpler, approaches such a GA.
P values with a constraint for synthetic accessibility and shows that the GA is as good as or better than the ML approaches for this particular property. The molecules found by the GB-GA bear little resemblance to the molecules used to construct the initial mating pool, indicating that the GB-GA approach can traverse a relatively large distance in chemical space using relatively few (50) generations. The paper also introduces a new non-ML graph-based generative model (GB-GM) that can be parameterized using very small data sets and combined with a Monte Carlo tree search (MCTS) algorithm. The results are comparable to previously published results (Sci. Technol. Adv. Mater., 2017, 18, 972–976) using a recurrent neural network (RNN) generative model, and the GB-GM-based method is several orders of magnitude faster. The MCTS results seem more dependent on the composition of the training set than the GA approach for this particular property. Our results suggest that the performance of new ML-based generative models should be compared to that of more traditional, and often simpler, approaches such a GA.
Introduction
Within the past few years several papers have been published on using machine learning (ML) to generate molecules with the aim of optimizing their properties.1–8 While the performances of these generative models have been impressive, they are usually not compared to those of more traditional approaches such as genetic algorithms (GAs),9–12 and recent work by Tsuda and co-workers13 suggests that non-ML approaches may be competitive. The lack of comparison is perhaps in part due to the fact that there are no free or open source versions of implementation of these GAs available (ACSESS11 uses the proprietary OpenEye cheminformatics toolkits).In this paper I present a comparison of graph-based GA and ML results for the optimization of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values with a constraint for synthetic accessibility and show that the GA is as good as or better than the ML approaches for this particular property. I also introduce a new non-ML graph-based generative model that can be parameterized using very small data sets and combined with a Monte Carlo tree search algorithm. The implementation of both methods relies on the open source RDKit cheminformatics package and the codes are made freely available.
P values with a constraint for synthetic accessibility and show that the GA is as good as or better than the ML approaches for this particular property. I also introduce a new non-ML graph-based generative model that can be parameterized using very small data sets and combined with a Monte Carlo tree search algorithm. The implementation of both methods relies on the open source RDKit cheminformatics package and the codes are made freely available.
Computational methodology
Graph-based genetic algorithm (GB-GA)
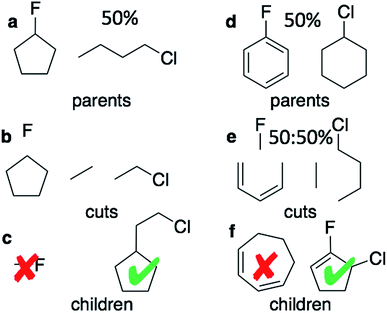
The graph-based genetic algorithm (GB-GA) combines the ideas from the algorithm developed by Brown et al.9 and the ACSESS algorithm developed by Virshup et al.11 and is implemented using the open source RDKit package. In this context “graph-based” means that crossovers and mutations are performed by altering a graph representation of the molecules as opposed to, say, a string based representation such as SMILES. The crossovers and mutations are defined using RDKit's reaction SMILES. Following Brown et al.9 a crossover can occur both at non-ring (Fig. 1a–c) and ring bonds (Fig. 1d–f), with equal probability and the positions of the cuts are chosen randomly. Molecules with macrocycles (seven atoms or more – Fig. 1f), allene centers in rings, fewer than five heavy atoms (Fig. 1c), incorrect valences as determined by RDKit, and more non-H atoms than the target size are discarded. The target size is a random number sampled from a distribution with a mean of 39.15 non-H atoms and a standard deviation of 3.50 non-H atoms as discussed later in the paper. The mutation operations are similar to those used by Virshup et al.11 (Fig. 2). The initial mating pool is drawn from a subset of the ZINC dataset used in previous studies,2,4,6 as described below, and molecules are sampled from the mating pool based on their normalized log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P scores.
P scores.
A graph-based generative model with Monte Carlo tree search (GB-GM-MCTS)
Tsuda and coworkers2,5 have combined the text-based generative model developed by Segler et al.1 with a Monte Carlo tree search (MCTS) algorithm to optimize molecular properties. In this approach each character in a SMILES string corresponds to a node in a tree network and each node is selected sequentially using the MCTS approach. Inspired by Virshup et al.11 we developed a graph-based generative model (GB-GM) that grows the molecule one atom at a time and that can be combined with a MCTS. The GB-GM uses the “append atom” and “insert atom” mutations (Fig. 2) for atom addition to non-ring and ring atoms, respectively, but with different probabilities as described below. In addition to these two mutation-types, a new tricyclic ring-creation mutation is used: X ∼ Y → X1 ∼ Z ∼ Y1 where “1” indicates that X and Y are bonded and “∼” indicates an arbitrary bond order.In order to create realistic looking molecules, such as those in the ZINC data set, the mutations and choice of element are chosen with probabilities obtained by an analysis of a subset of the molecules in the ZINC dataset. An analysis of first 1000 molecules in the ZINC dataset shows that 63% of the atoms are ring atoms, so the ring-creation or ring-insertion mutation is chosen 63% of the time. The most common 3-atom combination in rings is C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C, which accounts for 45% of all 3-atom combinations in rings (Table 1), so a C ∼ C → C
C–C, which accounts for 45% of all 3-atom combinations in rings (Table 1), so a C ∼ C → C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C mutation is chosen 45% of the time, and similarly for the 34 other X ∼ Y ∼ Z combinations found in the data set. The site of insertion/creation is chosen randomly and excludes aromatic and six-membered rings. Similarly, for addition the most common bond involving at least one non-ring atom is C–C, so a C → C–C mutation is chosen more often (see Table S1† for more details). A more specific bonding analysis, e.g. addition of C to C
C–C mutation is chosen 45% of the time, and similarly for the 34 other X ∼ Y ∼ Z combinations found in the data set. The site of insertion/creation is chosen randomly and excludes aromatic and six-membered rings. Similarly, for addition the most common bond involving at least one non-ring atom is C–C, so a C → C–C mutation is chosen more often (see Table S1† for more details). A more specific bonding analysis, e.g. addition of C to C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C vs. C–C, was considered but then the most probable bonding patterns are often not found in the early stages of molecule growth and the growth process effectively stops.
C vs. C–C, was considered but then the most probable bonding patterns are often not found in the early stages of molecule growth and the growth process effectively stops.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) [*]–[*] type bonding is increased to 80% (“GB-GM (80%)”)
[*]–[*] type bonding is increased to 80% (“GB-GM (80%)”)
| Bonding | ZINC | GB-GM (62%) | GB-GM (80%) |
|---|---|---|---|
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C C–C |
45% | 41% | 53% |
| C–C–C | 15% | 23% | 21% |
| C–C–N | 9% | 9% | 6% |
| C–N–C | 6% | 7% | 5% |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–N C–N |
4% | 6% | 4% |
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C C–C |
3% | 2% | 2% |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–C N–C |
2% | 2% | 1% |
| C–C–O | 2% | 2% | 2% |
N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–N C–N |
2% | 0% | 0% |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–N N–N |
2% | 0% | 0% |
| C–O–C | 1% | 1% | 1% |
| C–N–N | 1% | 1% | 1% |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–S C–S |
1% | 1% | 0% |
| C–S–C | 1% | 1% | 1% |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–O C–O |
1% | 1% | 1% |
The GB-GM-MCTS code is a modified version of the mcts.py code14 modified for leaf parallelization with a maximum of 25 leaf nodes. The exploration factor is 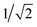 and rollout is terminated if the molecule exceeds the target size as described for the GB-GA. Any three- or four-membered alkene rings are subsequently expanded to five-membered rings by inserting C atoms. The reward function is 1 if the predicted J(m) value (see below) is larger than the largest value found so far and 0 otherwise. This reward function was found to work slightly better than the one used by Yang et al.2
and rollout is terminated if the molecule exceeds the target size as described for the GB-GA. Any three- or four-membered alkene rings are subsequently expanded to five-membered rings by inserting C atoms. The reward function is 1 if the predicted J(m) value (see below) is larger than the largest value found so far and 0 otherwise. This reward function was found to work slightly better than the one used by Yang et al.2
The penalized log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) P score
P score
Following Gómez-Bombarelli et al.4 and Yang et al.2 the goal is to maximize J(m):J(m) = log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P(m) − SA(m) − RingPenalty(m) P(m) − SA(m) − RingPenalty(m) | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P(m) is the octanol–water partition coefficient for a molecule (m) as predicted by RDKit, SA(m) is a synthetic accessibility score,15 and RingPenalty(m) penalizes unrealistically large rings by reducing the score by RingSize − 6 where RingSize is the number of atoms in a ring. Following previous studies, each property is normalized to have zero mean and unit standard deviation across the ZINC dataset.
P(m) is the octanol–water partition coefficient for a molecule (m) as predicted by RDKit, SA(m) is a synthetic accessibility score,15 and RingPenalty(m) penalizes unrealistically large rings by reducing the score by RingSize − 6 where RingSize is the number of atoms in a ring. Following previous studies, each property is normalized to have zero mean and unit standard deviation across the ZINC dataset.
J(m) depends both on the number and types of atoms and can be made arbitrarily large by increasing the molecular size. Therefore it is important to limit the molecular size in order to make a fair comparison to previous studies. Yang et al.2 predict SMILES strings with a maximum length of 81 characters, but it is difficult to translate that restriction directly to molecular size since many of the characters do not refer to atoms. Instead, the 20 molecules found by Yang et al.2 are used to determine an average target size of 39.15 ± 3.50 non-H atoms.
Results and discussion
GB-GA
Ten GA simulations are performed and the maximum J(m) scores for each simulation are averaged. The population size is 20 and 50 generations are used (i.e. 1000 J(m) evaluations per run). The initial mating pool is 20 random molecules sampled from the first 1000 molecules in the ZINC data set. The mean J(m)-score for this set is 0.2 and the maximum value is 3.6.The average maximum J(m)-score for the GA is 6.8 ± 0.7 and 7.4 ± 0.9 using a 50% and 1% mutation rate, respectively (Table 2). For comparison the best average maximum value found by Yang et al.2 is 5.6 ± 0.5, which required close to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 J(m)-score evaluations. The latter took 8 hours each, while the GB-GA calculations took 30 seconds each on a laptop. These J(m)-scores are also significantly larger than those of the other ML-based methods tried by Yang et al.2 (Table 2): a recurrent neutral network (RNN) with and without Bayesian optimization (BO), the continuous variational autoencoder4 (CVAE), and the grammar variational autoencoder3 (GVAE).
000 J(m)-score evaluations. The latter took 8 hours each, while the GB-GA calculations took 30 seconds each on a laptop. These J(m)-scores are also significantly larger than those of the other ML-based methods tried by Yang et al.2 (Table 2): a recurrent neutral network (RNN) with and without Bayesian optimization (BO), the continuous variational autoencoder4 (CVAE), and the grammar variational autoencoder3 (GVAE).
| Method | Average J(m) | No. molecules | CPU time |
|---|---|---|---|
| GB-GA (50%) | 6.8 ± 0.7 | 1000 | 30 seconds |
| GB-GA (1%) | 7.4 ± 0.9 | 1000 | 30 seconds |
| GB-GM-MCTS (62%) | 2.6 ± 0.6 | 1000 | 90 seconds |
| GB-GM-MCTS (80%) | 3.4 ± 0.6 | 1000 | 90 seconds |
| GB-GM-MCTS (80%) | 4.3 ± 0.6 | 5000 | 9 minutes |
| ChemTS | 4.9 ± 0.5 | ∼5000 | 2 hours |
| ChemTS | 5.6 ± 0.5 | ∼20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
8 hours |
| RNN + BO | 4.5 ± 0.2 | ∼4000 | 8 hours |
| Only RNN | 4.8 ± 0.2 | ∼20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
8 hours |
| CVAE + BO | 0.0 ± 0.9 | ∼100 | 8 hours |
| GVAE + BO | 0.2 ± 1.3 | ∼1000 | 8 hours |
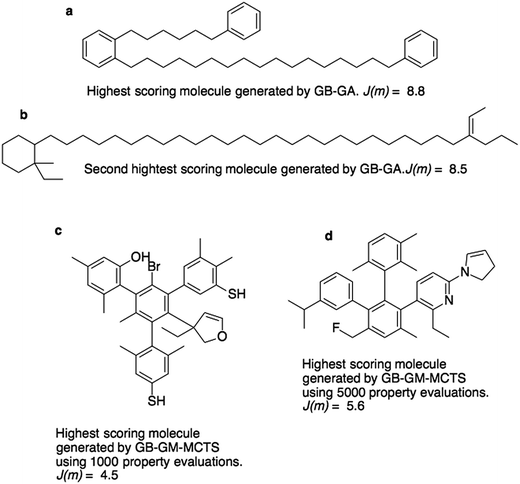
Fig. 3a and b show the molecules with the two highest J(m)-scores found by the GB-GA. These scores, 8.8 and 8.5, are slightly larger than the three largest values (7.8–8.0) obtained by You et al.6 using a graph convolutional policy network approach. The two molecules bear little resemblance to the molecules used to construct the initial mating pool. The molecules in the ZINC data set that are most similar to these two molecules have respective Tanimoto similarity scores of just 0.27 and 0.12 and corresponding J(m) values of 0.9 and −2.4 (Fig. S1†). This indicates that the GB-GA approach can traverse a relatively large distance in chemical space using relatively few (50) generations.
Fig. 4 shows an example of how the maximum J(m) value evolves with each generation for 10 different GB-GA runs. While most of the runs have mostly peaked after about 20 generations the three best performing runs (run 1, 6, and 10) show significant improvements between 30 and 40 generations, so running fewer than 50 generations cannot be recommended for J(m) maximisation. None of the runs increased J(m) significantly after periods of 20 generations with no or little change in J(m) (with the possible exception of run 7). So a good strategy may be to terminate the GB-GA run if the J(m) value has not changed for more than 20 generations (at least for J(m) maximisation).
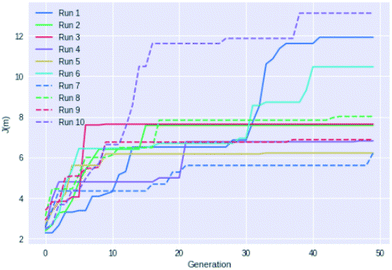 | ||
| Fig. 4 Plot of the highest J(m) value found as a function of generations for 10 different GB-GA runs with a mutation rate of 1%. | ||
GB-GM
As described in the Computational methodology section, the GB-GM method grows a molecule one atom at a time where the choice of bond order and atom type is chosen probabilistically based on a bonding analysis of the first 1000 molecules in the ZINC dataset (referred to hereafter as the reference set). The GB-GM model is tested by generating 1000 molecules using ethane as the “seed” molecule (which takes about 30 seconds on a laptop) and repeating the statistical bonding analysis. The average molecular size in the new data set is 23.2 ± 4.1 atoms, which is nearly identical to that of the training set: 23.2 ± 4.4 atoms. There are 2498 rings compared to 2768 in the reference set and 59% of the atoms are in rings, which also is close to the 63% in the reference set. 41% of the 3-atom combinations in rings is C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C, which is reasonably close to the 45% in the reference set (Table 1). This difference is probably due to the fact that at least one of the two carbons must be secondary to “accept” the double bond, and if such a bonding pattern is not present then no “
C–C, which is reasonably close to the 45% in the reference set (Table 1). This difference is probably due to the fact that at least one of the two carbons must be secondary to “accept” the double bond, and if such a bonding pattern is not present then no “![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–” atom will be added. It is thus a little bit more likely that a “–C–” atom will be “accepted”, compared to a “
C–” atom will be added. It is thus a little bit more likely that a “–C–” atom will be “accepted”, compared to a “![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–” atom.
C–” atom.
Not surprisingly, there are bigger differences for the larger scale features not specifically encoded in the rules such as the type of ring (Table 3). For example, there are many fewer benzene-type rings ([*]1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) [*]–[*]
[*]–[*]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) [*]–[*]
[*]–[*]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) [*]1) as well as cyclopentane ([*]1–[*]–[*]–[*]–[*]1) and cyclohexane ([*]1–[*]–[*]–[*]–[*]–[*]1) type rings, while there are more of most of the other types compared to the reference set. The reason is that the molecules in the ZINC data set are not made by randomly adding atoms, but by assembling larger functional groups such as aliphatic and aromatic rings. As a result the average ring composition does not reflect the most likely ring compositions. It is possible to scale the probabilities to skew the results towards one or the other ring-type. For example in the last column the probabilities are scaled such that the probability of X = Z–Y is 80% rather than the 62% in the reference set, which increases the number of benzene-like rings from 479 to 850 at the expense of the aliphatic rings.
[*]1) as well as cyclopentane ([*]1–[*]–[*]–[*]–[*]1) and cyclohexane ([*]1–[*]–[*]–[*]–[*]–[*]1) type rings, while there are more of most of the other types compared to the reference set. The reason is that the molecules in the ZINC data set are not made by randomly adding atoms, but by assembling larger functional groups such as aliphatic and aromatic rings. As a result the average ring composition does not reflect the most likely ring compositions. It is possible to scale the probabilities to skew the results towards one or the other ring-type. For example in the last column the probabilities are scaled such that the probability of X = Z–Y is 80% rather than the 62% in the reference set, which increases the number of benzene-like rings from 479 to 850 at the expense of the aliphatic rings.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) [*]–[*] type bonding is increased to 80% (“GB-GM (80%)”)
[*]–[*] type bonding is increased to 80% (“GB-GM (80%)”)
| Ring-type | ZINC | GM (62%) | GM (80%) |
|---|---|---|---|
| [*]1–[*]–[*]1 | 57 | 104 | 57 |
| [*]1–[*]–[*]–[*]1 | 17 | 33 | 10 |
| [*]1–[*]–[*]–[*]–[*]1 | 280 | 15 | 4 |
[*]1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) [*]–[*]–[*]–[*]1 [*]–[*]–[*]–[*]1 |
120 | 396 | 408 |
[*]1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) [*]–[*] [*]–[*]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) [*]–[*]1 [*]–[*]1 |
470 | 132 | 221 |
| [*]1–[*]–[*]–[*]–[*]–[*]1 | 409 | 64 | 2 |
[*]1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) [*]–[*]–[*]–[*]–[*]1 [*]–[*]–[*]–[*]–[*]1 |
77 | 363 | 104 |
[*]1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) [*]–[*] [*]–[*]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) [*]–[*]–[*]1 [*]–[*]–[*]1 |
100 | 591 | 405 |
[*]1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) [*]–[*]–[*] [*]–[*]–[*]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) [*]–[*]1 [*]–[*]1 |
7 | 321 | 202 |
[*]1![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) [*]–[*] [*]–[*]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) [*]–[*] [*]–[*]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) [*]1 [*]1 |
1206 | 479 | 850 |
| 7-Membered ring | 24 | 0 | 0 |
| 8-Membered ring | 1 | 0 | 0 |
| Total | 2768 | 2498 | 2263 |
GB-GM-MCTS
Ten GB-GM-MCTS simulations are performed using ethane as a seed molecule and the maximum J(m)-scores for each simulation are averaged. The tree is traversed 1000 times, i.e. there are 1000 J(m) evaluations per run. For GB-GM-MCTS the average maximum J(m)-score value is 2.6 ± 0.6, which is significantly lower than the lowest value in the study of Yang et al.2, 4.9 ± 0.4 (Table 2). The most likely explanation is that the GB-GM makes relatively few benzene rings (as discussed above), which, together with Cl atoms, is the defining structural feature of the high scoring molecules found by Yang et al.2 Indeed, if the probability of generating C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C containing rings is increased from 62% to 80% then the average maximum J(m)-score increases to 3.4 ± 0.6. Increasing the number of tree traversals to 5000 increases the value to 4.3 ± 0.6, which is similar to the 4.9 ± 0.4 obtained by Yang et al.2 using as similar number of tree traversals. The latter run takes about 9 minutes, compared to 2 h in the study of Yang et al.2.
C–C containing rings is increased from 62% to 80% then the average maximum J(m)-score increases to 3.4 ± 0.6. Increasing the number of tree traversals to 5000 increases the value to 4.3 ± 0.6, which is similar to the 4.9 ± 0.4 obtained by Yang et al.2 using as similar number of tree traversals. The latter run takes about 9 minutes, compared to 2 h in the study of Yang et al.2.
Fig. 3c and d show the highest scoring molecule found using 1000 and 5000 tree traversals. The molecules are similar to those found by Yang et al.2 in that they consist mostly of benzene rings, and the benzene ring is the most common hydrophobic structural motif in the ZINC data set. The GB-GA results show that higher J(m)-scores can be obtained using long aliphatic chains, but this structural motif is relatively rare in the ZINC data set and therefore rarely suggested by the generative models.
Conclusion and outlook
This paper presents a comparison of a graph-based genetic algorithm (GB-GA) and machine learning (ML) results, compiled by Yang et al.,2 for the optimization of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values with a constraint for synthetic accessibility (J(m)) and shows that the GA is as good as or better than the ML-based approaches for this particular property. The GB-GA predicts maximum J(m)-values that, on average, are 1.3–1.8 units higher than the best ML-based results reported by Yang et al.,2 while also being several orders of magnitude computationally more efficient. Similarly, the GB-GA method finds molecules with maximum J(m)-scores that, depending on the method, often are several units larger than those found with ML-based approaches. These molecules bear little resemblance to the molecules used to construct the initial mating pool, indicating that the GB-GA approach can traverse a relatively large distance in chemical space using relatively few (50) generations.
P values with a constraint for synthetic accessibility (J(m)) and shows that the GA is as good as or better than the ML-based approaches for this particular property. The GB-GA predicts maximum J(m)-values that, on average, are 1.3–1.8 units higher than the best ML-based results reported by Yang et al.,2 while also being several orders of magnitude computationally more efficient. Similarly, the GB-GA method finds molecules with maximum J(m)-scores that, depending on the method, often are several units larger than those found with ML-based approaches. These molecules bear little resemblance to the molecules used to construct the initial mating pool, indicating that the GB-GA approach can traverse a relatively large distance in chemical space using relatively few (50) generations.
The paper also introduces a new non-ML graph-based generative model (GB-GM) that can be parameterized using very small data sets and combined with a Monte Carlo tree search (MCTS) algorithm such as the one used by Yang et al.2 The results are comparable to the results obtained by Yang et al.2 using a recurrent neural network (RNN) generative model, with maximum J(m)-values of 4.3 ± 0.6 compared to 4.9 ± 0.6 found using 5000 property evaluations. While the results are slightly worse than the RNN results, the GB-GM-based method is several orders of magnitude faster. In both cases the MCTS approach essentially extracts the main hydrophobic structural motif (a benzene ring) found in the training set. The MCTS results thus seem more dependent on the composition of the training set than the GA approach for this particular property.
While the results are quite encouraging, it is important to perform similar comparisons for other properties before drawing general conclusions. In a very recent study Brown et al.16 have compared GB-GA and GB-GM-MCTS methods to SMILES-based ML and GA methods on 20 different optimization problems and conclude that “In terms of optimization performance, the best model is a genetic algorithm based on a graph representation of molecules”. Our and their results strongly suggest that the performance of new ML-based generative models should be compared to that of more traditional, and often simpler, approaches such as GAs. Both the GB-GA and GB-GM-MCTS codes used in this study are freely available with the open source RDKit toolkit as the only dependence.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
I thank Bowen Liu for helpful discussions.References
- M. H. S. Segler, T. Kogej, C. Tyrchan and M. P. Waller, ACS Cent. Sci., 2017, 4, 120–131 CrossRef PubMed.
- X. Yang, J. Zhang, K. Yoshizoe, K. Terayama and K. Tsuda, Sci. Technol. Adv. Mater., 2017, 18, 972–976 CrossRef CAS PubMed.
- M. J. Kusner, B. Paige and J. M. Hernandez-Lobato, Proceedings of 34th International Conference on Machine Learning, ICML, 2017, pp. 1945–1954 Search PubMed.
- R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276 CrossRef PubMed.
- M. Sumita, X. Yang, S. Ishihara, R. Tamura and K. Tsuda, ACS Cent. Sci., 2018, 4, 1126–1133 CrossRef CAS PubMed.
- J. You, B. Liu, R. Ying, V. Pande and J. Leskovec, arXiv:1806.02473, 2018.
- B. Sanchez-Lengeling and A. Aspuru-Guzik, Science, 2018, 361, 360–365 CrossRef CAS PubMed.
- D. Neil, M. Segler, L. Guasch, M. Ahmed, D. Plumbley, M. Sellwood and N. Brown, Exploring Deep Recurrent Models with Reinforcement Learning for Molecule Design, 2018 Search PubMed.
- N. Brown, B. McKay, F. Gilardoni and J. Gasteiger, J. Chem. Inf. Comput. Sci., 2004, 44, 1079–1087 CrossRef CAS PubMed.
- N. M. O'Boyle, C. M. Campbell and G. R. Hutchison, J. Phys. Chem. C, 2011, 115, 16200–16210 CrossRef.
- A. M. Virshup, J. Contreras-García, P. Wipf, W. Yang and D. N. Beratan, J. Am. Chem. Soc., 2013, 135, 7296–7303 CrossRef CAS PubMed.
- Y. Kanal and G. R. Hutchison, arXiv:1707.02949, 2017.
- N. Yoshikawa, K. Terayama, T. Honma, K. Oono and K. Tsuda, arXiv:1804.02134, 2018.
- Python Implementations of Monte Carlo Tree Search, https://github.com/haroldsultan/MCTS, accessed, 2018-10-23 Search PubMed.
- P. Ertl and A. Schuffenhauer, J. Cheminf., 2009, 1, 8 Search PubMed.
- N. Brown, M. Fiscato, M. H. S. Segler and A. C. Vaucher, arXiv:1811.09621, 2018.
Footnote |
| † Electronic supplementary information (ESI) available: The codes used in this study can be found on GitHub: github.com/jensengroup/GB-GA/tree/v0.0 and github.com/jensengroup/GB-GM/tree/v0.0. See DOI: 10.1039/c8sc05372c |
| This journal is © The Royal Society of Chemistry 2019 |