Open Access Article
Open Access ArticleFacile access to regio- and stereoselective synthesis of highly functionalized spiro[indoline-3,2′-pyrrolidines] incorporating a pyrene moiety: experimental, photophysical and theoretical approach†
Essam M. Hussein ab,
Ziad Moussac,
Nizar El Guesmiad and
Saleh A. Ahmed
ab,
Ziad Moussac,
Nizar El Guesmiad and
Saleh A. Ahmed *ab
*ab
aChemistry Department of Chemistry, Faculty of Applied Science, Umm Al-Qura University, 21955 Makkah, Saudi Arabia. E-mail: saahmed@uqu.edu.sa; saleh.a.ahmed@aun.edu.eg; saleh_63@hotmail.com
bDepartment of Chemistry, Faculty of Science, Assiut University, 71516 Assiut, Egypt
cDepartment of Chemistry, Faculty of Science, Taibah University, P.O. Box 30002, Almadinah, Almunawarrah, Saudi Arabia
dDépartement de chimie, Faculté des Sciences de Monastir, Avenue de l’Environnement, 5019 Monastir, Tunisia
First published on 3rd July 2018
Abstract
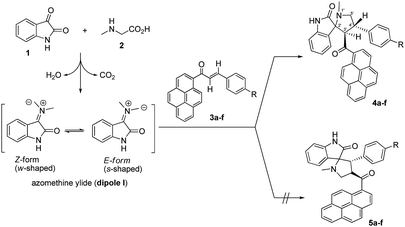
The regio- and stereochemical polar [3 + 2] cycloaddition of azomethine ylides, which were generated in situ by the reaction of isatin and sarcosine or benzylamine, with (E)-3-aryl-1-(pyren-1-yl)prop-2-en-1-ones as dipolarophiles, was studied using experimental and theoretical methods. The chemical structures and relative configurations of all products have been fully established by 1D and 2D homonuclear and heteronuclear correlation NMR spectrometry. The effects of the electronic and steric factors of the reactions were discussed. The photophysical properties of the synthesized spiro[indoline-3,2′-pyrrolidin]-2-ones and 5′-phenyl-spiro[indoline-3,2′-pyrrolidin]-2-ones were studied. The mechanism of the reactions was investigated using global and local reactivity indices and frontier molecular orbital (FMO) analysis at the B3LYP/6-31G level of theory. The relationship between the electrophilicity index ω of the dipolarophiles and the Hammett constant σp has been studied. The theoretical scale of reactivity correctly explains the electrophilic activation/deactivation effects promoted by electron-withdrawing and electron-releasing substituents in the para-position of the dipolarophiles.
Introduction
Multistep reactions are typically associated with high cost, low yields, and complex isolation procedures that often include hazardous and costly solvents after each step. However, higher efficiency, higher reaction yields, lower cost, shorter reaction duration, and improved selectivity can be achieved by designing multicomponent reactions (MCRs), which provide access to synthesis of a massive number of compounds that have interesting biological properties using readily available starting materials.1 Multicomponent [3 + 2] cycloaddition reactions, also known as Huisgen reactions, provide a direct and straightforward entry for the construction of many five-membered heterocyclic ring systems.2 In the past few decades, [3 + 2] cycloaddition of azomethine ylides, which represent one of the most reactive and versatile classes of 1,3-dipoles, has been used to trap a range of dipolarophiles to construct pyrrolidine, pyrrolizine and pyrrolothiazole derivatives in a regio and stereo controlled fashion.3 The spiro pyrrolidine-oxindole system is the core structure of several natural alkaloids and pharmacological agents such as spirotryptostatine A and B,4 elacomine,5 horsifiline,6 and coreleucine.7 The derivatives of spiropyrrolidine-oxindole have shown important biological applications such as modulation of the function of muscarinic serotonin receptor,8 inhibition of microtubule assembly,9 inhibition of human NK-1 receptor,10 potent non-peptide inhibition of the p53-MDM2 protein–protein interaction,11 poliovirus, rhinovirus 3C-proteinase inhibition,12 as well as antidiabetic,13 antibiotic,14 anticonvulsant actions,15 antibacterial, antiviral, anti-inflammatory, anticancer, and antitubercular activities.16 Moreover, the molecular mechanism and the origins of the regioselectivity in [3 + 2] cycloaddition reaction of azomethine ylides with various dipolarophiles have been theoretically studied based on DFT reactivity indices17 and molecular electron density theory.18 The pyrene moiety is considered one of the most useful frameworks for the construction of fluorogenic chemosensors for a diversity of important chemical species.19 However, there is little published work regarding the synthesis of spiroheterocyclic compounds which incorporate the pyrene moiety.20 Herein, as a part of our research program on [3 + 2] cycloaddition reactions,20,21 we describe the results of experimental and theoretical studies on the stereo- and regioselectivity of the [3 + 2] cycloaddition reaction of azomethine ylides, generated in situ from isatin (1) and sarcosine (2) or benzylamine (6), to a series of (E)-3-aryl-1-(pyren-1-yl)prop-2-en-1-ones 3a–f to afford a new series of 4′-aryl-3'-(pyrene-1-carbonyl)spiro[indoline-3,2′-pyrrolidin]-2-ones 4a–f.Results and discussion
Synthetic strategy
The choice of an appropriate reaction medium was of key importance for the successful synthesis. Initially, the three-component reaction of isatin (1), sarcosine (2), and (E)-3-phenyl-1-(pyren-1-yl)prop-2-en-1-one (3a) as a simple model substrate was investigated to assess the feasibility of the strategy and to optimize the reaction conditions (Scheme 1). Different solvents such as 1,4-dioxane, tetrahydrofuran (THF), dichloromethane (CH2Cl2), acetonitrile, methanol, and ethanol under reflux conditions and were shown to have a substantial influence on the reaction yield. The results are summarized in Table 1 (entries 1–6). As can be seen from Table 1, the cycloaddition adduct 4a was obtained as a single regioisomer in excellent yield (93%) with a comparatively short reaction time (4 h) when the reaction was carried out in ethanol (Table 1, entry 6). Moderate to poor yields of 50, 43, and 27% were obtained when 1,4-dioxane, THF, and dichloromethane were used as reaction solvents, respectively, even though the reaction time was increased to 10 h in order to drive the reaction forward (Table 1, entries 1–3).| Entry | Solvent | Time (h) | Yield (%) |
|---|---|---|---|
| a Reaction conditions: isatin (1, 1.1 mmol), sarcosine (2, 1.1 mmol), (E)-3-phenyl-1-(pyren-1-yl)prop-2-en-1-one (3a, 1.0 mmol), solvent (10 mL)/reflux. | |||
| 1 | Methanol | 5 | 80 |
| 2 | Ethanol | 4 | 93 |
| 3 | Acetonitrile | 7 | 79 |
| 4 | 1,4-Dioxane | 10 | 50 |
| 5 | Tetrahydrofuran | 10 | 43 |
| 6 | Dichloromethane | 10 | 27 |
Encouraged by this success, we extended this reaction of isatins (1) with sarcosine (2) to the remaining (E)-3-aryl-1-(pyren-1-yl)prop-2-en-1-ones 3b–f under the optimized conditions. Thus, the corresponding 1′-methyl-4′-aryl-3′-(pyrene-1-carbonyl)-spiro[indoline-3,2′-pyrrolidin]-2-ones 4a–f were smoothly synthesized in excellent yields (87–94%), and the results are summarized in Table 2. It can be seen from Scheme 1 that the nature of the substituents in aryl groups on the (E)-3-aryl-1-(pyren-1-yl)prop-2-en-1-ones 3a–f had no significant effect on the final yield of the products.
Regio- and stereoselectivity
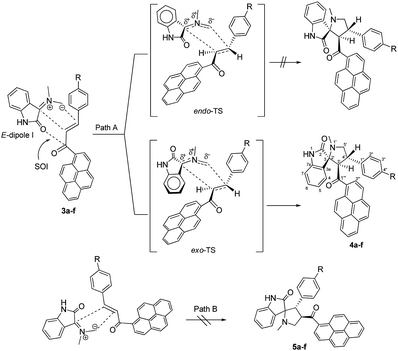
As shown in Schemes 1 and 2, the formation of 4a–f proceeds through the generation of an azomethine ylide (dipole I), via the decarboxylative condensation of isatin (1) with sarcosine (2), which then undergoes [3 + 2] cycloaddition reaction with the dipolarophile (3a–f) in a highly regio- and diastereoselective fashion, leading to the exclusive formation of one of four possible diastereomers in all cases.The cycloaddition reaction is regioselective where the electron-rich carbon atom of the dipole reacts with the β-carbon of the α,β-unsaturated moiety of the dipolarophile 3a–f. The regioselectivity in the product formation can be explained by considering the electronic effect due to resonance and the electron-withdrawing effect of the carbonyl group of the dipolarophile 3a–f causing the β-carbon to be most electrophilic. In addition, the regioselectivity may be expounded by the secondary orbital interaction (SOI) of the orbital of the carbonyl group of dipolarophile 3a–f with those of the azomethine ylide as suggested in Scheme 2. Accordingly, the observed regioisomer 4a–f via path A is more favorable than the other regioisomer 5a–f because of the secondary orbital interaction which is not possible in path B.
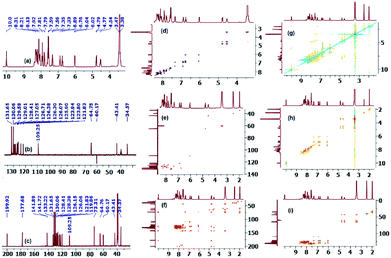
On the other hand, and although concerted cycloaddition reactions are inherently diastereoselective, one still expects two diastereomeric products due to the stereogenic center C3, of which only a single isomer was obtained in all examples. Thus, in order to fully establish the chemical structures of the products and assign the relative stereochemistry of the stereocenters for the isolated diastereomer in each reaction, extensive 1D (1H-, 13C-, 13C-DEPT-90/135-NMR), and 2D homonuclear and heteronuclear correlation NMR spectrometry experiments (1H–1H DQF-COSY, 1H–1H-TOCSY, HSQC-TOCSY, 13C–1H-HSQC, 13C–1H-HMBC, 1H–1H-ROESY) were conducted in DMSO-d6 on a selection of compounds (see ESI†). Hence, using (3S,3′R,4′S)-4′-(4-bromophenyl)-1′-methyl-3′-(pyrene-1-carbonyl)spiro[indoline-3,2′-pyrrolidin]-2-one (4c) as a representative example and a model for the remaining structurally-related compounds, the relevant spectra that were used in structural elucidation and stereochemical assignment are shown in Fig. 1.
Analysis of the 13C (Fig. 1, spectrum c, showing selected peak picking), 13C-DEPT-90 (ESI†), and 13C-DEPT-135 (Fig. 1, spectrum b) NMR spectra indicated the presence of 33 signals (15 aromatic CH's, 11 aromatic quaternary carbons, 2 carbonyl carbons, 1 quaternary sp3 spiro-center, one methylene, one methyl, and two methine carbons) which is consistent with all carbons being nonequivalent except C2′′/C3′′. The two carbonyl carbons, one due to the ketone and another due to the indolone group appear at δ 199.9 and 177.7 ppm, respectively, and the spiro-center carbon of the pyrrolidine ring resonates most downfield (δ 73.3 ppm) among all the carbon atoms of this ring which are also the only ones with chemical shifts in the aliphatic region besides the methyl group. The peak at δ 64.8 ppm has been attribute to the C3 carbon because the attached proton of C3′–H (d, δ 4.78 ppm) shows strong long range 1H–13C heteronuclear multiple bond correlation with the adjacent ketone (2JCH) as well as with the other carbonyl group (3JCH) (Fig. 1, spectrum f) and is the most deshielded aliphatic signal due to diamagnetic anisotropy. While the methylene 13C chemical shift (C5′/δ 60.2 ppm) was clearly identified as it was the only signal with a negative phase in the 13C-DEPT-135 spectrum, the attached diastereotopic protons appear as two doublets closely flanking the HOD peak (δ 3.43 ppm) and were correlated in the 1H–13C-HSQC-NMR spectrum by two contours to the corresponding C5′ carbon (Fig. 1, spectrum e). Although the C4′–H multiplicity was expected to be a three doublets (ddd) due to the surrounding non-equivalent protons, it appeared as a highly shifted downfield quartet (δ 4.53 ppm) and was correlated to the carbon at δ 43.4 ppm. The non-equivalent pyrrolidine protons were correlated to the same spin system by TOCSY (16-contour square in the aliphatic region, Fig. 1, spectrum h) and HSQC-TOCSY NMR (16-contour rectangle in the aliphatic region, Fig. 1, spectrum i) and the order of the chemical shifts was also confirmed by 1H–1H-DQFCOSY (Fig. 1, spectrum d). Clearly, the magnetic anisotropic effect impacted the chemical shifts for the pyrrolidine carbons and more so for its protons and outweighed the local atomic environment effect which warranted the above detailed NMR studies. Surprisingly, the –NH group of the indolone moiety (δ 10.0 ppm/1H NMR, Fig. 1, spectrum a) provided the only entry point that ultimately led to the unambiguous assignment of the correct stereochemistry for the isolated diastereomer. In the ROSEY spectrum (Fig. 1, spectrum g) there exists a strong correlation cross peak between the –NH proton (δ 10.0 ppm) and H-7 (doublet, δ 6.03 ppm) and identification of the latter triggers the assignment of all the indolone ring protons. Hence, while TOCSY (16-contour square in the aromatic region, Fig. 1, spectrum h) and HSQC-TOCSY NMR (16-contour rectangle in the aromatic region, Fig. 1, spectrum i) correlated the remaining three protons in the indolone spin system (δ 7.33, δ 6.89, δ 6.76 ppm) with δ 6.03 ppm, 1H–1H-DQFCOSY (Fig. 1, spectrum d) was used to assign their relative position on the aromatic ring. From the 1H–1H-COSY correlation of H-7 (off diagonal cross peak at δ 6.03/6.76), the triplet at δ 6.76 was assigned to the adjacent proton H-6. Further, from the correlation of the latter, as evident from the contour at δ 6.76/6.89, the triplet at δ 6.89 was assigned to the neighboring H-5 proton. A last cross peak at δ 6.89/7.33 correlated the doublet at δ 7.33 which was assigned to H-4. Having assigned the chemical shifts for the indolone and pyrrolidine protons, what remained was to examine the ROSEY spectrum for any significant spatial proximity contours that could be used to assign the relative stereochemistry of the three chiral centers.
Indeed, a very strong cross peak at δ 7.33/4.53 indicated the close proximity of H-4 to H-4′ which signified a syn-relationship between the indolinone aromatic ring and H-4′ and set the relative stereochemistry for the spirocenter (C3/C2′) and C4′. The syn-geometry of H-3′ and the C4′ p-bromophenyl moiety was evident from the off diagonal cross peak at δ 4.78/7.55 between C2′′–H (δ 7.55) and H-3′ (δ 4.78).
As suggested in Scheme 2 (path A), the formation of cycloaddition products 4a–f proceeds via an “exo”-transition state.22 This can be explained by the fact that the corresponding “endo”-transition state would require more free energy of activation than the “exo”-transition state due to the electrostatic repulsion between the cis carbonyl groups increasing the free energy of activation.22
To expand the scope of this three-component [3 + 2] cycloaddition reaction, the reaction of (E)-3-aryl-1-(pyren-1-yl)prop-2-en-1-ones 3a–f with a non-stabilized azomethine ylide generated from isatin (1) and benzylamine (6) rather than sarcosine (2) was attempted. The corresponding 4′-(aryl)-5′-phenyl-3′-(pyrene-1-carbonyl)-spiro[indoline-3,2′-pyrrolidin]-2-ones 7a–f were obtained regioselectively in good yields and the results are summarized in Scheme 3 (Table 3).
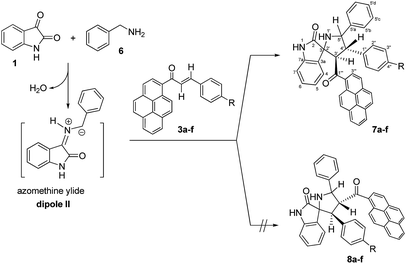 | ||
| Scheme 3 Synthesis of 4′-(aryl)-5′-phenyl-3′-(pyrene-1-carbonyl)-spiro[indoline-3,2′-pyrrolidin]-2-ones 7a–f. | ||
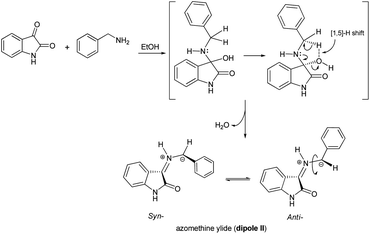
Although the detailed mechanism of the above reaction is not fully clear, the formation of regioisomer 7a–f could be explained as follows: there are two possible isomeric structures of the azomethine ylide (dipole II), “syn-”' and “anti-” would be formed from the reaction of isatin and benzylamine via pseudo-pericyclic [1,5]-hydrogen shift and subsequent deprotonation23 (Scheme 4) which then undergoes [3 + 2] cycloaddition reaction with the dipolarophile (3a–f) regioselectively as shown in Scheme 5 (path A). As mentioned, the observed regioisomer 7a–f via path A is more favorable than the other regioisomer 8a–f because of electronic effect and the secondary orbital interaction which is not possible in path B.
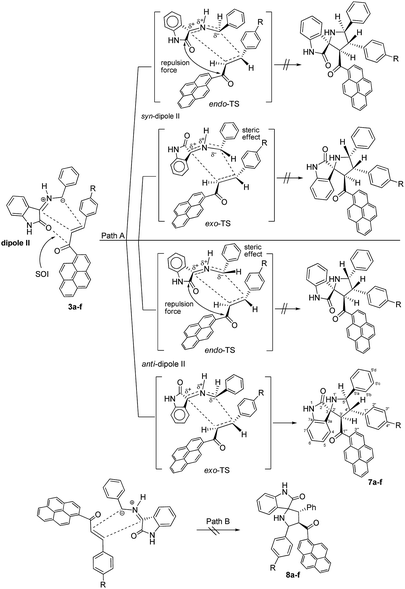 | ||
| Scheme 5 Plausible mechanism for the formation of 4′-(aryl)-5′-phenyl-3′-(pyrene-1-carbonyl)spiro[indoline-3,2′-pyrrolidin]-2-ones 7a–f. | ||
Similarly, the [3 + 2] cycloaddition of azomethine ylide (dipole II) to variously substituted (E)-3-aryl-1-(pyren-1-yl)prop-2-en-1-ones was highly diastereoselective, affording one of four possible diastereomers (8 diastereomers would be expected if the cycloaddition reaction was not inherently diastereoselective) in all cases as shown in Scheme 5. While the reaction of the electron-rich carbon atom of the dipole II with the β-carbon of the dipolarophile 3a–f set the regiochemical outcome, determining stereoselectivity required extensive 1D and 2D NMR analysis. Using (3S,3′R,4′S,5′R)-4′-(4-nitrophenyl)-5′-phenyl-3′-(pyrene-1-carbonyl)spiro[indoline-3,2′-pyrrolidin]-2-one (7e) as a representative example, the relative stereochemistry of the four chiral centers was set using the same techniques as before (see ESI†). However, in order to evade undertaking detailed discussions, only the most relevant correlations will be highlighted. Strong diamagnetic anisotropic effect stemming from the newly added benzene ring at C5′ caused unexpected strong deshielding to H-5′ (δ 5.04, J = 10.3 Hz) which was used as key to assign the remaining protons of the pyrrolidine ring. In some compounds (e.g. 7a, 7f) and under dilute conditions in DMSO-d6, H-5′ and the pyrrolidine N1′–H (δ 4.02–4.05) couple with each other and appear as a dd (J = 4.90–5.40 Hz for the smaller coupling constant) and d (J = 5.10–5.40 Hz), respectively, and were identified based on this observation. Long range 13C–1H-HMBC also corroborated this assignment by showing a cross peak between N1′–H (2JCH) and C5′. Accordingly, the chemical shifts for the other pyrrolidine protons were traced to δ 5.17 (3′-H) (d, J = 11.2 Hz) and 4.33 (4′-H) (t, J = 10.7 Hz) based on 1H–1H–COSY, 1H–1H-TOCSY, and HSQC-TOCSY analysis. It is noted that the chemical shifts for the indolone protons had the same order as determined before and showed the key contour between the –NH proton (δ 9.97 ppm) and H-7 (doublet, δ 5.98 ppm) in the ROSEY spectrum. As such, the other indolone ring protons were matched with δ 6.73 for H-6, δ 6.96 for H-5, and δ 7.62 for H-4 based on various 2D spectral analysis. Finally, the relative stereochemistry of the four chiral centers was set based on ROSEY correlation cross peaks between H-4 and H-4′, and H-4′ and H-5′b, pointing to the syn-arrangement of these groups. On the other hand, the syn- geometry of H-3′, H-5′, and the C4′ p-nitrophenyl ring was deduced from cross peaks between H-2′′, H-3′ and H-5′.
As suggested in Scheme 5, the stereochemistry of cycloaddition products 7a–f is described by considering the steric effect and the repulsion force. The formation of cycloaddition products 7a–f proceeds via anti-form of the dipole II through the exo-transition state. This can be explained by the fact that the endo-transition state would require more free energy of activation due to both the steric effect and the electrostatic repulsion between the cis carbonyl groups.
Moreover, concerning the syn-form of the dipole II, the transition states would require more free energy of activation due to either the steric effect or the electrostatic repulsion between the cis carbonyl groups.
Absorption and emission spectra of spiro[indoline-3,2′-pyrrolidin]-2-ones 4a–f and 5′-phenyl-spiro[indoline-3,2′-pyrrolidin]-2-ones 7a–f
Absorption spectra of compounds 4a–f and 7a–f (1 × 10−5 M) were recorded in dichloromethane at ambient temperature. Representative absorption spectra of both compounds recorded in dichloromethane are shown in Fig. 2 and the corresponding spectral data are summarized Table 4. As seen in Fig. 2 the compounds 4a–f and 7a–f show a broad absorption band at 390–395 nm. Generally, changing the substituent group had no significant influence on the λmax. The band absorption intensities (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε) of the compounds 4a–f and 7a–f under investigations were found between 4.13 and 4.33 (Table 4). On excitation at 390 nm, only one emission peak is observed for both compounds 4a–f and 7a–f, a large red shifted emission band is observed within the wavelength range 477–482 nm for compound 4a–f and 487–495 nm for 7a–f. A bathochromic shift by ∼10–13 nm was detected corresponding to the effect of adding the phenyl group on C5′. On the other hand, as seen in Fig. 3, a remarkable increase in fluorescence intensity was observed when going from system 4a–f to system 7a–f by a factor of ∼2.5. The fluorescence intensity was also observed to be weak for 4f and 7f (R
ε) of the compounds 4a–f and 7a–f under investigations were found between 4.13 and 4.33 (Table 4). On excitation at 390 nm, only one emission peak is observed for both compounds 4a–f and 7a–f, a large red shifted emission band is observed within the wavelength range 477–482 nm for compound 4a–f and 487–495 nm for 7a–f. A bathochromic shift by ∼10–13 nm was detected corresponding to the effect of adding the phenyl group on C5′. On the other hand, as seen in Fig. 3, a remarkable increase in fluorescence intensity was observed when going from system 4a–f to system 7a–f by a factor of ∼2.5. The fluorescence intensity was also observed to be weak for 4f and 7f (R![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CN) and to be strong for 4c and 7c (R
CN) and to be strong for 4c and 7c (R![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) Br). The fluorescence intensity of 4a–f and 7a–f strongly depended on the substituent.
Br). The fluorescence intensity of 4a–f and 7a–f strongly depended on the substituent.
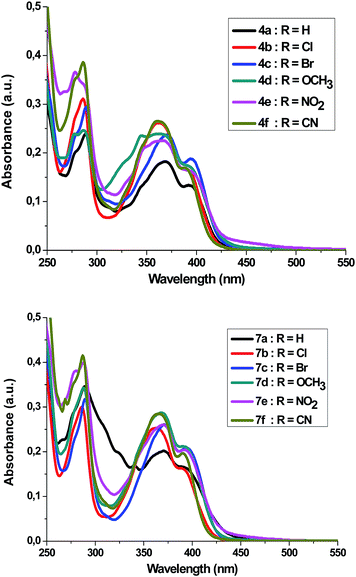 | ||
| Fig. 2 UV-Vis-spectrum of 4a–f and 7a–f in dichloromethane (c = 1 × 10−5 mol dm−3) at room temperature. | ||
| R | 4a–f | 7a–f | ||||
|---|---|---|---|---|---|---|
| λmax/nm, excitation | λmax/nm, emission | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε ε |
λmax/nm, excitation | λmax/nm, emission | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε ε |
|
| a; H | 369; 392 | 479 | 4.13 | 371; 392 | 492 | 4.22 |
| b; Cl | 363; 391 | 482 | 4.22 | 362; 390 | 494 | 4.21 |
| c; Br | 370; 394 | 478 | 4.27 | 371; 394 | 492 | 4.32 |
| d; OCH3 | 362; 392 | 479 | 4.24 | 368; 390 | 493 | 4.33 |
| e; NO2 | 367; 395 | 477 | 4.21 | 370; 392 | 495 | 4.31 |
| f; CN | 361; 391 | 480 | 4.22 | 366; 390 | 487 | 4.29 |
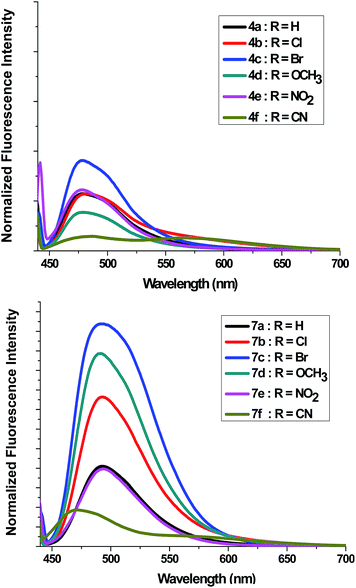 | ||
| Fig. 3 Fluorescence emission spectra of 4a–f and 7a–f in dichloromethane (c = 1 × 10−5 mol dm−3) at room temperature. | ||
Theoretical studies
Conceptual DFT provides different indices to rationalize and understand chemical structure and reactivity.24 Structures of dipoles I, II and dipolarophiles 3 were minimized according to the preceding parameters and frontier molecular orbital (FMO) (ie; the Highest Occupied Molecular Orbital (HOMO) and the Lowest Unoccupied Molecular Orbital (LUMO)) analysis and global/local reactivity indices were used to predict regioselectivity.In this study, the HOMO–LUMO energy gaps suggest that the LUMO(dipolarophile)–HOMO(dipole) interaction controls the cycloaddition reaction (normal electron demand reactions).25 The calculated frontier orbital energies for 1,3-dipoles I, II and dipolarophiles 3a–f are shown in Table 5. It's clear that the energy gaps ΔE = LUMO(dipolarophiles 3a–f) − HOMO(E-dipole I) and LUMO(dipolarophiles 3a–f) − HOMO(anti-dipole II) are lower than those of the corresponding Z-dipole I and syn-dipole II, respectively.
| Reactant | HOMO (eV) | LUMO (eV) | Energy barrier (ΔEa, eV) | |||
|---|---|---|---|---|---|---|
| Z-Dipole I | E-Dipole I | syn-Dipole II | anti-Dipole II | |||
| a ΔE = LUMO(dipolarophile) − HOMO(dipole). | ||||||
| Z-Dipole I | −7.6259 | −0.4895 | ||||
| E-Dipole I | −7.5615 | −0.4272 | ||||
| syn-Dipole II | −7.5272 | −1.1186 | ||||
| anti-Dipole II | −7.4689 | −1.0996 | ||||
| 3a | −8.2744 | −1.1466 | 6.4793 | 6.4148 | 6.3806 | 6.3223 |
| 3b | −8.3236 | −1.2092 | 6.4167 | 6.3522 | 6.3179 | 6.2597 |
| 3c | −8.3351 | −1.2264 | 6.3995 | 6.3350 | 6.3008 | 6.2425 |
| 3d | −8.2515 | −1.1197 | 6.5062 | 6.4417 | 6.4074 | 6.3492 |
| 3e | −8.4714 | −1.6212 | 6.0047 | 5.9402 | 5.9059 | 5.8477 |
| 3f | −8.3876 | −1.3140 | 6.3119 | 6.2474 | 6.2131 | 6.1549 |
Global reactivity indices (electronic chemical potential μ, chemical hardness η, global electrophilicity (ω)) were estimated according to the equations recommended by Parr26 and Domingo.27 In particular, the electronic chemical potentials and chemical hardness of the reactants studied here were evaluated in terms of the one-electron energies of the frontier molecular orbitals using the following equations: μ = 1/2(εH + εL); η = (εL − εH).27
The values of μ and η were then used to calculate an important and interesting global descriptor, which is called electrophilicity index ω according to the formula
| ω = μ2/2η. | (1) |
Electrophilicity index is a measure of the electrophilic power of a system and can be described as the maximal ability of a molecule to accept electrons in the neighborhood of an electron reservoir. Another informative index used by Domingo et al. is called ΔNmax parameter, defined by
| ΔNmax = −μ/η, | (2) |
Calculated values ω, μ, η, and ΔNmax of relevance for the study are collected in Table 6.
| Reactant | μ | η | ω | ΔNmax | |
|---|---|---|---|---|---|
| a Electronic chemical potential μ, chemical hardness η and global electrophilicities ω in eV as defined by eqn (1); ΔNmax in electron units (a.u.).b All computations were carried out with the Gaussian 03 suite of programs. Calculations based on the method of DFT were performed using the B3LYP exchange correlation functional, together with the standard 6-31G basis set. | |||||
| Z-Dipole I |  |
−4.05776 | 7.13646 | 1.153 | 0.568 |
| E-Ddipole I |  |
−3.99436 | 7.13428 | 1.118 | 0.560 |
| syn-Dipole II |  |
−4.32280 | 6.40855 | 1.458 | 0.675 |
| anti-Dipole II |  |
−4.28416 | 6.36937 | 1.441 | 0.673 |
| 3a |  |
−4.71056 | 7.12775 | 1.556 | 0.661 |
| 3b |  |
−4.76634 | 7.11442 | 1.596 | 0.670 |
| 3c |  |
−4.78077 | 7.10870 | 1.608 | 0.672 |
| 3d |  |
−4.68580 | 7.13183 | 1.539 | 0.657 |
| 3e |  |
−5.04635 | 6.85019 | 1.858 | 0.737 |
| 3f |  |
−4.85097 | 7.07360 | 1.663 | 0.686 |
The data summarized in Table 6 reveals that, the dipole I with configuration “E” and dipole II with configuration “anti” have an electronic chemical potential higher than its dipole counterparts dipole I with configuration “Z” and dipole II with configuration “anti”, respectively, which means that the electronic flow is again from the azomethine ylides type dipoles to chalcones 3a–f as dipolarophile. So, chalcones 3a–f and acts as an electrophile due to the larger value of its ω (1.539 < ω < 1.858) relatively to dipoles ω values. So, starting from the reference compound chalcone 3a (ω = 1.556 eV), the para substitution with chlorine (–Cl), and bromine (–Br) atoms results in an electrophilic activation in compounds chalcone 3b (ω = 1.596 eV) and chalcone 3c (ω = 1.608 eV). The highest activation effect is achieved by electron withdrawing nitro (–NO2) substitution, in compound chalcone 3e (ω = 1.858 eV). In this series, the electrophilic deactivation was caused by electron releasing groups as found, for example, with the methoxy substituting –OCH3 in compound chalcone 3d (ω = 1.539 eV). On the other hand, recent investigations have used the ω values to classify dipole and dipolarophiles on a unique scale.26–28 According to this model, the polar character of a dipole–dipolarophiles interaction can be assessed from the difference, Δω, in the global electrophilicities of the two reagents. It is clear that, the [3 + 2] cycloaddition of azomethine ylide I, II with chalcones 3a–f as dipolarophiles (Δω are in the range of ∼0.2 and 0.7 which are ≪4.5 eV) are reactions governed by a concerted mechanism.
Relationship between the electrophilicity ω index and Hammett constant σp
Recently, the global electrophilicity index ω of a series of dipolarophiles is used to illustrate the rationalization of the substituent effects on the electrophilic activation/deactivation of the substrates. Indeed, aromatic substrates were chosen because of the substantial electronic effect of the para-substituted group on carbon–carbon double bond facilitated by the electronic transmission through the aromatic π-conjugated system.It is known that the Hammett equation relates the relative magnitude of the equilibrium constants to a reaction constant (ρ) and a substituent constant (σp), according to eqn (3).29
| log(K/Ko) = ρσp | (3) |
Linear relationship between σp and ω have been recently obtained for para-substituent in the alkynes and azides series.30 Domingo et al. have systematically developed a statistical procedure to obtain intrinsic electronic contributions to σp based on the comparison between the experimental Hammett constant σp and the electrophilicity index ω.
The global values of electrophilicity indexes ω for the dipolarophiles 3a–f for the ground state of the substituting agents as well as the Hammett substituent constants σp are listed in Table 7.
| R | σp | ω (eV) | log(ω/ωH) |
|---|---|---|---|
| –H | 0.000 | 1.556 | 0.000000 |
| –Cl | 0.227 | 1.596 | 0.011023 |
| –Br | 0.232 | 1.608 | 0.014276 |
| –OCH3 | −0.268 | 1.539 | −0.004771 |
| –NO2 | 0.778 | 1.858 | 0.077036 |
| –CN | 0.660 | 1.663 | 0.028880 |
Fig. 4 show a positive slope in the relationship between the Hammett constants σp of para-substituents in the dipolarophiles and the logarithm of the global electrophilicity ratio (ω/ωH). It should be noted that the para position leads to the activation of the carbon–carbon double bond groups and then to a nice correlation log(ω/ωH) = f(σp) for the substituent H, Cl, Br, OCH3 and CN, while for the substituent NO2, a remarkable deviation is observed, this deviation can be explained by the fact that the nitro group does not act with its inductive effect but by its resonance effect in which in this case σ− = 1.27 is used and not σp = ∼0.78.
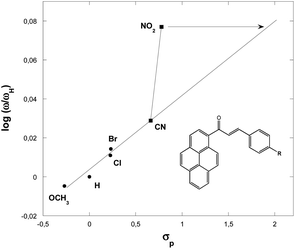 | ||
| Fig. 4 Plot of the global electrophilicity ratio (ω/ωH) against the Hammett constants for p-substituents in the dipolarophiles 3a–f. | ||
The electrophilicity scale correctly accounts for the electrophilic activation/deactivation effects promoted by the substituents in the ground state of the electrophiles involved in our cycloaddition reactions. Indeed, it is proven that the electron withdrawing substituents increase the global electrophilicity of the chalcones, unlike electron releasing substituents, which behave oppositely. This behavior is due to the great activation of the chalcones carbon–carbon double bond function promoted by electronic resonance effects of the electron withdrawing substituents, instead of the great stabilization and then deactivation promoted by the electron releasing groups in the chalcones derivatives.
Conclusions
In conclusion, the regio- and stereoselective polar [3 + 2] cycloaddition reactions of azomethine ylides generated in situ by the reaction of isatin and sarcosine or benzylamine, with (E)-3-aryl-1-(pyren-1-yl)prop-2-en-1-ones as dipolarophiles were carried out to produce a new series of (3S,3′R,4′S)-1′-methyl-4′-aryl-3′-(pyrene-1-carbonyl)spiro[indoline-3,2′-pyrrolidin]-2-ones or (3S,3′R,4′S,5′R)-4′-(aryl)-5′-phenyl-3′-(pyrene-1-carbonyl)spiro[indoline-3,2′-pyrrolidin]-2-ones, respectively, in good to excellent yields. Absorption and emission spectral properties corresponding to 4a–f and 7a–f were determined in dichloromethane. Its noticeable that, substituents affect on the fluorescence behavior. Global reactivity indices for dipoles I, II and dipolarophiles 3a–f were estimated based on the DFT/B3LYP method. It has been revealed a linear relationship between the experimental Hammett constant σp and the electrophilicity index ω. It can be concluded that the great activation of the dipolarophiles 3 carbon–carbon double bond function promoted by electronic resonance effects of the electron withdrawing substituents and then deactivation promoted by the electron releasing groups.Experimental
Materials and methods
All solvents used purchased from Sigma-Aldrich are spectroscopic grade and used without further purifications. Melting points were determined on a Stuart SMP3 melting point apparatus and are uncorrected. IR spectra were recorded on a Shimadzu IR-3600 FT-IR spectrometer in KBr pellets. NMR spectra were acquired on a Bruker Avance 400 instrument (at 400 MHz for 1H, 100 MHz for 13C) in DMSO-d6 solutions, using residual solvent signals as internal standards. Compounds (3a–f) were prepared according to described procedures.20Synthetic procedures
(3S,3′R,4′S)-1′-Methyl-4′-phenyl-3′-(pyrene-1-carbonyl)-spiro[indoline-3,2′-pyrrolidin]-2-one (4a). Orange crystals; mp 124–126 °C. IR (KBr): νmax = 3423 (NH), 3045 (CH arom.), 2939 (CH aliph.), 1714 (C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1678 (C
O), 1678 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 10.10 (s, 1H, NH), 8.30 (d, J = 7.5 Hz, 1H), 8.27 (d, J = 7.5 Hz, 1H), 8.22 (d, J = 9.0 Hz, 1H), 8.15–8.03 (m, 3H), 7.94 (d, J = 9.4 Hz, 1H), 7.85 (d, J = 8.1 Hz, 1H, C3′′′–H), 7.81 (d, J = 9.2 Hz, 1H), 7.61 (d, J = 7.1 Hz, 2H, C2′′–H), 7.43 (t, J = 7.1 Hz, 2H, C3′′–H), 7.37 (d, J = 7.1 Hz, 1H, C4–H), 7.29 (t, J = 7.4 Hz, 1H, C4′′–H), 6.93 (t, J = 7.2 Hz, 1H, C5–H), 6.80 (t, J = 7.4 Hz, 1H, C6–H), 6.09 (d, J = 7.4 Hz, 1H, C7–H), 4.84 (d, J = 9.4 Hz, 1H, C3′–H), 4.57 (q, J = 8.6 Hz, 1H, C4′–H), 3.46–3.40 (m, 2H, C5′–H), 2.01 (s, 3H, N–CH3) ppm. 13C NMR (100 MHz, DMSO-d6): δ 200.2 (C1′′′), 177.9 (C2), 142.4 (C1′′), 141.8 (C7a), 133.2 (C), 131.8 (C), 130.5 (C), 129.8 (C), 129.6 (CH), 129.0 (C6–H), 128.8 (C3′′–H), 128.4 (C4′′–H), 128.3 (C), 127.8 (C2′′–H), 127.1 (CH), 126.9 (CH), 126.7 (CH), 126.4 (C4–H & C3a), 126.3 (CH), 126.1 (C3′′′–H), 125.7 (CH), 124.0 (CH), 123.9 (CH), 123.6 (C), 123.1 (C), 121.9 (C5–H), 109.3 (C7–H), 73.4 (C3/C2′), 65.0 (C3′–H), 60.4 (C5′–H2), 44.2 (C4′–H), 34.6 (N–CH3) ppm.
O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 10.10 (s, 1H, NH), 8.30 (d, J = 7.5 Hz, 1H), 8.27 (d, J = 7.5 Hz, 1H), 8.22 (d, J = 9.0 Hz, 1H), 8.15–8.03 (m, 3H), 7.94 (d, J = 9.4 Hz, 1H), 7.85 (d, J = 8.1 Hz, 1H, C3′′′–H), 7.81 (d, J = 9.2 Hz, 1H), 7.61 (d, J = 7.1 Hz, 2H, C2′′–H), 7.43 (t, J = 7.1 Hz, 2H, C3′′–H), 7.37 (d, J = 7.1 Hz, 1H, C4–H), 7.29 (t, J = 7.4 Hz, 1H, C4′′–H), 6.93 (t, J = 7.2 Hz, 1H, C5–H), 6.80 (t, J = 7.4 Hz, 1H, C6–H), 6.09 (d, J = 7.4 Hz, 1H, C7–H), 4.84 (d, J = 9.4 Hz, 1H, C3′–H), 4.57 (q, J = 8.6 Hz, 1H, C4′–H), 3.46–3.40 (m, 2H, C5′–H), 2.01 (s, 3H, N–CH3) ppm. 13C NMR (100 MHz, DMSO-d6): δ 200.2 (C1′′′), 177.9 (C2), 142.4 (C1′′), 141.8 (C7a), 133.2 (C), 131.8 (C), 130.5 (C), 129.8 (C), 129.6 (CH), 129.0 (C6–H), 128.8 (C3′′–H), 128.4 (C4′′–H), 128.3 (C), 127.8 (C2′′–H), 127.1 (CH), 126.9 (CH), 126.7 (CH), 126.4 (C4–H & C3a), 126.3 (CH), 126.1 (C3′′′–H), 125.7 (CH), 124.0 (CH), 123.9 (CH), 123.6 (C), 123.1 (C), 121.9 (C5–H), 109.3 (C7–H), 73.4 (C3/C2′), 65.0 (C3′–H), 60.4 (C5′–H2), 44.2 (C4′–H), 34.6 (N–CH3) ppm.
(3S,3′R,4′S)-4′-(4-Chlorophenyl)-1′-methyl-3′-(pyrene-1-carbonyl)spiro[indoline-3,2′-pyrrolidin]-2-one (4b). Yellow powder; mp 157–159 °C. IR (KBr): νmax = 3398 (NH), 3043 (CH arom.), 2936 (CH aliph.), 1715 (C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1671 (C
O), 1671 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 10.00 (s, 1H, NH), 8.41–8.05 (m, 6H), 7.95 (d, J = 9.6 Hz, 1H), 7.92 (d, J = 8.0 Hz, 1H, C3′′′–H), 7.79 (d, J = 9.5 Hz, 1H), 7.62 (d, J = 8.3 Hz, 2H, C2′′–H), 7.47 (d, J = 8.3 Hz, 2H, C3′′–H), 7.35 (d, J = 7.3 Hz, 1H, C4–H), 6.89 (t, J = 7.5 Hz, 1H, C5–H), 6.78 (t, J = 7.7 Hz, 1H, C6–H), 6.04 (d, J = 7.7 Hz, 1H, C7–H), 4.79 (d, J = 9.5 Hz, 1H, C3′–H), 4.55 (q, J = 8.1 Hz, 1H, C4′–H), 3.42 (d, J = 8.6 Hz, 1H, C5′–H), 3.38 (d, J = 8.6 Hz, 1H, C5′–H), 1.99 (s, 3H, N–CH3) ppm. 13C NMR (100 MHz, DMSO-d6): δ 199.9 (C1′′′), 177.7 (C2), 141.7 (C1′′), 141.4 (C7a), 133.2 (C), 131.6 (C4′′–Cl), 131.4 (C), 130.5 (C), 129.8 (C), 129.6 (C2′′–H), 129.5 (C–H), 129.0 (C6–H), 128.7 (C3′′–H), 128.4 (C–H), 128.3 (C), 127.0 (CH), 126.7 (CH), 126.4 (C4–H), 126.3 (CH), 126.1 (C3a), 126.0 (C3′′′–H), 125.8 (CH), 123.9 (CH), 123.8 (CH), 123.6 (C), 123.1 (C), 121.8 (C5–H), 109.3 (C7–H), 73.3 (C3/C2′), 64.8 (C3′–H), 60.2 (C5′–H2), 43.4 (C4′–H), 34.6 (N–CH3) ppm.
O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 10.00 (s, 1H, NH), 8.41–8.05 (m, 6H), 7.95 (d, J = 9.6 Hz, 1H), 7.92 (d, J = 8.0 Hz, 1H, C3′′′–H), 7.79 (d, J = 9.5 Hz, 1H), 7.62 (d, J = 8.3 Hz, 2H, C2′′–H), 7.47 (d, J = 8.3 Hz, 2H, C3′′–H), 7.35 (d, J = 7.3 Hz, 1H, C4–H), 6.89 (t, J = 7.5 Hz, 1H, C5–H), 6.78 (t, J = 7.7 Hz, 1H, C6–H), 6.04 (d, J = 7.7 Hz, 1H, C7–H), 4.79 (d, J = 9.5 Hz, 1H, C3′–H), 4.55 (q, J = 8.1 Hz, 1H, C4′–H), 3.42 (d, J = 8.6 Hz, 1H, C5′–H), 3.38 (d, J = 8.6 Hz, 1H, C5′–H), 1.99 (s, 3H, N–CH3) ppm. 13C NMR (100 MHz, DMSO-d6): δ 199.9 (C1′′′), 177.7 (C2), 141.7 (C1′′), 141.4 (C7a), 133.2 (C), 131.6 (C4′′–Cl), 131.4 (C), 130.5 (C), 129.8 (C), 129.6 (C2′′–H), 129.5 (C–H), 129.0 (C6–H), 128.7 (C3′′–H), 128.4 (C–H), 128.3 (C), 127.0 (CH), 126.7 (CH), 126.4 (C4–H), 126.3 (CH), 126.1 (C3a), 126.0 (C3′′′–H), 125.8 (CH), 123.9 (CH), 123.8 (CH), 123.6 (C), 123.1 (C), 121.8 (C5–H), 109.3 (C7–H), 73.3 (C3/C2′), 64.8 (C3′–H), 60.2 (C5′–H2), 43.4 (C4′–H), 34.6 (N–CH3) ppm.
(3S,3′R,4′S)-4′-(4-Bromophenyl)-1′-methyl-3′-(pyrene-1-carbonyl)spiro[indoline-3,2′-pyrrolidin]-2-one (4c). Yellow powder; mp 157–159 °C. IR (KBr): νmax = 3206 (NH), 3046 (CH arom.), 2935 (CH aliph.), 1716 (C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1679 (C
O), 1679 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 10.02 (s, 1H, NH), 8.30 (d, J = 7.4 Hz, 1H), 8.27 (d, J = 7.7 Hz, 1H), 8.22 (d, J = 8.7 Hz, 1H), 8.17–8.03 (m, 3H), 7.93 (d, J = 9.5 Hz, 1H), 7.90 (d, J = 8.0 Hz, 1H, C3′′′–H), 7.80 (d, J = 9.7 Hz, 1H), 7.60 (d, J = 7.7 Hz, 2H, C3′′–H), 7.55 (d, J = 7.7 Hz, 2H, C2′′–H), 7.33 (d, J = 7.2 Hz, 1H, C4–H), 6.89 (t, J = 7.4 Hz, 1H, C5–H), 6.76 (t, J = 7.4 Hz, 1H, C6–H), 6.03 (d, J = 7.6 Hz, 1H, C7–H), 4.78 (d, J = 9.3 Hz, 1H, C3′–H), 4.53 (q, J = 8.7 Hz, 1H, C4′–H), 3.48 (d, J = 9.0 Hz, 1H, C5′–H), 3.37 (d, J = 9.6 Hz, 1H, C5′–H), 1.98 (s, 3H, N–CH3) ppm. 13C NMR (100 MHz, DMSO-d6): δ 199.9 (C1′′′), 177.7 (C2), 141.9 (C1′′), 141.7 (C7a), 133.2 (C), 131.7 (C3′′–H), 131.6 (C), 130.5 (C), 130.1 (C2′′–H), 129.8 (C), 129.6 (C–H), 129.0 (C6–H), 128.4 (C–H), 128.3 (C), 127.1 (CH), 126.7 (CH), 126.4 (C4–H), 126.3 (CH), 126.2 (C3a), 126.1 (C3′′′–H), 125.9 (CH), 123.9 (CH), 123.8 (CH), 123.6 (C), 123.1 (C), 121.8 (C5–H), 119.9 (C4′′–Br), 109.3 (C7–H), 73.3 (C3/C2′), 64.8 (C3′–H), 60.2 (C5′–H2), 43.4 (C4′–H), 34.6 (N–CH3) ppm.
O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 10.02 (s, 1H, NH), 8.30 (d, J = 7.4 Hz, 1H), 8.27 (d, J = 7.7 Hz, 1H), 8.22 (d, J = 8.7 Hz, 1H), 8.17–8.03 (m, 3H), 7.93 (d, J = 9.5 Hz, 1H), 7.90 (d, J = 8.0 Hz, 1H, C3′′′–H), 7.80 (d, J = 9.7 Hz, 1H), 7.60 (d, J = 7.7 Hz, 2H, C3′′–H), 7.55 (d, J = 7.7 Hz, 2H, C2′′–H), 7.33 (d, J = 7.2 Hz, 1H, C4–H), 6.89 (t, J = 7.4 Hz, 1H, C5–H), 6.76 (t, J = 7.4 Hz, 1H, C6–H), 6.03 (d, J = 7.6 Hz, 1H, C7–H), 4.78 (d, J = 9.3 Hz, 1H, C3′–H), 4.53 (q, J = 8.7 Hz, 1H, C4′–H), 3.48 (d, J = 9.0 Hz, 1H, C5′–H), 3.37 (d, J = 9.6 Hz, 1H, C5′–H), 1.98 (s, 3H, N–CH3) ppm. 13C NMR (100 MHz, DMSO-d6): δ 199.9 (C1′′′), 177.7 (C2), 141.9 (C1′′), 141.7 (C7a), 133.2 (C), 131.7 (C3′′–H), 131.6 (C), 130.5 (C), 130.1 (C2′′–H), 129.8 (C), 129.6 (C–H), 129.0 (C6–H), 128.4 (C–H), 128.3 (C), 127.1 (CH), 126.7 (CH), 126.4 (C4–H), 126.3 (CH), 126.2 (C3a), 126.1 (C3′′′–H), 125.9 (CH), 123.9 (CH), 123.8 (CH), 123.6 (C), 123.1 (C), 121.8 (C5–H), 119.9 (C4′′–Br), 109.3 (C7–H), 73.3 (C3/C2′), 64.8 (C3′–H), 60.2 (C5′–H2), 43.4 (C4′–H), 34.6 (N–CH3) ppm.
(3S,3′R,4′S)-4′-(4-Methoxyphenyl)-1′-methyl-3′-(pyrene-1-carbonyl)spiro[indoline-3,2′-pyrrolidin]-2-one (4d). Yellow powder; mp 118–120 °C. IR (KBr): νmax = 3394 (NH), 3040 (CH arom.), 2934 (CH aliph.), 1717 (C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1681 (C
O), 1681 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 8.61 (s, 1H, NH), 8.22–8.04 (m, 6H), 7.95 (d, J = 9.6 Hz, 2H), 7.93 (d, J = 8.0 Hz, 1H, C3′′′–H), 7.63 (d, J = 8.3 Hz, 2H, C2′′–H), 7.55 (d, J = 8.3 Hz, 2H, C3′′–H), 7.52 (d, J = 7.3 Hz, 1H, C4–H), 6.91–6.89 (m, 2H, C5–H, C6–H), 6.04 (d, J = 7.7 Hz, 1H, C7–H), 4.91 (d, J = 9.5 Hz, 1H, C3′–H), 4.71 (q, J = 8.1 Hz, 1H, C4′–H), 3.83 (s, 3H, O–CH3), 3.73 (d, J = 8.6 Hz, 1H, C5′–H), 3.56 (d, J = 8.6 Hz, 1H, C5′–H), 2.14 (s, 3H, N–CH3) ppm. 13C NMR (100 MHz, DMSO-d6): δ 196.3 (C1′′′), 161.8 (C2), 158.5 (C1′′), 146.2 (C7a), 133.2 (C4′′), 131.2 (C), 131.4 (C), 130.5 (C), 129.8 (C), 129.6 (C2′′–H), 129.5 (C–H), 129.0 (C6–H), 128.7 (C3′′–H), 128.4 (C–H), 128.3 (C), 127.0 (CH), 126.7 (CH), 126.4 (C4–H), 126.3 (CH), 126.1 (C3a), 126.0 (C3′′′–H), 125.8 (CH), 124.1 (CH), 123.9 (CH), 114.4 (C), 114.2 (C), 114.0 (C5–H), 109.6 (C7–H), 74.2 (C3/C2′), 64.8 (C3′–H), 60.9 (C5′–H2), 55.4 (O–CH3), 44.0 (C4′–H), 35.1 (N–CH3) ppm.
O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 8.61 (s, 1H, NH), 8.22–8.04 (m, 6H), 7.95 (d, J = 9.6 Hz, 2H), 7.93 (d, J = 8.0 Hz, 1H, C3′′′–H), 7.63 (d, J = 8.3 Hz, 2H, C2′′–H), 7.55 (d, J = 8.3 Hz, 2H, C3′′–H), 7.52 (d, J = 7.3 Hz, 1H, C4–H), 6.91–6.89 (m, 2H, C5–H, C6–H), 6.04 (d, J = 7.7 Hz, 1H, C7–H), 4.91 (d, J = 9.5 Hz, 1H, C3′–H), 4.71 (q, J = 8.1 Hz, 1H, C4′–H), 3.83 (s, 3H, O–CH3), 3.73 (d, J = 8.6 Hz, 1H, C5′–H), 3.56 (d, J = 8.6 Hz, 1H, C5′–H), 2.14 (s, 3H, N–CH3) ppm. 13C NMR (100 MHz, DMSO-d6): δ 196.3 (C1′′′), 161.8 (C2), 158.5 (C1′′), 146.2 (C7a), 133.2 (C4′′), 131.2 (C), 131.4 (C), 130.5 (C), 129.8 (C), 129.6 (C2′′–H), 129.5 (C–H), 129.0 (C6–H), 128.7 (C3′′–H), 128.4 (C–H), 128.3 (C), 127.0 (CH), 126.7 (CH), 126.4 (C4–H), 126.3 (CH), 126.1 (C3a), 126.0 (C3′′′–H), 125.8 (CH), 124.1 (CH), 123.9 (CH), 114.4 (C), 114.2 (C), 114.0 (C5–H), 109.6 (C7–H), 74.2 (C3/C2′), 64.8 (C3′–H), 60.9 (C5′–H2), 55.4 (O–CH3), 44.0 (C4′–H), 35.1 (N–CH3) ppm.
(3S,3′R,4′S)-1′-Methyl-4′-(4-nitrophenyl)-3′-(pyrene-1-carbonyl)spiro[indoline-3,2′-pyrrolidin]-2-one (4e). Pale brown powder; mp 161–163 °C. IR (KBr): νmax = 3340 (NH), 3047 (CH arom.), 2941 (CH aliph.), 1716 (C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1680 (C
O), 1680 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 10.0 (s, 1H, NH), 8.42–7.77 (m, 11H), 7.40–7.33 (m, 3H, C4–H and pyrene-H) 6.90 (t, J = 7.6 Hz, 1H, C5–H), 6.75 (t, J = 7.7 Hz, 1H, C6–H), 6.03 (d, J = 7.9 Hz, 1H, C7–H), 4.86 (d, J = 9.0 Hz, 1H, C3′–H), 4.71 (q, J = 8.1 Hz, 1H, C4′–H), 3.41 (d, J = 8.6 Hz, 1H, C5′–H), 3.37 (d, J = 8.6 Hz, 1H, C5′–H), 1.99 (s, 3H, N–CH3) ppm. 13C NMR (100 MHz, DMSO-d6): δ 199.6 (C1′′′), 177.4 (C2), 146.6 (C4′′–NO2), 146.4 (C1′′), 141.7 (C7a), 133.3 (C), 131.3 (C), 130.5 (C), 129.8 (C), 129.6 (CH), 129.5 (C–H), 129.1 (C2′′–H), 129.0 (C6–H), 128.4 (C–H), 127.0 (CH), 126.7 (C), 126.6 (CH), 126.3 (CH), 126.2 (C4–H), 126.0 (C3′′′–H), 125.8 (C3a), 123.9 (C3′′–H), 123.7 (CH), 123.5 (C), 123.1 (C), 122.8 (CH), 121.8 (C5–H), 109.3 (C7–H), 73.4 (C3/C2′), 64.6 (C3′–H), 60.0 (C5′–H2), 43.6 (C4′–H), 34.5 (N–CH3) ppm.
O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 10.0 (s, 1H, NH), 8.42–7.77 (m, 11H), 7.40–7.33 (m, 3H, C4–H and pyrene-H) 6.90 (t, J = 7.6 Hz, 1H, C5–H), 6.75 (t, J = 7.7 Hz, 1H, C6–H), 6.03 (d, J = 7.9 Hz, 1H, C7–H), 4.86 (d, J = 9.0 Hz, 1H, C3′–H), 4.71 (q, J = 8.1 Hz, 1H, C4′–H), 3.41 (d, J = 8.6 Hz, 1H, C5′–H), 3.37 (d, J = 8.6 Hz, 1H, C5′–H), 1.99 (s, 3H, N–CH3) ppm. 13C NMR (100 MHz, DMSO-d6): δ 199.6 (C1′′′), 177.4 (C2), 146.6 (C4′′–NO2), 146.4 (C1′′), 141.7 (C7a), 133.3 (C), 131.3 (C), 130.5 (C), 129.8 (C), 129.6 (CH), 129.5 (C–H), 129.1 (C2′′–H), 129.0 (C6–H), 128.4 (C–H), 127.0 (CH), 126.7 (C), 126.6 (CH), 126.3 (CH), 126.2 (C4–H), 126.0 (C3′′′–H), 125.8 (C3a), 123.9 (C3′′–H), 123.7 (CH), 123.5 (C), 123.1 (C), 122.8 (CH), 121.8 (C5–H), 109.3 (C7–H), 73.4 (C3/C2′), 64.6 (C3′–H), 60.0 (C5′–H2), 43.6 (C4′–H), 34.5 (N–CH3) ppm.
(3S,3′R,4′S)-4′-(4-Cyanophenyl)-1′-methyl-3′-(pyrene-1-carbonyl)spiro[indoline-3,2′-pyrrolidin]-2-one (4f). Orange crystals; mp 150–152 °C. IR (KBr): νmax = 3397 (NH), 3048 (CH arom.), 2939 (CH aliph.), 2226 (CN), 1716 (C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1682 (C
O), 1682 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 10.0 (s, 1H, NH), 8.44–8.06 (m, 6H), 7.96 (d, J = 9.4 Hz, 2H), 7.89 (d, J = 7.9 Hz, 2H, C3′′–H), 7.84–7.77 (m, 3H, C2′′–H and pyrene-H), 7.36 (d, J = 7.2 Hz, 1H, C4–H), 6.90 (t, J = 7.5 Hz, 1H, C5–H), 6.75 (t, J = 7.6 Hz, 1H, C6–H), 6.01 (d, J = 7.7 Hz, 1H, C7–H), 4.82 (d, J = 9.1 Hz, 1H, C3′–H), 4.65 (q, J = 8.0 Hz, 1H, C4′–H), 3.56–3.36 (m, 2H, C5′–H), 1.98 (s, 3H, N–CH3) ppm. 13C NMR (100 MHz, DMSO-d6): δ 199.6 (C1′′′), 177.4 (C2), 148.5 (C1′′), 141.7 (C7a), 133.2 (C), 132.7 (C3′′–H), 131.3 (C), 130.4 (C), 129.7 (C), 129.5 (CH), 129.0 (C6–H), 128.9 (C2′′–H), 128.4 (C–H & C overlapping), 127.0 (CH), 126.6 (CH), 126.3 (CH), 126.2 (C4–H), 126.0 (CH & C3′′′–H overlapping), 125.9 (C3a), 123.9 (C–H), 123.7 (CH), 123.5 (C), 123.0 (C), 121.8 (C5–H), 118.9 (CN), 109.6 (C4′′), 109.2 (C7–H), 73.3 (C3/C2′), 64.5 (C3′–H), 60.0 (C5′–H2), 43.8 (C4′–H), 34.5 (N–CH3) ppm.
O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 10.0 (s, 1H, NH), 8.44–8.06 (m, 6H), 7.96 (d, J = 9.4 Hz, 2H), 7.89 (d, J = 7.9 Hz, 2H, C3′′–H), 7.84–7.77 (m, 3H, C2′′–H and pyrene-H), 7.36 (d, J = 7.2 Hz, 1H, C4–H), 6.90 (t, J = 7.5 Hz, 1H, C5–H), 6.75 (t, J = 7.6 Hz, 1H, C6–H), 6.01 (d, J = 7.7 Hz, 1H, C7–H), 4.82 (d, J = 9.1 Hz, 1H, C3′–H), 4.65 (q, J = 8.0 Hz, 1H, C4′–H), 3.56–3.36 (m, 2H, C5′–H), 1.98 (s, 3H, N–CH3) ppm. 13C NMR (100 MHz, DMSO-d6): δ 199.6 (C1′′′), 177.4 (C2), 148.5 (C1′′), 141.7 (C7a), 133.2 (C), 132.7 (C3′′–H), 131.3 (C), 130.4 (C), 129.7 (C), 129.5 (CH), 129.0 (C6–H), 128.9 (C2′′–H), 128.4 (C–H & C overlapping), 127.0 (CH), 126.6 (CH), 126.3 (CH), 126.2 (C4–H), 126.0 (CH & C3′′′–H overlapping), 125.9 (C3a), 123.9 (C–H), 123.7 (CH), 123.5 (C), 123.0 (C), 121.8 (C5–H), 118.9 (CN), 109.6 (C4′′), 109.2 (C7–H), 73.3 (C3/C2′), 64.5 (C3′–H), 60.0 (C5′–H2), 43.8 (C4′–H), 34.5 (N–CH3) ppm.
(3S,3′R,4′S,5′R)-4′,5′-Diphenyl-3′-(pyrene-1-carbonyl)-spiro[indoline-3,2′-pyrrolidin]-2-one (7a). Orange crystals; mp 100–101 °C. IR (KBr): νmax = 3347 (NH), 3291 (NH), 3029 (CH arom.), 2971 (CH aliph.), 1706 (C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1675 (C
O), 1675 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 9.97 (s, 1H, N1–H), 8.35–8.04 (m, 6H, pyrene H), 7.97–7.84 (m, 3H, pyrene H), 7.63 (d, J = 7.3 Hz, 1H, C4–H), 7.52 (d, J = 7.6 Hz, 2H, Cph–H), 7.44 (d, J = 7.5 Hz, 2H, Cph–H), 7.35–7.10 (m, 6H, Cph–H), 7.02 (t, J = 7.6 Hz, 1H, C5–H), 6.83 (t, J = 7.6 Hz, 1H, C6–H), 6.10 (d, J = 7.5 Hz, 1H, C7–H), 5.10 (d, J = 11.1 Hz, 1H, C3′–H), 5.05 (dd, J = 10.2, 4.9 Hz, 1H, C5′–H), 4.22 (t, J = 10.7 Hz, 1H, C4′–H), 4.02 (d, J = 5.1 Hz, 1H, N1′–H) ppm. 13C NMR (100 MHz, DMSO-d6): δ 200.2 (C1′′′), 181.1 (C2), 142.4 (C1′′), 141.4 (C7a), 139.2 (C5′a), 133.1 (C), 132.1 (C), 130.8 (C), 130.4 (C), 129.7 (C), 129.5 (C–H), 128.5 (C6–H), 128.4 (C–H), 128.1 (C–H), 128.0 (C–H), 127.9 (C–H), 127.4 (C–H), 127.3 (C–H), 127.2 (C–H), 127.0 (C–H), 126.9 (C–H), 126.6 (C–H), 126.3 (C4–H), 126.0 (C–H), 125.6 (C–H), 124.0 (C–H), 123.8 (C–H), 123.7 (C), 123.5 (C), 123.1 (C), 121.8 (C5–H), 109.0 (C7–H), 67.9 (C3/C2′), 67.5 (C5′–H), 65.0 (C3′–H), 55.9 (C4′–H) ppm.
O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 9.97 (s, 1H, N1–H), 8.35–8.04 (m, 6H, pyrene H), 7.97–7.84 (m, 3H, pyrene H), 7.63 (d, J = 7.3 Hz, 1H, C4–H), 7.52 (d, J = 7.6 Hz, 2H, Cph–H), 7.44 (d, J = 7.5 Hz, 2H, Cph–H), 7.35–7.10 (m, 6H, Cph–H), 7.02 (t, J = 7.6 Hz, 1H, C5–H), 6.83 (t, J = 7.6 Hz, 1H, C6–H), 6.10 (d, J = 7.5 Hz, 1H, C7–H), 5.10 (d, J = 11.1 Hz, 1H, C3′–H), 5.05 (dd, J = 10.2, 4.9 Hz, 1H, C5′–H), 4.22 (t, J = 10.7 Hz, 1H, C4′–H), 4.02 (d, J = 5.1 Hz, 1H, N1′–H) ppm. 13C NMR (100 MHz, DMSO-d6): δ 200.2 (C1′′′), 181.1 (C2), 142.4 (C1′′), 141.4 (C7a), 139.2 (C5′a), 133.1 (C), 132.1 (C), 130.8 (C), 130.4 (C), 129.7 (C), 129.5 (C–H), 128.5 (C6–H), 128.4 (C–H), 128.1 (C–H), 128.0 (C–H), 127.9 (C–H), 127.4 (C–H), 127.3 (C–H), 127.2 (C–H), 127.0 (C–H), 126.9 (C–H), 126.6 (C–H), 126.3 (C4–H), 126.0 (C–H), 125.6 (C–H), 124.0 (C–H), 123.8 (C–H), 123.7 (C), 123.5 (C), 123.1 (C), 121.8 (C5–H), 109.0 (C7–H), 67.9 (C3/C2′), 67.5 (C5′–H), 65.0 (C3′–H), 55.9 (C4′–H) ppm.
(3S,3′R,4′S,5′R)-4′-(4-Chlorophenyl)-5′-phenyl-3′-(pyrene-1-carbonyl)spiro[indoline-3,2′-pyrrolidin]-2-one (7b). Yellow powder; mp 180–182 °C. IR (KBr): νmax = 3325 (NH), 3180 (NH), 3038 (CH arom.), 2940 (CH aliph.), 1705 (C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1670 (C
O), 1670 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 9.96 (s, 1H, N1–H), 8.62 (d, J = 8.0 Hz, 1H, C3′′′–H), 8.40 (d, J = 7.6 Hz, 1H), 8.32–8.25 (m, 5H), 8.10 (d, J = 8.0 Hz, 2H, C3′′–H), 8.09–8.01 (m, 2H), 7.98 (d, J = 8.6 Hz, 2H, C2′′–H), 7.94 (d, J = 7.3 Hz, 1H, C4–H), 7.91 (d, J = 7.3 Hz, 2H, C5′b–H), 7.84 (d, J = 7.3 Hz, 2H, C5′c–H), 7.60–7.54 (m, 1H, C5′d–H), 7.15 (t, J = 7.0 Hz, 1H, C5–H), 6.75 (t, J = 7.0 Hz, 1H, C6–H), 6.02 (d, J = 7.7 Hz, 1H, C7–H), 5.55 (d, J = 11.0 Hz, 1H, C3′–H), 5.01 (d, J = 11.2 Hz, 1H, C5′–H), 4.17 (t, J = 10.8 Hz, 1H, C4′–H), 4.01 (br, 1H, N1′–H) ppm. 13C NMR (100 MHz, DMSO-d6): δ 200.1 (C1′′′), 180.9 (C2), 142.9 (C4′′), 141.3 (C1′′), 139.1 (C7a), 135.9 (C5′a), 133.6 (C), 132.1 (C), 131.7 (C3a), 131.2 (C), 130.6 (C2′′–H), 130.6 (C), 130.3 (C–H), 130.2 (C–H), 129.6 (C), 128.7 (C6–H), 128.6 (C5′c–H), 127.8 (CH), 127.6 (C5′d–H), 127.5 (C5′b–H), 127.1 (CH), 126.8 (C–H), 126.5 (C3′′′–H), 125.1 (C4–H), 124.4 (CH), 124.0 (CH), 123.5 (C3′′–H), 122.4 (C), 122.3 (CH), 120.9 (C), 120.4 (C5–H), 109.3 (C7–H), 72.4 (C3/C2′), 67.5 (C5′–H), 65.2 (C3′–H), 55.4 (C4′–H) ppm.
O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 9.96 (s, 1H, N1–H), 8.62 (d, J = 8.0 Hz, 1H, C3′′′–H), 8.40 (d, J = 7.6 Hz, 1H), 8.32–8.25 (m, 5H), 8.10 (d, J = 8.0 Hz, 2H, C3′′–H), 8.09–8.01 (m, 2H), 7.98 (d, J = 8.6 Hz, 2H, C2′′–H), 7.94 (d, J = 7.3 Hz, 1H, C4–H), 7.91 (d, J = 7.3 Hz, 2H, C5′b–H), 7.84 (d, J = 7.3 Hz, 2H, C5′c–H), 7.60–7.54 (m, 1H, C5′d–H), 7.15 (t, J = 7.0 Hz, 1H, C5–H), 6.75 (t, J = 7.0 Hz, 1H, C6–H), 6.02 (d, J = 7.7 Hz, 1H, C7–H), 5.55 (d, J = 11.0 Hz, 1H, C3′–H), 5.01 (d, J = 11.2 Hz, 1H, C5′–H), 4.17 (t, J = 10.8 Hz, 1H, C4′–H), 4.01 (br, 1H, N1′–H) ppm. 13C NMR (100 MHz, DMSO-d6): δ 200.1 (C1′′′), 180.9 (C2), 142.9 (C4′′), 141.3 (C1′′), 139.1 (C7a), 135.9 (C5′a), 133.6 (C), 132.1 (C), 131.7 (C3a), 131.2 (C), 130.6 (C2′′–H), 130.6 (C), 130.3 (C–H), 130.2 (C–H), 129.6 (C), 128.7 (C6–H), 128.6 (C5′c–H), 127.8 (CH), 127.6 (C5′d–H), 127.5 (C5′b–H), 127.1 (CH), 126.8 (C–H), 126.5 (C3′′′–H), 125.1 (C4–H), 124.4 (CH), 124.0 (CH), 123.5 (C3′′–H), 122.4 (C), 122.3 (CH), 120.9 (C), 120.4 (C5–H), 109.3 (C7–H), 72.4 (C3/C2′), 67.5 (C5′–H), 65.2 (C3′–H), 55.4 (C4′–H) ppm.
(3S,3′R,4′S,5′R)-4′-(4-Bromophenyl)-5′-phenyl-3′-(pyrene-1-carbonyl)spiro[indoline-3,2′-pyrrolidin]-2-one (7c). Yellow powder; mp 234–235 °C. IR (KBr): νmax = 3345 (NH), 3327 (NH), 3036 (CH arom.), 2945 (CH aliph.), 1704 (C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1670 (C
O), 1670 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 9.93 (s, 1H, N1–H), 8.65 (d, J = 8.0 Hz, 1H, C3′′′–H), 8.42 (d, J = 7.6 Hz, 1H), 8.36–8.26 (m, 5H), 8.19 (d, J = 8.5 Hz, 2H, C3′′–H), 8.14–8.09 (m, 2H), 8.00 (d, J = 8.6 Hz, 2H, C2′′–H), 7.96 (d, J = 7.3 Hz, 1H, C4–H), 7.92 (d, J = 7.3 Hz, 2H, C5′b–H), 7.83 (d, J = 7.3 Hz, 2H, C5′c–H), 7.60–7.53 (m, 1H, C5′d–H), 7.16 (t, J = 7.0 Hz, 1H, C5–H), 6.73 (t, J = 7.0 Hz, 1H, C6–H), 6.01 (d, J = 7.7 Hz, 1H, C7–H), 5.54 (d, J = 11.0 Hz, 1H, C3′–H), 5.05 (d, J = 11.2 Hz, 1H, C5′–H), 4.15 (t, J = 10.8 Hz, 1H, C4′–H), 4.03 (br, 1H, N1′–H) ppm. 13C NMR (100 MHz, DMSO-d6): δ 200.3 (C1′′′), 181.4 (C2), 142.7 (C4′′), 141.8 (C1′′), 139.0 (C7a), 135.9 (C5′a), 133.7 (C), 132.1 (C), 131.9 (C3a), 131.2 (C), 130.9 (C2′′–H), 130.7 (C), 130.5 (C–H), 130.2 (C–H), 129.4 (C), 128.7 (C6–H), 128.6 (C5′c–H), 127.8 (CH), 127.6 (C5′dH), 127.5 (C5′b–H), 127.1 (CH), 126.8 (C–H), 126.5 (C3′′′–H), 124.9 (C4–H), 124.4 (CH), 124.0 (CH), 123.5 (C3′′–H), 122.4 (C), 122.3 (CH), 120.9 (C), 120.4 (C5–H), 109.4 (C7–H), 72.3 (C3/C2′), 68.2 (C5′–H), 64.9 (C3′–H), 55.2 (C4′–H) ppm.
O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 9.93 (s, 1H, N1–H), 8.65 (d, J = 8.0 Hz, 1H, C3′′′–H), 8.42 (d, J = 7.6 Hz, 1H), 8.36–8.26 (m, 5H), 8.19 (d, J = 8.5 Hz, 2H, C3′′–H), 8.14–8.09 (m, 2H), 8.00 (d, J = 8.6 Hz, 2H, C2′′–H), 7.96 (d, J = 7.3 Hz, 1H, C4–H), 7.92 (d, J = 7.3 Hz, 2H, C5′b–H), 7.83 (d, J = 7.3 Hz, 2H, C5′c–H), 7.60–7.53 (m, 1H, C5′d–H), 7.16 (t, J = 7.0 Hz, 1H, C5–H), 6.73 (t, J = 7.0 Hz, 1H, C6–H), 6.01 (d, J = 7.7 Hz, 1H, C7–H), 5.54 (d, J = 11.0 Hz, 1H, C3′–H), 5.05 (d, J = 11.2 Hz, 1H, C5′–H), 4.15 (t, J = 10.8 Hz, 1H, C4′–H), 4.03 (br, 1H, N1′–H) ppm. 13C NMR (100 MHz, DMSO-d6): δ 200.3 (C1′′′), 181.4 (C2), 142.7 (C4′′), 141.8 (C1′′), 139.0 (C7a), 135.9 (C5′a), 133.7 (C), 132.1 (C), 131.9 (C3a), 131.2 (C), 130.9 (C2′′–H), 130.7 (C), 130.5 (C–H), 130.2 (C–H), 129.4 (C), 128.7 (C6–H), 128.6 (C5′c–H), 127.8 (CH), 127.6 (C5′dH), 127.5 (C5′b–H), 127.1 (CH), 126.8 (C–H), 126.5 (C3′′′–H), 124.9 (C4–H), 124.4 (CH), 124.0 (CH), 123.5 (C3′′–H), 122.4 (C), 122.3 (CH), 120.9 (C), 120.4 (C5–H), 109.4 (C7–H), 72.3 (C3/C2′), 68.2 (C5′–H), 64.9 (C3′–H), 55.2 (C4′–H) ppm.
(3S,3′R,4′S,5′R)-4′-(4-Methoxyphenyl)-5′-phenyl-3′-(pyrene-1-carbonyl)spiro[indoline-3,2′-pyrrolidin]-2-one (7d). Yellow powder; mp 177–179 °C. IR (KBr): νmax = 3324 (NH), 3182 (NH), 3034 (CH arom.), 2941 (CH aliph.), 1700 (C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1668 (C
O), 1668 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 10.04 (s, 1H, N1–H), 8.59–8.42 (m, 3H), 8.37 (d, J = 8.5 Hz, 2H, C3′′–H), 8.33–8.28 (m, 4H), 8.23–8.10 (m, 2H), 8.08 (d, J = 8.4 Hz, 2H, C2′′–H), 7.91 (d, J = 7.3 Hz, 1H, C4–H), 7.80 (d, J = 7.3 Hz, 2H, C5′b–H), 7.26 (d, J = 7.3 Hz, 2H, C5′c–H), 7.12–7.10 (m, 1H, C5′d–H), 6.69 (t, J = 7.5 Hz, 1H, C5–H), 6.63 (t, J = 7.6 Hz, 1H, C6–H), 5.97 (d, J = 11.6 Hz, 1H, C7–H), 5.55 (d, J = 11.2 Hz, 1H, C3′–H), 5.05 (d, J = 10.3 Hz, 1H, C5′–H), 4.51 (t, J = 10.7 Hz, 1H, C4′–H), 4.18 (br, 1H, N1′–H), 3.60 (s, 3H, O–CH3) ppm. 13C NMR (100 MHz, DMSO-d6): δ 201.7 (C1′′′), 181.2 (C2), 143.2 (C4′′), 142.8 (C1′′), 133.7 (C7a), 133.4 (C5′a), 133.1 (C), 131.0 (C), 130.2 (C3a), 130.0 (C), 129.4 (C2′′–H), 129.2 (C), 129.0 (C–H), 128.8 (C–H), 128.1 (C), 127.8 (C6–H), 127.5 (C5′c–H), 127.1 (CH), 126.8 (C5′dH), 126.4 (C5′b–H), 124.9 (CH), 124.4 (C–H), 124.3 (C3′′′–H), 124.2 (C4–H), 123.9 (CH), 123.5 (CH), 122.2 (C3′′–H), 114.9 (C), 114.4 (CH), 114.0 (C), 113.8 (C5–H), 109.6 (C7–H), 72.4 (C3/C2′), 65.5 (C5′–H), 61.3 (C3′–H), 55.3 (O–CH3), 54.8 (C4′–H) ppm.
O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 10.04 (s, 1H, N1–H), 8.59–8.42 (m, 3H), 8.37 (d, J = 8.5 Hz, 2H, C3′′–H), 8.33–8.28 (m, 4H), 8.23–8.10 (m, 2H), 8.08 (d, J = 8.4 Hz, 2H, C2′′–H), 7.91 (d, J = 7.3 Hz, 1H, C4–H), 7.80 (d, J = 7.3 Hz, 2H, C5′b–H), 7.26 (d, J = 7.3 Hz, 2H, C5′c–H), 7.12–7.10 (m, 1H, C5′d–H), 6.69 (t, J = 7.5 Hz, 1H, C5–H), 6.63 (t, J = 7.6 Hz, 1H, C6–H), 5.97 (d, J = 11.6 Hz, 1H, C7–H), 5.55 (d, J = 11.2 Hz, 1H, C3′–H), 5.05 (d, J = 10.3 Hz, 1H, C5′–H), 4.51 (t, J = 10.7 Hz, 1H, C4′–H), 4.18 (br, 1H, N1′–H), 3.60 (s, 3H, O–CH3) ppm. 13C NMR (100 MHz, DMSO-d6): δ 201.7 (C1′′′), 181.2 (C2), 143.2 (C4′′), 142.8 (C1′′), 133.7 (C7a), 133.4 (C5′a), 133.1 (C), 131.0 (C), 130.2 (C3a), 130.0 (C), 129.4 (C2′′–H), 129.2 (C), 129.0 (C–H), 128.8 (C–H), 128.1 (C), 127.8 (C6–H), 127.5 (C5′c–H), 127.1 (CH), 126.8 (C5′dH), 126.4 (C5′b–H), 124.9 (CH), 124.4 (C–H), 124.3 (C3′′′–H), 124.2 (C4–H), 123.9 (CH), 123.5 (CH), 122.2 (C3′′–H), 114.9 (C), 114.4 (CH), 114.0 (C), 113.8 (C5–H), 109.6 (C7–H), 72.4 (C3/C2′), 65.5 (C5′–H), 61.3 (C3′–H), 55.3 (O–CH3), 54.8 (C4′–H) ppm.
(3S,3′R,4′S,5′R)-4′-(4-Nitrophenyl)-5′-phenyl-3′-(pyrene-1-carbonyl)spiro[indoline-3,2′-pyrrolidin]-2-one (7e). Pale brown powder; mp 203–205 °C. IR (KBr): νmax = 3349 (NH), 3185 (NH), 3028 (CH arom.), 2946 (CH aliph.), 1715 (C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1669 (C
O), 1669 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 9.97 (s, 1H, N1–H), 8.34–8.22 (m, 3H), 8.20 (d, J = 8.5 Hz, 2H, C3′′–H), 8.17–8.02 (m, 4H), 8.00–7.85 (m, 2H), 7.80 (d, J = 8.4 Hz, 2H, C2′′–H), 7.62 (d, J = 7.3 Hz, 1H, C4–H), 7.44 (d, J = 7.3 Hz, 2H, C5′b–H), 7.30 (d, J = 7.3 Hz, 2H, C5′c–H), 7.27–7.26 (m, 1H, C5′d–H), 6.96 (t, J = 7.5 Hz, 1H, C5–H), 6.73 (t, J = 7.6 Hz, 1H, C6–H), 5.98 (d, J = 7.7 Hz, 1H, C7–H), 5.17 (d, J = 11.2 Hz, 1H, C3′–H), 5.04 (d, J = 10.3 Hz, 1H, C5′–H), 4.33 (t, J = 10.7 Hz, 1H, C4′–H), 4.12 (br, 1H, N1′–H) ppm. 13C NMR (100 MHz, DMSO-d6): δ (ppm) 199.6 (C1′′′), 180.8 (C2), 147.3 (C4′′–NO2), 146.5 (C1′′), 141.2 (C7a), 141.0 (C5′a), 133.3 (C), 131.4 (C), 130.6 (C3a), 130.5 (C), 129.9 (C2′′–H), 129.8 (C), 129.7 (C–H), 128.7 (C–H), 128.5 (C), 128.4 (C6–H), 128.3 (C5′c–H), 127.7 (CH), 127.4 (C5′dH), 127.2 (C5′b–H), 127.0 (CH), 126.7 (C–H), 126.4 (C3′′′–H), 126.1 (C4–H), 126.0 (CH), 124.0 (CH), 123.6 (C3′′–H), 123.5 (C), 123.1 (CH), 123.0 (C), 122.1 (C5–H), 109.0 (C7–H), 67.8 (C3/C2′), 67.6 (C5′–H), 64.4 (C3′–H), 55.6 (C4′–H) ppm.
O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 9.97 (s, 1H, N1–H), 8.34–8.22 (m, 3H), 8.20 (d, J = 8.5 Hz, 2H, C3′′–H), 8.17–8.02 (m, 4H), 8.00–7.85 (m, 2H), 7.80 (d, J = 8.4 Hz, 2H, C2′′–H), 7.62 (d, J = 7.3 Hz, 1H, C4–H), 7.44 (d, J = 7.3 Hz, 2H, C5′b–H), 7.30 (d, J = 7.3 Hz, 2H, C5′c–H), 7.27–7.26 (m, 1H, C5′d–H), 6.96 (t, J = 7.5 Hz, 1H, C5–H), 6.73 (t, J = 7.6 Hz, 1H, C6–H), 5.98 (d, J = 7.7 Hz, 1H, C7–H), 5.17 (d, J = 11.2 Hz, 1H, C3′–H), 5.04 (d, J = 10.3 Hz, 1H, C5′–H), 4.33 (t, J = 10.7 Hz, 1H, C4′–H), 4.12 (br, 1H, N1′–H) ppm. 13C NMR (100 MHz, DMSO-d6): δ (ppm) 199.6 (C1′′′), 180.8 (C2), 147.3 (C4′′–NO2), 146.5 (C1′′), 141.2 (C7a), 141.0 (C5′a), 133.3 (C), 131.4 (C), 130.6 (C3a), 130.5 (C), 129.9 (C2′′–H), 129.8 (C), 129.7 (C–H), 128.7 (C–H), 128.5 (C), 128.4 (C6–H), 128.3 (C5′c–H), 127.7 (CH), 127.4 (C5′dH), 127.2 (C5′b–H), 127.0 (CH), 126.7 (C–H), 126.4 (C3′′′–H), 126.1 (C4–H), 126.0 (CH), 124.0 (CH), 123.6 (C3′′–H), 123.5 (C), 123.1 (CH), 123.0 (C), 122.1 (C5–H), 109.0 (C7–H), 67.8 (C3/C2′), 67.6 (C5′–H), 64.4 (C3′–H), 55.6 (C4′–H) ppm.
(3S,3′R,4′S,5′R)-4′-(4-Cyanophenyl)-5′-phenyl-3′-(pyrene-1-carbonyl)spiro[indoline-3,2′-pyrrolidin]-2-one (7f). Yellow powder; mp 199–201 °C. IR (KBr): νmax = 3335 (NH), 3185 (NH), 3049 (CH arom.), 2957 (CH aliph.), 2226 (CN), 1716 (C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1670 (C
O), 1670 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 9.92 (s, 1H, N1–H), 8.27–7.97 (m, 7H), 7.91 (d, J = 9.3 Hz, 1H, C–H), 7.83 (d, J = 9.2 Hz, 1H, C–H), 7.75 (d, J = 8.0 Hz, 2H, C3′′–H), 7.67 (d, J = 8.0 Hz, 2H, C2′′–H), 7.56 (d, J = 7.3 Hz, 1H, C4–H), 7.37 (d, J = 7.3 Hz, 2H, C5′b–H), 7.26 (d, J = 7.3 Hz, 2H, C5′c–H), 7.24–7.16 (m, 1H, C5′d–H), 6.90 (t, J = 7.6 Hz, 1H, C5–H), 6.68 (t, J = 7.6 Hz, 1H, C6–H), 5.94 (d, J = 7.6 Hz, 1H, C7–H), 5.09 (d, J = 11.1 Hz, 1H, C3′–H), 4.97 (dd, J = 10.2, 5.4 Hz, 1H, C5′–H), 4.23 (t, J = 10.7 Hz, 1H, C4′–H), 4.05 (d, J = 5.4 Hz, 1H, N1′–H) ppm. 13C NMR (100 MHz, DMSO-d6): δ 199.7 (C1′′′), 180.9 (C2), 145.2 (C1′′), 141.2 (C7a), 141.1 (C5′a), 133.3 (C), 132.4 (C3′′–H), 131.4 (C), 130.6 (C3a), 130.4 (C), 129.7 (C2), 129.6 (C2′′–H & CH overlapping), 128.6 (C6–H), 128.5 (C), 128.4 (C–H), 128.2 (C5′c–H), 127.6 (C5′d–H), 127.2 (C5′b–H), 127.0 (C–H), 126.6 (C–H), 126.3 (C3′′′–H), 126.0 (C4–H & 2CH overlapping), 124.0 (CH), 123.8 (C3–H), 123.5 (C), 123.0 (C), 121.9 (C5–H), 118.8 (CN), 109.8 (C4′′), 109.0 (C7–H), 67.8 (C3/C2′), 67.5 (C5′–H), 64.3 (C3′–H), 55.8 (C4′–H) ppm.
O) cm−1. 1H NMR (400 MHz, DMSO-d6): δ 9.92 (s, 1H, N1–H), 8.27–7.97 (m, 7H), 7.91 (d, J = 9.3 Hz, 1H, C–H), 7.83 (d, J = 9.2 Hz, 1H, C–H), 7.75 (d, J = 8.0 Hz, 2H, C3′′–H), 7.67 (d, J = 8.0 Hz, 2H, C2′′–H), 7.56 (d, J = 7.3 Hz, 1H, C4–H), 7.37 (d, J = 7.3 Hz, 2H, C5′b–H), 7.26 (d, J = 7.3 Hz, 2H, C5′c–H), 7.24–7.16 (m, 1H, C5′d–H), 6.90 (t, J = 7.6 Hz, 1H, C5–H), 6.68 (t, J = 7.6 Hz, 1H, C6–H), 5.94 (d, J = 7.6 Hz, 1H, C7–H), 5.09 (d, J = 11.1 Hz, 1H, C3′–H), 4.97 (dd, J = 10.2, 5.4 Hz, 1H, C5′–H), 4.23 (t, J = 10.7 Hz, 1H, C4′–H), 4.05 (d, J = 5.4 Hz, 1H, N1′–H) ppm. 13C NMR (100 MHz, DMSO-d6): δ 199.7 (C1′′′), 180.9 (C2), 145.2 (C1′′), 141.2 (C7a), 141.1 (C5′a), 133.3 (C), 132.4 (C3′′–H), 131.4 (C), 130.6 (C3a), 130.4 (C), 129.7 (C2), 129.6 (C2′′–H & CH overlapping), 128.6 (C6–H), 128.5 (C), 128.4 (C–H), 128.2 (C5′c–H), 127.6 (C5′d–H), 127.2 (C5′b–H), 127.0 (C–H), 126.6 (C–H), 126.3 (C3′′′–H), 126.0 (C4–H & 2CH overlapping), 124.0 (CH), 123.8 (C3–H), 123.5 (C), 123.0 (C), 121.9 (C5–H), 118.8 (CN), 109.8 (C4′′), 109.0 (C7–H), 67.8 (C3/C2′), 67.5 (C5′–H), 64.3 (C3′–H), 55.8 (C4′–H) ppm.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are highly indebted to the Deanship of the Scientific Research (DSR), Umm Al-Qura University for full financial support of this work through the project number 15-SCI-3-1-0010. S. A. Ahmed is highly indebted to Alexander von Humboldt Foundation (AvH) and Prof. Jochen Mattay, Bielefeld University, Germany for helping with some analytical and spectroscopic measurements in addition to some labwares donations.Notes and references
- (a) I. Ugi, A. Dömling and W. Hörl, Endeavour, 1994, 18, 115–122 CrossRef; (b) S. L. Dax, J. J. McNally and M. A. Youngman, Curr. Med. Chem., 1999, 6, 255–270 Search PubMed; (c) L. Weber, K. Illgen and M. Almstetter, Synlett, 1999, 366–374 CrossRef; (d) A. Dömling, Curr. Opin. Chem. Biol., 2002, 6, 303–313 CrossRef; (e) L. Weber, Drug Discovery Today, 2002, 7, 143–147 CrossRef PubMed; (f) E. M. Hussein, Z. Naturforsch., 2012, 67b, 231–237 CrossRef; (g) A. Dömling, W. Wang and K. Wang, Chem. Rev., 2012, 112, 3083–3135 CrossRef PubMed; (h) E. M. Hussein, Monatsh. Chem., 2013, 144, 1691–1697 CrossRef; (i) E. M. Hussein, Russ. J. Org. Chem., 2015, 51, 54–64 CrossRef; (j) E. M. Hussein and S. A. Ahmed, Chem. Heterocycl. Compd., 2017, 53, 1148–1155 CrossRef.
- (a) F. Shi, R. Mancuso and R. C. Larock, Tetrahedron Lett., 2009, 50, 4067–4070 CrossRef PubMed; (b) F. Shi, R. Zhu, X. Liang and S. Tu, Adv. Synth. Catal., 2013, 355, 2447–2458 CrossRef; (c) C. Wang, R. Zhu, J. Zheng, F. Shi and S. Tu, J. Org. Chem., 2015, 80, 512–520 CrossRef PubMed; (d) W. Dai, X. Jiang, Q. Wu, F. Shi and S. Tu, J. Org. Chem., 2015, 80, 5737–5744 CrossRef PubMed.
- (a) A. K. Ganguly, N. Seah, V. Popov, C. H. Wang, R. Kuang, A. K. Saksena, B. N. Pramanik, T. M. Chan and A. F. McPhail, Tetrahedron Lett., 2002, 43, 8981–8983 CrossRef; (b) K. A. Ahrendt and R. M. Williams, Org. Lett., 2004, 6, 4539–4541 CrossRef PubMed; (c) V. Nair and T. D. Suja, Tetrahedron, 2007, 63, 12247–12275 CrossRef; (d) M. Ghandi, A. Yari, S. J. T. Rezaei and A. Taheri, Tetrahedron Lett., 2009, 50, 4724–4726 CrossRef; (e) S. V. Karthikeyan, B. D. Bala, V. P. A. Raja, S. Perumal, P. Yogeeswari and D. Sriram, Bioorg. Med. Chem. Lett., 2010, 20, 350–353 CrossRef PubMed.
- T. Onishi, P. R. Sebahar and R. M. Williams, Org. Lett., 2003, 5, 3135–3137 CrossRef PubMed.
- M. N. G. James and G. J. B. Williams, Can. J. Chem., 1972, 50, 2407–2412 CrossRef.
- A. Jossang, P. Jossang, H. A. Hadi, T. Sevenet and B. Bodo, J. Org. Chem., 1991, 56, 6527–6530 CrossRef.
- N. Anderton, P. A. Cockrum, S. M. Colegate, J. A. Edgar, K. Flower, I. Vit and R. I. Willing, Phytochemistry, 1998, 48, 437–439 CrossRef.
- T. H. Kang, K. Matsumoto, Y. Murakami, H. Takayama, M. Kitajima, N. Aimi and H. Watanabe, Eur. J. Pharmacol., 2002, 444, 39–45 CrossRef PubMed.
- T. Usui, M. Kondoh, C.-B. Cui, T. Mayumi and H. Osada, Biochem. J., 1998, 333, 543–548 CrossRef PubMed.
- M. J. Kornet and A. P. Thio, J. Med. Chem., 1976, 19, 892–898 CrossRef PubMed.
- K. Ding, Y. Lu, Z. Nikolovska-Coleska, G. Wang, S. Qiu, S. Shangary, W. Gao, D. Qin, J. Stuckey, K. Krajewski, P. P. Roller and S. Wang, J. Med. Chem., 2006, 49, 3432–3435 CrossRef PubMed.
- J. W. Skiles and D. McNeil, Tetrahedron Lett., 1990, 31, 7277–7280 CrossRef.
- T. D. Aicher, D. C. Knorr and H. C. Smith, Tetrahedron Lett., 1998, 39, 8579–8580 CrossRef.
- J. E. Baldwin, R. T. Freeman, C. Lowe, C. J. Schofield and E. Lee, Tetrahedron, 1989, 45, 4537–4550 CrossRef.
- G. Trapani, M. Franco, A. Latrofa, A. Carotti, S. Cellamare, M. Serra, C. A. Ghiani, G. Tuligi, G. Biggio and G. Liso, J. Pharm. Pharmacol., 1996, 48, 834–840 CrossRef PubMed.
- (a) S. R. Murugan, S. Anbazhagan and S. Narayanan, Eur. J. Med. Chem., 2009, 44, 3272–3279 CrossRef PubMed; (b) K. Karthikeyan, R. S. Kumar, D. Muralidharan and P. T. Perumal, Tetrahedron Lett., 2009, 50, 7175–7179 CrossRef; (c) A. S. Girgis, Eur. J. Med. Chem., 2009, 44, 91–100 CrossRef PubMed; (d) R. R. Kumar, S. P. S. C. Manju, P. Bhatt, P. Yogeeswari and D. Sriram, Bioorg. Med. Chem. Lett., 2009, 19, 3461–3465 CrossRef PubMed.
- (a) L. R. Domingo, M. J. Aurell, P. Perez and R. Contreras, Tetrahedron, 2002, 58, 4417–4423 CrossRef; (b) L. R. Domingo, M. J. Aurell, P. Perez and R. Contreras, Tetrahedron, 2003, 59, 3117–3125 CrossRef; (c) P. Arroyo, M. T. Picher and L. R. Domingo, J. Mol. Struct., 2004, 709, 45–52 CrossRef; (d) P. Arroyo, M. T. Picher, L. R. Domingo and F. Terrier, Tetrahedron, 2005, 61, 7359–7365 CrossRef.
- (a) L. R. Domingo, Molecules, 2016, 21, 1 Search PubMed; (b) M. Hamzehloueian and Z. Davari, J. Mol. Graphics Modell., 2018, 80, 32–37 CrossRef PubMed.
- J. Weng, Q. Mei, Q. Q. Ling, Q. Fan and W. Huang, Tetrahedron, 2012, 68, 3129–3134 CrossRef.
- E. M. Hussein, S. A. Ahmed and I. I. Althagafi, Heterocycl. Commun., 2017, 23, 379–384 Search PubMed.
- (a) E. M. Hussein and M. I. Abdel-Monem, ARKIVOC, 2011, 10, 85–98 Search PubMed; (b) E. M. Hussein, S. A. Ahmed, N. El Guesmi and K. S. Khairou, J. Chem. Res., 2017, 41, 346–351 Search PubMed.
- (a) R. R. Kumar, S. Perumala, P. Senthilkumar, P. Yogeeswari and D. Sriram, Eur. J. Med. Chem., 2009, 44, 3821–3829 CrossRef PubMed; (b) J. He, G. Ouyang, Z. Yuan, R. Tong, J. Shi and L. Ouyang, Molecules, 2013, 18, 5142–5154 CrossRef PubMed.
- Y. Sarrafi, M. Hamzehloueian, K. Alimohammadi and S. Yeganegi, J. Mol. Struct., 2012, 1030, 168–176 CrossRef.
- (a) F. De Proft and P. Geerlings, Chem. Rev., 2001, 101, 1451–1464 CrossRef PubMed; (b) P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1873 CrossRef PubMed; (c) P. W. Ayers, J. S. M. Anderson and L. J. Bartolotti, Int. J. Quantum Chem., 2005, 101, 520–534 CrossRef; (d) J. L. Gázquez, J. Mex. Chem. Soc., 2008, 52, 3–10 Search PubMed; (e) P. Geerlings, S. Fias, Z. Boisdenghien and F. De Proft, Chem. Soc. Rev., 2014, 43, 4989–5008 RSC.
- M. Rahm and T. Brinck, J. Phys. Chem. A, 2008, 112, 2456–2461 CrossRef PubMed.
- (a) R. G. Parr and W. Yang, Density Functional Theory of Atoms and Molecules, Oxford University Press, New York, 1989 Search PubMed; (b) R. G. Parr, L. von Szentpaly and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef.
- (a) P. Pérez, L. R. Domingo and A. Aizman, in The electrophilicity index in organic chemistry, Theoretical aspects of chemical reactivity, ed. A. Toro-Labbe, Elsevier, Amsterdam, 2007, vol. 9, pp.139–201 Search PubMed; (b) P. Pérez, L. R. Domingo, M. J. Aurell and R. Contreras, Tetrahedron, 2003, 59, 3117–3125 CrossRef; (c) P. Pérez, L. R. Domingo, M. Duque-Noreña and E. Chamorro, J. Mol. Struct., 2009, 895, 86–91 CrossRef.
- (a) L. R. Domingo, M. J. Aurell, P. Perez and R. Contreras, Tetrahedron, 2002, 58, 4417–4423 CrossRef; (b) P. Arroyo, M. T. Picher and L. R. Domingo, J. Mol. Struct., 2004, 709, 45–52 CrossRef; (c) P. Arroyo, M. T. Picher, L. R. Domingo and F. Terrier, Tetrahedron, 2005, 61, 7359–7365 CrossRef; (d) D. V. Steglenko, M. E. Kletsky, S. V. Kurbatov, A. V. Tatarov, V. I. Minkin, R. Goumont and F. Terrier, J. Phys. Org. Chem., 2008, 22, 298–307 CrossRef; (e) S. Lakhdar, F. Terrier, D. Vichard, G. Berionni, N. El Guesmi, R. Goumont and T. Boubaker, Chem.–Eur. J., 2010, 16, 5681–5690 CrossRef PubMed.
- C. Hansch, A. Leo and R. W. Taft, Chem. Rev., 1991, 91, 165–195 CrossRef.
- H. Ayouchia, H. Anane, M. L. I. Moubtassim, L. R. Domingo, M. Julve and S. Stiriba, Molecules, 2016, 21, 1434 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra04312d |
| This journal is © The Royal Society of Chemistry 2018 |