Design principles for platinum nanoparticles catalysing electrochemical hydrogen evolution and oxidation reactions: edges are much more active than facets

Abstract

Improving the performance of hydrogen evolution and oxidation reactions using precious metal catalysts is key in reducing the cost of electrolysers and fuel cells. By considering the performance of these reactions as a function of platinum particle size (2.1–15 nm) under high mass transport conditions in acids, we find that the activity is composed of two components which vary in a defined way with the particle size. Geometrical considerations and electrokinetic modelling suggest that these two components correspond to the response of edges/vertices and the response of facets (Pt(100) and Pt(111)). Edges and vertices are much more active towards the hydrogen reaction. This assignment also rationalises the poor performance of platinum in alkaline environments. We predict that “ideal” particles made up of only edges/vertices would allow fuel cells and electrolysers to operate with only 1 μg_Pt cm⁻² – about two to three orders of magnitude lower than what is currently used.

---

Introduction

The surface sensitivity for the oxygen reduction reaction (ORR) has been well established on crystal facets. For the low index planes, the order of activity has been given as Pt(110) > Pt(111) > Pt(100) in perchloric acid,¹ while specifically adsorbing anions (e.g. sulfuric acid) are known to affect this order, changing it to Pt(110) > Pt(100) > Pt(111).² However, the particle size also has an effect on the ORR: reducing the particle size has been reported to decrease the specific activity (activity per surface area) of the catalyst.^3–7 Fig. 8 in ref. 6 shows this decrease in specific activity in terms of metal area, creating a peak in the mass activity at 80–110 m² g⁻¹; corresponding to a particle diameter between 3 and 5 nm, also seen and modelled by others.^3,4,7–10 Although there are some suggestions that rather than there being a decrease, there is a levelling out of specific activity for smaller size particles,¹¹ somewhat complicating the above discussion.

Knowing the ORR is structure sensitive with a peak mass activity between 3 and 5 nm diameter particle size has helped in the optimisation of Pt catalysts for the ORR. Due to the rapid kinetics of the hydrogen oxidation and evolution reactions (HOR/HER) under acidic conditions, it has proven to be more challenging than the ORR to measure the exchange current density without including mass transport effects; especially when using conventional techniques such as the rotating disk electrode (RDE).¹² This has impeded the study of the surface sensitivity of the HOR/HER on platinum, especially under acidic conditions.

Measuring the HOR under alkaline conditions has been more successful due to a reduction in kinetics by two orders of magnitude,^12–14 bringing the geometric current densities into boundaries which the RDE is capable of measuring. Pt single crystal studies^13,15 have shown an activity on the different facets to decrease in the order Pt(110) > Pt(111) > Pt(100), equivalent to the ORR in perchloric acid. Relating single crystal studies to nanoparticles is not directly comparable; however, this gives a good indication that there is surface sensitivity in the HOR.

While it is generally agreed that the surface facets have different activities toward the HOR, it is still not clear how this corresponds to nanoparticles. Vogel et al.¹⁶ showed no substantial difference when using polycrystalline Pt, Pt black and Pt/C nanoparticles using rapid potentiodynamic scanning and Sheng et al.¹² measured a comparatively similar exchange current density in alkaline environments for polycrystalline Pt and Pt/C catalysts; both suggesting that the surface is structurally insensitive.

However, Takasu et al.¹⁷ observed a clear increase in activity with decreasing particle size in acid using vacuum evaporated Pt onto a glassy carbon RDE at very low loadings (0.5–1.2 μg cm⁻²). This is in agreement with the study by Antoine et al.¹⁸ using a gas diffusion electrode half-cell to increase H₂ mass transport. Both also follow the conclusions from the single crystal studies, where the Pt(110) facet can be treated like the edge of a nanoparticle, and as it becomes the more dominant surface faction with reduced particle size (discussed below), the exchange current density increases.

In order to measure mass-transport free electrocatalysis some of us at Imperial College London have recently developed a new method for producing ultra-thin layers of catalyst on a thin gold coated porous hydrophobic polycarbonate membrane.¹⁹ This thin membrane is then floated on top of the electrolyte and the reactant gas is exposed to the back of the membrane where it diffuses through the pores to the catalyst.^19–21 We estimate that the mass transport rate constant for these electrodes is about 30 cm s⁻¹, about 10 000 times faster than what can be achieved using a rotating disk electrode at 1600 rpm in aqueous acid.

In this paper we have used this new technique to ascertain the particle size dependence of the HOR/HER under acidic conditions free from mass transport effects for Pt/C particles in the relevant 2–15 nm range. Combined with electrokinetic modelling results, we obtained new insights into the hydrogen reaction.

Experimental

Chemicals

Ultra-pure perchloric acid (VWR, Merck Suprapur, 4 mol dm⁻³) and ultra-pure water (Millipore Milli-Q, 18.2 MΩ cm) were used to make up electrolytes. Butyl acetate (Sigma, anhydrous grade), propan-2-ol (VWR, Normapur analytical reagent), perfluorosulfonic acid (PFSA) solution (DuPont DE521 Nafion solution, 5 wt%), Teflon AF 2400 fluoropolymer (DuPont De Nemours), and Fluorinert FC-40 (Sigma, F9755) were obtained from the aforementioned suppliers. Gas purities of ≥5.8 N (Air Products) were utilized with 6 N rated regulators (GCE DruVa). All glassware was first cleaned by soaking in acidified potassium permanganate for 8 h, rinsed with acidified hydrogen peroxide and then boiled in ultra-pure water, while being rinsed at least six times with ultra-pure water in between each step and before use.

Particle analysis

Particle size analysis was performed using a JEM 2800 (Scanning) transmission electron microscope at 200 kV with a C2 aperture of 70 and 40 μm, collecting images of at least 100 nanoparticles to give an average particle size for each catalyst. In this report the TEM particle size is used as it gives a particle number average size distribution. X-ray diffraction data were collected using Cu Kα radiation (λ = 1.5406 + 1.54439 Å) on a Bruker AXS D8. Crystallite sizes have been calculated from the Rietveld refinements using the LVol-IB method. CO metal area was measured via pulsed chemisorption in a helium carrier gas using a Micromeritics Autochem II chemisorption analyzer. After which the sample was analysed by ICP-OES (Thermo iCAP 7600 ICP-OES) to give the metal loading.

Electrode fabrication

The gold coated polycarbonate electrodes were prepared as in ref. 19. Polycarbonate (Sterlitech, PCTF0447100, 0.4 μm pore size) was coated with a 100 nm gold layer by sputter deposition (Emitech K575X). These electrodes were then cleaned by Soxhlet extraction in both propan-2-ol and ultra-pure water for 8 hours each. After catalyst deposition, the electrodes were again cleaned by Soxhlet extraction in ultra-pure water for 8 hours, and then the pores of the polycarbonate track etched membrane were hydrophobized with a coating of an amorphous fluoropolymer (Teflon AF 2400, 0.21 μg cm_Geo⁻²) dissolved in Fluorinert FC-40. These electrodes were then vacuum dried at 100 °C to remove the FC-40.

Stock solutions of the catalyst inks were made into the following mixture: the selected Pt/C catalyst (50 mg), butyl acetate (950 mg), propan-2-ol (570 mg) and a perfluorosulfonic acid (PFSA) solution (5 wt%, 380 mg). To deposit the catalyst, the volume of ink needed for the required catalyst loading was further diluted to 500 μl with a 50 : 50 mix of butyl acetate and propan-2-ol to ensure that the ink deposits evenly across the substrate. This ink was deposited onto the substrate via a vacuum filtered catalyst technique (VFC).¹⁹

Electrochemical measurement

Electrochemical measurements were performed in a three compartment electrochemical cell with a water jacket kept at 298 K. The reference electrode was an in-house reversible hydrogen electrode (RHE) in the Luggin capillary compartment and the counter electrode was a platinum wire. A Gamry Reference 600 potentiostat was used to make the measurements. All electrodes were tested using the same procedure; 10 cleaning cycles under nitrogen (0–1 V vs. the RHE at 100 mV s⁻¹), nitrogen CV's run at 100 and 20 mV s⁻¹ (0–1 V vs. the RHE) for H_UPD measurements, 10 cleaning cycles between the HOR (−0.1 to 1 V vs. the RHE at 50 mV s⁻¹) and the ORR (0.3–1 V vs. the RHE at 50 mV s⁻¹) with a brief flow of nitrogen in between, HOR measurement (−0.1 to 1 V vs. the RHE at 10 mV s⁻¹) then ORR measurement (0.3–1 V vs. the RHE at 10 mV s⁻¹, results to be published elsewhere), and finally nitrogen CVs measured at 10 mV s⁻¹ (0.3–1 V vs. the RHE) for ORR double layer corrections and 100 and 20 mV s⁻¹ (0–1 V vs. the RHE) for H_UPD measurement. CV's for the H_UPD measurements were obtained before and after the HOR and ORR measurements to ensure that any change in the surface area is accounted for. All presented values are averaged between the three electrodes. To keep the plots clear, the electrode corresponding most closely to the average was plotted, although the difference in activity between the three electrodes was found to be small. All HOR curves were corrected for uncompensated resistance (iR) measured from the high frequency intercept of the electrochemical impedance spectrum.

In our experiments we have had to use high concentrations of perchloric acid because of the large currents we experience even at the ultra-low loading electrodes we have developed. If we tried to use lower electrolyte concentrations or higher catalyst loadings, we would suffer from excessive iR drops and ohmic heating effects.

Results and discussion

Pt nanoparticles supported on carbon in the size range used in this paper (2–15 nm) are generally considered to be cubo-octahedron in nature, made up of edges and corners (herein collectively called edges) and Pt(111) and Pt(100) facets. Using the cubo-octahedral shape, the ratio of Pt(111), Pt(100) and edges can be calculated for a defect free particle where the square facets correspond to Pt(100) and the hexagonal facets to Pt(111)^22,23 and was used by Kinoshita,³Fig. 1A (see the ESI for calculation details†). Edge sites dominate the particle surface once the particle size becomes less than 1.8 nm, and Pt(111) sites are 4-fold more frequent than Pt(100) sites for large particles. This simple geometric model allows us to understand the variation in the facet ratio with size and shows good agreement with more advanced computational models.^9,10,24 Further understanding from imaging methods to visualise nanoparticles^25–27 could give a more realistic surface structure which includes defects and higher index planes.

Fig. 1 Details of supported platinum particles. (A) Fraction of Pt(111), Pt(100), edge and facet (Pt(111) + Pt(100)) sites on Pt cubo-octahedron particles (details in ESI†). Vertical black dotted lines show the particles tested in this study: 2.1, 3, 7 and 15 nm from TEM analysis. Inset shows a model of a cubooctahedral particle colour coding the different sites. (B) XRD pattern of carbon supported Pt particles used in this study. Pt indices and relative intensities from ref. 28. (C–F) TEM images of Pt particles supported on carbon used in this study for 2.1 nm, 2.7 nm, 6.9 nm and 14.6 nm with 200 nm and 5 nm scale bars. Inset: particle size distribution.

Representative catalysts in this size range were produced by sintering ∼40 wt% Pt/C catalysts supported on Ketjen black EC-300J at different temperatures, with XRD patterns provided in Fig. 1B. High resolution TEM analysis at two different magnifications and particle size analysis of the catalysts are shown in Fig. 1C–F. Details of the catalysts determined from the XRD, TEM electrochemical and elemental analysis are summarised in Table 1.

Table 1 Measured properties of catalysts used in this study

Crystallite size XRD/nm	Particle size TEM/nm	CO metal area/m^2 g^−1	Metal loading/wt%
13.3	14.6 ± 6.6	13	41.4
6.2	6.9 ± 2.3	28	40.0
3.6	2.7 ± 1.2	77	42.8
<2	2.1 ± 0.5	121	38.2

---

As there is some range in particle size as measured from image analysis, we take the error bounds into account and henceforth label the particles as 2.1, 3, 7, and 15 nm. Fig. 2A shows the adsorption and desorption of hydrogen (0.05–0.4 V) as a function of catalyst particle size in 4 mol dm⁻³ HClO₄ at 298 K. Fig. 2B shows the corresponding regions for the oxide formation/reduction regions (0.4–1 V) in the same electrolyte. The areas have been normalised using the charge under the H_UPD to give the specific surface area and the current associated with the double layer charging at 0.4 V vs. the RHE has been subtracted. The loadings were chosen to give a constant roughness factor of ∼50 (64–550 μg_Pt cm⁻²). This loading range is high when compared to the values of the results presented below and our previous results using the floating electrode technique,^19,20,29,30 but is beneficial for looking at the surface species as the effect of substrate capacitance is reduced.

Fig. 2 Electrochemical response of different sized platinum particles. (A) H_ads/H_des, (B) O_ad/O_des and (C) cumulative Q_H(des) of the hydrogen region for Pt/C of different particle sizes. (D) shows the fraction of sites from fitting two Gaussians to the oxide desorption region. The inset in (D) shows an example of the two Gaussian curve fit (black dashed line as O_des,1, red dashed line as O_des,2 and green dashed line as the sum of the two Gaussians) on the 2.1 nm particle size catalyst (blue line). All voltammograms were normalised by the H_UPD region with the double layer capacitance removed. Layer loadings 15 nm (550 μg_Pt cm⁻², black line), 7 nm (220 μg_Pt cm⁻², red dashed line), 3 nm (97 μg_Pt cm⁻², blue dashed dotted line) and 2.1 nm (64 μg_Pt cm⁻², green dotted line). The loadings give a range of roughness factors between 60 and 80. Electrolyte: 4 mol dm⁻³ HClO₄ at 20 mV s⁻¹ at 298 K. Arrows show the transition from a larger to a smaller particle size.

The H_ads/des region of polycrystalline Pt is often thought of as a combination of the Pt(110), Pt(111) and Pt(100) facets;³¹ the Pt(100) gives sharp peaks at ∼0.12 while the Pt(111) gives a broad peak underneath. This has been shown on individual single crystals in perchloric acid.¹ The shape of H_ads/des for Pt/C nanoparticles between 2.1 and 14.6 nm is shown in Fig. 2A for desorption and adsorption, with the scan normalised to specific current density giving the area under a peak as a fraction of each site. The H_ads regions for the larger two particles are fairly consistent with polycrystalline Pt in perchloric acid.^6,7,32 The peaks at 0.12 and 0.24 V decrease as the particle size increases whereas there is a rise in the peak at about 0.2 V.

Deconvoluting the H_ads/des region into surface sites is a challenging process due to the complex shape of the peaks on different facets and the broad feature due to the Pt(111) facet underneath the peaks.³³ However, some general conclusions can be taken from the changes in peak shapes.^7,34 The site at ∼0.26 V vs. the RHE referred to as Pt(100) decreases with particle size in line with expectation from a cuboctahedron (Fig. 1a), where there is hardly a noticeable component for the 2 nm particles. This site has been referred to as a strong hydrogen adsorption site, and its decrease with decreasing particle size agrees with previous literature.^17,34 At lower potentials, there are contributions from the edge and Pt(111) sites which the two smaller particle size catalysts are predominantly made up of.

While Fig. 2A shows that the Pt(100) sites at ∼0.12 V vs. the RHE decrease with decreasing particle size, it also broadens, suggesting the adsorption energetics are not as uniform across the surface. This broadening and overlapping with the Pt(111) site make it challenging to differentiate the H_ads current to the individual surface sites for the smaller particles. However, a general shift in charge under the peaks to lower potentials is observed with decreasing particle size, showing a higher fraction of sites with a weaker hydrogen binding energy, Fig. 2C.

Fig. 2B shows the oxide adsorption on the Pt/C catalysts of different Pt particle sizes (2.1–14.6 nm). The oxide formation begins at ∼0.75 V vs. the RHE, and the onset potential decreases with decreasing particle size. Also the desorption peak moves to lower potentials with decreasing particle size (see the ESI†). Both are indicative of the stronger adsorption of oxides on the surface which has been observed elsewhere.^4,6,7,10 The increased oxophilic nature has been used to explain the difference in ORR activity, with the surface oxygenated species acting as the site blocking species.^7,10,35–37

Upon fitting two Gaussians to the oxygen desorption peak in Fig. 2D, the ratio of the strongly adsorbed (lower desorption potential) to the weakly adsorbed (higher desorption potential) can be estimated, Fig. 2D. An example of the Gaussian fit for the 2 nm particle is shown in the inset of Fig. 2D. The ratio of O_des,1 and O_des,2 is very similar to ref. 34, especially for the larger particles. There are some slight differences in the change in surface fractions calculated from a perfect cuboctahedron (Fig. 1A), with the change in fraction of the difference sites being much smaller than that seen in the geometrical model. The reduced change in the proportion of different sites calculated from the oxide reduction peaks is likely because the real particles are imperfect and contain defects and higher order facets,^{7,22,23,25–27} with more variations in complex geometries as the particle size increases. The results from the fitting (see the ESI†) show that the position of O_des,1 remains relatively constant, while O_des,2 decreases slightly in potential with particle size. This decrease in O_des,2 is probably due to a change in the Pt(111) and Pt(100) facet ratio in the range of particle size measured (see Fig. 1A). In addition, Tritsaris et al.⁹ showed that the energetics of a facet site adjacent to an edge site tend towards those of an edge site, and as the facet diameters range from a few atoms (2.1 nm) to tens of atoms across (15 nm), it is also likely that the overall energetics of the facets change with particle size.

From the hydrogen and oxide adsorption/desorption profiles it can be seen that the particles have a decreasing hydrogen binding energy while having an increased oxygen binding energy (becoming more oxophilic) as they decrease in size.

Utilising our new floating electrode technique, we have examined the HOR/HER of the 4 different Pt particle sizes supported on carbon at very low loadings (0.65–7.8 μg_Pt cm⁻², chosen to give a roughness factor close to one for each respective catalyst), Fig. 3A. In this plot the current is normalised to the electrochemical surface area determined from the H_UPD peaks, and thus represent the area specific current densities. These low loadings are optimum for studying the HOR; a very thin catalyst layer provides a platform for homogeneous conditions throughout the catalyst, giving resolution to the peaks (which would otherwise be blurred on a thicker catalyst layer due to the gradation of reaction conditions), and relatively small currents reduce catalyst layer resistance and hence reduce the necessity for iR correction and local Joule heating within that layer.

Fig. 3 Voltammetry of the HOR/HER on different sized platinum particles. (A) Voltammograms (corrected to surface specific current density) of the HOR for Pt/C of different particle sizes with targeted loading to give a roughness factor in the range 0.7–1. The loadings of electrodes for the different particle sizes are 15 nm (7.8 μg_Pt cm⁻²); 7 nm (2.5 μg_Pt cm⁻²), 3 nm (1.2 μg_Pt cm⁻²) and 2.1 nm (0.7 μg_Pt cm⁻²). Inset: anodic scan normalised to the height of the second peak. (B) Plot of the ratio of peak current densities for the low and high peaks as a function of platinum particle size along with the best fit curves for the response expected if the peaks are due to facets and edges or just different facets (Pt(100) vs. Pt(111)). The CVs were run in 4 mol dm⁻³ HClO₄ at 10 mV s⁻¹ at 298 K. 1 bar hydrogen.

The voltammetry appears similar to that which we have seen before on 60% Pt on carbon HiSPEC 9100 catalysts from Alfa Aesar, with a 2.4 nm diameter particle size.^19,38 Immediately obvious are a number of distinct features:

The presence of two peaks in the voltammetry, the first at low potential (peak_low, where E(peak_low) < 0.18 V) and the second at slightly higher potentials (peak_high where 0.25 < E(peak_high) < 0.36 V);

• the relative magnitude of each of these peaks changes with particle size;

• there is an asymptotic decay in the HOR at higher potentials which is more significant for the smaller particles;

• HOR/HER activity increases with decreasing particle size.

The change in the peak ratio can be seen clearly by normalising the scans in the anodic direction from Fig. 3A by the height of the second peak showing strong particle size dependence, Fig. 3A inset. Fig. 3B shows the ratio of peak heights as a function of particle size (see ESI Table 2† for precise values). While we believe that this is the first time the peak ratio change with particle size has been observed, there is evidence from the literature that supports the presence of these peaks. Chen and Kucernak⁵ presented a shoulder in their HOR voltammogram (relatively small j_peak,low) using a 72 nm diameter single platinum particle deposited on a carbon ultra microelectrode, with a similar shape to the low over-potential region of the 15 nm catalysts in Fig. 3A. Likewise Wesselmark et al.³⁹ observed peaks of relatively similar size using sputtered Pt electrodes, which correspond to somewhere between the two intermediate particle sizes. Following our initial work,^19,21 Durst et al.⁴⁰ (with a 4.7 wt% Tanaka TEC10V05E Pt/C catalyst composed of 2.6 nm particles) presented a voltammogram obtained in a fuel cell similar to the 2.1 nm particle in Fig. 3A.

A further observation is the strong correlation of increasing HOR/HER current density close to the equilibrium potential as the peak at lower potential grows (i.e. as particle size decreases). This correlation suggests that the two peaks are different sites for the HOR with different exchange current densities; as the ratio of the more active site increases, the average activity of the particle increases. For nanoparticles, different geometrical possibilities for sites responsible for the peaks may be considered:

• the activity comes from the difference between the two facets (Pt(111) and Pt(100) as for the ORR);

• the change comes from the varying ratio of edges and facets;

• the change comes from some other combination of the above features.

Fig. 3B displays curves representing the ratio of the Pt(111)/Pt(100) facets and the facet/edge ratio over the range of nanoparticle sizes used in this study. The two facets, Pt(111) and Pt(100) reach a constant ratio quickly, once the particle size is around 8–10 nm. For cubo-octahedral particles the ultimate ratio is four surface atoms in the Pt(111) geometry for every atom in the Pt(100) geometry. On the other hand, the ratio of facets to edges increases linearly with particle size: at ∼10 nm the fraction of edge sites is <10% of the total available sites in agreement with ref. 3. This linear increase in the facet to edge ratio is much more similar to the decreasing peak height of peak_low. Indeed, fitting the ratio of peak current densities to the ratio of facets to edges as a function of particle size, we get a very good fit whereas if we try and correlate the current ratio to that of the area of the different facets, we get a very poor correlation, Fig. 3B. This suggests that the peak at low potential is correlated with edge sites, and that at higher potential is correlated with the facet sites. The peak assignment agrees with the PZTC discussion in the authors' previous paper,²⁹ whereby E(peak_low) is close to the PZTC measured for a step edge: measured to have a PZTC of ∼0.15 V vs. the RHE in 0.1 mol dm⁻³ HClO₄ (ref. 41) and E(peak_high) is close to the PZTCs of the Pt(111) and Pt(100) facets (0.34 V and 0.43 V vs. the RHE, respectively in 0.1 mol dm⁻³ HClO₄ (ref. 42)). Sun et al. have also suggested a similar interpretation based on their analysis of activity towards the HOR as a function of platinum particle size in RDE experiments.³⁴ This is also the case for what is seen in single crystal electrochemistry work in which surfaces with more step edges are more active towards the HOR/HER⁴³ and Pt adislands on Pt(111) significantly increase the HOR/HER activity.⁴⁴ We see that the PZTC of the particles increases with particle size (see the ESI†).

Hence it would be expected that E(peak_high), a contribution of both Pt(100) and Pt(111), shifts higher on larger nanoparticles. As observed, the difference in the shift between E(peak_high) for the 7 nm and 15 nm particles would also be much reduced compared to the 2.1 nm to 3 nm particle difference, as the ratio of the two facet plateaus out (Fig. 3B). This shift could also be helped by both the Pt(111) and Pt(100) facets becoming slightly less oxophilic as the particle size increases,⁴⁵ which would also move the PZTC and therefore the E(peak_high) to higher potentials.

In the past, attempts have been made to model the occurrence of the low potential peak by assuming it was a changeover from the Tafel–Volmer mechanism near the equilibrium potential to a Heyrovsky–Volmer mechanism at larger overpotentials.⁴⁶ However a change in the mechanism can only give a monotonic increase in current density with overpotential, and not the formation of a peak followed by a decrease in performance at higher potentials observed here and in other studies.³⁸ In contrast, Chen and Kucernak tried to model their results on the basis of different sites for the HOR.⁴⁷ Hence there must be some other aspect leading to a decrease in current as potential is increased.

On platinum the high activity towards the hydrogen reaction is a consequence of the low free energy of the adsorption of hydrogen, leading to an intermediate coverage of H_ad on the surface (i.e. a good balance between H_ad available to produce H₂ during the HER and adsorption sites free of H_ad to allow H₂ adsorption and subsequent reaction during the HOR). In our previous paper, we have estimated the value of this parameter to be close to +3 kJ mol⁻¹. Such a low value for the free energy of adsorption (which is of the order of kT) suggests that the process can be strongly influenced by other species which may have a higher adsorption strength, which can lead to site-blocking for the HOR/HER. Indeed, such a case has been seen for platinum where, for instance, the addition of adsorbing anions has been shown to massively suppress the HOR on platinum single crystal electrodes.^48,49 Furthermore, in our work we see that shifting from perchloric acid to sulfuric acid leads to a significant decrease in current densities at high potentials, positive of the PZTC, with little effect below the PZTC (see the ESI†).

In order to capture the decrease in performance at large overpotentials, we include the possibility that the sites may become blocked at high potentials. This site-blocking may occur through either electrosorption of anions from the solution^50–52 or the Nafion binder, or maybe the formation of an oxide like species at low potentials^53,54 or blocking by water. Hence these blocked sites become unavailable for the HOR/HER reactions. It is important to remember that the specific current densities we are measuring are more than two orders of magnitude larger than that measured using the RDE, and so it is hardly surprising that we can see effects when none are usually observable using the standard RDE measurements – this is simply a consequence of being able to “push the electrocatalyst harder”.

We have simultaneously fit the HOR/HER curves of all four of our platinum particles considering that there are two different sites (see the ESI for details†). We assume that the two sites are the same across all particles (i.e. have the same parameters), and the only difference between the four particles is the ratio of the coverage of the different sites (which is also a fit parameter). The fit (dashed lines) is shown overlaid on the experimental data for each of the particle sizes in Fig. 4A–D. The fit is performed on the reverse scans. The model overpredicts the currents at high potential because it does not take into account the surface area lost to oxides, which are only significantly removed once the potential is below 0.5 V (cf.Fig. 2B for the oxide reduction peak). Fits for the forward scan are given in the ESI.†

Fig. 4 Comparison of model to experimental data. Fitting of the HOR/HER curves in Fig. 3 from −0.02 to 0.5 V vs. the RHE using a two site model. The inset shows the data and fit close to the equilibrium potential. The data used were for the scan in the cathodic direction (see text) as shown in Fig. 3A. Summary of the fitting results are provided in Tables 1 and 2.

The inset in each plot is the absolute value of specific current density on a logarithmic scale for the region close to the equilibrium potential. It can be seen that the fit closely matches the response in this important region. Hence, we see that the fit not only captures the response over a wide potential range, but also accurately describes the response in the technologically relevant region close to the equilibrium potential. Each of the two sites is controlled by five fitting parameters, k^⊖_ad, k^⊖_des, k^⊖_+V, E′_anion and λ_anion. The molecular symmetry factor, β, was fixed at 1/2, and further details are provided in the ESI.† The values for the fit parameters and derived quantities from those fit parameters are provided in Table 2.

Table 2 Fitting parameters (under standard conditions) used to describe the HOR/HER on the two different sites associated with the nanoparticles. Parameters determined under standard conditions and with a β of 1/2, but in 4 M HClO₄. Details of fitting process are given in the ESI. k^eq_+T, k^eq_−T, and k^eq_+V are respectively the forward and reverse Tafel step, and forward Volmer step rate constants at equilibrium

Parameter	Type^a	Site
		Edge	Facet
Feature		Peaklow	Peakhigh
a F: fit parameter and D: derived from fit parameters. b Calculated assuming a saturated hydrogen concentration of 5.10 × 10^−7 mol cm^−3.^55 c See the ESI for calculation. d Values which would be measured by taking the slope of the micropolarisation region and applying 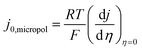see the ESI. e True exchange current density. N.B. see ref. 38 for discussion of the non-equivalence of the exchange current density with the value determined from the micropolarisation region. See the ESI for derivation. f Calculated in the absence of site-blocking effects, i.e. θanion,site(E) = 0.
k ^eq+T/mol cm^−2 s^−1	F	1.73 × 10^−5	1.30 × 10^−5
k ^eq+T/cm s^−1^b	D	33.9	25.5
k ^eq−T/mol cm^−2 s^−1	F	4.94 × 10^−5	1.76 × 10^−7
k ^eq+V/mol cm^−2 s^−1	F	1.24 × 10^−4	3.56 × 10^−7
E′/V	F	0.009	0.393
λ anion	F	0.11	0.03
	D	0.37	0.90
/kJ mol^−1^c	D	1.3	−5.3
J o,micropol/mA cm^−2^d	D	527	9
J o,true/mA cm^−2^e	D	2270	18
J o,micropol,anion-free/mA cm^−2^d^,^f	D	1650	20
J o,true,anion-free/mA cm^−2^e^,^f	D	4440	31

---

Table 3 provides the proportion of each site needed to produce the fits, i.e. ζ values for

j_total(E) = ζj_peak,low(E) + (1 − ζ)j_peak,high(E) (1)

Table 3 Variation of the proportion of each site (facet, edge) as determined from simultaneously fitting all four data sets. Also shown are the weighted exchange current densities for the different particles – either the true exchange current density, or the value which would be estimated from the linear dependence of the micropolarisation region

Particle size/nm	Proportion of the site		Effective exchange current density mA cm^−2
	ζ, edge	(1 − ζ), facet	True	Micropolarisation
14.6 ± 6.6	0.34	0.66	160	42
6.9 ± 2.3	0.39	0.61	320	79
2.7 ± 1.2	0.46	0.54	770	180
2.1 ± 0.5	0.58	0.42	970	230

---

It is thus assumed that a simple weighting process governs the total current, and that we can independently assess the performance of each of the independent sites. Thus, this approach neglects the case where the HOR/HER reaction is associated with edge sites and near edge sites which are nonetheless on a facet, although this aspect is handled in an implicit manner in the fitting process. Also shown in this table are the true exchange current densities and the effective exchange current density which would be determined from the micropolarisation region. The difference in these values is associated with simplifications involved with utilising the Butler Volmer formalism which we have discussed in a previous paper.³⁸

Utilising the fitting parameters, we can determine the performance of a surface entirely composed of edge sites or the corresponding case where the surface is entirely composed of facets (i.e. ratio 4 : 1 Pt(111) : Pt(100)), which represent the limits of a very small particle or a very large one. Such a plot is shown in Fig. 5A for each “pure” site, also showing the effect if we ignore site-blocking (Fig. 5B shows the data for potentials near the equilibrium potential). There are a number of striking observations. The first is that the current near the equilibrium potential (and for the HER) is dominated by the performance of edge sites, but these sites shut down for the HOR very quickly at positive potentials due to site-blocking. For the facets, the situation is reversed, the performance is relatively poor for the HOR close to the equilibrium potential (and for the HER), and only rises slowly, but is somewhat less affected by site-blocking. The peak currents for the HOR on both types of sites in the presence of site-blocking are only about 1/6 of the value which could be obtained without blocking, although both sites show similar limiting values which would be expected from the similarity of the adsorption rate constant for the Tafel step, k^eq_+T (Table 2). The sensitivity of edge sites to site blocking is hardly surprising, as it is to be expected that the under-coordinated platinum atoms along edges will preferentially fill their coordination sphere and this process may be associated with moderate charge transfer (λ_anion ∼ 0.1).⁵⁶ In contrast, for the facets, the degree of under-coordination is much lower, and so charge transfer is only about a quarter of that of the edges (λ_anion ∼ 0.03). These values should be compared to those of strongly adsorbing anions on single crystal surfaces (e.g. Br⁻ or I⁻) for which values of λ_anion are significantly larger.

Fig. 5 “Pure” HOR/HER performance of platinum edges and facets in the presence of and absence of blocking species (anions or oxides), determined from the fitting results to the data in Fig. 4. (A) Specific current density for facets and edges in the presence and absence of anions. Inset – comparison of the results with that obtained through rotating disk voltammetry of single crystal (Pt(100) and Pt(111)) electrodes in 0.1 mol dm⁻³ HClO₄ at 1600 rpm (data taken from ref. 57). For comparison, the performance of j_facet in the presence of anions is corrected for the mass transport limitation imposed by an RDE at the same rotation rate and overlaid (see ESI† for details of calculation of j_MT). (B) Expansion of data in (A) to show the variation in current in the micropolarisation region for the different sites and in the presence and absence of anions. (C) Variation of the coverage of site-blocking species, θ_anion, and hydrogen coverage, θ_Had, in the presence and absence of site-blocking for the different reaction sites as a function of applied potential.

Even though the performance of the facets is much less than that of the edges, it is important to note that the performance is still greater than that seen for Pt(111) and Pt(100) single crystal electrodes used in RDE measurements for the HOR under comparable conditions,⁵⁷Fig. 5A inset. In this inset we replot the data from Strmcnik et al.^57,58 for the HOR on Pt(111) and Pt(100) electrodes and compare it to the performance of the pure “edge” and “facet” surfaces in perchloric acid. Both of these sites show significantly increased performance compared to the single crystal electrodes, which is hardly surprising due to the high mass transport characteristics of our electrodes. In order to have a fair comparison, the modelled performance of the theoretical facet is modified to include the mass transport effects associated with a 1600 rpm RDE i.e. the same mass transport conditions as used by Strmcnik et al.⁵⁷ (see ESI† for details). The performance of the facet is slightly better than that of the Pt(100) surface and significantly better than that of the Pt(111) surface. This result shows that even though site blocking is visible in the response for the HOR on the floating electrodes, this effect would not be observable in RDE experiments as mass transport is too slow in those experiments.

In Fig. 5B we show the performance of the two sites close to the equilibrium potential. For comparison, we also plot the mass transport corrected (i.e. corrected to 1600 rpm on an RDE, see ESI† for details) performance of the facet site. In these plots it can be seen that the effect of site blocking is to suppress the HOR and HER across the micropolarisation region by about a factor of 3.5 for the edges and only about a factor of two for the facets.

However, the blocking effect has important consequences. If site-blocking is important for the HOR on edge sites, then in alkaline environments, it might be expected that hydroxide may act as a strongly blocking anion and shut down the performance of the edges, leaving just the facets on which the HOR can be performed. This would lead to a significantly reduced exchange current density for the HOR in an alkaline environment. This interpretation is corroborated by single crystal RDE work in alkaline environments which show HOR voltammetry for Pt(111) and Pt(100) at 275 K which closely matches that of the facet response in Fig. 5A.¹⁵

Displayed in Table 2 are also the calculated exchange current densities for each of the sites both in the presence and absence of site-blocking. It can been seen that in all cases the exchange current density for the edges is about two orders of magnitude larger than that for the facets, with significantly better performance achieved in the absence of site-blocking. Performance in the absence of site blocking might be important when, for instance, a platinum particle is deposited into a carbon support pore within the catalyst layer of a fuel cell or an electrolyser. In this case, when the particle is not in direct contact with the ionomer, but instead with pure water, performance will be enhanced. In order for such a particle to not suffer from excessive ionic resistance losses, the depth of the pore must not be too much, as the ionic resistivity of pure water is high (18.2 MΩ cm).

The strong effect of site-blocking species on the hydrogen adsorption/desorption reaction is also lent some credence by the values of the free energy of hydrogen adsorption, , calculated from .³⁸ We find that for the edge sites, this parameter is very close to zero (i.e. <kT at room temperature) and slightly positive, suggesting that hydrogen can be easily displaced by species with a stronger free energy of binding. The values calculated agree well with those we have determined in our previous studies. In contrast, the facets show ∼7 kJ mol⁻¹ stronger binding of hydrogen atoms compared to the edges, meaning that they are much less affected by electrosorption of blocking species.

Plotted in Fig. 6A is the calculated composite exchange current density as a function of particle size in the presence of site blocking derived from the exchange current densities of each site (Table 2) through the weighting function eqn (1) and assuming a simple cubooctahedral geometric model (see ESI† for calculation details). We plot both the true exchange current density and the slope of the micropolarisation region multiplied by RT/F. The latter value is frequently used as the value of the exchange current density, but as some of us have pointed out in a previous paper,³⁸ this equivalence does not hold for the HOR/HER on platinum (see the ESI for more details†).

Fig. 6 Continuous variation of kinetic parameters as a function of particle size. (A) Variation of exchange current density and exchange current density estimated from the micropolarisation region as a function of particle size assuming a cubooctahedral model. Squares represent the particle sizes studied in this paper. Limiting values for pure facets and pure edges are also shown. (B) Correlation between the fraction of sites giving the low potential peak determined from the kinetic fit and the fraction of oxide reduction charge in the deconvoluted low potential peak (Fig. 2). Each point is labelled with the average particle size. (C) Variation of the fraction of sites associated with the low potential HOR peak determined through fitting of the HOR/HER (Table 2). The data points are compared to the ratio of edge sites to total sites () and the ratio of edge and Pt(100) sites to total sites (), both for a cubooctahedral geometry and a power-law model for defect coverage (), eqn (2).

The increase in activity with decreasing particle size is the opposite trend observed for the ORR. This is reasonable if the edge or low co-ordination sites are both the most active sites and the most energetically favourable for blocking species to absorb on. Previously the authors showed how the anions effect Pt activity across the potential window of the HOR using two anions with different adsorption strengths; sulfuric acid and perchloric acid²⁹ (see the ESI†).

Below the PZTC little difference in the HOR activity was observed when the electrolyte was changed from perchloric to sulfuric acid showing that the coverage of adsorbed anions is limited. Above the PZTC, a larger suppression in the HOR was visible in sulfuric acid compared to perchloric acid, showing anion adsorption plays a large role in perturbing the activity at higher potentials. In fact, for the ORR, the edges are often taken to have negligible activity.^3,10,59 Hence, as the particle size decreases, the fraction of edge or low co-ordination sites increases, which in turn lowers the ORR activity but increases the HOR activity.

Displayed in Fig. 6B is the correlation between the proportion of different sites determined from both oxide reduction (strongly bound sites, Fig. 2B) and fitting of the HOR/HER kinetics (edges, Table 2) for the different particle sizes studied. It can be seen that there is a clear correlation between the surface responsible for the oxide peak and those responsible for the HOR peak at low potential (i.e. peak_low). We suggest that the strongly bound oxide peak is also associated with undercoordinated platinum surface atoms associated with defects and edges. In Fig. 6C we attempt to take the surface ratio of platinum sites for the HOR determined from the fitting procedure and compare the response to the proportion of edge sites on a perfect cubooctahedral particle. Although the cubo-octahedral model shows a similar trend to the experimentally derived data, they do not show the same range of variation, especially for the larger particles. This is hardly surprising as the larger particles are liable to have a significant number of defects, and these defects will look like edge sites, and hence it would be expected that especially at a larger particle size, the simple cubooctahedral model underestimates the number of edge sites. If we assume that the edge sites and Pt(100) sites are responsible for the peak at low potential and only the Pt(111) sites are responsible for the peak at high potential, then the geometrical model is somewhat improved.

It is well established that steps and/or other types of defects are inherently present on Pt(100) surfaces,^60,61 and so this interpretation is not so unlikely. Furthermore, single crystal studies of the HOR do show enhanced activity for Pt(100) over Pt(111). Note that in this case the fraction of sites responsible for the peak at low potential will stabilize at 20% for large particles. An alternative, empirical model, based on a simple power law model seems to approximate the data even better

The fitting results give a value of 5.4 for δ. In this case the proportion of sites responsible for the peak at low potentials will asymptotically approach zero for larger particles.

Conclusions

We have examined the performance of well-characterised platinum nanoparticles towards the HOR/HER as a function of particle size. We see that the HOR is characterised by two peaks which are correlated with the particle size. Furthermore, we see that the smallest particles show the highest activity and this effect seems to be correlated with a peak which occurs closest to the equilibrium potential. We interpret the two peaks as being due to different sites on the platinum particles with different activities towards the HOR/HER. In light of geometrical considerations, and the manner in which the peaks change as a function of particle size, we determine that the peak at lower potential is due to edges and vertices (and possibly the Pt(100) facets), whereas the peak at a higher potential is due predominantly to the Pt(111) facets of the particle. The decrease in activity towards the HOR at high potentials appears to be due to site-blocking of the hydrogen reaction which has a serious impact on the hydrogen reaction. Site-blocking may be due to anion adsorption or formation of an oxide-like species at low potentials. Site-blocking occurs because the free energy of formation of the H_ads electrokinetic intermediate on the platinum surface is low (as required for high activity for the HOR/HER reaction), and so the H_ads has to compete with weakly adsorbing species for access to the surface. By developing a two site electrokinetic model of the particle which incorporates the effect of site-blocking we are able to accurately model the kinetic performance of the particles across the entire oxide-free potential range. The results of the modelling yield an estimate of the ratio of the different surfaces on the particle as a function of particle size, and this seems reasonable if one assumes that the particles are somewhat defective (i.e. they have a greater number of edge sites than assumed from a simple cubooctahedral model). The ratio of different sites correlates well with two different peaks seen in the oxide reduction region. We show that site blocking due to weakly adsorbing species decreases the performance of the HOR by a factor of 2–3. Furthermore, we show that the edge sites are much more strongly affected than the facet sites, with the facet sites being about two orders of magnitude less active towards the HOR/HER. This result is the opposite to what is found for the oxygen reduction reaction in which it is usually assumed that edge sites are less active than facets. The strong interaction of the edges with blocking species suggests that the performance of platinum towards the HOR in alkaline environments may be stymied by excessive adsorption of hydroxide anions on the edges, meaning that the performance may drop to that of the facets.

What do these results mean? It seems that platinum is almost an ideal catalyst for the HOR/HER under acidic conditions. Indeed, were it possible to produce a catalyst which was composed only of edges (nanoparticle or extended surface), and which had a dispersion equivalent to that of a 2 nm diameter particle, then it should be possible to sustain the hydrogen oxidation reaction at 298 K in the absence of mass transport effects at a current density of 1 A cm⁻² and at 0.01 V overpotential using only 4 μg_Pt cm⁻². If site-blocking effects can be removed than this value drops to only 1 μg_Pt cm⁻². Such performance is also possible for hydrogen evolution at similar loadings and conditions (i.e. 1 A cm⁻² and 0.01 V overpotential).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank Manfred Schuster for the TEM images, Edward Bilbé for XRD measurements and the EPSRC for funding through EP/G030995/1 – Supergen Fuel Cell Consortium – Fuel cells – Powering a Greener Future – CORE; EP/K503733/1 – EPSRC Impact Acceleration Research Grant; and Hydrogen to Fuel Cells (H2FC SUPERGEN) Flexible Funding Award EPSRC Grant Ref. EP/J016454/1. The data used to produce the figures in this paper are available for download at DOI: 10.5281/zenodo.894289.

Notes and references

1. N. M. Marković, R. R. Adžić, B. D. Cahan and E. B. Yeager, J. Electroanal. Chem., 1994, 377, 249–259.
2. N. M. Markovic, H. A. Gasteiger and P. N. Ross, J. Phys. Chem., 1995, 99, 3411–3415.
3. K. Kinoshita, J. Electrochem. Soc., 1990, 137, 845–848.
4. Y. Takasu, N. Ohashi, X. G. Zhang, Y. Murakami, H. Minagawa, S. Sato and K. Yahikozawa, Electrochim. Acta, 1996, 41, 2595–2600.
5. S. Chen and A. Kucernak, J. Phys. Chem. B, 2004, 108, 3262–3276.
6. H. A. Gasteiger, S. S. Kocha, B. Sompalli and F. T. Wagner, Appl. Catal., B, 2005, 56, 9–35.
7. K. J. J. Mayrhofer, B. B. Blizanac, M. Arenz, V. R. Stamenkovic, P. N. Ross and N. M. Markovic, J. Phys. Chem. B, 2005, 109, 14433–14440.
8. M. Peuckert, T. Yoneda, R. A. D. Betta and M. Boudart, J. Electrochem. Soc., 1986, 133, 944–947.
9. G. A. Tritsaris, J. Greeley, J. Rossmeisl and J. K. Nørskov, Catal. Lett., 2011, 141, 909–913.
10. M. Shao, A. Peles and K. Shoemaker, Nano Lett., 2011, 11, 3714–3719.
11. M. Nesselberger, S. Ashton, J. C. Meier, I. Katsounaros, K. J. J. Mayrhofer and M. Arenz, J. Am. Chem. Soc., 2011, 133, 17428–17433.
12. W. Sheng, H. A. Gasteiger and Y. Shao-Horn, J. Electrochem. Soc., 2010, 157, B1529–B1536.
13. N. M. Marković, S. T. Sarraf, H. A. Gasteiger and P. N. Ross, J. Chem. Soc., Faraday Trans., 1996, 92, 3719–3725.
14. J. Durst, A. Siebel, C. Simon, F. Hasche, J. Herranz and H. A. Gasteiger, Energy Environ. Sci., 2014, 7, 2255–2260.
15. T. J. Schmidt, P. N. Ross Jr and N. M. Markovic, J. Electroanal. Chem., 2002, 524–525, 252–260.
16. W. Vogel, L. Lundquist, P. Ross and P. Stonehart, Electrochim. Acta, 1975, 20, 79–93.
17. Y. Takasu, Y. Fujii, K. Yasuda, Y. Iwanaga and Y. Matsuda, Electrochim. Acta, 1989, 34, 453–458.
18. O. Antoine, Y. Bultel, R. Durand and P. Ozil, Electrochim. Acta, 1998, 43, 3681–3691.
19. C. M. Zalitis, D. Kramer and A. R. Kucernak, Phys. Chem. Chem. Phys., 2013, 15, 4329–4340.
20. C. M. Zalitis, D. Kramer, J. Sharman, E. Wright and A. R. Kucernak, ECS Trans., 2013, 58, 39–47.
21. C. M. Zalitis, D. Kramer, J. Sharman, E. Wright and A. R. Kucernak, Presented in part at the Polymer Electrolyte Fuel Cells 13, 2013.
22. R. van Hardeveld and A. van Montfoort, Surf. Sci., 1966, 4, 396–430.
23. R. Van Hardeveld and F. Hartog, Surf. Sci., 1969, 15, 189–230.
24. I. E. L. Stephens, A. S. Bondarenko, U. Gronbjerg, J. Rossmeisl and I. Chorkendorff, Energy Environ. Sci., 2012, 5, 6744–6762.
25. A. I. Frenkel, C. W. Hills and R. G. Nuzzo, J. Phys. Chem. B, 2001, 105, 12689–12703.
26. L. C. Gontard, L.-Y. Chang, C. J. D. Hetherington, A. I. Kirkland, D. Ozkaya and R. E. Dunin-Borkowski, Angew. Chem., Int. Ed., 2007, 46, 3683–3685.
27. T. Li, P. A. J. Bagot, E. Christian, B. R. C. Theobald, J. D. B. Sharman, D. Ozkaya, M. P. Moody, S. C. E. Tsang and G. D. W. Smith, ACS Catal., 2014, 4, 695–702.
28. Swanson, Tatge, Natl. Bur. Stand (U.S.), 1953, Circ. 539 I, 31.
29. C. M. Zalitis, J. Sharman, E. Wright and A. R. Kucernak, Electrochim. Acta, 2015, 176, 763–776.
30. M. Markiewicz, C. Zalitis and A. Kucernak, Electrochim. Acta, 2015, 179, 126–136.
31. P. A. Christensen and A. Hamnett, Techniques and Mechanisms in Electrochemistry, Blackie Academic & Professional, London, 1994.
32. T. J. Schmidt, H. A. Gasteiger, G. D. Stab, P. M. Urban, D. M. Kolb and R. J. Behm, J. Electrochem. Soc., 1998, 145, 2354–2358.
33. J. Solla-Gullon, P. Rodriguez, E. Herrero, A. Aldaz and J. M. Feliu, Phys. Chem. Chem. Phys., 2008, 10, 1359–1373.
34. Y. Sun, Y. Dai, Y. Liu and S. Chen, Phys. Chem. Chem. Phys., 2012, 14, 2278–2285.
35. N. M. Marković, H. A. Gasteiger and P. N. Ross, J. Phys. Chem., 1996, 100, 6715–6721.
36. O. Antoine, Y. Bultel and R. Durand, J. Electroanal. Chem., 2001, 499, 85–94.
37. C. Baldizzone, L. Gan, N. Hodnik, G. P. Keeley, A. Kostka, M. Heggen, P. Strasser and K. J. J. Mayrhofer, ACS Catal., 2015, 5, 5000–5007.
38. A. R. Kucernak and C. Zalitis, J. Phys. Chem. C, 2016, 120, 10721–10745.
39. M. Wesselmark, B. Wickman, C. Lagergren and G. Lindbergh, Electrochem. Commun., 2010, 12, 1585–1588.
40. J. Durst, C. Simon, F. Hasché and H. A. Gasteiger, J. Electrochem. Soc., 2015, 162, F190–F203.
41. V. Climent, G. A. Attard and J. M. Feliu, J. Electroanal. Chem., 2002, 532, 67–74.
42. V. Climent, R. Gomez, J. M. Orts, A. Rodes, A. Aldaz and J. M. Feliu, in Interfacial Electrochemistry Theory, Experimental, and Application, ed. A. Wieckowski, Marcel Dekker, Inc., New York, 1999, ch. 26, p. 463.
43. R. Kajiwara, Y. Asaumi, M. Nakamura and N. Hoshi, J. Electroanal. Chem., 2011, 657, 61–65.
44. D. Strmcnik, D. G. Li, P. P. Lopes, D. Tripkovic, K. Kodama, V. R. Stamenkovic and N. M. Markovic, Top. Catal., 2015, 58, 1174–1180.
45. B. C. Han, C. R. Miranda and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 075410.
46. J. X. Wang, T. E. Springer and R. R. Adzic, J. Electrochem. Soc., 2006, 153, A1732–A1740.
47. S. Chen and A. Kucernak, J. Phys. Chem. B, 2004, 108, 13984–13994.
48. D. S. Strmcnik, P. Rebec, M. Gaberscek, D. Tripkovic, V. Stamenkovic, C. Lucas and N. M. Markovic, J. Phys. Chem. C, 2007, 111, 18672–18678.
49. V. Stamenkovic, N. M. Markovic and P. N. Ross, J. Electroanal. Chem., 2001, 500, 44–51.
50. J. Omura, H. Yano, D. A. Tryk, M. Watanabe and H. Uchida, Langmuir, 2014, 30, 432–439.
51. J. Omura, H. Yano, M. Watanabe and H. Uchida, Langmuir, 2011, 27, 6464–6470.
52. G. A. Attard, A. Brew, K. Hunter, J. Sharman and E. Wright, Phys. Chem. Chem. Phys., 2014, 16, 13689–13698.
53. M. J. T. C. van der Niet, N. Garcia-Araez, J. Hernández, J. M. Feliu and M. T. M. Koper, Catal. Today, 2013, 202, 105–113.
54. W. Schmickler and E. Santos, in Interfacial Electrochemistry, Springer-Verlag, Berlin, Heidelberg, 2010, ch. 6 – Adsorption on metal electrodes: principles, pp. 51–64,  DOI:10.1007/978-3-642-04937-8.
55. J. Jiang and A. Kucernak, J. Electroanal. Chem., 2004, 567, 123–137.
56. J. Tymoczko, F. Calle-Vallejo, W. Schuhmann and A. S. Bandarenka, Nat. Commun., 2016, 7, 10990.
57. D. Strmcnik, D. Tripkovic, D. van der Vliet, V. Stamenkovic and N. M. Markovic, Electrochem. Commun., 2008, 10, 1602–1605.
58. D. Strmcnik, P. P. Lopes, B. Genorio, V. R. Stamenkovic and N. M. Markovic, Nano Energy, 2016, 29, 29–36.
59. S. W. Lee, S. Chen, J. Suntivich, K. Sasaki, R. R. Adzic and Y. Shao-Horn, J. Phys. Chem. Lett., 2010, 1, 1316–1320.
60. A. López-Cudero, Á. Cuesta and C. Gutiérrez, J. Electroanal. Chem., 2006, 586, 204–216.
61. L. A. Kibler, A. Cuesta, M. Kleinert and D. M. Kolb, J. Electroanal. Chem., 2000, 484, 73–82.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ta05543a

---