Open Access Article
Open Access ArticleScaling behaviour and rate-determining steps in filamentous self-assembly†
Georg
Meisl
 a,
Luke
Rajah
a,
Samuel A. I.
Cohen
a,
Manuela
Pfammatter
a,
Luke
Rajah
a,
Samuel A. I.
Cohen
a,
Manuela
Pfammatter
 b,
Anđela
Šarić
b,
Anđela
Šarić
 c,
Erik
Hellstrand
d,
Alexander K.
Buell
e,
Adriano
Aguzzi
b,
Sara
Linse
c,
Erik
Hellstrand
d,
Alexander K.
Buell
e,
Adriano
Aguzzi
b,
Sara
Linse
 d,
Michele
Vendruscolo
a,
Christopher M.
Dobson
d,
Michele
Vendruscolo
a,
Christopher M.
Dobson
 *a and
Tuomas P. J.
Knowles
*a and
Tuomas P. J.
Knowles
 *a
*a
aDepartment of Chemistry, University of Cambridge, Lensfield Road, Cambridge CB2 1EW, UK. E-mail: tpjk2@cam.ac.uk; cmd44@cam.ac.uk
bInstitute of Neuropathology, University Hospital of Zurich, Schmelzbergstrasse 12, 8091 Zurich, Switzerland
cDepartment of Physics and Astronomy, Institute for the Physics of Living Systems, University College London, London WC1E 6BT, UK
dChemistry Department and Molecular Protein Science, Lund University, P. O. Box 124, SE221 00 Lund, Sweden
eInstitute of Physical Biology, University of Duesseldorf, Universitaetsstr. 1, 40225 Duesseldorf, Germany
First published on 31st August 2017
Abstract
The formation of filaments from naturally occurring protein molecules is a process at the core of a range of functional and aberrant biological phenomena, such as the assembly of the cytoskeleton or the appearance of aggregates in Alzheimer's disease. The macroscopic behaviour associated with such processes is remarkably diverse, ranging from simple nucleated growth to highly cooperative processes with a well-defined lagtime. Thus, conventionally, different molecular mechanisms have been used to explain the self-assembly of different proteins. Here we show that this range of behaviour can be quantitatively captured by a single unifying Petri net that describes filamentous growth in terms of aggregate number and aggregate mass concentrations. By considering general features associated with a particular network connectivity, we are able to establish directly the rate-determining steps of the overall aggregation reaction from the system's scaling behaviour. We illustrate the power of this framework on a range of different experimental and simulated aggregating systems. The approach is general and will be applicable to any future extensions of the reaction network of filamentous self-assembly.
Introduction
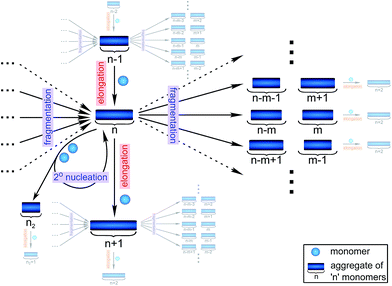
Filamentous self-assembly is observed for a range of different peptides and proteins1–5 and, in many cases, these assembly processes generate structures that are functional in living systems.1,6–11 In other cases, however, protein aggregation may have deleterious effects on an organism's health and is associated with a range of devastating diseases.3–5 At the core of all these phenomena is a fibrillar self-assembly reaction, which is generally homo-molecular in nature.1,5 Despite this apparent simplicity, several different events at the molecular level, such as nucleation, fragmentation and growth, contribute to the overall formation of filaments. Indeed a reaction network of fibrillar self-assembly is very complex and will involve thousands of different aggregate sizes inter-converting (see Fig. 1). The relative importance of the different microscopic processes controls the dominant reaction path resulting in a rich spectrum of observed macroscopic behaviour. Establishing which path the reactive flux from monomers to aggregates takes through this reaction network is a central question in the study of aggregating systems and a range of mechanistic descriptions exist for different aggregating systems.12–14 Here we consider different general cases of network connectivity and the resulting scaling of the aggregation rate with monomer concentration. This allows us to develop a simplified reaction network in the form of a Petri net, which unifies the different mechanistic descriptions and clarifies the meaning of rate-determining steps in the context of filamentous self-assembly reactions. By means of this Petri net, a measurement of the scaling of the characteristic lag-phase of the reaction allows us to determine the aggregation pathway and its rate-determining steps.Results and discussion
The Petri net of filamentous growth
In principle, a full kinetic description of filamentous aggregation in terms of a master equation15 is complex, involving infinitely many non-linear coupled differential equations to keep track of the time evolution of the concentration of each species, i.e. aggregate size, and the reactive fluxes between them, Fig. 1. However, a significant simplification of the equations can be achieved by considering only the total number concentration and the total mass concentration of aggregates of any size, rather than the concentrations of all aggregate sizes individually.12 These overall quantities, which are the zeroeth and first moments of the aggregate size distribution are often easily accessible through experiment. For example the aggregate mass can be measured by an amyloid reporter dye. In this description, the state of the aggregating system is defined by three quantities: the monomer concentration, m(t), the fibril number concentration, P(t), and the fibril mass concentration, M(t). One example of how these three quantities may interact and inter-convert is described by the differential eqn (1) and (2) in Table 1.| Differential equations for the moments | These are the equations produced when all processes in Fig. 3 are included (using the more general, 2-step versions of elongation and secondary nucleation), given certain approximations generally valid for systems of linear self-assembly (see ESI Section 1). Although these non-linear equations are not readily integrated, it is possible to derive closed-form solutions using a self-consistent scheme12,13 (see ESI Section 5). Eqn (1) and (2) are represented visually in the Petri net shown in Fig. 2. This Petri net explicitly includes the intermediate species for multi-step elongation and multi-step secondary nucleation, whilst in the above equations a steady state approximation has been used to treat these species in the context of kinetics (see ESI Section 5 for details and the relation of KE and KM to the rate constants in the Petri net) |
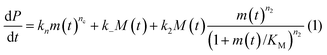
|
|
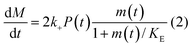
|
|
| Elongation | Elongation is the main process by which new fibril mass is generated. It proceeds by the addition of (usually monomeric) species from solution to the ends of existing fibrils and is modeled either as a single-step reaction (also referred to as unsaturated elongation), with rate constant k+ or more generally as a 2-step reaction, with an initial, monomer concentration-dependent attachment step, followed by a monomer concentration-independent rearrangement step (a ‘dock-lock’ mechanism),19,20 where KE determines the monomer concentration at which this process saturates (see ESI Section 5.2) |
| Primary nucleation | Primary nucleation creates an aggregate in a reaction involving only monomers in solution and is therefore always the most important process at the beginning of an aggregation reaction initiated from monomeric protein alone (see ESI Section 2). Here we treat primary nucleation as a process with single step kinetics, with rate constant kn and reaction order nc in monomer, which will in most cases constitute a coarse-graining of a nucleation cascade. Nucleation cascade descriptions can, however, also be included if appropriate, for example in order to explicitly model pre-fibrillar oligomer concentrations16 |
| Secondary processes/multiplication processes | Secondary processes/multiplication processes summarize processes which produce new growth competent fibrils and depend on the amount of fibrils present. They only become active once a finite quantity of fibrillar material is already present, for example formed via primary nucleation. Secondary processes include fragmentation and secondary nucleation. Due to their auto-catalytic nature, secondary processes can have a very significant effect on the aggregation behaviour of a protein and lead to near exponential increase in fibril mass over time, a feature characteristic of the behaviour of many disease-related proteins |
| Secondary nucleation | Secondary nucleation refers the formation of nuclei from monomeric protein molecules on the fibril surface.2,12,21–23 Secondary nucleation is modelled either as a single-step process (referred to as unsaturated secondary nucleation) with rate constant k2 and reaction order n2 in monomer, or more generally as a 2-step process with an initial step in which monomers attach to the fibril surface, followed by a monomer concentration independent rearrangement/detachment step, where KM determines the monomer concentration at which this process saturates (see ESI Section 5.3) |
| Fragmentation | Fragmentation exposes new growth competent fibril ends through breakage of existing fibrils.12,15,24,25 We model fragmentation by assuming an equal probability of fragmentation at each monomer in a fibril, given by the rate constant k− |
Here, we have taken into account the various possible mechanisms of fibrillar self assembly and have developed a Petri net to visualize the reaction in terms of the moments (Fig. 2). This Petri net is general in that it includes the fundamental processes of fibrillar self-assembly which will apply regardless of the nature of the aggregating species. If required, it can be extended to account for a less coarse-grained description of the individual processes, such as for example a multi-step process with on-pathway oligomers for primary nucleation.16–18 By analogy with the mathematical description, the abstraction to the fibril number and mass concentrations allows the reduction of a very large, complex reaction network that considers every species individually, to a much simpler, compact one as shown in Fig. 2. However, the behaviour of the system in terms of these moments may be less intuitive than in a Petri net representing a chemical reaction in conventional terms. Unlike in more standard chemical reaction networks, the quantities in this description do not necessarily refer to distinct chemical species, such as the concentration of aggregates of a certain size, but rather the properties of the entire population of all aggregates. It can be helpful to think of analogous chemical reactions, for example the elongation step can be seen as the conversion of monomeric species m to their aggregated form M via a catalyst P. If the mass produced by the nucleation processes is neglected (a viable approximation in systems where long fibrils are formed such as those presented here), the primary and secondary nucleation processes can be interpreted as the production of species P from monomer m, with the action of a catalyst M in the case of secondary nucleation. However, not all steps can be mapped to simple chemical reactions. For example, in the fragmentation process P is created without using up any other quantity, which would violate mass balance if P was a chemical species in a standard reaction. Therefore treatment of the systems in terms of the Petri net presented here is necessary and care needs to be taken when considering mappings to standard chemical reactions.
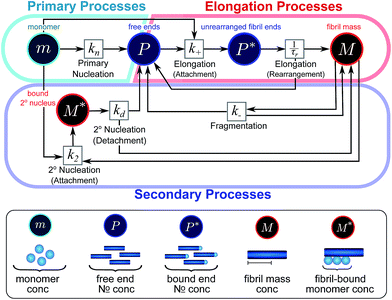 | ||
| Fig. 2 Reaction network of fibrillar self-assembly in terms of moments. The full reaction network, shown in Fig. 1, is significantly simplified by considering the moments of the fibril distribution rather than the concentration of species of all sizes individually. A closed reaction network can be formulated as a Petri net in terms of the first two moments of the fibril length distribution, the mass concentration (M) and the number concentration (P). Circles represent populations of different species, and squares represent the processes that inter-convert them. Note that fragmentation and monomer-dependent secondary nucleation have arcs going in both directions, to and from the fibril mass, because fibril mass is not removed when new ends are created in these processes. | ||
In this description of aggregation in terms of the moments P(t) and M(t), the fundamental processes comprising the reaction network naturally fall into two categories (see Fig. 3): growth processes, which generate the majority of new fibril mass, M, and nucleation/multiplication processes, which generate new aggregates or new growth competent ends, P. These processes are summarized in Fig. 3 and detailed in Table 1. The contribution of the nucleation/multiplication processes to the production of fibril mass is generally negligible because the fibrils formed are many hundreds to thousand monomers in length, whereas nuclei consist only of a few monomers, meaning most of the aggregate mass is produced through elongation (see ESI Section 1†). In the cases when the aggregates produced are not elongated structures, and their aggregate size is comparable to the nucleus size, this approximation is no longer valid and models other than linear self-assembly will be more suitable to describe these phenomena. It is important to note that these two properties of the system, fibril mass M and fibril number P, are controlled by different processes. The fibril number and the fibril mass are coupled, so the overall kinetics will be determined both by the process that dominates nucleation/multiplication as well as the process that dominates growth. It is therefore meaningless to talk about a single process being rate-determining overall for the fibrillar self-assembly (see ESI Section 4.4† for the mathematical explanation for this behaviour). Instead there are one or more processes that determine the rate of growth, dM/dt and one or more processes that determine the rate of nucleation/multiplication, dP/dt.
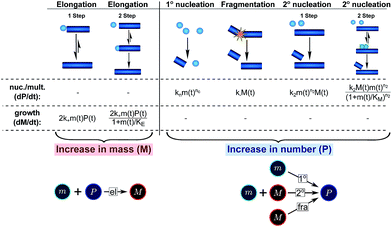 | ||
| Fig. 3 Processes of fibrillar self-assembly. The processes that make up the reaction network of filamentous self-assembly fall into two categories, nucleation/multiplication processes, which produce new fibril ends, P, and only a negligible quantity of new fibril mass, and growth processes, which produce fibril mass, M, but leave the fibril number unchanged. The contributions to the rates of growth and nucleation/multiplication are given below the schematic representation for each process. For elongation and secondary nucleation we use two alternative schemes, a single-step and a two-step one. Under certain conditions the single-step description may be sufficient, as discussed in the main text. The rate constants and reaction rates are defined in Table 1. | ||
Half times and scaling
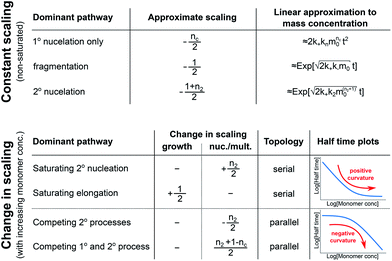
In order to obtain an easily accessible quantity that helps characterize the rate-determining steps in a given reaction network, we use the scaling of the half time of aggregation with monomer concentration. The half time, t1/2, is the time by which half the end-point concentration of fibrillar material (M) has been reached. The dependence of t1/2 on the monomer concentration, m, is written as a power law t1/2 ∝ mγ where γ is referred to as the scaling exponent. As the overall rate of aggregation is determined both by the process that controls the increase in number concentration and the process that controls the increase in mass concentration, the scaling exponent is determined by the monomer concentration-dependence of both of these processes. The rates of the two processes enter multiplicatively into the overall rate, hence their contributions to the scaling exponent are additive (see ESI Section 5.1†). The scaling exponents expected for different dominant mechanisms of aggregation are summarized at the end of this work in Fig. 7. In general, when new aggregate formation is dominated by secondary processes, it can be shown that the half times are approximately given by t1/2 ≈ 1/κ, where κ is of the form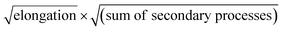 (see ESI Section 5.1†). In this case the scaling is determined by the monomer concentration dependence of the elongation process (referred to as γelon below) and the monomer concentration-dependence of the dominant secondary process.
(see ESI Section 5.1†). In this case the scaling is determined by the monomer concentration dependence of the elongation process (referred to as γelon below) and the monomer concentration-dependence of the dominant secondary process.
For a simple system, a double logarithmic plot of the half time versus monomer concentrations gives a straight line with slope γ. However, in some cases a variation of γ with monomer concentration, evident from curvature in the double logarithmic plots, is observed. Physically, a monomer concentration-dependent scaling exponent is an indication that the monomer dependence of the dominant pathway of either growth or nucleation/multiplication differs for different monomer concentrations, suggesting a switch in the corresponding rate-determining step. The relative change in scaling exponent, i.e. whether the monomer dependence increases or decreases with increasing monomer concentration, can provide insights into the reaction network topology.
Rate-determining steps and network connectivity
In very general terms, two individual steps on the path to a product can combine in two fundamentally different ways: they can occur in series, the product of one being the reactant for the next step, or they can occur in parallel, both forming the same product via different pathways. To illustrate how the rate-determining step for either growth or nucleation/multiplication is expected to change, depending on the monomer-dependence of the individual steps and their topological relationship, we consider two simple hypothetical reaction networks, both forming the same product.The first simple network consists of two steps in series, where in the serial reaction the conversion of intermediate to product is through the action of a catalyst (Fig. 4, left). The case without catalyst is discussed in ESI Section 4.3† and yields an analogous result. The second network consists of two steps in parallel (Fig. 4, right), forming the same product from different reactants. To obtain a scaling exponent, we consider the dependence of the formation of the product (dark blue squares) on the reagent concentration (light blue circles, which we will refer to as monomer in analogy to the aggregation reaction). In both networks one reaction is monomer-dependent (S1 or P1) and the other one is monomer-independent (S2 or P2). Note that the serial network is similar to Michaelis–Menten kinetics observed in enzyme kinetics. The scaling exponent is defined in the same way as for the aggregation reaction.
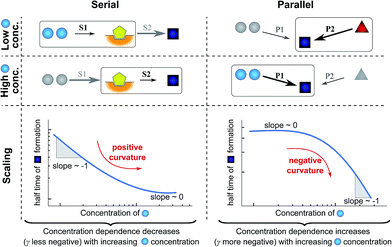 | ||
| Fig. 4 Rate-determining steps and scaling in serial and parallel reactions. The saturating serial process (left) consists of two steps, S1 and S2, in series where the intermediate (yellow pentagon) is bound to a catalyst which is released again upon formation of the product (blue square). The parallel process consists of two steps, P1 and P2, that both yield the same product, directly from monomer (blue circles) in the case of P1 and from a different species (red triangle) in the case of P2. The mechanisms are considered in the limits of high and low concentrations of starting material (blue circles) and the rate-determining step is highlighted in each case. The behaviour of each system over the range of monomer concentrations is summarized in the scaling plots, i.e. the double logarithmic plots of the half time versus monomer concentration (the equations used to generate these plots are given in the ESI Sections 4.1 and 4.2†). Note that for the parallel network the scaling exponent increases in magnitude with increasing concentration (i.e. the faster process dominates the reaction), whereas for the serial network the magnitude of the scaling exponent decreases with increasing concentration (i.e. the slower process limits the overall rate). | ||
First consider the limit of low concentration of monomer: for the serial process the first step, S1, will be slow compared to S2 because of the low concentration of monomer, most of the catalyst will be unbound and S1 will be rate-determining. Small changes in monomer concentration will affect the rate of product formation, the scaling exponent is close to −1. For the parallel process, step P1 will be slow due to the low monomer concentration, hence the formation of product is dominated by the monomer-independent process P2, giving a scaling exponent of zero.
In the limit of high monomer concentration, the first step of the serial network is very fast and most of the catalyst will be present in its bound form, hence the second step, S2, becomes rate-determining and the rate of product formation is unaffected by small changes in the monomer concentration. The parallel network by contrast is dominated by the now much faster step P1 and the scaling exponent is close to −1. A quantitative mathematical analysis of these two reaction networks is given in the ESI Section 4.†
In summary, a decrease in the magnitude of the scaling with increasing monomer concentration results in positive curvature (i.e. a positive second derivative of the curves or equally a positive first derivative of γ) in the scaling plots (Fig. 4B) and is characteristic of a serial (i.e. saturating) pathway. By contrast, an increase in the magnitude of the scaling becomes apparent through negative curvature in the scaling plots and is characteristic of a parallel pathway. The property of a parallel pathway to exhibit a greater monomer dependence upon an increase in monomer concentration, while a serial pathway shows exactly the reverse behaviour, serves as a convenient identification method. This identification method is general and can be applied to any selection of processes in the reaction network at hand, as well as potential future extensions of this network. It should be noted that while it can be shown that a switch between mechanisms in parallel gives negative curvature and a switch between mechanisms in series gives positive curvature (ESI section†), the reverse is not true in general. In more complex reaction networks that include the formation of significant populations of off-pathway species, positive curvature can arise without a switch in the mechanism of aggregate formation, simply through a depletion of monomeric species to form products other than fibrils. However, none of the datasets discussed here necessitate such a more complex mechanism. In the following we discuss the different possible interactions of the individual steps responsible for the increase in aggregate mass or number, illustrated with experimental and simulated aggregation data.
Examples of parallel and serial pathways in the reaction network of fibrillar self-assembly
The growth of existing fibrils, eqn (2), has been found to be well-described by a single mechanism in all proteins studied so far, with the elongation of fibril ends occurring by addition of proteins from solution. Although this mechanism may be multi-step (see Table 1), i.e. a serial reaction, there are no other processes acting in parallel with it, rendering the contribution of growth to the reaction network relatively simple (see Fig. 3 bottom). According to the above description the growth process can therefore either contribute a constant value to the scaling, if it does not saturate, or lead to a decrease in the monomer dependence if it does saturate. Indeed a decrease in the scaling due to a saturation of elongation can be observed experimentally.19,20By contrast, the increase in fibril number, eqn (1), can stem from one of three different sources (see Fig. 3 bottom): primary nucleation, secondary nucleation and fragmentation, which constitute three processes acting in parallel. For an aggregation beginning from monomers, primary nucleation is initially always the dominant process of aggregate production because secondary processes require fibrillar mass to be present to become active. However, if a secondary process is accessible, which is the case in all experimental systems presented here, this secondary process is usually observed to dominate the aggregation reaction as soon as small quantities (in the nM range) of fibrillar material have been formed. We also present simulation data in which the effect of primary nucleation is comparable to that of secondary nucleation even at later times during the aggregation reaction, but no experimental data indicative of such a system exist to our knowledge. Fragmentation and primary nucleation are well described by a single step reaction, but the two-step nature of secondary nucleation becomes evident under certain conditions (see Table 1). Therefore, in summary, nucleation/multiplication constitutes a system of one serial process, competing in parallel with two single step processes.
The contributions from growth and nucleation/multiplication can be distinguished to some extent based on the curve shape and their monomer-dependence, and more rigorously by considering seeded experiments, which allow the sampling of the elongation process alone (see ESI Section 3† for a discussion of seeded systems).
In the following, we show how the Petri net can be used in combination with the half time plots to determine the mechanism of aggregation. The individual cases are illustrated with experimental data on the fibril growth from the peptide hormone insulin and the Aβ peptide linked to Alzheimer's disease. The growth of fibrils from both of these polypeptide systems was studied starting from a supersaturated solution of monomeric protein, in the absence of pre-formed seed structures. The progress of the reaction was monitored using thioflavin-T (ThT) fluorescence; this amyloidophilic label binds preferentially to the fibrillar rather than monomeric states, and therefore acts as a reporter for the concentration of fibrillar material, proportional to M(t). Note that, in principle, competition or saturation of several processes could occur in the same experimental system, leading for example to half time plots that first show negative curvature (due to competition) and then positive curvature (due to saturation). However, in all experimental systems studied here, a single switch in one of the rate-determining steps is sufficient to explain the observed behaviour.
Serial processes in elongation and secondary nucleation
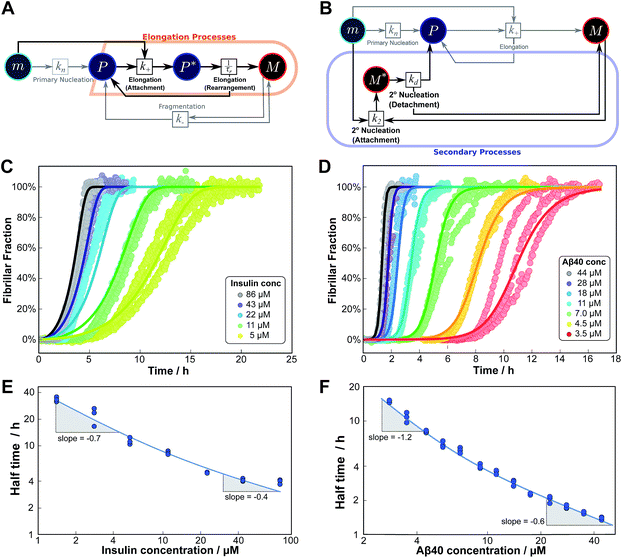
The mechanisms of aggregation of molecules as complex as proteins are likely to involve several intermediates. However, often these intermediates will not be kinetically visible and single-step kinetic descriptions are completely sufficient. By contrast, if intermediates accumulate and, in particular, if the individual steps display a different concentration dependence, it becomes necessary to extend the kinetic descriptions to explicitly include the individual steps. By inspection of the Petri net, Fig. 2, it is evident that such a scenario arises for the two mechanisms that involve both monomeric and fibrillar species, i.e. elongation and secondary nucleation. For these processes two steps with a different monomer dependence occur in series, so we expect positive curvature in the half time plots in the relevant range of monomer concentrations.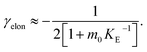 | (1) |
As an example of this saturation effect, we measured the fibril growth from monomeric insulin at concentrations between 1.4 μM and 86 μM (see Fig. 5C and E). Positive curvature was observed in the half time plots, indicative of a serial process. The low average value of the scaling exponent and the relatively small variation furthermore point towards a saturation of elongation, with fragmentation being the process responsible for fibril multiplication (see Fig. 7). The simplified Petri net for this mechanism is shown in Fig. 5A, (for the corresponding differential equations and solution see ESI Section 5.2†), the curves of relative fibril mass versus time, obtained from measurements of ThT fluorescence, were fitted using our fitting platform AmyloFit27 to this mechanism. There is good agreement for both the full time courses and double logarithmic half time plots. The saturation effect becomes evident in the decrease in the spacing of the aggregation curves at higher monomer concentrations (Fig. 5C): as the elongation step becomes monomer-independent the aggregation rate at different monomer concentrations becomes comparable and the curves begin to overlap. This effect is also evident in the low monomer dependence of the half times at high monomer concentrations (Fig. 5E).
 | ||
| Fig. 5 Serial processes. The saturation of elongation (left column) and the saturation of secondary nucleation (right column) are two examples of systems where a variation in monomer concentration leads to a change in the rate-determining step through a switch between two steps in series. (A) Petri net with two-step elongation. The relevant region is highlighted. (B) Petri net with two-step secondary nucleation. Again, the relevant region is highlighted. (C) Saturation of elongation occurs in the aggregation of bovine insulin, here starting from monomeric protein in solution, in triplicate repeats, at concentrations between 5 and 86 μM. The solid lines represent the best global fit to the model, using 3 free parameters. (The data at the lowest two concentrations are noisy and were therefore excluded from the fit, but they are shown in the half time plots to lie on the curve predicted from the fit.) (D) Saturation of secondary nucleation is observed for the aggregation of Aβ40 (pH 7.4).28 Solid lines are the global best fit using 3 free fitting parameters. Only curves at every other concentration are shown for clarity, however all the data were used to obtain the fit. (E) Half time versus initial monomer concentration for insulin. The solid line is plotted using the parameters obtained through the fit in (C). Note the positive curvature due to a decrease in the monomer dependence of the elongation step at high monomer concentrations. (F) Half time versus initial monomer concentration for Aβ40. The solid line is plotted using the parameters obtained from the fit in (D). Again positive curvature is evident, in this case due to a saturation of secondary nucleation at high monomer concentrations. | ||
The scaling exponent is given by:
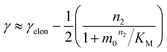 | (2) |
Saturation of secondary nucleation was observed experimentally in the aggregation of Aβ40 between monomer concentrations of 3.5 μM and 44 μM (data from Meisl et al.28). Again, the half time plots display positive curvature, but the large change in γ and additional seeding experiments (not shown) rule out saturation of elongation as in the case of insulin above. The kinetic curves are well fit globally by a model in which elongation does not saturate and multiplication is dominated by saturating secondary nucleation (Fig. 5D). The simplified Petri net for this mechanism is shown in Fig. 5B, the differential equations and solution are given in ESI Section 5.3.† The scaling exponent varies between −0.6 at high monomer concentrations and −1.2 at low monomer concentrations (Fig. 5F).
Competition between two processes in parallel
The previous cases considered processes combining in series, but as there are several distinct mechanisms by which new growth competent ends can be produced, competition between two processes in parallel may also emerge. Conceptually this effect is simpler than a saturation effect, as the faster process simply dominates over the slower one. By inspection of the Petri net three possible scenarios emerge: the two secondary processes, fragmentation and secondary nucleation, compete with each other, or either of the secondary processes competes with primary nucleation. In all cases we expect negative curvature in the half time plots; however, the two cases involving a competition with primary nucleation have to our knowledge not been observed experimentally yet. , from the secondary processes are k_M(t) for fragmentation and k2m(t)n2M(t) for secondary nucleation. While both depend on the concentration of aggregates, M(t), only secondary nucleation also depends on the monomer concentration, m(t). According to the simplified picture of a parallel system discussed in Fig. 4, the monomer-dependent secondary pathway should become dominant at sufficiently high monomer concentrations. At sufficiently low concentrations, by contrast, fragmentation may dominate.
, from the secondary processes are k_M(t) for fragmentation and k2m(t)n2M(t) for secondary nucleation. While both depend on the concentration of aggregates, M(t), only secondary nucleation also depends on the monomer concentration, m(t). According to the simplified picture of a parallel system discussed in Fig. 4, the monomer-dependent secondary pathway should become dominant at sufficiently high monomer concentrations. At sufficiently low concentrations, by contrast, fragmentation may dominate.
We expect the scaling exponents at low and high monomer concentration to be those found for a fragmentation dominated or a secondary nucleation dominated system respectively, i.e. ∼−1/2 at low concentrations and ∼−(n2 + 1)/2 at high concentrations in the case of unsaturated elongation. From the solution of the differential equations (see ESI Section 5.4†), the scaling exponent is given approximately by:
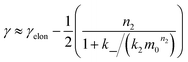 | (3) |
Experimentally, such behaviour emerges in the aggregation of Aβ42 at low ionic strengths, where clear negative curvature in the half time plots is apparent. The half times and kinetic curves of the aggregation of Aβ42 at monomer concentrations between 1.4 μM and 7 μM at an ionic strength of approximately 17 mM (4 mM phosphate buffer, 5 mM NaCl) are shown in Fig. 6C and E. The curve shapes and seeding experiments (not shown) rule out primary nucleation as the process dominating the increase in fibril number at all sampled monomer concentrations, indicating that aggregation proceeds via a mechanism in which secondary nucleation and fragmentation compete (simplified Petri net shown in Fig. 6A). The full kinetic time course fits well to our model and the half times calculated using the parameters obtained in this global fit of the aggregation data match closely the experimental results. The physical reason that, under these conditions, Aβ42 shows competition, whereas Aβ40 showed saturation in the system discussed above, is likely to be a combination of several factors. The lower monomer concentration and the increased electrostatic repulsion in the Aβ42 experiment compared to the Aβ40 experiment both decrease the rate of secondary nucleation. This allows the fragmentation of fibrils, which is less affected by the different conditions, to be fast enough compared to secondary nucleation to become kinetically visible. A more detailed discussion of effects of ionic strength and these data is given in Meisl et al.29
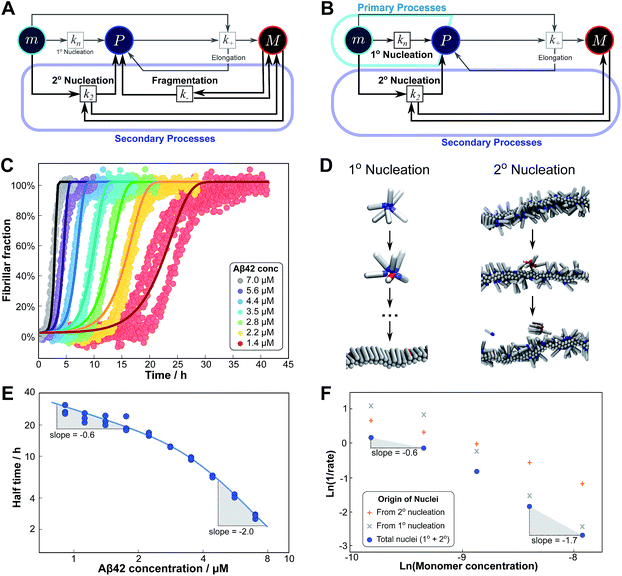 | ||
| Fig. 6 Parallel processes. Competition of two processes in parallel can be observed between fragmentation and secondary nucleation (left) and in simulations also between primary and secondary nucleation (right). (A) Petri net with both secondary processes active. The relevant region is highlighted. (B) Petri net with primary and secondary nucleation. Although primary nucleation was also present in all other nets presented, it was there assumed to be significant only at very early times. (C) Competition of secondary nucleation and fragmentation appears in the aggregation of Aβ42 at low ionic strengths (4 mM sodium phosphate buffer at pH 8.0, 5 mM NaCl). Points are the relative aggregate mass, measured by ThT fluorescence, solid lines are the global best fit using 4 free fitting parameters. Some curves at low monomer concentrations are omitted for clarity although all the data were used to obtain the fit. (D) A minimal model of secondary nucleation was used in a Monte-Carlo algorithm where proteins were modeled as rods with attractive patches; a visualization of the primary and secondary nucleation processes is shown.17,23 (E) Half time versus initial monomer concentration. The solid line is plotted using the parameters obtained through the fit in (C). Note the negative curvature due to an increase in the monomer dependence when secondary nucleation dominates over fragmentation at high monomer concentrations. (F) The overall rate of nucleus formation (blue circles), the rate of nucleus formation from primary nucleation (grey crosses) and from secondary nucleation (red pluses) as obtained from the Monte-Carlo simulations (D). The negative curvature agrees with the predicted behaviour and moreover the simulations allow one to directly establish the origin of the nuclei, again confirming the prediction that the more monomer-dependent process dominates at high monomer concentrations. | ||
Although there is currently no experimental evidence for systems displaying such a competition between primary and secondary processes, we have observed this behaviour in silico, in minimal simulations of aggregation.23 In these simulations, the monomer dependence of the secondary process is naturally lower than that of the primary process as new nuclei are formed from bound monomers on the surface and are stabilised by the presence of the surface, lowering the critical nucleus size. According to our description of parallel systems, secondary nucleation is therefore expected to be the main generator of new aggregates at low concentrations, whereas primary nucleation should dominate at high concentrations, resulting in an increase in the magnitude of the scaling exponent with increasing monomer concentration. The simulations are performed in the presence of a preformed seed, with a constant concentration of monomers, so the previous definition of the half time is not useful in this context. We instead consider the monomer dependence of the rate of nucleus formation, plotting its inverse in Fig. 6F to allow easier comparison with half time plots.
Although there is no half time in these simulations, they have a distinct advantage over experiment in that they allow the direct determination of the origin of each nucleus, hence giving separate rates of primary and secondary nucleation. As expected, at low monomer concentrations the overall rate of nucleus formation is determined by secondary process, whereas at high concentrations it is determined by primary nucleation in solution, leading to a negative curvature in the double logarithmic plots of monomer concentration versus inverse nucleation rate, Fig. 6F. Crucially, these data show that the change in scaling exponent is indeed due to a change in the dominant process of nucleus formation, confirming that the process with the higher monomer dependence, primary nucleation, produces more nuclei at high monomer concentrations whereas the process with the lower monomer dependence, secondary nucleation, dominates at low monomer concentrations.
Conclusions
In conclusion, we have condensed the complex reaction networks of filamentous growth into a simple Petri net in terms of the moments of the fibrillar distribution. This net unifies a range of previously described mechanistic models, providing a clear general picture of fibrillar self-assembly: the aggregation kinetics depend both on the rate at which new fibrillar mass is formed and on the rate at which the fibril number increases, hence the overall rate is controlled by distinct rate-determining steps for each of the two processes. In addition to this Petri net, we provide a general guide to the kinetics and concentration dependence of combining two reaction steps in series and in parallel. Through this approach, we are able to link the connectivity of the Petri net to variations in the scaling exponent, which characterizes the dependence of the aggregation half time on the protein concentration. In particular, we find that the sign of the change of the scaling exponent with protein concentration indicates whether a mechanism consists of two kinetically visible steps acting in series or if two distinct processes compete in parallel. Our findings are summarized in Fig. 7. The approach presented here to link the scaling exponent to the network topology is general and can be easily extended to variations and extensions of the Petri net, for example to account explicitly for the presence of oligomeric species18 or to take into account the formation of higher order assemblies from existing aggregates.31Materials and methods
Aβ40
The aggregation assay was performed in 20 mM sodium phosphate buffer at pH 7.4 in the presence of 100 μM ThT. For further details on purification see ref. 28.Aβ42
The aggregation assay was performed in 4 mM sodium phosphate buffer at pH 8.0, in the presence of 5 mM NaCl and 6 μM ThT. For further details on purification see ref. 29.Insulin
Bovine insulin was purchased from Sigma-Aldrich and used without further purification. Solutions of insulin in 50 mM NaCl (pH 1.6) containing 10 μM ThT were prepared in 96-well non-binding plates (Corning prod. no. #3881) and incubated at 45 °C in a Fluostar Omega plate reader (BMG Labtech). ThT fluorescence was measured every 180 s with 5 s shaking before each reading using 450/480 nm ex/em filters.Data fitting
All fits were performed on the fitting platform AmyloFit.27 The differential equations describing the kinetics and their approximate solutions which were used in the fitting are all given in the ESI.†Computer simulations
All computer simulations were performed using a coarse-grained Monte Carlo scheme, as described in our previous work.17,23 The parameters used here were: monomer–fibril interaction, εsf = 8 kT, monomer–monomer interaction, εss = 6 kT.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The research leading to these results has received funding from the European Research Council under the European Union's Seventh Framework Programme (FP7/2007-2013) through the ERC grant PhysProt (agreement no. 337969) (SL, TPJK), Sidney Sussex College Cambridge (GM), the Frances and Augusta Newman Foundation (TPJK), the Biotechnology and Biological Science Research Council (TPJK), the Swedish Research Council (SL), the Academy of Medical Sciences (AŠ), Wellcome Trust (AŠ), and the Cambridge Centre for Misfolding Diseases (CMD, TPJK, MV).References
- F. Oosawa and S. Asakura, Thermodynamics of the Polymerization of Protein, Academic Press, 1975 Search PubMed.
- F. Ferrone, Methods Enzymol., 1999, 309, 256–274 CAS.
- F. A. Ferrone, J. Hofrichter and W. A. Eaton, J. Mol. Biol., 1985, 183, 611–631 CrossRef CAS PubMed.
- C. M. Dobson, Nature, 2003, 426, 884–890 CrossRef CAS PubMed.
- C. M. Dobson, Trends Biochem. Sci., 1999, 24, 329–332 CrossRef CAS PubMed.
- F. Oosawa and M. Kasai, J. Mol. Biol., 1962, 4, 10–21 CrossRef CAS PubMed.
- B. Alberts, A. Johnson, J. Lewis, M. Raff, K. Roberts and P. Walter, Molecular Biology of the Cell, Garland Publishing, 4th edn, 2002 Search PubMed.
- T. L. Hill, Linear Aggregation Theory in Cell Biology, Springer, 1987 Search PubMed.
- J. W. Kelly and W. E. Balch, J. Cell Biol., 2003, 161, 461–462 CrossRef CAS PubMed.
- D. M. Fowler, A. V. Koulov, C. Alory-Jost, M. S. Marks, W. E. Balch and J. W. Kelly, PLoS Biol., 2006, 4, e6 Search PubMed.
- S. K. Maji, M. H. Perrin, M. R. Sawaya, S. Jessberger, K. Vadodaria, R. A. Rissman, P. S. Singru, K. P. R. Nilsson, R. Simon, D. Schubert, D. Eisenberg, J. Rivier, P. Sawchenko, W. Vale and R. Riek, Science, 2009, 325, 328–332 CrossRef CAS PubMed.
- S. I. A. Cohen, M. Vendruscolo, M. E. Welland, C. M. Dobson, E. M. Terentjev and T. P. J. Knowles, J. Chem. Phys., 2011, 135, 065105 CrossRef PubMed.
- S. I. A. Cohen, M. Vendruscolo, C. M. Dobson and T. P. J. Knowles, J. Chem. Phys., 2011, 135, 065106 CrossRef PubMed.
- S. I. A. Cohen, M. Vendruscolo, C. M. Dobson and T. P. J. Knowles, J. Chem. Phys., 2011, 135, 065107 CrossRef PubMed.
- T. P. J. Knowles, C. A. Waudby, G. L. Devlin, S. I. A. Cohen, A. Aguzzi, M. Vendruscolo, E. M. Terentjev, M. E. Welland and C. M. Dobson, Science, 2009, 326, 1533–1537 CrossRef CAS PubMed.
- G. A. Garcia, S. I. A. Cohen, C. M. Dobson and T. P. J. Knowles, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 032712 CrossRef PubMed.
- A. Šarić, Y. C. Chebaro, T. P. J. Knowles and D. Frenkel, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17869–17874 CrossRef PubMed.
- A. Šarić, T. C. T. Michaels, A. Zaccone, T. P. J. Knowles and D. Frenkel, J. Chem. Phys., 2016, 145, 211926 CrossRef PubMed.
- T. Scheibel, J. Bloom and S. L. Lindquist, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 2287–2292 CrossRef CAS.
- W. P. Esler, E. R. Stimson, J. M. Jennings, H. V. Vinters, J. R. Ghilardi, J. P. Lee, P. W. Mantyh and J. E. Maggio, Biochemistry, 2000, 39, 6288–6295 CrossRef CAS PubMed.
- A. M. Ruschak and A. D. Miranker, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 12341–12346 CrossRef CAS PubMed.
- S. I. A. Cohen, S. Linse, L. M. Luheshi, E. Hellstrand, D. A. White, L. Rajah, D. E. Otzen, M. Vendruscolo, C. M. Dobson and T. P. J. Knowles, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9758–9763 CrossRef CAS PubMed.
- A. Šarić, A. Buell, G. Meisl, T. C. T. Michaels, C. M. Dobson, S. Linse, T. P. J. Knowles and D. Frenkel, Nat. Phys., 2016, 12, 874–880 CrossRef.
- S. R. Collins, A. Douglass, R. D. Vale and J. S. Weissman, PLoS Biol., 2004, 2, e321 Search PubMed.
- M. Tanaka, S. R. Collins, B. H. Toyama and J. S. Weissman, Nature, 2006, 442, 585–589 CrossRef CAS PubMed.
- A. K. Buell, J. R. Blundell, C. M. Dobson, M. E. Welland, E. M. Terentjev and T. P. J. Knowles, Phys. Rev. Lett., 2010, 104, 228101 CrossRef PubMed.
- G. Meisl, J. B. Kirkegaard, P. Arosio, T. T. C. Michaels, M. Vendruscolo, C. M. Dobson, S. Linse and T. P. J. Knowles, Nat. Protoc., 2016, 11, 252–272 CrossRef CAS PubMed.
- G. Meisl, X. Yang, E. Hellstrand, B. Frohm, J. B. Kirkegaard, S. I. A. Cohen, C. M. Dobson, S. Linse and T. P. J. Knowles, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 9384–9389 CrossRef CAS PubMed.
- G. Meisl, X. Yang, C. M. Dobson, S. Linse and T. P. J. Knowles, Chem. Sci., 2017, 8, 4352–4362 RSC.
- P. Arosio, R. Cukalevski, B. Frohm, T. P. J. Knowles and S. Linse, J. Am. Chem. Soc., 2014, 136, 219–225 CrossRef CAS PubMed.
- S. Bolisetty, J. Adamcik and R. Mezzenga, Soft Matter, 2011, 7, 493–499 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7sc01965c |
| This journal is © The Royal Society of Chemistry 2017 |