Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Structural organization in the trimethylamine iodine monochloride complex†
William G.
Marshall‡
a,
Richard H.
Jones
 *b,
Kevin S.
Knight
a,
John
Clews
b,
Richard J.
Darton
*b,
Kevin S.
Knight
a,
John
Clews
b,
Richard J.
Darton
 b,
William
Miller
b,
Simon J.
Coles
b,
William
Miller
b,
Simon J.
Coles
 c and
Mateusz B.
Pitak
c
c and
Mateusz B.
Pitak
c
aISIS Facility, STFC Rutherford Appleton Lab, Harwell Oxford, Didcot OX11 0QX, Oxon, England, UK. Fax: +44 (0)1235 4455720; Tel: +44 (0)1235 445434
bBirchall Centre for Inorganic Materials, School of Chemical and Physical Sciences, Keele University, Keele, ST5 5BG UK. E-mail: Chemistry@keele.ac.uk; Fax: +44 (0)1792 712378; Tel: +44 (0)1782 733033
cUK National Crystallography Service, Chemistry, Faculty of Natural and Environmental Sciences, University of Southampton, Southampton SO17 1BJ, UK. E-mail: info@ncs.ac.uk; Fax: +44 (0)8059 6723; Tel: +44 (0)8059 6722
First published on 28th June 2017
Abstract
The structure of the complex formed between trimethylamine and iodine monochloride had been redetermined by a combination of neutron powder diffraction and X-ray single crystal diffraction techniques. The structure determined using NPD shows that the geometry of the trimethylamine moiety resembles that in trimethylammonium cations rather than in the free trimethylamine molecule. The structure shows the presence of weak C–D⋯Cl hydrogen bonds, The I–Cl bond length is in agreement with that derived from an analysis of the pKb values of a series of nitrogen bases and previously determined structures containing N⋯ICl fragments.
Introduction
Halogen bonding is an area of increasing importance in chemistry. The rapid rise in the number of papers mentioning halogen bonding has been commented on previously,1 with the number of papers discussing either halogen bonding or halogen bonds in the title or abstract having risen from 15 in 2002 to 305 in 2016.1,2The existence of halogen bonds has been known since the 19th century;3 however, the first modern description of the bonding in these compounds was not proposed until the 1950s,4 which was no doubt motivated by the first determination of the crystal structures of complexes formed between donor species such as C5H5N, (CH3)3N, and 1,4-dioxane in combination with acceptor molecules such as I2, Br2, ICl.5 The initial view of the halogen bonding interaction was that there was substantial charge donation from a lone pair on the donor atom into an anti-bonding σ* orbital of the acceptor molecule.4 However, the currently accepted view of the bonding concentrates on the electrostatic interaction between an area of negative potential on the donor and positive potential on the halogen (σ-hole).6 The σ-hole of the halogen is located on the extension of the axis of the bond between the halogen and the atom to which it is bonded6–8 This description of halogen bonding (also taking account polarization and dispersion effects7,8) has become the most widely accepted view for the majority of compounds in which such bonds occur.
In addition to fundamental questions of bonding in these complexes, halogen bonding has also been studied for its similarity to hydrogen bonding,9 and also for its role in many other areas of chemistry, for example, in supramolecular chemistry,10 liquid crystals,11 and biological systems.12 In the context of the latter, the potential role of secondary stabilising (C–H⋯X) interactions may be of relevance in dictating a specific orientation of a substrate molecule at an active site.13 Recently, calculations on the interaction of substituted bromobenzene with acetone predicted that there may also be secondary stabilising interactions between the hydrogen atoms of the acetone and an area of negative electrostatic potential encircling the bromine σ-hole.14 Using neutron powder diffraction techniques, we have recently observed in the complex formed between acetone and bromine that there is just such a stabilising weak C–H interaction.15 We have also observed similar interactions in the complexes formed between pyridine and ICl and IBr. As a consequence of the interplay between the halogen and weak hydrogen bonding interactions we have also observed unusual thermal expansion properties, such as negative thermal expansion and colossal thermal expansion.16
Complexes between FCl and CN–X (X = CN, NC, NO2, F, CF3, Cl, Br, H, CCF, CCH, CH3, SiH3) molecules have been studied recently.17 Some of which have properties which resemble those seen in the earliest structurally characterized halogen-bonded complexes. For example, linear geometries and Cl⋯C distances which, though they exceed the sum of the covalent radii, have values which are much closer to this value than the sum of the van der Waals radii.17 One of the conclusions that the authors derived from this study was that, as the basic strength of the isocyanide increased, “…the nature of the halogen bond changes from conventional chlorine-shared to ion pair”. These systems, together with SiN–R complexes, have also been recently investigated by Politzer and Murray7 (in which Cl2 was modelled as an acceptor), who attributed these effects to the group 14 elements being strongly polarized by the σ hole of the chlorine atom of the FCl molecule. They also noted that these polarization effects could merge into dative sharing and, as such, it is perhaps open to question whether these systems are true halogen-bonded complexes. We have recently reinvestigated several of the original halogen-bonded complexes containing nitrogen or oxygen as the donor (D) and either halogen (X2) or interhalogen (XY) molecules as the acceptor.15,16 These have some features similar to those seen in the FCl and CN–X complexes in that they typically contain a linear D⋯X–Y motif in which the D⋯X distance is typically 10% longer than the covalent radii.18 Historically, these systems were amongst the first to be characterised and are still often mentioned and discussed in standard undergraduate textbooks.19
In this work, we have re-investigated the structure of the complex formed between ICl and trimethylamine (TMA) using neutron powder diffraction (NPD) and variable-temperature single crystal X-ray diffraction. The molecular structure of this compound was first investigated by Hassel and Hope in 1960,20 who reported the characteristic indicators of a strong halogen-bonded complex, i.e. a linear N⋯I–Cl arrangement with a nitrogen⋯iodine distance longer than a covalent bond but shorter than a van der Waals contact, and a lengthened I–Cl distance. The original crystal structure determination was carried out using photographic methods (visual estimation of intensities) and Fourier refinement of the data. Given the success of recent crystallographic studies in determining accurate hydrogen positions in molecular solids,21 we thought it would be timely to reinvestigate this important crystal structure using modern crystallographic methods and so obtain somewhat more precise information on the positions of the hydrogen atoms and to investigate the possible occurrence of C–H⋯X bonds.
Experimental
The samples to be studied using X-ray diffraction were prepared by the slow addition of a commercial (Sigma Aldrich) 1.0 M solution of iodine monochloride to an ice-cold solution of trimethylamine (45% wt) in stoichiometric quantities. The resulting orange precipitate was collected and recrystallized from a solution in hot methanol, which was slowly cooled to produce suitable crystals. In the case of the sample for the neutron powder diffraction experiment, perdeuterated trimethylamine (Sigma Aldrich) was condensed into a graduated test tube which had been placed in Dewar flask (methanol–N2(l) cooling mixture) to which was added a stoichiometric amount of 1.0 M iodine monochloride in dichloromethane (Sigma Aldrich). As before, the resulting precipitate was recrystallized from hot methanol.For the X-ray diffraction study, a small single crystal (0.24 × 0.2 × 0.18 mm) was selected as a suitable specimen. Single-crystal X-ray diffraction data were collected using a ‘Bruker-Nonius Roper’ CCD camera on a κ-goniostat mounted at the window of a Bruker FR591 rotating anode X-ray source (Mo Kα, λ = 0.71073 Å). Diffraction data were collected at room temperature, i.e. 298 K, and 110 K.22,23 For the neutron powder diffraction study, the recrystallized deuterated sample material was gently ground in a cooled agate pestle and mortar and then transferred into a thin-walled quartz tube. Once filled, the quartz tube was placed in a thin-walled vanadium sample can which was then attached to a sample stick and then cooled to 110 K in an AS “Orange” helium cryostat. High-resolution neutron powder diffraction patterns were then collected from this sample using the HRPD time-of-flight diffractometer at the ISIS facility of the STFC Rutherford Appleton Laboratory.
The resulting single-crystal X-ray diffraction data were of sufficient completeness and quality for the crystal structures to be solved using ab initio methods24 and then refined by least squares25 using a Chebychev weighting scheme.26 One low angle reflection, that appeared to suffer from significant extinction effects, was omitted from the refinements. All of the hydrogen atoms were located from Fourier difference maps and allowed to refine independently with isotropic temperature factors. In the case of the 298 K data set, suitable restraints were applied to the H–C–N and H–C–H bond angles of the TMA molecule and one equivalent temperature factor was applied to all the hydrogen atoms of each methyl group. The 110 K X-ray structure was used as the starting model for the Rietveld profile refinement (using GSAS)27 of the neutron powder diffraction patterns. Isotropic thermal parameters were used for all atoms in the neutron diffraction structure refinement.
Results and discussion
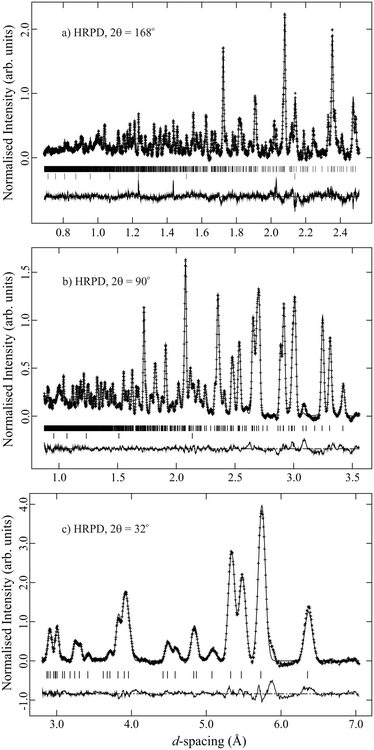
Crystallographic data resulting from the X-ray and neutron diffraction structure refinements are given in Table 1. Selected intramolecular contact distances and angles are shown in Tables 2 and 3. Fig. 1 illustrates the quality of fit of the GSAS Rietveld profile structure refinement with the observed 110 K NPD pattern from the deuterated TMA:ICl complex. The resulting molecular structures and packing diagrams for the TMA:ICl complex are shown in Fig. 2–4.| Compound | N(CH3)3 IClb | N(CH3)3 IClc | N(CD3)3 ICld |
|---|---|---|---|
| a I > 2σ(I). b CCDC deposition CCDC1531716. c CCDC deposition CCDC1531709. d CCDC deposition CCDC1531801. | |||
| Radiation | X-ray (Mo-Kα) | X-ray (Mo-Kα) | Neutron (TOF) |
| Crystal system | Orthorhombic | Orthorhombic | Orthorhombic |
| Space group | Pbca | Pbca | Pbca |
| Temperature/K | 298 | 110 | 110 |
| a/Å | 11.6168(4) | 11.5039(3) | 11.4812(7) |
| b/Å | 11.1573(4) | 10.9570(3) | 10.9618(6) |
| c/Å | 10.8342(3) | 10.6758(3) | 10.6723(6) |
| V/Å3 | 1404.24(8) | 1345.67(6) | 1343.16(21) |
| Formula | C3H9NICl | C3H9NICl | C3D9NICl |
| Mw/g mol−1 | 221.47 | 221.47 | 230.47 |
| D c/g cm−3 | 2.095 | 2.186 | 2.279 |
| Z | 8 | 8 | 8 |
| Size/mm | 0.24 × 0.2 × 0.18 | 0.24 × 0.2 × 0.18 | NA |
| λ/Å | 0.71073 | 0.71073 | NA |
| μ/mm−1 | 4.824 | 5.034 | NA |
| 2θmax/° | 54.96 | 54.96 | NA |
| N ref | 9848 | 9198 | 3165 |
| N unique | 1601 | 1539 | 2140 |
| T min T max | 0.35 0.42 | 0.30 0.40 | NA |
| R int | 0.033 | 0.030 | NA |
| N obs | 1333 | 1418 | |
| N param | 85 | 85 | 138 |
| wR2(all) | 0.040 | 0.035 | NA |
| R | 0.026 | 0.021 | NA |
| R wp | NA | NA | 0.014 |
| R p | NA | NA | 0.011 |
| 253 K XRD20 | 298 K XRD | 110 K XRD | 110 K NPD | |
|---|---|---|---|---|
| No SU are reported in ref. 20. | ||||
| Cl–I⋯N | 178.6(1) | 178.7(1) | 178.7(3) | |
| I⋯N–C(1) | 109 | 108.5(3) | 108.2(2) | 108.3(3) |
| I⋯N–C(2) | 104 | 108.7(3) | 108.6(2) | 109.5(2) |
| I⋯N–C(3) | 107 | 109.1(3) | 109.0(2) | 109.2(3) |
| C(1)–N–C(2) | 108 | 110.5(3) | 110.7(3) | 110.1(3) |
| C(1)–N–C(3) | 109 | 109.7(4) | 109.9(2) | 108.8(3) |
| C(2)–N–C(3) | 118 | 110.3(4) | 110.5(2) | 110.0(3) |
 | ||
| Fig. 2 a Thermal ellipsoid diagram for the TMA:ICl complex at 110 K (XRD data). b Ball and stick diagram for the TMA:ICl complex at 110 K (NPD data). | ||
Most of the bond lengths and angles given in the earlier X-ray structure determination of Hassel and Hope20 are in rough agreement with those obtained from our higher resolution structure refinements. The distances within the TMA:ICl complex merit some discussion. There is a significant difference in one key bond length, namely, the key I–Cl interhalogen bond length. In the earlier work this distance was reported as 2.52 Å; in this study the three structure refinements provided values between 2.5621(12) Å and 2.5790(8) Å. The N⋯I–Cl component of the complex has a bond angle of 178.7(1)° (NPD), 178.7(1)° XRD at 110 K and 178.6 (1)° XRD at 298 K. Both the N⋯I and I–Cl distances are significantly longer than either the sum of the covalent radii for the N–I bond (2.10 Å) or for I–Cl molecule in the gas phase (2.321 Å)28 but are significantly shorter than the sum of the van der Waals radii (3.67 Å and 3.79 Å, respectively).29 This feature of the N⋯ICl unit has been commented on in the past4 and has been attributed to the formation of a three-centre four-electron bond in which there is one bonding and one non-bonding electron pair.30 If this is the case, then the moiety is isoelectronic to (or would have the same type of bonding as seen in) ions such as [ICl2]−. This apparent similarity between N⋯X2 complexes to linear trihalide ions was first noted by Hassel towards the end of his work on these systems.31
A comparison of selected bond lengths for structural determinations of N⋯I–Cl complexes when N is either part of an heterocyclic aromatic ring or the TMA:ICl complex is given in Table 4 together with the pKb values for the donor compound. In all of these compounds the N–I–Cl fragments is close to linear with N–I–Cl bonds ranging between 175.33(5)° to 179.9(4)°. It can be seen that the longest I–Cl bond length within this series occurs for the TMA complex. It can also clearly be seen that the overall trend in the I–Cl distances follows that of the pKb values for the donor molecules; that is to say, the longer I–Cl distances are associated with more basic amines. This correlation is illustrated in Fig. 5 where we have plotted the data from low temperature studies. We have only used the low temperature data in constructing this plot as rigid body37 TLS calculations on the compound studied in this work suggest that librational corrections of the order of 0.008 Å need to be applied to room temperature data sets and 0.003 Å to data collected at 110 K. From Fig. 5 it can also be seen that the correlation between N⋯I distance and pKb is not of similar quality; furthermore, it can be seen that the value for the TMA:ICl complex appears anomalous. A much better correlation may be obtained when the value for the TMA complex is omitted and this is shown in Fig. 6. The origin for the anomalous position for the TMA:ICl complex probably arises either from the smaller covalent radius for a sp2 hybrid for the aromatic nitrogen of pyridine in comparison to the sp3 hybrid for TMA or the presence of charge delocalization in the aromatic ring, or a combination of both effects. However, even with the TMA:ICl complex omitted, the degree of correlation agreement is not as good. This may, perhaps, be due to the lower intrinsic accuracy of determining the position of the relative low-Z nitrogen atom in the presence of the much heavier iodine atom for the X-ray studies A plot of N⋯I bond length versus I–Cl bond length appeared to showed a linear correlation over the range of values that were used (barring the TMA complex). This did not correspond to the expected hyperbola, which is typically seen for linear triatomic species.38,39 The origin of this linear behaviour is unclear but may be a consequence of the limited range of data available.
| Donor compound | T/K | pKba | I–Cl/Å | I⋯N/Å |
|---|---|---|---|---|
DMAP = 4-(dimethylamino)pyridine.a Ref. 30;b ref. 16;c ref. 32;d ref. 33;e this work;f ref. 34;g ref. 35;h ref. 36.pKb = −log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Kb where Kb where  for the reaction. B + H2O ⇌ [BH+] + [OH−]. for the reaction. B + H2O ⇌ [BH+] + [OH−]. |
||||
| 3-Bromopyridinea | 120 | 11.16f | 2.4734(7) | 2.344(2) |
| Pyridineb | 110 | 8.77f | 2.523(1) | 2.284(3) |
| Pyridineb | 298 | 8.77f | 2.504(2) | 2.281(4) |
| DMAPa | 120 | 4.8g | 2.5615(7) | 2.246(2) |
| 2,2-Bipyridinea | 120 | 9.67h | 2.4974(7) | 2.321(2) |
| 2,2-Bipyridinea | 120 | 9.67h | 2.4879(9) | 2.337(2) |
| 2,2-Bipyridinec | 298 | 9.67h | 2.5421(4) | 2.336(7) |
| 2,2-Bipyridinec | 298 | 9.67h | 2.477(11) | 2.344(7) |
| 2 chloroquinolined | 293 | 13.59 | 2.432(8) | 2.446(3) |
| Trimethylaminee | 110 | 4.2f | 2.5790(8) | 2.304(3) |
| Trimethylaminee | 298 | 4.2 | 2.5621(12) | 2.299(3) |
A correlation between the interatomic N⋯I contacts with the calculated pKb values for the complexes formed between a series of fluorinated iodobenzenes with 4-(N,N-dimethylamino)pyridine DMAP has also been made.40 In this study, the I⋯N distances varied between 2.926 and 2.693 Å and thus represent much weaker interactions with negligible charge transfer. This was inferred from the observation that all the C–I bond lengths were the same within experimental error. The relationship between donor D⋯I contacts in halogen-bonded complexes was also the subject of a Cambridge Crystallographic Database investigation,41 in which the authors were able to show that there were clear correlations between the equilibrium formation constant for D⋯I2 complexes and both the elongation of the I–I bonds and the D⋯I distance. Furthermore, they showed that the elongation of the I–I bond and the D⋯I distance fell into distinct families which depended upon the nature of the donor D.
Whilst the use of experimentally determined equilibrium constants is undoubtedly correct and more rigorous than the use of pKb values to infer N⋯I distances, the use of pKb values, which can be relatively easily obtained from reference sources, or calculated using computer packages such as Gaussian-98,42 appears to be able to predict the I–Cl distances to surprising accuracy and, hence, via the conservation of bond number at the iodine atom, the N⋯I bond length. Furthermore, the use of pKb may enable us to predict the occurrence and nature of complexes formed between bases and interhalogens. The justification for this last statement makes use of the recognized similarity between hydrogen and halogen bonding. It is known that in a system containing a hydrogen bond X–H⋯Y–Z there is strong correlation in the strength of the hydrogen bond between the pKa value of X–H and the pKb value of Y–Z43 and also that hydrogen bonds can play a part in proton transfer reactions. What we may be seeing with the interactions that occur with the strongest bases are the initial steps in the transfer of an iodine atom in the reaction
| RN + ICl → [RNI]+ + Cl− |
Turning our attention to the TMA moiety, the bond lengths and angles show both similarities and differences to that of free TMA. In the crystal structure of pure TMA the molecule has crystallographically imposed 3-fold symmetry. In the TMA:ICl complex, the C–N bond lengths appear to have the same value within error in the X-ray structure but for the NPD structure two bonds are similar in length, while the third differs to a statistically significant degree; whether this finding is chemically significant is open to question. All the bond lengths differ markedly from those reported for pure trimethylamine, as determined by X-ray diffraction 1.4535(11) Å,44 electron diffraction 1.455(2) Å,45 microwave 1.451(3) Å (ref. 46) and DFT 1.4566.47 The average seen in our 110 K X-ray structure determination is 1.482(3) Å, which is closer to that seen in trimethylammonium cations (1.486(6) Å)48 or when TMA acts as a ligand in a complex. In the complexes formed between TMA and Cr(CO)5 and Mo(CO)5 the N–C bond length values range between 1.478 Å and 1.490 Å (ref. 49) or 1.477 Å in the adduct formed between GaH3 and TMA.50
The free TMA molecule itself has C3v symmetry, with a hydrogen atom on each of the methyl groups being orientated in an anti arrangement to the nitrogen lone pair. In the case of the complex formed with an ICl molecule, the latter occupies the coordination site where the nitrogen lone pair resides. The C–N–C bond angles again show differences between our X-ray and neutron structures. For the former, all the angles appear to have the same value within error, while for the neutron structure the differences are larger but at the margin of statistical significance. One final point worth noting is that the N–C–Hanti bond angle differs significantly from that reported in other structural studies, namely 114.3° (XRD44), 111.7° (microwave spectroscopy46) and 112.9° (DFT calculation47). The increase in this angle from the ideal tetrahedral value was ascribed to a hyperconjugative effect between the nitrogen lone pair and the C–Hanti bond47 as opposed to our study where the bond angle values ranged between 110.6° and 108.7°. Because of these changes in bond angle, the Hanti⋯Hanti distances are smaller in our structure (average 2.455 Å) than in the free molecule (2.562 Å). The smaller distances seen in the complex would not normally be expected on steric grounds. Furthermore, these changes are occurring at atoms which are not adjacent to the nitrogen and would thus not be significantly affected by steric demands on the nitrogen upon increasing its coordination number from 3 to 4. This is confirmed by the observation that whilst the C⋯C distance in the free molecule is 2.387 Å the average value in the complex is 2.436 Å, which suggests that any steric pressure caused by formation of the complex with I–Cl has already been accounted for by the increase in the C⋯C distance. In addition, since the larger bond angle was a consequence of the hyper conjugative interaction between the lone pair of the nitrogen and the Hanti atom, any changes involving the lone pair occurring on complex formation would change the N–C–Hanti angle. Our argument is analogous to the effect of protonation on TMA, where this angle was reported to decrease by 4.5° to 108.4°.48 A similar decrease in the N–Hanti angle to give an observed value of 109.7(3.3)° was seen in the X-ray study of the complex formed between GaH3 and TMA.50
From the changes seen both within the N⋯I–Cl moiety and the TMA molecule itself, it seems that some degree of electronic reorganization has occurred. This is clearly seen not only in the changes within the TMA molecule discussed above but also in the bond lengths and the bond numbers within the N⋯ICl moiety. Whilst bond number is an empirical concept, it serves a useful function and finds widespread use in chemistry, as do other empirical concepts such as electronegativity.39 It can be clearly seen that the I–Cl bond length of 2.578(6) Å is comparable to those found in symmetric ICl2− ions51 where a bond order of 0.5 is observed. Furthermore, the N⋯I distance of 2.290(6) Å (NPD) is similar to those found in symmetric N⋯I⋯N units seen in [I(NC5H5)2]+ BF4−, 2.259(3) Å;52 [C14H18IN2]+ IBr2−, 2.294(3) Å (ref. 53) and C14H18IN2+ ICl2−, 2.300(1) Å (ref. 29) where, again, a bond number of 0.5 would be inferred. The question which has already been advanced in the case of the compounds formed between FCl and CN–X is whether these compounds possess true halogen bonds. We believe that the recognition of the similarity between hydrogen and halogen bonds provides a solution. The origin of the bonding in hydrogen bonds has long been debated,54 and that “The importance of various components of hydrogen bonding may vary quite widely from system to system.”55 However, it is well known that in the case of hydrogen bonding there is a continuum from very strong to weak hydrogen bonds,56 though the terminology used for these interactions does depend upon the definitions of individual authors.57,58 It should of course be emphasised that there is a gradation of the properties in these systems and that to categorize hydrogen bonds into distinct groupings is probably a mistake. Of relevance to this work is the transition (using the classification of Desiraju and Steiner) between strong and very strong hydrogen bonds.58 In the former, electrostatic interactions are dominant and the degree of covalency is weak so that these bonds can have significant effects upon crystal packing. These types of bonds are exemplified by systems such O–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, N–H⋯O
C, N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and O–H⋯O–H. Adopting this approach would place complexes such as TMA:ICl into the same position as species such as [HF2]− occupy in the hydrogen bonding classification, namely very strong hydrogen bonds.
C and O–H⋯O–H. Adopting this approach would place complexes such as TMA:ICl into the same position as species such as [HF2]− occupy in the hydrogen bonding classification, namely very strong hydrogen bonds.
One of our objectives in this work was the accurate location of hydrogen atoms involved in weak C–H⋯X hydrogen bonds. Examination of the D⋯Cl distances obtained in the NPD study reveals that the four shortest D⋯Cl contact distances are Cl–D(23) 2.755(5) Å; Cl⋯D(13) 2.772(5) Å; Cl⋯D(22) 2.862(5); Cl⋯D(12) 2.901(5). The two shortest of these distances are significantly smaller than the sum of the van der Waals radii of Cl and H (2.86 Å (ref. 28)) and are thus possibly involved in C–D⋯Cl hydrogen bonds. The corresponding I–Cl⋯D angles are 114.0(2)° and 77.0(2)° respectively indicating that the deuterium atoms lie well away from the axis of the I–Cl moiety and the σ hole and, hence, towards areas of negative electron density. These bond angle values are similar to those seen in the neutron diffraction study of pyridine–IBr, where an I–Br⋯D angle of 81.17(14)° was observed for the shortest Br⋯D contact (2.787(4) Å). The occurrence of these hydrogen bonds together with the N–ICl hydrogen bond can be clearly seen in by examining the Hirschfeld surfaces (Fig. 7).59,60 These have been previously used to demonstrate the occurrence of intermolecular contacts.61,62
 | ||
| Fig. 7 Hirshfeld surface for the trimethylamine iodine monochloride complex in two different orientations. | ||
Unfortunately, we have neutron powder diffraction data at just one temperature. However, by comparing the changes in the relevant Cl⋯C distances as a function of temperature from the X-ray study, we may estimate what happens to these weak hydrogen bonds as the temperature increases. The increase in the C⋯Cl distances with temperature is roughly the same for both systems, namely Cl⋯C1 3.830(4) Å at 110 K, 3.899(5) Å at 298 K; and Cl⋯C2 3.825(4) Å at 110 K and 3.904(5) Å at 298 K. These results suggests that the Cl⋯H interactions associated with these carbon atoms weaken with increasing temperature. Further evidence for this comes from a broad line NMR study on the TMA:ICl complex.63 Compared to TMA itself, which cleanly lost the fine structure observed in the fine structure at 77 K when warmed to 110 K, the spectra for TMA:ICl evolved via a series of steps from the characteristic broadened fine structure at 77 K to a completely averaged spectrum at ∼150 K. This effect may well be due to C–H⋯Cl hydrogen bonding being operative at low temperature.
Since all the hydrogen bonds in the title compound are responsible for forming the sheet structures in the b-c plane of the crystal structure, weakening of the C–H⋯Cl hydrogen bonds with increasing temperature would be expected to lead to enhanced thermal expansion in this plane relative to the perpendicular direction, which is accord with our observations (αa = 52.2 MK−1αb = 97.2 MK−1αc = 78.9 MK−1).64
Conclusion
From our investigation of the TMA:ICl complex, in conjunction with the existing literature on N⋯ICl complexes, we suggest there is a simple linear relationship between the pKb values of the nitrogen bases and the bond lengths within the N⋯ICl moiety and that the changes in the bond lengths within this moiety for a series of nitrogen containing bases may signify progress along the reaction coordinate for the transformation N⋯ICl → [NI]+ + Cl−. We also see changes in the geometry of the TMA molecule are consistent with likely electronic changes within the molecule, as do changes within the ICl fragment The use of neutron diffraction has accurately and precisely located the positions of the deuterium atoms within the crystal structure and reveals the existence of weak C–H⋯Cl hydrogen bonds, which may be responsible, in part, for determining the packing in this crystal and its thermal expansion properties.Acknowledgements
We thank the EPSRC, STFC and the ISIS Facility for supporting this study, including the provision of neutron beam time. We also wish to acknowledge the late Bill Marshall for his incisive comments during this work and contribution to the study of molecular solids using neutron powder diffraction.Notes and references
- P. Metrangolo and G. Resnati, Cryst. Growth Des., 2012, 12, 5835 CAS.
- Web of Science “The Web of Science Service for UK Education” Thomson Reuters http://wok.mimas.ac.uk/.
- F. Guthrie, J. Chem. Soc., 1863, 239 RSC.
- R. S. Mulliken, J. Am. Chem. Soc., 1952, 74, 811 CrossRef CAS.
- (a) O. Hassel and C. Romming, Q. Rev., Chem. Soc., 1962, 16, 1 RSC; (b) O. Hassel, Science, 1970, 170, 3957 Search PubMed.
- (a) T. Brinck, J. S. Murray and P. Politzer, Int. J. Quantum Chem., 1992, 44, 57 CrossRef; (b) P. Politzer and J. S. Murray, ChemPhysChem, 2013, 14, 278 CrossRef CAS PubMed; (c) T. Clark, M. Hennemann, M. Murray, J. S. Murray and P. Politzer, J. Mol. Model., 2007, 13, 291 CrossRef CAS PubMed.
- P. Politzer and J. S. Murray, Theor. Chem. Acc., 2012, 131, 114 CrossRef.
- P. Politzer, K. E. Riley, F. A. Bulat and J. S. Murray, Comput. Theor. Chem., 2012, 198, 2 CrossRef.
- A. C. Legon, Struct. Bonding, 2008, 126, 17 CrossRef CAS; P. Metrangolo, H. Neukirch, T. Pilati and G. Resnati, Acc. Chem. Res., 2005, 38, 5 CrossRef PubMed; S. J. Grabpwski, Phys. Chem. Chem. Phys., 2013, 15, 2013 Search PubMed.
- (a) R. Bertani, P. Sgarbossa, A. Venzo, F. Lelj, M. Armati, G. Resnati, P. Metrangolo and G. Terraneo, Coord. Chem. Rev., 2010, 254, 677 CrossRef CAS; (b) K. Rissanen, CrystEngComm, 2008, 10, 1107 RSC; P. Metrangolo, F. Meyer, T. Pilati, G. Resnati and G. Terraneo, Angew. Chem., Int. Ed., 2008, 47, 6114 Search PubMed.
- (a) H. L. Nguyen, P. N. Horton, M. B. Hursthouse, A. C. Legon and D. W. Bruce, J. Am. Chem. Soc., 2004, 126, 16 CrossRef CAS PubMed; (b) C. M. Cho, X. B. Wang, J. J. Li, C. B. He and J. W. Xu, Liq. Cryst., 2013, 40, 185 CrossRef CAS; (c) C. Praesang, H. L. Nguyen, P. N. Horton, A. C. Whitwood and D. W. Bruce, Chem. Commun., 2008, 6164 RSC; (d) L. J. McAllister, C. Präsang, J. P.-W. Wong, R. J. Thatcher, A. C. Whitwood, B. Donnio, P. B. Karadakov and D. W. Bruce, Chem. Commun., 2013, 3946 RSC.
- (a) P. Auffinger, F. A. Hays, E. Westhof and P. S. Ho, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 16789 CrossRef CAS PubMed; (b) M. R. Scholfield, C. M. Vander Zanden, M. Carter and P. S. Ho, Protein Sci., 2013, 22, 139 CrossRef CAS PubMed.
- Y. Lu, Y. Wang, Z. Xu, X. Yan, X. Luo, H. Jang and W. Zhu, J. Phys. Chem. B, 2009, 113, 12615 CrossRef CAS PubMed.
- (a) K. E. Riley, J. S. Murray, P. Politzer, M. C. Concha and P. Hobza, J. Chem. Theory Comput., 2009, 5, 155 CrossRef CAS PubMed; (b) K. E. Riley, J. S. Murray, J. Fanfrik, J. Rezac, R. C. Sola, M. C. Concha, F. M. Ramos and P. Politzer, J. Mol. Model., 2011, 17, 3309 CrossRef CAS PubMed.
- R. H. Jones, K. S. Knight, W. G. Marshall, S. J. Coles, P. N. Horton and M. B. Pitak, CrystEngComm, 2014, 16, 237 RSC.
- R. H. Jones, K. S. Knight, W. G. Marshall, J. Clews, R. J. Darton, D. Pyatt, S. J. Coles and P. N. Horton, CrystEngComm, 2013, 15, 8572 RSC.
- J. E. del Bene, I. Alkorta and J. Elguero, J. Phys. Chem. A, 2010, 114, 12958 CrossRef CAS PubMed.
- B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Dalton Trans., 2008, 2832 RSC.
- M. Weller, T. Overton, J. Rourke and F. Armstrong, Inorganic ChemistryOxford, University Press Oxford, 6th edn, 2014 Search PubMed.
- O. Hassel and H. Hope, Acta Chem. Scand., 1960, 14, 391 CrossRef CAS.
- (a) D. M. S. Martins, D. S. Middlemiss, C. R. Pulham, C. C. Wilson, M. T. Weller, P. F. Henry, N. Shankland, K. Shankland, W. G. Marshall, R. M. Ibberson, K. S. Knight, S. Moggach, M. Brunelli and C. A. Morrison, J. Am. Chem. Soc., 2009, 131, 3884 CrossRef CAS PubMed; (b) S. Crawford, M. T. Kirchner, D. Blaeser, R. Boese, W. I. F. David, A. Dawson, A. Gehrke, R. M. Ibberson, W. G. Marshall, S. Parsons and O. Yamamuro, Angew. Chem., Int. Ed., 2009, 48, 755 CrossRef CAS PubMed; (c) D. R. Allan, S. J. Clark, R. M. Ibberson, S. Parsons, C. R. Pulham and L. Sawyer, Chem. Commun., 1999, 751 RSC.
- R. W. W. Hooft, Collect: Data Collection Software, ed. B. V. Nonius, Delft, The Netherlands, 1998 Search PubMed.
- G. M. Sheldrick, SADABS, Version 2.10, Bruker AXS Inc., Madison, Wisconsin, USA, 2003 Search PubMed.
- L. Palatinus and L. G. Chapuis, J. Appl. Crystallogr., 2007, 40, 786 CrossRef CAS.
- P. W. Betteridge, J. R. Carruthers, R. I. Cooper, K. Prout and D. J. Watkin, J. Appl. Crystallogr., 2003, 36, 1487 CrossRef CAS.
- J. R. Carruthers and D. J. Watkin, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1979, 35, 698 CrossRef.
- (a) A. C. Larson and R. B. Von Dreele, General Structure Analysis System (GSAS), Los Alamos National Laboratory Report LAUR 86-748 ( 2000) Search PubMed; (b) B. H. Toby, EXPGUI, a graphical user interface for GSAS, J. Appl. Crystallogr., 2001, 34, 210–213 CrossRef CAS.
- K. P. Huber and G. Herzberg, in Molecular Spectra and Molecular Structure. IV.Constants of Diatomic Molecules, van Nostrand, New York, 1979 Search PubMed.
- R. S. Rowland and R. Taylor, J. Phys. Chem., 1996, 100, 7384 CrossRef CAS.
- A. S. Batsanov, J. A. K. Howard, A. P. Lightfoot, S. J. R. Twiddle and A. Whiting, Eur. J. Org. Chem., 2005, 1876 CrossRef CAS.
- O. Hassel and C. Romming, Acta Chem. Scand., 1967, 21, 2659 CrossRef CAS.
- S. Soled and G. B. Carpenter, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1974, 30, 910 CrossRef.
- G. Bernardinelli and R. Gerdil, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1976, 32, 1906 CrossRef.
- CRC Handbook of Chemistry and Physics, ed. W. M. Hayes, 91st edn, 2010 Search PubMed.
- http://evans.harvard.edu/pdf/evans_pka_table.pdf (accessed 6th dec 2013).
- D. D. Perrin, Aust. J. Chem., 1964, 17, 484 CrossRef CAS.
- V. Schomaker and K. N. Trueblood, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1968, 24, 63 CrossRef CAS.
- (a) H. A. Bent, Chem. Rev., 1968, 68, 587 CrossRef CAS; (b) H. B. Burgi, Angew. Chem., Int. Ed. Engl., 1975, 14, 460 CrossRef.
- J. D. Dunitz, X-ray Analysis and the Structure of Organic Molecules, Verlag Helvetica Chimica Acta, Zurich, 1995 Search PubMed.
- C. Präsang, A. C. Whitwood and D. W. Bruce, Cryst. Growth Des., 2009, 9, 5319 Search PubMed.
- C. Ovvard, J.-Y. Le Questel, M. Berthelot and C. Laurence, Acta Crystallogr., Sect. B: Struct. Sci., 2003, 59, 512 Search PubMed.
- B. Ghalami-Choobar, A. Ghiami-Shomami and P. Nikparsa, J. Theor. Comput. Chem., 2012, 11, 283 CrossRef CAS.
- P. Gilli, L. Pretto, V. Bertolasi and G. Gilli, Acc. Chem. Res., 2009, 42, 33 CrossRef CAS PubMed.
- A. J. Blake, E. A. V. Ebsworth and A. J. Welch, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1984, 40, 413 CrossRef.
- B. Beagley and T. G. Hewitt, Trans. Faraday Soc., 1968, 64, 2565 RSC.
- J. E. Wollrab and V. W. Laurie, J. Chem. Phys., 1969, 5Z, 1580 CrossRef.
- A. K. Chandra, S. Parveen, S. Das and T. Zeegers-Huyskens, J. Comput. Chem., 2008, 29, 1490 CrossRef CAS PubMed.
- Average value for N–C in [HN(CH3)3]+ salts was determined from 19 low temperature (100–150 K) crystal structures which did not contain disorder and were error free. 20th November 2013.
- M. Findlater, N. J. Hill and A. H. Cowley, J. Chem. Crystallogr., 2010, 40, 64 CrossRef CAS.
- P. T. Brain, H. E. Brown, A. J. Downs, T. M. Greene, E. Johnsen, S. Parsons, D. W. H. Rankin, B. A. Smart and C. Y. Tang, J. Chem. Soc., Dalton Trans., 1998, 3685 RSC.
- Average value for I-Cl in [ICl2]− salts was determined from 23 symmeteric low temperature (100–150 K) crystal structures which did not contain.
- C. Álvarez-Rúa, S. García-Granda, A. Ballesteros, F. González-Bobes and J. M. González, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2002, 58, o1381 Search PubMed.
- A. S. Batsanov, A. P. Lightfoot, S. J. R. Twiddle and A. Whiting, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2006, 62, o901 CAS.
- (a) P. Macchi, N. Casati, W. G. Marshall and A. Sironi, CrystEngComm, 2010, 12, 2596 RSC; (b) B. Kojic-Prodic and K. Molcanov, Acta Chim. Slov., 2008, 55, 692 CAS.
- E. Arunan, G. R. Desiraju, R. A. Klein, J. Sadlej, S. Scheiner, I. Alkorta, D. C. Clary, R. H. Crabtree, J. J. Dannenberg, P. Hobza, H. G. Kjaergaard, A. C. Legon, B. Mennucci and D. J. Nesbitt, Pure Appl. Chem., 2011, 83, 1637–1641 CAS.
- T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48 CrossRef CAS.
- G. A. Jeffrey, An Introduction to Hydrogen Bonding, OUP Oxford, 1997 Search PubMed.
- G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond, OUP Oxford, 1999 Search PubMed.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129 CrossRef CAS.
- J. J. McKinnon, D. Jayatilaka and M. A. Spackman, CrystalExplorer 2.1, University of Western Australia (http://hirshfeldsurface.net/CrystalExplorer), Perth, 2007 Search PubMed.
- M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19 RSC.
- J. J. McKinnon, D. Jayatilaka and M. A. Spackman, Chem. Commun., 2007, 3814 RSC.
- C. A. Fyfe and J. Ripmeester, Can. J. Chem., 1970, 48, 2283 CrossRef CAS.
- K. S. Knight, Phys. Chem. Miner., 2010, 37, 529 CrossRef CAS.
Footnotes |
| † CCDC 1531709, 1531716 and 1531801. For crystallographic data in CIF or other electronic format see DOI: 10.1039/c7ce00869d |
| ‡ Deceased. |
| This journal is © The Royal Society of Chemistry 2017 |