Open Access Article
Open Access ArticleExchange-bias quantum tunnelling in a CO2-based Dy4-single molecule magnet†
Eufemio Moreno
Pineda
 a,
Yanhua
Lan
b,
Olaf
Fuhr
a,
Wolfgang
Wernsdorfer
*ab and
Mario
Ruben
a,
Yanhua
Lan
b,
Olaf
Fuhr
a,
Wolfgang
Wernsdorfer
*ab and
Mario
Ruben
 *ac
*ac
aInstitute of Nanotechnology (INT), Karlsruhe Institute of Technology (KIT), Hermann-von-Helmholtz-Platz 1, D-76344 Eggenstein-Leopoldshafen, Germany. E-mail: mario.ruben@kit.edu
bInstitut Néel, CNRS, Université Grenoble Alpes, 25 rue des Martyrs, F-38000 Grenoble, France
cInstitut de Physique et Chimie des Matériaux de Strasbourg (IPCMS), CNRS, Université de Strasbourg, 23 rue du Loess, BP 43, F-67034 Strasbourg Cedex 2, France
First published on 22nd September 2016
Abstract
Carbamate formation in green-plants through the RuBisCO enzyme continuously plays a pivotal role in the conversion of CO2 from the atmosphere into biomass. With this in mind, carbamate formation from CO2 by a lanthanide source in the presence of a secondary amine is herein explored leading to a lanthanide–carbamate cage with the formula [Dy4(O2CNiPr2)12]. Magnetic studies show slow relaxation leading to the observation of hysteresis loops; the tetranuclear cage being a single molecule magnet. Detailed interpretation of the data reveals: (i) the presence of two different exchange interactions, ferromagnetic and antiferromagnetic and (ii) the observation of exchange-bias quantum tunnelling with two distinct sets of loops, attributable to ferromagnetic interactions between dysprosium ions at longer distances and antiferromagnetic exchange between dysprosium ions at shorter distances. The results clearly demonstrate that the [Dy4(O2CNiPr2)12] cage acts as a quantum magnet which in turn could be at the heart of hybrid spintronic devices after having implemented CO2 as a feedstock.
Introduction
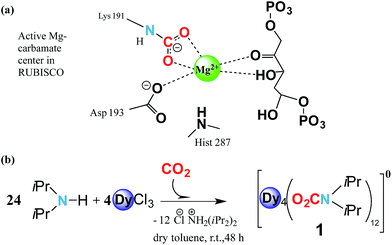
Carbamylation is the most important chemical process in the fixation, activation and capture of CO2 in nature, where CO2 is inserted into an M–N amide bond of a Mg2+ centre and an ε-amino residue of a lysine amino acid (Lys) resulting in the formation of a carbamate1 (Fig. 1a). The enzyme responsible for this process is ribulose-1,5-bisphosphate carboxylase/oxygenase, better known as RuBisCO, the most abundant protein in the world and the major contributor to the conversion of atmospheric CO2 into biomass.2 Despite the efficient role of RuBisCO, in the last 150 years the concentration levels of the most abundant greenhouse gas, CO2, have dramatically increased from 280 ppm to 400 ppm (ref. 3 and 4) due to growing industrial activity. However, due to the renewable character of CO2 it could, if well managed, in principle serve as a valuable feedstock source for the synthesis and production of added value materials.5–7Reminiscent of enzymatic CO2 activation, where an oxophilic Mg2+ centre is involved, transition metals have demonstrated that they can be versatile catalytic entities to activate and interconvert CO2 in organic compounds.8,9 Moreover, they have been shown to be successful in coordinating to CO2, forming metal complexes.10–13 Recently Long et al. have studied the cooperative insertion of CO2 into diamine-appended metal–organic frameworks (MOFs) where the removal of CO2 from solution can be directly achieved through the insertion of CO2 into amine groups leading to a carbamate-containing MOF.14
In this regard, lanthanide metal ions seem to be promising agents for CO2 capture due to their strong oxophilic characteristics which allow the concerted insertion of CO2 as a carbamate15–18 or as carbonate-containing compounds with high lanthanide/CO2 ratios.19,20 Several polymetallic carbonate-containing systems have been described, showing not just interesting structural motifs but also bewildering physical properties.20 Similarly, lanthanides are milestone entities in terms of their magnetism, and have also shown fascinating physical behaviours such as nuclear spin detection and manipulation21,22 blocking of magnetisation at high temperatures23–26 magnetic memory in chiral systems with a non-magnetic ground state27 and, very recently, blocking magnetisation at the atomic level.28 These properties have led researchers to envisage a diverse range of possible applications for lanthanide-based molecules, including their potential to act as qubits for quantum information technologies and prototype quantum spintronic devices such as molecular spin valves and transistors.22,29,30 Thus, the quantum correlations observed in lanthanide molecules (e.g. superposition, entanglement, coherence, etc.) are important resources for quantum communication and processing, particularly in quantum computing.31
Based on these two points, i.e. (i) CO2 abundance and (ii) the quantum physical properties of lanthanide units, we explore the physical implementation of CO2 as a feedstock for the synthesis of lanthanide molecular nanomagnets. Herein, we firstly explore the CO2 fixation of an amine in the presence of dysprosium chloride to form a complex with the formula [Dy4(O2CNiPr2)12] (1) (O2CNiPr2 = diisopropylcarbamate) (Fig. 1b and 2). Moreover, we explore the magnetic properties of such a material, which in turn could shed light on its possible applicability in quantum spintronic devices or quantum computing. Herein, through a combination of alternating current SQUID measurements, and μ-SQUID measurements along with a simple electrostatic analysis, we show that the [Dy4(O2CNiPr2)12] cage exhibits both ferro- and antiferromagnetic interactions, that can be associated with the intramolecular interactions between the Ising-like dysprosium ions within the compound, exhibiting exchange-bias quantum tunnelling, where the two different exchange interactions could, in principle, be employed in four-qubit quantum gate operations;32 these characteristics highlight the importance of our proposal to employ CO2 as a C1 building block to form added-value materials.
Results and discussion
Synthesis and structure
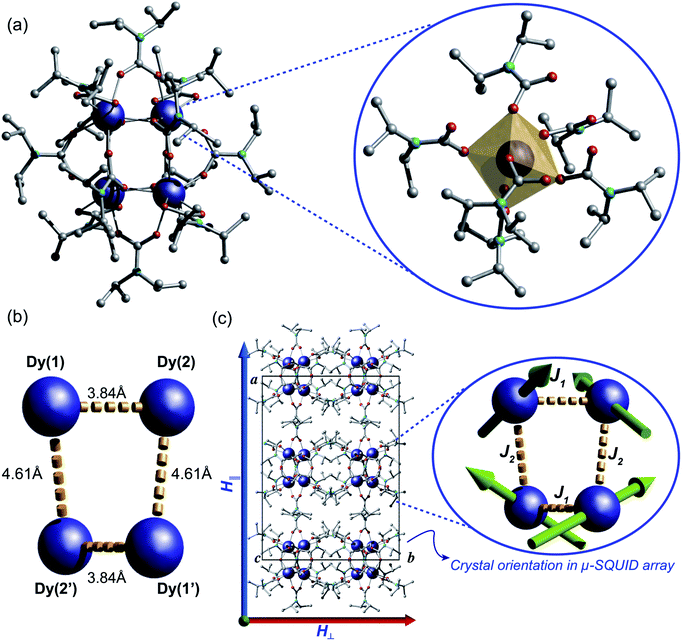
The reaction of anhydrous dysprosium chloride, with a six-fold excess of di-isopropylamine and CO2 in dry toluene, followed by crystallisation in toluene at 5 °C gave colourless block-shaped X-ray quality crystals in yields of 70%. Single crystal studies revealed the compound to be a neutral tetranuclear lanthanide–carbamate cage with the molecular formula [Dy4(O2CNiPr2)12]·2C7H8 (1)‡ (Fig. 2). Infrared analysis of 1 shows the typical carbamate stretching modes between 1300 and 1700 cm−1 (Fig. S1†). The molecule crystallises in the monoclinic C2/c space group with half of the molecule in the asymmetric unit (Table S1†).The neutral homoleptic tetramer 1 is composed of four Dy(III) ions and twelve carbamate groups resulting from the capture of twelve CO2 molecules under mild synthetic conditions. Two Dy(III) ions are found in the asymmetric unit, interrelated by a two-fold axis and both ions, i.e. Dy(1) and Dy(2) are hepta-coordinated featuring a capped trigonal prism geometry33 (Table S3†). The Dy(1)⋯Dy(2) and Dy(1)′⋯Dy(2)′ distances are 3.8381(6) Å whilst the Dy(1)⋯Dy(2)′ and Dy(1)′⋯Dy(2) distances are 4.6090(7) Å. The Dy⋯O distances are in the range of 2.238(5) to 2.404(4) Å. The versatility of carbamates as coordinating groups is evidenced with the three distinct coordination modes present in the cage, 1.11, 2.11 and 3.21 (ref. 34) (Fig. S2†). All carbamates are rather regular with C⋯N distances ranging between 1.33(1)–1.372(8) Å and C⋯O in the range of 1.25(1)–1.30(1) Å (Table S2†). The closest intermolecular Dy⋯Dy distance is 12.8530(8) Å.
Magnetism DC and AC measurements
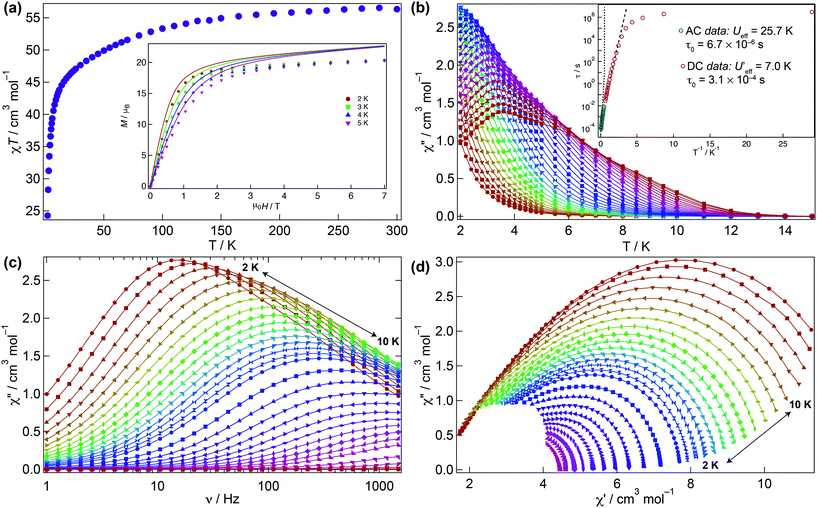
The magnetic behaviour of 1 was investigated under an applied direct current (DC) field of 1 kOe (Fig. 3). The room temperature χMT value for 1 (56.3 cm3 K mol−1) is close to that expected for four non-interacting Dy(III) ions (56.7 cm3 K mol−1) and upon cooling declines smoothly to ca. 30 K where it sharply drops to 24.3 cm3 K mol−1 due to depopulation of the Stark levels of the crystal field (CF) and antiferromagnetic interactions (vide infra). The molar magnetisation M(H) for 1 does not reach full saturation at 2 K (inset Fig. 3a).To probe the dynamic behaviour of compound 1, alternating current (AC) susceptibility measurements under an oscillating field of 3.5 Oe were undertaken. Compound 1 shows clear signatures of a Single Molecule Magnet (SMM) at zero field, i.e. strong frequency dependent magnetic behaviour with a maximum shifting upon frequency change and temperature. At zero field the out-of-phase component is observed in the χ′′M(T) below 12 K, with a broad maximum at about 3.8 K for a frequency of 1.5 kHz. The maximum shifts towards lower temperatures with decreasing frequency. In the χ′′M(ν) a single broad process is observed which can be fitted using a generalised Debye model. The Arrhenius plot is based on AC results and was fitted to data between 7.5 and 10 K yielding an energy barrier of Ueff = 25.7(1) K, a τ0 = 6.7(1) × 10−6 s, with α varying from 0.07 to 0.45 from high to low temperature indicating a wide distribution of relaxation times, which could be associated with the two slightly distinct dysprosium ions in 1 (Fig. 3b–d and S3†).
Given that the Ueff at zero field is small, the investigation of an optimal field was carried out to try to reduce the quantum tunnelling rate. An optimal field of 1.5 kOe was obtained and under this condition 1 was reinvestigated (Fig. S4–S6†). Likewise at zero field, upon application of the optimal field, the out-of-phase component in the temperature dependence χ′′M(T) begins from 12 K, with a very broad maximum at 6 K at the highest frequency (1.5 kHz) whilst the χ′′M(ν) shows just a single broad process, which can be fitted to a simple Debye model. Arrhenius treatment of the data above 7.5 K yields Ueff = 31.1(1) K, τ0 = 2.55(1) × 10−6 s, and 0.008 < α < 0.015 showing a narrower distribution of relaxation times but not considerable improvement in the Ueff. As evidenced, application of the optimal DC field does not completely slow down the fast tunnelling of 1 highlighting that the quantum tunnelling of the magnetisation (QTM) is not efficiently suppressed. This can be attributed to transverse anisotropy and to dipolar/exchange and/or hyperfine interactions. The linear dependence of ln(τ) at high temperatures indicates an Orbach relaxation mechanism, whilst the data at lower temperatures is markedly nonlinear at zero and under application of the optimal field, suggesting the onset of competing Orbach and/or Raman processes. The anisotropic nature of compound 1 does not allow fitting of the χMT(T) and M(H) without advanced and costly ab initio calculations.
μ-SQUID measurements
We have further explored the magnetic behaviour of 1 by employing a μ-SQUID array35 on an oriented crystal, with the field applied along and transverse to the easy-axis, from 0.03–2 K, and at different magnetic field scan rates. The opening of the hysteresis loops starts below 2 K and their coercivity fields widen with increasing sweep rates and with decreasing temperature, a signature of SMM (Fig. 4). Interestingly, two marked distinct magnetic behaviours are detected depending on the direction of the applied magnetic field: either (i) antiferromagnetic interactions, thus exhibiting double S-shaped loops and no significant QTM at zero field attributable to exchange biasing of antiferromagnetically coupled dimers and/or spin-canting (Fig. 4a and c); or (ii) ferromagnetic interactions with well opened loops (Fig. 4b and d). Below 1 K the loops display step-like features, indicating that resonant quantum tunnelling occurs below this temperature. Along the antiferromagnetic projection two sharp tunnelling steps at ±0.35 T are found; whilst in the ferromagnetic projection the zero-field resonance loop is shifted to μ0H = ±0.22 T and is then followed by three successive steps located at ±0.32, ±0.42 and ±0.62 T. These observations corroborate the SMM behaviour of 1 allowing now a more judicious analysis of the low temperature energy barrier (U′eff) employing the data obtained from the magnetisation decay measurements from the μ-SQUID data; a linear fit in the temperature range of 0.45–1.5 K leads to a U′eff value of 7.0 K with the quantum regime reached below 0.2 K and a τ0 = 3.1 × 10−4 s (inset of Fig. 3b).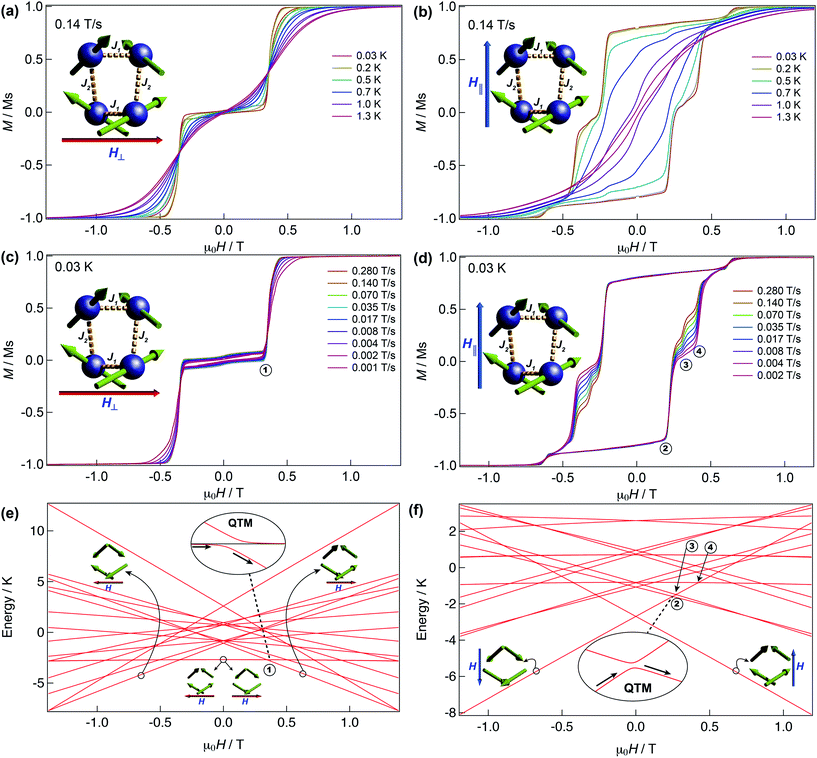 | ||
| Fig. 4 μ-SQUID measurements and Zeeman diagram for 1. Hysteresis loop measurements performed on a single crystal of 1; red and blue arrows represent the direction of the applied field with respect to the molecule’s orientation within the crystal lattice. Temperature dependence at a fixed sweep rate of 0.14 T s−1 with the field applied transverse (a) and parallel (b) to the average direction. Field sweep rate studies at a fixed temperature of 0.03 K with the fields transverse (c) and parallel (d) to the average direction. Panels (a) and (c) show the antiferromagnetic behaviour with a typical double S-shape whilst panels (b) and (d) show the ferromagnetic behaviour. Zeeman diagrams simulated using eqn (1) along the antiferromagnetic projection (e) and the ferromagnetic projection (f). Insets of the panels show the avoided level crossings observed alongside the antiferromagnetic projection at ±0.35 T and along the ferromagnetic projection at ±0.22 T. The spin structure in panels (e) and (f) (green arrows) represent the ground and excited states involved in the quantum tunnelling events (see text). | ||
Magnetic axes
A great deal of understanding of the magnetic behaviour of lanthanide-based SMMs has been achieved through multi-configurational complete active space self-consistent field (CASSCF) ab initio calculations,36 however these are very cost-ineffective methods often requiring expert theoretical knowledge and advanced computational power. Recently, a more intuitive and much less demanding electrostatic approach was described for the elucidation of the anisotropic axes of dysprosium complexes based on the charge distribution of ligands around the Dy(III) ions and the electrostatic optimisation of the oblate mJ = ±15/2 electron density.37 The SMM behaviour observed in dysprosium-based systems is associated with a well-defined mJ = ±15/2 ground state doublet and greatly axial g-tensors (ideally gxx = gyy = 0; gzz = 20) of the 6H15/2 manifold and has been well tested in a variety of complexes with very good agreement with the CASSCF calculations.26,37,41 Given the SMM behaviour clearly exhibited by 1 we employ the electrostatic calculation to obtain its anisotropic magnetic axes simply utilising the crystallographic coordinates of 1 and the partial charges of the carbamates and Dy(III) ions. As expected, due to crystallographic considerations, two slightly distinct sets of axes are found with a tilting angle of around ∼140° between Dy(1) and Dy(2) and Dy(1)′ and Dy(2)′ (Fig. 2c), consistent with the observation of spin-canting in the μ-SQUID experiments (Fig. 2c (inset) and 4). The projections of the anisotropy axes for each Dy(III) ion are better observed in terms of Euler rotations of the ZY′Z′′ scheme (Table S4†).38Discussion
Detailed analysis of the μ-SQUID data additionally shows that within the cage two exchange interactions could be present, ferromagnetic and antiferromagnetic; this is consistent with the electrostatic analysis. μ-SQUID analysis of the ferromagnetic projection (Fig. 4b and d) suggests possible quantum tunnelling between the ferromagnetic ground state and excited states at ±0.22, ±0.32, ±0.42 and ±0.62 T whilst a crossover is found in the antiferromagnetic projection at ±0.35 T (Fig. 4a and c), suggesting antiferromagnetic interactions.In order to understand these two distinct behaviours at the first stage, we invoke spin effective formalism38 (Seff = 1/2) employing pure axial g-tensors e.g. gxx = gyy = 0; gzz = 20 and the projection angles of the mJ = ±15/2 state for each Dy(III) ion obtained from the electrostatic analysis. Unfortunately, Seff = 1/2 can be, at first order, mixed very quickly by transverse fields leading to huge tunnelling splitting, not representative of the system. This would not be the case with a Dy(III) spin given that the mJ = ±15/2 levels only weakly mix by a transverse field (mixing in 15th order only). Unfortunately, due to the huge Hilbert space of the four Dy(III) ions (2S + 1)n = 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 536 and all the parameters involved i.e. ligand field splittings (LFS), g-values, Euler angles and exchange interaction(s), we cannot employ a J = 15/2 to understand the μ-SQUID data. To circumvent this problem, we therefore employ a fictitious S = 3/2 with an arbitrarily big LFS (D) of −100 cm−1, given that this spin value is less prone to mixing by transverse field. g-Values were kept isotropic (gxx = gyy = gzz = 20/3) and while the LFS were rotated employing the Euler angles obtained from the electrostatic analysis.39 The Hamiltonian describing our system is then given in eqn (1):
536 and all the parameters involved i.e. ligand field splittings (LFS), g-values, Euler angles and exchange interaction(s), we cannot employ a J = 15/2 to understand the μ-SQUID data. To circumvent this problem, we therefore employ a fictitious S = 3/2 with an arbitrarily big LFS (D) of −100 cm−1, given that this spin value is less prone to mixing by transverse field. g-Values were kept isotropic (gxx = gyy = gzz = 20/3) and while the LFS were rotated employing the Euler angles obtained from the electrostatic analysis.39 The Hamiltonian describing our system is then given in eqn (1):
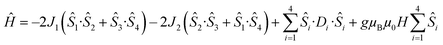 | (1) |
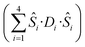 is the ligand field splitting, and the last term is the Zeeman term
is the ligand field splitting, and the last term is the Zeeman term 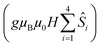 . For easiness, simulations of the Zeeman diagrams employing a single exchange interaction, i.e. J1 = J2 were performed, however no good agreement was obtained with this approach. For the antiferromagnetic projection the best agreement was found with J1 = −0.55 K, (Fig. 4e) while for the ferromagnetic projection the best agreement was found by employing anisotropic exchange J2x = J2y = +0.98 K and J2z = +0.32 K (Fig. 4f). At the experimental temperature of collection most of the excited spin states are not populated and can be neglected, thus Fig. 4e and f show only the low-lying states involved in the magnetisation reversal at very low temperatures. We calculated the dipolar couplings (Jdipi) for the Dy(III) pairs, leading to very anisotropic matrices (see Section E of the ESI†). Attempts to simulate the Zeeman diagram employing solely Jdipi yield no agreement (Fig. S8†), highlighting that these are not uniquely responsible for the μ-SQUID loops obtained for 1. Interestingly, Jdipi contains antiferromagnetic and ferromagnetic components, due to spin canting of the Dy(III) ion in 1 which, although weak, can account for the ferro- and antiferromagnetic exchange observed.
. For easiness, simulations of the Zeeman diagrams employing a single exchange interaction, i.e. J1 = J2 were performed, however no good agreement was obtained with this approach. For the antiferromagnetic projection the best agreement was found with J1 = −0.55 K, (Fig. 4e) while for the ferromagnetic projection the best agreement was found by employing anisotropic exchange J2x = J2y = +0.98 K and J2z = +0.32 K (Fig. 4f). At the experimental temperature of collection most of the excited spin states are not populated and can be neglected, thus Fig. 4e and f show only the low-lying states involved in the magnetisation reversal at very low temperatures. We calculated the dipolar couplings (Jdipi) for the Dy(III) pairs, leading to very anisotropic matrices (see Section E of the ESI†). Attempts to simulate the Zeeman diagram employing solely Jdipi yield no agreement (Fig. S8†), highlighting that these are not uniquely responsible for the μ-SQUID loops obtained for 1. Interestingly, Jdipi contains antiferromagnetic and ferromagnetic components, due to spin canting of the Dy(III) ion in 1 which, although weak, can account for the ferro- and antiferromagnetic exchange observed.
As observed in Fig. 4e, when the field is applied perpendicular to the a-crystallographic axis the ground state is a singlet. Upon sweeping the field only one quantum tunnelling event is present, in the experimental field range, at ±0.35 T, consistent with the observation in the μ-SQUID data (Fig. 4a, c and e). This event is associated with tunnelling between the ground state and nearest excited state which, at zero field, lies at ca. 1.6 K and involves a single spin flip. Conversely, when the field is applied parallel to the a-axis the situation leads to a well-defined ferromagnetic ground state with three close excited states lying at 3.3 K, 3.8 K and 3.9 K. Application of a negative magnetic field leads to a ground state characterised by ψ1 = ci|↓↓↓↓〉 (Fig. 4b, d and f). Upon field sweeping the first crossing point occurs at 0 T, where the possibility of tunnelling from ψ1 to ψ2 = cj|↑↑↑↑〉 is negligible since it would require all the spins to tunnel simultaneously. At +0.25 T and +0.27 T two crossovers are observed, involving ψ1 and the first and second excited states with ψ3 = ck|↑↑↑↓〉 and ψ4 = cl|↑↑↑↓〉. At these crossovers a tunnelling event occurs, due to the admixture of wavefunctions, which leads to a single spin flip. The third crossover is then observed at +0.42 T, occurring due to quantum tunnelling of ψ1 with a diamagnetic excited state with wavefunctions ψ5 = cm|↓↑↓↑〉, involving a double spin flip. These events are in good agreement with the crossings observed in the μ-SQUID loops, i.e. ±0.22, ±0.32 and ±0.42 T. Our model does not account for the crossings at ±0.62 T, which occur twice during the field sweep from −1 T to +1 T, which are not present in our simulation even after inclusion of off-diagonal dipolar terms, highlighting the weakness of our assumptions. Despite this, however, the simulations reproduce the ferromagnetic and antiferromagnetic behaviours and most of the tunnelling events observed in the μ-SQUID loops quite well. Several other crossing points at higher field occur, however due to the temperature of the characterisation and the applied field, the population of the ψ1f state at these crossing points is expected to be negligible.
Simulation of the M(H) data utilising parameters from the simulations of the Zeeman diagram is also possible by employing eqn (1) and the J1 and J2 (see the inset of Fig. 3a). The simulation is slightly higher than the experimental data, which could account for smaller g-values and some rhombicity on the Dy(III) ions. In order to compare our results with a similar structure, we obtained the isotropic analogue i.e. [Gd4(O2CNiPr2)12]18 (2) and interestingly simultaneous fitting of the χMT and M(H) data yields both ferromagnetic and antiferromagnetic interactions, as also observed in 1, highlighting the possible coexistence of two exchange pathways (see Fig. S7 and explanation therein†).
The average interactions projected onto the mJ = 15/2 states are found to be J1 = −0.022 K and J2 = +0.030 K, and are very weak as expected for lanthanide ions. To compare the magnitude of the exchange interaction obtained from our analysis, the exchange and g-values for compound 1 were re-scaled to the most commonly used spin effective (Seff = 1/2) formalism: leading to J1 = −4.95 K and J2x = +6.75 K, thus scaled to the magnitude of the exchange within the range of exchange observed in other reported Dy(III)-based SMMs.24,40,41
At this stage, we can understand why the application of an optimal field during the AC data collection had very little effect on the Ueff of compound 1. As observed in Fig. 4, due to the two exchange pathways in 1, the application of DC fields also induces many other level crossings, where the magnetisation can tunnel. Many other steps can be present upon application of the applied field in different directions of the molecule, therefore leading to the diminished SMM behaviour observed in the AC measurements of the powdered sample. Moreover, compound 1 shows clear exchange-biased quantum tunnelling,42 resulting from the magnetic exchange between neighbouring Dy(III)-ions and non-collinear arrangement of the anisotropic axes. Interestingly, two very different magnetic behaviours, ferro- vs. antiferromagnetic, can be clearly addressed by controlling the direction of the applied magnetic field along the crystal.
Conclusions
In summary, herein we report a concept where a molecular quantum magnet 1 is achieved by the capture and fixation of CO2. In the formed {Dy4} cage, 1, the four metal ions are held together by carbamates, arising from the activation and capture of twelve CO2 molecules per cage molecule resembling the CO2 activation pathway found in RuBisCO. Magnetic studies of 1 show this to be a SMM with a moderate Ueff even after application of an optimal field. μ-SQUID experiments at very low temperatures show the presence of two distinct magnetic interactions operating within the cage-complex giving rise to two different hysteresis loops depending on the direction of application of the magnetic field due to exchange bias, leading to suppression of QTM at zero field. The coexistence of two applied field direction dependent exchange pathway characteristics and the interesting dynamic magnetic behaviour observed in 1 could be of potential use in spintronic devices and/or quantum computing. In particular, facile tuning of the quantum tunnelling transitions upon manipulation of the field direction and/or the resonance fields, would signify that the molecule could be exploited in four-qubit quantum computing algorithms, paving the way for higher-level quantum gates.32 These results clearly demonstrate that from a simple green concept mimicking the capture and conversion of CO2, technological nanoscopic materials can be prepared generating added-value materials of cutting edge technological interest.Acknowledgements
MR, WW and YL acknowledge the EU for financial support within the FP7 FET-Proactive project MoQuaS No. 610449 and the ANR for ANR-13-BS10-0001-03 MolQuSpin. We acknowledge the Karlsruhe Nano-Micro Facility (KNMF) for X-ray time.Notes and references
- B. Stec, Proc. Natl. Acad. Sci. U. S. A., 2011, 109, 18790 Search PubMed.
- W. W. Cleland, T. J. Andrews, S. Gutteridge, F. C. Hartman and G. H. Lorimer, Chem. Rev., 1998, 98, 549 CrossRef CAS PubMed.
- P. M. Cox, R. A. Betts, C. D. Jones, S. A. Spall and I. J. Totterdell, Nature, 2000, 408, 184 CrossRef CAS PubMed.
- J. R. Petit, J. Jouzel, D. Raynaud, N. I. Barkov, J.-M. Barnola, I. Basile, M. Bender, J. Chappellaz, M. Davisk, G. Delaygue, M. Delmotte, V. M. Kotlyakov, M. Legrand, V. Y. Lipenkov, C. Lorius, L. Pépin, C. Ritz, E. Saltzmank and M. Stievenard, Nature, 1999, 399, 429 CrossRef CAS.
- Y. Xie, T.-T. Wang, X.-H. Liu, K. Zou and W.-Q. Deng, Nat. Commun., 2013, 4, 1960 Search PubMed.
- S. Wesselbaum, T. v. Stein, J. Klankermayer and W. Leitner, Angew. Chem., 2012, 124, 7617 CrossRef.
- T. Sakakura, J.-C. Choiand and H. Yasuda, Chem. Rev., 2007, 107, 2365 CrossRef CAS PubMed.
- Q. Liu, L. Wu, R. Jackstell and M. Beller, Nat. Commun., 2015, 6, 1 Search PubMed.
- L. J. Murphy, K. N. Robertson, R. A. Kemp, h. M. Tuononen and J. A. C. Clyburne, Chem. Commun., 2015, 51, 3942 RSC.
- Y. Yamazaki, H. Takeda and O. J. Ishitani, J. Photochem. Photobiol., C, 2015, 25, 106 CrossRef CAS.
- K. Sumida, D. L. Rogow, J. A. Mason, T. M. McDonald, E. D. Bloch, Z. R. Herm, T.-H. Bae and J. R. Long, Chem. Rev., 2012, 112, 724 CrossRef CAS PubMed.
- D. Walther, M. Ruben and S. Rau, Coord. Chem. Rev., 1999, 187, 67 CrossRef.
- D. A. Palmer and R. Van Eldik, Chem. Rev., 1983, 83, 651 CrossRef CAS.
- T. M. McDonald, J. A. Mason, X. Kong, E. D. Bloch, D. Gygi, A. Dani, V. Crocella, F. Giordanino, S. O. Odoh, W. S. Drisdell, B. Vlaisavljevich, A. L. Dzubak, R. Poloni, S. K. Schnell, N. Planas, K. Lee, T. Pascal, L. F. Wan, D. Prendergast, J. B. Neaton, B. Smit, J. B. Kortright, L. Gagliardi, S. Bordiga, J. A. Reimer and J. R. Long, Nature, 2015, 519, 303 CrossRef CAS PubMed.
- U. Baisch, D. B. Dell'Amico, F. Calderazzo, L. Labella, F. Marchetti and A. Merigo, Eur. J. Inorg. Chem., 2004, 6, 1219 CrossRef.
- D. B. Dell'Amico, F. Calderazzo, L. Labella, F. Marchettiand and G. Pampaloni, Chem. Rev., 2003, 103, 3857 CrossRef PubMed.
- D. Chaturvedi and S. Ray, Monatsh. Chem., 2006, 137, 127 CrossRef CAS.
- D. B. Dell'Amico, F. Calderazzo, F. Marchetti and G. Perego, J. Chem. Soc., Dalton Trans., 1983, 483 RSC.
- S.-D. Bian, J.-H. Jia and Q.-M. Wang, J. Am. Chem. Soc., 2009, 131, 3422 CrossRef CAS PubMed.
- E. Moreno-Pineda, G. Lorusso, K. H. Zangana, E. Palacios, J. Schnack, M. Evangelisti, R. E. P. Winpenny and E. J. L. McInnes, Chem. Sci., 2016, 7, 4891 RSC.
- S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Science, 2014, 344, 1135 CrossRef CAS PubMed.
- R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Nature, 2013, 488, 357 CrossRef PubMed.
- M. Gregson, N. F. Chilton, A.-M. Ariciu, F. Tuna, I. F. Crowe, W. Lewis, A. J. Blake, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and S. T. Liddle, Chem. Sci., 2016, 7, 155 RSC.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Nat. Chem., 2011, 3, 538 CrossRef CAS PubMed.
- N. Ishikawa, M. Sugita, T. Ishikawa, S.-Y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694 CrossRef CAS PubMed.
- R. J. Blagg, L. Ungur, F. Tuna, J. Speak, P. Comar, D. Collison, W. Wernsdorfer, E. J. L. McInnes, L. F. Chibotaru and R. E. P. Winpenny, Nat. Chem., 2013, 5, 673 CrossRef CAS PubMed.
- (a) A. Soncini and L. F. Chibotaru, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 220406 CrossRef; (b) L. F. Chibotaru, L. Ungur and A. Soncini, Angew. Chem., Int. Ed., 2008, 47, 4126 CrossRef CAS PubMed; (c) J. Luzon, K. Bernot, I. J. Hewitt, C. E. Anson, A. K. Powell and R. Sessoli, Phys. Rev. Lett., 2008, 100, 247205 CrossRef PubMed.
- F. Donati, S. Rusponi, S. Stepanow, C. Wäckerlin, A. Singha, L. Persichetti, R. Baltic, K. Diller, F. Patthey, E. Fernandes, J. Dreiser, Ž. Šljivančanin, K. Kummer, C. Nistor, P. Gambardella and H. Brune, Science, 2016, 352, 318 CrossRef CAS PubMed.
- M. Urdampilleta, S. Klayatskaya, M. Ruben and W. Wernsdorfer, ACS Nano, 2015, 9, 4458 CrossRef CAS PubMed.
- M. Urdampilleta, S. Klyatskaya, J.-P. Cleuziou, M. Ruben and W. Wernsdorfer, Nat. Mater., 2011, 10, 1 CrossRef PubMed.
- D. Loss and D. P. DiVincenzo, Phys. Rev. A: At., Mol., Opt. Phys., 1998, A57, 120 CrossRef.
- S. S. Ivanov, P. A. Ivanov and N. V. Vitanov, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 91, 032311 CrossRef.
- S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Coord. Chem. Rev., 2005, 249, 1693 CrossRef CAS.
- R. A. Coxall, S. G. Harris, D. K. Henderson, S. Parsons, P. A. Tasker and R. E. P. Winpenny, J. Chem. Soc., Dalton Trans., 2000, 2349 RSC.
- W. Wernsdorfer, Supercond. Sci. Technol., 2009, 22, 064013 CrossRef.
- L. F. Chibotaru and L. J. Ungur, Chem. Phys., 2012, 137, 064112 CAS.
- N. F. Chilton, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and A. Soncini, Nat. Commun., 2013, 4, 2551 Search PubMed.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Oxford Univ. Press, 1970 Search PubMed.
- S. Stoll and A. J. Schweiger, Magn. Reson., 2006, 178, 42 CrossRef CAS PubMed.
- J. Long, F. Habib, P.-H. Lin, I. Korobkov, G. Enright, L. Ungur, W. Wernsdorfer, L. F. Chibotaru and M. Murugesu, J. Am. Chem. Soc., 2011, 133, 5319 CrossRef CAS PubMed.
- E. Moreno-Pineda, N. F. Chilton, R. Marx, M. Dörfel, D. O. Sells, P. Neugebauer, S.-D. Jiang, D. Collison, J. v. Slageren, E. J. L. McInnes and R. E. P. Winpenny, Nat. Commun., 2014, 5, 5243 CrossRef CAS PubMed.
- W. Wernsdorfer, N. Aliaga-Alcalde, D. N. Hendrickson and G. Christou, Nature, 2002, 416, 406 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthesis, crystallographic and magnetic measurements and shape analysis details and figures. CCDC 1483884. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6sc03184f |
‡ Crystal data for 1 [Dy4N12O24C105H192]: Mr = 2656.69, monoclinic, T = 180.15(1) K, a = 28.1117(11), b = 20.1279(6), c = 22.8674(10) Å, β = 105.985(3)°, V = 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 438.7(8) Å3, Z = 4, r = 1.419 g cm−3, total data = 41 438.7(8) Å3, Z = 4, r = 1.419 g cm−3, total data = 41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 630, independent reflections 11 630, independent reflections 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 718 (Rint = 0.0723), μ = 2.442 mm−1, 699 parameters, R1 = 0.0723 for I ≥ 2σ(I) and wR2 = 0.1870. The data was collected employing a STOE StadiVari 25 diffractometer with a Pilatus 300 K detector using GeniX 3D HF micro focus with MoKα radiation (λ = 0.71073 Å). 718 (Rint = 0.0723), μ = 2.442 mm−1, 699 parameters, R1 = 0.0723 for I ≥ 2σ(I) and wR2 = 0.1870. The data was collected employing a STOE StadiVari 25 diffractometer with a Pilatus 300 K detector using GeniX 3D HF micro focus with MoKα radiation (λ = 0.71073 Å). |
| This journal is © The Royal Society of Chemistry 2017 |