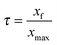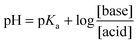A study of Moroccan pupils' difficulties at second Baccalaureat year in solving chemistry problems relating to the reactivity of ethanoate ions and to copper–aluminium cells

Abstract

This paper investigates the difficulties that Moroccan pupils (18–19) of the second Baccalaureat year encountered in solving chemical equilibrium problems relating to ethanoate ions' reactivity with water and methanoic acid, and to copper–aluminum cells. The pupils were asked to provide answers to questions derived from two problems. The questions were classified into different tasks according to whether their answers required declarative and (or) procedural knowledge. The written responses evaluated and counted as the percentage of successful, failed and unprocessed tasks revealed that pupils completed with success tasks on the reactivity of ethanoate ions with water more easily than those of two other studied cases. The pupils encountered difficulties in appropriating procedural knowledge on equilibriums involved in ethanoate ions' reactivity with methanoic acid and in copper–aluminum cells. The impact of the tasks' organization on knowledge development seems to be not verified as it was shown in the hierarchy prevalence of problems from simple to complex ones.

---

Introduction

The ability to solve problems is one of the most important manifestations of the ability to think and a crucial component of intelligence. It is rated as one of the most complex operations in taxonomies that categorize cognitive acts (D'Hainaut, 1985; Gagné, 1985). Problem solving was considered as a finalized cognitive activity that serves to achieve a task in one situation (Richard, 1990); it deals with mental activities and intellectual processes involving knowledge that would be acquired or built by means of anterior intellectual processes.

From a constructivist perspective, learning to solve problems implies undertaking in an active and cumulative way a process of construction and a change in the cognitive structure that allows developing effective actions. Problem solving leads not only to mastering basic knowledge and skills, but to combining and reorganizing data that has a subject before reaching the desired solution. However, the acquisition of knowledge in one context does not mean that an individual can use it at the appropriate time; the ability to use the knowledge is then essential to solve problems.

The solving of a closed-ended problem, that has only one solution leading to one answer, requires subjects to do simple applications and easy identifications of preceding and used data. The open-ended problems are assumed to have objective and verifiable solutions, but have not yet been solved, and require creativity and the application of high level thinking skills since the useful elements for solving them are not obvious (Goffard and Goffard, 2003; Overton et al., 2013); so the subjects must transform or reorganize the given data to find original solutions to these problems. During early learning years, pupils use simple techniques before applying most complex problem solving models. The pupils learn how to choose the correct method to solve a problem and apply it correctly. They learn that problem solving is a difficult process involving attempts, successes, failures, examination and rejection of some solutions.

This paper contains six parts. The first part tries to illustrate pupils' difficulties in solving chemistry problems in a Moroccan school context. The second part discusses some studies that have been carried out on learners’ difficulties in appropriating scientific concepts using problem solving activities. The third part is the conceptual framework which discusses declarative and procedural knowledge involved in solving problems as well as the impact of the tasks' organization on knowledge development. The fourth part is devoted to the methodology, the target population, the investigation methods and data collection instruments. In the fifth part, are presented the obtained results which are analyzed and discussed in the sixth part. This allows some difficulties that pupils of second Baccalaureate year encountered in solving chemistry problems involving acid reactivity with water and with a base, and copper–aluminum cells to be highlighted.

(I) Problem

The research studies carried out on problem solving are distributed in different areas ranging from the expert/novice paradigm (Chi et al., 1981) to studies focused on capacity development in solving problems to increase students' performance by classical evaluations (Rief, 1983; Caillot et al., 1988; Dumas-Carré and Goffard, 1997; Aka et al. 2010; Mazouze, 2016). The current preoccupation focus is on a pupil-centered learning environment, in which pupils are involved actively in the learning process, but should also be given counseling if they have difficulties in solving problems.

Problem solving is a method of student-centred, active learning and knowledge development (Aka et al., 2010) and more recently it was used as the primary domain of large-scale assessment systems around the world such as PISA (Grieff et al., 2013). From a methodological point of view, different research studies have been based on the analysis of written productions of “novice” learners in solving problems.

In chemistry, the representation of matter is characterized by three levels: symbolic (chemical equations and formulae), sub-microscopic (conceptualization of molecules and atoms) and macroscopic (observable phenomena: color, phase) (Johnstone, 1982; Talanquer, 2006; Gilbert and Treagust, 2009). According to Johnstone, the macroscopic level is real and corresponds to tangible and visible chemicals which may or may not be part of everyday students' experiences. The sub-microscopic level is also real comprising a particulate level that can be used to describe, for example, electrons, molecules or atoms' movement. The symbolic level involves a wide variety of pictorial representations, algebraic and computational forms of the submicroscopic representation.

It is only after mastering these three levels and their interrelation that a learner can use correctly chemistry models to predict and explain chemical reactions. The building-up of operational knowledge in chemistry requires an abstraction level, like atom and molecule imaginations, and this is more difficult than acquisition of declarative knowledge. The pupils' difficulties in solving problems involving procedural knowledge arise often from mathematical blockages.

At the Moroccan school level, chemistry problems are focused on total and reversible chemical reactions “chemical equilibriums” (Ouasri, 2016). From practice, it is difficult for these reactions to be understood by pupils who should know the involved substances, their names, their chemical formulas, their usual conditions and their physical and chemical properties. The chemistry problems imply implicit knowledge on necessary elements that could be used in the problems' representation and their solving: the nature of the entities involved in the reaction, the equation, the stoichiometric conditions or the physical conditions. The evaluation is used to elucidate and mobilize implicit knowledge to solve problems.

In the Moroccan context, the most used assessment tool is solving problems. Upon completion of the third year of upper secondary school, pupils sit an external examination administered by the Department of National Education that leads to several baccalaureate diplomas; the performance of Moroccan pupils in chemistry examinations is not satisfactory. In order to improve problem solving skills, the difficulties faced by pupils need to be understood and then a way to overcome these difficulties needs to be found. In this perspective, some questions may be asked about this: Why is pupils' performance in problem solving activities so low? Can we attribute this failure to a pupil himself, or to the received teaching, and consequently, to the teacher? To all these factors together or to the problem presented itself?

The educational facts can never be reduced to a single explanatory factor. Then, the present work tries to interpret, discuss and understand the difficulties of pupils of the second baccalaureate year in solving standard school chemistry problems used generally to evaluate the acquired pupils' knowledge. Before illustrating the knowledge categories, it seems important to review some pupils' difficulties in solving problems.

(II) The pupils' difficulties in problem solving

Several studies have been carried out on difficulties of learners' appropriation of scientific concepts related to problem solving practices in classes (Crahay and Lafontaine, 1986; Caillot et al., 1988; Goffard, 1994; Giordan, 1998; Ried and Yang, 2002; Orange, 2005; Drummond and Selvaratnam, 2008; Overton et al., 2013). Others research studies have focused on teachers' thoughts, their beliefs, their conceptions and their epistemological visions (Pajares, 1992; Tochon, 1993; Hashweh, 1996; Sale, 2002). It follows that pupils' difficulties in solving problems, especially in chemistry, could be due to:

Reading instructions

The success in solving problems depends on how pupils take into account the instructions. The non-understanding of some words or concepts would be an obstacle to read efficiently the instructions and such pupils cannot give the correct answers. In chemistry, several pupils read a text without understanding it, and this blocks the progress of pupils that remain paralyzed by certain unknown elements.

Lack of prerequisites

Several errors were due to lack of numerical and/or algebraic skills. If the lack of pre-requisites is punctual, the teacher can make a quick reminder; this is not possible when there is a lack of important prerequisites where teachers are confronted with complex problems that do not have immediate solutions.

Lack of competences in skills, strategies and logical reflexes

Many students' difficulties in solving chemistry problems are due to lack of competence in interlinked intellectual skills and strategies. In solving chemistry problems, four intellectual strategies (clarification and clear presentation of problems, identification of strategies to reach a required goal, identification of principles needed in solving, and proceeding step by step) were investigated (Drummond and Selvaratnam, 2008). Indeed, about 80% of students of North-West University, South Africa were found to be unable to use the required strategies, and many students who have the competence to use the strategies did not recognize the necessity for doing so. The pupils' failure in solving problems is not always be due to their inability to reason, but rather due to lack of experience and strategy (novice) to approach problems. The pupils without complex reference situations do not know how to treat problems, and search only to reproduce solutions of similar problems that have been seen previously.

Lack of mental representations

The pupils without good representations of what they read could not construct mental representations to treat such situations. Sweller (2003) defined the elaboration of schemas as abstract mental representations; these schemas stoked in memory allow us to analyze, to select, to structure and to interpret new information. They serve as a model to treat the information and direct the behavior. In chemistry problems describing experiments, the experiments' schematizations are necessary to understand and solve problems since they make it possible to reorganize and synthesize the given information.

Lack of attention, rigor, investment and weariness

Several pupils carry out such tasks that seem to be known to them without checking what is really requested. In calculations, pupils make errors in number signs and units for chemistry and physical sizes. These errors could be corrected by a precise re-reading of the proposed solution. A lack of investment and weariness were often felt in evaluations where pupils let the situations go very quickly, and did not try with all questions.

(III) Conceptual framework

Beyond the problems' classification (Greeno, 1978), the problem quality is twofold in education; an individual who faces a problem can achieve two objectives: testing his knowledge and also developing it. Problem solving is a privileged teaching tool that allows pupils to evaluate and develop their abilities. According to a purposed teaching situation, pupils should perform two tasks: solve the problem and learn from this solving situation.

From a didactic point of view, the problem solving concept has three perspectives: an assessment tool often used in the school context, a learning activity of scientific concepts less used in this context (Mazouze and Lounis, 2015) and support for research not used in the Moroccan school context. Psychologically, the problem solving concept was approached according to knowledge process acquisition; it is highly used in school activities to guide learning or to assess pupils' acquisition in the chemistry field. This highlights some key concepts such as teaching, learning, declarative and procedural knowledge. The conceptual framework tries to explain these concepts according to knowledge categories used by pupils to carry out tasks in solving problems. But, what do we mean by knowledge? What are the main knowledge categories? What are the main trends in research studies that are interesting in knowledge and solving problems?

III.1. Cognitivism and knowledge

Cognitivism seems to be a theoretical framework to explain cognitive behavior bases. Following the behaviorism decline, cognitivism was gradually imposed in education discourse and training practitioners. The cognitivism issues hypothesis proposes models on the thought structure and intellectual processes, and focuses on mechanisms of acquiring and integrating knowledge.

Constructivism (Piaget, Walloon, Vygotski and Bruner) clarifies the learning and the teaching process, including problem solving activities. The contribution of the two great figures of psychological constructivism, Piaget and Vygotski, had provided decisive insights into cognitive development, despite their crossed itineraries (Ravanis, 2010). While the intellectual development of Piaget is based on steps that determine learning in a dynamic way from the intra-psychic to the inter-psychic, Vygotski postulates the inverse movement. The cognitivism of Piaget and the socio-cognitivism of Vygotski can provide a theoretical framework that can interpret the multiple dimensions of the problem solving concept.

The cognitive psychology “Human information processing” (Newell and Simon, 1972; Gagné, 1985; Glover et al., 1990) can better inform questions relating to learning with problem solving. Based on theoretical foundations on knowledge structures and on information processing, cognitive psychology has provided concepts and approaches to better analyze and understand the involved processes in teaching/learning. Using structural concepts of a knowledge field that may build problem solving activities, the cognitive psychology seeks to verify the relevance, the models and the efficiency of knowledge in analysis of school learning situations. The Human information processing allowed operationalizing the analysis of complex cognitive processes in relation with knowledge and memory, two essential elements for a subject in solving problem.

The knowledge considered as basic concepts in Human information processing has attracted more attention in the problem of cognition through cognitive psychology. The knowledge is constituted in cognitive psychology meaning that a subject is assigned to a lived experience. The diversity of meaning derived from different experiments implies a wide range of knowledge that is essential to realize complex tasks. The role of specific knowledge and strategies is fundamental in learning and problem solving (Tardif, 1992).

The knowledge can be classified taking into account the experiences' diversity and the tasks' specificity. The first knowledge categorization was deduced from knowledge acquisition that was made in a process involving three distinct steps (Neves and Anderson, 1981): the encoding (declarative knowledge), the proceduralisation (procedural knowledge) and the composition or organization. The classification in terms of declarative, procedural and integration knowledge was refined by introducing contextual or conditional knowledge (Anderson, 1983, 1985; Glover et al., 1990). At the school level, only declarative and procedural knowledge were generally used. According to Neves and Anderson (1981), declarative knowledge firstly recorded (encoded) as domain facts implied static and passive information that could be enunciated without modification and treatment. It corresponds to principles, definitions, rules, laws and relations that are specific to one domain; although useful this knowledge does not allow the learner to undertake directly the action (Gagné, 1985).

In the second phase of knowledge acquisition, declarative facts were transformed into articulated procedures in the way that a subject passes to a procedural knowledge acquisition level that allows him to reach a fixed goal by using declarative knowledge (Neves and Anderson, 1981); at this level, the information is easily articulated in procedures, and this may be traduced by a faster action and better performance. The procedural knowledge involved in an action and know-how implies action steps and procedures for carrying out this action (Tardif, 1992). By the way, how do we pass from declarative knowledge to behavior? According to Anderson (1983, 1995), the process of producing procedural knowledge is divided into three non-discrete steps that characterized moments in qualitative skills' evolution. In the first step called the “cognitive step”, the learner can identify the needed information to solve problems by following instructions, applying general problem solving operators, and using analogies between declarative knowledge and anterior behaviors. In the second step, the declarative representation is transformed into a procedural one and errors characterizing the cognitive step are detected and eliminated. The transformation ability is accompanied by producing little errors and becomes then better coordinated and faster. In the third step, the “autonomous step”, the ability becomes more automated, faster and involves little cognitive intervention; it is then a step of adjustment and refinement of productions.

Anderson has developed an ATC (Adaptive Thinking Control) model to show how the most complex knowledge could be built by articulation of procedural and declarative knowledge. Indeed, building skills is a cumulative process in which a learner should be able to acquire knowledge elements and use appropriate skills according to the situation that he had to treat. The selection of appropriate knowledge depends on an activation process that traduced the success level of a skill in a particular context. This refers to works developed on progression from a novice to an expert problem solver (Larkin et al., 1980; Larkin and Simon, 1987). The authors have made significant contributions both to the study of expert and novice problem solving in physics and to the study of representation use by experts and novices. They also note that one of the major differences between expert and novice problem solvers is the span and organization of the expert's domain knowledge, as this allows them to access many stored problem schemas. The success in solving problem is based on two factors: knowledge base consisting of general or common knowledge and skills base consisting of specific cognitive activities or abilities (Gick, 1986; Taconis et al., 2001). When a person has both a strong knowledge base and skills base in a particular domain, that person is able to solve problems in that domain quickly, without hesitation, and with a high degree of accuracy. This combination of knowledge and skills is characteristic of an expert problem solver (Larkin et al., 1980).

III.2. Organization of tasks in problem solving

Various studies carried out on the impact of the tasks' organization on elaboration and development of knowledge are divided into three approaches:

– The first approach concerns contextual interference studies observing a prevalence of variability on consistency in solving problems (Carlson and Yaure, 1990; Schmidt and Bjork, 1992; Van Merriënboer et al., 2006). These studies showed that successful learning did not guarantee success in new problems and the high variability that blocks success in the learning phase seems to favor this learning because it allows for more success in problems of transfer. According to this approach, the tasks' organization is considered as a factor that influences learning in solving problems.

– The second approach “Instructional design” takes into account the cognitive load in the tasks' development in solving problems (Paas and van Merriënboer, 1993; Paas et al., 2003; Salden et al. 2006; de Croock and van Merriënboer, 2007). This approach emphasizes also the importance of how tasks are organized; it asks how to organize the learning of a skill/knowledge so that the learner may develop this skill/knowledge with success, retention, understanding, and with little error and good elaboration of schemas. Salden et al. (2006) distinguished between static and dynamic approaches as a mode of task selection. The tasks' organization is determined beforehand in a static situation where problems are presented according to an ascending difficulties' order that has been fixed a priori. However, the organization is adjusted during learning in dynamic situations according to the performance and attitude of the participants. Thus, the use of partial or complete tasks depends on the skill type that the learner wishes to acquire.

– The third approach suggests the prevalence of a hierarchy of problems from the simple to the complex (Gagné, 1962, 1968; Frederiksen and White, 1989) and considers that a competency is based on prerequisites or basic skills that must be acquired before more complex skills (Gagné, 1962). The learner has to master a new task (knowledge or skill) gradually at an increasingly hierarchical level until reaching the final level of this task. Frederiksen and White (1989) offered a mode of instruction based on decomposition of a task into sub-goals and on setting up of situations allowing gradual acquisition of skills relating to the sub-goals. They showed that learners being subjects to this type of organized instruction were more successful than others who directly realized the task.

(IV) Methodology

The methodology adopted in this study is based on the analysis of written responses of Moroccan pupils at the second Baccalaureate year in solving chemistry problems. In the analysis of pupils' responses, each question of the two problems is divided into tasks (steps) that could be carried out by the subjected pupils without giving them explicitly these steps. The obtained responses are counted in terms of the number of successful, failed and unprocessed tasks. Moreover, the tasks to be carried out according to whether their response requires pupils to mobilize declarative knowledge, procedural knowledge or both at the same time are classified and discussed. In the following, the target population, the investigation methods and the data collection instruments are defined and illustrated.

IV.1. Target population

This study targeted a population of 96 pupils (18–20 years) of three classes of second Baccalaureat year, Experimental Sciences, of Moulay Abdallah high school that is located in the Youssoufia prefecture of Rabat city (Morocco). The pupils of the classes profited from six hours of Physical and Chemistry course per week (three sessions of two hours). As in all Moroccan high schools, a weekly program of continuous teaching, from 8 h at 6 h, with a pause of two hours from 12:00 to 14 h, is adopted within this school. The choice of this population (classes of second Baccalaureate year) is made taking into account the importance of the problem solving approach for pupils in ongoing assessments and in the national Baccalaureate examination. The choice is also based on the fact that reactivity of an acid with water and a base as well as the cells also involved the chemical equilibrium concept that was not taught in Morocco before the second Baccalaureate year class; this is considered for pupils as an innovation which merits being analyzed and studied.

IV.2. Ethics

The participating pupils were subjected to a problem solving test from their teachers in coordination with me; the test was used both as an evaluation tool as well as to provide the data for this study. The school administration was well informed and approved the use of this test. In addition, the pupils were informed about the goals of the test and that their responses to the problem questions would be used in a research study. The test was announced to the pupils and administered to them after completion of chemical reactivities of ions and piles instruction. The test completed by those pupils who agreed to participate were given to me by their teachers. It should be noted that pupils' names were not provided (Taber, 2014).

IV.3. Investigation method and instruments

This study seeks to evaluate the Moroccan pupils' performance on two themes involving different chemical equilibriums. Indeed, it seems important to analyze the written outputs of pupils in solving chemistry problems in terms of successful, failed or unprocessed tasks (Tables 1a, b and 2) in order to identify some pupils' difficulties in problem solving activities. The tasks are identified and constructed from questions of problems 1 and 2 submitted to pupils, with a constructivist and cognitivist approach aiming to link the information treatment with the involved knowledge. This makes it possible to identify and analyze blockages and errors encountered by pupils during problem solving activities.

Table 1 (a) Results corresponding to the first part of problem 1: reactivity of ethanoate ions with water (Q: question; DC: declarative knowledge; PC: procedural knowledge). (b) Results corresponding to the second part of problem 1: reactivity of ethanoate ions with methanoic acid (Q: question; DC: declarative knowledge; PC: procedural knowledge)

Q	Tasks to be done (Ti)	DC	PC	Successful	Failed	Unprocessed
(a)
1.1	T1: identify the acid-base couples involved in base-water reaction.	*		12	0	84
	T2: identify the reagents and products	*		84	6	6
	T3: write the equation of base-water reaction	*		84	6	6
1.2	T4: establish the ICE table of the reaction	*		90	0	6
	T5: tate the relation:	*		90	0	6
	T6: determine from the ICE table: – the relation between xf and pH – the relation between xmax and C1 – the relation between τ1, C1 and pH		*	72	12	12
1.3	T7: know that K = Qeq relation is established at equilibrium	*		66	6	24
	T8: determine the present species' concentrations in solution as a function of C1 and τ1		*	36	24	36
	T9: express K as function of C1 and τ1		*	36	24	36
1.4	T10: know that K is a constant that is dependent only on the temperature	*		18	18	60
	T11: use the relation K = f(C1,τ1) in another case by replacing C1, τ1 by C2 and τ2		*	18	18	60
	T12: calculate τ2 by solving a quadratic equation		*	18	18	60
	T13: numeric application		*	18	18	60
	T14: check that 0 < τ2 < 1		*	18	18	60
	T15: conclude on the dilution effect on the degree of advancement τ	*		18	18	60
(b)
2.1.a	T1: know the relation K = Qeq	*		18	0	78
	T2: determine, by using the ICE table, the present species’ concentrations in solution as a function of Xeq	*	*	12	6	78
	T3: calculate Xeq from the conductivity relation	*	*	12	6	78
2.1.b	T4: express K as a function of KA1 and KA2	*	*	6	12	78
	T5: deduct the KA2 value		*	6	12	78
2.2	T6: use the relation	*		0	18	78
	T7: numeric application		*	0	18	78
	T8: compare pH with pKa for the two acid–base couples		*	0	18	78
	T9: deduct the predominant species in the solution	*	*	0	18	78

---

Table 2 Results corresponding to the problem 2: study of the copper–aluminium cell (Q: question; DC: declarative knowledge; PC: procedural knowledge)

Q	Tasks to be done (Ti)	DC	PC	Successful	Failed	Unprocessed
1.1	T1: calculate the reaction quotient at the initial state Qr,i for a reversible transformation	*	*	24	6	66
	T2: compare Qr,i with the equilibrium constant K and predict the direction of spontaneous evolution of a reversible transformation		*	24	6	66
1.2	T3: identify the positive and negative poles of the cell	*		36	6	54
	T4: know that: – oxidation is done in the anode, negative pole – reduction is done in the cathode, positive pole	*		36	0	60
	T5: Give the conventional representation of the cell	*		60	0	36
2.1	T6: establish the ICE table corresponding to functioning of the cell	*		24	0	72
	T7: express a product concentration, for example [Cu^2+], as a function of Co, x and V		*	24	0	72
	T8: express the relation between x, F, I and t	*		30	0	66
	T9: express [Cu^2+] as a function of Co, t, I, F and V		*	24	0	72
2.2	T10: use the [Cu^2+] = f(t) curve to determine the current intensity I delivered during the functioning of the cell		*	18	0	78
	T11: determine I by using the relation deduced from [Cu^2+] = f(t) curve		*	18	0	78
3	T12: determine from the curve the necessary time t for the cell to be completely depleted		*	18	0	78
	T13: numeric application		*	12	0	84

---

The two chemistry problems (Appendix) to which pupils were subjected include questions about chemical systems, particularly the reactivity of ethanoate ions in water and methanoic acid (problem 1) as well as the cell (problem 2). Pupils were asked to answer the problems' questions containing implicitly different tasks used as indications of declarative and procedural knowledge acquisition. It is worth noting that the problems were given in French to the subject pupils' who are second language speakers. The instruction languages are Arabic as first language speakers and French as the second language of instruction.

(V) Results

According to the hierarchy approach, the pupils' responses are divided and analyzed in terms of tasks (T1, T2,…) ranging from a simple to a more complex level in solving chemistry problems. The tasks carried out by pupils of three classes are identified and analyzed according to whether their answer requires declarative, procedural or both declarative and procedural knowledge (Tables 1a, b and 2).

(VI) Analysis and discussion

VI.1. Analysis in terms of tasks

Using Excel software, the results given in Tables 1a, b and 2 are transformed into graphs (Fig. 1a, b and 2) representing the tasks carried out by pupils in terms of percentage, according to three indicators (successful, failed and unprocessed).

Fig. 1 (a) Performance of pupils in tasks on reactivity of ethanoate ions with water. (b) Performance of pupils in tasks on reactivity of ethanoate ions with methanoic acid.

Fig. 2 Performance of pupils in tasks in the copper–aluminium cell study.

Problem 1: reactivity of ethanoate ions.
Part 1: reactivity of ethanoate ions with water. The representation in terms of percentage (%) of pupils that were successful, failed and did not attempt the tasks of the first part of problem 1 concerning the reactivity of ethanoate ions with water is given in Fig. 1a.

The first question corresponds to T1, T2 and T3 tasks that require pupils to mobilize only declarative knowledge without much reflection and strategies. Nevertheless, the T1 task aiming to identify the acid–base couples involved in the reaction of a base with water was successful with a low score of 12.5%. Both T2 and T3 considered as usual tasks were successfully completed by the majority of pupils (87.5%) even if task T1 was successfully completed less. So, the identification of the acid–base couples (T1) seems to be not decisive for most pupils to carry out the following tasks of the first question of this problem.

The question (1.2) refers to three tasks (T4, T5 and T6). The (T4 and T5) tasks involving declarative knowledge on representation of the ICE table and enunciation of the advancement ratio were carried out with a very high percentage 93.75%. The T6 task requiring procedural knowledge on using the ICE table to determine such relations between equilibrium chemical variables was successfully completed with a percentage of 75%. This explains why the percentage of pupils achieving this task has relatively decreased.

The question (1.3) consists of three tasks (T7, T8 and T9). The task T7 that was completed at 68.75% requires only declarative knowledge, i.e. prerequisites on relation between the equilibrium constant and the reaction quotient. The tasks T8 and T9 requiring pupils to mobilize procedural knowledge were realized at 37.5%. The task T8 concerns the determination of chemical species' concentrations in solution as a function of C₁ and τ₁, while task T9 is devoted to determining the equilibrium constant K as a function of C₁ and τ₁. So, two-thirds of pupils displayed difficulties in succeeding in these tasks requiring strategies and logical reflections to mobilize mathematical tools and to use the ICE table.

The dependent tasks T10 to T15 (question 1.4) were found to be successful with a very low score (18.75%). The declarative or procedural knowledge has no impact on the success percentage being the same for these tasks. Indeed, among 36 pupils succeeding in task 9, only 18 were able to succeed in task 10 which seems to be decisive in this question. The remaining 6 pupils that failed task 10 did not succeed in the following tasks (T11 to T15); this may be explained by the fact that task 10 requires prerequisites on dependence of the equilibrium constant K only on temperature; these prerequisites are not understand by all pupils. The failure in these tasks means that most pupils cannot acquire automated and fast skills within the autonomous step considered as a higher step in building a procedural knowledge process (Anderson, 1983, 1995).

Part 2: reactivity of ethanoate ions with methanoic acid. The percentage (%) of pupils that were successful, failed and did not ateempt tasks of the second part of problem 1 concerning the reactivity of ethanoate ions with methanoic acid is given in Fig. 1b.

The question (2.1.a) corresponds to (T1, T2, and T3) tasks. Except for the T1 task that requires only declarative knowledge, the success of the T2 and T3 tasks requires the mobilization of both declarative and procedural knowledge. The T1 task relating to K = Q_eq relation at chemical equilibrium was successful with a low score (18.75%). The tasks T2 and T3 were performed with an even lower score (12.5%). The results reveal that the majority of pupils had difficulties in succeeding in these unusual tasks, in contrast to tasks involving reactivity of ethanoate ions with water which have been successfully completed (Part 1 – problem 1). In the case of reactivity of ethanoate ions with acid, several pupils are not able to calculate the advancement X_eq value from the conductivity relation, since they do not have the required skills relating to the use of the ICE table to determine the present species' concentrations in solution at equilibrium as a function of X_eq.

The task T4 requiring both declarative and procedural knowledge on equilibrium constant K as a function of K_A1 and K_A2 was successful with a very low percentage (6.25%). The task T5 aiming to deduce the K_A2 value is even successful with the same percentage (6.25%). This implies that the majority of pupils did not mobilize the required declarative and procedural knowledge to carry out these tasks. The T6, T7, T8 and T9 tasks focus on the relation that should be used to determine concentrations and so the predominant species at equilibrium. These tasks were not carried out by all pupils, and this indicates clearly the major difficulties encountered by pupils in understanding acid–base equilibrium.

The modesty of the obtained results for the second part of problem 1 may be explained by the following factors:

– Lack of pupils' pre-requisites in terms of declarative and procedural knowledge (establishment of the concentrations' expression as a function of X_eq from the ICE table, calculation of X_eq using the concentrations determined by the conductivity relation, the equilibrium constant, acidity constant…).

– Lack of strategy and logical reflection: many pupils cannot organize and arrange declarative knowledge in a logical way to answer the asked questions.

– Lack of mental representation: several pupils did not understand and explain some implicit tasks to elaborate such schemas that would allow them to successfully complete the complex tasks.

Problem 2: study of copper–aluminium cells. The results traduced in terms of percentage of pupils that were successful, failed and did not attempt the tasks of problem 2 are given in Fig. 2.

The first question regroups two tasks: T1 requiring both declarative and procedural knowledge and T2 that needed procedural knowledge. These tasks aim to determine the chemical system direction by calculating the reaction quotient Q_i and using the spontaneous evolution criterion (comparison between Q_i and K); they have been completed successfully only by 25% of pupils. The majority of pupils then had difficulties in acquiring and using the spontaneous evolution criterion to predict the evolution direction of a chemical system. This can be due to the lack of prerequisites for the majority of pupils in solving this type of problem.

The question (1.2) corresponds to T3, T4 and T5 tasks involving only declarative knowledge. The task T3 aims to identify positive and negative cell poles, and the task T4 intends to enunciate that “the oxidation occurs at the anode (negative pole) and the reduction at the cathode (positive pole)”; these two tasks were carried out successfully by 37.5% of pupils. The task T5 that aims to give the cell conventional representation was realized by 62.5% of pupils. This reveals that many pupils can give the cell a conventional representation without being able to identify the poles where the oxidation and the reduction occurred; these pupils did not have pre-requisites on cell poles and what signified the anodic oxidation and cathodic reduction.

The question (2.1) involves T6, T7, T8 and T9 tasks. The success of T6 and T8 tasks requires declarative knowledge on the ICE table and the Faraday relation between x, F, I and t, respectively. The two procedural tasks (T7 and T9) make it possible to express the concentration of one product (for example [Cu²⁺]) as a function of C₀, t, I, F and V by using the ICE table and Faraday's relation. One quarter of pupils completed successfully the (T6, T7 and T9) tasks, and 31.25% of pupils succeeded in the T8 task. So, some pupils can enunciate Faraday's relation without being able to confront this relation with the ICE table to answer the asked questions.

The tasks (T10 and T11) require pupils to mobilize their procedural knowledge to determine the current intensity I delivered by the aluminum–copper cell by using the [Cu²⁺] = f(t) curve, and the relation deduced from this curve. It is found that 18.75% of pupils have completed with success the two tasks; this highlights the difficulties that are encountered by the majority of pupils (81.25%) who are unable to determine graphically the concentration [Cu²⁺]. For the procedural tasks (T12 and T13), one can state that only 18.75% of pupils succeeded in the T12 task aiming to determine from the [Cu²⁺] = f(t) curve the necessary time t for the cell to be completely worn out, while the T13 task that is a numerical application was successful with 12.5% of pupils; this indicates the difficulties encountered by the majority of pupils in calculation and homogenization of physical and chemical units. So, one can state that few pupils could pass to the “autonomous step” in problem solving activities relating to the chemical equilibrium in aluminum–copper cells.

VI.2. Analysis in terms of declarative and procedural knowledge

The success of a task in solving problems is related to pupils' ability to mobilize their declarative and procedural knowledge. Tables 1a, b and 2 show the tasks' classification made in terms of knowledge categories. Among 37 tasks identified in Tables 1a, b and 2, 20 were considered as tasks requiring pupils to mobilize declarative knowledge, 22 as tasks requiring the mobilization of procedural knowledge, and 5 as tasks requiring simultaneously both knowledge. It is worth noting that a task is considered to be successful when pupils achieving it exceed 2/3 of the pupils (i.e. ≥66.67%). By the way, 7 tasks are found to be performed, with 6 being declarative tasks and one being a procedural task. This indicates that more than 66.67% of pupils were able to mobilize chemical knowledge to achieve 6/20 (30%) of the declarative tasks and 1/22 (4.545%) of the procedural tasks derived from the two problems (Fig. 3). It seems that many pupils lack reasoning attitudes and strategies using procedural knowledge in solving chemistry problems. When it is required to mobilize and articulate both declarative and procedural knowledge, one can state that any task has been carried out (Fig. 3); this reveals the difficulties that were encountered by the majority of pupils to completing tasks involving knowledge articulation.

Fig. 3 Representation of declarative and procedural successful tasks in terms of percentage.

According to the “Instructional design” approach (Paas and van Merriënboer, 1993; Paas et al., 2003; Salden et al. 2006; de Croock and van Merriënboer, 2007), the failure in using and articulating declarative and procedural knowledge may be explained by lack of abstract mental representations due to the pupils' inability in elaboration of schemas. Generally, these results are not predicted and so merit to be taken into consideration in the teaching/learning processes in the future. For this, it would be interesting to break further tasks required for both knowledge types into sub-tasks.

VI.3. Discussion

The second Baccalaureat year pupils subjected to chemistry problem solving activities were found to be able to carry out easily declarative and procedural tasks in the case of reactivity of acid with water, in contrast to the cases related to the reactivity of acid with base and to copper–aluminum cells. Concerning the impact of tasks' organization on knowledge development among pupils considered as novices, the results’ analysis, based on closed-ended problems containing sometimes open (complex) tasks at the end, reveals clearly a decrease in the percentage of pupils achieving relatively complex tasks which required procedural knowledge; the decrease tends to be null for complex tasks requiring both knowledge categories. This is in agreement with the approach privileging the prevalence of problems' hierarchy from the simple to the complex (Gagné, 1962, 1968; Frederiksen and White, 1989). So, the majority of pupils did not acquire knowledge or skills at a significant hierarchical level to reach the final level (complex) task. Even if the proposed problems were divided into questions containing tasks going from the simple to the complex, the success of complex final tasks has not been completely realized by pupils. This indicates that the instruction based on tasks' decomposition into sub-goals and the setting up of learning situations allowing the gradual acquisition of competences relating to the sub-goals is not sufficient to obtain positive results.

Moreover, several indications of blockages, errors and difficulties have been identified for many subjected pupils who did not succeed in solving the two problems. Other pupils did not try again and quickly abandoned solving problems. This can be due to:

– Lack of understanding of certain keywords (concepts), and lack of semantic and linguistic skills, etc.

– Lack of strategies and logical reflexes for most pupils that did not pass to the autonomous step in the elaboration of the procedural knowledge process.

– Lack of mental representation of chemical phenomena (symbolic, sub-microscopic and macroscopic) that prevents pupils from developing schemas allowing them to solve chemistry problems; this is more evident in the case of acid–base reactivity and copper–aluminum cells.

– Lack of certain prerequisites, such as the spontaneous evolution criterion, the calculation of the reaction quotient and the spontaneous chemical transformation in cells.

– Lack of motivation, of investment and weariness, especially for the last tasks of problems.

Conclusions

This study tried to understand the difficulties encountered by Moroccan pupils of the second Baccalaureat year in solving chemistry problems including acid–water and acid–base reactivities, and spontaneous oxido-reduction transformations in copper–aluminum cells. From a methodological point of view, this research is based on the analysis of written responses of “novice” learners that have been administered problem solving activities.

The pupils' difficulties were analyzed and discussed in terms of declarative and procedural knowledge that pupils could mobilize to complete implicit tasks derived from questions of the proposed chemistry problems. The impact of tasks' organization on knowledge development among novice pupils seems to be not verified as it was indicated by the approach privileging the prevalence of a hierarchy of problems from the simple to the complex ones.

As a perspective, it will be important to provide some remedies to pupils by giving them explicitly the component tasks of such problems; this would allow novice pupils to develop their problem solving strategies and so to build their knowledge and their skills. This would be a useful contribution to the teaching of problem solving.

Appendix

Problem 1: reactivity of ethanoate ions

The sodium ethanoate chemical compound CH₃COONa is soluble in water and is considered as a source of ethanoate CH₃COO⁻ ions. The objective of this problem is to study the reaction of ethanoate ions with water and with methanoic acid.

Given data:

– The molar mass of sodium ethanoate: M(CH₃COONa) = 82 g mol⁻¹.

– The ionic product of water at 25 °C is: K_e = 1 × 10⁻¹⁴.

– The acidity constant of the (CH₃COOH/CH₃COO⁻) couple at 25 °C is: K_A1 = 1.6 × 10⁻⁵.

– All measurements are taken at a temperature of 25 °C.

(1) Study of the reaction of ethanoate ions with water

Sodium ethanoate crystals of mass m₁ = 140 mg are dissolved in distilled water to obtain an unsaturated solution S₁ of volume V = 500 ml and concentration C₁. The pH measured for the obtained solution is: pH = 8.4.

1.1. Write the equation of reaction between ethanoate ions and water.

1.2. By using the ICE table of reaction, express the final advancement ratio of this reaction as a function of K_e, C₁ and pH. Calculate τ₁.

1.3. Express the equilibrium constant K, associated with the equation of this reaction as a function of C₁ and τ₁; then check that K = 6.3 × 10⁻¹⁰.

1.4. A volume of the solution S₁ is taken and an amount of distilled water is added to it to obtain a solution S₂ of concentration C₂ = 10⁻³ mol l⁻¹. Calculate in this case the final advancement ratio τ₂ of the reaction between ethanoate ions and water. Conclude.

(2) Study of the reaction of ethanoate ions with methanoic acid

A volume V₁ = 90 ml of a sodium ethanoate aqueous solution of concentration C = 1 × 10⁻² mol l⁻¹ was mixed with a volume V₂ = 10 ml of an aqueous solution of methanoic HCOOH acid of the same concentration C. The transformation which takes place is traduced by a chemical reaction of the following equation:

CH₃COO⁻ + HCOOH ⇄ CH₃COOH + HCOO⁻

The conductivity of the chemical mixture is expressed at a time t as a function of the advancement x of the reaction by: σ = 81.9 + 1.37 × 10⁻⁴x, with σ in mS m⁻¹ and x in mol.

2.1. The conductivity of the chemical mixture measured at equilibrium is found to be σ = 83.254 mS m⁻¹.

(a) Check that the constant K associated with the equation of reaction is equal to: K ≅ 10.

(b) Deduce the acidity constant K_A2 value of the HCOOH/HCOO⁻ couple.

(2) Calculate the pH of the solution at equilibrium. Deuce the two predominant chemical species at equilibrium among: CH₃COOH, CH₃COO⁻, HCOOH, and HCOO⁻.

Problem 2: copper–aluminium cell

The cell involving “Metal ion/Metal” couples has been discovered when the telegraph evolution has needed continuous electric current sources. The objective of this problem is the study of the copper–aluminum cell.

Given data:

– The Faraday constant: F = 96 500 C mol⁻¹.

– The equilibrium constant associated with the equation of reaction between copper metal and aluminum ions: 3Cu_(s) + 2Al³⁺_(aq) ⇄ 3Cu²⁺_(aq) + 2Al_(s) is: K = 1 × 10⁻¹⁴.

The copper–aluminum cell is made of two compartments connected through an ammonium chloride (NH₄⁺, Cl⁻) salt bridge.

The first half-cell is constituted by a copper plate partially immersed in an aqueous solution of copper(II) sulfate (Cu²⁺, SO₄²⁻) with a concentration C₀ and a volume V = 50 ml.

The second half-cell is constituted by an aluminum plate partially immersed in an aqueous solution of aluminum chloride (Al³⁺, 3Cl⁻) of the same concentration C₀ and of the same volume V.

An Ohmic conductor (D), an amperemeter and an interceptor K are connected between the cell poles (Fig. 4). At time t = 0, the circuit is closed, an electrical current of intensity I circulates then in the circuit.

Fig. 4 Representation of the copper-aluminium cell.

The curve given in Fig. 5 represents the variation of the concentration [Cu²⁺] of copper(II) ions existing in the first half-cell as a function of time.

Fig. 5 Curve showing the variation of [Cu²⁺] ions' concentration as a function of time.

1.1.1. Using the spontaneous evolution criterion, determine the direction of the chemical system evolution in the given cell.

1.2. Give the conventional representation of the pile.

2.2.1. Express the concentration [Cu²⁺] as functions of t, C₀, I, V and F.

2.2. Deduce the value of the current intensity I passing through the circuit.

3. The cell was worn out fully after a time tc. Determine tc.

References

1. Aka E. I., Guven E. and Aydogdu M., (2010), Effect of problem solving Method on Science Process Skills and Academic Achievement, J. Turk. Sci. Educ., 7(4), 13–25.
2. Anderson J. R., (1983), The architecture of cognition, Cambridge, Massachusetts: Harvard University Press.
3. Anderson J. R., (1985), Cognitive Psychology and its applications, 2nd edn, San Francisco: W.H. Freeman.
4. Anderson J. R., (1995), Learning and memory: An integrated approach, New York: John Wiley & Sons.
5. Caillot M., Dumas-Carré A. and Goffard M., (1988), PROPHY: Une méthode pour résoudre des problèmes de physique. LIREST, Paris: Université de Paris VII.
6. Carlson R. and Yaure R. G., (1990), Practice schedules and use of component skills in problem solving, J. Exp. Psychol.: Learn. Mem. Cogn., 16(3), 484–496.
7. Chi M. T. H., Feltovitch P. J. and Glaser R., (1981), Categorization and representation of physics problems by experts and novices, Cogn. Sci., 5, 121–152.
8. Crahay M. and Lafontaine D., (1986), L'art et la science de l'enseignement, Bruxelles: Labor.
9. De Croock M. and van Merriënboer J., (2007), Paradoxical effects of information presentation formats and contextual interference on transfer of a complex cognitive skill, Comput. Hum. Behav., 23, 1740–1761.
10. D'Hainaut L., (1985), Des fins aux objectifs de l'éducation. Un cadre conceptuel et une méthode générale pour établir les résultats attendus d'une formation, 4^e édn, Bruxelles: Editions Labor.
11. Drummond H. P. and Selvaratnam M., (2008), Students' Competence in Intellectual Strategies Needed for Solving Chemistry Problems, S. Afr. J. Chem., 61, 56–62.
12. Dumas-Carré A. and Goffard M., (1997), Rénover les activités de résolution de problème en physique. Concept et démarches, Paris: Armand Collin.
13. Frederiksen J. and White B., (1989), An approach to training based upon principled task decomposition, Acta Psychol., 71, 89–146.
14. Gagné R., (1962), The acquisition of Knowledge, Psychol. Rev., 69(4), 355–365.
15. Gagné R., (1968), Learning hierarchies, Educ. Psychol., 6, 1–9.
16. Gagné E. D., (1985), The cognitive psychology of school learning, Boston, Toronto: Little Brown Company.
17. Gick M. L., (1986), Problem solving strategies, Educ. Psychol., 21, 99–120.
18. Gilbert J. K. and Treagust D. F., (2009), Macro, submicro, and symbolic representations and the relationship between them: key models in chemical education, in Dans Gilbert J. K. and Treagust D. F. (dir.), Multiple Representations in Chemistry Education, The Netherlands: Springer, pp. 1–8.
19. Giordan A., (1998), Une didactique pour les sciences expérimentales, Belin.
20. Glover J. A., Ronning R. R. and Brunning R. H., (1990), Cognitive psychology for teachers, New York: Macmillian Publishing Company.
21. Goffard M., (1994), Le problème de physique et sa pédagogie, Paris: ADAPT.
22. Goffard M. and Goffard S., (2003), Interactions entre élèves et résolution de problèmes, Aster, 37, 165–187.
23. Greeno J. G., (1978), A study of problem solving, in Glaser R. (ed.), Advances in instructional psychology, vol. 1, Hillsdale NJ: Lawrence Erlbaum Associates.
24. Grieff S., Holt D. V. and Funke J., (2013), Perspectives on problem solving in Educational Assessment: Analytical, Interactive, and Collaborative Problem Solving, J. Probl. Solving, 5(2), 71–91.
25. Hashweh M. Z., (1996), Effects of Sciences Teachers' epistemological Beliefs in Teaching, J. Res. Sci. Teach., 33(1), 47–63.
26. Johnstone A. H., (1982), Macro-and micro- chemistry, Sch. Sci. Rev., 64(227), 377–379.
27. Larkin J. and Simon H. A., (1987), Why a diagram is (sometimes) worth ten thousand words, Cogn. Sci., 11, 65–99.
28. Larkin J., McDermott J., Simon D. P. and Simon H. A., (1980), Expert and novice performance in solving physics problems, Science, 208(4450), 1335–1342.
29. Mazouze B., (2016), Des difficultés en résolution de problèmes de physique: quelles aides pour les élèves? Educational Journal of the University of Patras UNESCO Chair, 3(2), 258–268.
30. Mazouze B. and Lounis A., (2015), Résolution de problèmes et apprentissage des ondes: quels types de difficultés rencontrent les élèves? Review of Science, Mathematics and ICT Education, 9(2), 25–40.
31. Neves D. M. and Anderson J. R., (1981), Knowledge compilation: mechanisms for the automatization of cognitive skills, in Anderson J. R. (ed.), Cognitive skills and their acquisition, Hillsdate, NJ: Erlbaum, pp. 86–102.
32. Orange C., (2005), Problème et problématisation dans l'enseignement scientifique, Aster, 40, 3–11.
33. Overton T., Potter N. and Leng C., (2013), A study of Approaches to solving open-ended Problems in Chemistry, Chem. Educ. Res. Pract., 14, 468–475.
34. Newell A. and Simon H. A., (1972), Human Problem Solving, Englewood Cliffs, New Jersey: Prentice-Hall.
35. Ouasri A., (2016), Study of the appropriation by the pupils of second Baccalaureate year of knowledge objectifs relating to acide-bases titrations, Chemistry: Bulgarian Journal of Science Education, 25(5), 695–717.
36. Paas F. and van Merriënboer J., (1993), The efficiency of instructional conditions, Hum. Factors, 35(4), 737–743.
37. Paas F., Renkl A. and Sweller J., (2003), Cognitive Load theory and instructional design: recent developments, Educ. Psychol., 38(1), 1–4.
38. Pajares M. F., (1992), Teachers' beliefs and educational research: cleaning up a messy construct, Rev. Educ. Res., 62, 307–332.
39. Ravanis K., (2010), Représentations, Modèles Précurseurs, Objectifs-Obstacles et Médiation-Tutelle: concepts-clés pour la construction des connaissances du monde physique à l'âge de 5–7 ans, Revista Electrónica de Investigación en Educación en Ciencias, 5(2), 1–11.
40. Richard J.-F., (1990), Les activités mentales, Paris: Armand Collin.
41. Ried N. and Yang M. J., (2002), The Solving of Problems in Chemistry: the more open-ended problems, Res. Sci. Technol. Educ., 20(1), 83–98.
42. Rief F., (1983), Understanding and teaching problem solving in physics, in Delacôte G. and Tiberghien A. (ed.), Recherche en didactique de la physique, Paris: CNRS, pp. 15–53.
43. Salden R., Paas F. and van Merriënboer J., (2006), A comparison of approach to learning task selection in the training of complex cognitive skills, Comput. Hum. Behav., 22, 321–333.
44. Sall C. T., (2002), L'auto-évaluation du profil d'entrée: une stratégie constructiviste dans la formation professionnelle initiale des enseignants, in Actes des 2èmes Assises du CIFFERSE: l'enseignement des sciences expérimentales, Dakar, 8-10 Avril 2001.
45. Schmidt R. A. and Bjork R. A., (1992), New conceptualizations of practice: common principles in three paradigms suggest new concepts for training, Psychol. Sci., 3, 207–217.
46. Sweller J., (2003), Evolution of human cognitive architecture, in Ross B. (ed.), The psychology of learning and motivation, vol. 43, San Diego: Academic Press, pp. 215–266.
47. Taber K. S., (2014), Ethical considerations of chemistry education research involving human subjects, Chem. Educ. Res. Pract., 15, 109–113.
48. Taconis R., Ferguson-Hessler M. G. M. and Broekkamp H., (2001), Teaching science problem solving: an overview of experimental work, J. Res. Sci. Teach., 38(4), 442–468.
49. Talanquer V., (2006), Commonsense chemistry: a model for understanding students' alternative conceptions, J. Chem. Educ., 83(5), 811–816.
50. Tardif J., (1992), Pour un enseignement stratégique L'apport de la psychologie cognitive, Logique.
51. Tochon F. V., (1993), L'enseignante experte et l'enseignant expert, Collection Les repères Pédagogiques, Série Formation, Paris: Edition Nathan.
52. Van Merriënboer J., Kester L. and Paas F., (2006), Teaching complex rather than simple tasks, Appl. Cogn. Psychol., 20, 343–352.

---