Scaffolding the development of problem-solving skills in chemistry: guiding novice students out of dead ends and false starts

Abstract

To scaffold the development of problem-solving skills in chemistry, chemistry educators are exploring a variety of instructional techniques. In this study, we have designed, implemented, and evaluated a problem-solving workflow – “Goldilocks Help”. This workflow builds on work done in the field of problem solving in chemistry and provides specific scaffolding for students who experience procedural difficulties during problem solving, such as dead ends (not being able to troubleshoot) and false starts (not knowing how to initiate the problem-solving process). The Goldilocks Help workflow has been designed to scaffold a systematic problem-solving process with a designation of explicit phases of problem solving, to introduce students to the types of questions/prompts that should guide them through the process, to encourage explicit reasoning necessary for successful conceptual problem solving, and to promote the development of metacognitive self-regulation skills. The tool has been implemented and evaluated over a two-year period and modified based on student and instructor feedback. The evaluation demonstrated a shift in students’ beliefs in their capacities to use the strategies required to achieve successful problem solving and showed their capacity to employ such strategies.

---

Introduction

Teaching problem solving and developing problem-solving skills are at the heart of chemistry education and chemistry education research (Herron, 1996b). More specifically, the cornerstone questions are: why do some students struggle with solving problems? and how can we help these students develop problem-solving skills?

Problem solving is a multifaceted activity, influenced by a variety of cognitive, motivational, and behavioural factors. Cognitive factors include content knowledge, understanding of concepts, and process skills. In this study, we focused on approaches for developing students’ problem-solving process skills. Specifically, we have designed, implemented, and evaluated the problem-solving workflow “Goldilocks Help” (GH), which builds on work done in the field of problem solving in chemistry and related fields. In particular, it provides specific scaffolding for students who experience procedural difficulties during problem solving, such as dead ends (not being able to troubleshoot) and false starts (not knowing how to initiate the problem-solving process).

For the purpose of this study, we are focusing on problem-solving research in the field of chemistry education with the emphasis on (i) student difficulties in problem solving, (ii) problem-solving approaches by different problem solvers, and (iii) problem-solving processes.

Prior research on student difficulties in solving chemistry problems

Student difficulties, while solving problems in chemistry, are usually due to one or more of the following: lack of knowledge of subject matter (“chemical facts” (Herron and Greenbowe, 1986; Gulacar et al., 2013)), misconceptions or alternative conceptions (Taber, 2002), or poor problem-solving approaches and strategies. With respect to the latter, there is extensive literature describing such difficulties. We have analysed the literature to delineate the manifestations and causes of such difficulties.† The distinction between manifestations and causes is significant if educational approaches are to be aimed at addressing the latter.

One of often cited manifestations of student difficulties exhibited during problem solving is the application of memorised algorithms, either successful or not, without clear understanding of why they are appropriate (“black boxes”, “plug ‘n chug”) (Van Ausdal, 1988; Pushkin, 1998; Cohen et al., 2000; Drummond and Selvaratnam, 2008; Gulacar et al., 2014; Nyachwaya et al., 2014). Students resort to rote memorisation when they are not motivated to tackle problems conceptually or when they are cognitively overloaded and thus cannot “afford” the mental capacity required for conceptual problem solving (Overton and Potter, 2008; Gulacar et al., 2014). Some students also think that they are supposed “to know” how to solve a problem, and if they do not know at the first read of the problem (i.e. if they can not recall an appropriate algorithm) then there is no point trying (Harper, 2005).

Orientation on declarative and procedural knowledge and poor understanding of meaning of mathematical representations (Herron and Greenbowe, 1986) can cause students to superficially (sometimes, meaninglessly) manipulate mathematical equations (Van Ausdal, 1988; Comeford, 1997; Cohen et al., 2000; Drummond and Selvaratnam, 2008; Selvaratnam, 2011; Gulacar et al., 2014). While they are able to correctly execute mathematical operations, they could be failing to make strong connections between mathematical forms and the physical reality. This issue arises particularly sharply when a problem requires integration of mathematics, chemistry, and reasoning.

Some students may experience one or more of the following challenges: an inability to extract relevant information from a problem (Bodner and McMillen, 1986; Cohen et al., 2000; Gulacar et al., 2014) or recognise a need for additional information that may be required for solving a problem (Van Ausdal, 1988), impediments in language comprehension resulting from a limited scientific vocabulary, confusions with word meaning (Yuriev et al., 2016), or misreading the problem (Herron, 1996a), an impaired ability to handle complexity (i.e. multiple concepts) (Gulacar et al., 2014), and poor reasoning skills (Cohen et al., 2000). These issues often lead to ignoring assumptions and limitations associated with some algorithms (Herron and Greenbowe, 1986; Van Ausdal, 1988; Nyachwaya et al., 2014), rushing into the solution without first clarifying the problem (Harper, 2005; Drummond and Selvaratnam, 2008; Selvaratnam, 2011), guessing based on irrelevant data (Gulacar et al., 2014), not knowing where to start (Van Ausdal, 1988; Gulacar et al., 2014), or giving up (Harper, 2005; Drummond and Selvaratnam, 2008). The absence of a habit for checking and troubleshooting (Herron and Greenbowe, 1986; Van Ausdal, 1988) and/or failure to use units correctly or at all (Van Ausdal, 1988; Gulacar et al., 2014) may manifest in the reporting of an incorrect or intermediate result (Herron and Greenbowe, 1986) or an alternative result (Herron, 1996a) in place of the result called for in the problem.

Behavioural issues may also sometimes impede problem solving. These could manifest as negative attitudes and a lack of self-confidence in problem solving (Harper, 2005; Drummond and Selvaratnam, 2008), focus on the “right answer” in preference to the problem-solving process (Cohen et al., 2000; Harper, 2005), and a reluctance to try a new approach to problem solving (Van Ausdal, 1988; Comeford, 1997; Cohen et al., 2000).

The causes of problem-solving difficulties are not only student-driven. The instructor-driven causes include classroom practices and instructional materials, expecting students to apply procedures without requiring them to demonstrate their reasoning (Pushkin, 1998; Cohen et al., 2000; Zoller, 2000; Nyachwaya et al., 2014). While worked examples have their place, focusing purely on worked examples could inhibit the development of problem-solving skills (Bodner and McMillen, 1986; Harper, 2005). Finally, the development of problem-solving skills could suffer due to an insufficient emphasis on (meta)cognitive strategies and a lack of integration between explicit and continuous training of (meta)cognitive strategies and content teaching in a range of contexts (Cohen et al., 2000; Drummond and Selvaratnam, 2008; Selvaratnam, 2011; Yu et al., 2015). The main focus of this study is to address the latter issue along with a range of student-driven causes.

Problem-solving approaches

Any given task may represent a routine exercise for expert problem solvers, yet present as a novel problem for novices encountering it for the first time (Bodner, 1987). Novices and experts usually take distinct approaches to solving problems: when dealing with a task, novices look for an algorithm, while experts think conceptually and use general strategies (Herron, 1996b; Felder and Brent, 2016). Thus, it is experience and control of strategies, rather than intellectual ability, that turns problems into exercises.

Algorithms are stepwise procedures for solving of well-defined tasks, guaranteeing arrival at a solution if the procedures are applied correctly. A range of algorithmic methods have been developed in chemistry to guide students through problem solving: “networks” (e.g., Waddling, 1988), “pathways” (e.g., McCalla, 2003), or “solution maps” (e.g., Selvaratnam and Canagaratna, 2008). Algorithms decrease the overload of the working memory (Baddeley and Hitch, 1974) and allow individual steps in more complex sequences to be automated (Johnstone and Al-Naeme, 1991). However, such methods are not applicable for solving complex chemistry problems since they are limited to specific problem types and lack the generality requisite for authentic tasks (Bodner and McMillen, 1986).

On the other hand, strategic approaches give students a general direction, i.e. an overall sequence (not necessarily linear) of stages/phases of a solution process. While they do not guarantee arrival at a solution, they induce a systematic approach to problem solving (De Corte et al., 2012). They are useful for problem solving in the context of its definition by Wheatley: “what you do when you don’t know what to do” (Wheatley, 1984). In accordance with this definition, problem solving requires trial and error, sometimes involving backwards or sideways steps. An “anarchistic” strategy to solving chemical problems, one that allows for trial and error, has been proposed by Bodner and co-workers (Bodner, 2003). Bodner defined a successful problem solver as one who is able to extract relevant information from the problem statement, one who often uses drawing to represent a problem, is willing to “try something” when stuck, keeps track of the problem-solving process, and checks the answer to see if it makes sense (Bodner, 2015).

Research on problem-solving processes

To solve a problem, or to find a way to cross a knowledge gap, one needs to understand the problem (i.e. comprehend its elements and the relationships between them), plan a solution, implement it, and evaluate an outcome (Polya, 1945). While most problem-solving models (Table 1) include these four main steps, expressed in a variety of terms, several models specifically include a step that precedes a problem-representation step. One model specifically introduced a step to activate pre-knowledge related to the problem (Shahat et al., 2013). This activation is essential, particularly for students with weak understanding of concepts and therefore requiring such prompting. Finally, post-solution steps, such as delivering a solution (Deek et al., 1999) or consolidating gains (Hayes, 1989), have also been introduced.

Table 1 Problem-solving processes^a

Problem identification	Problem representation	Planning	Implementation	Evaluation	Process name (if available) and Ref.^b
a For the purpose of uniformity, all descriptions of stages were presented in the form of instructions, but otherwise were kept as close as possible to the original sources. b Evaluated problem-solving processes are shown in bold. c Dewey uses the term “difficulty” to indicate “problem”. d Herron discusses the processes of planning and implementation as a single process.
Locate the difficulty^c	Define the nature of the difficulty	Suggest explanation or possible solution	Develop an idea through reasoning	Corroborate the idea and form a concluding belief	(Dewey, 1910)
	Understand the problem	Devise a plan	Carry out a plan	Look back	(Polya, 1945)
Identify problems and opportunities	Define goals	Explore possible strategies	Anticipate outcomes and Act	Look back and learn	IDEAL (Bransford and Stein, 1984)
	Construct a representation	Search for a solution	Implement solution		(Gick, 1986)
Find the problem	Represent the problem	Plan the solution	Carry out the plan	Evaluate the solution	(Hayes, 1989)
	Information and rules	Plan	Mathematics and units	Review	EMPS (Bunce et al., 1991)
Understand the problem	Represent the problem	Plan a solution	Execute a plan^d	Verify	(Herron, 1996a)
	Formulate the problem	Plan a solution	Design and translate	Test	(Deek et al., 1999)
Engage	Define and explore	Plan a solution	Do it: carry out the plan	Evaluate: check and look back	McMaster strategy (Woods, 2000)
	Define a problem	Generate and justify solutions		Monitor and evaluate	(Ge and Land, 2003)
Recognize the problem	Describe the problem	Plan a solution	Execute the plan	Evaluate the solution	CPS (Heller and Heller, 2010)
Identify and formulate the problem	Define and represent the problem	Formulate an expected result (hypothesis); explore a possible way of solving the problem	Perform the problem-solving process; fix data and calculate	Look back to the idea (hypotheses) and evaluate	(Shahat et al., 2013)
	Define and analyse the problem	Collect data; generate potential solutions	Select and implement the optimum solution	Evaluate and revise	(Yu et al., 2015)

---

Whereas general problem-solving processes are very similar between different disciplines and reflect human problem solving (Simon and Newell, 1971), each discipline implements these processes in a field-specific manner. Since chemistry problems require specific terminology and ways of prompting, instructional approaches need to foster discipline-specific problem-solving process skills.

Theoretical framework

This study is underpinned by educational theories from both teaching and learning perspectives. The teaching standpoint is based on the concepts of scaffolding and prompting. The learning perspective stems from self-regulation of learning, more specifically – metacognitive self-regulation.

Scaffolding

Scaffolding is a pedagogical process that enables a novice to complete a learning task that could not be accomplished unassisted (Wood et al., 1976; Vygotsky, 1978; Pea, 2004; Belland, 2011). In the context of problem solving, scaffolding involves the structuring of the process, as well as metacognitive and procedural prompting (Reiser, 2004). Scaffolding enables learners to internalise the guidance through distributed practice and, eventually, self-regulate their cognitive actions. Common features of scaffolded instruction are: focusing learner's attention towards a goal, simplifying the task, modelling and demonstrating, prompting for ongoing diagnosis and assessment, and promoting the eventual transfer of responsibility (Reiser, 2004; Puntambekar and Hubscher, 2005; Zydney, 2012). The goals of scaffolds are: to assist students in skill development for problem-solving processes (Wood et al., 1976), to draw student attention to important process elements (Reiser, 2004), and to promote understanding by engaging in reflection (Davis, 2000). Scaffolding, which could be contextual, metacognitive, procedural, and strategic (Hannafin et al., 1999), can result in improved problem-solving performance (Belland, 2011). While human-facilitated scaffolds could be dynamically adjusted to address exhibited student difficulties, scaffolds could also be designed to anticipate projected student difficulties based on prior research and experience (Hannafin et al., 1999).

A critical component of scaffolding is prompting. Prompts, embedded within learning environments, are seen by students as integral, not additional, structural elements (Horz et al., 2009). Successful prompts direct student attention to important information they may have overlooked, facilitate awareness of potential knowledge gaps, help them organise their thoughts, make their thinking “visible”, and recognise a need to evaluate the validity of their solutions (Ge and Land, 2003). Guiding-through-questions, or Socratic questioning, effectively stimulates rational and logical thinking and reasoning and structures a problem-solving process. It promotes reflection and improves problem-solving skills (Ge and Land, 2003; Rhee, 2007). Question prompts convey transcendent messages about what is important in problem solving, e.g. a question “what are you asked to determine?” conveys a message about the need to identify the goal (Herron, 1996b).

Metacognition and self-regulation

Metacognition is the ability to monitor and critically evaluate one's understanding and learning/problem-solving processes (Flavell, 1979). Metacognitive awareness includes two main sub-constructs: knowledge of cognition and regulation of cognition (Schraw and Dennison, 1994). The knowledge of cognition is further divided into declarative knowledge (about one's skills, intellectual resources, and abilities as a learner), procedural knowledge (about how to implement learning procedures, such as strategies), and conditional knowledge (about when and why to use learning procedures). The regulation of cognition involves such aspects as planning (goal setting and allocating resources), information management strategies (skills and strategies to process information more efficiently, such as organising and summarising), monitoring (assessment of one's strategy use), debugging strategies (correcting comprehension and performance errors), and evaluation (analysis of performance and of the chosen approaches).

Self-regulated learning (SRL) represents proactive processes used by students to set goals, select and implement strategies, and self-monitor their effectiveness (Zimmerman and Pons, 1986; Pintrich et al., 1991; Zimmerman, 2008; Low and Jin, 2012). SRL is characterised by personal initiative, perseverance, and adaptive skill (Zimmerman, 2008) and involves metacognitive, motivational, and behavioural engagement by students. Metacognitive self-regulation is enacted via planning, monitoring, and regulating (Pintrich et al., 1991). Planning activities, e.g. task analysis, activate prior knowledge and assist with organising information. Monitoring activities, e.g. self-questioning, help to integrate new information with prior knowledge. Regulating/controlling activities, e.g. evaluation and checking, assist in adjusting problem-solving behaviour.

Research questions

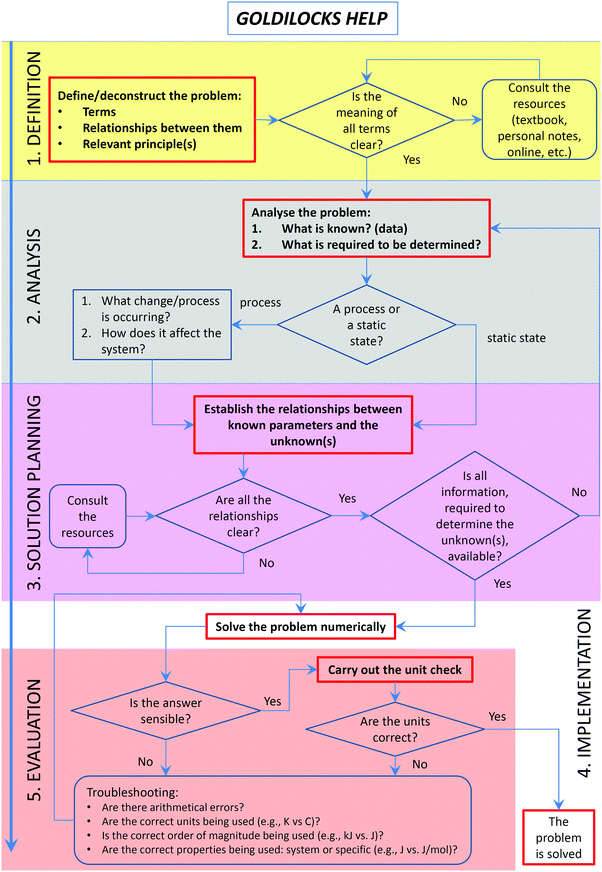
Solving problems often presents a challenge to students because of the issues associated with the problem-solving processes (Yu et al., 2015) and reasoning (Moon et al., 2016). The Goldilocks Help workflow (Fig. 1) is designed to: (i) scaffold a systematic problem-solving process with a designation of the explicit phases of problem solving; (ii) introduce students to the types of questions/prompts that should guide them through the process; (iii) encourage explicit reasoning necessary for successful conceptual problem solving, and (iv) foster the development of metacognitive self-regulation skills by the inclusion of feedback mechanisms for monitoring, evaluation, and reflection. The tool has been designed, implemented and evaluated over a two-year period (2015–2016). In the second year of implementation, the workflow has been modified based on feedback and paired with an explicit modelling instruction strategy to transparently demonstrate to students aspects of expert problem solving. Specific research questions we addressed in this study were:

Fig. 1 Goldilocks Help problem-solving workflow – original version.

(1) Do students change their approach to problem solving when exposed to explicit and scaffolded instruction, using a specially designed problem-solving workflow?

(2) Does students’ metacognitive self-regulation, as related to problem solving, develop as a result of such instruction?

Design and development of “Goldilocks Help” workflow

Recognising the function of each phase of the problem-solving process is critical to the success of problem solving (Yu et al., 2015). The development of the workflow has been in great respect informed by common student difficulties and their causes, summarised above and prior research on problem-solving processes (Table 1). Also, we specifically aimed to provide students with strategies to extricate themselves from the points where they commonly get stuck while solving problems: dead ends and false starts. Dead ends could result from: (i) following a misconception or an alternative conception; (ii) making inappropriate assumptions; (iii) ignoring dimensional aspects of a problem; and (iv) reporting an incorrect answer. All four manifestations of these difficulties may go unnoticed by students until the very end, and sometimes not realised at all. Students may proceed solving the problem incorrectly in the face of information that should indicate that something is not right. While a solver does not get stuck and arrives at a “solution”, we classify it as a dead end since the solution is not correct or is inappropriate for the problem being solved. False starts happen when students (i) do not recognise that they lack particular knowledge or (ii) “look for an equation” instead of thinking through the problem holistically.

The design of GH was informed by cognitive load (Sweller, 1988; Sweller et al., 2011a) and information processing (Roberts and Rosnov, 2006; St Clair-Thompson et al., 2010) theories. Specifically, GH provides students with useful prompts while avoiding overloading their cognitive structures. This consideration was taken into account when designing the original version as described below (Fig. 1), as well as when refining it, following the feedback from students and instructors (see Results section). Furthermore, we aimed for the right balance between prompts being useful (i.e. going further than generic “analyse” or “plan” instructions) but not too specific so as to turn the workflow into an algorithm (hence, the name “Goldilocks” which alludes to The Story of Goldilocks and the Three Bears or the Goldilocks zone in astronomy). Finally, the prompts were designed to increase students’ awareness of their comprehension failures, and to trigger the use of additional information when necessary. The prompts were fashioned after the Socratic questioning used by the lead author in the actual face-to-face instruction over many years. The following paragraphs describe the structure and attributes of the problem-solving process as implemented in the “Goldilocks Help” workflow.

Understanding

While ‘understanding’ the problem and ‘representing’ it may appear to be the same, they are not (Herron, 1996a). Based on known student difficulties in solving chemistry problems (i.e., conceptual and cognitive), we decided to split the first phase into two: one to trigger students to test their comprehension of the problem statement (“understand” step) and another to prompt them to explore it (“analyse” step). In the first version of the GH workflow, the first step was called “Definition”, later replaced by “Understand” to emphasise the need for comprehension.

The lack of knowledge, often not recognised by students, creates an obstacle at the very beginning of the problem-solving attempt (a false start of the first kind). In our workflow, students are encouraged to examine all the terms and concepts relevant to a given problem. In the first instance, it may simply entail reading a problem text and checking that all terms are clear, known, and their meaning understood. We have previously demonstrated the importance of a deep understanding of the terminology in promoting successful problem solving (Yuriev et al., 2016).

Misconceptions and alternative conceptions often do not manifest themselves until later in the process, where they may lead either to an incorrect solution or to getting stuck (a dead end of the first kind). An example of arriving at an incorrect solution is represented by solving this problem (presented in the context of reversible processes with no non-expansion work occurring): A sample containing two moles of oxygen gas is heated from 25.0 °C to 45.0 °C at atmospheric pressure. Predict enthalpy for this process. Unless students appreciate that the change in enthalpy is equal to energy absorbed or released as heat at constant pressure (IUPAC, 2014), they may use the constant-volume heat capacity, rendering the answer incorrect.

To help avoid these common pitfalls, the GH workflow starts by asking students to define relevant terms present in the problem statement, as well as relevant relationships and principles. Students are then prompted to consider whether the meaning of all terms is clear and to consult the resources (e.g., textbook), if it is not.

Analysis

Students often experience difficulties when starting or progressing a problem-solving process if they are “looking for an equation” instead of thinking their way through the problem (Harper, 2005). If an algorithm does not present itself, they are stuck (a false start of the second kind).

Bodner and McMillen emphasised the critical importance of the early holistic stage of problem solving, to which they referred as cognitive restructuring (Bodner and McMillen, 1986). Students need to recognise the initial and the goal states of the problem and then to use the results of this analysis for solving the problem. To quote Bodner and McMillen, these early steps “set the stage for the analytic thought processes that eventually lead to an answer”.

During problem analysis, any relevant assumptions need to be explicitly stated in order to select an appropriate course of action. For example, problems dealing with ionic equilibria of weak electrolytes often involve assuming a negligible extent of ionisation. If students do not explicitly make this assumption, they may internalise this concept as being a fact, characterising all solutions of weak electrolytes. This conjecture may be then inappropriately used in situations where it does not apply. For example, in problems where the extent of ionisation is known exactly or where it needs to be determined. Thus, ignoring the appropriateness/applicability of assumptions may lead to students embarking on an incorrect course of action (a dead end of the second kind) (Nyachwaya et al., 2014). To address these common pitfalls, the GH tool requires students to state the current and desired states (i.e., knowns and unknowns) and prompts students to consider their features.

Planning

Once the problem is deconstructed and restructured, students can proceed to setting up a solution. This step is often skipped by students. The most common manifestation of such omission is the superficial (sometimes, meaningless) manipulation of mathematical equations (Van Ausdal, 1988; Cohen et al., 2000; Drummond and Selvaratnam, 2008; Selvaratnam, 2011; Gulacar et al., 2014), often combined with a failure to use units correctly or use them at all (Van Ausdal, 1988; Gulacar et al., 2014). Novice problem solvers should be encouraged to meticulously set up relevant equations, using symbols and units before the actual numerical values are plugged in. The haptic actions of writing present opportunities for students to think about what they are doing and to catch mistakes (Mangen and Velay, 2010). Skipping these steps often leads to getting stuck as a result of incorrect mathematical operations or ignored dimensional aspects of a problem (a dead end of the third kind). For example in the heat capacity problem described above, the sample contains 2 moles of gas and the molar heat capacity has units of J K⁻¹ mol⁻¹. A failure to take this information into account leads some students to incorrect results. When prompted to provide units for the outcome of this calculation, students realise their mistake since once they observe the dimensional non-equivalence of the variables in equations, where the terms are expected to be equivalent. Another common occurrence of dimensional omissions leading problem solving astray is the use of degrees Celsius instead of Kelvins, for example in Clausius–Clapeyron or Arrhenius equations.

To deal with these common pitfalls, the GH workflow directs students to establish the relationships between known parameters and the unknown(s) and then prompts them to consider whether all the relationships are clear and to consult the resources, if they are not. At this stage, it is also appropriate to prompt students as to whether all the information, required to determine the unknown(s), is available and to return to the analysis, if it is not. Unlike many practice and assessment problems that students encounter in their studies, authentic real-world problems are not posed with all the relevant data in a neat statement. The necessary information needs to be identified and sourced. Furthermore, real-world problem presentation often contains information that is actually not required to reach a solution. All these elements of complexity should be tackled at the planning stage.

Implementation

The implementation stage is often simply an exercise in algebra, at least for quantitative problems. However, beyond solid mathematical skills, it requires that problem solvers be organised in their thinking, in their execution of necessary steps, and in their attention to detail (Van Ausdal, 1988). Careless mistakes at this stage often lead to incorrect solutions. While it is fairly straightforward as a workflow phase, the success of its execution depends to great extent on the quality of planning. As noted previously, students often enter the problem solving process laterally: by trying to implement it without prior analysis and planning. By explicitly stating that implementation cannot come before these crucial steps, instructors should be able to draw students’ attention to the importance of analysis and planning, to the need to spend significant time on these steps, and to the possible difficulties that may arise if these steps are omitted.

Evaluation

Problem-solving performance can be improved by engaging in the practice of reflection while solving problems (Belland, 2011). However, “teachers know that admonitions to do so fall on deaf ears” (p. 73) (Herron, 1996a). Frank (1986) suggested that while students appreciate the value of checking and verification in principle, they often do not do it simply because the exact verification strategies are not clear or known to them, particularly for more complex problems.

To deal with this lack of evaluation experience, the GH workflow prompts students to consider whether the answer is sensible and whether the units are correct. These two specific decision points have been selected based on common student difficulties. An example of a non-sensible answer is a numerically correct answer with a wrong sign: for example, confusing initial and final states of a process leads to a negative enthalpy for an endothermic process or vice versa (a dead end of the fourth kind). Another example of students producing non-sensible results is reporting negative temperature in Kelvin. Problem solving is impossible without making mistakes (Martinez, 1998). It is important for students, on the one hand, to understand this and to accept mistakes and, on the other hand, develop methods to deal with mistakes as a necessary part of problem solving (Herron, 1996b; Kapur and Toh, 2015). To demonstrate evaluation strategies, GH contains a list of exemplar (but by no means comprehensive) troubleshooting prompts.

Methods

Ethics approval

This study was designed to evaluate the GH workflow as a tool for scaffolding problem solving and was approved by the institutional Human Research Ethics Committee. The objectives of the study were explained to students in week one of semester, and they were invited to participate in the study. Their participation in the metacognitive awareness inventory was optional and anonymous. Written consent forms were signed by: students who agreed for their reflections to be used for this research, focus group participants, and the academics who evaluated the workflow.

Context and participants

First year students undertaking the Bachelor of Pharmaceutical Science degree took part in this study. In 2015 and 2016, there were 112 and 129 students enrolled in the course, respectively. Fortnightly problem-solving sessions (tutorials) entailed students working in groups of 4–5 to solve problems and present their workshopped solution to a class of 25–30.

While some tasks involved simple mathematical manipulations of data, others had added elements of complexity. For example, one element of complexity involved data (such as compound properties) not being provided in the problem statement, with only system properties being given (such as mass, temperature, etc.). Students were required to identify what information was required (as a result of early problem restructuring) and source it. The sources available to students (textbook tables, worksheet appendices) contained a wide range of data, so students needed to know what they were looking for rather than be guided by the data provided. Following is an example of such type of problem: Consider the chemical reaction 2H₂O₂(l) → 2H₂O(l) + O₂(g) in which liquid hydrogen peroxide decomposes into O₂and water at 25 °C. Analyse available thermodynamic data, provided in the appendix, and determine the standard enthalpy change for this reaction, using TWO different methods. Suggest a reason why the two results are not identical. In this case students were able to access standard enthalpies of formation and mean bond enthalpies.

Another element of complexity involved including data that was not actually required for solving a given problem, for example: Extracts containing benzylpenicillin were prepared for analysis in buffer at pH 6.5 at 25 °C. The rate constant for the hydrolysis of benzylpenicillin under these conditions is 1.7 × 10⁻⁷s⁻¹. What is the maximum length of time (in hours) the solutions can be stored before analysis so that no more than 1% decomposition occurs?

Problem-solving workshop

During the first week of semester, all students participated in an hour-long problem-solving workshop. Before any other activities, students were asked to fill out a metacognition and self-regulation inventory (details below). The first activity of the workshop was a group discussion of a chemistry-unrelated task: “You are a member of a group of people organising a music festival on the outskirts of Melbourne. You are in charge of catering and your first job is to produce a budget with a restricted bottom line. How do you go about doing that?” The task is fashioned after the one used by Randles and Overton (Randles and Overton, 2015); it is unfamiliar and open-ended, but does not require any scientific knowledge. The task is designed to elicit students’ comments relating to problem-solving approaches. At the end of a session spent brainstorming this scenario, students are asked to share with the class what would they do to action the task and what decisions they would have to make. Students’ suggestions usually cover the processes involved in problem solving: identifying what the challenge is (understanding), figuring out how variables such as costs relate to the goal, i.e. a balanced budget (analysis), collecting and organising necessary information (planning), calculating (implementation), and verifying that the budget is in the black (evaluation). Interestingly, both times when this exercise was presented to students, one particular term in the problem statement (i.e., bottom line) elicited clarification requests. This presented an opportunity to draw students’ attention to the importance of the understanding/comprehension step, when solving problems.

Following this chemistry-unrelated task, students were presented with two chemistry questions. Q1: What is the concentration (% w/v) of a solution of 5 g of a salt dissolved in 200 mL of aqueous solution? Q2: A sample of 5 g of Ephedrine is dissolved in 200 mL of aqueous solution. What is the molar concentration of this solution? As expected, many students were able to solve Q1 almost instantly without a need to write anything down or use a calculator. For Q2, students came up with responses and queries that aligned with the problem-solving workflow.

Novice problem solvers often do not recognise that they are using a specific problem-solving procedure (Herron, 1996a). The tasks, presented to students in this workshop, are designed to make the process “more visible” and to encourage students to become aware of things they do when they solve problems (“problem solving behaviour” (Herron, 1996a)), to pay attention to understanding problem terminology and to the early stages of problem analysis and solution planning.

Data collection and analysis

A convergent parallel mixed methods design (Creswell, 2014) was used to investigate the impact of the GH workflow. Quantitative scores from the metacognitive awareness inventory were combined with qualitative input from students’ reflections and focus group interviews and triangulated by incorporating feedback from the instructor survey.

Student reflections and focus groups. Seven students accepted an invitation to participate in 2015 focus group interviews, which were carried out by an education support staffer who was not known to students prior to the interviews. The interviews were audio recorded and transcribed verbatim. End-of-semester reflections were typed by students and submitted electronically.

The constant comparative method of qualitative data analysis was implemented using NVivo v.10 and v.11. The 2015 reflections (70 reflections, 13 600 words) were first read by all investigators, and initial open codes emerging from the data (i.e. grounded categories) were organised into nodes and sub-nodes (i.e. themes and sub-themes). A combination of deductive and inductive analysis allowed additional themes to emerge from the data, beyond the initial research questions. These were used to develop our sense of the students’ perceptions of problem solving.

The analysis followed the guidelines of Braun and Clarke (2006). The investigators met to discuss the emerging themes and to resolve the discrepancies before reaching consensus. During this meeting, themes were removed, merged, or divided. Based on this discussion the final coding scheme was generated. To ensure rigour, two investigators (E. Y. and J. S.) analysed 16 reflections from the 2016 set (84 reflections, 20 000 words), using the coding scheme previously developed, and compared results to verify the coding. One researcher (E. Y.) then coded the remaining 2016 reflections. No new themes or sub-themes were identified in the final round, suggesting that saturation was achieved.

Instructor feedback. Twenty one instructors from a range of scientific disciplines (general chemistry [5]; inorganic chemistry [1]; organic chemistry [7]; analytical chemistry [2]; physical chemistry [2]; pharmacology [1]; mathematics [1]; physics [1]; biology [1]) attended a series of briefing sessions to consider, critique, and make suggestions for improving the GH problem-solving workflow. They provided written comments and filled out an instructor survey.

Metacognitive awareness instrument. Self-assessment of metacognitive characteristics of problem solving was determined using a scale based on Schraw and Dennison's 52-item Metacognitive Awareness Inventory (MAI) (Schraw and Dennison, 1994). To suit the teaching context, the initial inventory was modified into a 30-item scale, with the two main sub-constructs remaining intact: knowledge of cognition containing three sub-categories (nine items), and regulation of cognition containing five sub-categories (21 items). Where necessary, the items were edited to make them more relevant for problem solving (Appendix 1). At the time of writing, we became aware of Physics Metacognition Inventory (PMI) (Taasoobshirazi et al., 2015). PMI has items directly related to the features of the Goldilocks Help tool. For example, PMI: “Before I start solving a physics problem, I plan out how I’m going to solve it”, inventory used in this work: “To solve a problem, I first develop a plan with the sequence of steps necessary for completion.”

Each year, the inventory was administered twice, during the first and last weeks of the semester (pretest and posttest). The pretest was completed prior to the problem-solving activities of the workshop described above and prior to the introduction of the GH workflow. The inventory items were scored on a 5-point Likert scale (never, rarely, sometimes, often, and very often). From 93 to 115 students have participated in the four instances of the inventory administration. Matched data from 106 students was available for analysis.

In order to confirm that the component items in the modified scale were inter-correlated, the internal reliability of the modified scale was determined by calculating Cronbach's α on data obtained from the 2015 and 2016 cohorts. Cronbach's α was determined using the Statistical Package for Social Sciences (SPSS; IBM, Chicago). According to the results of the Cronbach's alpha analyses, all the included items measured different aspects of the same construct or sub-constructs, with alpha values consistently greater than 0.7 (α [knowledge of cognition] = 0.75, α [regulation of cognition] = 0.83, α [overall] = 0.86). The calculated alpha values indicate that the desired level of internal consistency was achieved, and allows for the overall scores to be summed and analysed as a total, as an α value above 0.7 indicates that all of the items contained within a particular scale are measuring the same outcome, without unnecessary redundancy (α values were all less than 0.9).

To determine the effect of a semester-long problem-solving approach on student metacognitive awareness, matched paired t-tests were performed to compare the data from before and after the intervention. The total and mean scores for the overall inventory, knowledge of cognition, regulation of cognition, and their sub-categories were determined. The pretest scores were compared with the posttest scores from the same students, identified by student-selected 4-character codes. Where students did not respond to a particular item, their data for that item was removed from the analyses, at the item, category, sub-construct and overall level. Descriptive statistics and paired t-tests were calculated using GraphPad Prism version 6 (La Jolla, California). Cohen's d, or effect size, was calculated for the overall inventory, knowledge of cognition and regulation of cognition, by subtracting mean pretest scores from mean posttest scores, and dividing by the average of the standard deviations (SD) of the two groups.

Results

Workflow and instruction refinement based on student focus groups and academic feedback

During the 2015 focus group interviews, students were asked how the GH workflow (Fig. 1) affected their problem solving habits. Their responses (Table 2) revealed three perspectives. Some students reported that the GH workflow aligned well with their established problem-solving schema, some adopted or partially adopted it, and some students did not adopt it due to either a confusion caused by its complexity or to a conflict with their pre-existing schema.

Table 2 Focus group responses related to the GH workflow

Theme	Excerpts
Already adopted	– I find I – in like high school for chemistry, my teachers sort of ingrained quite a bit of that already, so I do a lot of it automatically.
	– Personally I got the gist of it and it was very similar to what I was doing already so I didn’t really feel the need
	– It makes me feel good that the process I was using is very similar.
Adopting	– It sort of helped because if you followed the steps and got it wrong you could go back through those steps and see where you went wrong and you can fix it.
Partial adopting	– I only really used the last step to summarise and see if I did it correctly and then…. I only really used it when I got it wrong. So first I would do it my way and then if I got it wrong I’d use the flowchart.
	– I used it in the first few times it was helpful, but I wouldn’t go through the whole pathway all the time. I would just use the rough idea of it.
	– Yeah like I mean the chart's great but I’m not gonna always – I never have it in front of me, all I think is like, remembering what my lecturer said like, “What do you know?” so like I always do that yeah and then I’ll see what I don’t know and then you know…
Not adopting due to a conflict with pre-existing schema	– Its kind of a process of solving problems but I have my own way of solving problems with the given conditions and definitions. So I’d rather use my own way.
	– I do have my own way of solving the problems and I do think they work at least for 90% of the time, so I’m pretty confident with it.
Not adopting due to a confusion with too many steps	– I thought it was too long. There was a lot on it.
	– you looked at it and thought “wow I have to do all this”
	– I feel sometimes if it comes to a step in that Goldilocks thing that I don’t think that I need I often will struggle to then write that step down in my working out it if I don’t quite understand where that step's come from and ‘cause I might have previously done it, so I’m thinking to myself that I’m repeating these steps and then I get confused. I just… yep.

---

Academic survey responses are summarised in Table 3. The survey confirmed the construct validity of the GH workflow, demonstrated by positive responses to items 1–4 and 7 (52–71% agreement with only 1 or 2 respondents disagreeing). The instructors have also noted that, while the workflow is not confusing to expert problem solvers such as themselves (19 out of 21 responses), it could be confusing to students (19 out of 21 responses). Written comments related to (i) the need to add a loop from the evaluation phase back to analysis, (ii) the requirement to incorporate extra prompts for dimensional analysis, reflecting common problem-solving difficulties associated with units, and (iii) suggesting prompts for additional information sourcing.

Table 3 Academic responses related to the GH workflow

	No	Yes	May be/somewhat
(1) The aspects of problem solving, included into the flowchart, are appropriate (i.e., reflect problem solving as taught in my classes)	1	15	5
(2) The aspects of problem solving, included into the flowchart, are relevant to my area of teaching	2	14	5
(3) I would use this flowchart (or an appropriately edited version) in my teaching	1	11	9
(4) I would recommend this flowchart (or an appropriately edited version) to my colleagues	1	15	5
(5) The flowchart is confusing to me	19	1	1
(6) The flowchart would be confusing to my students	7	2	12
(7) The flowchart addresses common difficulties in the problem-solving process	1	16	4

---

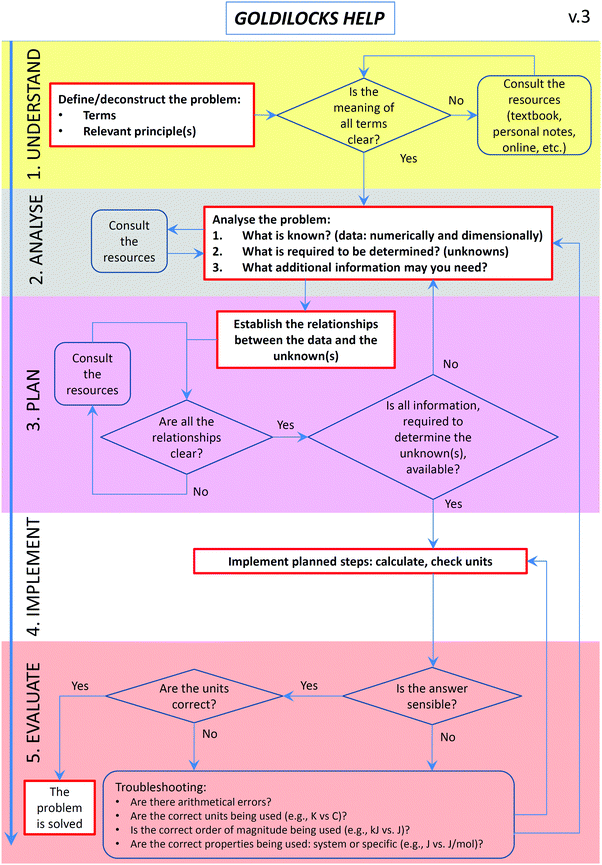
These findings led to two instructional modifications in 2016. Firstly, the GH workflow was decluttered to reduce confusion and modifications suggested by academics were implemented (Fig. 2). Secondly, modelling instruction was introduced into lectures and tutorials, where at least one of the problems allocated to each class period was worked through interactively, using explicit workflow prompts and colour-coding of the problem-solving stages.

Fig. 2 Goldilocks Help problem-solving workflow – final version.

End-of-semester reflections

Student comments expressed within end-of-semester reflections fell into two distinct but related themes: problem-solving processes and learning experiences in problem-solving sessions (tutorials). The themes, sub-themes, and specific categories are summarised in Table 4.

Table 4 Themes associated with problem solving expressed in end-of-semester reflections

Sub-themes	Categories	Excerpts
Theme: problem-solving processes
Understand	Importance for the subsequent steps	– The input of my group during discussion really helped me to understand the questions in another way and enlighten me on alternative ways to improve on my solution and offer advice on when I mistook or assumed something in the equation – I now do not just jump straight into the problem but I make sure I read everything carefully and fully understand all parts of the question before continuing
	Importance of preparation and building conceptual knowledge	– Absolutely necessary to in order to begin the understanding step in the problem solving model
Analyse	Relationships between concepts	– It had forced us to discuss the question from different perspectives which would lead to connections between ideas
	Restructuring the problem	– Dissecting – Unravelling – Breaking everything apart – Unpacking the question
	Focusing on the data and the goals	– Have learned how to solved problems strategically, analysing what being given and what need to be found
Plan	Consequences of the lack of planning	– It is crucial to plan out the steps taken to solve a problem instead of simply “plucking” numbers from the question. I was guilty of doing the latter in the first two tutorials and soon realized that it made me more confused and thus unable to obtain the correct answer. After discussing this with my fellow group members, I was able to plan out the appropriate steps and formulas needed to solve the given problems. This enabled me to not only obtain the correct answer but also made it clearer for me when I reviewed my solutions back
	The value of a well written-out plan for later revision
	Timing	– I have learnt how important it is to plan the response and know what you are trying to answer before starting calculations or formulating responses
Evaluate	Specific checking strategies	– How do you roughly ball-park your answer, confirming units – Double-check my solution before submission
	Critical assessment of the overall processes	– Evaluate my problem solving processes – Ask each other if our approach to the problem(s) seems to make sense, or if it answers the problem's question
	Evaluating regularly	– Critique the methods used in problem solving which was not observed during the first weeks of the semester
Overall workflow	Helps to commence, progress, and complete the problem-solving process	– It did help our group and myself, solve problems that we were unable to tackle – This allowed us to more easily solve questions without getting stuck – Pivotal towards how I go about in every question in each tutorial. Without it, I would have struggled to complete the questions
	Requires a change in problem-solving approaches	– My personal attitude to the problem-solving process has changed to become more accepting, although I’m still working towards it being an automatic approach
	Confusing	– Although it was beneficial to write down and approach the question in a different manner before jumping into a calculation right away, the flow chart itself was often confusing to follow
Theme: learning experiences in problem-solving sessions
Exposure to alternative problem-solving strategies	Different/others’ way of thinking	– It gave me useful insight into how other people think and helped me discover new ways of solving problems – I also learnt that people think differently
	Others’ way of querying	– Queries from other students challenged me to think in new ways and attack problems from different angles
	Strategising	– Various strategies on how to attack different types of problems
	Integration of problem-solving approaches	– It also shed some light on me that there might not necessarily be one approach to solve a problem and sometimes it is possible to integrate different approaches together
Cooperative problem solving	Enhanced understanding of concepts	– If I didn't understand something, someone in the group would be able to explain in it different terms to what I had previously heard, so i was also able to learn new things
	Disambiguation of misconceptions	– Cleared some of my misconceptions and misunderstandings about some topics, such as the phase equilibria topic
	Consolidation of ideas	– The group work aspect of the tutorial was the highlight and the most helpful, as peer learning is an effective way for students to consolidate information
	Complementarity	– There were many times when someone suggested something I hadn't considered
	Working with more knowledgeable peers	– The members who had a more proficient understanding about a particular topic would aid members who had a weak understanding about the respective topic, I was able gather a greater understanding in topics that I am particularly weak in (e.g. thermodynamics)
	Learning by teaching to less proficient peers	– It was very useful to me to explain to those in my group about things that they did not understand, which in a way helped in my own understanding quite significantly
	Negative attitude to group work	– I found this inefficient because everyone has their own way to solve the problems, so a lot of time was spent discussing rather than writing
Changes in problem-solving skills	General improvement	– Improved my overall problem solving skills
	Strengths and weaknesses	– Really helped with my understanding of strengths and weaknesses in terms of problem solving
	Improving skills is an ongoing process	– I realise I’ve improved but I haven’t perfected my abilities yet
	Grade motivation	– An opportunity to consolidate knowledge and gain experience in answering questions that may be similar to those that appear in exams
	Simplistic view of what problem solving	– I found that I was able to identify much better the equations that were required once performing questions in tutorials
Problem-solving challenges	Not knowing where to start	– Struggling to understand how to solve the problem
	Reasoning/verbalising the thought process	– Doing the questions was fairly simple, but explaining what I did was the hard part – Struggled to articulate her reasoning
	Challenges associated with changing to a process-driven approach	– The flow chart that was provided at the beginning of the tutorial first seemed quite confusing and unnecessary. But as we incorporated it into our problem solving process, it became increasingly important and we soon realised, as a group, that it helped everyone problem solve in a logical order. This allowed fewer mistakes and clearer understanding of the methods of problem solving.

---

Problem-solving processes. Students made statements about the individual phases of the problem-solving process and remarked on the workflow as a whole (sub-themes).

With respect to the “Understand” phase, students noted the importance of this stage for the subsequent steps. They also commented about the importance of preparation and building conceptual knowledge for performing this step. However, some students had a limited perception of class preparation as just a “speeding-up” of the process (“Working on the problems beforehand made it easier to discuss as everyone had read the problems and therefore did not have to waste time rereading and trying to understand the questions”), indicating a need for further instructional attention to explaining to students the value of re-reading questions as a problem-solving technique.

Students repeatedly referred to various elements of the “Analysis” phase, such as relationships between concepts, restructuring the problem, and focusing on the data and the goals. Skipping the “Plan” phase is a known manifestation of novice problem solving (Herron, 1996a). Reflections showed that students learned to appreciate the slow-down that is involved in attending to planning a solution. Specifically, the consequences of the lack of planning and the value of a well written-out plan for later revision emerged as a strong notion. The timing of the planning was also mentioned. Regarding the “Evaluate” phase, students referred to specific checking strategies as well as critically assessing the overall processes. Students’ reflections showed not only that they learned what exactly to do to evaluate their solutions, but that they actually started doing it more regularly.

With respect to the workflow as a whole, some noted it helped them to commence, progress, and complete the problem-solving tasks. Adopting the GH workflow clearly required a change in some students’ approaches. Also, confusion caused by it was regularly mentioned, particularly in 2015, prior to the workflow refinement.

Two selected extensive quotes capture student development of the problem-solving approaches, influenced by the GH workflow:

– I have realised the importance of understanding exactly what a problem is asking and planning my solution. Instead of jumping straight into solving problems, I now more and more take the time to identify what I do and don't know and the process I need to go through to solve it. I used to just plug things into equations but I now have a greater understanding of why I am calculating something in this way and appreciating how something is derived. It not only means I am more likely to answer correctly but forces me to fully understand what I am doing and why, so this knowledge can be applied to many situations, including unfamiliar ones

– In the past it was routine for me to see a couple of numbers, find a formula that has all the variables, then to just put them in the calculator and get an answer. Although I might get the right answer or not it was the equivalent of a guess as I didn’t understand as to why I chose those numbers. However, as the semester progressed I have learned to slow down whilst attempting each question and to first analyze all the information before jumping to the calculator. It occurred to me that I first have to recognize any assumptions that are being made which may affect which formula I chose. Then to accurately write down all variables is essential and with all this in mind, at the end of the analysis and understanding of the question, is the time to pick the formula that has the necessary variables to solve what is being asked

Learning experiences in problem-solving sessions. The learning experiences divided into sub-themes of exposure to alternative problem-solving strategies, cooperative problem solving, changes in problem-solving skills, and problem-solving challenges.

In tutorials, students worked in small groups of 4–5 and, at the end of each class, a presenter from each group delivered a workshopped solution to the whole class. This setup provided students with multiple opportunities to experience the problem-solving approaches of others, within and between groups. Students talked about others’ way of thinking and strategising. They emphasised different ways of thinking rather than using different algorithms and discovered that different approaches may not be truly alternative, but rather complementary and integrative. Some students appreciated that it is useful not only to be exposed to other's solutions, but particularly others’ questions.

We have used students’ reflections to carry out a detailed thematic analysis of students’ perceptions of group work and the change in their teamwork skills as a result of the instructional design used in the course. This analysis is outside of the scope of the present work and will be published separately. Here, we are presenting themes associated with the effects of cooperation specifically on problem solving. Students reported enhanced understanding of concepts, disambiguation of misconceptions, consolidation of ideas, and complementarity. They appreciated the benefits from working with more knowledgeable peers as well as learning by teaching to those less proficient. Student resistance to group work is well known (Hillyard et al., 2010), so it was not surprising to come across negative comments about it (“I found this inefficient because everyone has their own way to solve the problems, so a lot of time was spent discussing rather than writing”). This last quote represents an instructional challenge in that some students do not appreciate the value of peer discussion for their learning and improvement of problem-solving skills.

While many students have declared that their problem-solving skills have improved as a result of this teaching and learning approach, some of them have done so in a self-critical, metacognitive manner. Specifically, they commented on their strengths and weaknesses and demonstrated a mature appreciation of the fact that learning problem-solving process and improving relevant skills is a process in itself. However, some have revealed their grade, rather than intrinsic, motivation when it comes to skills development as well as somewhat simplistic view of what problem solving is.

Students recognised challenges associated with problem-solving. Reported were general difficulties summarised vide supra such as not knowing where to start or verbalising the thought process. Many students expressed concerns over challenges associated with using a process-driven approach.

Metacognition and self-regulation inventory scores

Total scores for the overall inventory and the knowledge of cognition and regulation of cognition sub-constructs are shown in Table 5. In 2015, the end-of semester scores were higher than the initial scores, with statistically significant increases of 5.3, 10.7, and 9.2% observed in the scores for the knowledge of cognition and regulation of cognition sub-constructs and the overall score, respectively (paired t-tests, p < 0.05). In 2016, statistically significant increases in scores were seen in the regulation of cognition and overall score (paired t-tests, p < 0.05). Effect size was estimated using Cohen's d, with the percentage changes for the overall inventory and regulation of cognition sub-construct in 2015 indicating a medium-to-large effect size, whereas the 2015 change in knowledge of cognition and the 2016 changes in overall inventory and regulation of cognition scores are small-to-medium in size.

Table 5 Total scores for the overall inventory and sub-constructs^a

	Pretest (before the intervention)		Posttest (after the intervention)		N	% change	p	SD	d
	Mean	SEM	Mean	SEM
a Overall score is a total for all 30 items, out of a possible 150, whereas sub-construct scores are out of a maximum 45 and 95, respectively. Scores are provided as mean ± SEM, with N indicating the number of students with matched pretest and posttest data, and p the significance reached after a paired t-test (p < 0.05 are indicated with an asterisk). Effect size was calculated as Cohen's d and also as a percentage of change.
2015 cohort
Overall	103.3	±1.9	112.8	±2.4	36	9.2	0.0003*	13.6	0.74
Knowledge of cognition	33.9	±0.6	35.6	±0.7	40	5.3	0.0090*	4.2	0.44
Regulation of cognition	69.3	±1.5	76.7	±1.8	36	10.7	0.0003*	10.4	0.75
2016 cohort
Overall	100.9	±1.5	105.9	±1.7	59	5.0	0.0078*	12.3	0.41
Knowledge of cognition	34.0	±0.5	34.5	±0.5	64	1.4	0.3168	3.9	0.12
Regulation of cognition	67.1	±1.2	70.8	±1.3	61	5.6	0.0047*	9.9	0.38

---

Mean scores for the overall inventory, knowledge of cognition and regulation of cognition sub-constructs, and the categories are shown in Table 6. The scores are provided as mean ± SEM, with N indicating the number of matched pairs, and p the significance reached after a paired t-test.

Table 6 Mean scores for the overall inventory, sub-constructs, and the categories

	Pretest (before the intervention; mean ± SEM)	Posttest (after the intervention; mean ± SEM)	N	% change	p
Mean values, out of a possible 5, reflecting the 5-point Likert scale, are provided as mean ± SEM, with N indicating the number of students with matched pretest and posttest data, and p the significance reached after a paired t-test.
2015 cohort
Overall	3.44 ± 0.06	3.76 ± 0.08	36	9.2	0.0003*
Knowledge of cognition	3.76 ± 0.02	3.96 ± 0.02	40	5.3	0.0090*
Conditional	3.88 ± 0.01	4.00 ± 0.01	40	3.2	0.1334
Declarative	4.00 ± 0.01	4.10 ± 0.01	40	2.5	0.4164
Procedural	3.56 ± 0.01	3.86 ± 0.01	40	8.4	0.0085*
Regulation of cognition	3.30 ± 0.05	3.65 ± 0.06	36	10.7	0.0003*
Debugging strategies	3.30 ± 0.01	3.66 ± 0.01	39	7.4	0.0302*
Evaluation	3.11 ± 0.01	3.42 ± 0.01	40	9.9	0.0372*
Information management strategies	3.56 ± 0.01	3.96 ± 0.01	40	11.4	0.0001*
Monitoring	3.18 ± 0.02	3.48 ± 0.01	37	9.4	0.0148*
Planning	3.13 ± 0.02	3.54 ± 0.01	40	13.14	0.0002*
2016 cohort
Overall	3.36 ± 0.05	3.53 ± 0.06	59	5.0	0.0078*
Knowledge of cognition	3.78 ± 0.02	3.83 ± 0.02	64	1.4	0.3168
Conditional	3.83 ± 0.01	3.96 ± 0.01	66	3.5	0.0532
Declarative	3.96 ± 0.00	3.92 ± 0.01	66	−1.2	0.6133
Procedural	3.64 ± 0.01	3.69 ± 0.01	64	1.3	0.5302
Regulation of cognition	3.19 ± 0.04	3.37 ± 0.04	61	5.6	0.0047*
Debugging strategies	3.35 ± 0.01	3.60 ± 0.01	66	7.5	0.0087*
Evaluation	2.94 ± 0.01	3.19 ± 0.01	66	8.2	0.0124*
Information management strategies	3.57 ± 0.01	3.72 ± 0.01	64	4.2	0.0346*
Monitoring	3.07 ± 0.01	3.17 ± 0.01	64	3.7	0.2033
Planning	3.09 ± 0.01	3.24 ± 0.01	65	5.0	0.0682

---

Discussion

No student population is uniform (Gulacar et al., 2014). In any given student cohort, there will be those with above average knowledge of content matter, advanced problem-solving skills, and superior metacognitive self-regulation abilities. Such students will benefit to varying degrees from metacognitive awareness and problem-solving skills training. Novice problem solvers are often referred to as low(er)-achieving (Gulacar et al., 2014), low-skilled comprehenders (Pyburn et al., 2014), or at-risk students (Chan and Bauer, 2014) and are defined as having low metacognitive self-regulation abilities (Chan and Bauer, 2014). Some students are also characterised by such cognitive variables as reduced functional M-capacity and disembedding ability as well as limited scientific reasoning and working memory (Johnstone and Al-Naeme, 1991; Niaz, 1996; Tsaparlis, 2005). In problem-solving tasks, these students often experience difficulties initiating their problem-solving process or get stuck at a particular stage in the process, situations we refer to as false starts and dead ends, respectively. These are the students who are the target of the intervention as part of this study.

The primary aim of the intervention described in this paper was to support students in developing the metacognitive habit of self-questioning and in learning what type of questions to ask themselves during the problem-solving process. Furthermore, the use of the GH workflow was designed to encourage students to incorporate the prompts and questions into their problem-solving schema and, ultimately, to internalise them. These prompts capture what an experienced instructor would ask students if they were to get stuck during problem solving. Goldilocks Help problem-solving workflow provides these prompts to students themselves or arms a less experienced instructor with a specific mechanism to guide students.

Student engagement with the GH problem-solving workflow

Problem solving, together with critical thinking, creativity, and decision-making, is recognised as one of the crucial twenty-first century skills, under the category of “ways of thinking” (Griffin and Care, 2015). Development of problem-solving competence, in turn, constitutes one of the central tenets of chemistry education (Bodner, 1991, 2015; Herron, 1996a, 1996b; Bodner and Herron, 2002). With respect to the problem-solving process embedded into the GH workflow, three main themes have been identified from the 2015 focus group interviews: students who (i) used the workflow as they found it useful; (ii) did not specifically use the workflow as they already used a similar approach to problem solving; and (iii) did not use the workflow as they found it confusing.

The first theme represented the successful outcome of the intervention designed and implemented in this study. The second theme concerns students that have been previously exposed to structured problem solving. They show the internalisation of the process, the removal of the need for an explicit support (Puntambekar and Hubscher, 2005), and therefore a student-controlled fading of scaffolding (Wood et al., 1976). The third theme is reminiscent of the earlier findings where students abandoned the problem-solving approach they were taught because they found it to be “too time consuming” (Bunce and Heikkinen, 1986). It is also possible that the intervention presents a hurdle to students with low functional M-capacity and disembedding ability as well as low levels of scientific reasoning and working memory (Tsaparlis, 2005). This theme demonstrated the need for workflow refinement and, together with feedback from instructors (Table 3), led to a more streamlined version (Fig. 2). The focus group and reflection comments about confusion also prompted us to implement an additional action in 2016, i.e. an emphasis on the steps within the process (gathering information, analysis, planning, and reflective evaluation) and explicit explanation and demonstration of what they entail, through modelling instruction.

How much structure and guidance is optimal? There are those who argue that providing excessive support structures confuses some learners, interferes with their own problem-solving schema, and leads to a decrease in performance (Horz et al., 2009; Nuckles et al., 2010), mostly due to cognitive overload (Sweller et al., 2011b). Others have argued that minimal structure and guidance do not work (Kirschner et al., 2006). Moreover, prompts may be too structured to be useful for some learners while others may be redundant once students have established their own internal schemas (Belland, 2011). The challenge of over-structuring was actually found to be greater for high-achieving students (Kalyuga, 2007). To address the issues of over-structuring, we have refined the original workflow to reduce excessive scaffolding. For example, we removed the planning prompt that asked students to consider the distinction between system properties (e.g., standard enthalpy of combustion) and process parameters (e.g., enthalpy for a given process with a specified mass of a compound being combusted). The concept of system-specific properties is an important one and is still included into the workflow, under the evaluation phase.

Importantly, when modifying the workflow, we did not aim to entirely eliminate possible confusion. Instead we used the instances of confusion, incidental as well as anticipated, to improve students’ problem-solving skills and metacognitive awareness. Specifically, one of the primary goals of presenting students with the GH workflow was to expose them to what expert problem-solving processes and expert thinking entail. Not unexpectedly, it is a long jump from algorithmic problem solving to conceptual thinking. It is challenging and, therefore, confusing and frustrating.

Contrary to how it is often perceived by students, confusion is not an entirely negative aspect of learning. Confusion, alongside flow, is an affective state that positively correlates with learning (Craig et al., 2004). Occasional complication of tasks by implementing specific scaffolds could be productive (Reiser, 2004). In other words, disciplined struggle is good for learning. However, failure to resolve confusion and struggle could also promote frustration and decrease learning (D’Mello and Graesser, 2010). Comments of the type “If you’d just tell me what equation to use, I’d be able to solve a problem” (Harper, 2005) or “there must be an easier way” (Van Ausdal, 1988) are not uncommon and convey frustration associated with problem solving. What we, instructors and students, do with that frustration makes the difference between learning and avoidance of learning. As instructors, we should take these instances of confusion and frustration to explain to students that problem solving is indeed a process and not a recall task and that the ability to see connections between initially abstract and seemingly disconnected pieces of information develops with practice and rests on organised, not memorised, knowledge.

Change in metacognitive awareness after one semester of the intervention

The results of the metacognitive awareness inventory demonstrate consistent increases in scores for all measures: the overall scale, the knowledge of cognition and regulation of cognition sub-constructs, and their constituent categories (Tables 5 and 6). The only exception is the declarative knowledge category in 2016, however the change is not statistically significant (p = 0.6). It is interesting to note that, in 2015, increases for all categories (except for declarative and conditional knowledge) were statistically significant and ranged from 5.3% to 13.1%. Conversely, in 2016, only three categories within the regulation of cognition sub-construct (information management strategies, debugging strategies, and evaluation) exhibited statistically significant increases of 4.2% to 8.2%. While the exact reason for such difference between the two cohorts is not known, we theorise that this may be due to the modelling instruction, introduced in 2016, which demonstrated to students what the different aspects of problem solving really entail. Students’ perceptions of their self-regulatory abilities could decrease as they progress through their education, even when they actually use more advanced self-regulatory strategies (Usher and Pajares, 2008). To test this idea we plan to interview students about how they make a decision when completing the inventory. Specifically, we plan to probe whether, after being exposed to problem solving by experts, they change their understanding of what different aspects of problem solving actually mean (e.g., strategies, planning, monitoring, etc.). For those students that improve their understanding of these constructs, it is not unreasonable to assume that their pretest response overestimates their practice and so later their posttest response is moderated, and thus their score may not increase significantly or may even decrease, as observed for some 2016 students on some items.

The increased scores for regulation of cognition are congruent with themes that emerged from students’ qualitative comments (Table 4). Specifically, the increased planning scores were illustrated by students appreciating the detrimental consequences of not attending to the planning stage and the value of a well written-out plan for later revision, and the importance of attending to planning before plunging into calculations. The scores for the evaluation, debugging, and monitoring were reflected in students’ comments about specific checking strategies, critical assessment of the overall processes, and the significance of evaluating each time a problem-solving cycle is undertaken. The items within the information management strategies category deal with such aspects of problem solving as focusing on important information and on overall meaning rather than specifics and organising and linking information. These aspects align well with student notions related to understanding and analysis of problems: importance of preparation and building conceptual knowledge, relationships between concepts, and restructuring the problem.

Limitations of the study and future work

Student success may be considered in the context of students’ learning experience, learning approach, and their learning outcomes. In this study, we have focused on collecting and analysing data relating to the first two aspects, through student-declared anonymous responses to the inventory (quantitative) and reflections (qualitative). The limiting factors in an anonymous process is that the responses cannot be used to correlate with student performance, and thus the third aspect of student success, as described above, cannot be linked to the change in their metacognitive awareness as reported by them for problem solving. Furthermore, using the inventory limits the measure of problem-solving proficiency to student-reported opinions. Analysing the relationship between metacognitive practice and students’ learning outcomes is currently underway and will be published separately. Specifically, we are investigating the relationships between a student's problem-solving process (demonstrated in their written work and through think-aloud interviews) and the success of their problem solving attempts.

This study was carried out in an authentic classroom setting with the cohorts of students taught by one of the authors (E. Y.). This context prevented the use of an experimental control vs. treatment design, which would not have been ethical. In keeping with within-subject design, independent variables (such as prior academic ability) were not manipulated. And finally, it should be noted that problem-solving abilities of students are likely to be affected by factors outside of the unit of study where the Goldilocks Help tool was implemented. Thus, rather than making any claims about cause and effect, we present possible relationships based on the collected data.

In this paper, we have described the design of a problem-solving workflow intended for use in general and physical chemistry courses. We have now implemented it for analytical and formulation chemistry courses (without any modifications), as well as developed versions for use in spectroscopy, organic chemistry, and pharmacology subject areas, and pilot studies were undertaken in 2016. Future work will evaluate their effectiveness. Furthermore, we are collecting data on the problem-solving skill development of the cohorts described in this paper in the context of a longitudinal study.

Finally, in this study, the problem-solving process was used by first-year students to develop problem-solving skills, while tackling essentially closed, numerical problems. The literature shows that open-ended and complex problems require a much less linear and more iterative approach. However, skills acquired by novice students, when dealing with simpler problems, form the foundation for solving open-ended and complex problems.

Conclusions

This paper describes the design, implementation, and evaluation of a scaffolding support for structured approach to problem solving in the context of one semester of physical chemistry. Students’ qualitative comments and inventory scores have indicated the shift in their beliefs in their capacities to use the strategies required to achieve successful problem solving, i.e. in their self-efficacy for self-regulated learning. The reflections demonstrated not only that students were aware of which strategies are needed for a successful outcome, but also that they were capable of employing such strategies.

Appendix 1

Problem-solving metacognition and self-regulation inventory

• Knowledge of cognition

○ Declarative knowledge

■ I understand my intellectual strengths and weaknesses.

■ I am a good judge of how well I understand something.

○ Procedural knowledge

■ I have a specific purpose for each strategy I use.

■ I am aware of what strategies I use when I solve problems.

■ I find myself using helpful problem-solving strategies automatically.

■ I try to use strategies that have worked in the past.

○ Conditional knowledge

■ I learn best when I know something about the topic.

■ I use different problem-solving strategies depending on the situation.

■ I use my intellectual strengths to compensate for my weaknesses.

• Regulation of cognition

○ Planning

■ I ask myself questions about the material before I begin.

■ I think of several ways to solve a problem and choose the best one.

■ I read instructions carefully before I begin solving a problem.

■ To solve a problem, I first develop a plan with the sequence of steps necessary for completion.

■ I define each problem carefully before attempting to solve it.

○ Information management strategies

■ I consciously focus my attention on important information.

■ I create my own examples/diagrams and/or write my own notes to make information more meaningful.

■ I ask myself if the information in the problem is related to other information I know.

■ I focus on overall meaning rather than specifics.

■ Before solving a problem, I assemble and organize all the necessary information.

○ Monitoring

■ I consider several alternatives to a problem.

■ I periodically review to help me understand important relationships.

■ I find myself analysing the usefulness of strategies I use for solving problems.

■ I find myself pausing regularly to check my comprehension.

■ While solving a problem, I consider various aspects of the problem.

○ Debugging strategies

■ I change strategies when I fail to understand.

■ I re-evaluate my assumptions when I get confused.

■ After a problem is solved, I look for improvements on the solution process.

○ Evaluation

■ I summarize what I have learned after I finish.

■ I ask myself if I have considered all options after I solve a problem.

■ After a problem is solved, I reflect on it and on how its solution could help to solve future problems.

Acknowledgements

The authors are indebted to Prof. Tina Overton for sharing her knowledge and experience. Dr Sheryl Maher's assistance in convening the focus group interviews and insightful discussions are gratefully acknowledged. The authors are also thankful to instructors who provided feedback on the GH workflow. This work was supported by the Monash University 2015 Better Teaching, Better Learning (BTBL) Small Grant.

References

1. Baddeley A. and Hitch G. J., (1974), Working memory, in Bower G. H. (ed.), The psychology of learning and motivation, New York: Academic, vol. 8, pp. 47–89.
2. Belland B. R., (2011), Distributed cognition as a lens to understand the effects of scaffolds: the role of transfer of responsibility, Educ. Psychol. Rev., 23, 577–600.
3. Bodner G. M., (1987), The role of algorithms in teaching problem solving, J. Chem. Educ., 64, 513–514.
4. Bodner G. M., (1991), A view from chemistry, in Smith M. U. (ed.), Toward a unified theory of problem solving: views from the content domains, Hillsdale, N.J.: Lawrence Erlbaum Associates, pp. 21–34.
5. Bodner G. M., (2003), The Nyholm Lecture – problem solving: the difference between what we do and what we tell students to do, U. Chem. Ed., 7, 37–45.
6. Bodner G. M., (2015), Research on problem solving in chemistry, in Garcia-Martinez J. and Serrano-Torregrosa E. (ed.), Chemistry education: best practices, opportunities and trends, 1st edn, Weinheim, Germany: Wiley-VCH Verlag GmbH & Co. KGaA, ch. 8, pp. 181–201.
7. Bodner G. M. and Herron J. D., (2002), Problem-solving in chemistry, in Gilbert J. K., De Jong O., Justi R., Treagust D. F. and Van Driel J. H. (ed.), Chemical education: towards research-based practice, Dordecht: Kluwer, ch. 11, pp. 235–266.
8. Bodner G. M. and McMillen T. L. B., (1986), Cognitive restructuring as an early stage in problem solving, J. Res. Sci. Teach., 23, 727–737.
9. Bransford J. D. and Stein B. S., (1984), The ideal problem solver: a guide for improving thinking, learning, and creativity, New York, NY: W.H. Freeman.
10. Braun V. and Clarke V., (2006), Using thematic analysis in psychology, Qual. Res. Psychol., 3, 77–101.
11. Bunce D. M. and Heikkinen H., (1986), The effects of an explicit problem-solving approach on mathematical chemistry achievement, J. Res. Sci. Teach., 23, 11–20.
12. Bunce D. M., Gabel D. L. and Samuel J. V., (1991), Enhancing chemistry problem-solving achievement using problem categorization, J. Res. Sci. Teach., 28, 505–521.
13. Chan J. Y. K. and Bauer C. F., (2014), Identifying at-risk students in general chemistry via cluster analysis of affective characteristics, J. Chem. Educ., 91, 1417–1425.
14. Cohen J., Kennedy-Justice M., Pai S., Torres C., Toomey R., dePierro E. and Garafalo F., (2000), Encouraging meaningful quantitative problem solving, J. Chem. Educ., 77, 1166–1173.
15. Comeford L., (1997), Writing assignments in physical chemistry, J. Chem. Educ., 74, 392.
16. Craig S. D., Graesser A. C., Sullins J. and Gholson B., (2004), Affect and learning: an exploratory look into the role of affect in learning, J. Educ. Media, 29, 241–250.
17. Creswell J. H., (2014), Research design – Qualitative, quantitative, and mixed methods approaches, LA: Sage.
18. D’Mello S. and Graesser A., (2010), Modeling cognitive-affective dynamics with hidden Markov models, in Catrambone R. and Ohlsson S. (ed.), Proceedings of the 32nd Annual Cognitive Science Society, Austin: Cognitive Science Society, pp. 2721–2726.
19. Davis E. A., (2000), Scaffolding students' knowledge integration: prompts for reflection in KIE, Int. J. Sci. Educ., 22, 819–837.
20. De Corte E., Verschaffel L. and Van Dooren W., (2012), Heuristics and problem solving, in Seel N. M. (ed.), Encyclopedia of the Sciences of Learning, Boston, MA: Springer US, pp. 1421–1424.
21. Deek F. P., Turoff M. and McHugh J. A., (1999), A common model for problem solving and program development, IEEE Trans. Educ., 42, 331–336.
22. Dewey J., (1910), The analysis of a complete act of thought, How we think, Boston: D.C. Heath & Co., ch. 6, pp. 68–78.
23. Drummond H. P. and Selvaratnam M., (2008), Students’ competence in intellectual strategies needed for solving chemistry problems, S. Afr. J. Chem., 61, 56–62.
24. Felder R. M. and Brent R., (2016), Problem-solving skills, Teaching and learning in STEM: a practical guide, San Francisco, CA: Jossey-Bass, ch. 9, pp. 189–212.
25. Flavell J. H., (1979), Metacognition and cognitive monitoring: a new area of cognitive-developmental inquiry, Am. Psychol., 34, 906–911.
26. Frank D. V., (1986), Implementing instruction to improve the problem-solving abilities of general chemistry students, PhD thesis, Purdue University.
27. Ge X. and Land S. M., (2003), Scaffolding students' problem-solving processes in an ill-structured task using questionprompts and peer interactions, Educ. Technol. Res. Dev., 51, 21–38.
28. Gick M. L., (1986), Problem-solving strategies, Educ. Psychol., 21, 99–120.
29. Griffin P. and Care E., (2015), Assessment and teaching of 21st century skills: methods and approach, Dordrecht: Springer.
30. Gulacar O., Overton T., Bowman C. R. and Fynewever H., (2013), A novel code system for revealing sources of students’ difficulties with stoichiometry, Chem. Educ. Res. Pract., 14, 507–515.
31. Gulacar O., Eilks I. and Bowman C. R., (2014), Differences in general cognitive abilities and domain-specific skills of higher- and lower-achieving students in stoichiometry, J. Chem. Educ., 91, 961–968.
32. Hannafin M., Land S. and Oliver K., (1999), Open learning environments: foundations, methods, and models, in Reigeluth C. M. (ed.), Instructional design theories and models, Mahwah, NJ: Erlbaum, vol. 2, pp. 115–140.
33. Harper K. A., (2005), Student problem-solving behaviors, Phys. Teach., 44, 250–251.
34. Hayes G. R., (1989), The complete problem solver, Hillsdale, NJ: L. Erlbaum Associates.
35. Heller K. and Heller P., (2010), Cooperative problem solving in physics: a user's manual, Minnesota, US: University of Minnesota.
36. Herron J. D., (1996a), Problem solving, The chemistry classroom, Washington, DC: ACS, ch. 7, pp. 63–82.
37. Herron J. D., (1996b), Teaching problem solving, The chemistry classroom, Washington, DC: ACS, ch. 8, pp. 83–104.
38. Herron J. D. and Greenbowe T. J., (1986), What can we do about Sue: a case study of competence, J. Chem. Educ., 63, 528–531.
39. Hillyard C., Gillespie D. and Littig P., (2010), University students’ attitudes about learning in small groups after frequent participation, Act. Learn. Higher. Ed., 11, 9–20.
40. Horz H., Winter C. and Fries S., (2009), Differential benefits of situated instructional prompts, Comput. Human Behav., 25, 818–828.
41. IUPAC, (2014), Enthalpy, Compendium of Chemical Terminology – The Gold Book, IUPAC, International Union of Pure and Applied Chemistry, p. 514.
42. Johnstone A. H. and Al-Naeme F. F., (1991), Room for scientific thought? Int. J. Sci. Educ., 13, 187–192.
43. Kalyuga S., (2007), Enhancing instructional efficiency of interactive e-learning environments: a cognitive load perspective, Educ. Psychol. Rev., 19, 387–399.
44. Kapur M. and Toh L., (2015), Learning from Productive Failure, in Cho Y. H., Caleon I. S. and Kapur M. (ed.), Authentic problem solving and learning in the 21st century, Singapore: Springer, ch. 12.
45. Kirschner P. A., Sweller J. and Clark R. E., (2006), Why minimal guidance during instruction does not work: an analysis of the failure of constructivist, discovery, problem-based, experiential, and inquiry-based teaching, Educ. Psychol., 41, 75–86.
46. Low R. and Jin P., (2012), Self-regulated learning, in Seel N. M. (ed.), Encyclopedia of the Sciences of Learning, Boston, MA: Springer US, pp. 3015–3018.
47. Mangen A. and Velay J.-L., (2010), Digitizing literacy: reflections on the haptics of writing, in Zadeh M. H. (ed.), Advances in haptics, InTech, ch. 20, pp. 385–401.
48. Martinez M. E., (1998), What is problem solving? The Phi Delta Kappan, 79, 605–609.
49. McCalla J., (2003), Problem solving with pathways, J. Chem. Educ., 80, 92–98.
50. Moon A., Stanford C., Cole R. and Towns M., (2016), The nature of students' chemical reasoning employed in scientific argumentation in physical chemistry, Chem. Educ. Res. Pract., 17, 353–364.
51. Niaz M., (1996), Reasoning strategies of students in solving chemistry problems as a function of developmental level, functional M-capacity and disembedding ability, Int. J. Sci. Educ., 18, 525–541.
52. Nuckles M., Hubner S., Dumer S. and Renkl A., (2010), Expertise reversal effects in writing-to-learn, Instr. Sci., 38, 237–258.
53. Nyachwaya J., Warfa A. R. M., Roehrig G. H. and Schneider J. L., (2014), College chemistry students’ use of memorized algorithms in chemical reactions, Chem. Educ. Res. Pract., 15, 81–93.
54. Overton T. L. and Potter N., (2008), Solving open-ended problems, and the influence of cognitive factors on student success, Chem. Educ. Res. Pract., 9, 65–69.
55. Pea R. D., (2004), The social and technological dimensions of scaffolding and related theoretical concepts for learning, education, and human activity, J. Learn. Sci., 13, 423–451.
56. Pintrich P. R., Smith D. A. F., García T. and McKeachie W. J., (1991), A manual for the use of the motivated strategies questionnaire (MSLQ), AnnArbor, MI: University of Michigan, National Center for Research to Improve Postsecondary Teaching and Learning.
57. Polya G., (1945), How to solve it; a new aspect of mathematical method, Princeton, NJ: Prinston University.
58. Puntambekar S. and Hubscher R., (2005), Tools for scaffolding students in a complex learning environment: what have we gained and what have we missed? Educ. Psychol., 40, 1–12.
59. Pushkin D. B., (1998), Introductory students, conceptual understanding, and algorithmic success, J. Chem. Educ., 75, 809–810.
60. Pyburn D. T., Pazicni S., Benassi V. A. and Tappin E. E., (2014), The testing effect: an intervention on behalf of low-skilled comprehenders in general chemistry, J. Chem. Educ., 91, 2045–2057.
61. Randles C. A. and Overton T., (2015), Expert vs. novice: approaches used by chemists when solving open-ended problems, Chem. Educ. Res. Pract., 16, 811–823.
62. Reiser B. J., (2004), Scaffolding complex learning: the mechanisms of structuring and problematizing student work, J. Learn. Sci., 13, 273–304.
63. Rhee R. J., (2007), The Socratic method and the mathematical heuristic of George Pólya, St. John's L. Rev., 81, 881–898.
64. Roberts M. C. and Rosnov D., (2006), Information Processing Theory, in Salkind N. J. and Margolis L. (ed.), Encyclopedia of Human Development, Thousand Oaks, CA: Sage Publications, vol. 2, pp. 713–715.
65. Schraw G. and Dennison R. S., (1994), Assessing metacognitive awareness, Contemp. Educ. Psychol., 19, 460–475.
66. Selvaratnam M., (2011), Chemistry students’ competence throughout their BSc course in some problem-solving strategies, S. Afr. J. Chem., 64, 44–48.
67. Selvaratnam M. and Canagaratna S. G., (2008), Using problem-solution maps to improve students' problem-solving skills, J. Chem. Educ., 85, 381–385.
68. Shahat M. A., Ohle A., Treagust D. and Fischer H. E., (2013), Design, development and validation of a model of problem solving for Egyptian science classes, Int. J. Sci. Math. Educ., 11, 1157–1181.
69. Simon H. A. and Newell A., (1971), Human problem solving, Am. Psychol., 26, 145–159.
70. St Clair-Thompson H., Overton T. L. and Botton C., (2010), Information processing: a review of implications of Johnstone's model for science education, Res. Sci. Technol. Educ., 28, 131–148.
71. Sweller J., (1988), Cognitive load during problem solving: effects on learning, Cogn. Sci., 12, 257–285.
72. Sweller J., Ayres P. and Kalyuga S., (2011a), Cognitive Load Theory, New York: Springer.
73. Sweller J., Ayres P. and Kalyuga S., (2011b), Intrinsic and extraneous cognitive load, Cognitive Load Theory, New York: Springer, pp. 57–69.
74. Taasoobshirazi G., Bailey M. and Farley J., (2015), Physics metacognition inventory part II: confirmatory factor analysis and rasch analysis, Int. J. Sci. Educ., 37, 2769–2786.
75. Taber K., (2002), Chemical misconceptions: prevention, diagnosis and cure, Cambridge: Royal Society of Chemistry.
76. Tsaparlis G., (2005), Non-algorithmic quantitative problem solving in university physical chemistry: a correlation study of the role of selective cognitive factors, Res. Sci. Technol. Educ., 23, 125–148.
77. Usher E. L. and Pajares F., (2008), Self-efficacy for self-regulated learning, Educ. Psychol. Meas., 68, 443–463.
78. Van Ausdal R. G., (1988), Structured problem solving in kinematics, Phys. Teach., 26, 518–522.
79. Vygotsky L. S., (1978), Interaction between learning and development, in Cole M., John-Steiner V., Scribner S. and Souberman E. (ed.), Mind in society the development of higher psychological processes, Cambridge, MA: Harvard University Press, pp. 79–91.
80. Waddling R. E. L., (1988), Pictorial problem-solving networks, J. Chem. Educ., 65, 260–262.
81. Wheatley G. H., (1984), Problem solving in school mathematics, West Lafayette, IN: School Mathematics and Science Center, Purdue University.
82. Wood D., Bruner J. S. and Ross G., (1976), The role of tutoring in problem solving, J. Child Psychol. Psychiatry, 17, 89–100.
83. Woods D., (2000), An evidence-based strategy for problem solving, J. Eng. Educ., 89(4), 443–459.
84. Yu K. C., Fan S. C. and Lin K. Y., (2015), Enhancing students' problem-solving skills through context-based learning, Int. J. Sci. Math. Educ., 13, 1377–1401.
85. Yuriev E., Capuano B. and Short J. L., (2016), Crossword puzzles for chemistry education: learning goals beyond vocabulary, Chem. Educ. Res. Pract., 17, 532–554.
86. Zimmerman B. J., (2008), Investigating self-regulation and motivation: historical background, methodological developments, and future prospects, Am. Educ. Res. J., 45, 166–183.
87. Zimmerman B. J. and Pons M. M., (1986), Development of a structured interview for assessing student use of self-regulated learning strategies, Am. Educ. Res. J., 23, 614–628.
88. Zoller U., (2000), Teaching tomorrow's college science courses - are we getting it right? Preparing students to become informed and responsible participants in the decision-making process, J. Coll. Sci. Teach., 29, 409–414.
89. Zydney J. M., (2012), Scaffolding, in Seel N. M. (ed.), Encyclopedia of the Sciences of Learning, Boston, MA: Springer US, pp. 2913–2916.

---

Footnote

† Some of the evidence has been drawn from physics education literature, dealing with very similar issues.

---