The effect of additional methyl on the magnetic relaxation and toroidal moment of Dy₆ complex

Abstract

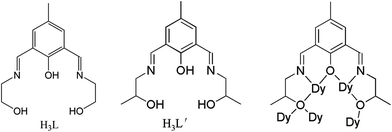
Two new μ₄-O bridged hexanuclear lanthanide complexes, [Dy₆L′₄(μ₄-O)(NO₃)₄]·4CH₃OH (1) and [Sm₆L′₄(μ₄-O)(CH₃COO)₄]·2CH₃OH (2), have been assembled by using methyl modified Schiff-base ligand H₃L′ (2,6-bis((2-hydroxypropylimino)methyl)-4-methylphenol). The complex 1 shares a similar μ₄-O bridged Dy₆ core as the parent Dy₆-2, while coordination geometries and magnetic interactions are slightly changed upon the modulation of the ligand, which results in distinct single-molecule magnetic (SMM) and single-molecule toroic (SMT) properties.

---

Introduction

The design and construction of single-molecule magnets (SMMs) has attracted increasing attention since the discovery of SMM behaviour,¹ because they have potential applications in processing and storing magnetic information at a molecular level.^2–7 Thus a large number of SMMs, including 3d complexes, 3d/4f complexes and 4f complexes, have been reported. Thereinto, 4f-based complexes are particularly appealing due to the strong magnetic anisotropy of 4f ions, and a flurry of groundbreaking results have been produced.^2,5,8–12 It is noteworthy that some cyclic Dy₃,^13–15 Dy₄,^16–18 and cyclic/local cyclic Dy₆ complexes^19–21 have exhibited SMM behaviours and toroidal moments that arise from a vortex arrangement of local magnetic moments of the individual Dy(III) centers. These systems are defined as single-molecule toroics (SMTs), which are promising candidates for future applications in quantum computing and information storage.^5,22 Toroidal moment is generally influenced by the molecular symmetry, local magnetic moment as well as magnetic interactions. However, the study on magneto-structural relationships of SMTs is rare.^16,21 Thus, it is of primary importance to design and construct a comprehensive (quasi)isostructural series of complexes to improve our knowledge of magneto-structural relationships.

In reality, most lanthanide SMMs have been synthesized by serendipitous approaches. Modulating the structure of complexes by design and choice of ligands is still a challenge. In general, one type of ligand affords a particular type of complexes possessing a certain nuclearity and topology.^23–26 In this regard, we have been interested to investigate the magneto-structural relationships of SMTs with one typic ligand. Recently, we have successfully assembled a Dy₆ SMTs with enhanced toroidal moment that was formed by linkage of two Dy₃ units (the complex is defined as Dy₆-2).²⁷ To go a step further, we modified slightly the Schiff-base ligand by adding a methyl, and assembled two μ₄-O bridged hexanuclear lanthanide clusters, [Dy₆L′₄(μ₄-O)(NO₃)₄]·4CH₃OH (1) and [Sm₆L′₄(μ₄-O)(CH₃COO)₄]·2CH₃OH (2). Though Dy₆-2 and complex 1 have similar structures, the coordination geometries and magnetic interactions are changed upon the slight modulation of the ligand. The coordination environment of Dy(III) ions will influence the local tensor of anisotropy and crystal-field splitting. Thus they exhibit dissimilar magnetic behaviour. Complex 1 shows SMM behaviour with obvious quantum tunnelling of the magnetization (QTM) and SMT property with large conventional magnetization.

Experimental section

General

All starting materials were of A.R. Grade and were used as commercially obtained without further purification. 2,6-Diformyl-4-methylphenol (DFMP) were prepared according to a previously published method.²⁸ The Schiff-base ligand H₃L′ (2,6-bis((2-hydroxypropylimino)methyl)-4-methylphenol) (shown in Scheme 1) was prepared by the in situ condensation of DFMP and (DL)-1-amino-2-propanol in a 1 : 2 ratio in methanol.

Scheme 1 Ligands H₃L and H₃L′ and the coordination formation of H₃L′.

Elemental analyses for C, H, and N were carried out on a Perkin-Elmer 2400 analyzer. Fourier transform IR spectra (4000–300 cm⁻¹) were measured using KBr pellets by a Fourier transform infrared spectrometer Nicolet 6700. All magnetization data were recorded on a Quantum Design MPMS-XL7 SQUID magnetometer equipped with a 7 T magnet. The variable-temperature magnetization was measured with an external magnetic field of 1000 Oe in the temperature range of 1.9–300 K. The experimental magnetic susceptibility data are corrected for the diamagnetism estimated from Pascal's tables and sample holder calibration.

X-ray crystallography

Suitable single crystals of 1 and 2 were selected for single-crystal X-ray diffraction analysis. Crystallographic data were collected at 185(2) K on a Bruker ApexII CCD diffractometer with graphite monochromated Mo-Kα radiation (λ = 0.71073 Å). The structure was solved by direct methods and refined on F² with full-matrix least-squares techniques using SHELXS-97 and SHELXL-97 programs.^29,30 The locations of Dy(III) ion were easily determined, and O, N, and C atoms were subsequently determined from the difference Fourier maps. Anisotropic thermal parameters were assigned to all non-hydrogen atoms. The H atoms were introduced in calculated positions and refined with a fixed geometry with respect to their carrier atoms. CCDC 1566095 and 1566096 contain the supplementary crystallographic data for this paper.†

Synthesis of [Dy₆L′₄(μ₄-O)(NO₃)₄]·4CH₃OH (1)

A solution of Dy(NO₃)₃·6H₂O (137.8 mg, 0.30 mmol) in 5 ml methanol was added in a solution of DFMP (0.15 mmol) and (DL)-1-amino-2-propanol (0.3 mmol) in 5 ml methanol in presence of triethylamine. The mixture was continual stirred at room temperature for 20 min. The resulting reaction mixture was sealed in an autoclave and maintained at 90 °C for 3 days, and then cooled slowly to room temperature to yield yellow single crystals suitable for X-ray diffraction. Yield: 33 mg, (27%, based on the metal). Elemental analysis (%) calcd for Dy₆C₆₄H₉₂N₁₂O₂₉: C, 31.14, H, 3.76, N, 6.81; found C, 30.96, H, 3.67, N, 6.50. IR (KBr, cm⁻¹): 2856 (w), 1646 (vs), 1549 (m), 1497 (m), 1452 (s), 1396 (m), 1368 (w), 1323 (s), 1281 (m), 1231 (m), 1082 (m), 1042 (s), 902 (w), 873 (w), 813 (m), 775 (m), 739 (w).

Synthesis of [Sm₆L′₄(μ₄-O)(CH₃COO)₄]·2CH₃OH (2)

A procedure similar to that for 1 was followed except that Dy(NO₃)₃·6H₂O was replaced by Sm(CH₃COO)₃·H₂O (0.3 mmol, 105.2 mg). Yield: 27 mg (23%, based on the metal salt). Elemental analysis (%) calcd for Sm₆C₇₀H₉₄N₈O₂₃: C, 36.27; H, 4.09; N, 4.83. Found: C, 36.16; H, 3.97; N, 4.53. IR (KBr, cm⁻¹): 2910 (w), 1644 (s), 1548 (vs), 1444 (s), 1395 (m), 1323 (m), 1231 (w), 1231 (w), 1138 (m), 1033 (s), 928 (w), 854 (w), 816 (w), 678 (w).

Results and discussion

To explore the effect of additional methyl groups on the lanthanide compound, the symmetrical Schiff-base H₃L′ (Scheme 1) was formed by the in situ condensation of DFMP and (DL)-1-amino-2-propanol (1 : 2) in methanol. Similar to the procedure for Dy₆-2, the reactions of in situ formed H₃L′ with Dy(NO₃)₃·6H₂O/Sm(CH₃COO)₃·H₂O in the presence of triethylamine under solvothermal condition produce block-shaped crystals of [Dy₆L′₄(μ₄-O)(NO₃)₄]·4CH₃OH (1) and [Sm₆L′₄(μ₄-O)(CH₃COO)₄]·2CH₃OH (2). The structures of 1 and 2 were established by single crystal X-ray diffraction. The crystal data and structure refinement are summarised in Table 1.

Table 1 Crystal data and structure refinement for complexes 1 and 2

Compound	1	2
Empirical formula	Dy6C64H92N12O29	Sm6C70H94N8O23
Fw (g mol^−1)	2468.50	2317.63
Crystal system	Triclinic	Monoclinic
Space group	P1̄	C2/c
a (Å)	12.4459(5)	18.6094(11)
b (Å)	13.8185(5)	17.218(1)
c (Å)	25.2852(10)	25.3390(14)
α (°)	82.073(1)	90
β (°)	81.870(1)	92.634(1)
γ (°)	75.400(1)	90
V (Å^3)	4142.1(3)	8110.5(8)
Z, ρcalcd (Mg m^−3)	2, 1.979	4, 1.898
F(000), Rint	2376, 0.0306	4504, 0.0744
R1, wR2 [I > 2σ(I)]	0.0455, 0.1085	0.0495, 0.1146
R1, wR2 (all data)	0.0750, 0.1271	0.0887, 0.1394
GOF	1.006	1.008

---

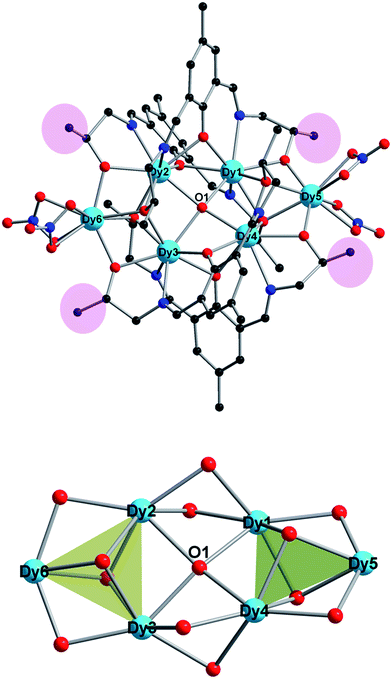
As shown in Fig. 1, complex 1 crystallizes in the triclinic space group P1̄ and consists of six Dy(III) ions, four (L′)³⁻ ligands, one μ₄-O anion and four NO₃⁻ anions. The core of 1, similar to the Dy₆-2, consists of two [Dy₃(μ₃-O)₂(μ₂-O)₂] triangular units linked by one μ₄-O²⁻ ion in an edge-to-edge arrangement. The triangular Dy₃ units in 1 are more equilateral than that in Dy₆-2 with Dy⋯Dy distances in range 3.4933(8)–3.4017(6) Å. The dihedral angle between the two Dy₃ planes in 1 is 30.101(12)° that is slightly larger than that in Dy₆-2 with 29.6568°.

Fig. 1 (Top) Structure of 1 with hydrogen atoms omitted for clarity. (Bottom) μ₄-O bridged hexanuclear core.

It is notable that all donors in ligand H₃L′ are coordinated, and each of the four (L′)³⁻ binds five Dy(III) ions utilizing their tridentate pocket (O₂N) along with bridging alkoxido oxygen (Scheme 1). This is different from some Schiff-base ligands that only coordinated partially.³¹ Two arms of alkoxido oxygens in ligands bridge distinctly: while one arm bridges two Dy(III) ions of one triangular edge, the other arm links three Dy(III) ions upon the other triangular unit. Additionally, the phenoxido oxygen bridges two Dy(III) ions from two triangular units. Therefore, alkoxido oxygens from four ligands fasten Dy₃ triangles, one μ₄-O anion and four phenoxido oxygens of ligands further strengthen the “Dy₃ + Dy₃” construction from center and periphery, respectively. This is the same with the reported Dy₆-2. Such a robust edge-to-edge arrangement will enhance the toroidal magnetic moment of the molecule.

The coordination spheres of Dy5 and Dy6 ions are completed respectively by two nitrate ions, and all Dy(III) ions are eight-coordinate (Fig. 2). This is different from Dy₆-2, where five Dy(III) centers are eight-coordinate and one Dy(III) ion is nine-coordinate. The exact geometries of all Dy(III) centers were determined by using the SHAPE 2.1 ^32,33 and the results are listed in Table S1.† For complex 1, Dy1/Dy3/Dy5/Dy6 centers are situated in distorted square antiprismatic geometries, and Dy2/Dy4 centers are situated in distorted triangular dodecahedron. For Dy₆-2, Dy1/Dy3/Dy5 centers are situated in distorted square antiprismatic geometries, Dy2/Dy4 centers are situated in distorted triangular dodecahedron, and Dy6 ion is in mono-capped square antiprism. The changes probably have a great impact on the magnetic anisotropy and further the magnetic properties.^34–37

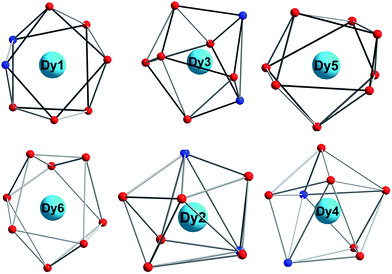Fig. 2 Coordination polyhedra (distorted square antiprism for Dy1, Dy3, Dy5 and Dy6; distorted triangular dodecahedron for Dy2 and Dy4) for six Dy³⁺ ions in 1.

In addition, the Dy–O bond lengths fall in the range of 2.235(6)–2.478(7) Å with the average bond of 2.37 Å, the Dy–N bond lengths fall in the range of 2.457(8)–2.490(8) Å with the average bond of 2.47 Å. Those average bonds in complex 1 are similar to that of Dy₆-2 (average bonds are 2.48 and 2.38 Å for Dy–O and Dy–N, respectively). This indicates the metal–ligand interactions of complex 1 and Dy₆-2 are similar.

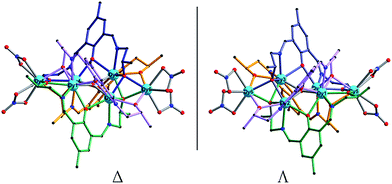
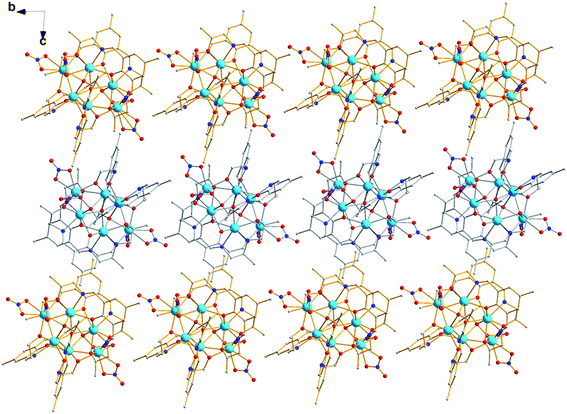
In [Dy₆L′₄(μ₄-O)(NO₃)₄] core, the four ligands are twisted along the C–N bonds, and each ligand straddles two triangles to coordinate five Dy(III) ions, resulting in formation of quadruple-stranded helicates (Fig. 3).^38–40 Significantly, two stereoisomers of right- (Δ) and left-hand (Λ) configurations are in crystal, forming a racemic mixture. The packing arrangement of 1 reveals that Δ- and Λ-configuration helicates are alternate along the crystallographic a axis (Fig. 4).

Fig. 3 Two stereoisomers of right- (Δ) and left-hand (Λ) configurations in 1.

Fig. 4 Crystal packing of 1 along the crystallographic a axis showing the stereoisomers.

Complex 2 crystallizes in the monoclinic space group C2/c, the asymmetric unit contains four Sm(III) ions, two (L′)³⁻ ligands and two CH₃COO⁻ ions. The structure of 2 is essentially isomorphous to 1 (Fig. S1†), consists of a μ₄-O²⁻ ion linked two triangular units in an edge-to-edge arrangement, where Sm⋯Sm distances are in range of 3.4439(10)–3.6234(96) Å, the dihedral angle between the two Sm₃ planes in 2 is 28.176° that is smaller than that in 1. In the asymmetric unit, Sm2 and Sm3 ions are eight-coordinate with 6O₂N, and both display distorted triangular dodecahedral geometries based on SHAPE 2.1 (Fig. S2 and Table S2†). The coordination spheres of Sm1 and Sm4 ions are filled respectively by two CH₃COO⁻ ions, forming eight-coordinate Sm1 and Sm4 ions with 8O. The exact geometries of Sm1 and Sm4 ions are both distorted square antiprisms based on SHAPE 2.1. In addition, the Sm–O bond lengths fall in the range of 2.331(6)–2.506(8) Å, the Sm–N bond lengths fall in the range of 2.507(9)–2.552(9) Å.

In [Sm₆L′₄(μ₄-O)(CH₃COO)₄] core, each of four ligands coordinates five Sm(III) ions and straddles two triangular units, producing formation of quadruple-stranded helicates (Fig. S3†). As shown in Fig. S4,† the two stereoisomers of Δ and Λ configurations form a racemic mixture, which can be seen in molecular structures and crystal packing.

Magnetic studies

The direct current (dc) susceptibility studies of complexes 1 and 2 were investigated under a 1000 Oe field in the temperature range 2–300 K (Fig. 5). At room temperature, the χ_MT value of complex 1 is 86.37 cm³ K mol⁻¹. The value is in agreement with the expected theoretical value (85.02 cm³ K mol⁻¹) for six free Dy(III) ions (₆H^15/2, S = 5/2, L = 5, g = 4/3, C = 14.17 cm³ K mol⁻¹). On cooling, χ_MT decreases throughout the whole temperature range: firstly, χ_MT decreases monotonously down to 50 K, then decreases abruptly to 21.03 cm³ K mol⁻¹ at 2.0 K. The thermal variation of the χ_MT indicates the progressive depopulation of the excited Stark sublevels of Dy(III) ions and/or weak molecular magnetic interactions.^41,42 Actually, this profile of χ_MT is similar but higher to that of Dy₆-2, and the minimum is larger than that of Dy₆-2 (6.59 cm³ K mol⁻¹ at 2.0 K), which indicates the weaker magnetic interaction in complex 1. The large minimum (21.03 cm³ K mol⁻¹) also indicates the magnetic ground state of complex 1 is different from the net toroidal moment.^16,20,43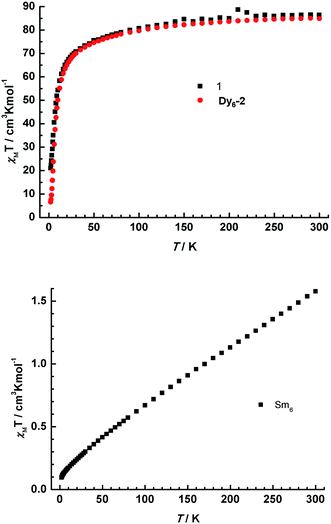

Fig. 5 (Top) Plots of χ_MT vs. T for 1 (black square) and Dy₆-2 (red circle) in a dc field of 1000 Oe (2–300 K); (bottom) plots of χ_MT vs. T for 2 in a dc field of 1000 Oe.

For complex 2, the χ_MT value (Fig. 5) observed at room temperature is 1.58 cm³ K mol⁻¹, which is significantly larger than the theoretical one. This is attributed to the first or even the higher excited states (₆H^7/2, ₆H^9/2,…, ₆H^15/2) of the Sm(III) ion that can be populated obviously at room temperature.⁴⁴ On cooling, the χ_MT value decreases continuously to a minimum of 0.10 cm³ K mol⁻¹ at 2.0 K.

The field dependence of magnetization (M) was measured between 1.9 and 5 K. As shown in Fig. 6, it is obviously that M under variable field at 1.9 K shows a “S” shape, which is consistent with SMTs.²² The peak (d(M/M_s)/dH) vs. field suggests inflection around 12 kOe. The inflection is less evident than that in Dy₆-2. M reaches a maximum value 33.83 μ_B at about 45 kOe, which is far lower than the expected saturation value of 60 μ_B for six noninteracting Dy(III) ions. This can be mostly attributed to crystal-field effects and the possible weak antiferromagnetic interactions that make the low-lying excited states accessible. Meanwhile, the non-superposition of the M vs. H/T data implies the presence of significant magnetic anisotropy. The static magnetic behaviours, including the dc susceptibility and the field dependence of M, reveal that the ground state of 1 could be toroidal magnetic moment and the conventional magnetic moment should be larger than that of Dy₆-2.²²

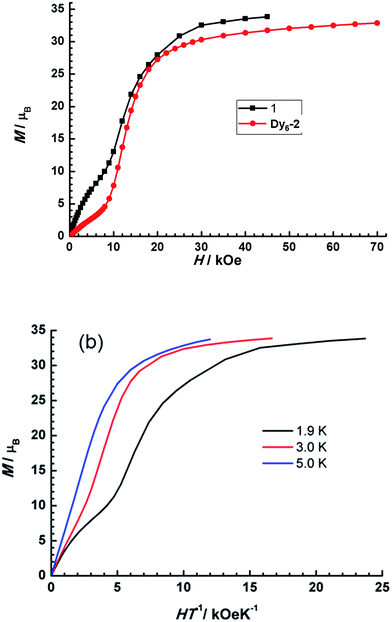Fig. 6 (Top) Field dependence of magnetization at 1.9 K for 1 and Dy₆-2. (Bottom) M versus H/T plots for 1 at 1.9 K, 3 K and 5 K.

Furthermore, the anisotropy axes of complex 1 were calculated using the Magellan program^45–47 based on an electrostatic model (Fig. 7 and Table S3†). The results indicate that complex 1 shows toroidal moment in both Dy₃ units. This agrees with the magnetic properties. The ab initio calculations^48–50 are planned to provide quantitative evaluation of the anisotropy axes and Dy–Dy coupling interactions.

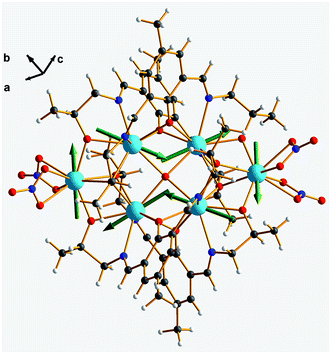Fig. 7 Ground-state magnetic anisotropy of complex 1. The green arrows represent the orientations of the anisotropic axes for each Dy(III) ion, as calculated by the electrostatic model.

To compare the magnetic relaxation been Dy₆-2 and 1, the dynamics of the magnetization of 1 were investigated using alternating current (ac) susceptibility measurements (Fig. 8). Under zero dc field, the variable-temperature ac susceptibility of 1 shows the temperature dependence maximum, which signals the freezing of the spins by the anisotropy barrier and is typical for SMM behaviour. Both 1 and Dy₆-2 show broad peak in the out-of-phase susceptibility, but the former appears at 7 K that is lower than that of Dy₆-2 (at about 9 K). This indicates lower effective energy barrier for complex 1. Obviously, unlike the Dy₆-2, the rise in the out-of-phase and in-phase susceptibility on cooling at low temperatures indicates the presence of QTM for 1, which may be due to the weak magnetic interaction that is too weak to suppress the QTM.^51–53 This agrees well with dc magnetic susceptibility that indicates weaker magnetic interaction in complex 1.

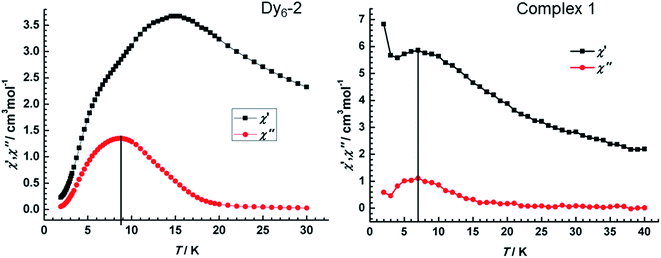Fig. 8 Temperature dependence of the out-of phase and in-phase ac susceptibility for Dy₆-2 (left) and 1 (right) at 1000 Hz under zero dc field.

The reported isomorphous Dy₆-2 displayed impressive dynamic magnetic properties with effective suppression of QTM and remarkable toroidal moment. However, obvious QTM is present and toroidal moment is less distinct in 1. Comparing the structure data of complex 1 and Dy₆-2, they have the identical metal–ligand interaction, but distinctive coordination geometries mainly on Dy6 ion. For Dy₆-2, Dy6 ion is nine-coordinate with a mono-capped square antiprism. While Dy6 center in complex 1 is eight-coordinate situated in distorted square antiprismatic geometries, which is due to the steric hindrance from additional methyl groups of ligands (Fig. 1). The changes in coordination geometries have a great impact on the orientation of the easy axes. Consequently, the toroidal moment retains in complex 1 but with a large conventional magnetization, SMM behaviour also is observed but with a non-ignorable QTM. It should be note that the weaker magnetic interaction in complex 1 could not suppress the QTM.

Conclusions

In conclusion, methyl modified Schiff-base ligand has been successfully used to synthesize two new hexanuclear lanthanide complexes, [Dy₆L′₄(μ₄-O)(NO₃)₄]·4CH₃OH (1) and [Sm₆L′₄(μ₄-O)(CH₃COO)₄]·2CH₃OH (2), under solvothermal condition. Single crystal X-ray diffraction studies revealed that complex 1 has a μ₄-O bridged Dy₆ core, μ₄-O bridged two [Dy₃(μ₃-O)₂(μ₂-O)₂] triangular units in an edge-to-edge arrangement, that is the same as the parent Dy₆-2. While the coordination geometries especially on Dy6 site and magnetic interactions change, which result in distinct magnetic properties. Complex 1 shows SMM behaviour with a non-ignorable QTM and SMT behaviour with a large conventional magnetization. The work provides an efficient strategy to probe the magneto-structural relationships of SMTs, further to design the special SMTs and SMMs.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research work was supported by the National Natural Science Foundation of China (no. 21401034), the Natural Science Foundation of Heilongjiang Province (QC2015008), the Innovative Talents Training Plan for Young Undergraduates in Heilongjiang Province (UNPYSCT-2016074), and the Open Funds of the State Key Laboratory of Rare Earth Resource Utilization (RERU2017018).

References

1. R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141–143.
2. D. N. Woodruff, R. E. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148.
3. S. Sanvito, Chem. Soc. Rev., 2011, 40, 3336–3355.
4. P. Zhang, L. Zhang and J. Tang, Dalton Trans., 2015, 44, 3923–3929.
5. S. Liu, T. J. Cui, Q. Xu, D. Bao, L. Du, X. Wan, W. X. Tang, C. Ouyang, X. Y. Zhou, H. Yuan, H. F. Ma, W. X. Jiang, J. Han, W. Zhang and Q. Cheng, Light: Sci. Appl., 2016, 5, e16076.
6. M. Gu, X. Li and Y. Cao, Light: Sci. Appl., 2014, 3, e177.
7. N. Papasimakis, S. Thongrattanasiri, N. I. Zheludev and F. J. Garcia de Abajo, Light: Sci. Appl., 2013, 2, e78.
8. P. Zhang, Y.-N. Guo and J. Tang, Coord. Chem. Rev., 2013, 257, 1728–1763.
9. Y.-S. Meng, S.-D. Jiang, B.-W. Wang and S. Gao, Acc. Chem. Res., 2016, 49, 2381–2389.
10. H. Wang, B.-W. Wang, Y. Bian, S. Gao and J. Jiang, Coord. Chem. Rev., 2016, 306, 195–216.
11. Y.-J. Liang, F. Liu, Y.-F. Chen, X.-J. Wang, K.-N. Sun and Z. Pan, Light: Sci. Appl., 2016, 5, e16124.
12. C. C. Lin, W.-T. Chen, C.-I. Chu, K.-W. Huang, C.-W. Yeh, B.-M. Cheng and R.-S. Liu, Light: Sci. Appl., 2016, 5, e16066.
13. L. Ungur, W. V. d. Heuvela and L. F. Chibotaru, New J. Chem., 2009, 33, 1224–1230.
14. S. Xue, X.-H. Chen, L. Zhao, Y.-N. Guo and J. Tang, Inorg. Chem., 2012, 51, 13264–13270.
15. J. Tang, I. Hewitt, N. T. Madhu, G. Chastanet, W. Wernsdorfer, C. E. Anson, C. Benelli, R. Sessoli and A. K. Powell, Angew. Chem., Int. Ed., 2006, 45, 1729–1733.
16. J. F. Wu, S. Y. Lin, S. Shen, X. L. Li, L. Zhao, L. Zhang and J. K. Tang, Dalton Trans., 2017, 46, 1577–1584.
17. C. Das, S. Vaidya, T. Gupta, J. M. Frost, M. Righi, E. K. Brechin, M. Affronte, G. Rajaraman and M. Shanmugam, Chem.–Eur. J., 2015, 21, 15639–15650.
18. S. Biswas, S. Das, T. Gupta, S. K. Singh, M. Pissas, G. Rajaraman and V. Chandrasekhar, Chem.–Eur. J., 2016, 22, 18532–18550.
19. S. K. Langley, B. Moubaraki, C. M. Forsyth, I. A. Gass and K. S. Murray, Dalton Trans., 2010, 39, 1705–1708.
20. L. Ungur, S. K. Langley, T. N. Hooper, B. Moubaraki, E. K. Brechin, K. S. Murray and L. F. Chibotaru, J. Am. Chem. Soc., 2012, 134, 18554–18557.
21. X.-L. Li, J. Wu, J. Tang, B. Le Guennic, W. Shi and P. Cheng, Chem. Commun., 2016, 52, 9570–9573.
22. L. Ungur, S.-Y. Lin, J. Tang and L. F. Chibotaru, Chem. Soc. Rev., 2014, 43, 6894–6905.
23. L. Zhang, P. Zhang, L. Zhao, S.-Y. Lin, S. Xue, J. Tang and Z. Liu, Eur. J. Inorg. Chem., 2013, 2013, 1351–1357.
24. R. J. Blagg, L. Ungur, F. Tuna, J. Speak, P. Comar, D. Collison, W. Wernsdorfer, E. J. L. McInnes, L. F. Chibotaru and R. E. P. Winpenny, Nat. Chem., 2013, 5, 673–678.
25. J. Wu, L. Zhao, M. Guo and J. Tang, Chem. Commun., 2015, 51, 17317–17320.
26. S. Biswas, S. Das, J. Acharya, V. Kumar, J. van Leusen, P. Kogerler, J. M. Herrera, E. Colacio and V. Chandrasekhar, Chem.–Eur. J., 2017, 23, 5154–5170.
27. S.-Y. Lin, W. Wernsdorfer, L. Ungur, A. K. Powell, Y.-N. Guo, J. Tang, L. Zhao, L. F. Chibotaru and H.-J. Zhang, Angew. Chem., Int. Ed., 2012, 51, 12767–12771.
28. R. R. Gagne, C. L. Spiro, T. J. Smith, C. A. Hamann, W. R. Thies and A. K. Shiemke, J. Am. Chem. Soc., 1981, 103, 4073–4081.
29. G. M. Sheldrick, SHELXS-97, Program for Crystal Structure Solution, University of Göttingen, Germany, 1997.
30. G. M. Sheldrick, SHELXL-97, Program for Crystal Structure Refinement, University of Göttingen, Germany, 1997.
31. S.-Y. Lin, C. Wang and Z. Xu, RSC Adv., 2016, 6, 103035–103041.
32. E. C. Mazarakioti, J. Regier, L. Cunha-Silva, W. Wernsdorfer, M. Pilkington, J. K. Tang and T. C. Stamatatos, Inorg. Chem., 2017, 56, 3568–3578.
33. M. Llunell, D. Casanova, J. Girera, P. Alemany and S. Alvarez, SHAPE, version 2.1.
34. M. E. Boulon, G. Cucinotta, J. Luzon, C. Degl'innocenti, M. Perfetti, K. Bernot, G. Calvez, A. Caneschi and R. Sessoli, Angew. Chem., Int. Ed., 2013, 52, 350–354.
35. S.-Y. Lin, J. F. Wu, C. Wang, L. Zhao and J. K. Tang, Eur. J. Inorg. Chem., 2015, 2015, 5488–5494.
36. Y. Bi, Y.-N. Guo, L. Zhao, Y. Guo, S.-Y. Lin, S.-D. Jiang, J. Tang, B.-W. Wang and S. Gao, Chem.–Eur. J., 2011, 17, 12476–12481.
37. G.-J. Chen, Y.-N. Guo, J.-L. Tian, J. Tang, W. Gu, X. Liu, S.-P. Yan, P. Cheng and D.-Z. Liao, Chem.–Eur. J., 2012, 18, 2484–2487.
38. S.-Y. Lin, G.-F. Xu, L. Zhao, Y.-N. Guo, Y. Guo and J. Tang, Dalton Trans., 2011, 40, 8213–8217.
39. A. Stephenson and M. D. Ward, Chem. Commun., 2012, 48, 3605–3607.
40. L. Zhang, P. Zhang, L. Zhao, J. Wu, M. Guo and J. Tang, Dalton Trans., 2016, 45, 10556–10562.
41. D. Aguila, L. A. Barrios, V. Velasco, L. Arnedo, N. Aliaga-Alcalde, M. Menelaou, S. J. Teat, O. Roubeau, F. Luis and G. Aromi, Chem.–Eur. J., 2013, 19, 5881–5891.
42. S.-Y. Lin, X.-L. Li, H. Ke and Z. Xu, CrystEngComm, 2015, 17, 9167–9174.
43. P.-H. Guo, J.-L. Liu, Z.-M. Zhang, L. Ungur, L. F. Chibotaru, J.-D. Leng, F.-S. Guo and M.-L. Tong, Inorg. Chem., 2012, 51, 1233–1235.
44. Molecular Magnetism, ed. O. Kahn, VCH Publishers, New York, 1993.
45. N. F. Chilton, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and A. Soncini, Nat. Commun., 2013, 4, 2551.
46. S.-D. Jiang and S.-X. Qin, Inorg. Chem. Front., 2015, 2, 613–619.
47. Y. Peng, V. Mereacre, A. Baniodeh, Y. Lan, M. Schlageter, G. E. Kostakis and A. K. Powell, Inorg. Chem., 2016, 55, 68–74.
48. L. Ungur and L. F. Chibotaru, Inorg. Chem., 2016, 55, 10043–10056.
49. L. F. Chibotaru and L. Ungur, in Programs SINGLE_ANISO and POLY_ANISO, University of Leuven, 2006.
50. L. Ungur and L. F. Chibotaru, Phys. Chem. Chem. Phys., 2011, 13, 20086–20090.
51. Y.-N. Guo, X.-H. Chen, S. Xue and J. Tang, Inorg. Chem., 2011, 50, 9705–9713.
52. Y.-N. Guo, G.-F. Xu, W. Wernsdorfer, L. Ungur, Y. Guo, J. Tang, H.-J. Zhang, L. F. Chibotaru and A. K. Powell, J. Am. Chem. Soc., 2011, 133, 11948–11951.
53. J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Nat. Chem., 2011, 3, 538–542.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 1566095 and 1566096. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c7ra09619d

---