Formation of environmentally-persistent free radicals (EPFR) on α-Al₂O₃ clusters

Abstract

Alumina oxides assume prominent catalytic applications in a wide range of industrial processes. However, alumina surfaces also serve as potent promoters in the heterogeneous formation of the notorious environmentally-persistent free radicals (EPFR). Herein, we theoretically examine dissociative adsorption mechanisms of phenol molecules over Al₂O₃ and hydrated Al₂O₃·nH₂O clusters that mimic dehydrated and hydrated alumina structures, respectively. We show that fission of the phenol's hydroxyl bond over dehydrated alumina systematically incurs lower energy barriers in reference to the hydrated structures. A 1,2-water elimination step marks the most feasible channel in the interaction of phenol with hydrated clusters. The relevance of the acidity sites to the catalytic activity of alumina is clearly supported by the finding that the catalytic activity of the alumina surface in producing the phenoxy/phenolate species reversibly correlates with the degree of hydroxyl coverage. Desorption of adsorbed phenolates requires sizable desorption energies, and thus is expected to facilitate surface-mediated condensation into dioxin-like moieties.

---

1. Introduction

Alumina oxide represents one of the most important catalytic and catalyst-support materials,^1–3 for chemical reactions. It also finds direct applications in dielectric materials, substrates for electronics, packing materials and radiation dosimeters.^4,5 Over the last two decades, the surface chemistry of alumina oxides has been a distinct research topic in catalysis chemistry. Most of these studies have focused on the surface/water interface conditions, where the chemistry of the surface is greatly affected and accordingly alters its reactivity and catalytic performance.^6–8 The interaction of alumina surfaces with water molecules^6,9–14 results in water- and hydroxyl-covered surfaces, in which the degree of coverage is highly sensitive to temperature.¹⁵ Heating and cooling processes can reversibly either add or remove hydroxyl groups from the surfaces, as confirmed experimentally by IR and NMR measurements.^16,17 For instance, X-ray diffraction data by Dyer et al.¹⁸ revealed the formation of Al(OH)₃ on the γ-Al₂O₃ surface, which disappeared after heating to 473.15 K. This has also been confirmed by Raman and infrared spectroscopy where several sharp peaks in the region around 3600 cm⁻¹ have been observed after hydration of the γ-Al₂O₃ powder. X-ray photoemission experiments by Liu et al.¹⁹ pointed out to water dissociation; most likely at surface defect sites.

It has become evident that,^3,15,20,21 the differences of the coordination of Al atoms of the alumina surface lead to form different terminal hydroxyl termination or interactive phases. An experimental study by Pimentel and McClellan²² revealed that, surfaces encompasses two main categories of surface hydroxyl groups; isolated hydroxyl groups with a sharp infrared bands (>3600 cm⁻¹), and self-associated hydroxyl groups with a broad, intense band (<3600 cm⁻¹). Apart from this, self-associated hydroxyl groups differ from the isolated groups in the presence of the hydrogen bond connection between adjacent moieties. Detailed examination of chemical sites on Al₂O₃ surface^23,24 confirmed the findings of Pimentel and McClellan.²² Overall, five different classes of isolated hydroxyl groups have been detected by IR spectroscopy.^21,24 Knözinger et al.³ attribute the difference in vibrational frequencies among these classes to the coordination number of alumina (i.e.; either tetrahedral and/or octahedral coordination).

The chemical makeup (i.e.; adsorption and decomposition) of the hydroxyl groups over alumina surface constitutes a key factor in clarifying the reactive/catalytic nature of alumina. As stated earlier, heating can reversibly remove the hydroxyl groups from the alumina surface,^16,17,25 leading to the formation of Lewis acid–base pair sites, and thus increases the catalytic activity of the surface. Along a similar line of enquiry, Ballinger and Yates²⁶ have performed a detailed investigation into the correlation between Al–OH group removal and the number of Lewis acid sites via CO molecular adsorption. The authors have found that, heating leads to the decomposition of the associated hydroxyl groups, leaving only isolated hydroxyl groups on the surface at a temperature range of 475–800 K. This has been viewed as the driving force of the catalytic activity of alumina, either via hydrogen bonding to the hydroxyl group and/or via lone pair donation to Lewis acid sites. A study by Hendriksen et al.²⁷ measure the heat of adsorption of water on both α- and γ-alumina powders via immersion calorimetry. It has been indicated that, the heat of adsorption on both termination depends primarily on the degree of hydration prior to water adsorption.

Over a wide range of operational pressure and temperatures, alumina exhibits a variety of crystallographic structures such as α phase or corundum, which is the most thermodynamically stable phase,²⁸ and other alumina phases such as δ, β, κ, η, θ and γ.^29,30 Literature density function theory (DFT) investigations have considered water adsorption and dissociation over α-Al₂O₃ surfaces from the dry to the fully hydroxylated surfaces. A detailed analysis and discussion on the subject was presented by Wang et al.³¹ The authors have found that, a fully hydrated alumina α-Al₂O₃ (0001) surface, when the surface Al atom is triply hydroxylated, exhibits relatively inertness toward further hydroxylation. In an insightful analysis into the interaction of water molecules and a α-Al₂O₃ (0001) surface, Wirth and Saalfrank³² found that 1,2-dissociation pathway is the most kinetically feasible mechanism, where Al surface atoms are hydroxylated and the nearby oxygen atoms are protonated.

Recent theoretical investigations addressed the interaction of hydrated and dehydrated α-Al₂O₃ surfaces towards different molecules.^33–35 Shukla and Hill³³ have performed a detailed investigation of the molecular interaction of 2,4,6-trinitrotoluene (TNT) molecule with the α-Al₂O₃ (0001) surface demonstrating that TNT acquires strong covalent interaction in a parallel orientation with the surface. The same group³⁴ found that molecular adsorption of TNT over hydroxylated alumina surface is much weaker when compared to the dehydrated surface. Similarly, Rohmann et al.³⁵ investigated molecular interaction of carbon monoxide with hydroxylated alumina surface, reporting that molecular CO exhibits strong interaction with a 25% degree of hydroxylated surface and this interaction is significantly stronger when compared with that over the clean dehydrated alumina. In a follow-up study on H₂S removal via γ-Al₂O₃ surfaces with different hydroxyl coverage, Ren et al.³⁶ revealed that, the bonding strength of H₂S on hydrated alumina surface is lower than that the over a dehydrated termination. For example, calculated binding energy for 8.9 OH per nm² hydroxyl coverage for γ-Al₂O₃ (110) amounts to −68 kJ mol⁻¹ whereas the corresponding value of the dehydrated surface stands at −114 kJ mol⁻¹. XPS studies by Kelber et al.³⁷ investigated the interaction between Cu and the hydrated α-Al₂O₃ (0001) surface to report an enhanced interaction of copper to the surface of alumina owing to the presence of a surface hydrated layer. There is a rather limited literature account on reactions of hydrocarbons on alumina clusters. Most of relevant studies have considered extended surfaces of alumina.^34,35,38 Nonetheless, it has been shown that alumina clusters encompass effective catalytic active sites present on surfaces; i.e., the surface Al–O bonds.^39,40 Therefore, alumina clusters in many theoretical studies (i.e. (Al₂O₃)_n=4) are being applied as representative models for both α-Al₂O₃ and γ-Al₂O₃ surfaces. Alumina clusters imitate both the experimental measurements and DFT surface properties. Additionally, clusters^41,42 were shown to illustrate an effective stability against relaxation often encountered in extended alumina surfaces.

Phenol molecule is among the most commonly discussed precursors for the synthesis of poly chlorinated dibenzo-p-dioxins and dibenzofurans (PCDD/Fs).^43–45 Heterogeneous formation of PCDD/Fs via surface-mediated coupling of chlorinated phenols were investigated on many oxide systems, including Al₂O₃,^46,47 Co₃O₄,⁴⁶ CuO,^48,49 TiO₂ (ref. 47) and Fe₂O₃.⁵⁰ In our recent study,⁵¹ we theoretically investigate the interaction of phenol molecule with the dehydrated α-Al₂O₃ (0001) surface. We have found that, alumina surface is catalytically very active in producing phenolate (i.e., surface-bounded phenoxy) with a modest activation energy of 43 kJ mol⁻¹, thus, signifying as an accessible route for the formation of persistent surface-bound radicals. However, when considering the temperature range of the cooling-down zone of the combustor (i.e.; 746–1146 K), all models of alumina (i.e.; polymorphs, surfaces and\or clusters) assume different hydration coverage. Therefore, the effect of the degree of hydration, on dissociative adsorption of phenol, can play an important role in attaining a detailed understanding of the catalytic activity of the surface. Thus, it is very important to shed light into the generation of the environmentally persistent free radicals (EPFRs)^52,53 on alumina surface with varying hydroxyl coverages.

In summary, the current work is part of our ongoing effort to reveal mechanistic and kinetic factors dictating the catalytic role of alumina surfaces in surface-mediated formation of phenoxy-type EPFR. The study provides a detailed investigation of the interaction of a phenol molecule with different hydration coverage of alumina clusters and therefore offers important insights into the role of the surface adsorbed water in the catalytic activity of alumina toward the generation of adsorbed phenoxy radicals. The present study expands on our recent investigation,⁵¹ in which we considered a dehydrated α-Al₂O₃ (0001) surface. Overall, this study has a three-fold aim; (i) to report modes of interaction of phenol with different hydration coverages of alumina clusters, (ii) to compare between the catalytic activity of hydrated and dehydrated alumina clusters toward the formation of the adsorbed phenolate via two distinct pathways; namely direct fission of the phenol' O–H bond and elimination of water molecules and to (iii) to construct a simplified kinetic model for the conversion of phenol into adsorbed phenoxy radicals.

2. Methodology

DMol³ program^54,55 performs all structural optimization, energy calculations and vibrational frequencies based on the generalized gradient approximation (GGA) of the Perdew–Burke–Ernzerhof (PBE) functional.⁵⁶ The computational methodology comprises Grimme dispersion correction,⁵⁷ together with the basis set of double numerical plus polarization (DNP). Total energy and forces on each atom converge with tolerance to less than 10⁻⁶ eV and 10⁻⁴ eV Å⁻¹, respectively.

We computed the binding energies (E_b) for the adsorption based on the energies of a phenol/Al₂O₃ system E_{cluster+phenol}, the clean alumina cluster E_cluster, and an isolated phenol molecule E_phenol:

E_b = E_{cluster+phenol} − E_cluster − E_phenol (1)

Reaction rate constants were estimated based on the conventional transition state theory (TST),⁵⁸ we fit reaction rate constants to the two-parameters Arrhenius formula, k(T) = A exp(−E_a/(RT), over the temperature range of 300 K to 1000 K, according to:

where: k_B is Boltzmann's constant, h signifies Plank's constant, R is the universal gas constant. Calculated vibrational frequencies enable to calculate thermodynamic functions; i.e., entropies and enthalpies. ΔS^≠ and ΔH^≠ stand for temperature-depended entropy and enthalpy of activation, correspondingly. σ_e represents the reaction degeneracy number. DMol³ computes entropy values based on well-documented statistical thermodynamics equations.⁵⁹ The enthalpy (at the desired temperature) has been competed relatively to the zero-point energy at 0 K.

3. Results and discussions

3.1. Water adsorption on Al₂O₃ cluster

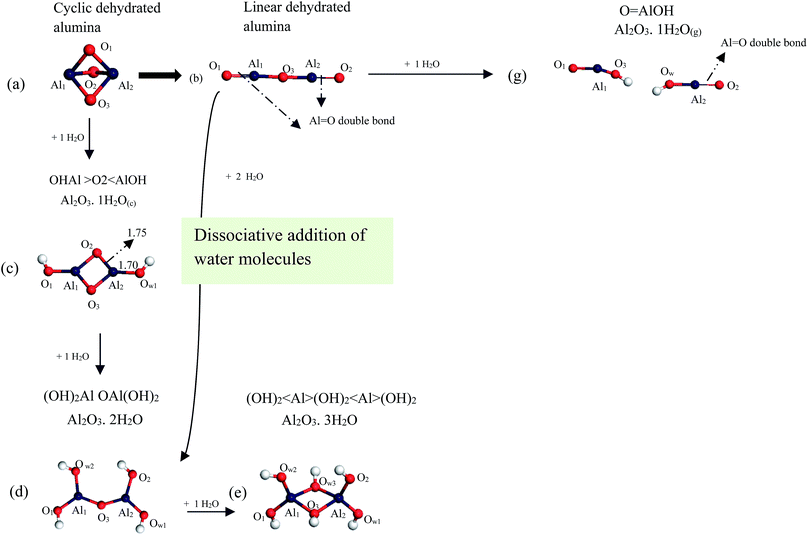
Starting with dehydrated alumina clusters, Fig. 1 displays two water-free geometrical monomers of alumina near-cyclic AlO₃Al that adapt D_3h symmetry, and a linear O=Al–O–Al=O chain structure. As illustrated in Fig. 1, the cyclic dehydrated alumina, AlO₃Al, contains three Al–O bonds with distances of ∼1.82 Å. This structure was found to be energetically less stable⁶⁰ than the linear chain structure due to the repulsion between the two cations (Al³⁺). In the latter configuration, alumina adapts a linear structure with one bridging and two non-bridging oxygen atoms. Calculated bond angle and bond lengths, in both structures, are in agreement with the literature analogous values.^60,61

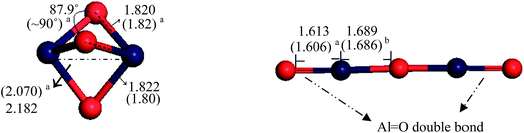Fig. 1 Optimised geometries for dehydrated Al₂O₃ clusters with the main geometrical parameters (in Å). Bond lengths in parentheses signify the corresponding experimental or theoretical values from the literature a,⁶⁰ b.⁶¹

Moving on now to consider how the geometries of alumina cluster are compared with those in alumina surface. Fig. 2 displays top and side views of α-Al₂O₃ (0001) surface (i.e., the thermodynamically most stable alumina surface^62,63) and the D_3h structure. As can be seen from the figure, Al–O bonds lengths in both structures are within 0.01 Å. This close agreement serves to testify that considered cyclic dehydrated structure contains similar active sites to those present in the surface.

Fig. 2 Geometrical comparison between Al₂O₃ cyclic cluster and the α-Al₂O₃ (0001) surface.

A study by Johnson and Panas⁶⁰ examine water adsorption and hydrolysis on molecular Al oxides and hydroxides solvation versus cluster formation. They found that, dehydrated alumina clusters, both cyclic and linear chain, reacts with water molecules through accessible energy barriers in the range of 33–110 kJ mol⁻¹. Further addition of water molecules leads to a series of Al₂O₃·nH₂O structures.

Fig. 3 illustrates mechanism of successive addition of water molecules to the dehydrated cluster of alumina (i.e.; cyclic and linear clusters). Starting with the cyclic structure of alumina, D_3h, the addition of a water molecule to the Al₂–O₁ bond results in the formation of the Al₂O₃·1H₂O_(c) cluster (c) which has been reported to be the most stable structure among the various configurations of Al₂O₄H₂ clusters.⁶⁰ Typically, this structure assumes cis and trans configurations, with very similar thermodynamic stability.⁶⁰ Thus, we have performed our subsequent calculations considering the cis planar molecule configurations with the C_2v symmetry as it is marginally more thermodynamically stable than its trans counterpart; by 3 kJ mol⁻¹. Calculated Al₂–O₂ and Al₂–O_w1 bond lengths amount to 1.75 Å and 1.70 Å, respectively. These values concur very well with the corresponding literature values by Johnson and Panas;⁶⁰ i.e., 1.75 Å and 1.69 Å, respectively.

Fig. 3 Structures of the Al₂O₃ + nH₂O.

Turning now to the linear chain structure, the addition of water can proceed either via cluster Al=O double bond site or via cleaving the central Al–O–Al bond.⁶⁰ This results in the formation of the Al₂O₃·2H₂O cluster (d) and O=AlOH (g), respectively. Considering the double bond pathway; further addition of a water molecule produces the cluster Al₂O₃·3H₂O (e), with the C_2h symmetry. Energetics for the formation of the hydrated alumina structures in Fig. 3 has been reported by Johnson and Panas.⁶⁰ The authors found that formation of (c) and (e) structures display an exothermic process with calculated enthalpies of −310 kJ mol⁻¹ and −184 kJ mol⁻¹, respectively. The formation of structure (g) is slightly endothermic with a low activation enthalpy at 33 kJ mol⁻¹.⁶⁰

3.2. Reaction of phenol with dehydrated alumina cluster

We studied the interaction of a phenol molecule with the two dehydrated alumina clusters (i.e.; cyclic and linear clusters in Fig. 3a and b). Two different reactions have been considered, denoted as pathway a and pathway b. These pathways involve the interaction of phenol molecule with cyclic and linear dehydrated alumina clusters, respectively. The optimized geometries for the reactants, transition states and products are presented in Fig. 4. Table 1 lists energies for physisorbed configurations and dissociative structures as well as prominent interatomic distances for all pathways.

Fig. 4 Optimised geometries for species in the reaction of phenol with dehydrated alumina clusters. Values (in kJ mol⁻¹) of energies are in reference to physisorbed reactant.

Table 1 Binding energies (using eqn (1)) and geometrical parameters for phenol interaction with Al₂O₃ and Al₂O₃·nH₂O clusters

Structure	Phenol-cluster spacing in the reactant (Å)	O–H phenol bond distance in the reactant (Å)	Al–O bond distance in the reactant (Å)	Binding (for reactants) and reaction (for products) energies (kJ mol^−1)
Pathway a	1.909	0.982	1.788	Ra = −129
				Pa = −241
Pathway b	2.260	0.985	2.260	Rb = −152
				Pb = −345
Pathway c1	2.007	0.997	1.793	Rc1 = −143
				Pc1 = −225
Pathway c2	1.979	0.991	1.739	Rc2 = −147
				Pc2 = −167
Pathway c3	1.997	0.990	1.742	Rc3 = −129
				Pc3 = 17
Pathway g	1.940	1.009	1.630	Rg = −166
				Pg = −360
Pathway d	1.725	1.004	1.733	Rd = −81
				Pd = −74
Pathway e	1.75	1.007	1.738	Re = −99
				Pe = −135

---

We first consider the interaction along the cyclic alumina structure, pathway a. Fig. 4(a) shows, phenol molecule physically adsorbed on the cluster through a van der Waals interaction between O_phenol atom and Al_cluster atom with a binding distance of 1.909 Å. The interaction proceeds via fission of the hydroxyl's bond over Al–O cluster bond where phenoxy moiety attaches to Al_cluster and deducted hydrogen atom binds to O_cluster atom. This has resulted in the optimised dissociation product P_a. Hence, the length of this bond increases by 13.4% with respect to that of the clean cyclic cluster (1.822 Å). This value concurs with results obtained in our recent study⁵¹ of the dissociative adsorption of phenol on the dehydrated α-Al₂O₃ (0001) surface (11.9%). In comparison, Wang et al.³¹ showed that the elongation of Al–O bond increased by 6.4% upon the dissociation of a water molecule over this Al–O bond.

The reaction is highly exothermic with an energy barrier of only 41 kJ mol⁻¹. Calculated binding energy of the reactant, R_a, and the product, P_a, are −129 kJ mol⁻¹ and −241 kJ mol⁻¹, respectively (based on eqn (1) in reference to separated reactants). These values also agree with the results obtained in our recent study.⁵¹ We found that, phenol molecule strongly interacts with the dehydrated α-Al₂O₃ (0001) surface via physisorbed binding energies in the range of −127 kJ mol⁻¹ to −202 kJ mol⁻¹, leading to the formation of an adsorbed phenolate with a modest activation energy of 48 kJ mol⁻¹.

Considering the second reaction, where phenol molecule interacts with the linear cluster chain of alumina (pathway b), phenol molecule physically adsorbs on the active Al=O double bond site of the cluster with a calculated binding distance of 2.26 Å. The O–H bond length of phenol molecule in R_b (Fig. 4) increases from the equilibrium 0.97 Å distance in the gas phase to 1.016 Å. The exothermic formation of the product P_b requires a trivial activation energy of 10 kJ mol⁻¹ (via direct fission of the phenol's O–H bond catalysed by the cluster's Al–O linkage). Calculated binding energies of the reactant, R_b, and the product, P_b, are −152 kJ mol⁻¹ and −345 kJ mol⁻¹, respectively (in reference to the separated reactants, Fig. 4). P_b appears relatively more stable than P_a. Activation barrier via pathway b is lower by 31 kJ mol⁻¹ than that along pathway a. This indicates that, the linear chain cluster of alumina is catalytically more active in producing phenolate than the cyclic dehydrated cluster.

Test computations employing the dependence of the reactivity of alumina cluster on the cluster size has been considered. We investigated physisorption and chemisorption interactions of phenol with the larger (Al₂O₃)₄ reported in the literature.⁶⁴ Stable optimised structures are shown in Fig. 5 calculated binding energies of the physisorbed and the chemisorbed structures are −150 kJ mol⁻¹ and −315 kJ mol⁻¹, respectively, both values are in a good agreement with the corresponding values we obtained for the smaller dehydrated clusters (i.e., −129 to −152 kJ mol⁻¹ and −241 to −345 kJ mol⁻¹, respectively). Furthermore, binding energies obtained for the larger (Al₂O₃)₄ cluster are consistent with the calculated binding energies in our recent study⁵¹ for the interaction of phenol with a seven-layer slab of the 2 × 2 (0001) surface alumina (−127 kJ mol⁻¹ to −202 kJ mol⁻¹). Thus, it can be concluded that energies of the surface interaction of phenol with alumina surface do not display sensitivity toward the cluster size. The same observation has been observed by Pan et al.⁶⁵ in their study of the reaction of 2-chlorophenol over the dehydrated and hydroxylated silica clusters with (SiO₂)₃ and (SiO₂)₈ clusters. They have found that binding energies of reactants and products using both structures are within (0.4–17.4) kJ mol⁻¹.

Fig. 5 Optimised geometries for the reaction of phenol with the (Al₂O₃)₄ cluster.

3.3. Reaction of phenol with Al₂O₃·nH₂O cluster

We now turn our attention to investigate the interaction of a phenol molecule with hydrated alumina clusters entailing different hydroxylation coverages, (i.e., all the hydrated alumina clusters shown in Fig. 3). The detailed mechanism of the interaction is presented in Scheme 1. Fig. 6 depicts optimised geometries of reactants, transition states, and products; along with their energy profiles.

Scheme 1 Reaction of phenol with the hydrated Al₂O₃ cluster. The highlighted reactions proceed via H₂O elimination (presenting H₂O elimination mechanism over the same Al–OH bond (1,2 non-bridging)).

Fig. 6 Optimised geometries involved in the reaction of phenol with c and g clusters. Values (in kJ mol⁻¹) of energies are in reference to physisorbed reactants.

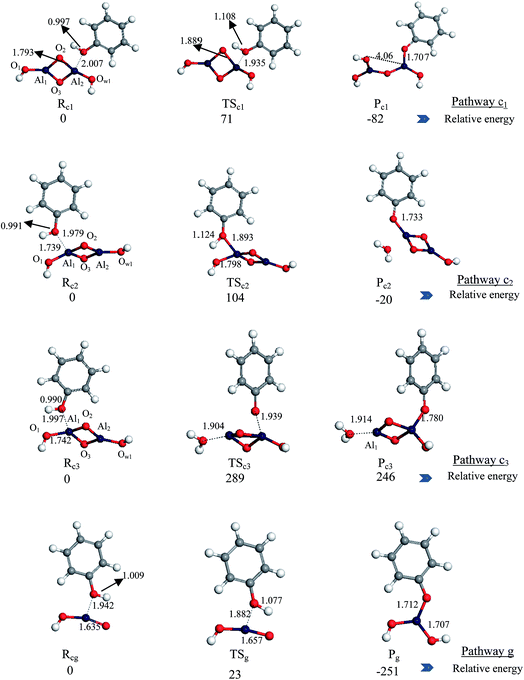
First, we have studied the interaction of a phenol molecule with the (c) structure, Fig. 3. Three possible pathways have been considered, denoted as c₁, c₂ and c₃ in Scheme 1. As Scheme 1 demonstrates, these reaction pathways characterise (i) fission of hydroxyl's bond over the same Al₂–O₂ bond (bridging bond), (ii) H₂O elimination mechanism over the same Al–OH bond (1,2 non-bridging) and (iii) H₂O elimination route over two Al–OH bonds (1,4 non-bridging linkage), respectively (Fig. 3 illustrates atomic numberings). The reaction is initiated by the physisorbed-type interaction between O_phenol and Al_cluster via binding spacings of 2.007 Å, 1.979 Å and 1.997 Å in the reactants R_c1, R_c2 and R_c3, respectively (Fig. 6). Calculated binding energies of the three reactants stand at −143 kJ mol⁻¹, −147 kJ mol⁻¹ and −129 kJ mol⁻¹, respectively (in reference to the separated reactants). Regarding to the structural changes induced to the cluster; we observe that Al₂–O₂ bridging bond in Fig. 6, R_c1 elongates by 2.4% when compared with the corresponding value in the Fig. 3(c) structure while Al₁–O₁ in R_c2 and Fig. 6, R_c3 increases by 8.1% and 8.2%, respectively. Dissociative desorption of phenol via these pathways leads to the formation of P_c1, P_c2 and P_c3 (Fig. 6) intermediates with reaction energies of −225 kJ, −167 kJ mol⁻¹ and 17 kJ mol⁻¹, respectively. The thermodynamic penalty associated with the product P_c3 most likely stem from the low coordinated Al₁ that display a 2-fold coordination.⁶⁶

Next, we examine the dissociative adsorption of phenol over the Fig. 3(g) structure. The reaction proceeds via the active Al=O double bond site of the cluster. We found a slight increase in the O–H bond length of the physisorbed phenol in pathway g (1.009 Å, Scheme 1), in reference to the gas phase value (0.97 Å). The corridor g in Scheme 1 characterises fission of the O–H bond in the phenol molecule in a noticeably exothermic reaction of 360 kJ mol⁻¹. The physisorbed state Fig. 6 (R_g) in this channel resides 166 kJ mol⁻¹ below the separated reactants. Compared to Fig. 3(d), the size of hydrated alumina cluster (g) with one water molecule is smaller and it has a planner structure. Therefore, as temperature increases, molecules move faster and they are more likely to collide and hence positively affect the collision frequency, A.

Reaction pathways c₁, c₂ and g proceeds via modest energy barriers of 71 kJ mol⁻¹, 104 kJ mol⁻¹ and 23 kJ mol⁻¹, respectively, whereas pathway c₃ incurs a very sizable energy barrier of 289 kJ mol⁻¹. Three concluding remarks can be drawn from values in Fig. 6. First, within Al₂O₃·1H₂O system (i.e.; pathways: g, c₁, c₂, c₃), as expected, reaction pathway g is the most favourable channel, presumably due to the presence of the active Al=O double bond site. Second, phenol dissociation catalysed/accompanied with water elimination (pathways c₂ and c₃) is more energy demanding than phenol decomposition through surface-assisted fission of its hydroxyl O–H bond (pathways c₁). For instance, the activation energy in pathway c₁ is lower by 33 kJ mol⁻¹ than that along pathway c₂. Third, the activation energy in reaction pathway c₃ as well as the calculated binding energy of the product P_c3 are higher when contrasted with the corresponding values in pathway c₂, this indicates that water elimination preferentially occurs at the same A-OH linkage; i.e., 1.2-elimination step rather than at different A-OH sites (i.e., 1,4-elimination). This has prompted us to exclude this mechanism (i.e.; pathway c₃) from further consideration in our subsequent discussion.

Phenol interaction with higher hydrated alumina clusters (Al₂O₃·2H₂O (d) and Al₂O₃·3H₂O Fig. 3(e)) is presented in pathways d and e in Scheme 1, with Fig. 7 illustrates optimised geometries and relative energies for species involved in pathways d and e.

Fig. 7 Optimised geometries involved in the reaction of phenol with d and e clusters. Values (in kJ mol⁻¹) of energies are in reference to physisorbed reactants.

Water elimination via pathways d and e (Scheme 1) results in the formation of a phenolate moiety via activation barriers of 110 kJ mol⁻¹ and 142 kJ mol⁻¹, respectively. Pathways d and e characterise dissociative adsorption of phenol via water elimination through 1,2-route; i.e., attachment of the phenoxy'O at the Al atom and the simultaneous departure of the OH group attached to the same Al atom with the hydroxyl'H as a water molecule. Higher energy barrier for pathway e in reference to pathways c₂ and d can be rationalised in energy penalty required for the rupture of the Al–O linkage in the former. The degree of hydration of alumina; could be viewed as a factor that partially dictates the catalytic activity of alumina via controlling the surface-acid properties.⁶⁷ In this regard, Al atom in structure (e) (the Al₂O₃·3H₂O system), is coordinated by four hydroxyl groups, whereas Al atom in c₂ and d, is less coordinated presenting more acidic structures as illustrated in Scheme 2. From the scheme, we can see that, the addition of water molecule in the structure dblocks the Lewis active site and accordingly decreases the catalytic activity of the cluster. This view is supported by Digne et al.⁶⁸ who argued that the lower the Al atom coordination, the stronger – the Lewis acidity. Calculated atomic Mullikan charges on Al atom for (c), (d) and (e) were shown to have more positive values on the four coordinated Al atom of 1.69e (structure (e)) when compared to the three coordinated Al atom (i.e., 1.52e in structures (c) and (d)). A positive correlation is found between the calculated energy barrier and calculated Mulliken atomic charges; i.e., the higher the atomic charges on Al atom, the higher energy required to break Al–OH bond toward generating water molecule (accompanied with the dissociative adsorption of phenol). Thus, the observed increase in barrier for pathway e in reference to pathways c₂ and d correlates with partial atomic charges; i.e., a prominent electronic descriptor that determines the acidity character.

Scheme 2 Structure of acidic and basic site of alumina cluster.

Overall, we can compare between hydrated and dehydrated alumina from two different perspectives. First, within fission of hydroxyl's bond reactions over the same Al–O bond; contrasting pathway Fig. 6 c₁ with pathway a reveals that, the energy barrier required in hydrated alumina clusters (i.e.; c₁ = 71 kJ mol⁻¹) are significantly higher than that over the dehydrated one (i.e.; a = 41 kJ mol⁻¹), respectively. Second, saturation of Al=O double bonds in the course of the hydroxylation of cluster b into d (refer to Fig. 3) significantly increases the barrier required for water elimination from only 10 kJ mol⁻¹ to 110 kJ mol⁻¹. Together, these findings indicate that dehydrated alumina cluster are more active in producing phenolate than hydrated alumina clusters. This observation agrees with the findings of Pan et al.⁶⁵ who found that, the dehydrated silica cluster (with the presence of two ends of S=O double bonds sites) produces chlorophenolate from 2-chlorophenol through an energy barrier of only 21 kJ mol⁻¹, compared with 70 kJ mol⁻¹ over the hydrated cluster (the same cluster after the two Si=O double bonds sites become saturated).

The most obvious finding to emerge from inspection of data in Table 1 is that, in both hydrated and dehydrated alumina, the dissociated product via Al=O double bonds site of the cluster is more stable than that leading to Al–O bond cleaving. For example, reaction energies that mark the formation of P_g and P_b (double bonds sites) amount to −360 kJ mol⁻¹ and −345 kJ mol⁻¹, respectively, while the analogous energies of P_c1 and P_a are −225 kJ mol⁻¹ and −241 kJ mol⁻¹, (A–O bond fission), respectively. This finding is in agreement with those obtained by Pan et al.⁶⁵ The authors found that dissociative adsorption of 2-chlorophenol through rupture of its hydroxyl's bond over a S=O double bonds site forms more stable product by 136 kJ mol⁻¹ than that leading to Si–O bond cleaving.

Desorption of the phenolate moiety from both dehydrated alumina cluster and hydrated alumina clusters, was found to be highly endothermic by 334–373 kJ mol⁻¹. This finding is in accord with those reported in our recent study for the interaction of phenol⁵¹ and chlorophenol⁶⁹ molecules over alumina surfaces and silica clusters, 394 kJ mol⁻¹ and 379 kJ mol⁻¹ respectively. This profound stability of phenolate enables it to undergo bimolecular reactions via the so called Eley–Rideal (ER) and Langmuir–Hinshelwood (LH) mechanisms⁴⁸ to produce dibenzo-p-dioxin and dibenzofuran; respectively. In alternative corridor, decomposition of phenolate on the surface is expected to initiate the formation of soot.

3.4. Kinetic consideration

We conclude the study by implementing a microkinetic analysis of the abovementioned reactions in this study. Fig. 8 represents Arrhenius plots while Table 2 displays the calculated reaction rate parameters. Within the considered temperature limit, reactions pathway c₃ displays the highest activation energy and relatively high dependence on temperature. For all reactions, the fitted Arrhenius energy of activation (E_a) largely reflects corresponding energy barriers presented in Fig. 3, 6 and 7. Calculations of the conversion-temperature profiles were carried out based on a simplified plug flow reactor (PFR) model. The material balance equations were solved by Polymath software:⁷⁰

Fig. 8 Arrhenius plots for the studied reactions.

Table 2 Arrhenius kinetic parameters

Reaction	Ea (kJ mol^−1)	A (s^−1)
Pathway a	27	2.76 × 10^13
Pathway b	7	7.50 × 10^13
Pathway c1	67	5.60 × 10^13
Pathway c2	90	6.35 × 10^11
Pathway c3	285	2.09 × 10^14
Pathway g	19	1.50 × 10^16
Pathway d	102	3.29 × 10^10
Pathway e	136	6.28 × 10^14

---

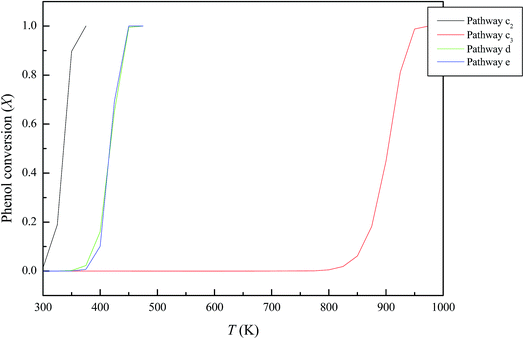
In the considered reaction, (A → B), A and B represents the molecularly adsorbed phenol and the dissociative structures; respectively. r denotes the reaction rate, F symbolizes the molar flow rate of phenol in mol s⁻¹, and W stands for alumina catalyst weight in kg. The reaction is considered to be first order with respect to phenol. The model utilises reaction rate constants given in Table 2. The catalytic destruction of phenol molecule over Al₂O₃·nH₂O catalysts as a function of temperature is presented in Fig. 9. It can be seen that all hydrated coverage of alumina clusters exhibits a highly catalytic destruction activity for phenol molecule, evident by high conversion at low temperatures. Calculated temperature of 90% destruction of phenol molecule (T₉₀%) occurs at 350 K, 925 K, 425 K and 425 K for pathways c₂, c₃, d and e, respectively. To the best of our knowledge, literature provides no conversion values pertinent to interaction of phenol with α-Al₂O₃. Considering the very high desorption energy for phenolate, formation of gas phase phenoxy should be hindered. The LR and LH mechanisms operated by the highly stable surface-bounded phenolate species, remains largely speculative.

Fig. 9 Conversion values for phenol molecule decomposition over Al₂O₃·nH₂O clusters.

4. Conclusion

This study sets out to assess the effect of surface acidity on the interaction of alumina with phenol molecules. Interaction of phenol molecule with dehydrated alumina clusters proceeds via fission of the hydroxyl's bond over either Al–O single bond or Al=O double bond. Clusters with the active Al=O double bond (i.e., b) are catalytically more active in producing phenolate when compared to structures where all bonds are saturated (i.e., a, Al–O single bonds). Overall, c channels that proceeds through fission of the hydroxyl's bond over Al–O (i.e.; c₁) are more feasible than those proceeding via H₂O elimination routes (i.e.; c₂ and c₃). The most obvious finding to emerge from this study is that adding water molecules increases the coordination number of Al atoms and acts to black available Lewis acid sites for uptake of phenol molecules. Simplified kinetics model suggests dissociation of phenol molecules at low temperatures; however, subsequent desorption of adsorbed phenolate into gas phase phenoxy radicals is hindered by very sizable desorption energies.

Conflicts of interest

There are no conflicts of interests to declare.

Acknowledgements

This work has been supported by the Australian Research Council (ARC) (Project no. DP140104493). The National Computational Infrastructure (NCI), Australia and Pawsey Supercomputing Centre in Perth are also acknowledged grants of computational time. N. A. and J. A. greatly appreciated Murdoch University for the award of a postgraduate scholarship.

References

1. K. Tanabe, Catalysis science and technology, Springer-Verlag, Berlin, 1981.
2. H.-P. Boehm and H. Knözinger, Catalysis science and technology, Springer, Berlin, 1983.
3. H. Knözinger and P. Ratnasamy, Catal. Rev.: Sci. Eng., 1978, 17, 31–70.
4. W. H. Gitzen, Alumina as a ceramic material, American Ceramic Society, Columbus, 1970.
5. R. H. French, J. Am. Ceram. Soc., 1990, 73, 477–489.
6. P. J. Eng, T. P. Trainor, G. E. Brown Jr, G. A. Waychunas, M. Newville, S. R. Sutton and M. L. Rivers, Science, 2000, 288, 1029–1033.
7. J. W. Elam, C. E. Nelson, M. A. Cameron, M. Tolbert and S. M. George, J. Phys. Chem. B, 1998, 102, 7008–7015.
8. K. C. Hass, W. F. Schneider, A. Curioni and W. Andreoni, J. Phys. Chem. B, 2000, 104, 5527–5540.
9. S. E. Mason, C. R. Iceman, T. P. Trainor and A. M. Chaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 125423–125439.
10. D. Argyris, T. Ho, D. R. Cole and A. Striolo, J. Phys. Chem. C, 2011, 115, 2038–2046.
11. K. C. Hass, W. F. Schneider, A. Curioni and W. Andreoni, Science, 1998, 282, 265–268.
12. A. C. Thomas and H. H. Richardson, J. Phys. Chem. C, 2008, 112, 20033–20037.
13. L. Zhang, C. Tian, G. A. Waychunas and Y. R. Shen, J. Am. Chem. Soc., 2008, 130, 7686–7694.
14. H. A. Al-Abadleh and V. H. Grassian, Langmuir, 2003, 19, 341–347.
15. D. B. Mawhinney, J. A. Rossin, K. Gerhart and J. T. Yates, Langmuir, 1999, 15, 4789–4795.
16. O. Glemser and G. Rieck, Angew. Chem., 1956, 68, 182.
17. O. Glemser, Angew. Chem., 1961, 73, 785–805.
18. C. Dyer, P. J. Hendra, W. Forsling and M. Ranheimer, Spectrochim. Acta, Part A, 1993, 49, 691–705.
19. P. Liu, T. Kendelewicz, G. E. Brown, E. J. Nelson and S. A. Chambers, Surf. Sci., 1998, 417, 53–65.
20. J. B. Peri and R. B. Hannan, J. Phys. Chem., 1960, 64, 1526–1530.
21. J. Peri, J. Phys. Chem., 1965, 69, 220–230.
22. G. C. Pimentel and A. L. McClellan, The Hydrogen Bond, Freeman, San Francisco, 1960.
23. T. H. Ballinger and J. Yates, J. Phys. Chem., 1992, 96, 1417–1423.
24. M. I. Zaki and H. Knözinger, Mater. Chem. Phys., 1987, 17, 201–215.
25. D. D. Eley, H. Pines and P. B. Weisz, Advances in Catalysis, Academic Press, New York, London, 1966.
26. T. H. Ballinger and J. T. Yates Jr, J. Phys. Chem., 1992, 96, 1417–1423.
27. B. A. Hendriksen, D. R. Pearce and R. Rudham, J. Catal., 1972, 24, 82–87.
28. J. M. McHale, A. Navrotsky and A. J. Perrotta, J. Phys. Chem. B, 1997, 101, 603–613.
29. C.-K. Lee, E. Cho, H.-S. Lee, K. S. Seol and S. Han, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 245110–245117.
30. I. Levin and D. Brandon, J. Am. Ceram. Soc., 1998, 81, 1995–2012.
31. B. Wang, H. Hou, Y. Luo, Y. Li, Y. Zhao and X. Li, J. Phys. Chem. C, 2011, 115, 13399–13411.
32. J. Wirth and P. Saalfrank, J. Phys. Chem. C, 2012, 116, 26829–26840.
33. M. K. Shukla and F. Hill, J. Phys. Chem. C, 2013, 117, 13136–13142.
34. M. K. Shukla and F. Hill, J. Comput. Chem., 2014, 35, 1977–1985.
35. C. Rohmann, J. B. Metson and H. Idriss, Phys. Chem. Chem. Phys., 2014, 16, 14287–14297.
36. R.-P. Ren, X.-W. Liu, Z.-J. Zuo and Y.-K. Lv, RSC Adv., 2015, 5, 55372–55382.
37. J. A. Kelber, C. Niu, K. Shepherd, D. R. Jennison and A. Bogicevic, Surf. Sci., 2000, 446, 76–88.
38. S. D. Chakarova-Käck, Ø. Borck, E. Schröder and B. I. Lundqvist, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 155402.
39. E. Fernández, R. Eglitis, G. Borstel and L. Balbás, Comput. Mater. Sci., 2007, 39, 587–592.
40. A. D. Zdetsis and A. B. Kunz, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 32, 6358.
41. J. Wittbrodt, W. Hase and H. Schlegel, J. Phys. Chem. B, 1998, 102, 6539–6548.
42. S. Biswas, A. Pramanik and P. Sarkar, Nanoscale, 2016, 8, 10205–10218.
43. M. Altarawneh and B. Z. Dlugogorski, Environ. Sci. Technol., 2015, 49, 2215–2221.
44. M. Altarawneh, M. W. Radny, P. V. Smith, J. C. Mackie, E. M. Kennedy, B. Z. Dlugogorski, A. Soon and C. Stampfl, J. Chem. Phys., 2009, 130, 184505–184512.
45. M. Altarawneh and B. Z. Dlugogorski, Phys. Chem. Chem. Phys., 2015, 17, 1822–1830.
46. Y. Qian, M. Zheng, W. Liu, X. Ma and B. Zhang, Chemosphere, 2005, 60, 951–958.
47. M. C. Patterson, N. D. Keilbart, L. W. Kiruri, C. A. Thibodeaux, S. Lomnicki, R. L. Kurtz, E. D. Poliakoff, B. Dellinger and P. T. Sprunger, Chem. Phys., 2013, 422, 277–282.
48. S. Lomnicki and B. Dellinger, J. Phys. Chem. A, 2003, 107, 4387–4395.
49. S. Lomnicki and B. Dellinger, Proc. Combust. Inst., 2002, 29, 2463–2468.
50. S. Nganai, S. Lomnicki and B. Dellinger, Environ. Sci. Technol., 2008, 43, 368–373.
51. N. W. Assaf, M. Altarawneh, I. Oluwoye, M. Radny, S. M. Lomnicki and B. Z. Dlugogorski, Environ. Sci. Technol., 2016, 50, 11094–11102.
52. B. Dellinger, S. Lomnicki, L. Khachatryan, Z. Maskos, R. W. Hall, J. Adounkpe, C. McFerrin and H. Truong, Proc. Combust. Inst., 2007, 31, 521–528.
53. M. C. Patterson, C. A. Thibodeaux, O. Kizilkaya, R. L. Kurtz, E. D. Poliakoff and P. T. Sprunger, Langmuir, 2015, 31, 3869–3875.
54. B. Delley, Chem. Phys., 1990, 92, 508–517.
55. B. Delley, Chem. Phys., 2000, 113, 7756–7764.
56. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
57. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
58. K. J. Laidler and M. C. King, J. Phys. Chem., 1983, 87, 2657–2664.
59. R. H. Fowler and E. A. Guggenheim, Statistical Thermodynamics, 1941.
60. J. R. T. Johnson and I. Panas, Phys. Chem. Chem. Phys., 2001, 3, 5482–5488.
61. R. Li and L. Cheng, Comput. Theor. Chem., 2012, 996, 125–131.
62. I. Manassidis and M. J. Gillan, J. Am. Ceram. Soc., 1994, 77, 335–338.
63. M. Gautier-Soyer, F. Jollet and C. Noguera, Surf. Sci., 1996, 352, 755–759.
64. S. M. Woodley, Proc. R. Soc. A, 2011, 467, 2020–2042.
65. W. Pan, W. Zhong, D. Zhang and C. Liu, J. Phys. Chem. A, 2011, 116, 430–436.
66. R. Cavallotti, J. Goniakowski, R. Lazzari, J. Jupille, A. Koltsov and D. Loison, J. Phys. Chem. C, 2014, 118, 13578–13589.
67. S. Yoshida, in Theoretical Aspects of Heterogeneous Catalysis, Van Nostrand-Reinhold, New York, 1990.
68. M. Digne, P. Sautet, P. Raybaud, P. Euzen and H. Toulhoat, J. Catal., 2004, 226, 54–68.
69. S. Mosallanejad, B. Z. Dlugogorski, E. M. Kennedy, M. Stockenhuber, S. M. Lomnicki, N. W. Assaf and M. Altarawneh, Environ. Sci. Technol., 2016, 50, 1412–1418.
70. POLYMATH is copyrighted by M. Shacham, B. M. Cutlip and M. Elly, POLYMATH, http://www.polymath-software.com/, accessed Feb 23, 2016.

---