Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Time–temperature superposition in the grain and grain boundary response regime of A2HoRuO6 (A = Ba, Sr, Ca) double perovskite ceramics: a conductivity spectroscopic analysis
Saswata Halder *a,
Alo Duttab and
T. P. Sinhaa
*a,
Alo Duttab and
T. P. Sinhaa
aDepartment of Physics, Bose Institute, 93/1, Acharya Prafulla Chandra Road, Kolkata 700009, India. E-mail: saswata.h88@gmail.com
bDepartment of Condensed Matter Physics and Material Sciences, S. N. Bose National Centre for Basic Sciences, Block-JD, Sector-III, Salt Lake, Kolkata 700098, India
First published on 11th September 2017
Abstract
The pursuit for a universal scaling factor to satisfy the time–temperature superposition principle for grain and grain boundary responses has been explored in the ac conductivity domain for polycrystalline double perovskite oxides A2HoRuO6 (AHR; A = Ba, Sr, Ca). The samples show different structural phases, from cubic to monoclinic, with decreasing ionic radii. The degree of distortion in the materials is correlated to the strength of the bonding through the bond valence sum (BVS) formalism. The conductivity spectra for all of the samples obey the power law variation. The contribution of different microstructural domains to the conduction process is established. Thermal variation of the dc resistivity points towards a gradual crossover from nearest neighbour to variable range hopping. The activation energies obtained from the dc conductivity, hopping frequency and relaxation frequency show close correlation between the conduction and relaxation mechanisms. The scaled conductivity curves for AHR display the presence of two different conduction processes with dissimilar activation energies in the grain boundary and the grain response regimes. It is thus concluded that a single scaling parameter is insufficient to satisfy the time temperature superposition principle universally when two different thermally activated regions are present simultaneously in the materials.
1. Introduction
The solid state chemistry of 4d Ru-based materials has always been an intriguing subject to the scientific community since the discovery of spin-glass behavior in Sr2FeRuO6.1–3 Ru-based double perovskite oxides (DPOs) have emerged as a fertile ground for the exploration of novel transport phenomena resulting from a delicate balance between localised and delocalised electron behaviour driven by spin–orbit coupling (SOC), coulombic interactions (U) and crystal field interactions.4–15 In the case of DPO with Ru at the B-site, an increase in orbital overlap with the decrease in unit cell volume has been shown to increase the Ru-d electron delocalisation.16 The sensitivity of the narrow itinerant 4d band of Ru is dependent on the degree of hybridization between the Ru-t2g and the O-2p orbitals along with the distortions present in the octahedral environment of Ru. Since the B-site of a DPO provides a dominant influence in determining the transport properties of the material, Ru at the octahedral B-site plays a major role in determining the electrical and magnetic properties of the host material. This research article focusses on the octahedral distortion induced electrical response of a specific DPO series A2HoRuO6 (AHR; A = Ba, Sr, Ca) in the radio frequency regime.The crystal and magnetic properties of AHR have been studied in details by many research groups. The crystal structure and magnetic properties of Ba2HoRuO6 (BHR) was studied by Hinatsu et al.17 The crystal structure was reported to be cubic Fm3m. The magnetic susceptibility and specific heat measurements showed the presence of two anomalies at 22 K and 50 K due to the magnetic ordering of Ho3+ ions and Ru5+ ions respectively. The crystal structure and magnetic properties of Sr2HoRuO6 (SHR) was explored by Doi et al.18 SHR was shown to crystallize in a monoclinic space group P21/n, with an antiferromagnetic transition at 36 K and a high Weiss constant. Neutron diffraction measurements suggested that both BHR and SHR have long range antiferromagnetic ordering with a type I arrangement of both the Ho3+ and Ru5+ ions. The crystal structure of Ca2HoRuO6 (CHR) was reported by Battle et al.19 to have a partial distribution of both Ca2+ and Ho3+ ions at both the A and B sites respectively. In the case of CHR, Ru5+ ions adopted a type I antiferromagnetic ordering at 4.2 K but no evidence of long range magnetic ordering among the Ho3+ ions was observed.
Although reports about the magnetic properties of AHR exist in literature, the knowledge about the ac electrical properties and dynamics of charge carriers in the radio frequency region remain a scarcity in literature. An understanding of the charge carrier dynamics is imperative in order to tailor the electrical properties of materials. The charge carrier dynamics can be extracted with the help of either the conductivity spectra20 or the modulus spectra.21 The conductivity spectra follow a power law behaviour22,23 consisting of a frequency independent (dc) region and a frequency dependent dispersive component. The crossover frequency which is also known as the hopping frequency provides the transition from the dc to the ac region. The hopping frequency can be related to the dc conductivity through the Nernst–Einstein relation (eqn (1)) and can be used to estimate the thermal variation of charge carrier concentration
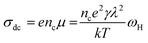 | (1) |
 | (2) |
2. Experimental details: material synthesis and characterization
AHR was synthesized using the standard solid state reaction method. Powders of BaCO3 (Loba Chemie, 99% pure), SrCO3 (Loba Chemie, 99% pure), CaCO3 (Loba Chemie, 99% pure), Ho2O3 (Sigma-Aldrich, 99% pure) and RuO2 (Alfa-Aesar, 99% pure) were taken in appropriate proportions in accordance with stoichiometric analysis. The ingredients were mixed homogeneously in an agate mortar by hand grinding in dry form and then in acetone medium at periodic intervals for 10 h. The mixture was initially raised to 1300 °C in an alumina crucible at a heating rate of 260 °C h−1, then calcined at 1300 °C for 10 h and brought to room temperature at the cooling rate of 90 °C h−1. In the next step, the calcined powder was pelletized into discs of 8 mm diameter and 1.7 mm thickness using polyvinyl alcohol as binder. Finally, the discs were raised to 1350 °C at a heating rate of 270 °C h−1, sintered at 1350 °C for 10 h followed by cooling down to room temperature at the rate of 1.6 °C min−1.The X-ray diffraction (XRD) patterns of the samples were collected using X-ray powder diffractometer (Rigaku Miniflex II diffractometer, Tokyo, Japan) using CuKα radiation in the 2θ range of 10–80° at a scanning rate of 0.02° per step. Rietveld refinement of the XRD data is performed by the Fullprof code.33 For dielectric measurements, the sintered pellets were polished on both the sides and kept between two thin gold electrodes. The scanning electron micrographs (SEM) of BHR, SHR and CHR were obtained at magnifications of 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 14
000, 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 10
000 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 respectively by the FEI Quanta 200 scanning electron microscope. The complex impedance (Z*), phase angle (ϕ) and conductance (G) were measured using a computer controlled LCR meter (HIOKI-3552, Nagano, Japan) in the frequency range from 42 Hz to 5 MHz and temperature range 303 K to 613 K at an oscillation voltage of 1.0 V. The temperature was controlled by a Eurotherm 2216e programmable temperature controller connected with the oven and each measured temperature was kept constant with an accuracy of ±1 K. The error in the experimental data was found to be less than the symbol size used in plotting the experimental data.
000 respectively by the FEI Quanta 200 scanning electron microscope. The complex impedance (Z*), phase angle (ϕ) and conductance (G) were measured using a computer controlled LCR meter (HIOKI-3552, Nagano, Japan) in the frequency range from 42 Hz to 5 MHz and temperature range 303 K to 613 K at an oscillation voltage of 1.0 V. The temperature was controlled by a Eurotherm 2216e programmable temperature controller connected with the oven and each measured temperature was kept constant with an accuracy of ±1 K. The error in the experimental data was found to be less than the symbol size used in plotting the experimental data.
3. Results and discussions
3.1. Structural characterization
The room temperature XRD patterns of BHR, SHR and CHR are shown in Fig. 1(a)–(c) respectively. The structural and fitted parameters for BHR, SHR and CHR are given in Table 1. The Rietveld refinement of the XRD pattern of BHR shows a cubic phase with space group Fm3m. The space group allows a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ordered arrangement between Ho3+ and Ru5+ ions. Superlattice lines such as [111] and [311] which arise from the alternate ordering of Ho and Ru sites in BHR are observed in the XRD pattern (Fig. 1(a)). The superlattice reflection [111] and its adjacent fundamental reflection [220] are selected for comparison in order to study the ordering of the B-site in the cubic DPO lattice. The development of ordered geometry at the B-site is given by the ratio of the intensity of the [111] reflection and the [220] fundamental reflection. The occurrence of superlattice reflections ensures a non-zero value of the intensity ratio thereby showing the presence of an ordered B-site. The intensity ratio I[111]/I[220] is found to be 0.04, indicating the ordering in the Ho and Ru site in BHR.34,35 The degree of ordering within a given compound was determined by the Long Range Order (LRO) parameter: LRO = [2xB − 1], where xB is the fractional occupancy of the B site cation on the predominantly occupied octahedral site. The refinement is done varying the occupancy parameter xB and the best result is obtained with xB = 1 which implies complete ordering of the B site cations36 as shown in Fig. 2(a)–(c).
1 ordered arrangement between Ho3+ and Ru5+ ions. Superlattice lines such as [111] and [311] which arise from the alternate ordering of Ho and Ru sites in BHR are observed in the XRD pattern (Fig. 1(a)). The superlattice reflection [111] and its adjacent fundamental reflection [220] are selected for comparison in order to study the ordering of the B-site in the cubic DPO lattice. The development of ordered geometry at the B-site is given by the ratio of the intensity of the [111] reflection and the [220] fundamental reflection. The occurrence of superlattice reflections ensures a non-zero value of the intensity ratio thereby showing the presence of an ordered B-site. The intensity ratio I[111]/I[220] is found to be 0.04, indicating the ordering in the Ho and Ru site in BHR.34,35 The degree of ordering within a given compound was determined by the Long Range Order (LRO) parameter: LRO = [2xB − 1], where xB is the fractional occupancy of the B site cation on the predominantly occupied octahedral site. The refinement is done varying the occupancy parameter xB and the best result is obtained with xB = 1 which implies complete ordering of the B site cations36 as shown in Fig. 2(a)–(c).
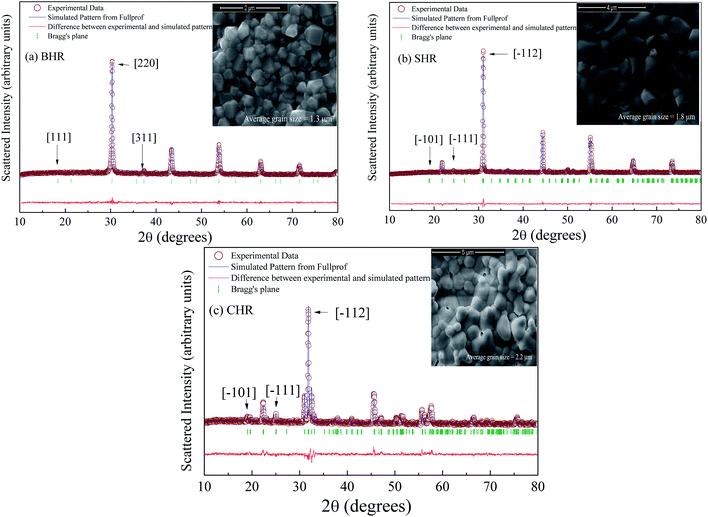 | ||
| Fig. 1 Room temperature XRD profile of (a) Ba2HoRuO6 (BHR), (b) Sr2HoRuO6 (SHR) and (c) Ca2HoRuO6 (CHR). The SEM images for BHR, SHR and CHR are shown in the inset of the figures. | ||
| Atoms | Wyckoff | x | y | z | Lattice parameters | Bond length (Å) | Bond angle | χ2 | |
|---|---|---|---|---|---|---|---|---|---|
| BHR | Ba | 8c | 0.25 | 0.25 | 0.25 | a = 8.3337 Å | <Ho–O> = 2.20 | <Ho–O–Ru> = 180° | 1.22 |
| Ho | 4a | 0.00 | 0.00 | 0.00 | <Ru–O> = 1.95 | ||||
| Ru | 4b | 0.50 | 0.50 | 0.50 | |||||
| O | 24e | 0.266(2) | 0.00 | 0.00 | |||||
| SHR | Sr | 4e | 0.5017(0) | 0.5284(0) | 0.2414(0) | a = 5.7529 Å | <Ho–O> = 2.21 | <Ho–O1–Ru> = 164° | 1.38 |
| Ho | 2c | 0.00 | 0.50 | 0.00 | b = 5.7739 Å | <Ru–O> = 1.94 | <Ho–O2–Ru> = 154° | ||
| Ru | 2d | 0.50 | 0.00 | 0.00 | c = 8.1464 Å | <Ho–O3–Ru> = 152° | |||
| O1 | 4e | 0.2199(0) | 0.2118(0) | −0.0043(0) | |||||
| O2 | 4e | 0.3051(0) | 0.7254(0) | −0.0385(0) | β = 89.87° | ||||
| O3 | 4e | 0.4142(5) | −0.0117(5) | 0.2329(5) | |||||
| CHR | Ca1 | 4e | 0.5245(2) | 0.5682(8) | 0.2631(1) | a = 5.5013 Å | <Ho1–O> = 2.44 | <Ho2–O1–Ru> = 149° | 1.82 |
| Ho1 | 4e | 0.5245(2) | 0.5682(8) | 0.2631(1) | b = 5.7594 Å | <Ho2–O> = 2.33 | <Ho2–O2–Ru> = 151° | ||
| Ca2 | 2c | 0.00 | 0.50 | 0.00 | c = 7.9333 Å | <Ru–O> = 1.88 | <Ho2–O3–Ru> = 152° | ||
| Ho2 | 2c | 0.00 | 0.50 | 0.00 | |||||
| Ru | 2d | 0.50 | 0.00 | 0.00 | |||||
| O1 | 4e | 0.3301(2) | 0.2238(2) | −0.063(2) | |||||
| O2 | 4e | 0.3260(1) | 0.7299(1) | −0.043(9) | β = 90.17° | ||||
| O3 | 4e | 0.4093(1) | −0.0054(8) | 0.2356(8) |
 | ||
| Fig. 2 Crystal structures at different orientations for (a)–(c) Ba2HoRuO6 (BHR), (d)–(f) Sr2HoRuO6 (SHR) and (g)–(i) Ca2HoRuO6 (CHR). | ||
The XRD profiles of SHR and CHR with monoclinic space group P21/n present contrasting features. The XRD pattern of SHR sample in Fig. 1(b) show two superlattice reflection peaks at 2θ ≈ 18° [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01] and 24° [
01] and 24° [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 11] respectively. The degree of site ordering in the monoclinic lattice is given by the intensity ratio I[
11] respectively. The degree of site ordering in the monoclinic lattice is given by the intensity ratio I[![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01]/I[
01]/I[![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 12] of the superlattice reflection peak. This intensity ratio is found to be 0.03, indicating the ordering of Ho and Ru at the B-site in SHR as evident in Fig. 2(d)–(f). The reflection at 2θ ≈ 18° [
12] of the superlattice reflection peak. This intensity ratio is found to be 0.03, indicating the ordering of Ho and Ru at the B-site in SHR as evident in Fig. 2(d)–(f). The reflection at 2θ ≈ 18° [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 01] is a consequence of the antiphase tilting of the octahedra around the principal 2-fold axis.37 The other reflection located at 2θ ≈ 24° [
01] is a consequence of the antiphase tilting of the octahedra around the principal 2-fold axis.37 The other reflection located at 2θ ≈ 24° [![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 11], arises from the in-phase tilt of the octahedra around the primitive axis.38 The total intensity of the [002] and [110] reflections are significantly decreased when Ca replaces Sr at the A-site as evident from the comparative study of the XRD profiles of SHR and CHR thus showing the A-site is partially occupied by the Ca2+ ions giving rise to a different cationic distribution in CHR as compared to SHR. The cationic distributions that best fits the intensity profile of CHR is Ca2+/Ho3+ (4e), Ca2+/Ho3+ (2d), Ru5+ (2c) corresponding to the formula (Ca1.46Ho0.54)(Ca0.54Ho0.46)RuO6 showing the partial occupation of the Ca and Ho ions at both the A-site and the B-site of the double perovskite in agreement to the suggestion by Battle et al.19 There exists no cationic ordering between the Ca2+ and Ho3+ ions at either of the A or B-sites although the Ca2+/Ho3+ ions form a 1
11], arises from the in-phase tilt of the octahedra around the primitive axis.38 The total intensity of the [002] and [110] reflections are significantly decreased when Ca replaces Sr at the A-site as evident from the comparative study of the XRD profiles of SHR and CHR thus showing the A-site is partially occupied by the Ca2+ ions giving rise to a different cationic distribution in CHR as compared to SHR. The cationic distributions that best fits the intensity profile of CHR is Ca2+/Ho3+ (4e), Ca2+/Ho3+ (2d), Ru5+ (2c) corresponding to the formula (Ca1.46Ho0.54)(Ca0.54Ho0.46)RuO6 showing the partial occupation of the Ca and Ho ions at both the A-site and the B-site of the double perovskite in agreement to the suggestion by Battle et al.19 There exists no cationic ordering between the Ca2+ and Ho3+ ions at either of the A or B-sites although the Ca2+/Ho3+ ions form a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ordered arrangement with the Ru5+ ions at the B-site as seen in Fig. 2(g)–(i). The intensity ratio of the superlattice reflection in CHR (I[011]/I[
1 ordered arrangement with the Ru5+ ions at the B-site as seen in Fig. 2(g)–(i). The intensity ratio of the superlattice reflection in CHR (I[011]/I[![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 12]) is found to be 0.12 which also signifies the B-site ordering in the sample.
12]) is found to be 0.12 which also signifies the B-site ordering in the sample.
Bond valence sum (BVS) for AHR are given in Table 2. The BVS of the A2+ cations are significantly less than 2.0 which demonstrates that the average A–O distances are longer than optimal.39 The BVS for Ba2+ and Sr2+ in BHR and SHR is 1.992 and 1.783 respectively. The Ca2+ (BVS = 1.382) at the A-site is comparatively more under-bonded than the Ca2+ (BVS = 1.801) at the B-site showing that the bonding strength in CaO6 octahedra is more than in the CaO12 octahedra. The increased bond valency reflects that the A-site is becoming more convenient for the A2+ cation thereby reducing the requirement for octahedral tilting resulting in a more symmetrical crystal structure. The bond lengths and BVS provide further insight into the bonding requirement of the two B-site cations of significant size difference which are distributed in an ordered perovskite structure. In case of BHR and SHR, the Ho3+ are over-bonded with the Ho–O bond lengths being shorter than the expected value. In the case of CHR, both Ho atoms are considerably under-bonded which is reflected in the respective bond lengths which are greater than the calculated values. This can be attributed to the increase in the distortion resulting in the lengthening and shortening of different axes to attain the lowest energy stable crystal structure. The Ru-atom in all three materials are overbonded as observed from Ru–O bond length which is shorter than the expected value. The Ho–O bond lengths systematically increase whereas the Ru–O bond length decreases as Ca replaces Ba/Sr at the A-site. This shows that with distortion the Ho–O axis elongates and Ru–O axis shortens. Although minor variations in determining the BVS values may arise due to the low scattering coefficient of oxygen ions, the BVS formalism still provides a very qualitative analysis of the bonding environment inside AHR. The ease with which any cation pair can form a perovskite structure is expressed in terms of a geometrical quantity known as the tolerance factor (t) given by.40,41
 | (3) |
| Atoms | Charge | BVS | Eaσdc (eV) | EaωH (eV) | Eaωm (eV) | |
|---|---|---|---|---|---|---|
| BHR | Ba | +2 | 1.992 | Eta = 0.27 eV | Eta = 0.26 eV | Egba = 0.25 eV |
| Ho | +3 | 3.573 | ||||
| Ru | +5 | 5.240 | ||||
| SHR | Sr | +2 | 1.783 | Eta = 0.31 eV | Eta = 0.29 eV | Egba = 0.29 eV |
| Ho | +3 | 3.423 | ||||
| Ru | +5 | 5.379 | Ega = 0.22 eV | |||
| CHR | Ca1 | +2 | 1.382 | Eta = 0.37 eV | Eta = 0.35 eV | Egba = 0.31 eV |
| Ho1 | +3 | 2.106 | ||||
| Ca2 | +2 | 1.801 | Ega = 0.26 eV | |||
| Ho2 | +3 | 2.662 | ||||
| Ru | +5 | 5.392 |
It predicts that for a given pair of B-site cations (Ho and Ru in the present case) an increase in the size of the A-site cation increases the tolerance factor of the perovskite system. A cubic perovskite structure is obtained for t close to unity, whereas the structure progressively undergoes distortion for lower values of t due to the mismatch of the A-site and B-site ionic radii. The values of the geometric tolerance factor t for BHR, SHR and CHR are calculated to be 1.004, 0.95 and 0.91 respectively, which is in agreement with the cubic structure of BHR and the monoclinic structures for SHR and CHR respectively as shown in Fig. 2(a)–(i). The increased bond valency reflects that the size of the A-site is becoming more suitable for the A2+ cation reducing the requirement for octahedral tilting in the perovskite structure resulting in an increase in the symmetry of the materials due to the volumetric resemblance of the BO6 and AO12 octahedra. The crystal structure approaches the higher symmetry configuration as one moves from CHR to BHR reducing the octahedral distortion in the system as is reflected in the <B′–O–B′′> bond angles which approach 180°.
The SEM images of the samples are shown in the inset of Fig. 1(a)–(c) for BHR, SHR and CHR respectively. The SEM images indicate high density of the materials as well as uniform distribution of grains of different sizes and shapes in the samples. The average grain size for BHR, SHR and CHR is found to be 1.3 μm, 1.8 μm and 2.2 μm respectively. The density of BHR, SHR and CHR is 7.307 g cc−1, 6.594 g cc−1 and 5.897 g cc−1 respectively which is 97%, 95% and 94% of the theoretical density.
3.2. Electrical characterization
Dynamical processes in materials are studied by a variety of spectroscopic techniques. Electrical relaxation measurements are commonly used, mostly as a function of frequency, to study the charge dynamics in materials.42 With the advancement of ac conductivity measurement techniques, impedance analysis has become a widely accepted tool for the characterization of the experimental data. Fig. 3(a)–(c) present the spectroscopic plots of the real part of ac conductivity for BHR, SHR and CHR respectively at selected temperatures. The symbols represent the experimental data and the solid lines represent the fit of the experimental conductivity spectra in accordance to the power law (eqn (4)) suggested by Almond and West:43,44
 | (4) |
In eqn (4), σdc represents the dc conductivity, ω is the angular frequency, n is the power law exponent describing the electrical relaxation behaviour of the material and ωH represents the hopping frequency of the charge carriers which marks the crossover from long range translational to the dispersive conduction region at ω > ωH. In a polycrystalline ceramic system, conductivity relaxation occurs due to grain, grain-boundary and electrode-specimen interface contributions. In absence of electrode polarization, electro-ceramics show the presence of plateaus and dispersion regions in their conductivity spectra due to the contribution from different microstructural regions.45–47 The spectroscopic plots for BHR, SHR and CHR have been divided into different regimes revealing different microstructural contribution to the conductivity of the materials. In the case of BHR (Fig. 3(a)), a single plateau in the low frequency region (region I) followed by a dispersion region (region II) is observed. The single plateau can be assigned to the total conductivity of the sample measuring the overall dc conductivity of the sample in the limit ω → 0 i.e. (σdc = σt(ω → 0)). The dispersion region can be attributed to the grain boundary relaxation of the sample. In the case of SHR and CHR (Fig. 3(b) and (c)), the presence of another plateau is observed along with regions I and II. This plateau denoted by region III can be assigned to the contribution of the grains to the total conductivity.
The frequency dependent conductivity can be interpreted in terms of the grain boundary conductivity and jump relaxation model.48,49 In this model, the total conductivity, which is a measure of the dc conductivity at ω → 0, is caused by the long range translational motion of charge carriers between localised sites. The ac conductivity in the dispersion regime is caused by the correlated backward and forward hopping motion of the charge carriers which can be visualised as a competition between two relaxation processes; successful and unsuccessful hopping of charge carriers. The conductivity of BHR is found to be greater than SHR and CHR for a particular temperature. The conductivity of the materials are enhanced with increase in temperature due to the thermal activation of charge carriers across the energy gap. As previously mentioned the conduction in AHR is dependent on the degree of hybridization between the Ru t2g and O-2p orbitals along with the distortions present in the Ru octahedral surroundings. As Ca replaces Ba and Sr at the A-site of the perovskite lattice, the degree of distortion increase which lowers the hybridization between the Ru t2g and O-2p orbitals. The decrease in electron delocalisation around the Ru-atom inhibits the facilitative transfer of electrons from the valence band to the conduction band. Thus the conductivity decreases as the distortions in the octahedra increase from BHR (t = 1.004) to CHR (t = 0.91). It seems plausible that due to the ordered arrangement of the octahedra, the complete electron delocalization of Ru cation could be inhibited by the HoO6 octahedra by the physical separation of the two successive RuO6 octahedra. In AHR, every second Ru is substituted by Ho forming a rock-salt arrangement and disrupting the Ru–O perovskite motif of intersecting 1D chains. As a result the AHR shows more localised electrical behaviour than most of the parent perovskite derived ruthenates.50–54
If the dc conductivity is Arrhenius activated, then 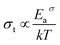 , where Eaσ is the activation energy for dc conductivity, k represents the Boltzmann constant and T is the absolute temperature. For a fixed number of sites N and fixed hopping length R, it can be shown that the hopping frequency also varies as
, where Eaσ is the activation energy for dc conductivity, k represents the Boltzmann constant and T is the absolute temperature. For a fixed number of sites N and fixed hopping length R, it can be shown that the hopping frequency also varies as  .27 If the power law exponent ‘n’ is independent or a weakly varying function of temperature then ωH activates with the same energy as σt. In the present study, ‘n’ is found to be weakly temperature dependent. Arrhenius representation of dc conductivity (σt) and hopping frequency (ωH) for BHR, SHR and CHR are shown in Fig. 4 and 5 respectively. The activation energy for grain boundary is found to be higher than the activation energy for grains. Both dc conductivity (σt) and hopping frequency (ωH) show identical profiles with a linear behaviour in the investigated temperature range. The activation energies for σt and ωH, determined from the slope of the linear fit to the experimental data, are given in Table 2. It is observed that the activation energies of dc conductivity are close to the activation energies of hopping frequency for all the three samples showing that σt is proportional to ωH. The value of the activation energy for bulk conductivity suggests that the conduction mechanism occurs due to the hopping of small polarons. In general, an activation energy of more than 0.2 eV is reminiscent of polaronic conduction of holes. On this basis it can be inferred that p-type carriers are responsible for the charge conduction in AHR.55,56
.27 If the power law exponent ‘n’ is independent or a weakly varying function of temperature then ωH activates with the same energy as σt. In the present study, ‘n’ is found to be weakly temperature dependent. Arrhenius representation of dc conductivity (σt) and hopping frequency (ωH) for BHR, SHR and CHR are shown in Fig. 4 and 5 respectively. The activation energy for grain boundary is found to be higher than the activation energy for grains. Both dc conductivity (σt) and hopping frequency (ωH) show identical profiles with a linear behaviour in the investigated temperature range. The activation energies for σt and ωH, determined from the slope of the linear fit to the experimental data, are given in Table 2. It is observed that the activation energies of dc conductivity are close to the activation energies of hopping frequency for all the three samples showing that σt is proportional to ωH. The value of the activation energy for bulk conductivity suggests that the conduction mechanism occurs due to the hopping of small polarons. In general, an activation energy of more than 0.2 eV is reminiscent of polaronic conduction of holes. On this basis it can be inferred that p-type carriers are responsible for the charge conduction in AHR.55,56
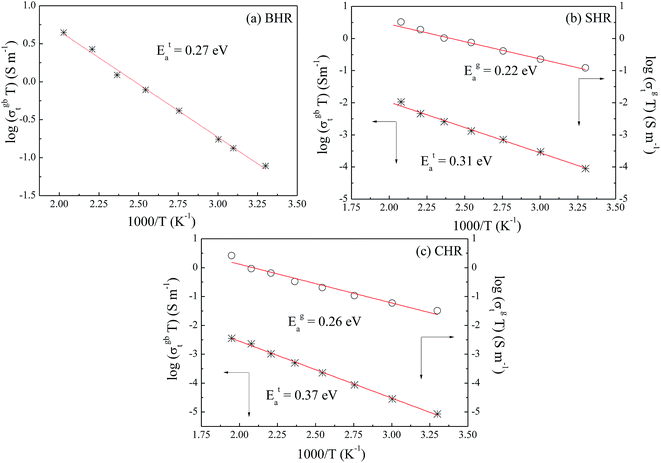 | ||
| Fig. 4 Thermal variation of dc conductivity (σdc) for (a) Ba2HoRuO6 (BHR), (b) Sr2HoRuO6 (SHR) and (c) Ca2HoRuO6 (CHR). | ||
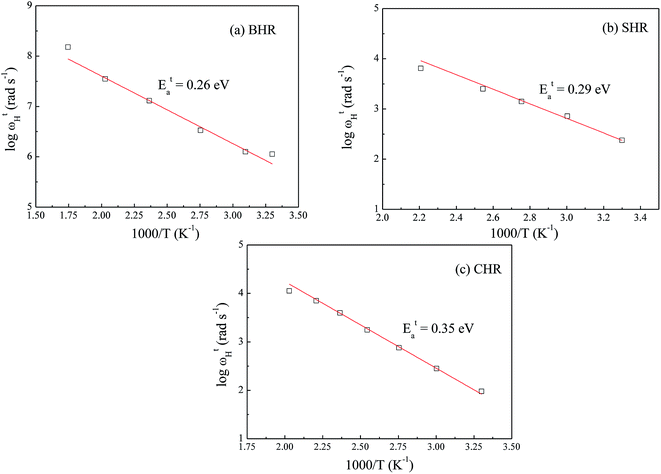 | ||
| Fig. 5 Thermal variation of hopping frequency (ωH) at grain boundaries for (a) Ba2HoRuO6 (BHR), (b) Sr2HoRuO6 (SHR) and (c) Ca2HoRuO6 (CHR). | ||
To examine the correlation between dc conductivity (σt) and hopping frequency (ωH), the logarithmic plot are drawn between these two parameters as shown in Fig. 6(a)–(c). The figures show a near linear nature with a slope of almost unity indicating a power law dependency of the form σt ∝ ωHn where ‘n’ is the slope of the graph. This implies that the dc and ac conductivity are correlated in AHR.57
 | ||
| Fig. 6 Correlation between dc conductivity (σdc) and hopping frequency (ωH) at grain boundaries for (a) Ba2HoRuO6 (BHR), (b) Sr2HoRuO6 (SHR) and (c) Ca2HoRuO6 (CHR). | ||
The electrical resistivity ρ can be deduced from the dc conductivity σt using the relation ρ = 1/σt. To understand the possible conduction mechanism, it is customary to investigate the variation of electrical resistivity with temperature. The results are analysed in terms of the hopping models namely, (i) nearest neighbour hopping or small polaron hopping (SPH) and (ii) variable range hopping (VRH).58,59 The general form of the hopping equation can be written as  where A = To and x = 0.25 represents VRH whereas A = Ea/kB and x = 1 describes the nearest neighbour hopping limit. In order to obtain the exponent ‘x’ which determines the nature of the hopping process, a plot of log(log
where A = To and x = 0.25 represents VRH whereas A = Ea/kB and x = 1 describes the nearest neighbour hopping limit. In order to obtain the exponent ‘x’ which determines the nature of the hopping process, a plot of log(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρ) vs. log
ρ) vs. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T is shown in Fig. 7(a)–(c) for BHR, SHR and CHR respectively. The slope of the graph determines the value of the exponent ‘x’.60 In all the three materials, the high temperature domain is dominated by the nearest neighbour hopping process (x ∼ 1) with a gradual cross-over towards variable range hopping limit near room temperature (x ∼ 0.30). With further decrease in temperature, the VRH limit of x ∼ 0.25 should be achieved.
T is shown in Fig. 7(a)–(c) for BHR, SHR and CHR respectively. The slope of the graph determines the value of the exponent ‘x’.60 In all the three materials, the high temperature domain is dominated by the nearest neighbour hopping process (x ∼ 1) with a gradual cross-over towards variable range hopping limit near room temperature (x ∼ 0.30). With further decrease in temperature, the VRH limit of x ∼ 0.25 should be achieved.
 | ||
| Fig. 7 Temperature dependence of electrical resistivity (a) Ba2HoRuO6 (BHR), (b) Sr2HoRuO6 (SHR), and (c) Ca2HoRuO6 (CHR). | ||
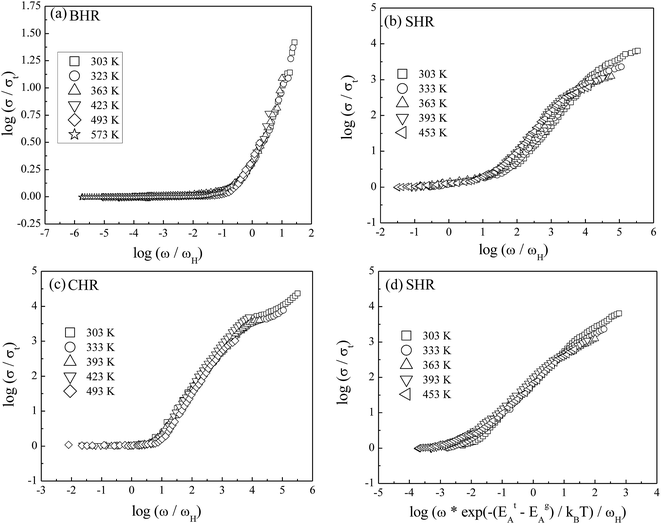
To gain valuable insight into the temperature dependence of the conduction mechanism and the response of grains and grain boundaries to the conductivity, the scaling behaviour of frequency dependent conductivity has been performed. In the present study, two different scaling formalisms, Summerfield scaling61 and Ghosh scaling,62,63 have been applied to perform the scaling of the conductivity spectroscopic plots. The conductivity axis of the ac conductivity spectra for BHR, SHR and CHR is scaled by the dc conductivity (σt) whereas the frequency axis is scaled by ωs = σtT and ωs = ωH as shown in Fig. 8(a)–(c) and 9(a)–(c) respectively. The ac conductivity spectra for BHR, SHR and CHR are superimposed into a single master curve at the grain boundary region although in the grain response region the ac conductivity data do not collapse into a single master curve. It shows that the relaxation processes at the grain boundary region follow the time–temperature superposition principle (TTSP). However, the deviation of the scaled conductivity curves at the grain region implies that the relaxation phenomena in the grains are different from that in the associated grain boundary response regions. The grain boundaries require higher activation energy than the grains as is evident from Table 2. This difference is in agreement with the dissimilar activation energies of the grains and the grain boundaries (ΔE = Eta − Ega = 0.09 eV for SHR and 0.11 for CHR). The higher activation energy of the grain boundary conductivity can be due to the combination of a number of serial barriers in the interfacial region and therefore the total conductivity is dictated by the grain boundary impedance. The parameters, such as the diffusion coefficient (D), which affect the bulk and grain conductivity can be obtained from the differently activated response regions. In order to consider the activation energy difference between the bulk and grain interiors the frequency axis has been scaled by the parameter  and
and 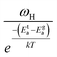 (ref. 64) for SHR as shown in Fig. 8(d) and 9(d) respectively. The scaled grain boundary curves are superimposed into a single curve whereas the grain response curve deviate more than previously. The factor
(ref. 64) for SHR as shown in Fig. 8(d) and 9(d) respectively. The scaled grain boundary curves are superimposed into a single curve whereas the grain response curve deviate more than previously. The factor  compensates for the different energy barriers that the mobile ion encounters between the grain boundaries and the grain regions during its percolation. The conductivity scaled isotherms for BHR, SHR and CHR show that the scaling formalism with ωs = ωH provides a better superposition than the scaling formalism with ωs = σtT due to the fact that σt has a power law dependence on ωH.
compensates for the different energy barriers that the mobile ion encounters between the grain boundaries and the grain regions during its percolation. The conductivity scaled isotherms for BHR, SHR and CHR show that the scaling formalism with ωs = ωH provides a better superposition than the scaling formalism with ωs = σtT due to the fact that σt has a power law dependence on ωH.
 | ||
Fig. 8 Summerfield scaling of ac conductivity for (a) Ba2HoRuO6 (BHR), (b) Sr2HoRuO6 (SHR), (c) Ca2HoRuO6 (CHR) and (d) scaling of ac conductivity for SHR with frequency axis scaled by  . . | ||
Previous studies have revealed that some school of thought prefer the use of electric modulus formalism in the interpretation of the conduction dynamics by eliminating the electrode polarization effect. The electric modulus formalism was first introduced by Macedo et al.65 in exploring the space-charge relaxation phenomena and is used in conjunction with the impedance and permittivity formalisms to differentiate between the grain and grain boundary regions and to recognize the microscopic processes responsible for localized dielectric relaxations and long-range conductions.66,67 Fig. 10(a)–(c) display the spectroscopic plots for the imaginary component of electric modulus, M′′, at selected temperatures for BHR, SHR and CHR respectively. BHR displays a single relaxation peak in the entire frequency domain whereas both SHR and CHR have two relaxation peaks, one at low frequency due to grain boundary response and the other at high frequency due to the grain response.68 The M′′ peaks are much broader than an ideal Debye peak showing that the relaxation behaviour is non-ideal and the relaxation times are distributed. The increase in frequency as one approaches the peak from the left facilitates the mobility of the charge carriers and represents a region of long range conduction. To the right of the peak, localized forward backward hopping motion occurs as the charge carriers are confined to trapped centres due to their decreased mobility.69,70 With increase in temperature charge carrier dynamics is boosted with a decrease in relaxation time which manifests itself as a shift in the relaxation frequency (ωm) towards the higher frequency side. A natural conclusion thus follows that the relaxation process is thermally activated with charge carrier hopping determining the conduction dynamics in AHR.
The scaling behaviour of M′′ has been performed to obtain an insight into the thermally influenced relaxation dynamics of AHR.71 The insets of Fig. 10(a)–(c) provide the scaled spectra in which each axis has been scaled by its corresponding peak value obtained from the relaxation maxima at individual temperatures. The figures show that the modulus spectra at different temperatures nearly collapse into a single master curve at the grain boundary response regime, whereas the grain response domain shows a deviation from the scaling behaviour. Similar nature was also obtained from the conductivity scaling behaviour. This indicates that the dynamical process controlling the conductivity relaxation at the grain boundaries is the same over the entire temperature range although it deviates greatly from the conductivity relaxation dynamics at the grain region. It is therefore concluded that there exists no single scaling parameter that can account for the validation of the time–temperature superposition principle when two dissimilar thermally activated processes are simultaneously present within a material.
Fig. 10(d) represents the thermal variation of relaxation frequency (ωm) for AHR. The activation energies obtained from the linear fit of the experimental data are 0.25 eV, 0.29 eV and 0.31 eV for BHR, SHR and CHR respectively. A comparison of the activation energies of all the samples for dc conductivity (σt), hopping frequency (ωH) and relaxation frequency (ωm) show that the values lie close to each other. The close proximity of the values of EH and Eωmax indicate that the hopping frequency and the relaxation frequency provide the limiting bound to the crossover from short range hopping to long range percolation.
4. Conclusion
A comprehensive quantitative investigation of electrical conduction for polycrystalline double perovskite oxides A2HoRuO6 (AHR; A = Ba, Sr, Ca) prepared by solid state technique has been presented over the temperature range of 303–613 K and frequency range 42 Hz to 5 MHz. The room temperature XRD data confirmed the single phase formation of all the materials. The bond valence sum (BVS) formalism correlates the degree of octahedral distortion to the strength of the bonding of the A-site cation. The conductivity spectra for AHR follow a power law variation. The contributions of the different microstructural regimes to the conduction mechanism are observed in the conductivity spectra. The dc conductivity and the hopping frequency are correlated in a power law form. The activation energy of the materials in the grain boundary lies in the range of 0.27–0.37 eV whereas the grain response region have energies of 0.22–0.26 eV. The polaronic conduction mechanism shows a gradual crossover from the nearest neighbour hopping to the variable range hopping mechanism with decrease in temperature. The electric modulus spectra show a thermally activated conduction mechanism. The activation energies obtained from the linear fit of the thermal variation of relaxation frequency (ωm) are in close proximity to the activation energies obtained from the hopping frequencies (ωH) showing that both (ωm) and (ωH) are correlated. Our investigations show that the time temperature superposition principle using the conductivity scaling formalism is valid only at the specific microstructural response domains and not universally. Hence, we conclude if two electroactive regions have simultaneous dissimilar thermally activated conduction processes in them then there exists no single scaling parameter that can account for the time–temperature superposition principle (TTSP) universally.Conflicts of interest
There are no conflict of interests to declare.Acknowledgements
Alo Dutta thanks the Department of Science and Technology of India for providing financial support through DST Fast Track Project under grant no. SR/FTP/PS-175/2013.References
- P. D. Battle, T. C. Gibb, C. W. Jones and F. Studer, Spin-Glass Behavior in Sr2FeRuO6 and BaLaNiRuO6: A Comparison with Antiferromagnetic BaLaZnRuO6, J. Solid State Chem., 1989, 78, 281 CrossRef CAS.
- J. Chang, K. Lee, M. H. Jung, J. H. Kwon, M. Kim and S. K. Kim, Emergence of Room-Temperature Magnetic Ordering in Artificially Fabricated Ordered-Double-Perovskite Sr2FeRuO6, Chem. Mater., 2011, 23, 2693 CrossRef CAS.
- T. C. Gibb, A study of superexchange interactions in the perovskite Sr2FeRuO6 by Monte Carlo analysis, J. Mater. Chem., 2005, 15, 4015 RSC.
- B. Ranjbar, E. Reynolds, P. Kayser and B. J. Kennedy, Structural and Magnetic Properties of the Iridium Double Perovskites Ba2−xSrxYIrO6, Inorg. Chem., 2015, 54, 10468 CrossRef CAS PubMed.
- P. Kayser, B. J. Kennedy, B. Ranjbar, J. A. Kimpton and M. Avdeev, Spin–Orbit Coupling Controlled Ground State in the Ir(V) Perovskites A2ScIrO6 (A = Ba or Sr), Inorg. Chem., 2017, 56, 2204 CrossRef CAS PubMed.
- L. T. Corredor, G. Aslan-Cansever, M. Sturza, K. Manna, A. Maljuk, S. Gass, T. Dey, A. U. B. Wolter, O. Kataeva, A. Zimmermann, M. Geyer, C. G. F. Blum, S. Wurmehl and B. Buchner, Iridium double perovskite Sr2YIrO6: A combined structural and specific heat study, Phys. Rev. B, 2017, 95, 064418 CrossRef.
- G. J. Nilsen, C. M. Thompson, G. Ehlers, C. A. Marjerrison and J. E. Greedan, Diffuse magnetic neutron scattering in the highly frustrated double perovskite Ba2YRuO6, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 054415 CrossRef.
- A. A. Aczel, D. E. Bugaris, L. Li, J.-Q. Yan, C. de la Cruz, H.-C. zur Loye and S. E. Nagler, Frustration by competing interactions in the highly distorted double perovskites La2NaBO6 (B = Ru, Os), Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 014435 CrossRef.
- C. M. Thompson, C. A. Marjerrison, A. Z. Sharma, C. R. Wiebe, D. D. Maharaj, G. Sala, R. Flacau, A. M. Hallas, Y. Cai, B. D. Gaulin, G. M. Luke and J. E. Greedan, Frustrated magnetism in the double perovskite La2LiOsO6: A comparison with La2LiRuO6, Phys. Rev. B, 2016, 93, 014431 CrossRef.
- H.-R. Fuh, Y.-P. Liu, S.-H. Chen and Y.-K. Wang, Electronic structures of compensated magnetism in double perovskites A2CrRu(Os)O6 (A = Si, Ge, Sn, and Pb) from ab initio calculations, J. Alloys Compd., 2013, 547, 126 CrossRef CAS.
- B. Ranjbar, A. Pavan, B. J. Kennedy and Z. Zhang, Structural and magnetic properties of the ruthenium double perovskites Ba2−xSrxYRuO6, Dalton Trans., 2015, 44, 10689 RSC.
- P. D. Battle, J. B. Goodenough and R. Price, The Crystal Structures and Magnetic Properties of Ba2LaRuO6 and Ca2LaRuO6, J. Solid State Chem., 1983, 46, 234 CrossRef CAS.
- P. D. Battle and C. W. Jones, The crystal and magnetic structures of Sr2LuRuO6, Ba2YRuO6, and Ba2LuRuO6, J. Solid State Chem., 1989, 78, 108 CrossRef CAS.
- P. D. Battle and W. J. Macklin, The crystal and magnetic structures of Ca2YRuO6 and the electronic properties of the series M22+X3+Ru5+O6 (M = Ca, Sr, Ba; X= La, Y), J. Solid State Chem., 1984, 54, 245 CrossRef CAS.
- A. V. Powell, J. G. Gore and P. D. Battle, The magnetic properties of iridium in mixed-metal oxides, J. Alloys Compd., 1993, 201, 73 CrossRef CAS.
- A. Maignan, C. Martin, M. Hervieu and B. Raveau, Ferromagnetism and metallicity in the CaMn1−xRuxO3 perovskites: a highly inhomogeneous system, Solid State Commun., 2001, 17, 377 CrossRef.
- Y. Hinatsu, Y. Izumiyama, Y. Doi, A. Alemi, M. Wakeshima, A. Nakamura and Y. Morii, Studies on magnetic and calorimetric properties of double perovskites Ba2HoRuO6 and Ba2HoIrO6, J. Solid State Chem., 2004, 177, 38 CrossRef CAS.
- Y. Doi and Y. Hinatsu, Crystal structures and magnetic properties of ordered perovskites Sr2LnRuO6 (Ln = Eu–Lu), J. Phys.: Condens. Matter, 1999, 11, 4813 CrossRef CAS.
- P. D. Battle, C. W. Jones and F. Studer, The Crystal and Magnetic Structures of Ca2NdRuO6, Ca2HoRuO6, and Sr2ErRuO6, J. Solid State Chem., 1991, 90, 302 CrossRef CAS.
- J. C. Dyre, The random free∼energy barrier model for ac conduction in disordered solids, J. Appl. Phys., 1988, 64, 2456 CrossRef.
- K. L. Ngai and C. T. Moynihan, The Dynamics of Mobile Ions in Ionically Conducting Glasses and Other Materials, Mater. Res. Soc. Bull., 1998, 23, 51 CrossRef CAS.
- A. K. Jonscher, The universal dielectric response, Nature, 1977, 267, 673 CrossRef CAS.
- D. P. Almond and A. R. West, Anomalous conductivity prefactors in fast ion conductors, Nature, 1983, 306, 456 CrossRef CAS.
- B. Roling and C. Martiny, Non-universal Features of the ac Conductivity in Ion Conducting Glasses, Phys. Rev. Lett., 2000, 85, 1274 CrossRef CAS PubMed.
- R. Murugaraj, G. Govindaraj and D. George, AC conductivity and its scaling behavior in lithium and sodium bismuthate glasses, Mater. Lett., 2003, 57, 1656 CrossRef CAS.
- S. Saha and T. P. Sinha, Low-temperature scaling behavior of BaFe0.5Nb0.5O3, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 134103 CrossRef.
- P. Singh, R. Pandey, O. Parkash and D. Kumar, Scaling of low-temperature conductivity spectra of BaSn1−xNbxO3 (x ≤ 0.100): Temperature and compositional-independent conductivity, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 174306 CrossRef.
- S. Murugavel and B. Roling, ac Conductivity Spectra of Alkali Tellurite Glasses: Composition-Dependent Deviations from the Summerfield Scaling, Phys. Rev. Lett., 2002, 89, 195902 CrossRef CAS PubMed.
- H. Kahnt, Ionic Transport in Oxide Glasses and Frequency Dependence of Conductivity, Ber. Bunsen-Ges., 1991, 95, 1021 CrossRef CAS.
- B. Roling, A. Happe, K. Funke and M. D. Ingram, Carrier Concentrations and Relaxation Spectroscopy: New Information from Scaling Properties of Conductivity Spectra in Ionically Conducting Glasses, Phys. Rev. Lett., 1997, 78, 2160–2163 CrossRef CAS.
- D. L. Sidebottom, Universal Approach for Scaling the ac Conductivity in Ionic Glasses, Phys. Rev. Lett., 1999, 82, 3653 CrossRef CAS.
- S. D. Baranovskii and H. Corder, On the conduction mechanism in ionic glasses, J. Chem. Phys., 1999, 111, 7546 CrossRef CAS.
- J. Rodriguez-Carvajal, Recent advances in magnetic structure determination neutron powder diffraction, Phys. B, 1993, 192, 55 CrossRef CAS.
- R. Mukherjee, A. Dutta and T. P. Sinha, Dielectric Relaxation of Rare Earth Ordered Double Perovskite Oxide Ba2ErTaO6, J. Electron. Mater., 2016, 45, 846 CrossRef CAS.
- G. Y. Liu, G. H. Rao, X. M. Feng, H. F. Yang, Z. W. Ouyang, W. F. Liu and J. K. Liang, Atomic ordering and magnetic properties of non-stoichiometric double-perovskite Sr2FexMo2−xO6, J. Phys.: Condens. Matter, 2003, 15, 2053 CrossRef CAS.
- P. M. Woodward, R. D. Hoffman and A. W. Sleight, Order-disorder in A2M3+M5+O6 perovskites, J. Mater. Res., 1994, 9, 2118 CrossRef CAS.
- W. T. Fu and D. J. W. Ijdo, X-ray and neutron powder diffraction study of the monoclinic perovskites Sr2MSbO6 (M = In, Y), Solid State Commun., 2005, 134, 177 CrossRef CAS.
- S. Halder, A. Dutta and T. P. Sinha, Dielectric relaxation and electrical conduction mechanism in A2HoSbO6 (A = Ba, Sr, Ca) Double Perovskite Ceramics: An impedance spectroscopic analysis, J. Phys. Chem. Solids, 2017, 102, 79 CrossRef CAS.
- P. J. Saines, B. J. Kennedy and M. M. Elcombe, Structural phase transitions and crystal chemistry of the series Ba2LnB′O6 (Ln = lanthanide and B′ = Nb5+ or Sb5+), J. Solid State Chem., 2007, 180, 401 CrossRef CAS.
- H. D. Megaw, Crystal structure of double oxides of the perovskite type, Proc. Phys. Soc., 1946, 58, 133 CrossRef CAS.
- H. D. Megaw, Crystal Structures: A Working Approach, W. B. Saunders Company, London, 1973 Search PubMed.
- D. P. Almond and A. R. West, Impedance and Modulus spectroscopy of Real dispersive conductors, Solid State Ionics, 1983, 11, 57 CrossRef CAS.
- D. P. Almond, G. K. Ducan and A. R. West, The Determination of Hopping Rates and Carrier Concentrations in Ionic Conductors by a new analysis of ac conductivity, Solid State Ionics, 1983, 8, 159 CrossRef CAS.
- K. Funke, B. Heimann, M. Vering and D. Wilmer, Concept of Mismatch and Relaxation Explains DC and AC Conductivities of Fragile Glass-Forming Ionic Melts, J. Electrochem. Soc., 2001, 148, 395 CrossRef.
- D. A. Payne and L. E. Cross, Microstructure-Property Relations for Dielectric Ceramics: II. The Brick-Wall Model of Polycrystalline Microstructure Microstructure and Properties of Ceramic Materials, 1984, vol. 380 Search PubMed.
- R. Waser, Bulk Conductivity and Defect Chemistry of Acceptor-Doped Strontium Titanate in the Quenched State, J. Am. Ceram. Soc., 1991, 74, 1934 CrossRef CAS.
- M. Vollman and R. Waser, Grain Boundary Defect Chemistry of Acceptor-Doped Titanates: Space Charge Layer Width, J. Am. Ceram. Soc., 1994, 77, 235 CrossRef CAS.
- K. Funke, Jump relaxation in solid electrolytes, Prog. Solid State Chem., 1993, 22, 111 CrossRef CAS.
- A. A. Youssef Ahmed, The Permittivity and AC Conductivity of the Layered Perovskite [(CH3)(C6H5)3P]2HgI4, Z. Naturforsch., 2002, 57, 263 Search PubMed.
- J.-S. Zhou, K. Matsubayashi, Y. Uwatoko, C.-Q. Jin, J.-G. Cheng, J. B. Goodenough, Q. Q. Liu, T. Katsura, A. Shatskiy and E. Ito, Critical Behavior of the Ferromagnetic Perovskite BaRuO3, Phys. Rev. Lett., 2008, 101, 077206 CrossRef PubMed.
- B. Szymanik and A. Edgar, Electrical Conductivity of BaRuO3 Ceramics, Solid State Commun., 1991, 79, 355 CrossRef CAS.
- A. Ito, H. Masumoto and T. Goto, Microstructure and Electrical Conductivity of CaRuO3 Thin Films Prepared by Laser Ablation, Mater. Trans., 2008, 49, 158 CrossRef CAS.
- V. Markovich, M. Auslender, I. Fita, R. Puzniak, C. Martin, A. Wisniewski, A. Maignan, B. Raveau and G. Gorodetsky, Interplay between itinerant and localized states in CaMn1−xRuxO3 (x ≤ 0.5) manganites, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 014416 CrossRef.
- V. Vashook, D. Nitsche, L. Vasylechko, J. Rebello, J. Zosel and U. Guth, Solid state synthesis, structure and transport properties of compositions in the CaRu1−xTixO3−δ system, J. Alloys Compd., 2009, 485, 73 CrossRef CAS.
- H. Rahmouni, R. Jemai, M. Nouiri, N. Kallel, F. Rziguac, A. Selmi, K. Khirouni and S. Alayaa, Admittance spectroscopy and complex impedance analysis of Ti-modified La0.7Sr0.3MnO3, J. Cryst. Growth, 2008, 310, 556 CrossRef CAS.
- J. Yang, B. C. Zhao, Y. Q. Ma, R. L. Zhang, R. Ang, W. H. Song and Y. P. Sun, Small-polaron hopping conduction in La0.9Te0.1MnO3 above the metal-insulator transition, Mater. Lett., 2006, 60, 3281 CrossRef CAS.
- O. N. Verma, N. K. Singh, R. Pandey and P. Singh, Study of ion dynamics in lanthanum aluminate probed by conductivity spectroscopy, RSC Adv., 2015, 5, 21614 CAS.
- N. F. Mott and E. A. Davis, Electronic Processes in Noncrystalline Materials, Clarendon, Oxford, 1979 Search PubMed.
- P. N. Vishwakarma and S. V. Subramanyam, Hopping conduction in boron doped amorphous carbon films, J. Appl. Phys., 2006, 100, 113702 CrossRef.
- A. K. Biswal, J. Ray, P. D. Babu, V. Siruguri and P. N. Vishwakarma, Dielectric relaxations in La2NiMnO6 with signatures of Griffiths phase, J. Appl. Phys., 2014, 115, 194106 CrossRef.
- S. Summerfield, Universal low-frequency behaviour in the a.c. hopping conductivity of disordered systems, Philos. Mag. B, 1985, 52, 9 Search PubMed.
- A. Ghosh and A. Pan, Scaling of the Conductivity Spectra in Ionic Glasses: Dependence on the Structure, Phys. Rev. Lett., 2000, 84, 2188 CrossRef CAS PubMed.
- A. Ghosh and M. Sural, Conductivity spectra of sodium fluorozirconate glasses, J. Chem. Phys., 2001, 114, 3243 CrossRef CAS.
- C. R. Mariappan, AC conductivity scaling behaviour in grain and grain boundary response regime of fast lithium ionic conductors, Appl. Phys. A, 2014, 117, 847 CrossRef CAS.
- P. B. Macedo, C. T. Moynihan and R. Bose, Role of ionic diffusion in polarization in vitreous ionic conductors, Phys. Chem. Glasses, 1972, 13, 171 CAS.
- I. M. Hodge, M. D. Ingram and A. R. West, Impedance and modulus spectroscopy of polycrystalline solid electrolytes, J. Electroanal. Chem., 1976, 74, 125 CrossRef CAS.
- G. M. Tsangaris, G. C. Psarras and N. Kouloumbi, Electric modulus and interfacial polarization in composite polymeric systems, J. Mater. Sci., 1998, 33, 2027 CrossRef CAS.
- S. Halder, M. S. Sheikh, B. Ghosh and T. P. Sinha, Electronic structure and Electrical conduction by polaron hopping mechanism in A2LuTaO6 (A = Ba, Sr, Ca) Double Perovskite Oxides, Ceram. Int., 2017, 43, 11097 CrossRef CAS.
- M. Bakr Mohamed, H. Wang and H. Fuess, Dielectric relaxation and magnetic properties of Cr doped GaFeO3, J. Phys. D: Appl. Phys., 2010, 43, 455409 CrossRef.
- J. M. Bobe, J. M. Reau, J. Senegas and M. Poulain, F-ion conductivity and diffusion properties in ZrF4-based fluoride glasses with various NaF concentrations (0 < xNaF < 0.45), Solid State Ionics, 1995, 82, 39 CrossRef CAS.
- J. R. Macdonald, Scaling and modeling in the analysis of dispersive relaxation of ionic materials, J. Appl. Phys., 2001, 90, 153 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |