Open Access Article
Open Access ArticleGap maximum of graphene nanoflakes: a first-principles study combined with the Monte Carlo tree search method†
Zhi-Peng Cao,
Yu-Jun Zhao,
Ji-Hai Liao and
Xiao-Bao Yang *
*
Department of Physics, South China University of Technology, Guangzhou 510640, P. R. China. E-mail: scxbyang@scut.edu.cn
First published on 8th August 2017
Abstract
The energy gap of graphene nanoflakes is important for their potential application in nano-devices; however, it is still a challenge to perform a systemic search of systems with large gaps due to the presence of numerous candidates. Herein, we showed an ideal feasible approach that involved structural recognition, simplified effective evaluation, and successive optimization strategy. Considering the local bonding environment of carbon atoms, we first proposed a tight-binding model with the parameters fitted from the first-principles calculations of possible GNFs; this model provided an ideal avenue to screen the candidates with high accuracy and efficiency. Via combining the Monte Carlo tree search method and the congruence check, we determined the correlation between structures and the gap distributions according to the carbon numbers, and the results were confirmed via the first-principles calculations. The structural stabilities of the candidates with different numbers of hydrogen atoms might be modulated by the chemical potential of hydrogen, whereas the candidates with larger gaps might be more stable for the isomers with the same number of C and H atoms. Note that the gap variation is dominated by the structural features despite the quantum confinement effect since the gap maximum fluctuates rather than gradually decreasing with the increase in size. Our finding shows the gap variety of GNFs due to the configuration diversity, which may help explore the potential application of GNFs in nano-devices and fluorescence labeling in biomedicine.
1. Introduction
Graphene, a two-dimensional honeycomb crystal structure consisting of carbon atoms, is a zero band gap semiconductor.1,2 With the confinement of the edge, the gaps of graphene nano-ribbons (GNRs) appear where the effects are different for armchair and zigzag edges.3–7 The edge will also rearrange the sub-bands8 and introduce the anti-ferromagnetic edge states to break the symmetry9–11 that effectively modulate the band gap of armchair and zigzag GNRs. Some numerical simulation methods such as classic Monte Carlo (MC) simulation, mean field theory, and series expansion have been widely used in carbon nanomaterials12–15 and some alloys16–19 to investigate their magnetic properties. For graphene nanoflakes (GNFs), it has been reported that the photoluminescence (PL) peak energy reduces with the increase in size from 5 to 17 nm due to the quantum confinement effect (QCE), whereas the PL peak energy anomalously increases for the larger GNFs due to the change in the edges.20Theoretically, the structural stabilities and electronic properties of GNFs have been intensively investigated. With hydrogen passivation, the carbon cluster tends to be a graphene-like structure with zigzag edges.21 The energy gaps Eg of GNFs with zigzag edges are smaller than those with armchair structures in general.22 On the basis of the Lieb's theorem, the energy gaps will disappear when the number of carbon atoms NC is odd due to the imbalance of sublattices.23–27 Herein, we focused on the GNFs with even NC. To date, it is challenging to systematically investigate the GNFs due to two main obstacles: (i) for a given NC, it is difficult to screen the possible structures in a fast way, and there are numerous candidates as the NC increases and (ii) for a given structure, we have to determine the corresponding electronic properties, especially Eg, where the first-principles calculations are often computationally expensive.
To make the screening efficient, we can either reduce the time of evaluating the candidates or speed up the seeking procedure. Structure recognition and comparison28,29 are necessary to avoid the repetitious calculations, and we have developed an effective indexing scheme for the lattice clusters that enables fast structure comparison and congruence check. In our recent study,30 the Hückel molecular orbital (HMO) method was used for the fast estimation of the gaps of GNFs with NC < 25; however, there is disagreement for some structures with large gaps. In addition, the successive optimization strategy31 should be adopted to search larger GNFs based on the properties of the smaller GNFs since the enumeration is impossible due to the numerous possible candidates. Thus, a systemic search of candidates should include structural recognition, simplified and effective evaluation, and successive optimization strategy.
Herein, we have proposed an effective tight-binding (TB) model for the electronic properties of the hydrogen-terminated GNFs focusing on the effect of carbon atoms' local bonding. The parameters were fitted with the enumerated structures of GNFs with NC ≤ 34 based on the first-principles calculations. For larger GNFs, we combined the Monte Carlo tree search method with the congruence check to search the structures with large Eg under the TB model that were further confirmed by the first-principles calculations with higher accuracy. Finally, we obtained the maximum Eg as a function of size, and the typical structures with large gaps have been summarized for discussion.
2. Methods
2.1. Tight-binding model for the gaps of GNFs
The first-principles calculations were based on the density functional theory (DFT), as was implemented in the Vienna ab initio simulation package (VASP).32,33 We employed the projector augmented wave (PAW) method and the Perdew–Burke–Ernzerhof (PBE) functional of generalized gradient approximation (GGA)34,35 for the calculations of Eg. The plane wave cut-off energy was 520 eV, with the Brillouin zone sampled by a 1 × 1 × 1 Gamma-centered mesh. All the structures were fully relaxed by the conjugate gradient minimization, and the convergence of the energy on each atom was less than 10−3 eV.Taking into account the pz orbit of carbon atoms, the Hamiltonian can be written as follows:
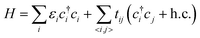 | (1) |
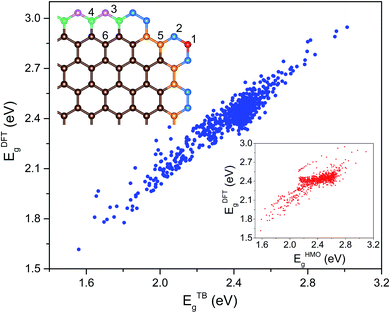
To characterize the environment effect, we divided the carbon atoms into six types according to the number of nearest neighbor carbon atoms, as shown in Fig. 1; this procedure resulted in thirteen types of hopping integral. We adopted the following procedure to fit these parameters. We performed DFT calculations on the 541 GNF structures with NC ≤ 34, which contained all the parameters, where all these 13 values were initialized in the range of ±0.5 eV around a general hopping integral of −3 eV.27 With the limitation in a range of ±2 eV, the parameters were optimized to make average deviations between TB and DFT results below the given precision.
Considering that there exist all 541 proper GNF structures when NC ≤ 34, the number is only 451 when NC = 36. Note that the GNF structures are the fragments of the planar hexagonal lattice with hydrogen atoms on the edge to maintain the sp2 hybridizations of graphene, where the center points of hexagons correspond to the fragments of the triangular lattice. As shown in Fig. S2 and S3,† an effective indexing scheme was adopted for the congruence check, where the structures with obvious deformation (Fig. S4†) were excluded. To balance the accuracy and efficiency, we enumerated 541 GNF structures with NC ≤ 34 and obtained the Hamilton matrices containing all transfer energies, where the Eg calculated by the DFT method was used to fit these thirteen parameters. These parameters are
| t′11 = −2.54, t′12 = −2.67, t′22 = −3.02, t′24 = −2.97, t′25 = −2.69, t′34 = −2.84, t′35 = −2.40, t′44 = −3.19, t′45 = −2.24, t′46 = −2.26, t′55 = −2.66, t′56 = −2.65, t′66 = −3.11 |
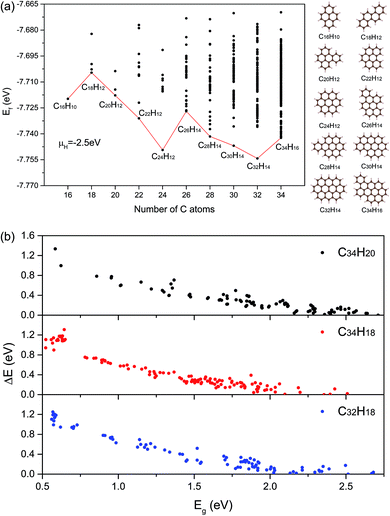
To describe the structural stabilities of GNFs, we defined the formation energy (Ef) as follows:36
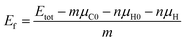 | (2) |
2.2. Monte Carlo tree search method
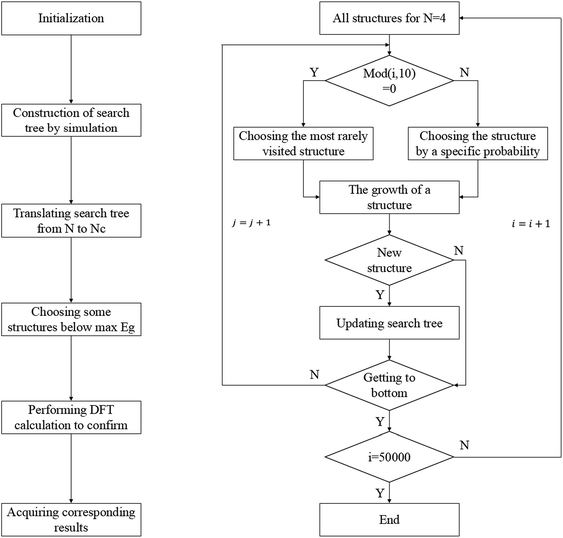
According to the enumeration with the congruence check, we obtained the gap distribution of the GNF structures with NC ≤ 34, as shown in Fig. S6.† Note that the gap maximum of GNFs with the given NC would not gradually decrease. In our TB model, the gap of GNFs can be easily estimated. However, the enumeration is impossible due to numerous candidates. Therefore, we introduced the Monte Carlo tree search with the previous TB method to screen possible structures with large Eg and confirmed the results using the DFT calculations with higher accuracy. Note that our Monte Carlo tree search method has a great difference from the classic MC simulation. Our method tends to find the GNF structures with large Eg rather than a simulation from initial states to equilibrium states. Therefore, the detailed balance is not pledged in our method.Fig. 3 shows the flow chart for searching the max Eg of GNFs with the Monte Carlo tree search method. The main idea of our strategy to screen the triangular candidates is select → expand → select. For example, we selected a structure with N centers of hexagons from the candidates according to a specific probability and randomly added a center to expand the structure to that with N + 1 centers of hexagons. The congruence check was performed to confirm that this new candidate has not been visited previously. These operations are repeated until N = 20, such that a simulation step gets finished. The probability of choosing a structure is determined by its Eg, which has been found by our TB model, where the selection probability (Pc) of searching for larger Eg structures can be written as follows:
| Pc = e−βEg | (3) |
3. Results and discussion
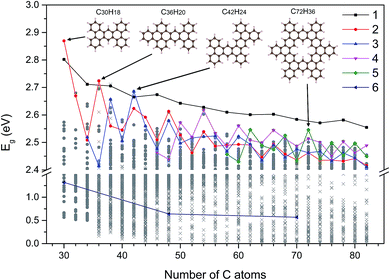
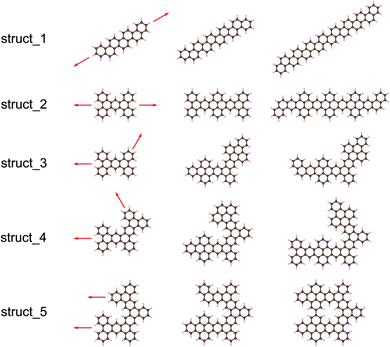
Using the Monte Carlo tree search method, we obtained the gap distribution of the possible largest Eg candidates and determined the structures with the largest Eg for various given NC. As shown in Fig. 4, we have screened the gap distribution for the structures with NC from 36 to 82 via our TB model; this data points indicate the breadth of the Monte Carlo tree search. The structures with large Eg are confirmed by the first-principles calculations, where those with the largest Eg are listed (Fig. S7†). There is a linear dependence between the results obtained from the first-principles calculations and those obtained from our TB model, where the structures with large gaps are screened, reflecting the reliability and efficiency of our method.Herein, we extracted five typical kinds of structures with the largest Eg, as shown in Fig. 5. Struct_1 has the shape of a straight line and all consist of armchair edge atoms, with similar electronic properties to the narrowest armchair GNRs.3 As shown in Fig. 4, the gaps of struct_1 in most cases are the largest, which would decrease slowly and close to 2.5 eV. Struct_2 is also a kind of candidates with a line shape, where the edge is of saw-tooth. For struct_3–5, the corners gradually appear to form a hexagon ring, where the red arrows indicate the expansion of the GNFs. The Eg curves of struct_2–5 show more fluctuations, which are commonly below that of struct_1. The gap variation of struct_6 is for the GNFs with the shape of rhombus with zigzag edges, where the gaps gradually decrease with the size. On comparing struct_6 with struct_1–5, it was found that the former had pure zigzag edges and the latter had high proportions of armchair edges. The type of edges for a GNF structure would have great effect on the Eg. We could expect that a narrow structure with a high proportion of armchair edges would be that with a large Eg, which is less influenced by the increase in size. These results are in agreement with the experimental20 observation, where the PL peak energy is anomalously increased with the increasing size due to the change in edge types. Note that struct_2 and struct_3 have larger Eg than struct_1 at NC = 30, NC = 36, NC = 42, where the three corresponding structures are of axial symmetry. Interestingly, the Eg of C72H36 is the local maximum of struct_5, with the symmetry of D6h. Thus, the GNFs' gap is dominated by the structural details since the largest Eg might fluctuate rather than gradually decreasing with the increasing size.
4. Conclusions
In summary, we have theoretically performed a systemic investigation of GNFs. The structures with NC ≤ 34 were enumerated with the structural recognition for the first-principles calculations, which were used to fit the parameters in our TB model considering the local bonding of carbon atoms. The average deviation of gap estimation with our TB model is as small as 0.04 eV, which provides a proper prediction of the GNFs' gaps. For the structures with NC > 34, the gap distribution was determined by the Monte Carlo tree search method, as confirmed by the first-principles calculations, where the typical structures with large gaps were found. Despite the QCE, the gap maximum fluctuates rather than gradually decreasing with the increasing size. The properties of GNFs should be further modulated via the control of structural details; this phenomenon might extend the potential application of GNFs. In addition, the Monte Carlo tree search combined with structural recognition provides an inversed property design approach for GNFs as well as other nanomaterials.Acknowledgements
This work was supported by NSFC (Grant No. 11474100 and 11574088) and Guangdong Natural Science Funds for Distinguished Young Scholars (Grant No. 2014A030306024).References
- A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109 CrossRef CAS.
- D. S. L. Abergel, V. Apalkov, J. Berashevich, K. Ziegler and T. Chakraborty, Adv. Phys., 2010, 59, 261 CrossRef CAS.
- Y.-W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216803 CrossRef PubMed.
- S. Okada, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 041408 CrossRef.
- L. Pisani, J. A. Chan, B. Montanari and N. M. Harrison, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 064418 CrossRef.
- L. Brey and H. A. Fertig, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 235411 CrossRef.
- O. Hod, J. E. Peralta and G. E. Scuseria, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 233401 CrossRef.
- H. Zheng, Z. F. Wang, T. Luo, Q. W. Shi and J. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 165414 CrossRef.
- H. Lee, Y.-W. Son, N. Park, S. Han and J. Yu, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 174431 CrossRef.
- K. Nakada, M. Fujita, G. Dresselhaus and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 17954 CrossRef CAS.
- M. Fujita, K. Wakabayashi, K. Nakada and K. Kusakabe, J. Phys. Soc. Jpn., 1996, 65, 1920 CrossRef CAS.
- R. Masrour and A. Jabar, J. Magn. Magn. Mater., 2017, 426, 225 CrossRef CAS.
- R. Masrour and A. Jabar, Superlattices Microstruct., 2016, 98, 78 CrossRef CAS.
- R. Masrour, A. Jabar, A. Benyoussef and M. Hamedoun, J. Magn. Magn. Mater., 2015, 395, 7 CrossRef CAS.
- R. Masrour, L. Bahmad, M. Hamedoun, A. Benyoussef and E. K. Hlil, Solid State Commun., 2013, 162, 53 CrossRef CAS.
- R. Masrour, A. Jabar, E. K. Hlil, M. Hamedoun, A. Benyoussef, A. Hourmatallah, A. Rezzouk, K. Bouslykhane and N. Benzakour, J. Magn. Magn. Mater., 2017, 428, 12 CrossRef CAS.
- R. Masrour, E. K. Hlil, M. Hamedoun, A. Benyoussef, O. Mounkachi and H. El Moussaoui, J. Magn. Magn. Mater., 2014, 361, 197 CrossRef CAS.
- R. Masrour, E. K. Hlil, M. Hamedoun, A. Benyoussef, O. Mounkachi and H. El Moussaoui, Phys. A, 2014, 414, 249 CrossRef CAS.
- R. Masrour, L. Bahmad, M. Hamedoun, A. Benyoussef and E. K. Hlil, Phys. Lett. A, 2014, 378, 276 CrossRef CAS.
- S. Kim, et al., ACS Nano, 2012, 6, 8203 CrossRef CAS PubMed.
- D. P. Kosimov, A. A. Dzhurakhalov and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 195414 CrossRef.
- A. Kuc, T. Heine and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 085430 CrossRef.
- E. H. Lieb, Phys. Rev. Lett., 1989, 62, 1201 CrossRef PubMed.
- J. Fernández-Rossier and J. J. Palacios, Phys. Rev. Lett., 2007, 99, 177204 CrossRef PubMed.
- O. V. Yazyev, Phys. Rev. Lett., 2008, 101, 037203 CrossRef PubMed.
- W. L. Wang, O. V. Yazyev, S. Meng and E. Kaxiras, Phys. Rev. Lett., 2009, 102, 157201 CrossRef PubMed.
- M. Ezawa, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 245415 CrossRef.
- L. Liao, Y. Zhao, Z. Cao and X. Yang, Sci. Rep., 2017, 7, 392 CrossRef PubMed.
- X. Li, X. Yang and Y. Zhao, J. Chem. Phys., 2017, 146, 154108 CrossRef PubMed.
- L. Qu, Z. Liu and X. Yang, Mol. Simul., 2017, 43, 558 CrossRef CAS.
- D. Silver, et al., Nature, 2016, 529, 484 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1998, 80, 891 CrossRef CAS.
- X. Yang, Y. Zhao, H. Xu and B. I. Yakobson, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 205314 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra06891c |
| This journal is © The Royal Society of Chemistry 2017 |