V–VO₂ core–shell structure for potential thermal switching

Abstract

Since the cold start of the internal combustion engine is not fuel efficient for vehicles, a warm start is desired. In this work, we propose to use thermal switching materials to warm-up the engine quickly at the cold start. We found that the V–VO₂ core–shell structure can be a thermal switching material, which yields a higher electrical conductivity due to the electron transfer from V to VO₂ above the insulator to metal transition temperature. The surface of V particles was converted into VO₂ by controlled annealing in air, resulting in a V–VO₂ core–shell structure. With such a V–VO₂ core–shell structure, electrical conductivity increased from 2.1 × 10⁵ to 5.1 × 10⁵ S m⁻¹ through the insulator-to-metal transition, resulting in an electronic thermal conductivity increase from 1.51 to 4.87 W m⁻¹ K⁻¹.

---

Introduction

The internal combustion (IC) engine converts chemical energy in fuel to mechanical energy. The average fuel conversion efficiency of an IC engine is in the range of 35–40%,¹ when the engine is completely warmed up with the lubricant temperature at 100–110 °C.^2,3 However, it is only about 9% at the beginning when the engine is cold (with the lubricant below 25 °C).^3,4 Therefore, knowledge of how to get the engine warmed up to its optimum temperature very quickly, is extremely important to the overall fuel efficiency of especially personal cars, since vehicles need about 5 to 10 minutes to warm up to their optimal efficiency.³ A warming up time of 5–10 min for each cold start is a very significant portion of the total driving time for personal cars. Ideally, the engine will warm up to the optimal temperature in the shortest time, if the thermal loss is zero below that temperature, but very high above that temperature to keep the engine at the optimal temperature for the best efficiency. This requires materials with thermal conductivity very low, to prevent heat from leaking out, below a certain temperature and very high above that temperature, to dissipate the heat when the engine is warmed up, preventing the engine from overheating. Such a function can only be achieved by a thermal switch: off/on, meaning a significant thermal conductivity change from very low to very high at the required temperature. Unfortunately such a thermal switch within the required temperature range does not exist. Our study mainly aims at demonstrating such a concept in a material structure.

It is well known that thermal energy in solid is transported by two components: lattice (κ_L) and charges⁵ (κ_e = L_oσT, where L_o = 2.44 × 10⁻⁸ W Ω K⁻² is the Lorenz number, σ the electrical conductivity, and T the absolute temperature).⁶ In order to have a significant change, a phase change is necessary since two different structures will have different κ_L and κ_e. With increase in κ_e, we can expect increase in κ, if κ_L does not change too much.

In previous studies, some of the materials on their solid–liquid phase transition showed high switching capability, for example, Zn₃Sb₂,⁷ Cd_0.999SbAg_0.001,⁸ CdSb,^8,9 AlSb,^10–12 InSb¹³ etc., undergoes semiconductor to metal transition on melting, with κ_high/κ_low ratio of 15.4, 8.25, 4.95, 5.05, 3.76, respectively. However, due to their higher melting temperature, these materials are not suitable for our proposed application in IC engines. Additionally, (C₂H₄)_n¹⁴ and NbO₂ (ref. 15–18) undergo solid–solid phase transition at 395 and 1080 K. For NbO₂ thermal conductivity increases above transition temperature with κ_high/κ_low ratio is only 1.02, and thermal conductivity decreases above transition temperature for (C₂H₄)_n. Recently, different strategies have been used to demonstrate thermal switching,^19–23 including in homogeneously mass-loaded carbon and boron nitride nanotubes,¹⁹ bulk material made of two oxides with different thermal conductivities,²² graphite/hexadecane suspension,²⁴ van der Waals interface effect on boron nano ribbons,²⁵ and electrochemical change on LiCoO₂,²⁶ however either thermal conductivity decreases at higher temperature or if increases, the values of κ_high/κ_low is less than 2. Furthermore, the thermal conductivity ratio (κ_high/κ_low) of 2–5 have been observed by electrochemically tuning the intercalated amount of lithium (Li) in the van der Waals gaps in the bulk MoS₂.²⁷

Vanadium dioxide VO₂ has recently been studied for its insulator(solid)–metal(solid) phase transition at 68 °C, from monoclinic (insulating) to tetragonal rutile (metallic) crystal structure in bulk materials,^28–33 thin films^34–40 and nanocrystals.^41–45 The associated electrical conductivity increases from 10² S m⁻¹ at room temperature to 10³–10⁵ S m⁻¹ at 120 °C.^28–46 Accordingly, thermal conductivity increase is expected^34,35 due to the increase in κ_e.

The best reported values of the thermal conductivity of the VO₂ thin film³⁴ and polycrystalline³¹ samples are shown in Fig. S1a in the ESI.† It is clear that even though the electrical conductivity changes by a factor of ∼10 in polycrystalline and more than 100 in film (Fig. S1b in the ESI†), the thermal conductivity only changes by a factor of less than 2, either increases in thin film^34,35 or decreases in polycrystalline.³¹ The reason is that the absolute electrical conductivity of both materials above the insulator–metal transition is not high enough to result in a high κ_e, so the total κ is not high in metallic phase. It is clear only when the electrical conductivity is high enough, then change in κ_e can lead to a high total thermal conductivity. Since the total thermal conductivity of VO₂ in the insulating state is of 3.5–4.5 W m⁻¹ K⁻¹, according to Wiedemann–Franz (W–F) relationship,⁶ we need to have electrical conductivity higher than 6 × 10⁶ S m⁻¹ in the metallic state to result in electronic thermal conductivity of about 10 times higher. We know that the electrical conductivity of VO₂ cannot satisfy this requirement, so we have to look for new ideas to get the required high electrical conductivity.

Core–shell structure has been proved as a noble way to improve the material properties including electrochemical catalytic performances,^47–50 photocatalytic performances,^51,52 as well as electrical properties.^51,53–56 Such core–shell structure has been reported in the form of nanoparticle,^47–50 nano rod,^51,52 and nanowire.^53–56 In this paper, we report our studies on a V–VO₂ core–shell structure (Fig. 1(a)), hoping for the free electrons transferring from V to VO₂ above the phase transition temperature to reach the electrical conductivity close to that of V: 5 × 10⁶ S m⁻¹.⁵⁷ Below the phase transition temperature, it is insulator, since all the electrons of V are confined in V by VO₂ shell. However, above the phase transition temperature, VO₂ becomes metallic and the free electrons of V can move into VO₂ to make the bulk more conducting when VO₂ is thin enough. For our V–VO₂ core–shell system, it could be possible to achieve thermal conductivity increase by a factor of 5, if we can get dense sample so that in the metallic phase κ would be close to that of vanadium (∼30.7 W m⁻¹ K⁻¹)⁵⁸ and in the insulating phase κ would be close to that of VO₂ (3–6 W m⁻¹ K⁻¹) when each vanadium particles in sample enclosed completely by thin insulating VO₂ layer. We're interested in this system because of its temperature driven solid-state thermal switching at temperature close to the optimum temperature of lubricant in the IC engine.

Fig. 1 (a) Schematic of the V–VO₂ core–shell structure, (b) XRD pattern of the step annealed V–VO₂ powder samples, (c) electrical conductivity of core–shell V–VO₂ bar samples annealed in air at different conditions as shown, and (d) XPS spectrum of 7 + 7 + 7 h sample, showing the chemical state of V.

Previously, different methods have been used to prepare VO₂ thin film. Some of the literatures have reported the preparation of VO_x film first, and anneal it at different atmospheres (in air, O₂, N₂, Ar, etc.) in order to get or improve VO₂ phase.^59–62 The annealing temperature is different in different reports. Similarly, the preparation of VO₂ films from V precursors have been reported in many papers.^63–75 Annealing V resulted in different oxides depending on availability of oxygen through the depth, with V₂O₅ on the top, VO₂ in the middle, and VO_0.5–1.0 close to the substrate of the film.^69–73 Such variation in oxidation state of V was controlled either by supplying low pressure oxygen or by making very thin V film to make the oxygen availability similar throughout the thickness of the film.⁷⁵

In our case, the V–VO₂ core–shell structure was formed by making the compacted pellet first and then converted the surface of each V particle into VO₂ by controlled annealing in air. The formation of VO₂ was confirmed by different measurements such as DSC heat flow curve and electrical resistivity. The XRD characterization and TEM analysis further confirmed it. The electrical and thermal conductivity near the phase transition temperature was also studied to support the concept.

Experimental

The V–VO₂ core–shell structure was developed by a three step annealing of the pressed pellets in air. The V metal powder (99.5%, Alfa Aesar) with particle size <44 micron was cold pressed at ∼460 MPa pressure for 3 minutes to make porous disks. The disks were then cut into bars of 1.5 mm × 1.5 mm × 11 mm, and finally the bars were annealed in air in a tube furnace. The annealing was done at 350, 380, and 425 °C for 7 hour at each temperature, with a heating rate of 2 K min⁻¹. For the XRD analysis, V powder was annealed. The phase formation was studied by XRD (X'Pert PRO PANalytical) with Cu-Kα radiation at room temperature and transmission electron microscope (TEM JEOL 2100F). The microstructure of the polished surface of the sample was studied by a scanning electron microscope (SEM, JEOL 6304F). The electrical as well as thermal conductivity of the samples were measured in the same direction by a four probe method using the thermal transport option (TTO) of a physical properties measurement system (PPMS, D060, Quantum Design) from room temperature to 120 °C. The latent heat of the sample was measured by the differential scanning calorimetry (DSC, 404 C, Netzsch). The errors for electrical conductivity and thermal conductivity are 3% and 5%, respectively.

Results and discussion

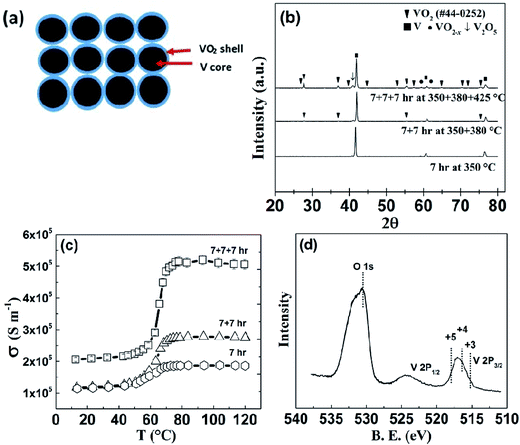
The formation of V–VO₂ core–shell structure (Fig. 1(a)) by oxidizing the surface of V particles is shown in the XRD patterns (Fig. 1(b)). The electrical conductivity of the samples prepared at different conditions is shown in Fig. 1(c). As shown, the sample annealed at 350 °C for 7 h clearly shows the transition in electrical conductivity across the phase transition of VO₂. This transition at 68 °C indicates the initiation of formation of VO₂, but very thin, since there is no visible peaks of VO₂ on XRD pattern of powder sample, annealed in the same condition (Fig. 1(b)). Another sample was annealed at 350 °C for 7 hours plus 380 °C for 7 hour, and it was found that the transition in conductivity is sharper. Upon further annealing, a third sample annealed at 350 °C for 7 hours, then 380 °C for 7 hours, and then 425 °C for 7 hour, shows a much sharper change in electrical conductivity (Fig. 1(c)) by a factor of 2.5, as well as clear appearance of the peaks of VO₂ in the XRD pattern (Fig. 1(b)). In comparing the XRD peak intensity, we noticed that the VO₂ is still thin, but V₂O₅ started to form indicated by the arrow, which led us to not anneal the samples at even higher temperature. X-ray photoelectron spectroscopy (XPS) analysis (Fig. 1(d)) also shows that the sample annealed at 350 °C for 7 h + 380 °C for 7 h + 425 °C for 7 h (named as “7 + 7 + 7 h”) contains VO₂ as well as V₂O₅. As we know the 2P_3/2 peak of V³⁺, V⁴⁺, and V⁵⁺ lies at 515.29 eV,⁷⁶ 516.35 eV,⁷⁷ and 517.91 eV (ref. 77) respectively. For our 7 + 7 + 7 h annealed sample, VO₂ is present as major phase, with trace amount of other oxides of vanadium with oxidation states from +3 to +5 as impurity phase. As the sample annealed at 350 + 380 + 425 °C has the highest electrical conductivity above the transition, we chose this annealing condition for further study. With increase in annealing temperature and time, the sample is also denser, that's probably why the electrical conductivity in the insulating phase is also increased.

HRTEM analysis of the V–VO₂ core–shell samples is shown in Fig. 2. The high magnification image (Fig. 2(b)) taken at the edge of the sample (Fig. 2(a)) shows the lattice spacing of 0.206 nm, corresponding to the (120) plane of VO₂.

Fig. 2 (a) Low magnification TEM image of 7 + 7 + 7 h sample, (b) HRTEM image of the edge of 7 + 7 + 7 h sample, and (c) specific heat absorption curve of the 7 + 7 + 7 h sample compared with that of VO₂ bulk polycrystalline sample.

The amount of VO₂ formed on V is calculated by the latent heat measurement using DSC. Fig. 2(c) shows the heat absorption curve of the sample by DSC measurement. It is interesting to note that the peak of DSC curve for V–VO₂ core–shell structured sample is shifted towards lower temperature due to the size effect.^37,38,46 The latent heat for polycrystalline VO₂ is found to be 43.37 J g⁻¹ (which is a little bit lower than the reported value (51.65 ± 0.25) J g⁻¹ for the single crystal³⁰), but that of the V–VO₂ core–shell sample is 4.97 J g⁻¹, meaning only about 9–11% (mass) is VO₂ and the rest about 90% is still V with trace amount of other vanadium oxides as impurity phase.

The thermal conductivity of the samples is shown in Fig. 3(a). It clearly shows a gradual thermal conductivity increase across the phase transition. For the 7 + 7 + 7 h annealed sample, thermal conductivity increased from 8.08 W m⁻¹ K⁻¹ at room temperature to 9.89 W m⁻¹ K⁻¹ at 120 °C, by about 22%. The room temperature total thermal conductivity increased with increasing temperature and time, which is probably due to better and better structure connection of the grains. Hall measurement shows that the carrier concentration increases across the transition (Fig. 3(d)), a clear demonstration of the core–shell modulation doping concept: electrons spill from V into VO₂ above the transition. Since the carrier concentration of 7 + 7 + 7 h sample is higher than polycrystalline bulk VO₂ sample³³ (inset in Fig. 3(d)) before and after phase transition, which further confirms that the increase in electron density of 7 + 7 + 7 h sample above transition temperature is due to the electron spill from V into VO₂. The Hall mobility (Fig. 3(e)) increases with temperature across the transition, which also supports the increase in electrical conductivity above the transition, different from most of the reports on VO₂ (ref. 33, 36, 78 and 79) showing decrease in mobility. The small change in carrier density indicates that either in the metallic phase the electrons transferred from V to VO₂ are not as many as we hope for, or the electrons blocked within V by VO₂ in the insulating phase are not as many as we hoped for, or both, which is not understood right now. The electronic thermal conductivity (κ_e) (Fig. 3(b)) calculated by using W–F relationship, increased from 1.51 W m⁻¹ K⁻¹ at room temperature to 4.87 W m⁻¹ K⁻¹ at 120 °C for 7 + 7 + 7 h sample, with the lattice contribution decreased by 1.55 W m⁻¹ K⁻¹ (Fig. 3(c)). Previous reports^29,31,33,80 also showed similar type of decrease in lattice thermal conductivity for sample with VO₂ only, however, our sample has VO₂ only 9–11% of the whole mass of the sample.

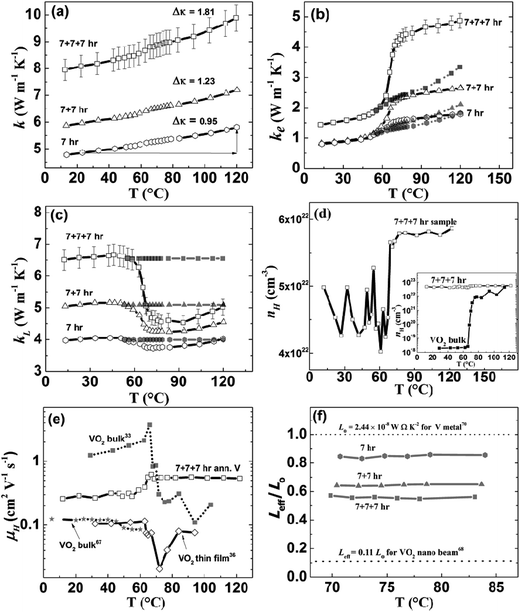Fig. 3 (a) Thermal conductivity of V–VO₂ core–shell samples, (b) electronic thermal conductivity of V–VO₂ core–shell samples (empty symbol: using W–F law and filled symbol: effective value), (c) lattice thermal conductivity of V–VO₂ core–shell samples (empty symbol: using W–F law and filled symbol: effective value), (d) carrier concentration of 7 + 7 + 7 h sample and inset shows the comparison of carrier concentration of polycrystalline bulk VO₂ (ref. 33) with that of 7 + 7 + 7 h sample, (e) comparison of mobility of the 7 + 7 + 7 h sample with that of reported polycrystalline bulk as well as thin film VO₂, and (f) effective Lorenz number of core–shell V–VO₂ samples prepared at three different conditions.

Even though the electrical conductivity of V could be close to 5 × 10⁶ S m⁻¹ at room temperature,⁵⁷ our V–VO₂ core–shell samples only showed an electrical conductivity of about 5 × 10⁵ S m⁻¹, an order of magnitude lower, which is most likely due to the low density of 5.28 g cm⁻³ for our V–VO₂ core–shell sample (only about 90% of the theoretical density of 5.90 g cm⁻³). Such a low density will certainly results in low electrical conductivity due to the electron scattering in porous areas (SEM image in Fig. S3 in the ESI†). Another possible reason for the low electrical conductivity is the presence of V₂O₅ phase, since it has very low electrical conductivity (∼50 S m⁻¹ at 120 °C).⁸¹ According to the XRD pattern of 7 + 7 + 7 h sample (after polishing its surface), there exist a trace amount of other oxides like VO_2−x (VO_0.5, etc.), which might also be responsible for the lowered electrical conductivity. For our sample, VO_2−x phase couldn't be avoided completely, since there exist an oxygen gradient along the radial direction of each particle. We also found that the V₂O₅ phase is present only on the outer surface of each particle since XRD of the polished samples don't have V₂O₅ peak (Fig. S2 in the ESI†).

In principle, the intrinsic thermal conductivity of V–VO₂ core–shell above the transition could be close to that of V (∼30 W m⁻¹ K⁻¹),⁵⁸ but it is actually much lower (9.89 W m⁻¹ K⁻¹) due to the high porosity (low electrical conductivity), as shown in SEM image in Fig. S3 in the ESI,† as well as the presence of other vanadium oxides (XRD pattern in Fig. 1(b) and S2 in the ESI†). We now face a challenge how to oxidize the outer surface of each particle of a 100% dense pellet. Similarly, we were unable to avoid V₂O₅ phase on outer surface of each core–shell particle.

The electronic thermal conductivity of 7 + 7 + 7 h sample is increased by 3.36 W m⁻¹ K⁻¹; however, total thermal conductivity increased only by 1.81 W m⁻¹ K⁻¹, across the phase transition. Since, VO₂ is only 10% (by mass) present in our sample, the lattice thermal conductivity across the transition shouldn't change by such a large amount (by ∼24% as in Fig. 3(c)), as previous reports shows ∼11% decrease in pure VO₂ nano beam⁸⁰ (calculated theoretically) and ∼27% decrease in VO₂ polycrystalline samples^29,31 (calculated using W–F relationship). Therefore, we can assume lattice thermal conductivity in the metallic phase (filled symbol in Fig. 3(c)), similar to that in the insulating phase. The effective electrical thermal conductivity (κ^eff_e) in the metallic phase can be calculated by subtracting lattice thermal conductivity in the insulating phase from the total thermal conductivity in the metallic phase, as shown by filled symbol in Fig. 3(b). The effective Lorenz number in the metallic phase can be calculated by using 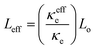. The effective Lorenz number (Fig. 3(f)) of 7 h sample is found to be ∼0.85 L_o which is closer to Sommerfeld value (L_o); however, with increase in amount of VO₂ on sample, the effective Lorenz number (L_eff) decreased to 0.65 L_o for 7 + 7 h and 0.56 L_o for 7 + 7 + 7 h sample, which indicates the deviation of W–F law with increase in concentration of VO₂ in the sample. Such a large deviation in W–F law with only 10% VO₂ could be due to the fact that each V particle is surrounded by very thin VO₂ layer and effect is significant. The decrease in value of effective Lorenz number with increased amount of VO₂ is in agreement with the report by Lee et al.,⁸⁰ as they have reported effective Lorenz number for pure VO₂ nano-beam in the metallic phase equal to only ∼0.11 L_o. They also show the switching behavior of thermal conductivity on VO₂ samples doped with the tungsten (W). This further indicates that, with only VO₂ it is not possible to get increased total thermal conductivity by pursuing higher electrical conductivity. However, the core–shell concept is clearly demonstrated and can be applied to the W doped VO₂ materials, which requires a significant amount of work and is out of the scope of this paper. Similarly, the material having phase transition temperature ∼100 °C is better for the application. Therefore, VO₂ need to be modified to meet the requirement of phase transition temperature or need to search for new materials with phase transition temperature between 80 and 100 °C to get better performance.

Conclusion

We designed and studied a V–VO₂ core–shell structure to realize a potential large change of thermal conductivity at the phase transition of VO₂ due to transfer of the free electrons from V to VO₂ above the transition temperature via modulation doping principle. The V–VO₂ core–shell structure can potentially be used for thermal switching. The VO₂ shell was formed by annealing V in air at limited temperatures to avoid formation of V₂O₅ and other higher oxides. We indeed observed higher electrical conductivity in V–VO₂ core–shell samples than any of the reported polycrystalline bulk VO₂ materials, but still about an order of magnitude lower than the expected value due to mainly low density (about 90%). Electronic thermal conductivity increased by 3.36 W m⁻¹ K⁻¹; however, total thermal conductivity increased by only 1.81 W m⁻¹ K⁻¹ across the phase transition, indicating the effective Lorenz number to be 0.56 L_o in the metallic phase. Even though the overall thermal conductivity increased only by 22%, it demonstrated the concept: increase thermal conductivity through increase of electronic thermal conductivity as a result of solid–solid phase transition.

Acknowledgements

This work was supported by the US Department of Energy under a Contract DE-SC0010831 and Toyota Motors of North America.

References

1. J. B. Heywood, Internal Combustion Engine Fundamentals, McGraw-Hill, New York, 1988.
2. J. P. Zammit, P. J. Shayler and I. Pegg, presented in part at 10th Vehicle Thermal Management Systems Conference and Exhibition, Coventry, United Kingdom, 2010.
3. J. Trapy and P. Damiral, SAE [Tech. Pap.], 1990, 902089.
4. F. Will and A. Boretti, SAE Int. J. Engines, 2011, 4, 175–187.
5. C. A. Wert and R. M. Thomson, Physics of Solids, McGraw-Hill, New York, 1970.
6. R. Franz and G. Weidemann, Ann. Phys., 1853, 165, 497–531.
7. A. Bath, J. G. Gasser and R. Kleim, Phys. Lett. A, 1982, 91, 355.
8. S. Wang, J. Yang, L. Wu, P. Wei, J. Yang, W. Zhang and Y. Grin, Chem. Mater., 2015, 27, 1071.
9. S. Nakamura, T. Hibiya and F. Yamamoto, J. Appl. Phys., 1990, 68, 5125.
10. E. F. Steigmeier and I. Kudman, Phys. Rev., 1966, 141, 767.
11. W. Nakwaski, J. Appl. Phys., 1988, 64, 159.
12. N. F. Mott and A. S. Alexandrov, Sir Nevill Mott: 65 Years in Physics, World Scientific, Singapore, 1995.
13. V. I. Fedorov and V. I. Machuev, Fiz. Tekh. Poluprovodn., 1972, 6, 173.
14. T. Zhang and T. Luo, ACS Nano, 2013, 7, 7592.
15. M. Kaviany, Heat Transfer Physics, Cambridge University Press, New York, 2014.
16. R. F. Janninck and D. H. Whitmore, J. Phys. Chem. Solids, 1966, 27, 1183.
17. A. O'Hara, T. N. Nunley, A. B. Posadas, S. Zollner and A. A. Demkov, J. Appl. Phys., 2014, 116, 213705.
18. A. Y. Wu and R. J. Sladek, Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 26, 2159.
19. C. W. Chang, D. Okawa, A. Majumdar and A. Zettl, Science, 2006, 314, 1121–1124.
20. H. Tian, D. Xie, Y. Yang, T.-L. Ren, G. Zhang, Y.-F. Wang, C.-J. Zhou, P. G. Peng, L.-G. Wang and L.-T. Liu, Sci. Rep., 2012, 2, 523.
21. G. Zhang and H. Zhang, Nanoscale, 2011, 3, 4604–4607.
22. W. Kobayashi, Y. Teraoka and I. Terasaki, Appl. Phys. Lett., 2009, 95, 171905.
23. D. Sawaki, W. Kobayashi, Y. Moritomo and I. Terasaki, Appl. Phys. Lett., 2011, 98, 081915.
24. R. Zheng, J. Gao, J. Wang and G. Chen, Nat. Commun., 2011, 2, 289.
25. J. Yang, Y. Yang, S. W. Waltermire, X. Wu, H. Zhang, T. Gutu, Y. Jiang, Y. Chen, A. A. Zinn, R. Prasher, T. T. Xu and D. Li, Nat. Nanotechnol., 2012, 7, 91–95.
26. J. Cho, M. D. Losego, H. G. Zhang, H. Kim, J. Zuo, I. Petrov, D. G. Cahil and P. V. Braun, Nat. Commun., 2013, 5, 4035.
27. G. Zhu, J. Liu, Q. Zheng, R. Zhang, D. Li, D. Banerjee and D. G. Cahill, Nat. Commun., 2016, 7, 13211.
28. F. J. Morin, Phys. Rev. Lett., 1959, 3, 34.
29. V. N. Andreev, F. A. Chudnovskii, A. V. Petrov and E. I. Terukov, Phys. Status Solidi A, 1978, 48, K153.
30. C. N. Berglund and H. J. Guggenheim, Phys. Rev., 1969, 185, 1022.
31. J. Chen, X. Liu, X. Yuan, Y. Zhang, Y. Gao, Y. Zhou, R. Liu, L. Chen and N. Chen, Chin. Sci. Bull., 2012, 57, 3393–3396.
32. M. Liu, A. J. Sternbach, M. Wagner, T. V. Slusar, T. Kong, S. L. Bud'ko, S. Kittiwatanakul, M. M. Qazilbash, A. Mcleod, Z. Fei, E. Abreu, J. Zhang, M. Goldflam, S. Dai, G. X. Ni, J. Lu, H. A. Bechtel, M. C. Martin, M. B. Raschke, R. D. Averitt, S. A. Wolf, H. T. Kim, P. C. Canfield and D. N. Basov, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 245155.
33. K. Dahal, Q. Zhang, R. He, I. K. Mishra and Z. Ren, J. Appl. Phys., 2017, 121, 155103.
34. H. Kizuka, T. Yagi, J. Jia, Y. Yamashita, S. Nakamura, N. Taketoshi and Y. Shigesato, Jpn. J. Appl. Phys., 2015, 54, 053201.
35. D.-W. Oh, C. Ko, S. Ramanathan and D. G. Cahill, Appl. Phys. Lett., 2010, 96, 151906.
36. D. Ruzmetov, D. Heiman, B. B. Claflin, V. Narayanamurti and S. Ramanathan, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 153107.
37. L. Dai, C. Cao, Y. Gao and H. Luo, Sol. Energy Mater. Sol. Cells, 2011, 95, 712–715.
38. H. Liu, J. Lu, M. Zheng, S. H. Tang, C. H. Sow, X. Zhang and K. Lin, Opt. Express, 2014, 22, 30748.
39. J. Lu, K. G. West and S. A. Wolf, Appl. Phys. Lett., 2008, 93, 262107.
40. K. G. West, J. Lu, J. Yu, D. Kirkwood, W. Chen, Y. Pei, J. Claassen and S. A. Wolf, J. Vac. Sci. Technol., A, 2008, 26, 133.
41. J. Wu, Q. Gu, B. S. Guiton, N. P. de Leon, L. Ouyang and H. Park, Nano Lett., 2006, 6, 2313.
42. J. Cao, E. Ertekin, V. Srinivasan, W. Fan, S. Huang, H. Zheng, J. W. L. Yim, D. R. Khanal, D. F. Ogletree, J. C. Grossman and J. Wu, Nat. Nanotechnol., 2009, 4, 732–737.
43. A. Tselev, E. Strelcov, I. A. Luk'yanchuk, J. D. Budai, J. Z. Tischler, I. N. Ivanov, K. Jones, R. Proksch, S. V Kalinin and A. Kolmakov, Nano Lett., 2010, 10, 2003–2011.
44. T. J. Huffman, P. Xu, M. M. Qazilbash, E. J. Walter, H. Krakauer, J. Wei, D. H. Cobden, H. A. Bechtel, M. C. Martin, G. L. Carr and D. N. Basov, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 115121.
45. X. He, T. Xu, X. Xu, Y. Zeng, J. Xu, L. Sun, C. Wang, H. Xing, B. Wu, A. Lu, D. Liu, X. Chen and J. Chu, Sci. Rep., 2014, 4, 6544.
46. L. Dai, S. Chen, J. Liu, Y. Gao, J. Zhou, Z. Chen, C. Cao, H. Luo and M. Kanehira, Phys. Chem. Chem. Phys., 2013, 15, 11723–11729.
47. H. A. Esfahani, L. Wang, Y. Nemoto and Y. Yamauchi, Chem. Mater., 2010, 22, 6310–6318.
48. L. Wang and Y. Yamauchi, Chem. Mater., 2011, 23, 2457–2465.
49. C. Li and Y. Yamauchi, Phys. Chem. Chem. Phys., 2013, 15, 3490–3496.
50. H. A. Esfahani, M. Imura and Y. Yamauchi, Angew. Chem., Int. Ed., 2013, 52, 13611–13615.
51. D. E. Schipper, Z. Zhao, A. P. Leitner, L. Xie, F. Qin, M. K. Alam, S. Chen, D. Wang, Z. Ren, Z. Wang, J. Bao and K. H. Whitmire, ACS Nano, 2017, 11, 4051–4059.
52. S. Khanchandani, S. Kundu, A. Patra and A. K. Ganguli, J. Phys. Chem. C, 2012, 116, 23653–23662.
53. P. Parkinson, H. J. Joyce, Q. Gao, H. H. Tan, X. Zhang, J. Zou, C. Jagadish, L. M. Herz and M. B. Johnston, Nano Lett., 2009, 9, 3349–3353.
54. B.-M. Nguyen, Y. Taur, S. T. Picraux and S. A. Dayeh, Nano Lett., 2014, 14, 585–591.
55. B. Ganjipour, S. Sepheri, A. W. Dey, O. Tizno, B. M. Borg, K. A. Dick, L. Samuelson, L.-E. Wernersson and C. Thelander, Nanotechnology, 2014, 25, 425201.
56. D. C. Dillen, K. Kim, E.-S. Liu and E. Tutuc, Nat. Nanotechnol., 2014, 9, 116–120.
57. P. D. Desai, H. M. James and C. Y. Ho, J. Phys. Chem. Ref. Data, 1984, 13, 1097.
58. W. D. Jung, F. A. Schmidt and G. C. Danielson, Phys. Rev. B: Solid State, 1977, 15, 659.
59. C. Chen, X. Yi, J. Zhang and X. Zhao, Infrared Phys. Technol., 2001, 42, 87–90.
60. S. B. Wang, S. B. Zhou, G. Huang and X. J. Yi, Surf. Coat. Technol., 2005, 191, 330–334.
61. J. H. Li and N. Yuan, Formation Mechanism of the VO2 Polycrystalline Film Prepared by Modified Ion-beam Enhanced Deposition 2004, Proc. SPIE 5774, Fifth International Conference on Thin Film Physics and Applications, 2004.
62. K. van Steensel, F. van de Burg and C. Kooy, Philips Res. Rep., 1967, 22, 170.
63. G. A. Rozgonyi and W. J. Polito, J. Electrochem. Soc., 1968, 115, 56.
64. R. J. Powell, C. N. Berglund and W. E. Spicer, Phys. Rev., 1969, 178, 1410.
65. I. Balberg and S. Trokman, J. Appl. Phys., 1975, 46, 2111.
66. A. A. Bugaev, V. V. Gudyalis, B. P. Zakharchenya and F. A. Chudnovskiy, Soviet Journal of Quantum Electronics, 1979, 9, 855.
67. S. J. Jiang, C. B. Ye, M. S. Khan and C. G. Granqvist, Appl. Opt., 1991, 30, 847–851.
68. G. Golan, A. Axelevitch, B. Sigalov and B. Gorenstein, Microelectron. J., 2003, 34, 255–258.
69. V. I. Andreev, A. S. Oleinik and Y. I. Sarov, Sov. Phys. Solid State, 1980, 22, 2163.
70. V. G. Mokerov, A. R. Verishev and A. S. Ignat'ev, Sov. Phys. Solid State, 1979, 21, 855.
71. A. S. Oleinik, Neorg. Mater., 1991, 27, 534.
72. A. S. Oleinik, Zh. Tekh. Fiz., 1993, 63, 97.
73. S. N. Svistasheva and V. N. Kruchinin, Thin Solid Films, 1998, 319, 313–314.
74. Y.-H. Han, I.-H. Choi, H.-K. Kang, J.-Y. Park, K. T. Kim, H. J. Shin and S. Moon, Thin Solid Films, 2003, 425, 260.
75. M. Gurvitch, S. Luryi, A. Polyakov, A. Shabalov, M. Dudley, G. Wang, S. Ge and V. Yakovlev, J. Appl. Phys., 2007, 102, 033504.
76. M. C. Biesinger, L. W. M. Lau, A. R. Gerson and R. S. C. Smart, Appl. Surf. Sci., 2010, 257, 887–898.
77. G. Silversmit, D. Depla, H. Poleman, G. B. Marin and R. D. Gryse, J. Electron Spectrosc. Relat. Phenom., 2004, 135, 167–175.
78. D. Fu, K. Liu, T. Tao, K. Lo, C. Cheng, B. Liu, R. Zhang, H. A. Bechtel and J. Wu, J. Appl. Phys., 2013, 113, 043707.
79. I. Kitahiro, T. Ohashi and A. Watanabe, J. Phys. Soc. Jpn., 1966, 21, 2422.
80. S. Lee, K. Hippalgaonkar, F. Yang, J. Hong, C. Ko, J. Suh, K. Liu, K. Wang, J. J. Urban, X. Zhang, C. Dames, S. A. Hartnoll, O. Delaire and J. Wu, Science, 2017, 355, 371–374.
81. A. M. Abo El Soud, B. Bansour and L. I. Soliman, Thin Solid Films, 1994, 247, 140–143.

---

Footnote

† Electronic supplementary information (ESI) available: Electrical and thermal conductivity of VO₂ (Fig. S1), XRD pattern of polished surface of 7 + 7 + 7 h sample (Fig. S2) and its SEM image (Fig. S3). See DOI: 10.1039/c7ra05766k

---