Exotic thermoelectric behavior in nitrogenated holey graphene

Abstract

Combining first-principles approaches with the Boltzmann transport equation and semi-classical analysis we investigate the thermal conductivity κ, thermopower S, electrical conductivity σ, and carrier mobility μ of newly synthesized nitrogenated holey graphene (NHG). Strikingly, the NHG possesses exceedingly high S and σ but a fairly low lattice thermal conductivity κ_L, and therefore extraordinary thermoelectric properties, with a figure of merit zT even exceeding 5.0, are obtained in the n-type doped NHG. The outstanding thermoelectric behavior of NHG is attributed to its exotic atomic and electronic structure: (i) strong anharmonic phonon scattering results in a very low κ_L; (ii) flat bands around the Fermi level together with a large band gap cause high S; and (iii) conduction band dipping at the Brillouin zone center leads to a high electron mobility μ and thus high σ.

---

1 Introduction

In the last decade, environmental challenges as well as limited fossil resources have prompted an intense search for alternative methods for sustainable, efficient, and clean power generation. In these circumstances, the focus on thermoelectric (TE) materials has increased drastically due to their potential for converting heat into electricity, which offers a clean way to capture the enormous amount of wasted heat from various high-temperature industrial, transportation and electronic processes.^1–4

For a TE power generator, the conversion efficiency depends on the dimensionless figure of merit zT = S²σT/κ, where S is the thermopower (Seebeck coefficient), σ is the electrical conductivity, T is the absolute temperature, and κ is the thermal conductivity, which includes the lattice thermal conductivity κ_L and electronic contribution κ_el. According to the Wiedemann–Franz formula κ_el = LσT, where L is the Lorenz number with a value of 2.44 × 10⁻⁸ WΩ K⁻², the figure of merit can be further written as zT = S²/(L + κ_L/σT). Therefore, a complete solution to the optimization of zT requires both enhancement of the thermopower S and electrical conductivity σ, and the reduction of the lattice thermal conductivity κ_L.

To date there have been many schemes proposed for the enhancement of S and σ in order to increase zT. For instance, in the Tl-doped p-type PbTe a resonant impurity-induced distortion of the electronic density of states (EDOS) leads to a drastic improvement of S, and thus results in a high zT of 1.5 at 773 K.^2,5 In low dimensional Bi₂Te₃ both S and σ can be tuned by a highly anisotropic effective-mass tensor via the quantum confinement effect, which causes an increase of zT by a factor of 13 over the bulk value.⁶ The conduction band convergence in Mg₂Si_1−xSn_x solid solutions leads to a significantly enhanced S with no adverse effect on the carrier mobility.⁷

Besides these approaches to meliorating TE performance, the reduction of κ_L could also significantly enhance the figure of merit zT. Via all-scale hierarchical structures, a significant reduction of κ_L to about 0.5 W m⁻¹ K⁻¹ leads to a high zT of 2.2 in bulk spark-plasma-sintered Na-doped PbTe:SrTe at 900 K.⁸ A zT of 2.0 was achieved in Na-doped PbTe at 773 K through optimizing the nanostructures to reduce κ_L.⁹ An extraordinary zT of 2.6 was reported in undoped monocrystalline SnSe at 923 K, because of the ultra-low intrinsic κ_L of SnSe crystals.¹⁰ Nowadays, with the booming of nanomaterials, superior TE properties can be expected in these materials owing to a significant reduction in κ_L due to the lower dimensions.^11,12 As an example, monolayer transition metal dichalcogenides (TMDs) such as MoS₂ and MoSe₂ possess much smaller thermal conductivities than that of graphene,^13–19 and, on account of this, a great many TMDs have been confirmed to be good TE materials.^20–23 More recently, binary SnSi and SnGe sheets have been suggested to be feasible TE candidates due to the fairly low intrinsic κ_L in these two-dimensional (2D) sheets.²⁴

Ideally, a material with both a high power factor S²σ and low κ_L is the best candidate for TE applications. To meet both requirements, we identify a newly synthesized 2D crystal, nitrogenated holey graphene (NHG),²⁵ to be a perfect candidate with exotic thermoelectric properties. Recently, κ_L values of 40.00, 64.80, and 82.22 W m⁻¹ K⁻¹ for NHG at 300 K were reported based on classical molecular dynamics (MD) simulations and first-principles calculations.^26–28 Although these studies show the heat transport results for NHG, to date no evidence of the thermoelectric transport properties and figure of merit zT of this new 2D crystal has been reported. The unique holey structure of this new 2D crystal not only brings potential applications in molecular sieves^29–31 and nanoscale devices,³² but also bestows the coexistence of low thermal conductivity, high thermopower, and high electron mobility. Therefore a figure of merit zT even exceeding 5.0 is predicted in n-type doped NHG, which is significantly higher than other materials with similar structures and compositions. The outstanding thermoelectric behavior of NHG is attributed to its exotic atomic and electronic structure. The strong anharmonic phonon scattering originating from the holey structure results in very low κ_L. The flat bands near the Fermi level and a large band gap cause a high value of S. Finally, conduction band dipping at the center of the Brillouin zone leads to a high electron mobility μ, and thus high σ. Our results strongly support the idea that NHG is a perfect candidate material with great potential for exotic TE applications.

2 Methodology

To build a complete picture revealing the thermoelectric behavior of NHG, we calculate all of the relevant quantities in this paper. We use the phonon Boltzmann transport equation (BTE), together with the interatomic force constants (IFCs) obtained from first-principles techniques, to calculate κ_L, and this been demonstrated to be an accurate and predictive method for the study of the thermal transport performance.^33–36

From the solution of the BTE,³⁷ the lattice thermal conductivity along the α direction is written as

where k_B, Ω, N, and f₀ are the Boltzmann constant, the volume of the unit cell, the number of q points in the first Brillouin zone, and the equilibrium Bose–Einstein distribution function, respectively. ω_λ represents the phonon frequency at the phonon mode λ, which comprises the wave vector q and the phonon branch ν. ħ is the reduced Planck constant, and v_g^α,λ represents the phonon group velocity of mode λ along the α direction. The last term, F_λ^α, is determined by F_λ^α = τ_λ(v_g^α,λ + Δ_λ), where τ_λ is the phonon lifetime in the relaxation time approximation (RTA). Δ_λ is a correction term used to eliminate the inaccuracy of the RTA via solving the BTE iteratively. If Δ_λ is ignored, the RTA result of κ_L^αα is obtained.

The ShengBTE package³⁷ is employed to calculate κ_L. The harmonic IFCs (IFC2) and anharmonic IFCs (IFC3) required in the BTE calculations are computed by the density functional theory (DFT) software VASP,^38,39 combined with the PHONOPY code⁴⁰ and THIRDORDER.PY script.³⁷ IFC2 and IFC3 are both generated within 3 × 3 × 1 supercells via the finite-difference approach, and interaction up to the third-nearest neighbor is included in the IFC3 calculations. In the DFT calculations, the ion cores are modeled using the projector augmented wave potentials (PAW),⁴¹ and the valance electrons are modeled using a plane-wave basis set with a cutoff energy of 550 eV and the exchange–correlation functional of Perdew–Burke–Ernzerhof (PBE).⁴² For relaxation of the primitive cell, the force acting on each atom is less than 10⁻⁸ eV Å⁻¹ with the electronic convergence criterion of 10⁻⁸ eV, and a 9 × 9 × 1 Monkhorst–Pack k-point mesh is used to simulate the Brillouin zone integration. To estimate the Born effective charges and dielectric tensor required in both the ShengBTE and PHONOPY calculations, the density functional perturbation theory (DFPT) implemented in VASP is employed within a dense k-mesh of 36 × 36 × 1. Finally, for the ShengBTE calculations, a q-mesh of 27 × 27 × 1 is selected to simulate the corresponding q space integration.

The semi-classical electronic Boltzmann theory and the rigid band model coded in the BoltzTraP package⁴³ are utilized to calculate S, σ, and κ_el within the constant scattering time approximation. To obtain accurate derivatives of the Kohn–Sham eigenvalues, the electronic structure is calculated by VASP on a dense k-mesh of 45 × 45 × 1. In this approach, the only empirical parameter is the scattering time τ, which determines the value of σ and κ_el. According to σ ∼ neμ, the experimental results of carrier concentration n, mobility μ, and electrical conductivity σ can be employed to estimate τ. Here, due to the lack of experimental data on the conductive characteristics of NHG, we use a simple model of τ ∼ d/v, where d is the average electron–electron distance and v is the corresponding electron velocity, to calculate τ at a high doping concentration n, while the value of τ at a low n is estimated via the calculation of the carrier mobility μ.

3 Results and discussion

As shown in the inset of Fig. 1(a), the atomic structure of NHG consists of hexagonal C-rings terminated by N atoms, which results in a stoichiometry of C₂N with the symmetry group P6/mmm. The optimized lattice constant is 8.33 Å, which is consistent with the experimental result of 8.24 ± 0.96 Å and the calculated value of 8.30 Å.²⁵ In each primitive cell, there is one kind of C–N bond with a length of 1.34 Å and two kinds of C–C bonds with lengths of 1.43 Å for one (located inside) and 1.47 Å for another (facing the holey side), which are same as previous results.³²

Fig. 1 (a) Phonon dispersion and PDOS of NHG. The inset shows the primitive cell of the crystal outlined by a dashed rhombus. Nitrogen and carbon atoms are shown by green and orange balls, respectively. (b) The original and re-scaled lattice thermal conductivity κ_L as a function of T for NHG. The square (triangle) and circle (star) lines represent the original (re-scaled) ITS and RTA results, respectively. The inset shows the original ITS result of cumulative thermal conductivity κ_C as a function of the phonon maximum mean-free path (MFP) at 300 K.

The calculated phonon dispersion and phonon density of states (PDOS) are plotted in Fig. 1(a). There are 54 phonon branches due to the presence of 18 atoms in each primitive cell. The highest eigenfrequency is about 295.2 rad ps⁻¹, which can be compared to 301.4 rad ps⁻¹ of graphene.⁴⁴ Among all of the branches, the flexural ZA acoustic branch is the softest vibration mode, corresponding to the out-of-plane transverse motion or bending of the NHG sheet, and this possesses an approximate parabolic dispersion feature around the Γ point. Being similar to graphene, the ZA mode is coupled with the softest optical mode at the high symmetry point K. In addition, the partial PDOS shows that a large proportion of the optical modes above 130.0 rad ps⁻¹ originate from the vibrations of C atoms due to the lighter mass of C than that of N. Another important point is that the phonon dispersion for the branches around the high symmetry point K is almost linear because of the trigonal symmetry structure. Similar features induced by trigonal or hexagonal crystal symmetry have been also observed in some other 2D structures such as defect-patterned graphene nanomeshes, metal adatom decorated silicene, etc.^45–48

The calculated intrinsic κ_L of NHG with naturally occurring isotope concentrations as a function of T is plotted in Fig. 1(b). According to eqn (1), the original κ_L obtained from the BTE calculations should be re-scaled by a factor of c/h, where c is the lattice constant along the perpendicular direction and h is the thickness of the NHG sheet. In our calculations, c is fixed at 15.00 Å and h is set to be 3.30 Å, based on the interlayer spacing shown in previous work.²⁵ The iterative solutions (ITS) of the BTE and RTA results are both shown in Fig. 1(b), which reveals a difference of less than 6% between them for T ≥ 200 K. Strikingly, due to the particular holey structure, the values of κ_L are very low, especially at high temperature. For instance, at 600 K the ITS (RTA) values of original and re-scaled κ_L are 6.49 (6.13) and 29.52 (27.87) W m⁻¹ K⁻¹, respectively, which are much lower than those of graphene at the same temperature.⁴⁴ At 300 K, the re-scaled κ_L values are 48.72 and 45.86 W m⁻¹ K⁻¹ from the ITS and RTA results, respectively, which are lower than the results of 64.80 and 82.22 W m⁻¹ K⁻¹ reported in ref. 26 and ref. 28, but higher than the value of about 40.00 W m⁻¹ K⁻¹ reported in ref. 27. In addition, the isotopic effect is also calculated, which has almost no influence (<0.8%) on the determination of κ_L for T ≥ 200 K.

Furthermore, we also calculate the cumulative thermal conductivity κ_C with respect to the allowed phonon maximum mean-free path (MFP) in order to reveal the size dependence of κ_L. The κ_C values at 300 K are plotted in the inset of Fig. 1(b). The total accumulation continues increasing with the increase of MFPs, approaching a plateau after the MFPs reach about 140 nm. The contribution of phonons with a MFP shorter than 40 nm is about 81% of the total κ_L, implying that nanostructures with the characteristic of a MFP length shorter than 40 nm are required to reduce κ_L significantly.

In order to reveal the detailed thermal transport mechanism, we show the anharmonic three-phonon scattering rates (ASRs) and isotopic scattering rates (ISRs) as functions of frequency in Fig. 2(a). In the BTE calculations, due to the exclusion of boundary scattering rates, total scattering rates 1/τ_λ in RTA can be obtained using ASRs and ISRs through the relationship 1/τ_λ = 1/τ^anh_λ + 1/τ^iso_λ. As shown in Fig. 2(a), the ISRs are much smaller than the ASRs, which indicates a negligible influence of the isotopic effect on calculations of κ_L. Thus, the ASRs are responsible for κ_L of NHG. Compared with previous TE materials, the total ASRs are very high, and even larger than those of CoSb₃ and IrSb₃,⁴⁹ implying a very strong three-phonon scattering and thus a low κ_L. In addition, for phonon modes below about 20.0 rad ps⁻¹ the ASRs are relatively small, which signifies that the low-frequency modes contribute to the majority of the κ_L. In detail, for low-frequency phonon modes, most of the ASRs of phonon emission processes (ASRs⁻) are smaller than the ASRs of phonon absorption processes (ASRs⁺), while for high-frequency modes the ASRs⁻ are slightly larger than the ASRs⁺.

Fig. 2 (a) Anharmonic three-phonon scattering rates (ASRs) and isotopic scattering rates (ISRs) as functions of frequency for NHG at 300 K. The ASRs of phonon absorption processes (ASRs⁺) and phonon emission processes (ASRs⁻) are also shown. (b) The corresponding weighted phase space W. The W of the phonon absorption processes (W⁺) and phonon emission processes (W⁻) are also shown.

Interestingly, there is a sudden jump for part of the ASRs⁻ when the frequency reaches about 2.5 rad ps⁻¹. As is well known, 1/τ^anh_λ is obtained by the sum of three-phonon transition probabilities Γ^±_{λλ′λ′′}, which depend on the anharmonic IFC3 and weighted phase space W (a direct measure of the number of scattering processes).^50,51 Our calculations show that the weighted phase space of the phonon emission processes (W⁻) also possesses a jump near the frequency of 2.5 rad ps⁻¹, as shown in Fig. 2(b), which explains the sudden jump of the ASRs⁻ around this frequency. In addition, for high-frequency phonon modes, much of W⁻ is slightly larger than the weighted phase space of the phonon adsorption processes (W⁺), causing the larger ASRs⁻ than ASRs⁺ in high frequencies.

Another important factor determining thermal transport is the phonon group velocity v_g = dω_ν/dq, where ν represents the νth branch within the whole first Brillouin zone. Our results show that the maximum group velocities for three acoustic branches are about 2.50, 17.76, and 18.48 km s⁻¹, while those for most of optical modes are in the range from 1.55 to 13.16 km s⁻¹. For detailed phonon group velocities see S1 in the ESI.†⁵² In view of κ_L ∼ v_g² in the RTA, these relatively high group velocities support the observation that the values of the re-scaled κ_L for NHG are two or three times higher than those of CoSb₃ and IrSb₃,⁴⁹ even though larger ASRs are observed in NHG.

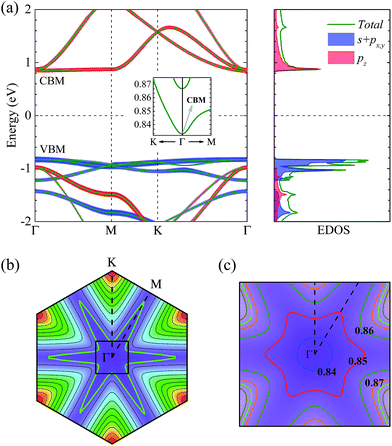
The low κ_L of NHG would make it a promising TE candidate if its thermopower S and electronic transport performances are good. Since electronic transport properties depend on the electronic structure, we show the projected band structure and partial EDOS for NHG in Fig. 3(a). It is found that NHG possesses a direct band gap of about 1.68 eV, with the conduction band minimum (CBM) and valence band maximum (VBM) at the Γ point. This finding is consistent with the previous first-principles calculation, which gives a band gap of about 1.70 eV, although a slightly larger band gap of ∼1.96 eV is detected experimentally.²⁵ The projections on band structure together with the partial EDOS indicate that the valence band is contributed to mainly by the s + p_x,y orbitals, while the conduction band is formed from only the p_z orbitals, as shown in Fig. 3(a). Prominently, the band gap of 1.68 eV for NHG is much larger than the gaps of most of the known TE materials. Usually, a large band gap guarantees the high specific heat of carriers, which is a part of reason why most of the best TE candidates are semiconductors.¹

Fig. 3 (a) The projected band structure and EDOS of NHG. The thickness of the blue and red colored lines represent the s + p_x,y and p_z projections, respectively. The inset shows the band structure for the conduction band around the Γ point. (b) Corresponding contour plot of the lowest conduction band in the whole Brillouin zone. The green snowflake-like curve represents the isoenergy at 40 meV above the CBM. (c) Zoomed-in view of the contour plot in the region surrounded by the black square in (b). The blue circle is the isoenergy at 5 meV above the CBM.

We also note that there exists very little dispersion in the conduction band along the ΓM line and the valence band in the whole Brillouin zone, which makes the bands around band extremes fairly flat. As a result, the total EDOS changes very rapidly around the CBM and VBM. For instance, the EDOS reaches nearly 18.6 (36.2) states/(eV cell) at only 40 meV above (below) the CBM (VBM). This behavior of the conduction band and valence band implies that there is a large effective mass of electrons in NHG. As is well known, at a constant carrier concentration, the thermopower S is proportional to the electronic effective mass. Thus, high thermopower S is expected in NHG.

In addition, to further understand the behavior of bands just above the CBM, we also plot the lowest conduction band in the whole Brillouin zone, shown in Fig. 3(b). The green snowflake-like contour represents the isoenergy (Fermi surface) for the Fermi level E_F taken 40 meV above the CBM. The nearly parallel curve around the ΓM line indicates weak dispersion and thus the quasi step function of the EDOS in NHG, while the dense contours along the ΓK line indicate strong dispersion.

To quantitatively estimate the electronic transport performances and TE properties, we calculate the thermopower S and electrical conductivity σ/τ as functions of temperature T and doping concentration n for NHG. The calculations with a scissors shift of 0.28 eV are also performed, and show that a slight underestimation of the band gap has no influence on S and σ/τ. Our calculations show that the best TE performance is obtained in the NHG with n-type doping. The calculated S and σ/τ as functions of T and n for the n-type doped NHG are plotted in Fig. 4(a) and (b), respectively. Similar to the case for the lattice thermal conductivity κ_L, the original and re-scaled σ/τ are both shown. The results show that σ/τ increases with n and it does not depend on T, which is consistent with electronic Boltzmann theory.⁴³ Being in accordance with the tendency observed in most TE materials, the thermopower S increases with T at the same n, and decreases with n at the same T. Strikingly, S is extraordinarily high, as is expected from the analyses of electronic structure. For instance, as T increases from 500 to 1200 K, the values of S are in the range from 2.02 × 10⁻⁴ to 2.72 × 10⁻⁴ V K⁻¹ at n ∼ 2.00 × 10¹³ cm⁻², as shown in Fig. 4(a). As is known, the typical S value for a high-zT material varies between 2.00 × 10⁻⁴ and 3.00 × 10⁻⁴ V K⁻¹. The results of high S suggest a possible high zT in NHG, although the accurate value of σ is not confirmed at present.

Fig. 4 Thermoelectric parameters for the heavily n-type doped NHG at temperatures ranging from 500 to 1200 K. (a) Thermopower S. (b) Electrical conductivity σ/τ. (c) Power factor S²σ. (d) Total thermal conductivity κ (full lines) and electronic thermal conductivity κ_el (dashed lines). (e) Figure of merit zT. In (c)–(e), the curves represent the values with τ = 13 fs, and have the same legends as (a). The upper and lower limits of the vertical bars represent the values at 1000 K with τ = 23 and 6 fs, respectively.

For calculations of σ, we firstly use a simple model of τ ∼ d/v to assess the amplitude of the scattering time τ in heavily n-type doped NHG, where d is the average electron–electron distance estimated by the doping concentration n and the effective thickness h ∼ 3.30 Å,²⁵ represents the corresponding electron velocity. In the n-type doping range from n ∼ 8.33 × 10¹² to 7.17 × 10¹³ cm⁻², which corresponds to the doping of from 0.05 to 0.43e into each primitive cell and thus gives rise to an isoenergy at 30 to 60 meV above the CBM, d is estimated to be from 7.87 to 16.13 Å. Correspondingly, in this doping range, the maximum electron velocity v varies from about 7.30 × 10⁴ to 11.25 × 10⁴ m s⁻¹ via the derivative analyses of band structure. As a result, τ is found to be in the range from 6 to 23 fs, as shown in Fig. S2 in the ESI.†⁵² Furthermore, at the medium doping concentration n ∼ 2.00 × 10¹³ cm⁻², which corresponds to 0.13e doping into each primitive cell and results in an isoenergy at 40 meV above the CBM, as shown by the green snowflake-like curve in Fig. 3(b), τ is found to be about 13 fs. Therefore, we choose the value of τ = 13 fs to calculate the electrical conductivity σ, electronic thermal conductivity κ_el, and corresponding TE parameters, and use the values calculated with τ = 6 and 23 fs as the lower and upper limits of these parameters.

In calculations of the figure of merit zT, the original κ_L and σ/τ are used to estimate the power factor S²σ and total thermal conductivity κ. According to the definition of zT, the results obtained from this method are in the same spirit as those calculated using all the re-scaled parameters. To obtain a more relevant zT, κ_el is also included, although it is small compared to κ_L, as shown in Fig. 4(d). Our results show that zT for the n-type doped NHG often exceeds 1.0 at T ≥ 500 K as τ varies between 6 and 23 fs. With τ = 13 fs, zT changes from about 1.00 to 2.32 when T increases from 750 K to 1200 K. As an example, a high zT ∼ 1.71 with a fairly large S²σ ∼ 1.00 × 10⁻² W m⁻¹ K⁻² is reached at T = 1000 K and n ∼ 2.00 × 10¹³ cm⁻², as shown in Fig. 4(c) and (e). At the same temperature, as τ increases to 23 fs an extraordinarily high zT ∼ 2.50 can be reached, while a maximum zT of 0.96 is obtained when τ lowers to 6 fs, as shown in Fig. 4(e). These results show that good TE performance is possible in heavily n-type doped NHG.

From the model τ ∼ d/v, the scattering time τ will approach infinity when n decreases to zero. Thus, to estimate the TE properties at weak doping levels, other models should be selected. Here we calculate the electron mobility μ to estimate τ and the corresponding TE performance at low doping concentration n. In 2D materials, the carrier mobility μ at the band extremes (CBM and VBM) is calculated by the formula^53–57

where e is the electron charge, m* ( or ) is the effective mass along the transport direction, m_a is the average effective mass calculated via , and E_lⁱ = ΔV_i/(Δl/l₀) represents the deformation potential constant of the CBM for the electron or VBM for the hole in the transport direction. Here l₀ is the lattice constant in the transport direction, Δl is the deformation of l₀, and ΔV_i represents the change of energy for the ith band under proper cell dilatation and compression. C is the elastic modulus of the longitudinal strain in the propagation directions (both zigzag and armchair) of the longitudinal acoustic wave, and is determined by (E − E₀)/S₀ = C(Δl/l₀)²/2, where E is the total energy and S₀ is the cell volume at equilibrium for a 2D structure. This estimation only includes the simplest electron–phonon interaction and provides the upper limit of μ for realistic cases, in which many extrinsic factors will further reduce the estimated values. However, this formula is so sophisticated that it can capture the anisotropic nature of μ for 2D systems. From the conduction band around the CBM, as shown in the inset of Fig. 3(a), we find that there is a conduction band dip at the Γ point, which results in an isotropic dispersion relation until the isoenergy, at 5 meV above the CBM, as shown in Fig. 3(c). A similar case is also observed around the VBM. Thus, the isotropic approximation for the carrier mobility μ of both electron and hole is used. The μ at 300 K together with the effective mass m*, deformation potential constant E_l, and elastic modulus C are listed in Table 1. Obviously, due to the conduction band dipping at the Brillouin zone center, a much smaller effective mass is obtained at the CBM compared with that at the VBM. This leads to an electron mobility of about 2.10 × 10³ cm² V⁻¹ s⁻¹ in NHG at 300 K, which is about 1.4% of that of graphene and much higher than the values of phosphorene.⁵⁵

Table 1 The calculated carrier mobility μ in NHG at 300 K. m* is in units of free electron mass m_e

Type	m*/me	El (eV)	C (J m^−2)	μ (cm^2 V^−1 s^−1)
VBM	15.27	6.15	291.52	0.70
CBM	0.38	4.51	291.52	2.10 × 10^3

---

The high electron mobility μ indicates a large average electron scattering time τ. At low doping concentrations n, τ can be estimated according to the relationship τ = μm*/e. As T increases from 300 to 1200 K, the estimated τ varies in the range from 450 to 112 fs. Such large values of τ signify high electrical conductivities σ and thus possible good TE performances at weak doping levels. Here, we choose the lowest τ of 112 fs to recalculate the TE properties, as shown in Fig. 5. Since the highest isotropic isoenergy is the contour at 5 meV above the CBM, shown in Fig. 3(c), which corresponds to the doping of n ∼ 1.66 × 10¹² cm⁻² (0.01e in each primitive cell), we only consider the values for n ≤ 1.66 × 10¹² cm⁻¹ in Fig. 5. Remarkably, the calculated figure of merit zT even exceeds 5.0 at 1000 K, while a zT of 3.0 can be obtained at 700 K, which is much higher than the values for the case of heavy doping. It is worth noting that, besides the drastic increase of τ, the thermopower S is also improved greatly in weak doping conditions, for example varying from 3.73 × 10⁻⁴ to 5.02 × 10⁻⁴ V K⁻¹ at n ∼ 1.66 × 10¹² cm⁻² when T changes from 500 to 1200 K, as shown in Fig. 4(a). These results indicate that weakly n-type doped NHG possesses outstanding TE properties. Furthermore, the doping concentration n ∼ 1.66 × 10¹² cm⁻² is easily realized by adsorbing an alkali metal atom or creating a C atom replacement by N in about 100 unit cells, supporting the idea that TE application of NHG is easily accessible in experiments.

Fig. 5 The figure of merit zT calculated for weakly doped NHG, with τ = 112 fs at 500 to 1200 K. The curves have the same color legends as those in Fig. 4. The orange vertical line denotes the doping concentration n ∼ 1.66 × 10¹² cm⁻², which corresponds to the isoenergy at 5 meV above the CBM shown in Fig. 3(c).

In addition, according to eqn (2) and Fig. 3, μ decreases quickly as the isoenergy exceeds about 15 meV above the CBM, because of the drastic enhancement of the electron effective mass in the ΓM direction. To reassess τ at high doping concentrations, we only take the anisotropy of the effective mass into account in eqn (2) while other quantities remain the same, and find that the largest μ at 300 K decreases to about 126 cm² V⁻¹ s⁻¹ at the high doping concentration n ∼ 2.00 × 10¹³ cm⁻². As a result, a scattering time τ of 7 to 27 fs is found in the temperature range from 500 to 1200 K, which is consistent with the result of 6 to 23 fs obtained from the model of τ ∼ d/v.

Finally, in order to estimate the stabilities of the n-type doped NHG at high temperature, we also carry out ab initio molecular dynamics (MD) simulations, where NHG in a 4 × 4 × 1 supercell containing 288 atoms is simulated using the canonical ensemble with a time step of 2 fs. Through 10 ps MD at 1500 K, the structure remains intact without any lattice destruction, which suggests good structural stability of the n-type doped system at high temperature (see S3 in the ESI†⁵²

4 Conclusions

In conclusion, we have used first-principles techniques combined with semi-classical analysis and Boltzmann transport theory to compute the thermoelectric properties of the recently fabricated 2D crystal NHG. The calculated κ_L is fairly low, dominantly contributed to by strong anharmonic three-phonon scattering. Thanks to its large band gap and flat bands around the Fermi level, the thermopower S of NHG is extraordinarily high. With estimated electron scattering times τ in the range from 6 to 23 fs, a figure of merit zT exceeding 2.0 is achieved in the heavily n-type doped system (∼0.1e per primitive cell). Weakly n-type doped NHG at concentrations below 1.66 × 10¹² cm⁻² (∼0.01e per primitive cell) has an electron mobility μ of about 1.4% of that for graphene and τ > 112 fs at room temperature, resulting from conduction band dipping at the Brillouin zone center. Consequently, an extraordinary figure of merit zT even exceeding 5.0 can be reached for weakly n-type doped samples, which are easily accessible in experiments by adsorbing an alkali metal atom or creating a C atom replacement by N in about 100 unit cells. Our results strongly support the idea that among all newly synthesized, low-dimensional materials, NHG is perhaps the most promising candidate. Its exotic thermoelectric properties show great potential in clean energy and thermoelectric applications, which can be readily tested by experimental approaches.

Acknowledgements

This research was supported by the National Key Research and Development Program of China under Grant No. 2016YFA0300902, and the MOST Project of China under Grant No. 2012CB921403 and 2015CB921001.

References

1. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114.
2. J. P. Heremans, V. Jovovic, E. S. Toberer, A. Saramat, K. Kurosaki, A. Charoenphakdee, S. Yamanaka and G. J. Snyder, Science, 2008, 321, 554–557.
3. J. R. Sootsman, D. Y. Chung and M. G. Kanatzidis, Angew. Chem., Int. Ed., 2009, 48, 8616–8639.
4. M. Zebarjadi, K. Esfarjani, M. S. Dresselhaus, Z. F. Ren and G. Chen, Energy Environ. Sci., 2012, 5, 5147–5162.
5. Y. Pei, A. LaLonde, S. Iwanaga and G. J. Snyder, Energy Environ. Sci., 2011, 4, 2085–2089.
6. L. D. Hicks and M. S. Dresselhaus, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 12727–12731.
7. W. Liu, X. Tan, K. Yin, H. Liu, X. Tang, J. Shi, Q. Zhang and C. Uher, Phys. Rev. Lett., 2012, 108, 166601.
8. K. Biswas, J. He, I. D. Blum, C.-I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, Nature, 2012, 489, 414–418.
9. H. Wang, J.-H. Bahk, C. Kang, J. Hwang, K. Kim, J. Kim, P. Burke, J. E. Bowers, A. C. Gossard and A. Shakouri, et al., Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 10949–10954.
10. L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Nature, 2014, 508, 373–377.
11. H. Alam and S. Ramakrishna, Nano Energy, 2013, 2, 190–212.
12. X. Zhang, L. Gao, Z.-P. Liu and L. Chen, BMC Bioinf., 2015, 16, 92.
13. X. Liu, G. Zhang, Q.-X. Pei and Y.-W. Zhang, Appl. Phys. Lett., 2013, 103, 133113.
14. X. Gu and R. Yang, Appl. Phys. Lett., 2014, 105, 131903.
15. W. Li, J. Carrete and N. Mingo, Appl. Phys. Lett., 2013, 103, 253103.
16. K. Kaasbjerg, K. S. Thygesen and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 115317.
17. C. Sevik, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 035422.
18. X. Wei, Y. Wang, Y. Shen, G. Xie, H. Xiao, J. Zhong and G. Zhang, Appl. Phys. Lett., 2014, 105, 103902.
19. R. Yan, J. R. Simpson, S. Bertolazzi, J. Brivio, M. Watson, X. Wu, A. Kis, T. Luo, A. R. Hight Walker and H. G. Xing, ACS Nano, 2014, 8, 986–993.
20. D. Wickramaratne, F. Zahid and R. K. Lake, J. Chem. Phys., 2014, 140, 124710.
21. C. Wan, X. Gu, F. Dang, T. Itoh, Y. Wang, H. Sasaki, M. Kondo, K. Koga, K. Yabuki and G. J. Snyder, et al., Nat. Mater., 2015, 14, 622–627.
22. A. N. Gandi and U. Schwingenschlögl, Chem. Mater., 2014, 26, 6628–6637.
23. S. Kumar and U. Schwingenschlögl, Chem. Mater., 2015, 27, 1278–1284.
24. Y. Ding and Y. Wang, Appl. Surf. Sci., 2017, 396, 1164–1169.
25. J. Mahmood, E. K. Lee, M. Jung, D. Shin, I.-Y. Jeon, S.-M. Jung, H.-J. Choi, J.-M. Seo, S.-Y. Bae, S.-D. Sohn, N. Park, J.-H. Oh, H.-J. Shin and J.-B. Baek, Nat. Commun., 2015, 6, 6486.
26. B. Mortazavi, O. Rahaman, T. Rabczuk and L. F. C. Pereira, Carbon, 2016, 106, 1–8.
27. T. Zhang and L. Zhu, Phys. Chem. Chem. Phys., 2017, 19, 1757–1761.
28. T. Ouyang, H. Xiao, C. Tang, X. Zhang, M. Hu and J. Zhong, Nanotechnology, 2017, 28, 045709.
29. B. Xu, H. Xiang, Q. Wei, J. Q. Liu, Y. D. Xia, J. Yin and Z. G. Liu, Phys. Chem. Chem. Phys., 2015, 17, 15115–15118.
30. L. Zhu, Q. Xue, X. Li, T. Wu, Y. Jin and W. Xing, J. Mater. Chem. A, 2015, 3, 21351–21356.
31. Y. Yang, W. Li, H. Zhou, X. Zhang and M. Zhao, Sci. Rep., 2016, 6, 29218.
32. H. Sahin, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 085421.
33. H. Dekura, T. Tsuchiya and J. Tsuchiya, Phys. Rev. Lett., 2013, 110, 025904.
34. J. W. L. Pang, W. J. L. Buyers, A. Chernatynskiy, M. D. Lumsden, B. C. Larson and S. R. Phillpot, Phys. Rev. Lett., 2013, 110, 157401.
35. L. Lindsay, D. A. Broido and T. L. Reinecke, Phys. Rev. Lett., 2013, 111, 025901.
36. Y. Zhao, Z. Dai, C. Zhang, C. Lian, S. Zeng, G. Li, S. Meng and J. Ni, Phys. Rev. B, 2017, 95, 014307.
37. W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747–1758.
38. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
39. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
40. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
41. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
42. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
43. G. K. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67–71.
44. L. Lindsay, W. Li, J. Carrete, N. Mingo, D. A. Broido and T. L. Reinecke, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 155426.
45. H. Sahin and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 035452.
46. H. Sahin, S. Cahangirov, M. Topsakal, E. Bekaroglu, E. Akturk, R. T. Senger and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155453.
47. H. Sahin and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 085423.
48. H. Sahin and S. Ciraci, J. Phys. Chem. C, 2012, 116, 24075–24083.
49. W. Li and N. Mingo, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 094302.
50. W. Li and N. Mingo, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 144304.
51. W. Li and N. Mingo, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 184304.
52. See ESI† for the phonon group velocity, electron scattering time, and bond length evolution in the MD simulation of nitrogenated holey graphene.
53. Y. Cai, G. Zhang and Y.-W. Zhang, J. Am. Chem. Soc., 2014, 136, 6269–6275.
54. R. Fei and L. Yang, Nano Lett., 2014, 14, 2884–2889.
55. J. Qiao, X. Kong, Z.-X. Hu, F. Yang and W. Ji, Nat. Commun., 2014, 5, 4475.
56. J. Xie, Z. Y. Zhang, D. Z. Yang, D. S. Xue and M. S. Si, J. Phys. Chem. Lett., 2014, 5, 4073–4077.
57. S. Bruzzone and G. Fiori, Appl. Phys. Lett., 2011, 99, 222108.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7ra03597g

---