Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Kinetics of phosphine substitution in CpRu(PPh3)2X (X = Cl, Br, I, N3, and NCO)†
David Hilla,
Connor Delaneya,
Miles Clarka,
Mathew Eatona,
Bakar Hassana,
Olivia Hendricksb,
Duy Khoi Danga and
Rein U. Kirss *a
*a
aDepartment of Chemistry and Chemical Biology, Northeastern University, Boston, MA 02115, USA. E-mail: r.kirss@neu.edu
bDepartment of Chemistry, Wellesley College, Wellesley, MA 02481, USA
First published on 7th July 2017
Abstract
The kinetics of phosphine substitution in CpRu(PPh3)2X (X = Br, 1b, X = I, 1c, X = N3, 1d, and X = NCO, 1e) have been measured under pseudo-first order conditions in THF solution and compared with data for CpRu(PPh3)2X (1a). The relative rate of substitution is found to be 1a > 1d > 1b > 1e > 1c. Substitution rates decrease in the presence of added PPh3 and are independent of added X consistent with a dissociative process. Activation parameters for 1a–1c (ΔH† = 113–135 kJ mol−1, ΔS† = 21–102 J mol−1 K−1) and DFT calculations support a dissociative or dissociative interchange pathway even though negative activation entropies (ΔS† = −48 ± 16 to −105 ± 5 J mol−1 K−1) are observed for 1d–e. Differences in Ru–ligand bond angles in 1d–e point to different π-acceptor properties of the pseudohalide ligands, contributing to the faster rate of substitution for the azide complexes, 1d relative to the cyanate derivative 1e. Substitution is not observed when X = F, 1f, X = H, 1g, X = SnF3, 1h, or X = SnCl3, 1i. Compounds 1b–1e also react with chloroform to yield 1a. The rates of halide exchange are comparable to phosphine substitution for 1c and 1d. The latter reaction is inhibited by excess triphenylphosphine and is unaffected by both radical inhibitors and radical traps suggesting that a radical mechanism is unlikely.
Introduction
Cyclopentadienyl ruthenium bis(triphenylphosphine) chloride, CpRu(PPh3)2Cl (1a), is a versatile catalyst for a range of useful transformations.1 Changing the halide ligand in CpRu(PPh3)2Cl for other halides or pseudohalides affects both the reactivity and selectivity in these processes.2 For example, CpRu(PPh3)2I (generated in situ) is reported to be more effective than CpRu(PPh3)2Cl in catalyzing the cycloaddition of norbornene and norbornadiene.3 A mechanism based on faster phosphine dissociation is proposed as the explanation for the increased catalytic activity of CpRu(PPh3)2I. On the other hand, CpRu(PPh3)2X catalyzed conversion of cyclohexylamine and methanol to CyNMe2 is nearly quantitative after 6 hours at 100 °C for X = Cl while only 40% conversion to 2.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.8
2.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of cyclohexylimine, methylcyclohexylamine and CyNMe2 is observed for X = I.4 In this case, the ionization of the Ru–X bond is proposed as the key step the reaction mechanism. The conversion rate of methanol to methyl acetate in the presence of catalytic amounts of CpRu(PPh3)2X (X = F, Cl, Br, SnF3, SnCl3 and SnBr3) follows the order: X = SnF3 > SnCl3 ≈ SnBr3 > F > Cl ≈ Br.5 In this case, dissociation of chloride is thought to be counterproductive to efficient catalysis with the greater activity of CpRu(PPh3)2SnF3 attributed to phosphine dissociation. The kinetics of phosphine substitution in CpRu(PAr3)2Cl6,7 and the rate of solvolysis of the halide in CpRu(PR2R′)2X (R = Ph, Me, X = Cl, Br, I)8 have both been measured but the effect of X on the rate of phosphine substitution (eqn (1)) has not been extensively explored. Only for the related Cp*Ru(PMe3)2X9 has the effect of the ancillary X ligand on the rate of phosphine substitution been systematically investigated. The data for the latter were consistent with a dissociative mechanism with a marked increase in rate for better π-donor X ligands. In the present study we report on the phosphine substitution in CpRu(PPh3)2X (eqn (1), 1b–i where X = Br, I, N3, NCO, H, F, SnCl3, and SnF3) in THF as well as on the unexpected halide exchange reaction between 1b–e and CDCl3. The results provide some insight into the relative importance of Ru–P dissociation in catalytic reactions involving 1a–i.
1 ratio of cyclohexylimine, methylcyclohexylamine and CyNMe2 is observed for X = I.4 In this case, the ionization of the Ru–X bond is proposed as the key step the reaction mechanism. The conversion rate of methanol to methyl acetate in the presence of catalytic amounts of CpRu(PPh3)2X (X = F, Cl, Br, SnF3, SnCl3 and SnBr3) follows the order: X = SnF3 > SnCl3 ≈ SnBr3 > F > Cl ≈ Br.5 In this case, dissociation of chloride is thought to be counterproductive to efficient catalysis with the greater activity of CpRu(PPh3)2SnF3 attributed to phosphine dissociation. The kinetics of phosphine substitution in CpRu(PAr3)2Cl6,7 and the rate of solvolysis of the halide in CpRu(PR2R′)2X (R = Ph, Me, X = Cl, Br, I)8 have both been measured but the effect of X on the rate of phosphine substitution (eqn (1)) has not been extensively explored. Only for the related Cp*Ru(PMe3)2X9 has the effect of the ancillary X ligand on the rate of phosphine substitution been systematically investigated. The data for the latter were consistent with a dissociative mechanism with a marked increase in rate for better π-donor X ligands. In the present study we report on the phosphine substitution in CpRu(PPh3)2X (eqn (1), 1b–i where X = Br, I, N3, NCO, H, F, SnCl3, and SnF3) in THF as well as on the unexpected halide exchange reaction between 1b–e and CDCl3. The results provide some insight into the relative importance of Ru–P dissociation in catalytic reactions involving 1a–i.
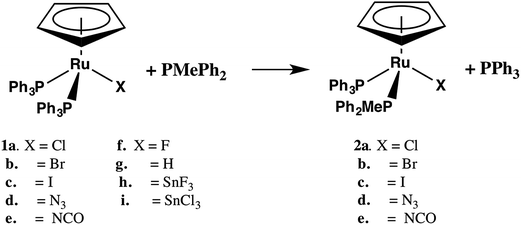 | (1) |
Experimental
All compounds described in this work were handled using Schlenk techniques or a M. I. Braun glove box under purified nitrogen atmospheres.10 RuCl3·xH2O was purchased from Pressure Chemical, Inc. Tertiary phosphines, PMePh2 and PPh3, were obtained from Strem Chemical, Inc. and used as received. Solvents were purified by refluxing over Na/benzophenone (toluene, tetrahydrofuran, benzene, hexane, pentane), P2O5 (dichloromethane) or MgSO4 (ethanol) and distilled prior to use. Chloroform-d1 and benzene-d6 (Cambridge Isotope Laboratories) were purified by distillation from CaH2 and Na/benzophenone, respectively. Ruthenium(II) compounds CpRu(PPh3)2Cl (1a),11 CpRu(PPh3)2Br (1b),12 CpRu(PPh3)2I (1c),12 CpRu(PPh3)2N3 (1d),13 CpRu(PPh3)2NCO (1e),12 CpRu(PPh3)2H (1f),12 CpRu(PPh3)2F (1g),14 CpRu(PPh3)2SnF3 (1h),13 CpRu(PPh3)2SnCl3 (1i),13 and CpRu(PPh3)(PPh2Me)Cl (2a),15 were prepared by literature procedures. Melting points were determined in capillary tubes using an Electrothermal 9110 melting point apparatus and are uncorrected. Elemental analyses (C, H) were performed by Columbia Analytical Services, Inc. Tucson, AZ.NMR spectra were recorded at 400 MHz for 1H and 162 MHz for 31P{1H} on a Mercury XL300 spectrometer. Proton chemical shifts are reported relative to residual protons in the solvent (CD2HCl at δ 7.24 ppm relative to TMS at 0.00 ppm). Phosphorus chemical shifts are reported relative to 85% H3PO4 at 0.0 ppm.
Electrochemical measurements were made under nitrogen on a BAS 100 B/W electrochemical workstation at 22 °C using 1 × 10−3 M solutions in dry CH2Cl2, 0.1 M nBu4NPF6 as supporting electrolyte at a scan rate of 100 mV s−1. The working electrode was a 3 mm Pt disk with a Pt wire as auxiliary electrode. A silver wire was used as a pseudo-reference electrode with ferrocene added as an internal standard. All potentials for 1a–e, h and i (Table 1) are referenced to ferrocene (E1/2 = 0.00 V).
| Compound | E° (mV) | Compound | E° (mV) |
|---|---|---|---|
| a 1 × 10−3 M solutions in dry CH2Cl2, 0.1 M nBu4NPF6 as supporting electrolyte at a scan rate of 100 mV s−1 at 22 °C vs. Fc/Fc+ at 0.00 mV.b 1h is not sufficiently soluble for the experiment. | |||
| X = Cl, 1a | 136 | X = NCO, 1e | 168 |
| X = Br, 1b | 138 | X = F, 1g | 790 |
| X = I, 1c | 182 | X = SnF3, 1h | b |
| X = N3, 1d | 20 | X = SnCl3, 1i | 730 |
Synthesis of CpRu(PPh3)(PMePh2)X (X = Br, I, NCO, N3, SCN, and SnCl3)
CpRu(PPh3)(PMePh2)Br (2b). Yellow-orange solid, 75% yield. Mp turns dark brown without melting above 160 °C.
Calculated for C36H33P2RuBr·CH2Cl2: 56.01% C, 4.45% H; found: 56.53% C, 5.35% H.
1H (CDCl3) δ 1.19 d (J = 8.8 Hz, 3H, PCH3), 4.20 s (5H, Cp), 5.29 s (2H, CH2Cl2), 7.0–7.8 m (25 H, aryl).
31P (CDCl3) δ 42.9 d (JPP = 43 Hz), 29.9 d (JPP = 43 Hz).
CpRu(PPh3)(PMePh2)I (2c). Yellow-orange solid, 51% yield. Mp turns dark brown without melting above 140 °C.
Calculated for C36H33P2RuI·CH2Cl2: 52.87% C, 4.20% H; found: 53.08% C, 4.67% H.
1H (CDCl3) δ 1.31 d (J = 8.8 Hz, 3H, PCH3), 4.27 s (5H, Cp), 5.24 s (2H, CH2Cl2), 7.0–7.8 m (25 H, aryl).
31P (CDCl3) δ 42.9 d (JPP = 43 Hz), 30.0 d (JPP = 43 Hz).
CpRu(PPh3)(PMePh2)N3 (2d). Yellow-orange solid, 15% yield. Mp turns dark brown without melting above 163 °C.
Calculated for C36H33N3P2Ru: 64.47% C, 4.96% H; found: 63.93% C, 5.31% H.
1H (CDCl3) δ 1.17 d (J = 8.8 Hz, 3H, PCH3), 4.23 s (5H, Cp), 7.21–7.46 m (25 H, aryl).
31P (CDCl3) δ 41.3 d (JPP = 43 Hz), 30.3 d (JPP = 43 Hz).
CpRu(PPh3)(PMePh2)NCO (2e). Yellow-orange solid, 74% yield. Mp turns black without melting above 160 °C.
Calculated for C37H33NOP2Ru: 66.26% C, 4.96% H; found: 66.45% C, 5.28% H.
1H (CDCl3) δ 1.06 d (J = 8.8 Hz, 3H, PCH3), 4.15 s (5H, Cp), 7.18–7.3 m (25 H, aryl).
31P (CDCl3) δ 39.5 d (JPP = 43 Hz), 30.7 d (JPP = 42 Hz).
CpRu(PPh3)(PMePh2)SnCl3 (2i). A solution of 172 mg (0.26 mmol) 2a and 54 mg (0.28 mmol) SnCl2 in 50 mL absolute ethanol was refluxed for 90 minutes. The resulting precipitate was isolated by filtration, washed 2 × 5 mL methanol and dried under vacuum. Compound 2i was isolated in 68% yield as an orange solid. Mp. turns dark brown without melting 151–153 °C.
Calculated for C36H33P2RuSnCl3: 50.65% C, 3.90% H; found: 50.83% C, 4.54% H.
1H (CDCl3) δ 1.19 d (J = 8.8 Hz, 3H, PCH3), 4.19 s (5H, Cp), 6.9–7.7 m (28 H, aryl).
31P (CDCl3) δ 43.4 d (JPP = 44 Hz), 30.4 d (JPP = 44 Hz).
Kinetic measurements
To assess the effect of excess PPh3 and X−, additional experiments were carried out by adding 600 μL of the stock solution to weighed amounts of PPh3 (3–10 equivalents) or nBu4NX (≈10 equivalents). The resulting solutions were transferred to NMR tubes and sealed as described above. These experiments were typically limited to a single measurement of the substitution rate at one temperature.
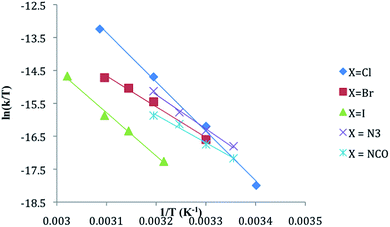
Activation parameters were determined using the Eyring equation by plotting ln(kobs/T) vs. 1/T where the slope = −ΔH‡/R and the intercept = ΔS‡/R + ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kB/h as described in our prior work.6 The activation entropies and enthalpies were also calculated from the slope and intercept of a plot of T
kB/h as described in our prior work.6 The activation entropies and enthalpies were also calculated from the slope and intercept of a plot of T![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(k/T) vs. T, respectively.16 The same values for ΔH‡ and ΔS‡ were obtained using each method within error. Errors in ΔS‡ and ΔH‡ were calculated using the statistical packages in Excel and by procedures described in standard analytical chemistry texts.17
ln(k/T) vs. T, respectively.16 The same values for ΔH‡ and ΔS‡ were obtained using each method within error. Errors in ΔS‡ and ΔH‡ were calculated using the statistical packages in Excel and by procedures described in standard analytical chemistry texts.17
Computational methods
All calculations were conducted using density functional theory (DFT) as implemented in the Gaussian09 Revision B.01 suite of ab initio quantum chemistry programs as described for phosphine substitution in 1a and related CpRu(PAr3)2Cl complexes.6Results
Kinetics of phosphine exchange
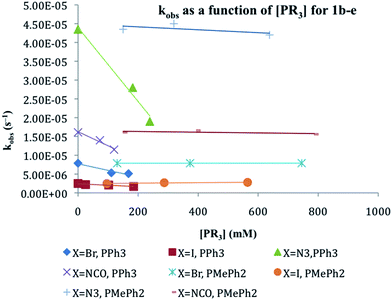
The substitution of one PPh3 in 1b–e by PPh2Me (10–15 equivalents, pseudo first order conditions) was followed by 31P NMR in both CDCl3 and THF/10% C6D6 (v/v) solution between 25 and 60 °C. The singlet resonance for the starting material is replaced by a pair of doublets assigned to the mono-substituted products, CpRu(PPh3)(PPh2Me)X (2b–e) with concurrent appearance of resonances for PPh3 (δ − 4.4 ppm in CDCl3, −4.6 ppm in THF/10% C6D6). The 31P chemical shifts of the products were verified by comparison with independently synthesized and characterized samples of 2b–f. Formation of CpRu(PPh2Me)2X (i.e. di-substitution) is not observed during the reaction period even in the presence of ≈10 equivalents of PMePh2. Formation of 1b–c from reactions between 2b–c and PPh3 is not observed. Qualitatively, the rate of reaction at 40 °C is found to be 1a > 1d > 1b ≈ 1e > 1c.Reactions between CpRu(PPh3)2X and PMePh2 in THF solution follow first order kinetics over several half-lives. Rate constants, half-lives and activation parameters for reactions in THF/C6D6 mixtures are summarized in Fig. 1 and Table 2. The reaction rates are largely independent of the [PMePh2], up to 60 equivalents (Fig. 2 and Table S3†). By comparison, the reaction rate decreases dramatically in the presence of added PPh3. In addition, the reaction rates are unaffected by the addition of excess nBu4NX in all four cases.18 The rates of phosphine substitution in 1a in both CDCl3 and in THF are known.6,7 The remaining complexes, 1f–g and 1i fail to react with excess PMePh2 in THF/C6D6, dioxane/C6D6 or other solvent mixtures up to the boiling point of the solvents even after 30 days or more. Compound 1h has minimal solubility in THF and dioxane hampering comparable studies, however, phosphine substitution was not observed.
| X | k30,THF (×106 s−1) | t1/2 (h) | ΔH‡ (kJ mol−1) | ΔS‡ (J mol−1 K−1) | ΔG‡ (kJ mol−1) |
|---|---|---|---|---|---|
| a Concentrations of 1b–e ranged from 8 to 17 mM with a ≈ 10–15 fold excess of PMePh2. Benzene-d6 is added to lock and shim the spectrometer.b From ref. 7. | |||||
| 1a, Cl− | 29 ± 2b | 0.66 | 121 ± 4b | 71 ± 8b | 100 |
| 1b, Br− | 7.89 ± 0.79 | 24 | 135 ± 7 | 102 ± 23 | 105 |
| 1c, I− | 2.49 ± 0.3 | 77 | 113 ± 4 | 21 ± 12 | 107 |
| 1d, N3− | 24.6 ± 1.5 | 7.8 | 86 ± 5 | −48 ± 16 | 100 |
| 1e, NCO− | 16.1 ± 3.6 | 12 | 70 ± 7 | −105 ± 23 | 101 |
The activation parameters reveal different trends for the halide complexes 1a–c and the pseudohalide complexes 1d–e. Activation enthalpies for the former are generally larger and the activation entropies are positive. The activation entropies for 1d and 1e, however, are negative. The free energies of activation (ΔG‡) calculated at 25 °C (298 K) for 1a–e are similar to those reported for Cp*Ru(PMe3)2X: 109 kJ mol−1, 106 kJ mol−1 and 113 kJ mol−1 for X = Cl, Br, and I, respectively.9 Pseudohalide derivatives in the Cp*Ru(PMe3)2X series were not studied.
Reactions between 1b–e and PMePh2 were also investigated in CDCl3 but were complicated by the appearance of 1a (δ 39.9 ppm) and 2a as the reaction progressed. The formation of 1a is the result of reaction between the starting materials and the solvent since the starting materials were pure by 31P NMR at the outset of the reaction. Thus the final reaction mixtures in CDCl3 contain 2b–e and 2a. Nevertheless, the rate of reaction between excess PMePh2 (10–15 equivalents, i.e. pseudo first order conditions in PMePh2) and 1b–e at early reactions times could be measured by integration of the 31P resonances for reactant and product before halide exchange led to measurable quantities of 1a. Qualitatively, the order of the rates for the reaction of 1b–e with PMePh2 in CDCl3 is the same as in THF: 1a > 1d > 1b > 1e > 1c. Reasonable estimates of first order rate constants (ksubs,CDCl3) for the substitution reactions in CDCl3 at early reaction times, when less than 5% of 1a (and no 2a) is observed in the solution, are summarized in Table 3. The substitution is slowed by the addition of excess PPh3 and the formation of 1a in these reactions is suppressed in the presence of added nBu4NX. The rate of substitution, however, remains unaffected by the presence of excess X−. Comparison of the values for ksubs,THF with ksubs,CDCl3 for 1a–e indicate that reactions are between 1.5 and 5 times faster in THF solution.
| X | k30,susb,CDCl3 (×106 s−1) | k30,THF/k30,susb,CDCl3 | k30,CDCl3 (×106 s−1) | k30,susb,CDCl3/k30,CDCl3 |
|---|---|---|---|---|
| a Concentrations of 1a–e ranged from 12 to 18 mM in CDCl3 with a ≈ 10 fold excess of PMePh2.b From data in ref. 6 and 7. | ||||
| 1a, Cl | 13b | 2.2b | — | — |
| 1b, Br | 5.0 ± 0.3 | 1.6 | — | |
| 1c, I | 1.8 ± 0.2 | 1.4 | 0.54 ± 0.2 | 3 |
| 1d, N3 | 6.1 ± 0.1 | 4.0 | 6.6 ± 0.4 | 1 |
| 1e, NCO | 3.5 ± 0.5 | 4.6 | — | — |
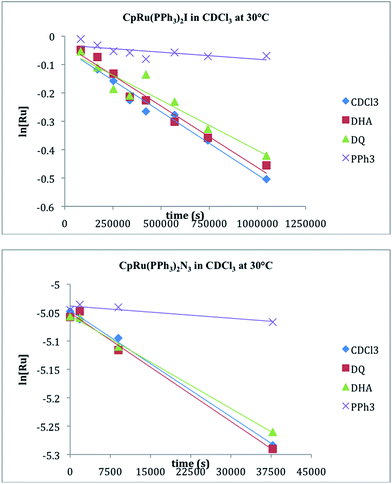
Kinetics of halide exchange between 1c–d and CDCl3
The rates of the halide exchange reactions between 1c and 1d with CDCl3 were measured independently by integration of the 31P resonances for reactants (1c–d) and product (1a) in CDCl3 at 30 °C. Linear plots of ln[CpRu(PPh3)2X] vs. time are observed for both compounds, with first order rate constants for the reaction (kCDCl3) being listed in Table 3. The rate of reaction with CDCl3 reflects the same order observed for phosphine substitution: 1d > 1c. The reaction rates of 1c–d in CDCl3 were further investigated in the presence of excess PPh3, (6–21 eq.), a radical initiator, 9,10-dihydroanthracene, (3–16 eq.), and a radical trap, duroquinone, (2–24 eq.). Fig. 3 reveals that the reaction rates are essentially independent of radical initiators and traps but are slowed significantly by the presence of PPh3. The ksubs,CDCl3/kCDCl3 ratio in Table 3 reveals that the rate of reaction with CDCl3 is competitive with the rate of phosphine substitution for 1c–d.Computational studies
DFT calculations were initially used to optimize the structures of 1a–e (Table 4). The calculated values for bond distances and bond angles for 1a–b and 1d compare favorably with the published structures determined by X-ray crystallography: the calculated bond distances are only slightly longer than the observed values.19| Compound | dRu–X (Å) | dRu–P1 (Å) | dRu–P2 (Å) | dRu–Cp,centroid (Å) | ∠Ru–X (°) |
|---|---|---|---|---|---|
| a The isocyanate ligand is treated as N bonded. Calculations use the B3LYP functional and the DGDZVP basis set on the Gaussian 09 suite. Normal convergence conditions were applied and geometries were determined to be of a minimal through a frequency calculation.b From X-ray crystallography see ref. 19. This value seems abnormally short for a Cp–Ru bond. | |||||
| 1a | 2.513 | 2.401 | 2.396 | 2.27 | — |
| 2.448b | 2.323b | 2.329b | 2.20b | — | |
| 1b | 2.648 | 2.406 | 2.411 | 2.27 | — |
| 2.568b | 2.323b | 2.329b | 2.214b | — | |
| 1c | 2.842 | 2.416 | 2.413 | 2.275 | — |
| 1d | 2.196 | 2.401 | 2.400 | 2.275 | 118.5 |
| 2.135b | 2.329b | 2.330b | 1.843b | 124.5b | |
| 1e | 2.136 | 2.400 | 2.3999 | 2.27 | 153.5 |
Computational chemistry was then applied to the calculation of the relative energies of potential intermediates in a dissociation of PPh3 in 1a–e. The free energies for the 16-electron intermediate that results from PPh3 dissociation from 1a–e (second column in Table 5) are quite similar to each other and lower than the energies for intermediates resulting from halide dissociation and coordination of THF (third column in Table 5). The calculated free energy changes for the overall conversion of 1a–e to 2a–e are listed in the fourth column of Table 5 indicating a fairly narrow range of value for ΔG of about 12 kJ mol−1.
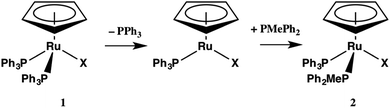 | (2) |
| CpRu(PPh3)2X | ΔG (kJ mol−1) | ΔG (kJ mol−1) | ΔG (kJ mol−1) |
|---|---|---|---|
| CpRu(PPh3)2X ⇒ CpRu(PPh3)X + PPh3 | CpRu(PPh3)2X + THF ⇒ CpRu(PPh3)2(THF)+ + X− | CpRu(PPh3)2X + PMePh2 ⇒ CpRu(PMePh2)(PPh3)X + PPh3 | |
| a Geometry optimizations were optimized in the gas phase using the B3LYP exchange–correlation functional and DGDZVP basis set followed by a single point energy calculation using a polarizable continuum model (PCM) for THF solvation. | |||
| 1a, X = Cl | 43.5 | 70.9 | −35.8 |
| 1b, X = Br | 40.7 | 59.0 | −40.8 |
| 1c, X = I | 43.6 | 47.2 | −45.2 |
| 1d, X = N3 | 47.2 | 105.1 | −32.6 |
| 1e, X = NCO | 43.9 | 108.8 | −31.9 |
The energies of the transition states for the two steps in eqn (2) were also calculated (Table 6). The data indicate that the activation energy for the dissociation of PPh3 is greater than for the reaction of the 16 e− intermediate, CpRu(PPh3)X, with PMePh2, consistent with the kinetic measurements. The calculated values of ΔG for the transitions states of 1a–e are also quite close in energy, covering a range of <4 kJ mol−1 for the rate-determining step and about 8–12 kJ mol−1 less than the values of ΔG‡ from experiment.
| CpRu(PPh3)2X | ΔG‡TS1 (kJ mol−1) | ΔG‡TS2 (kJ mol−1) |
|---|---|---|
| CpRu(PPh3)2X ⇒ [CpRu(PPh3)X⋯PPh3]‡ | CpRu(PPh3)2X + PMePh2 ⇒ [CpRu(PMePh2)(PPh3)X]‡ | |
| a The transition state optimization was performed using the synchronous transit and quasi-Newton methods (STQN). The guess structure used was the maximum of a relaxed PES scan along the Ru–P bond. They were confirmed as first order saddle points by harmonic frequency analysis. | ||
| 1a, X = Cl | 92.1 | 73.7 |
| 1b, X = Br | 93.2 | 75.7 |
| 1c, X = I | 91.1 | 80.0 |
| 1d, X = N3 | 89.6 | 79.9 |
| 1e, X = NCO | 91.1 | 79.5 |
Discussion
The effect of the X group on phosphine substitution rates in 1a–e is qualitatively similar to those reported previously for Cp*Ru(PMe3)2X for the same set of X ligands. An increase in the rate of substitution in Cp*Ru(PMe3)2X is observed for X ligands with lone pairs of electrons on the donor atom, e.g. X = Cl, Br, I, NPh2, NHPh, OPh, OH, and SH relative to such σ-donor ligands such as H, CH3, CH2Ph, Ph and CH2SiMe3.9 Kinetic data for phosphine exchange between Cp*Ru(PMe3)2X and PMe3 in aromatic hydrocarbon solution are consistent with a dissociative process through 16-electron Cp*Ru(PMe3)X intermediates.9 The relative rates of substitution in Cp*Ru(PMe3)2X were judged to reflect both ground state and transition state effects of X.9 The observation that 1g–i (X = H, SnF3, and SnCl3) do not react at all with PMePh2 under the reaction conditions is consistent with the observations for Cp*Ru(PMe3)2X: good σ-donors lead to slower reaction. The corresponding indenyl complex, (η5-C9H7)Ru(PPh3)2H, is also known to be inert toward phosphine substitution.20 The effect of σ-donor, π-donor, and possibly π-acceptor properties of the ligands on both ground state and transition state energies are likely to be relevant to interpretations of the rate data for 1a–e.We start by considering the halide derivatives 1a–c. The observed order of substitution rates in 1a–c are the same as for Cp*Ru(PMe3)2X: Cl > Br > I. The substitution rates in 1a–c span a relatively small range; kobs for 1a (X = Cl) is ≈ 50 times greater than for 1c (X = I) in THF, a slightly broader range of kobs values for 1a–c than for Cp*Ru(PMe3)2X for the same X ligands. A dissociative mechanism for phosphine substitution has been suggested for reactions of 1a with PMePh2 in both THF and CDCl3.6,7 The kinetic data for substitution in 1b and 1c in Table 1 in THF are also consistent with a dissociative or dissociative interchange mechanism with the loss of PPh3 as the rate-determining step.6 This conclusion is supported by the observed decrease in rate in the presence of added PPh3, the independence of the rate on PMePh2 concentration and the observed positive activation entropies. Closer examination of the effect of added PPh3 on the substitution rate reveals that the effect is not the same across the series 1b–e.
Ionization of Ru–X bonds in CpRu(PR2R′)2X (R = Ph, Me, X = Cl, Br, I) systems in Lewis basic solvents such as alcohols, acetonitrile, or dimethylsulfoxide is well established but does not seem to play a significant role in the substitution reactions in THF.21 The absence of any significant effect of added X− on the rate suggests that formation of [CpRu(PPh3)2(THF)]+ and X− ions in THF solution is unlikely to be the rate determining step; one would expect a decrease in rate if dissociation of X− was the rate determining step. With the exception of 1c calculations of the relative energies of CpRu(PPh3)X and [CpRu(PPh3)2(THF)]+[X]− confirm that the latter is significantly higher in energy than the former. Even in the case of CpRu(PPh3)2I (1c), the 16 e− intermediate is 3–4 kJ mol−1 lower in energy than [CpRu(PPh3)2(THF)]+[I]− (in the gas phase).
The absence of significant differences in the Ru–P or Ru–Cp bond distances in 1a–c in either the crystal structures or in the calculated structures (Table 4) suggests that only small differences exist in the ground state energies of 1a–c. Despite a significantly larger ionic radius and a longer Ru–X bond distance, the iodide (1c), reacts slower than the chloride (1a). Increasing the size of X (X = I > Br > Cl) does not increase the rate of the reaction suggesting that transition state effects also contribute to the order of substitution rates for 1a–c.9,22 The electrochemical potentials of CpRu(PPh3)2X (Table 1) reveal surprisingly similar E° values for 1a–c. The E° values for 1a–c are essentially indistinguishable: 136 vs. 138 mV vs. Fc/Fc+ for 1a and 1b, respectively and less than a 50 mV difference in E° between the chloride and iodide complexes. Although 1c does react slower than 1a–b, the small difference in E° values remains consistent with minimal contribution from ground state effects to the substitution reaction. Further support for small ground state effects of chloride, bromide and iodide is seen in the νCO for CpRu(CO)2X (νCO X = Cl > Br > I) which differ by only 11 cm−1.23
Interestingly CpRu(PPh3)2F (1f) has a significantly larger positive E°, 790 mV, which may help explain the lack of reactivity toward PMePh2. Fluoride is a weaker σ-donor and a stronger π-donor than Cl−, Br− and I−.2 One not on might expect greater π-donation to accelerate the substitution rate but the opposite is observed. The much greater electronegativity of fluoride as reflected by E°, suggests that the Ru–PPh3 bond is significantly stronger in 1f than in 1a–c contributing to the failure of CpRu(PPh3)2F (1f) to react with PMePh2 under the conditions of the experiment. No data is available for Cp*Ru(PMe3)2F for CpRu(CO)2F making further comparisons difficult.
The calculated free energies of the 16-electron CpRu(PPh3)X fragments span a narrow range, about 10 kJ mol−1 (Table 5). It was previously shown that PPh3 dissociation from 1a yields a lower energy intermediate than dissociation of Cl− to form CpRu(PPh3)2+, the common intermediate from halide dissociation from 1a–c.6 The computational results for the free energies of the CpRu(PPh3)X intermediate must be treated with caution when comparing calculations in the gas phase to the kinetic measurements in solution. As expected, the calculated free energy changes for substitution of one PPh3 by PMePh2 for the halide compounds are exergonic (ΔG < 0, Table 5) and differ by <15 kJ mol−1 as a function of the halide ligand.
Support for the role of transition state effects on the reactivity of 1a–c comes from decades-old studies of carbonyl substitution reactions of M(CO)5X (M = Re, Mn) and M(CO)5X− (M = Cr, Mo, where X = Cl, Br and I).24 Substitution cis to the X group is observed in all cases and kinetic data for these reactions are consistent with a dissociative pathway. The rate of substitution in the chloride complexes is between 15 and 250 times the rate of substitution in the corresponding iodides. This effect was attributed to stabilization of the 16-electron intermediate or transition state by the stronger σ-donation from the halide ligand: Cl > Br > I.24 There are strong parallels between the substitution rates in these mononuclear metal carbonyl halides and 1a–c. The observed order of rates, Cl > Br > I, is the same and substitution in 1a–c also occurs cis to the X group if one considers the Cp ligand to occupy a fac geometry in a pseudo-octahedral geometry. A stabilizing role for π-donation from X is less likely because the order of π-donation, I > Br > Cl, does not match the relative rates of phosphine substitution.1,22 The kinetics of carbonyl substitution in CpRu(CO)2X provide an even better comparison with the reactions of 1a–c.25 In xylene, the rate of substitution in CpRu(CO)2Cl with P(OPh)3 is faster than for the bromide and iodide. A dissociative process is proposed for all three CpRu(CO)2X compounds.
Finally, the calculated transition state energies (ΔG‡) for the reactions of 1a–c with PMePh2 support the interpretation of the experimental data. The first step, dissociation of PPh3, is the rate determining step with subsequent reaction of the coordinatively unsaturated CpRu(PPh3)X intermediate with PMePh2: ΔG‡TS1 > ΔG‡TS2. The difference between ΔG‡TS1 and ΔG‡ (Table 2) is small. The range of values for ΔG‡TS1 is quite narrow and mirrors the trend for ΔG‡ in Table 2 suggesting that only small differences in the transition state contribute to the observed order of reaction rates: 1a > 1b > 1c. For 1c, the similar energies for two intermediates, CpRu(PPh3)I and [CpRu(PPh3)2(THF)]+[I]− in Table 5 may account for the greater difference between ΔG‡TS1 and ΔG‡.
The compounds with pseudohalide ligands (N3− and NCO−), 1d and 1e, introduce ligands with both π-donating and π-accepting properties. Compounds 1d and e react with PMePh2 as fast, or even faster, than 1b. Unlike 1a–c, the activation entropies for 1d and 1e are negative: ΔS‡ = −48 ± 16 and −105 ± 23 J mol−1 K−1, respectively. This raises the possibility of a change in mechanism from a dissociative interchange to an associative interchange pathway. Nevertheless, the observation that the substitution rate in both 1d and 1e decreases in the presence of excess PPh3 and is unchanged when excess pseudohalide is added to the solution argues for a dissociative or dissociative interchange mechanism for 1a–e. The greatest effect of added PPh3 on rate is seen for 1d, the compound that reacts the fastest and the smallest effect is seen for 1c, which exhibits the slowest rate of phosphine substitution. One possible explanation is that the halide complexes, 1b–c react by a dissociative interchange mechanism while substitution in 1d–e follows a more dissociative pathway.
If ionization of the pseudohalide ligand in 1d–e represents the rate determining step, then one expects a decrease in rate when excess N3− or NCO− is added to the reaction mixture, yet the rate is unchanged. Calculated values of ΔG for product of substitution of N3− or NCO− by THF, [CpRu(PPh3)2(THF)]+[X]−, are more than double the ΔG for CpRu(PPh3)X, suggesting that dissociation of X− also does not play a role in the reaction with PMePh2. Large negative values for ΔS‡ were also reported for phosphine substitution in (η5-pentadienyl)Ru(PPh3)2Cl in what appears to be a dissociative mechanism and have been observed in halide exchange reactions of CpRu(prophos)Cl.26 The large positive ΔS‡ values for substitution in Cp*Ru(PMe3)2X were attributed to a late or product like transition state9 so one possible explanation for the differences in ΔS‡ values between 1a–c and 1d–e is an earlier, more ordered transition state in 1d–e than in 1a–c. For comparison, the activation entropy for substitution in Re(CO)5NCO, ΔS‡ = +8 J mol−1 K−1, is less positive than ΔS‡ = +73 and +44 J mol−1 K−1 for substitution in Re(CO)5Cl and Re(CO)5Br, respectively.27 The rate of substitution in the rhenium(I) series reveals that Re(CO)5NCO reacts slightly slower than Re(CO)5Cl but faster than the bromide derivative similar to our observations for 1a–b and 1e.27 Detailed calculations of the structure of the transition state for 1a–e are in progress but the data for ΔG‡TS1 indicate a lower activation energy for 1d and correlate well with the values for ΔG‡ in Table 2, as observed for 1a–c.
The Ru–P bond distances in the solid state structure of 1d19c and the results of DFT calculations (Tables 4 and 5) for 1d–1e do not reveal any striking structural anomalies. The electrochemical potential for 1e is again indistinguishable from the values for 1a–1c suggesting similar ground state energies. The electrochemistry of 1d, however, indicates that it is much easier to oxidize than 1a or 1b by about 160 mV. The significance of this E° value on the relative value of kobs is not entirely clear but may indicate a slightly higher energy for the ground state in 1d.
Crystallography confirms that the azide ligand in 1d is bent with a Ru–N–N bond angle of 124.5°.19c DFT calculations are consistent with this geometry yielding a calculated bond angle, ∠Ru–N–N = 118.5°. The calculated Ru–N–C bond angle in 1e (153.5°) reveals that the NCO ligand is more linear in 1e, consistent with a greater contribution of resonance forms C and D in Fig. 4, while structures A and B are likely to be the major contributors to the bonding of N3− in 1d. The importance of structures C and D may make the linear NCO ligand a better π-acceptor than the bent N3 ligand.
Transition state stabilization and increased substitution rates for square planar complexes bearing ancillary π-acceptor ligands is well established but the effect of π-acceptor ligands on substitution rates in octahedral complexes is less documented.22 Seminal studies on dissociative substitution reactions of group 6 and group 7 carbonyls suggest that 16 e− transition states are stabilized by electron donors and destabilized by acceptor ligands.22,24,27 If this is true, than the bent N3 ligand in 1d stabilizes the transition state and accounts for the faster reaction of 1d compared to 1e. Conversely, the better π-acceptor, linear NCO ligand may destabilize (raise the energy of) the transition state decreasing the reaction rate. The linear π-accepting phenylacetylide ligand in Cp*Ru(PMe3)2CCPh increases the Ru–PMe3 bond energy by about 38 kJ mol−1 and reduces the rate of phosphine dissociation.9 Significantly slower phosphine substitution was also observed in reactions of (η5-C9H7)Ru(PPh3)2CCPh compared to (η5-C9H7)Ru(PPh3)2Cl.20
In addition to 1f, phosphine substitution was also not observed in 1g–i all of which contain good σ-donors: hydride and trihalotin (SnX3−, X = Cl, F) ligands. To understand the lack of reaction, we turn to the studies of phosphine substitution that include Cp*Ru(PMe3)2Cl, Cp*Ru(PMe3)2H, and Cp*Ru(PMe3)2CH3.9 The data for the latter three compounds suggests that the activation enthalpy, ΔH‡, for the reaction closely approximates the Ru–PMe3 bond energies, leading to the conclusion that the Ru–PMe3 bonds in Cp*Ru(PMe3)2H and Cp*Ru(PMe3)2CH3 are 29–59 kcal mol−1 greater than for Cp*Ru(PMe3)2Cl. The lack of phosphine substitution in 1g–i is therefore, most likely the result of a small, strong σ-donor hydride ligands that substantially greater Ru–P bond strength.
The observation of halide exchange reactions between CpRu(PPh3)2X and CDCl3 has not been previously reported28 for 1b–e although reaction between 1a and acetyl halides, CH3COX where X = Br and I, was recently reported to yield 1b–c.29 An increase in the rate of halide exchange was observed in the presence of 9,10-dihydroanthracene (radical initiator) and a concomitant decrease in conversion when TEMPO (radical trap) is added to the reaction mixture supporting a radical mechanism. Computational chemistry suggested a pathway where phosphine dissociation is followed by halogen atom abstraction from CH3COX and formation of a radical pair.29 Further support for radical intermediates in the chemistry of 1 is found in the catalytic activity of CpRu(PPh3)(PMe3)Cl in the atom transfer radical addition (ATRA) reactions of CCl4 and styrene.30 There are also two reports of the reaction between 1a and excess iodomethane yielding 1c in situ and as a synthetic method but the mechanism of the reaction was not explored.3
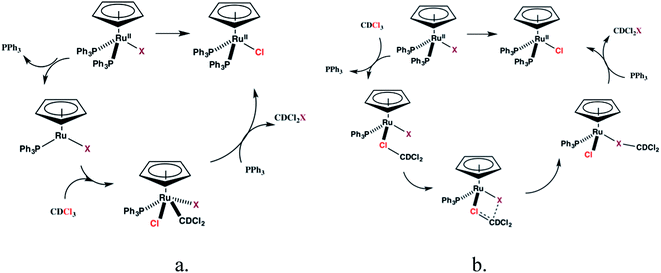
The reactions between 1c–d and CDCl3, however, are inconsistent with radical mechanisms given the absence of any noticeable effect of 1–16 equivalents of 9,10-dihydroanthracene or duroquinone (Fig. 3).25a The addition of PPh3 significantly reduces the rate of the halide exchange reaction. The latter observation argues for phosphine substitution as the potential rate-limiting step in the halide exchange reaction. The relative rates of halide exchange for 1c and 1d mimic the trend for the phosphine substitution rates in these two compounds. Both the oxidative addition of C-halide bonds and concerted mechanisms (Fig. 5) must be considered for the conversion of 1c–d to 1a.
Limited evidence for both mechanisms can be found in the literature. Oxidative addition of allyl chloride to CpRu(PPh3)2Cl yields CpRu(C3H5)Cl2 (ref. 31) while a halocarbon complex, [CpRu(PPh3)2(CH3I)][PF6] is isolated from reaction of 1a with Ag+ and methyl iodide.32 A further mechanistic proposal for the halide exchange reaction is the formation of quaternary phosphonium salts by reaction between the dissociated PPh3 and CDCl3 followed by dissociation of Cl− and subsequent halide exchange with 1b–e. The latter pathway was proposed for the catalytic halogen exchange between MeI and CH2Cl2 catalyzed by a broad range of group 9 transition metal complexes.33 Although no new resonances are observed in the 31P NMR spectrum of PPh3 in CDCl3, the possibility of halide exchange in 1b–e by this mechanism cannot be excluded at this time.
The rate data for phosphine substitution in 1a–i provide some insight into reaction mechanisms where 1a–i show catalytic activity. The assertion that faster phosphine dissociation accounts for higher yields in the cycloaddition of norbornene and norbornadiene3 when 1c is used in place of 1a is inconsistent with the relative rates of phosphine substitution reported herein. In fact, our data suggest that any catalytic process that relies on phosphine dissociation from 1a–e should proceed fastest for X = Cl with X = N3 as the next most active catalyst precursor. The effect of 1b–e on the rate and selectivity of ruthenium-catalyzed dimerization of alkynes34 and the 1,3-dipolar addition of azides to alkynes35 represent potential future studies of the effect of the X ligand on catalytic properties. Phosphine substitution in trihalotin ligands in 1h–i are clearly slow and consistent with the high temperatures required for converting methanol to methylacetate5 in their presence.
Conclusions
The results of the kinetic study of phosphine substitution in CpRu(PPh3)2X for five halide and pseudohalide derivatives in THF and CDCl3 solution reveals a likely dissociative or dissociative interchange process. These data suggest that dissociative substitution mechanisms reported for CpRu(PAr3)2Cl6 and Cp*Ru(PMe3)2X complexes9 are a general reaction pathway for 18-electron, cyclopentadienyl ruthenium(II) derivatives. Differences in the rate of substitution in 1a–e are likely a combination of ground state and transition state effects. Dissociation of phosphine in 1b–e is a likely step in the exchange of Ru–X bonds for Ru–Cl bonds when CpRu(PPh3)2X is dissolved in CDCl3, however, further mechanistic studies are needed to identify the likely mechanism.For reactions where Ru–X bond ionization is important, the data on phosphine substitution in 1a–e offer more limited insight. Compounds 1a, 1c–d, 1g and 1i all catalyze the N-methylation of cyclohexylamines4 to varying degrees in methanol solution. An order of relative rates, 1a > 1g > 1c ≥ 1d ≫ 1i (no reaction), can be inferred from the observed product ratios of CyNMe2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CyNHMe
CyNHMe![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CyNH2. Among these, 1a is by far the best catalyst but the position of the hydride complex, 1g, is anomalous suggesting that more work is needed to understand the effect of different ligand environments on the reactivity of cyclopentadienyl ruthenium(II) complexes in carbon–carbon and carbon–nitrogen bond forming processes.
CyNH2. Among these, 1a is by far the best catalyst but the position of the hydride complex, 1g, is anomalous suggesting that more work is needed to understand the effect of different ligand environments on the reactivity of cyclopentadienyl ruthenium(II) complexes in carbon–carbon and carbon–nitrogen bond forming processes.
References
- Ruthenium in Organic Synthesis, ed. S.-I. Murahashi, Wiley-VCH, 2004 Search PubMed.
- For a review of halide effect in transition metal catalyzed reactions see K. Fagnou and M. Lautens, Angew. Chem., Int. Ed., 2002, 41, 26–47 CrossRef CAS.
- (a) A. Tenaglia and L. Giordano, Synlett, 2003, 2333–2336 CrossRef CAS; (b) A. Tenaglia and M. Sylvain, J. Org. Chem., 2008, 73, 1397–1402 CrossRef CAS PubMed; (c) A. Tenaglia, L. Giordano, M. Sylvain and I. De Riggi, Angew. Chem. Int. Ed., 2011, 50, 9062–9065 CrossRef CAS PubMed.
- A. Del Zotto, W. Baratta, M. Sandri, G. Verardo and P. Rigo, Eur. J. Inorg. Chem., 2004, 524–529 CrossRef CAS.
- P. A. Robles-Dutenhefner, E. M. Mora, G. J. Gama, H. G. L. Siebald and E. V. Gusevskaya, J. Mol. Catal. A: Chem., 2000, 164, 39–47 CrossRef CAS.
- (a) M. J. Verschoor-Kirss, O. Hendricks, L. Renna, D. Hill and R. U. Kirss, Dalton Trans., 2014, 43, 15221–15227 RSC; (b) C. Peng and H. B. Schlegel, Isr. J. Chem., 1993, 33, 449 CrossRef CAS.
- M. P. Gamasa, J. Gimeno, C. Gonzalz-Bernardo, B. M. Martin-Vaca, D. Monti and M. Bassetti, Organometallics, 1996, 15, 302–308 CrossRef CAS.
- (a) R. J. Haines and A. L. DuPreez, J. Organomet. Chem., 1975, 84, 357–367 CrossRef CAS; (b) P. M. Treichel and P. J. Vincenti, Inorg. Chem., 1985, 24, 228–230 CrossRef CAS.
- H. E. Bryndza, P. J. Domaille, R. A. Paciello and J. E. Bercaw, Organometallics, 1989, 8, 379–385 CrossRef CAS.
- D. F. Shriver, Manipulation of Air Sensitive Compounds, McGraw Hill, 1969 Search PubMed.
- M. I. Bruce, C. Hameister, A. G. Swincer and R. C. Wallis, Inorg. Synth., 1990, 28, 270 CrossRef CAS.
- T. Wilczewski, M. Bochenska and J. F. Biernat, J. Organomet. Chem., 1981, 215, 87–96 CrossRef CAS.
- E. M. Moura, H. G. L. Siebald and G. M. de Lima, Polyhedron, 2002, 21, 2323–2331 CrossRef CAS.
- (a) M. I. Bruce, C. Hameister, A. G. Swincer and R. C. Wallis, Inorg. Synth., 1982, 21, 78–84 CrossRef CAS; (b) M. I. Bruce, R. C. F. Gardner and F. G. A. Stone, J. Chem. Soc., Dalton Trans., 1976, 81–89 RSC.
- P. M. Treichel and D. A. Komar, Synth. React. Inorg. Met.-Org. Chem., 1980, 10, 205–218 CrossRef CAS.
- G. Lente, I. Fabian and A. J. Poe, New J. Chem., 2005, 29, 759–760 RSC.
- D. A. Skoog, D. M. West and J. Holler, Analytical Chemistry: An Introduction, Saunders, 7th edn, 2000 Search PubMed.
- See ESI† for plots of ln[Ru] vs. time, complete tables of rate constants and Eyring plots for reactions of 1b–e with PMePh2.
- (a) M. I. Bruce, F. S. Wong, B. W. Skelton and A. H. White, J. Chem. Soc., Dalton Trans., 1981, 1398–1405 RSC; (b) M. I. Bruce, P. J. Low, B. W. Skelton, E. R. T. Tietink, A. Werth and A. H. White, Aust. J. Chem., 1995, 48, 1887–1892 CrossRef CAS; (c) M. M. T. Khan, M. M. Bhadbhade, M. R. H. Siddiqui and K. Venkatasubramanian, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1994, 50, 502–504 CrossRef.
- M. Bassetti, S. Marini, F. Tortorella, V. Cadierno, J. Diez, M. P. Gamasa and J. Gimeno, J. Organomet. Chem., 2000, 593–594, 292–298 CrossRef CAS.
- Rate constants for solvation for CpRu(PPh2OMe)2X and CpRu(PPh2Me)2X in CD3CN comparable to the substitution rates for CpRu(PPh3)2X at 30 °C require more than doubling the reaction temperature to 67 °C. Compound 1a–c do not dissolve sufficiently in CD3CN for a direct comparison. See ref. 8.
- J. M. Atwood, Inorganic and Organometallic Reaction Mechanisms, Wiley-VCH, 2nd edn, 1997 Search PubMed.
- R. J. Haines and A. L. duPreez, J. Chem. Soc., Dalton Trans., 1972, 944–948 RSC.
- J. D. Atwood and T. L. Brown, J. Am. Chem. Soc., 1976, 98, 3160–3166 CrossRef CAS.
- (a) K. Tabataiana and K. White, Inorg. Chem., 1981, 20, 2020–2022 CrossRef; (b) D. A. Brown, H. J. Lyons and R. T. Sane, Inorg. Chim. Acta, 1970, 4, 621–625 CrossRef CAS.
- (a) M. Daniels and R. U. Kirss, J. Organomet. Chem., 2007, 692, 1716–1725 CrossRef CAS; (b) H. Brunner, M. Muschiol, T. Tsuno, T. Takahashi and M. Zabel, Organometallics, 2008, 27, 3514–3525 CrossRef CAS.
- R. J. Angelici and G. C. Faber, Inorg. Chem., 1971, 10, 514–517 CrossRef CAS.
- Halide exchange is also observed between 1c and benzylbromide but not with bromobenzene.
- H. Kuniyasu, A. Sanagawa, T. Nakajima, T. Iwasaki, N. Kambe, K. Bobuatong and M. Ehara, J. Organomet. Chem., 2014, 769, 34–39 CrossRef CAS.
- R. P. Nair, T. H. Kim and B. J. Frost, Organometallics, 2009, 28, 4681–4688 CrossRef CAS.
- H. Nagashima, K. Mukai, Y. Shiota, K. Yamaguchi, K.-I. Ara, T. Fukahori, H. Suzuki, M. Akita, Y. Moro-oka and K. Itoh, Organometallics, 1990, 9, 799–807 CrossRef CAS.
- (a) R. J. Kulawiec, J. W. Faller and R. H. Crabtree, Organometallics, 1990, 9, 745–755 CrossRef CAS; (b) A related complex, [CpRu(PPh3)(CNtBu)(CH3I)]+ is also known: F. M. Conroy-Lewis, A. D. Redhouse and S. J. Simpson, J. Organomet. Chem., 1989, 366, 357–367 CrossRef CAS.
- D. Forster, J. Chem. Soc., Chem. Commun., 1975, 917–918 RSC.
- M. Daniels and R. U. Kirss, J. Organomet. Chem., 2007, 692, 1716–1725 CrossRef CAS.
- L. Zhang, X. Cheng, P. Xue, H. H. Y. Sun, I. D. Williams, K. B. Sharpless, V. V. Fokin and G. Jia, J. Am. Chem. Soc., 2005, 127, 15998–15999 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Representative plots ln[CpRu(PPh3)2X] vs. t for phosphine substitution and halide exchange, Eyring plots, and coordinates for the optimized geometries for 1a–e. See DOI: 10.1039/c7ra02793a |
| This journal is © The Royal Society of Chemistry 2017 |