Open Access Article
Open Access ArticleDichroic nonlinear absorption response of silver nanoprism arrays
Tiziana Cesca *a,
Emma Vianey García-Ramírezb,
Hectór Sánchez-Esquivelc,
Niccolò Michielia,
Boris Kalinica,
Juan Manuel Gómez-Cervantesb,
Raul Rangel-Rojoc,
Jorge Alejandro Reyes-Esquedab and
Giovanni Matteia
*a,
Emma Vianey García-Ramírezb,
Hectór Sánchez-Esquivelc,
Niccolò Michielia,
Boris Kalinica,
Juan Manuel Gómez-Cervantesb,
Raul Rangel-Rojoc,
Jorge Alejandro Reyes-Esquedab and
Giovanni Matteia
aDepartment of Physics and Astronomy, University of Padova, via Marzolo 8, I-35131 Padova, Italy. E-mail: tiziana.cesca@unipd.it
bInstituto de Física, Universidad National Autónoma de México, Circuito de la Investigación Científica, Ciudad Universitaria, Delegación Coyoacán, C.P. 4510, Ciudad de México, México
cDivisión de Física Aplicada, Centro de Investigación Científica y de Educación Superior de Ensenada, Carretera Ensenada-Tijuana No. 3918, Zona Playitas, C.P. 22860, Ensenada, México
First published on 22nd March 2017
Abstract
The properties of dichroism in the nonlinear absorption response of silver nanoprism arrays are experimentally investigated by the z-scan technique. Open aperture z-scan measurements are performed with a picosecond laser at a low repetition rate to excite the third-order electronic component of the optical nonlinearity for different linear polarization directions of the incident beam. A strong saturable absorber behavior is observed for all the linear polarization orientations and a continuous, sinusoidal modulation of the nonlinear absorption coefficient (up to about 30% of its absolute value) is demonstrated as a function of the polarization angle. The dichroic nonlinear absorption of the samples is explained by taking into account the polarization-dependent local electric-field distribution in the nanoprism arrays, as demonstrated by finite elements method electrodynamic simulations. These findings make silver nanoprism arrays an ideal platform for the development of nanophotonic devices with fast, strong and tunable nonlinear optical responses.
Recent years have seen a tremendous burst of research activity towards the development of novel nonlinear optical (NLO) materials for advanced applications in photonics and optoelectronics.1–5 From this point of view, plasmonic nanomaterials are of great interest for their strong and ultra-fast nonlinear response.6 By coupling light to surface plasmons, an intense enhancement and the confinement of the local electromagnetic field at the plasmonic nanostructures can be obtained,7 which is of paramount importance to develop metamaterials with properly tuned and enhanced optical nonlinearity.8–13 In recent years a variety of different plasmonic nanosystems, both with random distribution and as ordered arrays, have been developed and characterized for NLO applications.14–25 Among them, 2D ordered nanoprism arrays (NPAs) represent a very interesting configuration.26,27 The confinement of the electromagnetic field at the nanoprisms’ sharp tips gives rise to the formation of intense hot-spots (further amplified by near-field interactions among the nanoprisms in the array) that significantly boost the nonlinear optical response of these nanomaterials.18,26,28
Besides a strong and ultra-fast nonlinear optical response, a very important requirement for NLO applications is the capability to control and modulate the material nonlinearity in a desired way. For plasmonic nanosystems, an effective approach to obtain such a control is by properly engineering the structural and compositional parameters of the nanomaterials.25,26,29 As an example, regarding the nanoprism array configuration, we recently demonstrated that the nonlinear absorption properties of bimetallic Au–Ag NPAs can be varied by properly selecting the bimetallic composition of the nanoprisms, without changing any other structural parameter of the nanoarray.26 On the other hand, the capability to modify the nonlinear response of nanomaterials in a reversible way by switching on some external parameters would be of great interest for NLO applications. To this aim, in the present work we studied the possibility of using the linear polarization of a laser beam to get the desired external control of the material nonlinearity. To do this, we investigated the effects of dichroism in the nonlinear absorption response of silver NPAs synthesized via nanosphere lithography.30 Nonlinear optical characterization was performed using z-scan measurements.31 A picosecond laser source at a low repetition rate was used to excite the fast, electronic, third-order component of the nonlinear response of the NPAs, inducing minimal thermal load to the samples. Strong saturable absorber (SA) behavior was observed for all the polarization orientations of the laser beam explored. Moreover, it was demonstrated that a continuous modulation of the nonlinear absorption coefficient can be obtained by rotating the polarization, leaving at the same time the linear absorption properties of the nanomaterial globally unaffected. The linear polarization of an external laser beam therefore represents a useful degree of freedom to get the external fine control of the material nonlinear absorption properties. These findings, combined with the cost-effectiveness and high throughput of the nanosphere lithography technique used for the synthesis of the samples, make silver nanoprism arrays a very interesting and highly promising platform for the development of all-optical nanophotonic devices with fast, strong and tunable nonlinear optical responses.
1 Experimental section
1.1 Synthesis of nanoprism arrays
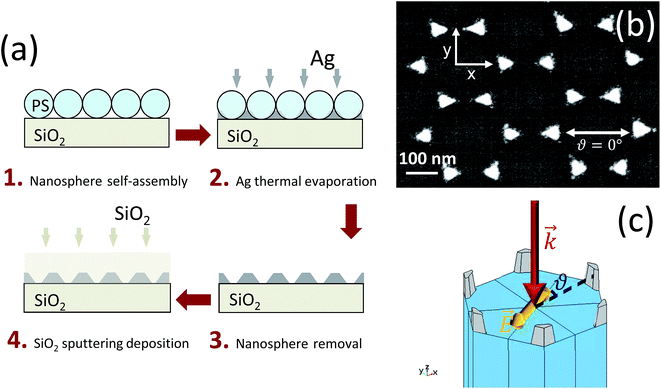
Silver nanoprism arrays (NPAs) were produced using the nanosphere lithography (NSL) technique.26,30,32 The main steps of fabrication are schematically illustrated in Fig. 1a. First, a colloidal monolayer of polystyrene (PS) nanospheres was formed, by self-assembling, on top of a silica glass substrate previously cleaned in a “piranha” solution (H2SO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O2, 3
H2O2, 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). Commercial PS nanospheres (Microparticles GmbH) with a nominal diameter of 248 nm were used. As the second step, silver was thermally evaporated in an orthogonal configuration on the PS monolayer. The thickness of the evaporated layer was controlled with a calibrated quartz microbalance. The PS nanospheres were then mechanically removed by stripping with an adhesive tape. After this step, an ordered array of triangular Ag nanoprisms, the same as the one shown in Fig. 1b, is left on the surface of the silica substrates. Finally, to protect the nanoprism arrays from possible physical damage and Ag oxidation (which would alter the optical properties of the samples), a layer of silica with thickness of about 160 nm was deposited on the samples by magnetron sputtering.
1). Commercial PS nanospheres (Microparticles GmbH) with a nominal diameter of 248 nm were used. As the second step, silver was thermally evaporated in an orthogonal configuration on the PS monolayer. The thickness of the evaporated layer was controlled with a calibrated quartz microbalance. The PS nanospheres were then mechanically removed by stripping with an adhesive tape. After this step, an ordered array of triangular Ag nanoprisms, the same as the one shown in Fig. 1b, is left on the surface of the silica substrates. Finally, to protect the nanoprism arrays from possible physical damage and Ag oxidation (which would alter the optical properties of the samples), a layer of silica with thickness of about 160 nm was deposited on the samples by magnetron sputtering.
1.2 Structural and linear optical characterizations
Morphological characterizations of the NPAs were performed using scanning electron microscopy (SEM). The measurements were made with a Zeiss Sigma field-emission scanning electron microscope (FE-SEM) working in the 0.2–30 kV range. An energy-dispersive spectrometer (EDS) is also mounted in the microscope for compositional analysis. Atomic force microscopy (AFM) measurements were performed to measure the height of the nanoprisms. A NT-MDT Solver PRO-M AFM microscope with a 100 × 100 μm scanner was used, operated in the semi-contact mode.Optical absorbance spectra in the 300–900 wavelength range were collected using a dual beam UV-Vis spectrophotometer (JASCO V670) with unpolarized light. Absorbance measurements as a function of the incident polarization orientation were also performed using an Ocean Optics USB2000 spectrometer coupled with optical fibers to a deuterium–halogen dual lamp.
1.3 Nonlinear absorption measurements
The third-order nonlinear absorption properties of the synthesized nanoprism arrays were investigated using open aperture (OA) z-scan measurements.31 The measurements were performed using the second harmonic (λ = 532 nm) of a picosecond pulsed mode-locked Nd:YAG laser (pulse duration of 26 ps, repetition rate 10 Hz). A 400 mm converging lens was used to focus the laser beam in the z-scan set-up. The beam waist w0 at the lens focal point was measured using the knife-edge method33 and it was w0 = 35 ± 1 μm. OA measurements were performed for different orientations of the linear polarization of the laser beam with respect to the plane of incidence (horizontal). The polarization was rotated by means of a half-wave plate.1.4 FEM simulations
Simulations were carried out using the Finite Elements Method (FEM).34 The software COMSOL Multiphysics 5.1 was used to solve the Helmholtz equation in the frequency domain. Fig. 1c shows the 3D geometry of the model. In the horizontal ( ) plane, the array of nanoprisms was modeled by considering a hexagonal unit cell. In this configuration, the nanoprisms are placed at the vertices of the cell and each cell embeds a third of a prism per vertex. The tips of the prisms are oriented along the boundaries of the unit cell. Such a choice of the unit cell was done since, as we checked, it does not introduce differences with respect to the standard rhomboidal unit cell, but assures at the same time a greater numerical stability. In the vertical direction (i.e., the light propagation direction), the nanoprism base is on the z = 0 plane, surrounded by silica on top and bottom. Over and below the simulated domains, two additional domains assure the absorption of unphysical backscattered radiation from external boundaries by using Perfectly Matched Layers (PML). The boundary conditions in the
) plane, the array of nanoprisms was modeled by considering a hexagonal unit cell. In this configuration, the nanoprisms are placed at the vertices of the cell and each cell embeds a third of a prism per vertex. The tips of the prisms are oriented along the boundaries of the unit cell. Such a choice of the unit cell was done since, as we checked, it does not introduce differences with respect to the standard rhomboidal unit cell, but assures at the same time a greater numerical stability. In the vertical direction (i.e., the light propagation direction), the nanoprism base is on the z = 0 plane, surrounded by silica on top and bottom. Over and below the simulated domains, two additional domains assure the absorption of unphysical backscattered radiation from external boundaries by using Perfectly Matched Layers (PML). The boundary conditions in the ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) and ŷ directions are periodic (PBC). The Ag dielectric function used in the simulations was experimentally obtained by ellipsometry measurements performed on continuous films evaporated under the same conditions as those used for the NPAs. A J. Woolham V-VASE spectroscopic ellipsometer was used for these measurements. The refractive index of the silica layer was set to n = 1.45. The shape of the nanoprisms was modeled using the FE-SEM images of the samples; their height was determined by AFM measurements. The mesh of the model was carried out by carefully assuring that it had the same hexagonal symmetry of the unit cell, to prevent spurious angular dependencies due to a non-uniform meshing. In the model, the nanoprisms were illuminated by plane waves traveling in the ẑ direction. The angle of polarization of the incident light (θ) was varied from θ = 0° to θ = 180°, with respect to the
and ŷ directions are periodic (PBC). The Ag dielectric function used in the simulations was experimentally obtained by ellipsometry measurements performed on continuous films evaporated under the same conditions as those used for the NPAs. A J. Woolham V-VASE spectroscopic ellipsometer was used for these measurements. The refractive index of the silica layer was set to n = 1.45. The shape of the nanoprisms was modeled using the FE-SEM images of the samples; their height was determined by AFM measurements. The mesh of the model was carried out by carefully assuring that it had the same hexagonal symmetry of the unit cell, to prevent spurious angular dependencies due to a non-uniform meshing. In the model, the nanoprisms were illuminated by plane waves traveling in the ẑ direction. The angle of polarization of the incident light (θ) was varied from θ = 0° to θ = 180°, with respect to the ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) direction in the
direction in the  plane (see Fig. 1).
plane (see Fig. 1).
2 Results and discussion
By nanosphere lithography, ordered arrays of triangular nanoprisms arranged in a honeycomb lattice can be synthesized.30 As an example, Fig. 1b shows a FE-SEM image of the silver nanoprism arrays (NPAs) investigated in the present work. The image was taken before the deposition of the silica top layer (step 3 in the synthesis process shown in Fig. 1a). The geometrical parameters of the nanoarrays were: lattice parameter a0 = 248 ± 5 nm, nanoprism side length L = 45 ± 1 nm and nanoprism height h = 40 ± 1 nm. The optical absorbance spectrum of the samples, measured after the silica deposition under unpolarized light illumination, is reported in Fig. 2a. Two peaks are visible in the spectrum, which can be interpreted as the dipolar (at λD = 520 nm) and the quadrupolar (at λQ = 392 nm) surface plasmon resonances (SPRs) of the nanoprism array.26,35,36 The linear absorption properties of the investigated NPA were also characterized as a function of the incident polarization. To do this, optical absorbance spectra were taken, with a linearly polarized light source, for different polarization orientations. The measurements are reported in Fig. 2b; the spectra are vertically shifted by a constant amount to improve the readability of the graph. The linear optical response of the NPA was found to be insensitive to the orientation of the incident electric field and no major differences were observed in the spectra. Such a behavior was expected taking into account the high degree of symmetry of the plasmonic lattice (honeycomb) in the samples, in agreement with literature data on similar samples37 and it was also confirmed by FEM simulations: consistent with the experimental findings, indeed, we did not highlight any dependence on the polarization in the simulated absorbance spectra.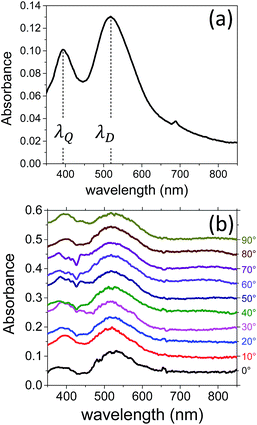 | ||
| Fig. 2 (a) Optical absorbance spectrum of a Ag NPA taken with unpolarized light after the silica sputtering deposition (step 4 in Fig. 1a): the two peaks correspond to the dipolar (at λD = 520 nm) and the quadrupolar (at λQ = 392 nm) surface plasmon resonances of the array. (b) Absorbance spectra as a function of the linear polarization orientation (in degrees, right-hand scale) of the incident light source; the spectra are vertically shifted by a constant amount to improve the readability of the graphs. | ||
The nonlinear absorption properties of the synthesized samples were studied using the z-scan technique in the open aperture (OA) configuration.31 The basic idea of this technique is to measure the intensity, transmitted by the sample, of a laser beam focused by a converging lens, as a function of the position of the sample along the focal axis of the lens (z direction). In this way, the laser beam intensity on the sample varies with z, being maximum at the lens focus (z = 0), and nonlinear absorption processes can be revealed as changes in the measured transmittance. The intensity-dependent absorption coefficient is usually written in the form α(I) = α0 + βI, where α0 and β are the linear and nonlinear absorption coefficients, respectively. The open aperture z-scan measurements allow both the magnitude and sign of the nonlinear absorption coefficient of the samples to be determined. Particularly, if saturable absorption (SA) phenomena are activated in the sample, they can be described by a negative nonlinear absorption coefficient (β < 0) and this would give rise to a peak in the OA transmittance scans at the lens focal point (z = 0). Conversely, reverse saturable absorption (RSA) processes are described by a positive nonlinear absorption coefficient (β > 0) and would be revealed by a minimum in the OA transmittance scans. In the present work, in order to reveal and investigate the possible effects of dichroism in the nonlinear absorption response of the samples, open aperture z-scan measurements were performed for different orientations of the linear polarization of the incident laser beam. For this experiment, the second harmonic of a ps Nd:YAG laser (λ = 532 nm) was used to excite the dipolar resonance of the samples. All the measurements were performed with a laser peak intensity (i.e., the beam intensity at the focal point of the converging lens used in the z-scan set-up) of I0 = 280 MW cm−2. This prevented possible physical damage or modifications of the samples during the scans (as it was further checked by performing forward and backward scans). Fig. 3a shows the OA scan obtained with the incident polarization oriented at 0° with respect to the plane of incidence (horizontal polarization). The continuous curve is the best fit to the experimental data obtained with the equation:31
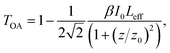 | (1) |
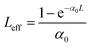 ). The scan shows a maximum of transmittance at the lens focus (z = 0) that corresponds to a saturable absorption (SA) behavior. The response can be characterized in this case by a negative nonlinear absorption coefficient (β < 0). To perform OA measurements with different polarization orientations, the electric field of the incident beam was rotated by means of a half-wave plate with increments of 15° with respect to the horizontal direction (0°), without changing the sample position. All the scans were fitted with eqn (1) and the results for the β parameter are summarized in Fig. 3b (red dots). A similar SA behavior was observed for all of the polarization orientations,38 but a continuous, sinusoidal modulation of the nonlinear absorption coefficient, β, was obtained as a function of the polarization angle. Such a modulation is well described by the function:
). The scan shows a maximum of transmittance at the lens focus (z = 0) that corresponds to a saturable absorption (SA) behavior. The response can be characterized in this case by a negative nonlinear absorption coefficient (β < 0). To perform OA measurements with different polarization orientations, the electric field of the incident beam was rotated by means of a half-wave plate with increments of 15° with respect to the horizontal direction (0°), without changing the sample position. All the scans were fitted with eqn (1) and the results for the β parameter are summarized in Fig. 3b (red dots). A similar SA behavior was observed for all of the polarization orientations,38 but a continuous, sinusoidal modulation of the nonlinear absorption coefficient, β, was obtained as a function of the polarization angle. Such a modulation is well described by the function:
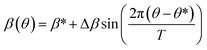 | (2) |
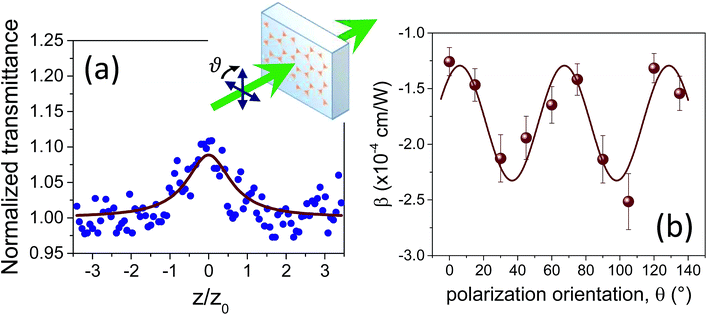 | ||
| Fig. 3 (a) Open aperture (OA) z-scan of the Ag NPA measured with horizontal polarization of the laser beam (θ = 0°); the continuous curve is the best fit to the experimental data performed with eqn (1). The inset shows a sketch of the sample orientation with respect to the laser beam during the z-scan measurements. (b) Nonlinear absorption coefficient, β, as a function of the polarization orientation obtained by fitting the corresponding OA scans with eqn (1). All the measurements were taken at λ = 532 nm, and the laser peak intensity was I0 = 280 MW cm−2. | ||
The effects of dichroism observed in the nonlinear absorption response of the investigated samples can be explained as a consequence of the local field enhancement in the NPA. Following the approach by Debrus et al.39,40 (recently used by Zheludev and co-workers to describe the nonlinear response of plasmonic metamaterials21), the nonlinear absorption coefficient of the NPA investigated in the present work can be expressed in terms of the distribution of local electric-field in the nanoprism array (E) according to the equation:
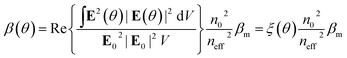 | (3) |
Therefore, according to eqn (3), an angle-dependent nonlinear absorption coefficient can be predicted for the investigated NPA due to the polarization-dependent local electric-field distribution in the array (i.e., the term ξ(θ)). No angular dependence is instead expected for the other parameters in eqn (3). Particularly, the effective linear refractive index of the array, neff, was computed from the same field distribution data using the S-matrix method:41 the same value (neff = 0.198) was obtained for all the polarization orientations. In Fig. 4a–f we report the electric field enhancement maps (at the z = 0 plane), calculated using FEM simulations for the incident polarization oriented at the different indicated angles with respect to the ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) axis. The simulations were performed at the wavelength of the dipolar resonance peak (λD = 520 nm). The maps show that the highest values of the electric-field enhancement factor, F = |E|/E0, are localized on the nanoprism tips that are oriented along the direction parallel to the incident polarization. The white contours indicate the levels of enhancement factor F = 1.5, 3, 5 and 25. These maps were used to compute the integral term ξ(θ) in eqn (3). The results of this calculation are reported in Fig. 4g (blue dots). The data show an oscillating trend as a function of the polarization angle well described by the sin function (blue continuous curve) with a period of 60°, in perfect agreement with the experimental results shown in Fig. 3b. A modulation amplitude of about 20% of the average value is obtained in this case, still in agreement with the experimental result. A small phase shift is present between the simulated and the experimental data, due to the fact that, while for the simulations the polarization angle is perfectly defined with respect to the
axis. The simulations were performed at the wavelength of the dipolar resonance peak (λD = 520 nm). The maps show that the highest values of the electric-field enhancement factor, F = |E|/E0, are localized on the nanoprism tips that are oriented along the direction parallel to the incident polarization. The white contours indicate the levels of enhancement factor F = 1.5, 3, 5 and 25. These maps were used to compute the integral term ξ(θ) in eqn (3). The results of this calculation are reported in Fig. 4g (blue dots). The data show an oscillating trend as a function of the polarization angle well described by the sin function (blue continuous curve) with a period of 60°, in perfect agreement with the experimental results shown in Fig. 3b. A modulation amplitude of about 20% of the average value is obtained in this case, still in agreement with the experimental result. A small phase shift is present between the simulated and the experimental data, due to the fact that, while for the simulations the polarization angle is perfectly defined with respect to the ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) direction in the unit cell of the array, an a priori alignment of the NPA with respect to the polarization direction of the laser beam during the z-scan measurements was not possible. Such a shift is taken into account in the parameter θ* in eqn (2).
direction in the unit cell of the array, an a priori alignment of the NPA with respect to the polarization direction of the laser beam during the z-scan measurements was not possible. Such a shift is taken into account in the parameter θ* in eqn (2).
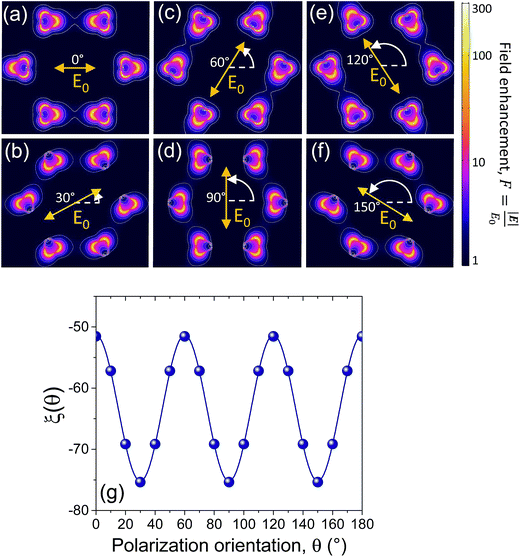 | ||
Fig. 4 (a–f) Simulated maps of electric field enhancement at the z = 0 plane (silica substrate interface) evaluated at λD = 520 nm. The incident light beam is orthogonal to the sample surface and the electric field is linearly polarized at the different indicated angles with respect to the ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) direction (see Fig. 1c). The white contours indicate enhancement factors F = 1.5, 3, 5 and 25. (g) Values of ξ(θ) in eqn (3) as a function of the polarization angle (blue dots); the blue curve is the best fit to the data performed with the sin function. direction (see Fig. 1c). The white contours indicate enhancement factors F = 1.5, 3, 5 and 25. (g) Values of ξ(θ) in eqn (3) as a function of the polarization angle (blue dots); the blue curve is the best fit to the data performed with the sin function. | ||
These findings further confirm the key role of the hot-spot formation in controlling the nonlinear optical properties of the investigated nanoprism arrays, giving rise to the demonstrated dichroic nonlinear absorption response. On the other hand, it is important to point out that if we calculate the average of the field enhancement factor over the whole unit cell of the array, no angular dependence comes out and a constant value F = 1.2 is obtained for all the polarization orientations. This is due to the fact that the tip region is small compared to the unit cell (a volume ratio of about 4.3% was estimated), and thus the field enhancement averaged over the whole cell is weakly influenced by the hot-spots at the nanoprism tips. As a consequence, this explains why, differently from the nonlinear absorption response, the linear optical absorbance, which is dependent on the linear component of the electric field, does not exhibit any dependence on the incident polarization (Fig. 2).
3 Conclusions
The properties of dichroism in the nonlinear absorption response of Ag nanoprism arrays synthesized via nanosphere lithography were experimentally investigated using the z-scan technique. A picosecond laser beam with a low repetition rate was used to highlight the third-order electronic contribution in the optical nonlinearity of the samples, minimizing possible thermal effects. The measurements were performed by exciting the dipolar surface plasmon resonance of the synthesized nanoprism arrays. Open aperture z-scan measurements were performed for different linear polarization directions of the incident laser beam, in order to investigate the polarization-dependent nonlinear absorption properties of the investigated samples. The results showed that the samples have a strong saturable absorber character, and a continuous, sinusoidal modulation of the nonlinear absorption coefficient up to about 30% of its average value can be obtained by rotating the incident polarization. From FEM simulations, it was demonstrated that the observed dichroic nonlinear absorption behavior can be quantitatively explained by taking into account the polarization-dependent local electric-field distribution in the nanoarray. The properties highlighted in the present work make plasmonic nanoprism arrays a very interesting platform for the development of all-optical nanophotonic devices with fast, strong and tunable nonlinear optical response. As fast saturable absorbers, they could be used, for example, to develop solid-state mode-locking systems in ultra-fast laser devices, with low saturation intensity and in which the incident polarization can be exploited for the fine-tuning of the nonlinear absorption properties. Finally, as a last comment it has to be pointed out that the approach developed in the present work to explain the polarization-dependent nonlinear optical properties of the investigated nanoprism arrays can be used as well to characterize other plasmonic metamaterials. Thus, the incident polarization becomes an important parameter to take into account when comparing the nonlinear optical properties of different nanosystems.Acknowledgements
This work has been supported by the Project of Major Importance Italy-México (Progetto di Grande Rilevanza Italia-Messico) MX14MO09 of the Italian Ministry of Foreigner Affairs and International Cooperation (MAECI). The authors thank CONACYT-México for grant 222485, and H. S. E. also thanks CONACYT for scholarship No. 221750 and mixed-funds grant 290842-359816. Financial support from PAPIIT-UNAM (México) through grant IN117116 is also acknowledged.References
- R. W. Boyd, Nonlinear Optics, Academic Press, 3rd edn, 2008 Search PubMed.
- X. Hu, Y. Zhang, Y. Fu, H. Yang and Q. Gong, Adv. Mater., 2011, 23, 4295–4300 CrossRef CAS PubMed.
- M. Kauranen, Science, 2013, 342, 1182–1183 CrossRef PubMed.
- D. Cotter, R. J. Manning, K. J. Blow, A. D. Ellis, A. E. Kelly, D. Nesset, I. D. Phillips, A. J. Poustie and D. C. Rogers, Science, 1999, 286, 1523–1528 CrossRef CAS PubMed.
- R. A. Ganeev, Nonlinear Optical Properties of Materials, Springer, 2013 Search PubMed.
- M. Kauranen and A. V. Zayats, Nat. Photonics, 2012, 6, 737–748 CrossRef CAS.
- S. A. Maier, Plasmonics: Fundamentals and Applications, Springer, New York, USA, 2007 Search PubMed.
- T. Cesca, P. Calvelli, G. Battaglin, P. Mazzoldi and G. Mattei, Opt. Express, 2012, 20, 4537–4547 CrossRef CAS PubMed.
- S. Gwo, C.-Y. Wang, H.-Y. Chen, M.-H. Lin, L. Sun, X. Li, W.-L. Chen, Y.-M. Chang and H. Ahn, ACS Photonics, 2016, 3, 1371–1384 CrossRef CAS.
- H. Harutyunyan, G. Volpe, R. Quidant and L. Novotny, Phys. Rev. Lett., 2012, 108, 217403 CrossRef PubMed.
- P. Genevet, J. Tetienne, E. Gatzogiannis, R. Blanchard, M. A. Kats, M. O. Scully and F. Capasso, Nano Lett., 2010, 10, 4880–4883 CrossRef CAS PubMed.
- S. Kim, J. Jin, Y. Kim, I. Park, Y. Kim and S. Kim, Nature, 2008, 453, 757–760 CrossRef CAS PubMed.
- Y. Zhu, X. Hu, Y. Fu, H. Yang and Q. Gong, Sci. Rep., 2013, 3, 2338 Search PubMed.
- R. Philip, P. Chantharasupawong, H. Qian, R. Jin and J. Thomas, Nano Lett., 2012, 12, 4661–4667 CrossRef CAS PubMed.
- A. L. Stepanov, Rev. Adv. Mater. Sci., 2011, 27, 115–145 CrossRef CAS.
- J. A. Reyes-Esqueda, V. Rodríguez-Iglesias, H.-G. Silva-Pereyra, C. Torres-Torres, A.-L. Santiago-Ramírez, J. C. Cheang-Wong, A. Crespo-Sosa, L. Rodríguez-Fernández, A. Lopez-Suarez and A. Oliver, Opt. Express, 2009, 17, 12849–12868 CrossRef CAS PubMed.
- A. López-Suárez, C. Torres-Torres, B. Can-Uc, R. Rangel-Rojo, C. E. Valencia and A. Oliver, J. Opt. Soc. Am. B, 2015, 32, 805–811 CrossRef.
- X.-L. Liu, J.-H. Wang, S. Liang, D.-J. Yang, F. Nan, S.-J. Ding, L. Zhou, Z.-H. Hao and Q.-Q. Wang, J. Phys. Chem. C, 2014, 118, 9659–9664 CAS.
- G. A. Wurtz, R. Pollard, W. Hendren, G. P. Wiederrecht, D. J. Gosztola, V. A. Podolskiy and A. V. Zayats, Nat. Nanotechnol., 2011, 6, 107–111 CrossRef CAS PubMed.
- S.-W. Chu, H.-Y. Wu, Y.-T. Huang, T.-Y. Su, H. Lee, Y. Yonemaru, M. Yamanaka, R. Oketani, S. Kawata, S. Shoji and K. Fujita, ACS Photonics, 2014, 1, 32–37 CrossRef CAS.
- M. Ren, B. Jia, J.-Y. Ou, E. Plum, J. Zhang, K. F. MacDonald, A. E. Nikolaenko, J. Xu, M. Gu and N. I. Zheludev, Adv. Mater., 2011, 23, 5540–5544 CrossRef CAS PubMed.
- J. Y. Suh, M. D. Huntington, C. H. Kim, W. Zhou, M. R. Wasielewski and T. W. Odom, Nano Lett., 2012, 12, 269–274 CrossRef CAS PubMed.
- Y. Zhang, J. J. Wang, K. E. Ballantine, P. R. Eastham and W. J. Blau, Adv. Opt. Mater., 2014, 2, 331–337 CrossRef CAS.
- J. Butet and O. J. F. Martin, ACS Nano, 2014, 8, 4931–4939 CrossRef CAS PubMed.
- A. D. Neira, N. Olivier, M. E. Nasir, W. Dickson, G. A. Wurtz and A. V. Zayats, Nat. Commun., 2015, 6, 7757 CrossRef CAS PubMed.
- T. Cesca, N. Michieli, B. Kalinic, A. Sánchez-Espinoza, M. Rattin, V. Russo, V. Mattarello, C. Scian, P. Mazzoldi and G. Mattei, Nanoscale, 2015, 7, 12411–12418 RSC.
- N. Michieli, PhD thesis, Doctoral School in Physics, 2014.
- Z. Li, Y. Yu, Z. Chen, T. Liu, Z.-K. Zhou, J.-B. Han, J. Li, C. Jin and X. Wang, J. Phys. Chem. C, 2013, 117, 20127–20132 CAS.
- K. O’Brien, H. Suchowski, J. Rho, A. Salandrino, B. Kante, X. Yin and X. Zhang, Nat. Mater., 2015, 14, 379–383 CrossRef PubMed.
- J. C. Hulteen and R. P. Van Duyne, J. Vac. Sci. Technol., A, 1995, 13, 1553–1558 Search PubMed.
- M. Sheik-Bahae, A. Said, T. Wei, D. Hagan and E. V. Stryland, IEEE J. Quantum Electron., 1990, 26, 760–769 CrossRef CAS.
- G. Perotto, V. Bello, T. Cesca, G. Mattei, P. Mazzoldi, G. Pellegrini and C. Scian, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 3211–3214 CrossRef CAS.
- J. M. Khosrofian and B. A. Garetz, Appl. Opt., 1983, 22, 3406–3410 CrossRef CAS PubMed.
- N. Michieli, B. Kalinic, C. Scian, T. Cesca and G. Mattei, Biosens. Bioelectron., 2015, 65, 346–353 CrossRef CAS PubMed.
- L. J. Sherry, R. Jin, C. A. Mirkin, G. C. Schatz and R. P. Van Duyne, Nano Lett., 2006, 6, 2060–2065 CrossRef CAS PubMed.
- N. Félidj, J. Grand, G. Laurent, J. Aubard, G. LÃľvi, A. Hohenau, N. Galler, F. R. Aussenegg and J. R. Krenn, J. Chem. Phys., 2008, 128, 094702 CrossRef PubMed.
- A. D. Humphrey and W. L. Barnes, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 075404 CrossRef.
- T. Cesca, H. Sanchez-Esquivel, E. Gemo, N. Michieli, B. Kalinic, E. V. García Ramírez, J. M. Gómez Cervantes, R. Rangel-Rojo, J. A. Reyes Esqueda and G. Mattei, Proc. SPIE 9894, Nonlinear Optics and its Applications IV, 2016, p. 98941A Search PubMed.
- S. Debrus, J. Lafait, M. May, N. Pincon, D. Prot, C. Sella and J. Venturini, J. Appl. Phys., 2000, 88, 4469–4475 CrossRef CAS.
- H. Ma, R. Xiao and P. Sheng, J. Opt. Soc. Am. B, 1998, 15, 1022–1029 CrossRef CAS.
- D. Smith, D. Vier, T. Koschny and C. Soukoulis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 036617 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2017 |