Phase diagram, stability and electronic properties of an Fe–P system under high pressure: a first principles study

Abstract

Fe–P binary compounds have attracted much attention, particularly under high pressure, since they are the constituents of the Earth's core. However, most studies focus on the single stoichiometry of Fe–P binary compounds at high pressure, and their whole phase diagram and relative stabilities have been unexplored thus far. Herein, first principles swarm structure predictions are performed to find stable structures of Fe–P compounds with various Fe_xP_y (x = 1–4 and y = 1, or x = 1 and y = 2) compositions. Then, their phase diagram and relative stabilities are reliably determined based on predicted structures. Specifically, the FeP, Fe₂P and Fe₄P compounds are found to be stable in the pressure range of 0–400 GPa. The Fe₃P compound decomposes into Fe₂P and Fe₄P above 214 GPa. FeP₂ becomes unstable above 82 GPa. Notably, two new phases (i.e. C2/c-structured Fe₄P and Cmcm-structured Fe₃P) are found to be more stable than the previously reported phases. In addition, the XRD pattern of the predicted Cmcm-structured Fe₃P matches the experimental patterns, and we are awaiting future experimental confirmation. Electronic band calculations show that the Fe–P binary compounds are metallic, with a pronounced Fe 3d component crossing the Fermi level. Cmcm-structured Fe₃P is ferromagnetic. Our study not only provides useful information for the further study of Fe–P binary compounds but also for the determination of the Earth's core components.

---

1. Introduction

Geochemical and geophysical studies show that light elements (i.e. hydrogen, oxygen, carbon, sulfur, phosphorus and silicon) play important roles in the Earth's core.^1,2 Early models of the Earth's core consisted of a considerable amount of schreibersite, cohenite, and troilite.³ The Fe content of the Earth's core is rather rich (90.67%).³ Several phases of iron compounds, such as iron–sulfur, iron–silicon, and iron–oxygen, with light elements under high pressure have been determined by a large number of experimental and theoretical studies.^4–7 Notably, the phosphorus content of the Earth's core was estimated to be around 0.20 wt%, and up to 4 wt% of phosphorus was found to be soluble in crystalline iron at 23 GPa in the Fe–S–P system.^8,9 Since the structures of Fe–P compounds are similar to that of Fe–S, iron phosphides should have a stable composition in the cores. As a consequence, investigation of the structures and properties of iron-phosphorus (Fe–P) compounds is worthy of attention.

To date, extensive studies have been carried out on Fe–P binary compounds, and although most of these studies were based on single stoichiometry, the relative stabilities of the Fe–P binary compounds remain undetermined, particularly at high pressure. For example, several stoichiometric compounds (i.e. Fe₄P, Fe₃P, Fe₂P, FeP and FeP₂) were separately investigated. Fe₄P is known as melliniite, which is a mineral from Northwest Africa 1054 acapulcoite. The cubic polymorph with the P2₁3 space group symmetry (AlAu₄-type structure) was determined using single-crystal X-ray diffraction data (XRD).¹⁰ Under high pressure, the Fe₄P phase is relatively stable compared to Fe₃P + Fe.¹¹ The tetragonal structure Fe₃P was discovered from schreibersite at ambient pressure.¹² Its possible high-pressure polymorph is either a P4/mnc or Pnma structure, as predicted by theoretical calculations, and the pressure-induced phase transition from I4̄ to P4/mnc has been observed at 64 GPa.¹³ For the Fe₂P compound, it is a terrestrial garnet peridotite with implications for the Earth's core. A hexagonal structure of Fe₂P with P6̄2m symmetry exists at ambient conditions, and the Co₂Si-type structure (space group Pnma) is found to be more stable above 8.0 GPa (ref. 14) or 16.8 GPa,¹⁵ as observed through high-pressure and high-temperature X-ray diffraction experiments. Based on first principles calculations, another P3̄m-structured Fe₂P was reported at 153 GPa.¹⁶ Several studies on FeP have been carried out because FeP is also an important member in the planetary cores. FeP crystallizes in the regular MnP-type structure (space group Pnma) at ambient conditions and undergoes a structural phase transition to a simple cubic FeSi-type phase (space group P2₁3) at 87.5 GPa.^17,18 FeP₂ crystallizes in the regular marcasite structure (space group Pnnm) at ambient conditions with no unpaired spins in the low-spin configuration.¹⁹ Under high-pressure and high-temperature conditions, a new phase of FeP₂ with I4/mcm symmetry was observed at 70 GPa.²⁰ Recent studies show that Fe–P binary compounds (i.e. Fe₃P, Fe₂P, FeP, FeP₂ and FeP₄) are stable at ambient pressure,²¹ in which all the structures came from reported compounds. By all appearance, it is necessary to establish the whole phase diagram of Fe–P binary compounds under high pressure.

Recently, the first principles structural prediction method has become an irreplaceable tool to discover new materials and determine their stable structures.^22–24 For example, a recent breakthrough in the superconductivity field is the observation of remarkably high superconductivity (with T_c up to 203 K),²⁵ in which H₃S is the main stoichiometry of the superconducting phase.²⁶ This observation was achieved by direct investigation on the theoretical prediction of high-T_c superconductivity in compressed solid H₂S.²⁷ A new clathrate sodalite-like BN structure was predicted with a high energy density and large hardness.²⁸ The reaction of iron with xenon has been predicted in the Earth's inner core environment through theoretical calculations, which provides a solution to the missing Xe paradox.²⁹ Numerous unusual stoichiometric compounds with exotic physical or chemical properties have been discovered under high pressure.^30–37

Herein, the most stable structures of the Fe–P binary compounds (Fe₄P, Fe₃P, Fe₂P, FeP and FeP₂) are reliably determined using the first principles calculations in combination with the swarm structural search technology.^23,38 The relative stabilities of these considered compounds are reliably established. Two new phases (C2/c-structured Fe₄P, and Cmcm-structured Fe₃P) are found to be more stable than the previously reported phases. Cmcm-structured Fe₃P meets the Stoner criterion and is ferromagnetic. Our study provides some useful information for the investigation of the constituents of the Earth's core.

2. Computational details

To search the stable structures for the given chemical compositions, structural predictions of the Fe–P system were performed at 0, 50, 100, 200, 300, and 400 GPa using the Crystal structure AnaLYsis by the Particle Swarm Optimization (CALYPSO) code.^23,39 The CALYPSO method can successfully find stable structures just depending on chemical compositions and has demonstrated success in predicting the high-pressure structures of various systems.^40–44 The ab initio structural relaxations and electronic calculations are based on the density functional theory (DFT) within the Perdew–Burke–Ernzerhof (PBE) of the generalized gradient approximation (GGA),⁴⁵ as implemented in the Vienna ab initio simulation package (VASP) code.⁴⁶ The electron–ion interaction was described using the all-electronic projector-augmented wave (PAW) method⁴⁷ with 3s²3p⁶3d⁷4s¹ and 3s²3p³ valence electrons for the Fe and P atoms, respectively. Hubbard U is necessary to correct the effective on-site electron–electron interaction of the transition metal, with valence electrons on the d and f orbits.^48,49 Hubbard U parameters with U = 2 eV and J = 0.95 eV were applied to the Fe atoms in the Fe₂P compounds.¹⁶ It successfully reproduces the experimental magnetic moments of Fe atoms.⁵⁰ As a consequence, we chose Hubbard U with 2 eV at a fixed value of 0.95 eV (i.e. U_eff = U − J) to calculate the properties and fine structure optimization. U = 2.2 eV was verified to be suitable to elemental iron by the linear response approach.⁵¹ The cutoff energy of 700 eV and Monkhorst–Pack⁵² k-meshes with a grid spacing of 2π × 0.03 Å⁻¹ were used to ensure that the total energy calculations converged well. The phonon calculations were carried out using the finite displacement approach to determine the dynamical stability of the predicted structures, as implemented in the Phonon code.⁵³ To study the interatomic interaction, the integrated crystal orbital Hamilton populations (ICOHPs) were calculated as implemented in the LOBSTER package.⁵⁴

3. Results and discussion

3.1. Phase stabilities of Fe–P compounds

Herein, we mainly considered Fe-rich phosphorus compounds (i.e. Fe₄P, Fe₃P, Fe₂P, FeP and FeP₂) since the Fe content of the Earth's core is estimated to be around 90.67% and P content is about 0.17%.³ In this study, the pressure ranges up to 400 GPa are considered. The predicted structures of Fe–P binary compounds were used to evaluate the formation enthalpy (ΔH) relative to the elemental solids Fe and P according to eqn (1), in order to explore the thermodynamic stabilities of Fe–P compounds.

ΔH(Fe_mP_n) = [H(Fe_mP_n) − mH(Fe) − nH(P)]/(m + n), (m = 1–4 and n = 1, or m = 1 and n = 2) (1)

where H = U + PV is the enthalpy of each composition and ΔH is the enthalpy of formation per atom. Herein, U, P, and V are the internal energy, pressure, and volume, respectively. The relative stabilities of the considered compositions at the selected pressures of 0, 50, 100, 200, 300, and 400 GPa, with ΔH evaluated per atom, are shown in Fig. 1a. The stable phase lies on the convex hulls (the global stability lines). As can be seen, all the considered compositions are stable at 0 GPa, which is well in agreement with the recent theoretical study.²¹ It should be noted that the Fe₄P compound is not included in the study by Jing Wu et al.²¹ P2₁3-structured Fe₄P has been found from melliniite and is confirmed to be stable at ambient pressure.¹⁰ The known Fe₄P, Fe₃P, Fe₂P, FeP, and FeP₂ structures^{10,17,19,55,56} at ambient pressure were well reproduced in our calculations, which validates our structure searching method applied to the Fe–P system. In addition, our calculated lattice parameters for Fe₃P (space group I4̄, 8 formula units per cell) are a = b = 9.13 Å and c = 4.40 Å, which are in excellent agreement with the experimental values at a = b = 9.10 Å and c = 4.46 Å.¹² These lattice parameter calculations support the validity of the pseudo potentials adopted in this study.

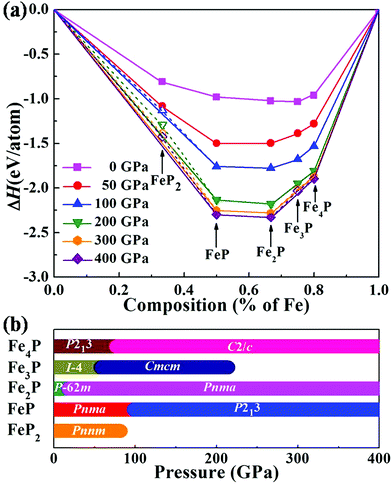Fig. 1 Relative thermodynamic stabilities of Fe–P compounds. (a) Convex hulls of the calculated formation enthalpy per atom of the Fe–P system relative to the elemental solids Fe and P are shown as solid lines. Compounds corresponding to data points located on the convex hulls are thermodynamically stable. The bcc structure,⁵⁷ and hcp structure⁵⁸ of solid Fe, and the phases I (Cmca), II (Pm3̄m), III (P6/mmm), IV (Im3̄m), and V (I4̄3d) of solid P^59,60 are used to calculate the enthalpy of formation. Detailed information about the element solids can be found in Fig. S1.† (b) Pressure–composition phase diagram of the Fe–P system.

Under high pressure, the relative stabilities of our considered compositions are significantly different from that at ambient pressure. Specifically, the FeP₂ compound becomes unstable above 82 GPa, whereas the iron-rich compounds are relatively stable under high pressure. These phases of Fe₄P, Fe₂P and FeP are stable in the entire considered pressure range (0–400 GPa). Notably, the Fe₃P phase is unstable compared above 214 GPa (Fig. S2†) and decomposes into Fe₂P plus Fe₄P. The pressure–composition phase diagram of the Fe–P system is shown in Fig. 1b. For all the predicted structures, the calculated phonon dispersion curves confirm their dynamical stability with no imaginary frequencies observed in the entire Brillouin zone (Fig. S4†).

3.2. Geometry structure of the stable phases

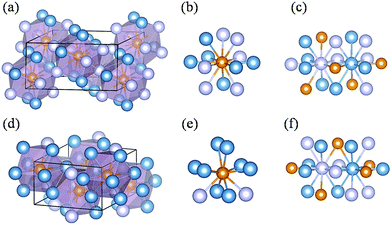
Two new phases (i.e. C2/c-structured Fe₄P and Cmcm-structured Fe₃P) were discovered by comparing previous structures and our predicted structures, and their structural characters are shown in Fig. 2. The predicted C2/c-structured Fe₄P (4 formula units) is more stable than the phase with P2₁3 symmetry above 37 GPa (Fig. S3a†). Its lattice parameters are a = 7.342 Å, b = 3.772 Å and c = 5.627 Å at 200 GPa. The structure contains two inequivalent Fe atoms occupying 8f (0.297, 0.337, 0.850) and 8f (0.900, 0.671, 0.551) sites and one equivalent P atom sitting at the 4e (0.000, 0.170, 0.750) position (Fig. 2a). To distinguish the two Fe atoms at different sites, we labelled the inequivalent Fe atoms with two different colors (Fig. 2c). In this structure, each P atom is in 12-fold coordination with the Fe atoms (Fig. 2b), forming a tetrakaidecahedron. The adjacent polyhedrons are interconnected through common edges or co-vertices. The distance of the two nearest Fe–Fe is 2.11 Å, which is smaller than the Fe–Fe distance of 2.48 Å in bulk Fe with Im3̄m symmetry under ambient conditions⁵⁷ and 2.44 Å in Fe₂SH₃ at 100 GPa.⁴³ However, this structure is nonmagnetic, as will be discussed later. To determine the interatomic interaction in the C2/c-structure Fe₄P, the integrated crystal orbital Hamilton populations (ICOHPs) for the Fe–P and Fe–Fe.

Fig. 2 Crystal structures of the Fe₄P and Fe₃P compounds at 200 GPa. (a) Fe₄P in the C2/c structure. (b) Coordination environment of the P atom in Fe₄P. (c) Coordination environment of the Fe atoms in Fe₄P. (d) Fe₃P in the Cmcm structure. (e) Coordination environment of the P atom in Fe₃P. (f) Coordination environment of the Fe atom in Fe₃P. Here, the large shallow blue or dark blue and small orange spheres represent Fe and P atoms, respectively.

Pairs at 200 GPa were calculated and are shown in Table S1.† The values of ICOHP between the Fe–P and Fe–Fe pairs are −1.80 and −4.97 eV, respectively. The ICOHP value of the Fe–Fe pair is very close to −4.90 eV in Fe₂SH₃.⁴³ Apparently, the Fe–Fe interaction plays an important role in determining the structural stability of the compound. Further analysis indicates that the major contribution of the Fe–Fe interaction originates from 4s–3d, which corresponds to the decomposed ICOHP of −1.908 eV per pair.

The Fe₃P compound with the I4̄ structure symmetry is stable at ambient conditions, and the first phase transition is observed at 64 GPa.¹³ This phase is assigned as the P4/mnc or Pnma structure. Notably, we discovered an orthorhombic structure of Fe₃P (space group Cmcm, 4 formula units per cell) above 58 GPa. This structure is much more stable than the P4/mnc or Pnma structure in the pressure range of 0–400 GPa (Fig. S3b†). The lattice parameters of the Cmcm-structure Fe₃P are a = 5.446 Å, b = 6.569 Å and c = 3.255 Å. This structure contains two inequivalent Fe atoms occupying the 4c (0.500, 0.900, 0.750), and 8g (0.784, 0.117, 0.750) positions, and one equivalent P occupying the 4c (0.000, 0.170, 0.250) site. For each P atom, there are 10 nearest neighbours of Fe atoms, forming a P–Fe hendecahedron (Fig. 2e). The adjacent polyhedrons have common edges. The two inequivalent Fe atoms are labelled with two different colors (Fig. 2f). The nearest Fe–Fe distance in the Cmcm phase is 2.10 Å, which is comparable to 2.14 Å in Fe₄P. Unlike Fe₄P with C2/c symmetry, the Cmcm-structured Fe₃P structure is magnetic. An experimental study investigated the phase transitions of Fe₃P, in which the P4/mnc or Pnma structure is stable above 64 GPa.¹³ However, our predicted Cmcm phase is more stable than the P4/mnc or Pnma phase at 64 GPa. The specific ΔH values of the three Fe₃P phases can be found in Table S2.† To confirm the existence of the Cmcm phase, the simulated XRD pattern of the Cmcm phase is shown in Fig. 3 along with the experimental patterns. Several possible structures of Fe₃P are also included in Fig. 3. Clearly, the main peak of Cmcm-structured Fe₃P is close to the experimental peaks or that of the other phases. Thus, Cmcm-structured Fe₃P might disappear under these experimental conditions.

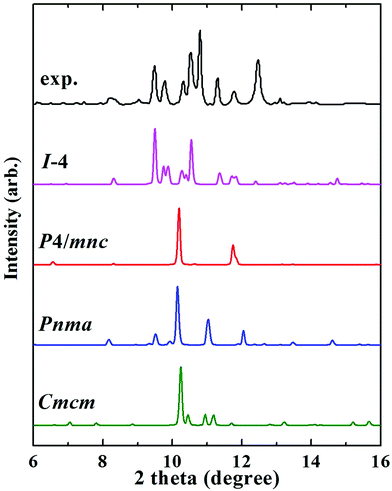Fig. 3 XRD patterns of Fe₃P selected in synchrotron X-radiation with a fixed wavelength of 0.3344 Å at 64 GPa. The XRD pattern of Fe₃P is described by a black line, which was collected in an experimental work.¹³ The XRD patterns of I4̄, P4/mnc, Pnma, and Cmcm structures are labelled by pink, red, blue, and green lines, respectively.

3.3. Electronic properties of stable phases

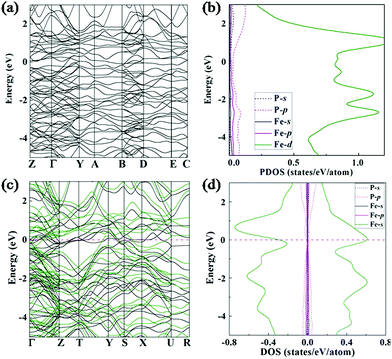
The electronic band structures and projected density of states (PDOS) of the Fe₄P and Fe₃P compounds are shown in Fig. 4. Similar to the electronic properties of the other Fe–P species,¹⁸ there are several bands crossing the Fermi level, which indicate that they are metallic. As can be seen in Fig. 4, there is a common character of a pronounced Fe 3d component near the Fermi level. Interestingly, the Cmcm-structured Fe₃P is a ferromagnetic phase with the magnetic moment of 3.31μ_B per cell at 200 GPa by our calculations. Its electronic band structures and spin-polarized DOS based on spin up and spin down can be found in Fig. 4c and d. The calculated DOS per Fe atom at the Fermi level is about 1.0 eV⁻¹ (Fig. 4d), which satisfies the Stoner criterion.⁶¹

Fig. 4 Electronic band structures and projected density of states (PDOS) of the C2/c-structured Fe₄P (a and b), and the Cmcm-structured Fe₃P (c and d). The electronic band structures of spin up and spin down are described by the black and green lines, respectively.

4. Conclusion

To find the stable phases of Fe–P binary compounds, we explored the crystal structures and stabilities of the Fe–P system with Fe_xP_y (x = 1–4 and y = 1, or x = 1 and y = 2) compositions under high pressure using first principles calculations combined with swarm structural searches. It is found that the FeP, Fe₂P and Fe₄P compounds are stable in the whole pressure range of 0–400 GPa, and Fe₃P becomes unstable above 214 GPa. Several phases of iron-rich compounds can be synthesized at elevated conditions, which may be the possible phases in the Earth's cores. The Fe₄P and Fe₃P compounds are metallic, with a pronounced Fe 3d component across the Fermi level. Our study provides the theoretical basis for the further investigation of Fe–P binary compounds. It is also important to explore the constituents of the Earth's core.

Acknowledgements

This study is supported by the Natural Science Foundation of China under No. 21573037; The Natural Science Foundation of Jilin Province (No. 20150101042JC); The Postdoctoral Science Foundation of China (under Grant No. 2013M541283). Parts of the calculations were performed in the High Performance Computing Centre of Jilin University.

Notes and references

1. J.-P. Poirier, Phys. Earth Planet. Inter., 1994, 85, 319–337.
2. A. S. Côté, L. Vačadlo and J. P. Brodholt, Geophys. Res. Lett., 2008, 35, L05306.
3. H. S. Washington, Am. J. Sci., 1925, 53, 352–378.
4. S. Ono, A. R. Oganov, J. P. Brodholt, L. Vočadlo, I. G. Wood, A. Lyakhov, C. W. Glass, A. S. Côté and G. D. Price, Earth Planet. Sci. Lett., 2008, 272, 481–487.
5. D. Errandonea, D. Santamaría-Perez, A. Vegas, J. Nuss, M. Jansen, P. Rodríguez-Hernandez and A. Muñoz, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 94113.
6. N. Sata, K. Hirose, G. Shen, Y. Nakajima, Y. Ohishi and N. Hirao, J. Geophys. Res.: Solid Earth, 2010, 115, B09204.
7. D. M. Sherman, Earth Planet. Sci. Lett., 1995, 132, 87–98.
8. W. F. Mcd, Treatise Geochem., 2003, 2, 547–568.
9. A. J. Stewart and M. W. Schmidt, Geophys. Res. Lett., 2007, 34, L13201.
10. G. Pratesi, L. Bindi and V. Moggi-Cecchi, Am. Mineral., 2006, 91, 451–454.
11. X. Wu, M. Mookherjee, T. Gu and S. Qin, Geophys. Res. Lett., 2011, 38, L20301.
12. H. P. Scott, S. Huggins, M. R. Frank, S. J. Maglio, C. D. Martin, Y. Meng, J. Santillán and Q. Williams, Geophys. Res. Lett., 2007, 34, L06302.
13. T. Gu, Y. Fei, X. Wu and S. Qin, Earth Planet. Sci. Lett., 2014, 390, 296–303.
14. P. Dera, B. Lavina, L. A. Borkowski, V. B. Prakapenka, S. R. Sutton, M. L. Rivers, R. T. Downs, N. Z. Boctor and C. T. Prewitt, Geophys. Res. Lett., 2008, 35, L10301.
15. T. Gu, X. Wu, S. Qin, C. McCammon and L. Dubroksky, Eur. Phys. J. B, 2013, 83, 311.
16. X. Wu and S. Qin, J. Phys.: Conf. Ser., 2010, 215, 12110.
17. T. Gu, X. Wu, S. Qin and L. Dubrovinsky, Phys. Earth Planet. Inter., 2011, 184, 154–159.
18. H. Yan, Comput. Mater. Sci., 2015, 107, 204–209.
19. E. Dahl, Acta Chem. Scand., 1969, 23, 2677–2684.
20. T.-T. Gu, X. Wu, S. Qin, J. Liu, Y.-C. Li and Y.-F. Zhang, Chin. Phys. Lett., 2012, 29, 26102.
21. J. Wu, X. Chong, R. Zhou, Y. Jiang and J. Feng, RSC Adv., 2015, 5, 81943–81956.
22. P. F. McMillan, Chem. Soc. Rev., 2006, 35, 855–857.
23. Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 94116.
24. Y. Wang, J. Lv, L. Zhu, S. Lu, K. Yin, Q. Li, H. Wang, L. Zhang and Y. Ma, J. Phys.: Condens. Matter, 2015, 27, 203203.
25. A. P. Drozdov, M. I. Eremets, I. A. Troyan, V. Ksenofontov and S. I. Shylin, Nature, 2015, 525, 73–76.
26. D. Duan, Y. Liu, F. Tian, D. Li, X. Huang, Z. Zhao, H. Yu, B. Liu, W. Tian and T. Cui, Sci. Rep., 2014, 4, 6968.
27. Y. Li, J. Hao, H. Liu, Y. Li and Y. Ma, J. Chem. Phys., 2014, 140, 174712.
28. Y. Li, J. Hao, H. Liu, S. Lu and J. S. Tse, Phys. Rev. Lett., 2015, 115, 105502.
29. L. Zhu, H. Liu, C. J. Pickard, G. Zou and Y. Ma, Nat. Chem., 2014, 6, 644–648.
30. W. Zhang, A. R. Oganov, A. F. Goncharov, Q. Zhu, S. E. Boulfelfel, A. O. Lyakhov, E. Stavrou, M. Somayazulu, V. B. Prakapenka and Z. Konopkova, Science, 2013, 342, 1502–1505.
31. M. S. Miao, X. L. Wang, J. Brgoch, F. Spera, M. G. Jackson, G. Kresse and H. Q. Lin, J. Am. Chem. Soc., 2015, 137, 14122–14128.
32. D. Pinkowicz, M. Rams, M. Misek, K. V. Kamenev, H. Tomkowiak, A. Katrusiak and B. Sieklucka, J. Am. Chem. Soc., 2015, 137, 8795–8802.
33. F. Peng, M. Miao, H. Wang, Q. Li and Y. Ma, J. Am. Chem. Soc., 2012, 134, 18599–18605.
34. H. Wang, J. S. Tse, K. Tanaka, T. Iitaka and Y. Ma, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 6463–6466.
35. J. Botana, X. Wang, C. Hou, D. Yan, H. Lin, Y. Ma and M. S. Miao, Angew. Chem., Int. Ed., 2015, 127, 9412–9415.
36. L. Zhu, H. Liu, C. J. Pickard, G. Zou and Y. Ma, Nat. Chem., 2014, 6, 644–648.
37. X. Zhong, H. Wang, J. Zhang, H. Liu, S. Zhang, H. F. Song, G. Yang, L. Zhang and Y. Ma, Phys. Rev. Lett., 2016, 116, 57002.
38. Y. Wang and Y. Ma, J. Chem. Phys., 2014, 140, 40901.
39. Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070.
40. J. Lv, Y. Wang, L. Zhu and Y. Ma, Phys. Rev. Lett., 2011, 106, 15503.
41. L. Zhu, H. Wang, Y. Wang, J. Lv, Y. Ma, Q. Cui, Y. Ma and G. Zou, Phys. Rev. Lett., 2011, 106, 145501.
42. M. Zhang, H. Liu, Q. Li, B. Gao, Y. Wang, H. Li, C. Chen and Y. Ma, Phys. Rev. Lett., 2015, 114, 15502.
43. S. Zhang, L. Zhu, H. Liu and G. Yang, Inorg. Chem., 2016, 55, 11434–11439.
44. G. Yang, Y. Wang, F. Peng, A. Bergara and Y. Ma, J. Am. Chem. Soc., 2016, 138, 4046–4052.
45. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
46. G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169–11186.
47. P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953–17979.
48. A. Jain, G. Hautier, C. J. Moore, S. Ping Ong, C. C. Fischer, T. Mueller, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2011, 50, 2295–2310.
49. C. Rdl, F. Fuchs, J. Furthmller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 235114.
50. A. Koumina, M. Bacmann, D. Fruchart, S. Niziol, P. Wolfers, M. Mesnaoui, J. Tobola, S. Kaprzyk, R. Zach and N. Techniques, Ann. Chimie Sci. Materiaux, 1998, 23, 177–180.
51. M. Cococcioni and S. de Gironcoli, Phys. Rev. B, 2005, 71, 35105.
52. J. D. Pack and H. J. Monkhorst, Phys. Rev. B, 1977, 16, 1748–1749.
53. A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106.
54. R. Dronskowski and P. E. Blöchl, J. Phys. Chem., 1993, 97, 8617–8624.
55. R. Skála and M. Drábek, Mineral. Mag., 2003, 67, 783–792.
56. S. Rundqvist and F. Jellinek, Acta Chem. Scand., 1959, 13, 425–432.
57. N. Kohlhaas, R. Dunner and P. Schmitz-Pranghe, Z. Angew. Phys., 1967, 23, 245.
58. T. Takahashi, W. a. Basett and H.-K. Mao, J. Geophys. Res., 1968, 73, 4717–4725.
59. T. Sugimoto, Y. Akahama, H. Fujihisa, Y. Ozawa, H. Fukui, N. Hirao and Y. Ohishi, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 24109.
60. H. Katzke and P. Tolédano, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 24109.
61. J. F. Janak, Phys. Rev. B, 1977, 16, 255–262.

---

Footnote

† Electronic supplementary information (ESI) available: Pressure phase diagram of the elementary substances of Fe and P; the calculated enthalpy difference as a function of pressure, for the reaction equation: 2Fe₃P ↔ Fe₂P + Fe₄P; enthalpy differences of the Fe₃P and Fe₄P compounds as a function of pressure; calculated phonon spectra for the Fe₃P and Fe₄P compounds; calculated ICOHPs of Fe–Fe, and Fe–P pairs in Fe₄P. See DOI: 10.1039/c7ra01567d

---