Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dynamic contact angle on a reconstructive polymer surface by segregation
Manabu Inutsuka a,
Hirokazu Tanouea,
Norifumi L. Yamadab,
Kohzo Itoa and
Hideaki Yokoyama*a
a,
Hirokazu Tanouea,
Norifumi L. Yamadab,
Kohzo Itoa and
Hideaki Yokoyama*a
aGraduate School of Frontier Sciences, The University of Tokyo, 5-1-5 Kashiwanoha, Kashiwa-shi, Chiba 277-8561, Japan. E-mail: yokoyama@molle.k.u-tokyo.ac.jp
bNeutron Science Laboratory, High Energy Accelerator Research Organization, Ibaraki 319-1108, Japan
First published on 20th March 2017
Abstract
We report the peculiar time evolution of the contact angle of water on reconstructive polymer surface. Surface reconstruction is driven by segregation of amphiphilic diblock copolymer to the water interface of the elastomer, in which amphiphilic diblock copolymer is mixed. In other words, the brush of hydrophilic block is spontaneously formed at the elastomer/water interface and can be called dynamic polymer brush. The contact angle measurement of water droplet was carried out as a function of time after a droplet was placed on the surface. The contact angles stay the same value for certain induction period before decrease monotonically with time. We also proposed a simple model to explain the experimental results quantitatively. The model is based on two hypotheses: water droplet starts to spread only after a depletion layer of the hydrophilic block at the air interface is dissolved, and segregated block copolymer brush begins to repel one another.
1. Introduction
A number of research groups are trying to find the best way to prevent biofouling such as protein and cell adsorption onto material surfaces.1–4 The modification by tethered water-soluble polymer chains, which is often called “polymer brush”, is one of the simplest and most effective methods.5,6 These polymer brushes are usually fabricated by following two methods: attaching a functional end of polymer chain to the surface chemically or physically (graft-to method),7 or polymerizing the polymer chains from the initiator on the surface (graft-from method).8,9 There are also several reports in which the amphiphilic diblock copolymers are used to realize to the antifouling properties and affinity to aqueous environment.10–14Recently we proposed the polymer brush by “inverted graft-to” method,15,16 which is spontaneously formed at the elastomer/water interface utilizing the surface segregation of diblock copolymer.17–20 Since the brush formation is driven by spontaneous process toward thermodynamic equilibrium state in rubbery matrix at room temperature, we can call the brush as “dynamic polymer brush”.
We added a small amount of diblock copolymer consisting of hydrophilic poly(ethylene glycol) (PEG) block and hydrophobic poly(dimethyl siloxane) (PDMS) block into a matrix of cross-linked PDMS elastomer. In this system, the glass transition temperature (Tg) of PDMS matrix is much lower than room temperature, and the copolymer can diffuse in the flexible PDMS matrix even at room temperature. The PEG block with high surface energy avoids the air surface, but segregates to the water interface to form a brush layer with PDMS anchor block. Fabricating such a grafted PEG chain on PDMS surface, which is widely used for biomedical devices, is advantageous for biomedical applications.21–23 We confirmed that a dense and extremely stretched polymer brush can be formed spontaneously by this segregation method. Moreover, our brush by segregation is expected to be applied to anti-fouling and anti-thrombotic surfaces of medical devices with self-healing capability: when the brush is lost by some physical damage, the copolymer remaining in the bulk immediately segregates to reconstruct the brush layer. These advantages have never been available with the previous system based on covalent immobilization of the polymer chain.24 It is, therefore, extremely important to know the time scale of the reconstruction. The reconstruction time scale is tough to be revealed experimentally; however, the construction time scale after the surface fist meets water should be the same and can be traceable.
In this paper, we report the unique time evolution of contact angle of water on dynamic polymer brush driven by the segregation of amphiphilic diblock copolymer. We placed a water droplet on the sample film, and observed its contact angle decreasing due to the surface reconstruction. We found that the surface was turned from hydrophobic to hydrophilic, after a characteristic delay time for several to several tens of seconds. In order to explain this peculiar behaviour, we propose a simple model considering “pinning effect” and “depletion layer”, which are unique in our surface-reconstructive system with dynamic polymer brush.
2. Experiments and materials
Film preparation
PEG-PDMS with Mn of 1000 for PEG block and 600 for PDMS block (Polymersoruce, Inc. Based on the information by supplier, polydisperse indexes of each block are 1.02 for PEG and 1.2 for PDMS.), hydride-terminated PDMS with molecular weight of ∼63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 (PDMS-H, Gelest, Inc.) and poly(methylvinylsiloxane-co-dimethylsiloxane) with molecular weight of ∼27
600 (PDMS-H, Gelest, Inc.) and poly(methylvinylsiloxane-co-dimethylsiloxane) with molecular weight of ∼27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (4–5% of methylvinylsiloxane, PMVS, Gelest, Inc.) were dissolved in dehydrated tetrahydrofuran (THF, Wako Pure Chemical Industries, Ltd). The ratios of PDMS-H to PMVS and PEG-PDMS to (PDMS-H + PMVS) were 9 to 1 and 2 to 8, respectively. The resulting block copolymer fraction was 20 wt% and the total polymer concentration in THF was 2.5 wt%. Platinum-1,3-divinyl-1,1,3,3-tetramethyldisiloxane complex in xylene (Aldrich, Inc., ∼2% platinum) was added to the polymer solution as catalyst for cross-linking and then immediately the solution was spin-coated at 2000 rpm onto silicon or thick quartz wafers. The cross-linking reaction of homo-PDMS undergoes in part during evaporation of solvent. These films were further annealed at 70 °C for 6 hours in vacuo for the remaining functional groups of PDMS to be fully cross-linked. The thicknesses of the PDMS films on silicon substrates were estimated by ellipsometry (JASCO, M-150).
000 (4–5% of methylvinylsiloxane, PMVS, Gelest, Inc.) were dissolved in dehydrated tetrahydrofuran (THF, Wako Pure Chemical Industries, Ltd). The ratios of PDMS-H to PMVS and PEG-PDMS to (PDMS-H + PMVS) were 9 to 1 and 2 to 8, respectively. The resulting block copolymer fraction was 20 wt% and the total polymer concentration in THF was 2.5 wt%. Platinum-1,3-divinyl-1,1,3,3-tetramethyldisiloxane complex in xylene (Aldrich, Inc., ∼2% platinum) was added to the polymer solution as catalyst for cross-linking and then immediately the solution was spin-coated at 2000 rpm onto silicon or thick quartz wafers. The cross-linking reaction of homo-PDMS undergoes in part during evaporation of solvent. These films were further annealed at 70 °C for 6 hours in vacuo for the remaining functional groups of PDMS to be fully cross-linked. The thicknesses of the PDMS films on silicon substrates were estimated by ellipsometry (JASCO, M-150).
X-ray photoelectron spectroscopy (XPS) measurement
The surface analysis of the sample films in vacuum was conducted by XPS (JEOL, Ltd., JPS-90SX). X-ray source was Al Kα operated at 8 kV and 10 mA.Contact angle measurement
Surface reconstruction by the segregation of PED-PDMS was observed by contact angle measurement (Kyowa Interface Science Co., LTD., CA-V) of water droplet on the sample films. A droplet of distilled water (5 μl) was placed onto the sample film via a needle from a syringe. Images of the droplets were captured by a camera every 1 second just after the contact, and analyzed to obtain the contact angles by fitting the contour of the water droplet.Neutron reflectivity measurement
Neutron reflectometry experiments were conducted with Soft Interface Analyzer (SOFIA)25,26 at J-PARC. Specular neutron reflectivity of the interface between the polymer and D2O was measured more than 1 hour after the contact with water. The depth profiles of SLD were computed by fitting the reflectivity curves using Parratt32 (version 1.6, developed by C. Braun at the Hahn–Meitner-institut Berlin). We fitted the reflectivity curves with a multi-layer model consisted of quartz substrate, PDMS matrix film, D2O-swollen brush layer and D2O ambient. The SLDs of quartz, PDMS matrix, PEG and D2O were assumed to be 4.2, 0.06, 0.56 and 6.36 × 10−4 nm−2, respectively. The brush layer was divided into 63 sub-layers whose SLD were fixed at 0.1, 0.2,…, 6.3 × 10−4 nm−2 with 0.1 increment and the thickness of each layer was used as fitting variables. Employing this fitting method automatically assumes monotonic decrease of volume fraction of PEG ϕPEG along the distance from matrix surface z. The thicknesses of 63 sub-layers as fitting parameters were optimized to obtain the SLD profiles around the sample film/D2O interfaces.3. Results and discussion
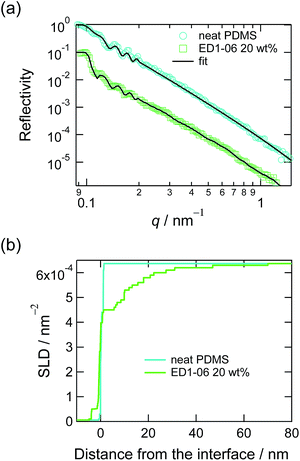
Panel (a) in Fig. 1 shows the neutron reflectivity curves of the neat PDMS film and the PDMS film with 20 wt% of EGD1-06. By fitting these reflectivities with multi-layer models mentioned in Experimental section, we obtained the SLD depth profiles as shown in panel (b) in Fig. 1. Whereas the SLD profile for the neat PDMS exhibited only a sharp interface with roughness less than 1 nm, that for the PDMS with EGD1-06 exhibited an intermediate layer at the interface between PDMS and D2O. The intermediate layer of ED1-06 amphiphilic block copolymer remains at the interface at least for several hours, from the contact with water to the measurement of neutron reflectivity. The PEG brush layer at the interface between PDMS and water appeared and hence reduces the interfacial tension between PDMS and water.This interfacial layer is not a mere brush layer reported in previous study because it is thicker than the contour length of the PEG block with the Mn of 1000. Compared to PEG-b-PDMS with Mn of 2100-b-1000, which forms a clear brush layer as reported in the previous study,16 ED1-06 is consisting with similar symmetrical block ratio, but its Mn is about a half. Therefore, ED1-06 may be forming multiple layers to expose more PEG block to water. It should be noted, however, that the multilayer formation of ED1-06 occurred the later stage of segregation but the dynamic contact angle measurement was carried out in relatively short time scale, i.e. less than 200 s, where the PDMS/water interface has not been fully covered by amphiphilic block copolymer. Therefore, the contact angle measurement probes the change from the interface with no brush to that with a single layer of PEG brush.
The formation of dynamic PEG brush alters the surface property of the PDMS film from hydrophobic to hydrophilic. Fig. 2 shows the typical images of water droplets on the PDMS film with 20 wt% of EGD1-06. At the moment of contact, the PEG brush has not formed yet, and thus the surface of the film is still pure PDMS and hydrophobic as indicated by the large contact angle of water droplet at t = 1 s in Fig. 2. After the contact with water, however, the surface is reconstructed from hydrophobic to hydrophilic as indicated by increasing the contact area and decreasing the contact angle by the dynamic PEG brush formation. After a sufficient time for the segregation and surface reconstruction, the contact angle of water droplet reaches equilibrium values.
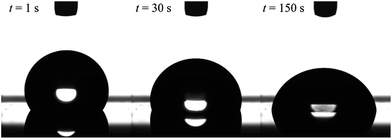 | ||
| Fig. 2 Images of a water droplet on cross-linked PDMS film with 20 wt% of ED1-06. Volume of the droplet is 5 μl. | ||
The decreasing water contact angles indicate the time-scale of the segregation and the formation process of the dynamic PEG brush formation. In order to analyze this behaviour in detail, we plotted the contact angles of water droplets on the PDMS films with various concentrations of ED1-06 against time as shown in Fig. 3. We found a characteristic induction period before the contact angle starts to decrease. The PDMS with lower copolymer concentration exhibited the longer induction period. To the best of our knowledge, such induction periods of the contact angles on reconstructive surfaces have not been reported.27–29 A typical example is the dynamic contact angle behaviour of water droplet on poly(methyl methacrylate) (PMMA), due to the reconstruction of the chain conformation at the surface.30 In this system, the PMMA surface exhibits an exponential decay without delay time. The segregation dynamics of a copolymer with low surface energy fluorine block to air interface was reported by Kramer et al.31 Their experimental results do not suggests such delay time in the segregation behaviour of the block copolymer in polymeric matrix. Therefore, the induction period of the water contact angle should be reflecting the characteristic feature of dynamic polymer brush system.
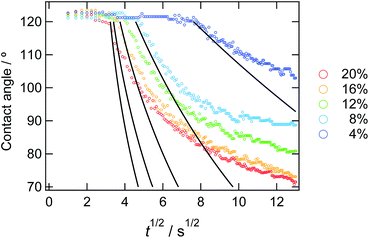 | ||
| Fig. 3 Time dependence of static contact angle of water droplets on the sample films with various copolymer concentrations. The solid lines represent the result from the eqn (10) from the calculation. | ||
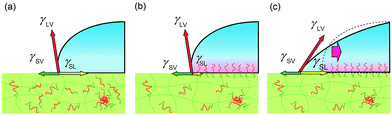
To explain the behaviours, we propose a model considering pinning effect and a depletion layer of the hydrophobic block at the air interface. In this model, contact area (line) is pinned and does not move until the certain criteria are satisfied as described later. A schematic illustration of pinning effect is shown in Fig. 4. When a water droplet is placed on the ED1-06/PDMS blend film, ED1-06 start to segregate to cover the interface. Notice that segregation occurs only underneath the water droplet and the air interface remains hydrophobic. Therefore, the force balance can be described as in Fig. 4. With the reduction of the interfacial energy by dynamic polymer brush formation of PDMS/water (γSL) as indicated from panel (a) to panel (b), the contact line is supposed to move outwards to decrease the contact angle, however, such a move exposes neat PDMS surface to water and increases γSL, which pushes the contact line backwards. Consequently, the contact line of the water droplet would be “pinned” and thus the contact angle does not reflect the change of interfacial tension γSL between water and elastomer. Similar pinning effect has been already reported for reconstructive surface of block copolymers consisting of both hydrophobic perfluoroalkyl group and hydrophilic PEO chain.32 We believe this should be a reason for the observed induction period.
When would the pinned contact line start to move and water droplet expand? We propose that the water droplet starts expanding when the contact area is fully occupied by mushrooms of segregated PEG block and start to repel each other. In order to segregate more ED1-06 than this state to earn more hydration energy gain between PEG and water, there are two possible ways: one is stretching the PEG block in the perpendicular direction and increasing the brush density without changing the contact line of water droplet. The other is expanding the contact area and increasing the number of PEG chains without paying the stretching energy. Therefore the repulsive energy between PEG chains eventually overcomes the pinning effect and push the contact line outwards.
Based on this idea, we predicted the dynamic behaviour of the contact angle quantitatively. We assume that the segregation of ED1-06 is based on the diffusion with diffusion constant D. The amount of the segregated ED1-06 per unit area t s after the contact with water, σ(t), would be equal to the product of diffusion length D1/2t1/2 and ED1-06 concentration in the PDMS matrix C0:
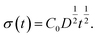 | (1) |
The contact area A is occupied by the segregated mushrooms after the delay time by the pinning effect t0,p, then
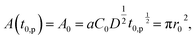 | (2) |
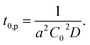 | (3) |
In Fig. 5, observed delay time t0 is plotted against C0−2. The data points can be fitted with a line and thus eqn (3) describes the behaviour quite well. However, the intercept is not 0, but 10 second.
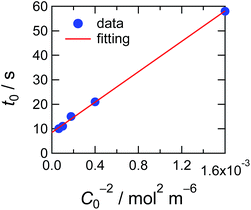 | ||
| Fig. 5 Delay time plotted against the concentration of the ED1-06. Red line indicates the simulation result considering the pinning effect and depletion layer shown in eqn (4). | ||
Here, we introduce another factor in our model to explain the delay time of 10 second: the presence of a depletion layer. As mentioned above, it is most likely that PEG block of ED1-06 with high surface energy should avoid air interface and burry themselves into the bulk. As the results, a surface depletion layer with lower ED1-06 concentration would be generated near the surface. When the surface is placed in water, the depletion layer would be resolved by diffusion and then the surface is covered by segregated brush layer. Experimental results of angle-resolved XPS support this picture, as shown in Fig. 6. Almost no signal corresponding to C 1s of PEG was detected, and all spectra with analysis angle of 90, 60 and 30° exhibited only a peak originating from PDMS, respectively. This means that PEG block of ED1-06 do not exist at the air interface with the analytical depth of about 10 nm.
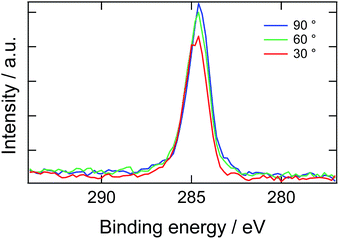 | ||
| Fig. 6 X-ray photoelectron spectroscopic C 1s narrow scan of the PDMS film containing 20 wt% of ED1-06. | ||
Considering this effect, we add another term, t0,d, corresponding to the delay time to resolve the depletion layer to the eqn (3):
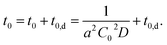 | (4) |
With eqn (4), we can fit the data shown in Fig. 5 and obtained various parameters: from the slope of the eqn (4), we can estimate the D to be about 10−18 m2 s−1, and the thickness of the assumed depletion layer to be about 3 nm by considering diffusion distance ld ∼ D1/2t0,d1/2. Compared to the analytical depth of XPS measurement, the value of ld might be underestimated. This should be because it is beyond the tether of our simple model or the sensitivity of XPS measurement. Therefore, we conclude that the values are reasonable for ED1-06.
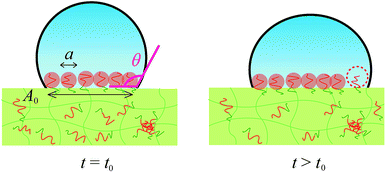
By using these estimated values, next we describe the initial contact angle decreasing behaviour with assuming a simple model. At t > t0, A should be determined by the contact area which should be corresponding to the total area of the mushrooms of segregated block copolymer, as shown in Fig. 7
| A(t) = aA0C0D1/2(t − t0,d)1/2 = πr2. | (5) |
Then, we obtain r as a function of t.
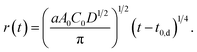 | (6) |
In order to obtain the θ from the r, we assume that the shape of the water droplet on the sample is expressed as a part of the sphere with ignoring the deformation by the gravity, as shown in Fig. 8, and the volume V of the water droplet (=5 μl) does not change through the experiment.
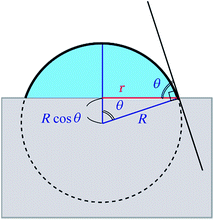 | ||
| Fig. 8 An illustration of the model for the water droplet with contact radius r and contact angle θ. | ||
Considering the geometry of the water droplet shown in Fig. 8, time dependence of V, r, R and θ are described by below 2 equations.
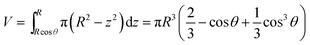 | (7) |
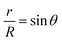 | (8) |
From eqn (7) and (8), we can express the relationship between r and θ as below:
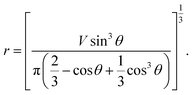 | (9) |
From eqn (6) and (9), t dependence of θ is described below.
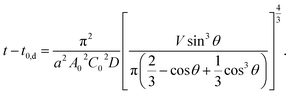 | (10) |
In Fig. 3, we overlay the lines by eqn (10). Here, we have succeeded in explaining both the depletion time and the initial contact angle decreasing with time, and their concentration dependence with only 2 fitting parameters: diffusion constant of block copolymer D and the thickness of the depletion layer ld.
Our model is too simplified to describe the behaviour for longer time scale and the lines deviate from the experimental values. In our model, the water droplet on the film would keep expanding and the contact angle would reach zero if the block copolymer were supplied infinitely. Of course, this would never be realized, and the contact angle would approach the equilibrium value. Therefore our model is only available in the early sate. In order to describe the all time stage, we need some detailed computation simulation. Our model should also be tentative, since it is lack of supporting evidence. Though, it explains the characteristic time-evolution behaviour of the contact angle on the reconstructive polymer surface by segregation of amphiphilic diblock copolymer.
4. Conclusions
In this paper we studied the processes of dynamic polymer brush formation by the segregation of amphiphilic diblock copolymer to elastomer/water interface by using the contact angle measurement. A peculiar induction period was found before the surface turned to be hydrophilic and the contact angle start to decrease due to the formation of dynamic polymer brush. The results were analyzed quantitatively by a model with initial “depletion layer” and “pinning effect” of contact angle, which are unique in our surface-reconstructive system. The advance of contact line occurs only when the interface between the water droplet and elastomer is fully occupied with the mushroom of hydrophilic PEG chains. The experimentally observed time evolution of contact angles were well described by the simple model with reasonable values of diffusion constant and molecular size of the block copolymer.Conflict of interest
The authors declare no competing financial interest.Acknowledgements
This research was partly supported by Grant-in-Aids for the Scientific Research (B) (no. 15H03862) from the Ministry of Education, Culture, Sports, Science and Technology, Japan. NR measurements were performed on BL-16 at the Materials and Life Science Facility (MLF), J-PARC, Japan, under program no. 2009S08 and no. 2014S08.References
- C. Nojiri, T. Okano, H. A. Jacobs, K. D. Park, S. F. Mohammad, D. B. Olsen and S. W. Kim, J. Biomed. Mater. Res., 1990, 24, 1151–1171 CrossRef CAS PubMed.
- M. Gosecka and T. Basinska, Polym. Adv. Technol., 2015, 26, 696–706 CrossRef CAS.
- M. Tanaka, T. Hayashi and S. Morita, Polym. J., 2013, 45, 701–710 CrossRef CAS.
- Y. Oda, C. Zhang, D. Kawaguchi, H. Matsuno, S. Kanaoka, S. Aoshima and K. Tanaka, Adv. Mater. Interfaces, 2010, 51, 5283–5293 Search PubMed.
- S. I. Jeon, J. H. Lee, J. D. Andrade and P. G. de Gennes, J. Colloid Interface Sci., 1991, 142, 149–158 CrossRef CAS.
- A. Halperin, Langmuir, 1999, 15, 2525–2533 CrossRef CAS.
- A. Halperin, M. Tirrell and T. P. Lodge, in Macromolecules, Synthesis, Order and Advanced Properties, Springer Berlin Heidelberg, Berlin, Heidelberg, 1992, pp. 31–71 Search PubMed.
- B. Zhao and W. J. Brittain, Prog. Polym. Sci., 2000, 25, 677–710 CrossRef CAS.
- Y. Tsujii, K. Ohno, S. Yamamoto, A. Goto and T. Fukuda, in Surface-Initiated Polymerization I, ed. R. Jordan, Springer Berlin Heidelberg, Berlin, Heidelberg, 2006, pp. 1–45 Search PubMed.
- X. Zhang, G. Lin, S. R. Kumar and J. E. Mark, Polymer, 2009, 50, 5414–5421 CrossRef CAS.
- E. Martinelli, E. Guazzelli, C. Bartoli, M. Gazzarri, F. Chiellini, G. Galli, M. E. Callow, J. A. Callow, J. A. Finlay and S. Hill, J. Polym. Sci., Part A: Polym. Chem., 2015, 53, 1213–1225 CrossRef CAS.
- S. J. Stafslien, D. Christianson, J. Daniels, L. VanderWal, A. Chernykh and B. J. Chisholm, Biofouling, 2015, 31, 135–149 CrossRef CAS PubMed.
- F. Faÿ, M. L. Hawkins, K. Réhel, M. A. Grunlan and I. Linossier, Green Mater., 2016, 4, 53–62 CrossRef.
- E. Martinelli, D. Gunes, B. M. Wenning, C. K. Ober, J. A. Finlay, M. E. Callow, J. A. Callow, A. Di Fino, A. S. Clare and G. Galli, Biofouling, 2016, 32, 81–93 CrossRef PubMed.
- H. Yokoyama, T. Miyamae, S. Han, T. Ishizone, K. Tanaka, A. Takahara and N. Torikai, Macromolecules, 2005, 38, 5180–5189 CrossRef CAS.
- M. Inutsuka, N. L. Yamada, K. Ito and H. Yokoyama, ACS Macro Lett., 2013, 2, 265–268 CrossRef CAS.
- L. Leibler, Makromol. Chem., Macromol. Symp., 1988, 16, 1–17 CrossRef CAS.
- F. S. Bates and G. H. Fredrickson, Annu. Rev. Phys. Chem., 1990, 41, 525–557 CrossRef CAS PubMed.
- P. F. Green and T. P. Russell, Macromolecules, 1991, 24, 2931–2935 CrossRef CAS.
- K. H. Dai, E. J. Kramer and K. R. Shull, Macromolecules, 1992, 25, 220–225 CrossRef CAS.
- G. Sui, J. Wang, C.-C. Lee, W. Lu, S. P. Lee, J. V. Leyton, A. M. Wu and H.-R. Tseng, Anal. Chem., 2006, 78, 5543–5551 CrossRef CAS PubMed.
- J. Zhou, H. Yan, K. Ren, W. Dai and H. Wu, Anal. Chem., 2009, 81, 6627–6632 CrossRef CAS PubMed.
- S. Lee and J. Vörös, Langmuir, 2005, 21, 11957–11962 CrossRef CAS PubMed.
- H. Chen, Z. Zhang, Y. Chen, M. A. Brook and H. Sheardown, Biomaterials, 2005, 26, 2391–2399 CrossRef CAS PubMed.
- K. Mitamura, N. L. Yamada, H. Sagehashi, N. Torikai, H. Arita, M. Terada, M. Kobayashi, S. Sato, H. Seto, S. Goko, M. Furusaka, T. Oda, M. Hino, H. Jinnai and A. Takahara, Polym. J., 2013, 45, 100–108 CrossRef CAS.
- N. L. Yamada, N. Torikai, K. Mitamura, H. Sagehashi, S. Sato, H. Seto, T. Sugita, S. Goko, M. Furusaka, T. Oda, M. Hino, T. Fujiwara, H. Takahashi and A. Takahara, Eur. Phys. J. Plus, 2011, 126, 1–13 Search PubMed.
- J. A. Crowe and J. Genzer, J. Am. Chem. Soc., 2005, 127, 17610–17611 CrossRef CAS PubMed.
- X. Wang, X. Wang and Z. Chen, Polymer, 2007, 48, 522–529 CrossRef CAS.
- B. Zuo, Y. Hu, X. Lu, S. Zhang, H. Fan and X. Wang, J. Phys. Chem. C, 2013, 117, 3396–3406 CAS.
- A. Horinouchi, Y. Fujii, N. L. Yamada and K. Tanaka, Chem. Lett., 2010, 39, 810–811 CrossRef CAS.
- D. R. Iyengar, S. M. Perutz, C.-A. Dai, C. K. Ober and E. J. Kramer, Macromolecules, 1996, 29, 1229–1234 CrossRef CAS.
- K. Tokuda, M. Kawasaki, M. Kotera and T. Nishino, Langmuir, 2015, 31, 209–214 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2017 |