1. Introduction

Boron-10 is one of the stable isotopes of boron with a natural abundance of ∼20%. It is known to exhibit a high propensity to absorb thermal neutrons with a neutron-capture cross-section of 3835 barns (1 barn = 10⁻²⁸ m²), which is about six times greater than that of uranium-235 and three orders of magnitude greater than that of the nuclei of living tissues.¹ On absorption of a slow neutron, a fission reaction occurs with the release of two energetic heavy ions: an α-particle (1.47 MeV) and, in ∼94% of all reactions, a ⁷Li³⁺ nucleus in its first excited state (0.84 MeV) which quickly returns to its ground state (half-life of ∼10⁻¹³ s) by releasing a low-energy γ-ray (478 keV).² These heavy charged particles have path lengths in the range of ∼5–8 μm in water or biological tissues and exhibit high linear energy transfer (LET, or energy loss per unit path length −dE/dx, in units of eV nm⁻¹) characteristics, as shown in Fig. 1.^3,4 Because of this high energy deposition to the surrounding environment and the α and Li recoils' short travel distances, which are typically of the order of a cell diameter, the ¹⁰B(n,α)⁷Li nuclear reaction has been used in clinical studies of biochemically targeted radiotherapies for cancer treatment known as “boron neutron capture therapy” (BNCT).^1,5

BNCT is a potentially ideal radiotherapy modality for glioblastoma, which is a type of brain tumor that is rarely removed surgically. When a cancer cell is allowed to take up preferentially a sufficient concentration of ¹⁰B, it can be selectively irradiated by the very densely ionizing ion recoils from the ¹⁰B(n,α)⁷Li reaction without damaging the surrounding normal tissue. This basic idea was first proposed by Locher in 1936,⁶ shortly after the discovery of the neutron by Chadwick.⁷ Interest in BNCT was spurred by Kruger's study in 1940, who reported a low transplantation efficiency for tumors treated by BNCT in vitro and subsequently implanted in mice.^8,9 Although the full clinical application of BNCT presents several difficulties, including the inadequate selectivity and toxicity of ¹⁰B delivery agents and the poor distribution of neutron flux, clinical trials of BNCT are still under way and new neutron irradiation facilities continue to be developed in Japan, the United States, Finland, and several other countries.^1,5,10–12

Apart from BNCT, the unique properties of boron-10 have also been extensively applied in the field of nuclear industry. For example, boron carbide (B₄C), enriched in ¹⁰B, is used as a control-rod material (neutron absorber) in boiling water reactors (BWRs). In addition, boron as boric acid (H₃BO₃) is generally added as a water-soluble neutron poison in the primary coolant of pressurized water reactors (PWRs) to control the neutron flux and the reactivity in the core.^13–16 However, recoil ions arising from the ¹⁰B(n,α)⁷Li reaction act as sources of high-LET radiation in the primary coolant of PWRs, thereby leading to the formation of oxidizing species, such as hydrogen peroxide and oxygen, due to the radiolysis of water.^17,18

The radiolysis of water is closely linked to the corrosion of structural materials. Water, which is used as the neutron moderator and the reactor coolant, is unavoidably exposed to extreme conditions of high temperature (∼275–325 °C), pressure (∼7–15 MPa), and intense mixed neutron and β–γ radiation fields (which have characteristically different LET values). Under these conditions, the radiolysis of water results in the formation of free radical (e_aq⁻, H˙, ˙OH, and HO₂˙/O₂˙⁻) and molecular (H₂, H₂O₂, and O₂) species which alter the chemical environment of the coolant.^18–20 The presence of the oxidizing species H₂O₂ and O₂ can significantly increase the corrosion potential of coolant water in BWRs.^16,21,22 In PWRs, the presence of boron-10 results in high-LET recoil ions and complicates the radiolytic process. Although ¹⁰B has been widely studied both in nuclear technology and clinical research, little attention has been devoted to ¹⁰B-induced reactions. In particular, data on the formation of primary products and their yields (G-values) for ¹⁰B(n,α)⁷Li recoil irradiation of neutral water are scarce and uncertain.^15,19 In fact, the only reported measurements at room temperature were made in acid (0.4 M H₂SO₄) solution.^23–25 Similarly, the G-values at reactor temperatures are not well known. To the best of our knowledge, there is only one report¹⁹ that estimated a complete set of water decomposition yields induced by the ¹⁰B(n,α)⁷Li reaction at 289 °C.

Understanding the radiation chemistry of the coolant water in reactors is important for maintaining the proper chemical environment that will minimize the degradation of materials. Recently, computer simulations have played a substantial role in evaluating the concentrations of oxidizing species produced from coolant-water radiolysis, which is difficult to observe directly because of the extreme operating conditions involved. In this current work, Monte Carlo track chemistry simulations were undertaken to predict the G-values for the various primary radical and molecular products formed from the radiolysis of pure, neutral water and 0.4 M H₂SO₄ aqueous solutions by the ¹⁰B(n,α)⁷Li reaction as a function of temperature from 25 to 350 °C.

The paper is organized as follows. The main features of our simulation approach are given in the next section. Sections 3 and 4 present, respectively, the results of our simulations of the ¹⁰B(n,α)⁷Li radiolysis of water at neutral pH and of 0.4 M H₂SO₄ aqueous solutions at 25 °C and as a function of temperature up to 350 °C, and their discussion. Conclusions are drawn in the final section.

A brief preliminary report of this work has been presented elsewhere.²⁶

2. Monte Carlo track chemistry simulations

The entire sequence of events generated in the radiolysis of liquid water by ¹⁰B(n,α)⁷Li recoil ions was modeled using our Monte Carlo track chemistry simulation code called IONLYS-IRT. This computer program simulates, in a 3D geometrical environment, the highly nonhomogeneous distribution of reactive species initially produced by the absorption of incident radiation and all of the energetic secondary electrons, as well as the subsequent diffusion and chemical reactions of these species. A detailed description of the current version of the code at both ambient and elevated temperatures and under low- and high-LET irradiation conditions has been reported previously.^27–30 In brief, the IONLYS step-by-step simulation program models all of the events of the early “physical” and “physicochemical” stages³¹ of radiation action up to ∼1 ps in the track development. The complex, highly nonhomogeneous spatial distribution of reactants formed at the end of the physicochemical stage [e_aq⁻, H⁺, OH⁻, H˙, ˙OH, H₂, H₂O₂, HO₂˙/O₂˙⁻, ˙O˙(³P), O(¹D), O₂,…], which is provided as an output of the IONLYS program, is then used directly as the starting point for the subsequent “nonhomogeneous chemical” stage³¹ (typically, from ∼1 ps to the μs time scale at 25 °C). This third stage, during which the different radiolytic species diffuse randomly at rates determined by their diffusion coefficients and react with one another (or with dissolved solutes, if any) until all track processes are complete, is covered by our IRT program. This program employs the “independent reaction times” (IRT) method,^32–34 a computationally efficient stochastic simulation technique that is used to simulate reaction times without having to follow the trajectories of the diffusing species. The IRT method relies on the approximation that the reaction time of each pair of reactants is independent of the presence of other reactants in the system. Its ability to give accurate time-dependent chemical yields under different irradiation conditions has been well validated by comparison with full random flights (or step-by-step) Monte Carlo simulations, which do follow the reactant trajectories in detail.^35,36 This IRT program can also be used to efficiently describe the reactions that occur in the bulk solution during the “homogeneous chemical” stage,³¹i.e., in the time domain beyond a few microseconds. The model assumptions and procedures employed to carry out the Monte Carlo simulations of the radiolysis of aqueous 0.4 M H₂SO₄ solutions (pH ∼ 0.46) with IONLYS-IRT have already been given.^37,38

In the current version of IONLYS-IRT, we used the self-consistent radiolysis database, including rate constants and diffusion coefficients, recently compiled by Elliot and Bartels.²⁰ This new database provides recommendations for the best values to use in high-temperature modeling of water radiolysis over the range of 20–350 °C.

Pre-simulations were performed using the SRIM simulation program³⁹ to calculate 1000 tracks of 1.47 MeV α-particles and 0.84 MeV lithium nuclei emitted from the ¹⁰B(n,α)⁷Li reaction, and the energies and LET values of the 2 recoil ions as a function of penetration depth in water (Fig. 2). As shown, the initial LETs of helium and lithium ions were ∼193 and 304 eV nm⁻¹, respectively. The LET of 1.47 MeV ⁴He²⁺ ions calculated using our Monte Carlo simulations agreed very well with the SRIM simulation results. Since the SRIM program incorporates the change of charge state of the moving ion as it goes into and through the target (due to the effects of electron capture and loss by the ion), this agreement indicates that the helium ion, when it travels with this energy, is fully stripped of its electrons. However, for 0.84 MeV ⁷Li³⁺ ions, our calculations gave a LET which is more than twice the expected value. This difference was explained as being caused by a change in the charge state of the lithium ion, which always acts to reduce its LET relative to the LET of the bare nucleus. Our Monte Carlo simulations were used to calculate the “effective charge” (Z*) of a 0.84 MeV lithium ion in water that was required to reproduce the SRIM LET value of 304 eV nm⁻¹. A value very close to +2 (instead of +3) was actually obtained, clearly indicating a partial neutralization of the lithium ion at this energy.

The above results confirm the importance of making charge-state calculations for each recoil ion in this study. In this work, however, to avoid complexity arising from energy-dependent charge exchange processes, simulations were performed under the simplifying approximation that the energies of the two recoil ions remained constant when passing through the water medium. These constant average energy values and were chosen according to the following procedure: (1) Watt's compilation of quantities for radiation dosimetry in liquid water³ was first used to determine the “dose-average” LET values for both 1.47 MeV helium and 0.84 MeV lithium ions. The values thus obtained were ∼196 and 225 eV nm⁻¹, respectively; (2) using Fig. 2(c), these two LET values were then related to the corresponding penetration depths of the two recoil ions in water, namely, ∼5.5 and 1.5 μm, respectively; and (3) and were finally deduced from Fig. 2(b) as being equal to the energies of the two ions at these penetration depths, namely, ∼0.3 and 0.4 MeV, respectively. Once these two energies known, the actual effective charges carried by the two helium and lithium ions having these energies were determined as described above by using our Monte Carlo simulations and by adjusting Z* so as to reproduce the expected LET values. and were found to be about +1.6 and +1.7, respectively.

All calculations were performed by simulating short (typically, ∼1–5 μm) ion track segments, over which the energy and LET of the ion are well defined and remain nearly constant. Such model calculations thus gave “track segment” yields⁴⁰ at a well defined LET. The number of individual ion “histories” (usually ∼2–100, depending on the irradiating ion and energy) was chosen to ensure only small statistical fluctuations in the computed averages of chemical yields, while keeping acceptable computer time limits.

Finally, the yields of primary free radical or molecular products of water radiolysis induced by the recoil ions of the nuclear reaction ¹⁰B(n,α)⁷Li were calculated by summing the G-values for each recoil ion (obtained from our Monte Carlo simulations) weighted by its fraction of the total energy absorbed according to^38,41 (1) where G(X_i)_He and G(X_i)_Li are the yields of species X_i associated with the recoil helium and lithium ions, respectively, and E_T = E_He + E_Li is the sum of the initial energies of the ion products of the reaction (i.e., 2.31 MeV).

Absorption of the accompanying 0.478 MeV γ-ray in the aqueous solution (see Fig. 1) is small in our area of interest. Indeed, the range of an electron of this energy is ∼1 mm in liquid water at 25 °C;⁴² this is more than 100 times larger than the penetration ranges of the He and Li ions, which are only 5–8 μm. Thus, its contribution to the overall chemical reaction was neglected in this study.

Throughout this paper, G-values are quoted in units of molecules formed or consumed per 100 eV of radiation energy absorbed. For conversion into SI units, 1 molecule/100 eV = 0.10364 μmol J⁻¹.

3. Results and discussion

The temperature dependences of our computed yields of e_aq⁻, ˙OH, H˙, H₂O₂, and H₂ in pure, deaerated liquid water irradiated by the ¹⁰B(n,α)⁷Li recoil ions from ambient up to 350 °C are shown in Fig. 3 along with estimated G-values at 20 °C (ref. 15) and 289 °C.¹⁹ For the sake of comparison, our G-values were calculated at two different times, namely 10⁻⁷ and 10⁻⁶ s after energy deposition at all temperatures (solid, blue and red lines shown in Fig. 3, respectively). Compared with the data obtained for low-LET radiation (γ-rays from ⁶⁰Co or fast electrons), our computed yields for ¹⁰B(n,α)⁷Li recoil irradiation show essentially similar temperature dependences over the range of temperatures studied, but with much lower values for yields of free radicals and higher values for molecular yields. This is particularly true for the yields of e_aq⁻ and H˙ atoms, which remain extremely small at the microsecond time scale even at high temperatures [Fig. 3(a) and (c)]. This general trend is a result of the high-LET character of the ¹⁰B(n,α)⁷Li recoil ions. Indeed, upon increasing the LET of the radiation, there is an increased intervention of radical–radical reactions as the local concentrations of radicals along the radiation tracks are high and many radical interactions occur before the products can escape into the bulk solution. This allows fewer radicals to escape combination and recombination reactions during the expansion of tracks and in turn leads to the formation of more molecular products.²⁸

A striking feature of our simulated results is the marked downward inflection that is observed above ∼150 °C in the yields of H₂ and H₂O₂. This is in contrast to the corresponding estimates of Christensen¹⁹ at 289 °C, which seem to indicate a rather monotonic variation of G(H₂) [Fig. 3(e)] and G(H₂O₂) [Fig. 3(d)] with temperature. Similar non-monotonic behavior in the temperature dependence of the yields of primary products in low-^29,45,46 and high-^47,48 LET irradiated water has already been predicted, and is due to the fact that the rate constant for the bimolecular self-reaction of the hydrated electron (k₂): e_aq⁻ + e_aq⁻ (+2H₂O) → H₂ + 2OH⁻ (2) drops sharply between ∼150 and 200 °C.²⁰ This non-Arrhenius behavior of reaction (2) above ∼150 °C readily explains the sharp decrease in H₂ yields in Fig. 3(e). Moreover, as a consequence of the drop in k₂, more and more e_aq⁻ are available as the temperature increases to either react in other intra-track reactions, such that²⁰ e_aq⁻ + ˙OH → OH⁻ (k₃ = 3.34 × 10¹⁰ M⁻¹ s⁻¹, 20 °C), (3) or escape into the bulk solution. As hydrogen peroxide is formed predominantly by the reaction²⁰ ˙OH + ˙OH → H₂O₂ (k₄ = 4.54 × 10⁹ M⁻¹ s⁻¹, 20 °C), (4) the increased occurrence of reaction (3) above 150 °C also leads to a downward inflection in G(H₂O₂), as shown in Fig. 3(d).

In connection with these predicted non-monotonic variations of G(H₂) and G(H₂O₂), we should briefly mention here the current controversy concerning the temperature dependence of k₂ (Fig. 4). In this work, we adopted the values of k₂, including the drop between 150 and 200 °C, recommended by Elliot and Bartels²⁰ as the “best values to use to model water radiolysis at temperatures up to 350 °C” [represented by the black dashed line, denoted k_a, in Fig. 4(a)]. However, this drop in k₂ has been measured only under alkaline conditions. Its applicability to neutral or slightly acidic (as the pH of water at 150–200 °C is about 5.7–6)¹⁵ solution remains uncertain because it could be a function of the pH of the solution.⁵⁰

Until recently, most computer modelers of the radiolysis of water at elevated temperatures have employed, in neutral solution, an Arrhenius extrapolation of the values of k₂ below 150 °C to 200–350 °C, as proposed previously by Elliot⁵⁰ and Stuart et al.,⁵¹ and recently by Hatomoto et al.⁵² This approach assumes that such an abrupt change in k₂ does not occur and that reaction (2) is diffusion controlled at temperatures greater than 150 °C. This assumption was originally justified by the good agreement between models and experiments.^45,46

To show the sensitivity of G(H₂) and G(H₂O₂) to k₂, our simulations were carried out for the temperature dependence of k₂ obtained by using an Arrhenius extrapolation procedure above ∼150 °C (ref. 49–52) [represented by the red solid line, denoted k_b, in Fig. 4(a)]. The red solid lines in Fig. 4(b) and (c) display our calculated H₂ and H₂O₂ yields at 10⁻⁶ s after the ionizing event over the temperature range of 25–350 °C. A comparison with our results obtained using the temperature dependence of k₂ measured in alkaline water (k_a) [black dashed lines in Fig. 4(b) and (c)] clearly indicates that G(H₂) and G(H₂O₂) are strongly affected by the choice of k₂. In particular, the sharp downward inflections predicted for G(H₂) and G(H₂O₂) above ∼150 °C no longer appear. Considering the importance of the self-reaction of e_aq⁻ in high-temperature water radiolysis, further measurements of its rate constant in near-neutral water are obviously highly desirable.

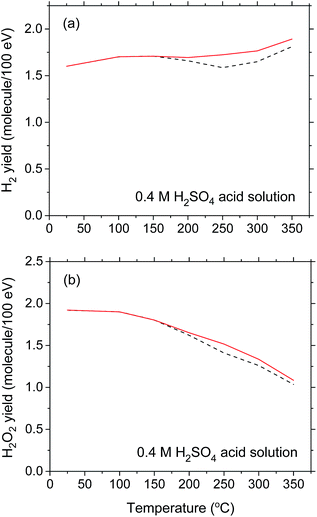
Turning now to the ¹⁰B(n,α)⁷Li radiolysis of deaerated 0.4 M sulfuric acid aqueous solutions, we present in Fig. 5 the results of our Monte Carlo simulations showing the variations of the G-values for H˙ (considering the conversion of e_aq⁻ to H˙ in the tracks in acidic solution),⁵⁵ ˙OH, H₂O₂, and H₂ (at 10⁻⁶ s) as a function of temperature over the range of 25–350 °C. As can be seen, the simulations agree reasonably well with the experimental data of Barr and Schuler²³ at 25 °C, which are also shown in the figure for the sake of comparison. Compared with the primary (or “escape”) yield data obtained for low-LET radiation (⁶⁰Co γ-rays or fast electrons) (shown as dashed lines in Fig. 5), it is seen that, as in neutral water, our computed G-values for the ¹⁰B(n,α)⁷Li radiolysis of deaerated 0.4 M H₂SO₄ aqueous solutions show essentially similar temperature dependences over the 25–350 °C temperature range studied. The same general trend is observed, but with much lower values for yields of radical species and higher values for molecular yields, reflecting again the high-LET character of the ¹⁰B(n,α)⁷Li recoil ions.

For the sake of completeness, we show in Fig. 6 the sensitivity of G(H₂) and G(H₂O₂) to the temperature dependence for the (e_aq⁻ + e_aq⁻) reaction rate constant k₂ chosen in the simulations. Compared to the results obtained in near-neutral water and shown in Fig. 4(b) and (c), the choice of k₂ [namely, k_a or k_b in Fig. 4(a)] in acidic solution is relatively unimportant. Indeed, as can be seen from Fig. 6(a) and (b), the H₂ and H₂O₂ yield (red solid) curves obtained using k₂ = k_a differ only slightly from the corresponding (black dashed) curves calculated for k₂ = k_b and the downward inflections predicted for G(H₂) and G(H₂O₂) above ∼150 °C are practically no longer apparent. This is easily understandable since in 0.4 M H₂SO₄ solutions, hydrated electrons are very rapidly (<10⁻⁹ s) transformed into H˙ atoms in the tracks,³⁷ thereby making reaction (2) quickly inoperative in contributing to these yields whatever the temperature. Removal of this reaction thus prevents the possibility of observing any clear difference in the temperature dependence of G(H₂) and G(H₂O₂) above ∼150 °C when either k_a or k_b is used for the (e_aq⁻ + e_aq⁻) reaction rate constant.

4. Conclusion

In this work, Monte Carlo simulations were used to calculate the G-values for the primary species of the radiolysis of neutral liquid water and 0.4 M H₂SO₄ aqueous solutions by the recoil ions of the ¹⁰B(n,α)⁷Li nuclear reaction at temperatures between 25 and 350 °C. Overall, the simulation results for neutral deaerated water agreed well with existing estimates at 20 and 289 °C. For 0.4 M H₂SO₄ solutions, reasonable agreement between experiment and simulation was also found at room temperature. Compared with the data obtained for low-LET radiation, our computed yields showed essentially similar temperature dependences over the range of temperatures studied, but with lower values for yields of free radicals and higher values for molecular yields, which reflect the high-LET character of the densely ionizing ¹⁰B(n,α)⁷Li recoil ions. More experimental data are required for both neutral and acidic solutions to better describe the dependence of radiolytic yields on temperature and to test our modeling calculations more thoroughly. Moreover, measurements of the (e_aq⁻ + e_aq⁻) reaction rate constant in near-neutral water would help us to determine whether the predicted non-monotonic inflections above ∼150 °C in G(H₂) and G(H₂O₂) are confirmed.

Acknowledgements

The authors thank Professor Takayuki Terai, Professor Yusa Muroya, and Dr Shin-ichi Yamashita for their support and advices. They are also grateful to Professor James F. Ziegler for his helpful correspondence with regard to the use of the SRIM simulation software. M. M. I. is the recipient of a scholarship from the “Centre de Recherche Médicale de l’Université de Sherbrooke”. P. L. thanks the Ministry of Education, Culture, Sports, Science, and Technology (MEXT) of Japan for financial support through a MEXT scholarship. The research of J.-P. J.-G. is supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) Grant No. RGPIN-2015-06100.

Notes and references

Footnote