Two impurity energy level regulation leads to enhanced thermoelectric performance of Ag_1−xCd_xIn₅Se₈

Abstract

The tetrahedrally bonded diamond-like compound AgIn₅Se₈ is proved to be a promising thermoelectric material due to its intrinsically low thermal conductivity. For the pristine AgIn₅Se₈ compound, however, the inferior electrical properties generally result in a limited zT value, owing to its wide band gap, up to 1.1 eV. Here, we report on the synthesis of AgIn₅Se₈ compound through a quick and convenient solid-state reaction route. Furthermore, the two impurity energy levels are regulated in those doped samples by incorporating Cd²⁺ ions at Ag⁺ lattice sites; the electron concentration dramatically increases, resulting in greatly enhanced electrical conductivity and thus a thermoelectric power factor over the entire temperature range. Combined with the intrinsically low lattice thermal conductivity, Cd-doped Ag_1−xCd_xIn₅Se₈ with x = 0.05 reaches the highest zT value of 0.63 at 883 K, favorably improved by 40% compared with that of the pristine AgIn₅Se₈.

---

1. Introduction

Thermoelectric (TE) materials can convert heat into useful electricity through the Seebeck effect, showing great potential for waste recovery or powering deep-space missions.^1–4 The fundamental physics and applications of TE materials have motivated a variety of relevant research areas in physics, chemistry and engineering for decades. The overall performance of TE material is determined by the dimensionless thermoelectric figure of merit zT, which can be defined as zT = S²σT/κ, where S is the Seebeck coefficient, σ the electrical conductivity, T the absolute temperature and κ the thermal conductivity.

Given the strong interrelation among the three transport parameters, S, σ and κ, it is difficult to optimize zT values by tuning one of these parameters alone without degrading the other two. The total thermal conductivity is composed of a lattice part and electronic part; fortunately, the lattice part of thermal conductivity is independent of electrical transport properties or power factor σS², which, to some extent, allows us optimize the electrical transport and lattice thermal conductivity separately. The most common and convenient way to enhance the power factor is to optimize carrier concentration while lattice thermal conductivity can be reduced by solid solution or directly choosing material with high disordered structure.^5–7

Traditionally, a good TE material should be a narrow gap semiconductor with band gap around 6–10K_BT depending on the operation temperature in order to attain good electrical conductivity and avoid the bipolar effect at high temperature. However, there is no theoretical upper limit for the band gap of TE materials. The preference of narrow band semiconductors for TE application relies on the experimental observation that wide band semiconductors typically have limited solubility for dopants, high lattice thermal conductivity or low carrier mobility. Most recently, the ternary wide gap family A^IB^IIIC₂^VI compounds with diamond-like structure (A = Cu, Ag; B = Al, Ga, In; C = S, Se, Te) have been reported to show promising TE properties.⁸ The lattice thermal conductivity (κ_l) of those compounds is fairly low due to the strong phonon scatting by the ordered vacancy defects or highly distorted crystal structures.^8–15 Besides, the three constituent elements give numerous choices of dopants, providing great opportunity to tune electrical transport properties.^8,16,17

The ternary compound AgIn₅Se₈ belongs to the A^IB₅^IIIC₈^VI – type wide band gap semiconductor family, which is regarded as being composed of an In₂Se₃-based (In₂Se₃)₂(AgInSe₂) or (In₂Se₃)_2.5(Ag₂Se)_0.5 pseudo binary alloy.¹⁸ Besides, the structure of these ternary compound is analogous to B₂^IIIC₃^VI – type crystalline structures,^19,20 which allows the incorporated foreign elements to take the most stable valence state,²⁰ resulting in the reduction in band gap. This is caused by the preference of Ag or Cu incorporation in α-In₂Se₃, favoring the formation of Ag₂Se or Cu₂Se slab.^18,21 The crystal structure and thermoelectric properties of the novel ternary AgIn₅Se₈ were first reported by Cui et al.,¹⁸ who investigated the thermoelectric performance of the pristine AgIn₅Se₈ compounds with different annealing time. In this study, in order to explore the possibility of further enhancing the electrical conductivity, we investigate and regulate the thermoelectric properties of ternary compound Ag_1−xCd_xIn₅Se₈ through Cd doping in addition to the intrinsic Se vacancy. The highest zT value of 0.63 at 883 K was achieved for the x = 0.05 sample, which is greatly improved by 40% in contrast with that of the pristine AgIn₅Se₈.

2. Experimental procedure

Alloys of composition Ag_1−xCd_xIn₅Se₈ (x = 0.0, 0.01, 0.03, 0.05) samples were synthesized by melting and annealing procedure. Firstly, high purity elements Ag (granular, 99.99999%), In (silk, 99.99999%), Se (granular, 99.99999%), Cd (granular, 99.99999%) were weighed in stoichiometric quantities, followed by mixing and putting into quartz tubes. Secondly, all the tubes were evacuated by vacuum pump to 10⁻⁴ Pa, and then quickly were sealed. Thirdly, the tubes were put into the muffle furnace, slowly heated from room temperature to 1273 K in 14 hours, and kept at this temperature for 15 hours. Subsequently, the samples were cooled down to 873 K in 6 hours and held for 20 hours. Thereafter, the samples were left for natural cooling. The obtained ingots were grinded into fine powders and annealed for 30 hours at 923 K. Finally, these annealed fine powders were consolidated by Spark Plasma Sintering (SPS) at 873 K for 5 minutes under the pressure of 45 MPa in an Ar-flow atmosphere. The final products were confirmed to have 98% of theoretical density by using the Archimedes method.

The composition phase analysis was performed by using X-ray diffraction (XRD). Powder X-ray diffraction (XRD) patterns of all samples after SPS were collected using a PANalytical X'Pert apparatus with Cu Kα radiation. The XRD data was analyzed by the commercial software JADE 8.0.

The thermoelectric properties of the samples were measured in the temperature range of 300–883 K. The electrical conductivity (σ) and Seebeck coefficient (σ) were measured by Linseis LSR-3 system, while the thermal conductivity were calculated from the formula κ = λρC_p. The thermal diffusivity (λ) was gained by Netzsch LFA 457 lasher flash system, and the heat capacity (C_p) value was measured by a differential scanning calorimeter, Netzsch, 404 F3. The Hall carrier concentration (n_H) and Hall mobility (u_H) were calculated from Hall coefficient (R_H) at room temperature based on the equations and u_H = R_Hσ, which was characterized by a home-made Hall system. The absorption coefficients were obtained by using a UV-vis spectrophotometer apparatus (Shimadzu UV-3600), and a strong absorption is observed at about 1127 nm when the photon wavelength is scanned from 300 nm to 1500 nm.

3. Results and discussions

3.1 Crystal structure and phase analysis

AgIn₅Se₈ crystallizes in the space group P4̄2m with unit cell parameters: a = 6.1952 Å, b = 6.1952 Å, c = 12.419 Å, V = 390.08 ų. The cation Ag⁺ and In³⁺ are orderly positioned in the network of Se²⁻ lattices, in which both In³⁺ (In1, In2) and Se²⁻ (Se1, Se2) occupy two inequivalent sites. The whole structure can be well described as a frame work of distorted AgSe₄ and InSe₄ tetrahedrons connected by common faces. As an ordered vacancy compound in chalcopyrite family, AgIn₅Se₈ possesses a cation deficiency. Namely, each anion is coordinated by two In atoms, one Ag atom while each cation is coordinated by four anions. Fig. 1 shows atomic positions of AgIn₅Se₈ projected along the b axis. As can be seen, the structure is characterized by a close packed and alternatively arranged Se1²⁻ and Se2²⁻ anion lattice, completed by the Ag, In1 and In2 cations. The atomic sites on In1 planes are totally occupied while those on the Ag and In2 planes are partially occupied, leaving voids along the 010 direction, as shown in Fig. 1.²²

Fig. 1 Shows atomic positions of AgIn₅Se₈ projected along the b axis.

Fig. 2(a) displays the room temperature X-ray diffraction pattern of Ag_1−xCd_xIn₅Se₈ with nominal stoichiometric component (x = 0.0, 0.01, 0.03, 0.05) after SPS. Room temperature XRD analysis for the polycrystalline sample Ag_xCd_1−xIn₅Se₈ indicate that the samples are single phase. We observe that all peaks of the samples can be indexed with the standard AgIn₅Se₈ card (PDF #76-1439, space group P4̄2m, No. 111), and no impurity peaks were found.

Fig. 2 (a) XRD pattern of Ag_1−xCd_xIn₅Se₈ (x = 0.0, 0.01, 0.03, 0.05); (b) UV-vis optical absorption spectrum of AgIn₅Se₈; the inset in (b) shows UV-vis optical absorption spectrum of Ag_1−xCd_xIn₅Se₈ (x = 0.01, 0.03, 0.05).

Fig. 2(b) shows the photon energy dependence of the relational expression of the Ag_1−xCd_xIn₅Se₈ (x = 0.0, 0.01, 0.03, 0.05) in terms of (αhν)² = A(hν − E_g). In this relational expression, α stands for the absorption coefficient, h signifies the Planck constant, hν stands for the photon energy and A is a constant. By extracting the intercept on the horizontal axis of the function (αhν)² = A(hν − E_g), we obtained the band gap of the tested AgIn₅Se₈ is 1.1 eV, which is consistent with the previous study.^18,23

3.2 Electrical transport properties

The electrical transport properties are shown in Fig. 3. Fig. 3(a) displays the temperature dependence of the electrical conductivity of Ag_1−xCd_xIn₅Se₈ with nominal stoichiometric component (x = 0.0, 0.01, 0.03, 0.05). In this figure, the pristine AgIn₅Se₈ shows a relatively low electrical conductivity at room temperature and the electrical conductivity for each of sample increases with increasing temperature as a result of more carriers being activated.

Fig. 3 (a) Temperature dependence of the electrical conductivity for Ag_1−xCd_xIn₅Se₈ (x = 0.01, 0.03, 0.05); (b) temperature dependence of the Seebeck coefficient for Ag_1−xCd_xIn₅Se₈ (x = 0.0, 0.01, 0.03, 0.05). (c) Temperature dependence of the power factor for Ag_1−xCd_xIn₅Se₈ (x = 0.0, 0.01, 0.03, 0.05); (d) the relationship between carrier concentration, mobility and the Cd concentration for Ag_1−xCd_xIn₅Se₈ (x = 0.0, 0.01, 0.03, 0.05).

By substituting the Cd atoms for Ag atoms, the carrier concentration increases rapidly with respect to Cd content due to the extra valence electron provided by Cd atom, which is confirmed by the results of Hall measurement shown in Fig. 3(d). The carrier concentration of pristine AgIn₅Se₈ is only 1.8 × 10¹⁶ cm⁻³ while that of x = 0.05 sample is 2.3 × 10¹⁹ cm⁻³, which is more than 3 orders of magnitude enhancement. Consequently, the dramatically increased carrier concentration leads to the significantly enhanced electrical conductivity. Specifically, the electrical conductivity is raised by 78 times when x = 0.05 as compared with pristine compound. As shown in Fig. 3(d), the mobility of all the Ag_1−xCd_xIn₅Se₈ samples at room temperature drops sharply with respect to Cd content, from 498 cm² V⁻¹ s⁻¹ for pristine AgIn₅Se₈ to 31 cm² V⁻¹ s⁻¹ for Ag_0.95Cd_0.05In₅Se₈ sample. The reduction in carrier mobility can be attributed to the enhanced point defect scattering caused by the heavy doping, which largely shortens the mean free path of the carriers. This is probably the reason for the diminished electrical conductivity of doped samples at higher temperature.²⁴

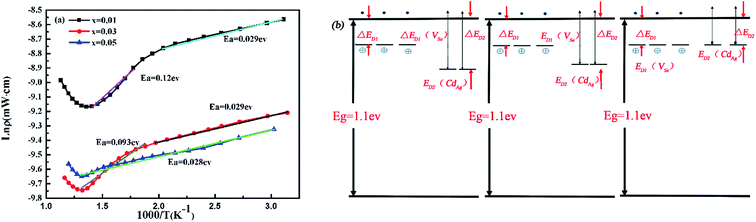
By carefully checking the curves of electrical conductivity, we observe two segments with varied slopes in the temperature dependence of electrical conductivity. In order to understand the intrinsic mechanism for the abrupt electrical conductivity enhancement of the doped samples Ag_1−xCd_xIn₅Se₈ (x = 0.01, 0.03, 0.05), the Arrhenius equation is applied to explain these different behaviors. Herein, the activation energy (E_a) for carriers is used in the Arrhenius eqn (1),²⁵ which means the energy barrier the electrons need to overcome for conducting. Fig. 4(a) displays the Arrhenius plot with linear fit for Ag_1−xCd_xIn₅Se₈ (x = 0.0, 0.01, 0.03, 0.05). For x = 0.01 and x = 0.03 samples, the same activation energy 0.029 eV from room temperature to 473 K is identified, which may be ascribed to the shallow donor levels created by Se vacancy (V_Se).²⁶ While above 473 K, the activation energies of these two samples are found to be 0.12 eV, 0.093 eV, resulting from the deeper donor states caused by the Cd impurities (Cd_Ag).²⁷ Nevertheless, only one donor level can be identified with activation energy of 0.028 eV in the whole measured temperature range for x = 0.05 sample. Here, we assume that the donor impurity level of the Cd may gradually move close to the conduction band edge as the Cd concentration increasing. When x = 0.05, the donor level of Cd may coincide with the impurity level of the selenium vacancy. The corresponding variation of donor impurity level with rising Cd concentration in Ag_1−xCd_xIn₅Se₈ samples is schematically displayed in Fig. 4(b). The additional Cd_Ag impurity level located below the energy level of Se vacancy (V_Se), provides more electrons for conducting in Ag_1−xCd_xIn₅Se₈ compounds, yielding a rapidly increased carrier concentration and thus the enhanced electrical conductivity, as compared with the pristine AgIn₅Se₈ the with only one V_Se impurity level. The temperature for Cd_Ag impurity level starting to function gradually shifts to room temperature with increasing Cd content, indicating the movement of Cd_Ag impurity level towards bottom of conducting band. As a result, associated with the intrinsic Se vacancy impurity level, the two impurity levels regulation leads to the enhanced electrical performance of Ag_1−xCd_xIn₅Se₈ over the entire temperature.

Fig. 4 (a) The Arrhenius plot with linear fit for Ag_1−xCd_xIn₅Se₈ (x = 0.01, 0.03, 0.05). (b) Shows the schematic about the donor impurities ionize from donor impurities to conduction band of all the doped samples Ag_1−xCd_xIn₅Se₈ (x = 0.01, 0.03, 0.05).

Fig. 3(b) displays the temperature dependence of the Seebeck coefficient of Ag_1−xCd_xIn₅Se₈ (x = 0.0, 0.01, 0.03, 0.05). For all these samples, negative values of the Seebeck coefficients are observed from 300 to 883 K, indicating that the major carrier of these Ag_1−xCd_xIn₅Se₈ samples are electrons. At room temperature, the absolute Seebeck values decrease from 358 to 97 μV K⁻¹ with the Cd concentration increasing, which is consistent with the general inverse relationship between electrical conductivity and Seebeck coefficient. The Seebeck coefficient of the pristine AgIn₅Se₈ firstly increases with lifted temperature, and then decreases as the temperature continues to raise, which is typical for non-degenerate semiconductors with low carrier concentration.

Compared with the pristine samples, the Cd doped samples shows entirely different temperature dependence behavior. Here, the eqn (2) based on a single parabolic band model is employed to provide a general understanding of the change in Seebeck coefficients of degenerate semiconductors as those Cd doped samples.^28,29 The relatively lightly doped sample with x = 0.01 and x = 0.03 exhibit three segments in the curve of Seebeck coefficients with respect to temperature. Initially, the Seebeck coefficients increases with the increasing temperature since the carrier concentration in this region increases slowly and the Seebeck coefficient is mainly governed by the temperature. Then the Seebeck coefficient shows a slight decrease from 500 to 700 K due to the rapidly increased carrier concentration caused by the activation of the deep impurity donor level through lifted temperature. In this case, a large number of carriers are activated, playing a dominant role in the Seebeck coefficient change, which is given by the relationship . After that, the Seebeck coefficients of these two samples continue to arise most of the carriers on the deep impurity level have been activated for transport and temperature dominates again for determining the absolute value of Seebeck coefficients. For the x = 0.05 sample, the Seebeck coefficient monotonically increases as a function of temperature, revealing a highly degenerate semiconductor behavior.

Combining the electrical conductivity with Seebeck coefficient, the maximum power factor of 0.42 mW m⁻¹ K⁻² is obtained when the Cd content reaches x = 0.05 at 883 K, which is larger than that of the pristine AgIn₅Se₈ sample (0.31 mW m⁻¹ K⁻² at 883 K), as shown in Fig. 3(c). The enhanced power factor is attained primarily through the optimization of carrier concentration, regulated by the contributions from two impurity levels.

3.3 Thermal transport properties

Fig. 5(a) presents the temperature dependence of the total thermal conductivity κ of the Ag_1−xCd_xIn₅Se₈ (x = 0.0, 0.01, 0.03, 0.05) samples. As temperature increases, from 300 to 883 K, the total thermal conductivity rapidly decreases, where the Umklapp process dominates. In order to investigate the intrinsic lattice thermal conductivity, the electronic contribution, which is estimated by the Wiedemann–Franz law κ_e = LσT, is subtracted from the total thermal conductivity. The Lorenz number L is calculated through eqn (3)–(5), based on a single parabolic model,³⁰where S is the measured Seebeck coefficient and r is the scattering factor related to the scattering mechanism. When the acoustic scatting dominates, r equals to −1/2. The Fermi–Dirac integral F_n(ξ) can expressed as formula (4).

Fig. 5 (a) Temperature dependence of the total thermal conductivity κ for Ag_1−xCd_xIn₅Se₈ (x = 0.0, 0.01, 0.03, 0.05); (b) temperature dependence of the electrical thermal conductivity for κ_l Ag_1−xCd_xIn₅Se₈ (x = 0.0, 0.01, 0.03, 0.05); (c) temperature dependence of the lattice conductivity κ_e for Ag_1−xCd_xIn₅Se₈; (d) temperature dependence of the zT values for Ag_1−xCd_xIn₅Se₈ (x = 0.0, 0.01, 0.03, 0.05).

After deriving the reduced Fermi energy ξ from the eqn (3). The Lorenz number can be calculated from the following formula (5).

Fig. 5(b) plots the electronic thermal conductivity as a function of the temperature by using the calculated Lorenz number. It seems that the electronic contribution should be taken into account only for the heavily doped samples (x = 0.03 and 0.05) at high temperature. As shown in Fig. 5(c), the lattice thermal conductivity of all the samples roughly follows a T⁻¹ law, indicating the predominant phonon scattering mechanism here is phonon–phonon scattering.³⁰ In addition, it is important to note that the minimum lattice thermal conductivity of 0.6 W m⁻¹ K⁻² obtained in this study is among the lowest values for wide band gap diamond-like semiconductors.^12,16,17

Combining the electronic transport and the total thermal conductivity data, we obtained the temperature dependence of the dimensionless thermoelectric figure of merit of the Ag_1−xCd_xIn₅Se₈ (x = 0.0, 0.01, 0.03, 0.05) samples, shown in Fig. 5(d). Apparently, for all the samples, the zT values monotonously increase with the increasing temperature in the measured temperature range. Also, it is found that the zT value in the doped samples shows a significant increase with increasing Cd content due to the enhancement of the power factor and the slightly reduced lattice thermal conductivity in spite of the enlarged electronic thermal conductivity. The maximum zT value achieved in this study is 0.63 at 883 K for x = 0.05 sample, which is 40% enhancement compared with that of pristine sample. Similar thermoelectric performance was found in previous study,¹⁸ in which we believe the long-term annealing process (more than 30 days) would produce more Se vacancy in those compounds and give rise to similar carrier concentration to our best sample.

4. Conclusion

In summary, the n-type Ag_1−xCd_xIn₅Se₈ (x = 0.0, 0.01, 0.03, 0.05) samples were synthesized via the solid state reaction method followed by the spark plasma sintering technique. The thermoelectric performance of Cd-doped Ag_1−xCd_xIn₅Se₈ compounds has been investigated from room temperature to 883 K. With increasing Cd content, the regulation of two impurity levels arising from Cd and Se vacancy results in a rapidly increased carrier concentration, leading to a maximum power factor of 0.42 mW m⁻¹ K⁻² for x = 0.05 sample. Furthermore, the lattice thermal conductivity of Ag_1−xCd_xIn₅Se₈ samples is found to be around 0.6 W m⁻¹ K⁻¹, which is comparable to that of the other state of art TE materials with diamond-like structure. As a result, the maximum zT of 0.63 at 883 K is attained for Ag_0.95Cd_0.05In₅Se₈. Although the zT value obtained in this study is not as high as the mainstream TE materials, it is demonstrated here that the wide band gap semiconductors with diamond-like structure can possess low lattice thermal conductivity at high temperature. After carefully doping, those materials can also have moderate power factor, which implies the great potential in TE application. To further enhance the thermoelectric performance AgIn₅Se₈, more effective doping elements or method should be investigated to avoid the diminished carrier mobility.

Acknowledgements

This work was financially supported in part by the National Natural Science Foundation of China (Grant No. 11344010, 11404044, 51472036), the Fundamental Research Funds for the Central Universities (106112016CDJZR308808). The work conducted at the Chongqing Institute of Green and Intelligent Technology, Chinese Academy of Sciences is supported by the 100 Talent Program of the Chinese Academy of Sciences (Grant No. 2013-46), the National Natural Science Foundation of China (Grant No. 51672270, 51401202), and the Project for Fundamental and Frontier Research in Chongqing (CSTC2015JCYJBX0026).

References

1. B. C. Sales, Science, 2002, 295, 1248–1249.
2. F. J. DiSalvo, Science, 1999, 285, 703–706.
3. L. E. Bell, Science, 2008, 321, 1457–1461.
4. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114.
5. Y. Z. Pei, A. D. LaLonde, N. A. Heinz, X. Y. Shi, S. Iwanaga, H. Wang, L. D. Chen and G. J. Snyder, Adv. Mater., 2011, 23, 5674–5678.
6. Y. Z. Pei, A. F. May and G. J. Snyder, Adv. Energy Mater., 2011, 1, 291–296.
7. X. Lu, W. Yao, G. W. Wang, X. Y. Zhou, D. Morelli, Y. S. Zhang, H. Chi, S. Hui and C. Uher, J. Mater. Chem. A, 2016, 4, 17096–17103.
8. R. H. Liu, L. L. Xi, H. L. Liu, X. Shi, W. Q. Zhang and L. D. Chen, Chem. Commun., 2012, 48, 3818–3820.
9. Y. Dong, A. R. Khabibullin, K. Wei, Z. H. Ge, J. Martin, J. R. Salvador, L. M. Woods and G. S. Nolas, Appl. Phys. Lett., 2014, 104, 252107.
10. K. Kurosaki, H. Matsumoto, A. Charoenphakdee, S. Yamanaka, M. Ishimaru and Y. Hirotsu, Appl. Phys. Lett., 2008, 93, 012101.
11. T. Plirdpring, K. Kurosaki, A. Kosuga, M. Ishimaru, A. Harnwunggmoung, T. Sugahara, Y. Ohishi, H. Muta and S. Yamanaka, Appl. Phys. Lett., 2011, 98, 172104.
12. M. L. Liu, I. W. Chen, F. Q. Huang and L. D. Chen, Adv. Mater., 2009, 21, 3808–3812.
13. X. Y. Shi, F. Q. Huang, M. L. Liu and L. D. Chen, Appl. Phys. Lett., 2009, 94, 122103.
14. C. Sevik and T. Cagin, Appl. Phys. Lett., 2009, 95, 112105.
15. X. Y. Shi, L. L. Xi, J. Fan, W. Q. Zhang and L. D. Chen, Chem. Mater., 2010, 22, 6029–6031.
16. A. Yusufu, K. Kurosaki, A. Kosuga, T. Sugahara, Y. Ohishi, H. Muta and S. Yamanaka, Appl. Phys. Lett., 2011, 99, 061902.
17. T. Plirdpring, K. Kurosaki, A. Kosuga, T. Day, S. Firdosy, V. Ravi, G. J. Snyder, A. Harnwunggmoung, T. Sugahara, Y. Ohishi, H. Muta and S. Yamanaka, Adv. Mater., 2012, 24, 3622–3626.
18. J. L. Cui, Y. Y. Li, Y. Deng, Q. S. Meng, Y. L. Gao, H. Zhou and Y. P. Li, Intermetallics, 2012, 31, 217–224.
19. T. Colakoglu, M. Parlak and S. Ozder, J. Non-Cryst. Solids, 2008, 354, 3630–3636.
20. T. Colakoglu, M. Parlak, M. Kulakci and R. Turan, J. Phys. D: Appl. Phys., 2008, 41, 115308.
21. J. L. Cui, X. J. Zhang, Y. Deng, H. Fu, Y. M. Yan, Y. L. Gao and Y. Y. Li, Scr. Mater., 2011, 64, 510–512.
22. P. Benoit, P. Charpin and C. Djegamariadassou, Mater. Res. Bull., 1983, 18, 1047–1057.
23. L. Y. Huang, H. Xu, Y. P. Li, H. M. Li, X. N. Cheng, J. X. Xia, Y. G. Xu and G. B. Cai, Dalton Trans., 2013, 42, 8606–8616.
24. C. G. Fu, S. Q. Bai, Y. T. Liu, Y. S. Tang, L. D. Chen, X. B. Zhao and T. J. Zhu, Nat. Commun., 2015, 6, 8144.
25. K. S. Weldert, W. G. Zeier, T. W. Day, M. Panthofer, G. J. Snyder and W. Tremel, J. Am. Chem. Soc., 2014, 136, 12035–12040.
26. H. Y. Ueng and H. L. Hwang, J. Phys. Chem. Solids, 1989, 50, 1297–1305.
27. H. Y. Ueng and H. L. Hwang, J. Phys. Chem. Solids, 1990, 51, 11–18.
28. C. Xiao, Z. Li, K. Li, P. C. Huang and Y. Xie, Acc. Chem. Res., 2014, 47, 1287–1295.
29. J. P. Heremans, V. Jovovic, E. S. Toberer, A. Saramat, K. Kurosaki, A. Charoenphakdee, S. Yamanaka and G. J. Snyder, Science, 2008, 321, 554–557.
30. Q. F. Chen, G. W. Wang, A. J. Zhang, D. F. Yang, W. Yao, K. L. Peng, Y. C. Yan, X. N. Sun, A. P. Liu, G. Y. Wang and X. Y. Zhou, J. Mater. Chem. C, 2015, 3, 12273–12280.

---