View PDF VersionPrevious ArticleNext Article

Open Access Article
This Open Access Article is licensed under a Creative Commons Attribution-Non Commercial 3.0 Unported Licence
DOI: 10.1039/C6RA27208H (Paper) RSC Adv., 2017, 7, 7610-7618

Role of Tf2N− anions in the ionic liquid–water distribution of europium(III) chelates†

Hiroyuki Okamura*a, Noboru Aoyagib, Kojiro Shimojoa, Hirochika Naganawaa and Hisanori Imura*c
aAdvanced Science Research Center, Japan Atomic Energy Agency, Tokai, Ibaraki 319-1195, Japan. E-mail: okamura.hiroyuki@jaea.go.jp
bNuclear Science and Engineering Center, Japan Atomic Energy Agency, Tokai, Ibaraki 319-1195, Japan
cFaculty of Chemistry, Institute of Science and Engineering, Kanazawa University, Kakuma, Kanazawa 920-1192, Japan. E-mail: imura@se.kanazawa-u.ac.jp

Received 23rd November 2016 , Accepted 9th January 2017

First published on 23rd January 2017

Abstract

The role of bis(trifluoromethanesulfonyl)imide (Tf2N−) anions in the ionic liquid–water distribution systems of Eu(III) chelates with 2-thenoyltrifluoroacetone (Htta) was investigated by liquid–liquid distribution and time-resolved laser-induced fluorescence spectroscopy (TRLFS). The extraction constants of neutral Eu(tta)3 and anionic Eu(tta)4− chelates in 1-alkyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide ([Cnmim][Tf2N]) were determined by analyzing the distribution equilibrium. The effect of the ionic liquids on the distribution constant of the neutral Eu(tta)3 chelate was evaluated by the regular solution theory. The distribution constant of Eu(tta)3 in [Cnmim][Tf2N] was increased dramatically by the solvation effects of Eu(tta)3 in [Cnmim][Tf2N]. TRLFS for [Eu(tta)3(H2O)3] synthesized revealed that the Eu(tta)3 chelate was almost completely dehydrated in a series of [Cnmim][Tf2N] (n = 2–10). The Eu(tta)3 chelate exists as di- or tri-hydrates in 1-ethyl-3-methylimidazolium perchlorate ([C2mim][ClO4]) containing 20 mol dm−3 water, whereas mono-hydrated chelate was formed in [C2mim][Tf2N, ClO4] in the presence of 0.50 mol dm−3 Tf2N− and 20 mol dm−3 water. These results show that the coordinated water molecules of [Eu(tta)3(H2O)3] were replaced by the Tf2N− anions. In fact, an anionic adduct, [Eu(tta)3(Tf2N)]−, was observed by electrospray ionization mass spectrometry in the presence of [C4mim][Tf2N].

Introduction

Ionic liquids (ILs) have been widely investigated as novel alternatives to conventional organic molecular solvents.1 They are defined as room-temperature molten salts that have extremely low vapor pressure and high thermal stability, and exhibit electrical conductivity. Chemical and physical properties such as viscosity, polarity, hydrophobicity, and Lewis acidity and basicity can be adjusted by judicious combination of a cationic and an anionic component in the IL. These unique features of ILs have potentially been exploited in various fields of analytical chemistry,2–4 electrochemistry,5–7 synthesis and catalysis,8–10 and materials chemistry.11–13 In particular, several reviews have investigated extensively water-immiscible hydrophobic ILs composed of a bis(trifluoromethanesulfonyl)imide (Tf2N−) anion as extraction media in liquid–liquid distribution (LLD).14–18

Application of ILs in LLD has many advantages.19 Because ILs can act as liquid ion exchangers, not only neutral species but also positively or negatively charged species can be extracted into the IL by ion exchange via the cationic or anionic constituent of the ILs.20–22 These unique mechanisms in an IL system often lead to an enhancement in the extractability of a particular metal ion. However, when the extracted ionic species becomes a part of the IL, it is generally difficult to recover metal ions extracted into the IL phase. Acidic chelating reagents such as β-diketones can potentially overcome these problems.23–31 Although it has been found that IL distribution systems for neutral complexes also exhibit high extraction performance compared with conventional organic solvent systems, the cause of the extraction enhancement except the ion-exchange mechanism23 has yet to be clarified. Therefore, in-depth systematic studies on IL distribution systems of metal chelates are required.

Time-resolved laser-induced fluorescence spectroscopy (TRLFS) has been widely used as an analytical technique for the speciation of fluorescent metal ions such as lanthanides(III) and actinides(III).32–39 Because the fluorescence is sensitive to the inner-sphere coordination environment of the metal ion, the fluorescence intensity, spectral shape, and fluorescence lifetime change are dependent on the solvation or coordination structure of the metal chelate. Especially, the fluorescence lifetime, τ, gives the hydration state in the first coordination sphere of the metal ion. Stumpf et al. reported on the solvation of the Eu-perchlorate and -triflate salts and the ligand exchange reaction in 1-butyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide ([C4mim][Tf2N]) by TRLFS.32 The hydration properties of Eu(Tf2N)3 in Tf2N-based IL were reported by Brandner et al., indicating that the added water in the solution binds quantitatively to Eu(III) ion.35 Furthermore, Ansari et al. reported that the complexation of Ln(Tf2N)3 (Ln = lanthanides) with nitrate in wet [C4mim][Tf2N] proceeds via the replacement of water molecules from the inner solvation spheres of Ln(III) ions.37,38 The coordination environment of Ln(III) ion in ILs was well studied,40 whereas the interaction between hydrophobic lanthanide chelates and other potential ligands such as water, halide ions, and IL components in ILs has seldom been documented.

The number of coordinated water molecules (nH2O) of the central Eu(III) ion in various complexes can be estimated by the following equation:41

 
nH2O = 1.05(kH2O − kD2O), (1)
where kH2O and kD2O (k = 1/τ) are the fluorescence decay constants in H2O- and D2O-containing solvents, respectively. The uncertainty in the calculated values of nH2O is approximately ±0.5. Although modified equations having uncertainties <0.5 have been reported,42 those equations include contributions to quenching from bulk water outside the first coordination sphere.35 The calculation method for eqn (1) is appropriate for evaluating the first coordination sphere of Eu(III) ions in the IL and organic solutions.

Recently, one of the present authors studied the distribution of 2-thenoyltrifluoroacetone (Htta) and its nickel(II) and copper(II) chelates between the 1-alkyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide ([Cnmim][Tf2N]; Fig. 1) phase and the aqueous phase to clarify the specific solvent effect of ILs.27 The values of the distribution constants of the neutral metal chelates in IL systems were evaluated on the basis of the regular solution theory. Additionally, the present authors have found the solvation of the neutral Eu(III)-tta chelate (Eu(tta)3) in [C4mim][Tf2N] by TRLFS and infrared absorption spectroscopy, and proposed specific solute–solvent interactions between the Eu(III) chelate and [C4mim][Tf2N].28


image file: c6ra27208h-f1.tif
Fig. 1 Chemical structures of ionic liquids employed in this study.

In the present study, the extraction constants for both neutral and anionic Eu(III) chelates with Htta in the [Cnmim][Tf2N] systems where n = 6 and 8 were determined by analyzing the distribution equilibrium. The effect of the ILs on the distribution constant of Eu(tta)3 (KD,M) was evaluated with the aid of the regular solution theory using the two-phase stability constant of the chelate (KD,Mβ3). The hydration state in the first coordination sphere of Eu(tta)3 in a series of [Cnmim][Tf2N] (n = 2–10) and in an organic solvent containing different concentrations of [C4mim][Tf2N] was examined by TRLFS. Furthermore, the effect of the water and Tf2N− concentrations on the hydration of Eu(tta)3 in [C2mim][Tf2N, ClO4] (mixed solvent of [C2mim][Tf2N] with 1-ethyl-3-methylimidazolium perchlorate, [C2mim][ClO4]; Fig. 1) was investigated to clarify the role of the Tf2N− anions in the IL–water distribution system. A stable solvated species of the Eu(III) chelate in the presence of [C4mim][Tf2N] was measured by electrospray ionization mass spectrometry (ESI-MS).

Experimental

Reagents

The ILs, [Cnmim][Tf2N] (n = 2, 4, 6, 8, and 10) and 1-butyl-2,3-dimethylimidazolium bis(trifluoromethanesulfonyl)imide ([C4dmim][Tf2N]), were synthesized and purified in the same manner as described previously.28 The hydrophilic IL, [C2mim][ClO4], was synthesized from 1-ethyl-3-methylimidazolium ethyl sulfate and lithium perchlorate according to the published procedure.43 An acidic chelating reagent, Htta, was obtained from Dojindo Laboratories (Japan, 98% purity), and was used without further purification. A hydrated Eu(III) chelate, [Eu(tta)3(H2O)3], was synthesized according to the published method.44 Yield 26.9%. Anal. calc. for EuC24H18F9S3O9: Eu, 17.48; C, 33.15; H, 2.09; N, 0.00. Found: Eu, 17.18; C, 33.48; H, 2.09; N, 0.00%. Three water molecules in the hydrated complex were confirmed by Karl Fischer titration in anhydrous toluene. All other chemicals used were of analytical or guaranteed reagent grade, and were used as received. High purity deionized water (18.2 MΩ cm) was used throughout this study.

Distribution procedure

An aliquot of an aqueous solution containing 1.0 × 10−4 mol dm−3 Eu(III), 1.0 × 10−1 mol dm−3 LiCl, and 1.0 × 10−2 mol dm−3 acetate buffer was shaken for 30–90 min with a [Cnmim][Tf2N] solution containing 1.0 × 10−3 to 1.6 × 10−2 mol dm−3 Htta at 25 ± 1 °C. After phase separation by centrifugation (5000 rpm), the equilibrium pH value in the aqueous phase was measured. The Eu(III) concentration in the aqueous phase was determined by inductively coupled plasma mass spectrometry (Hewlett Packard HP 4500 or PerkinElmer NexION 300X). The Eu(III) concentration in the [Cnmim][Tf2N] phase was determined in the same manner after back-extraction with 1 mol dm−3 HNO3. The distribution ratio (D) of Eu(III) was calculated from the Eu(III) concentrations in both phases.

Time-resolved laser-induced fluorescence spectroscopy

Sample solutions containing 1.0 × 10−4 mol dm−3 Eu(III) chelate were prepared by dissolving an appropriate amount of solid [Eu(tta)3(H2O)3] in [Cnmim][Tf2N] (n = 2, 4, 6, 8, and 10), [C4dmim][Tf2N], or organic solvents such as diisopropyl ether (DIPE), isobutyl methyl ketone (MIBK), benzene, and 1,2-dichloroethane (DCE), which were pre-saturated with H2O or D2O. To prepare the solution of [Eu(tta)3(D2O)3], a small amount of [Eu(tta)3(H2O)3] was dissolved in D2O-saturated solvents, which contain large excess of D2O over H2O arising from solid [Eu(tta)3(H2O)3]. The sample solutions of [Eu(tta)3(D2O)3] were covered with D2O until just before measurement in order to prevent isotope exchange with atmospheric water. Mixed solvents were prepared as given below, and used to examine the effect of the water and Tf2N− concentrations in ILs on the hydration number of Eu(tta)3. The water concentration in [C2mim][Tf2N, ClO4] and [C2mim][ClO4] was adjusted to be 5.0 (9.0 vol%) or 20 (36 vol%) mol dm−3 by adding water, while the Tf2N− concentration in [C2mim][Tf2N, ClO4] was kept constant at 0.50 mol dm−3 (13 vol%). On the other hand, the Tf2N− concentration in sample solutions was made to vary from 0 to 1.7 (50 vol%) mol dm−3 by dilution of [C4mim][Tf2N] with DCE.

The fluorescence spectrum and lifetime of the Eu(III) chelate in [Cnmim][Tf2N], the organic solvents, and the mixed solvents were measured using a pulse-laser detection system. The excitation pulse used in this study was obtained from the fourth harmonic of a Nd:YAG laser (Quantel) coupled with an optical parametric oscillator unit (Opotek Inc.) and the second harmonic of a Ti:sapphire laser (Tsunami, Spectra-Physics) coupled with a regenerative amplifier (Spitfire, Spectra-Physics) and a frequency doubler/pulse selector (model 3890, Spectra-Physics) to increase the output energy and to convert the wavelength of the laser light to 394 nm. For the measurements by the Nd:YAG laser, the pulse width was about 5 ns and the laser power at the sample location was generally 1–3 mJ per pulse at a repetition rate of 10 Hz. For the measurements by the Ti:sapphire laser, the pulse width, the laser power at the sample location, and the repetition rate were 130 fs, 0.1–0.5 mJ per pulse, and 100 Hz, respectively. The fluorescence spectrum was measured by a time-gated ICCD camera (iStar, Andor Technology), and multiple measurements were performed. The gate width and step were both 100 μs and the initial delay was 10 or 10.5 μs. The fluorescence emission of the 5D0 → 7F2 transition at 613 nm was processed using a least-squares fitting to obtain the fluorescence lifetime and the decay constant of the Eu(III) chelate.

Electrospray ionization mass spectrometry

The sample solution was prepared by dissolving 3.0 × 10−2 mol dm−3 [Eu(tta)3(H2O)3] in water-saturated DCE containing 1.0 vol% [C4mim][Tf2N]. The mass spectrum of [Eu(tta)3(H2O)3] in the [C4mim][Tf2N]–DCE-mixed solvent was measured by ESI-MS (JEOL JMS-T100TD) immediately after sample dilution (100-fold) with pure DCE. The measurements were carried out in negative ion mode, and operating parameters were as follows: needle voltage, −2350 V; ring lens voltage, −10 V; orifice 1 voltage, −30 V; orifice 2 voltage, −5 V; desolvation temperature, 250 °C; orifice 1 temperature, 80 °C.

Results and discussion

Distribution equilibrium of Eu(III) chelates between IL and water

The distribution ratio of Eu(III) with 5.0 × 10−3 mol dm−3 Htta in [Cnmim][Tf2N] was investigated as a function of pH in the aqueous phase. The average recovery of Eu(III) after the extraction in [C6mim][Tf2N] and [C8mim][Tf2N] was 95%. The D values in the pH region of 3–5 decreased in the following order: [C8mim][Tf2N] ≈ [C6mim][Tf2N] ≫ [C4mim][Tf2N]. This suggests that the hydrophobic property of the ILs or the mutual solubility with water is an important factor in the distribution of Eu(III) chelates. Since the slopes of log[thin space (1/6-em)] D vs. pH plots ranged from 3 to 4 in each IL, it is found that 3–4 protons take part in the distribution equilibrium of Eu(III) chelates.

Hence, given that Eu(III) is extracted with Htta in [Cnmim][Tf2N] as a mixture of neutral Eu(tta)3 and anionic Eu(tta)4− chelates as reported previously,23,28 the distribution ratio of Eu(III) can be expressed as follows:

 
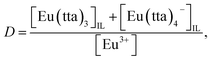image file: c6ra27208h-t1.tif(2)
where the subscript IL denotes the IL phase. The distribution equilibria and the extraction constants of the neutral (Kex,3) and anionic (Kex,4) chelates can be written as:
 
Eu3+ + 3HttaIL ⇌ Eu(tta)3,IL + 3H+, (3)
 
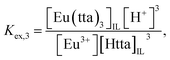image file: c6ra27208h-t2.tif(4)
and
 
Eu3+ + 4HttaIL + Tf2N−IL ⇌ Eu(tta)4−IL + 4H+ + Tf2N−, (5)
 
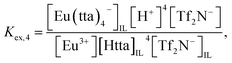image file: c6ra27208h-t3.tif(6)
respectively. Given that [Tf2N−] and [Tf2N−]IL for the respective ILs are constant under the stated conditions, eqn (6) may be rewritten as follows:
 
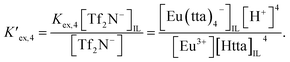image file: c6ra27208h-t4.tif(7)

From eqn (2), (4) and (7), the following equation can be derived:

 
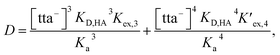image file: c6ra27208h-t5.tif(8)
where [tta−], KD,HA, and Ka are the concentration of tta− dissociated in the aqueous phase, the distribution constant of Htta, and the acid-dissociation constant of Htta, respectively. The constants used in this study were Ka = 10−6.33 (ref. 45) and KD,HA = 101.61, 101.68, and 101.64 for [C4mim][Tf2N], [C6mim][Tf2N], and [C8mim][Tf2N],27 respectively. The value for the tta− concentration in the aqueous phase can be calculated as follows:
 
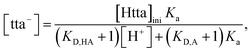image file: c6ra27208h-t6.tif(9)
where [Htta]ini and KD,A are the initial concentration of Htta in [Cnmim][Tf2N] and the apparent distribution constant of tta−, respectively. The KD,A values used were 100.96, 101.18, and 101.40 for [C4mim][Tf2N], [C6mim][Tf2N], and [C8mim][Tf2N],27 respectively.

To determine the extraction constants of the Eu(III) chelates, the distribution equilibria in the [Cnmim][Tf2N] systems were examined in detail. Fig. 2 shows the distribution ratio of Eu(III) as a function of the tta− concentration in the aqueous phase (pH 2.5–5.4) at the different concentrations of Htta in [Cnmim][Tf2N]. The slopes of the plots increased from 3 to 4 at the lower and higher tta− concentration, respectively. Therefore, in the [Cnmim][Tf2N] systems, Eu(III) was extracted into [Cnmim][Tf2N] as the neutral Eu(tta)3 and the anionic Eu(tta)4− chelates. The values of Kex,3 and K′ex,4 in the [Cnmim][Tf2N] systems were determined by a non-linear least-squares fitting of the plots, and the results are shown in Table 1. The Kex,3 values in the organic solvent systems were calculated from the distribution data in the respective references for DIPE,46 MIBK,47,48 benzene,46 and DCE.49 Additionally, the two-phase stability constant, KD,Mβ3, can be calculated from the Kex,3 value as follows:

 
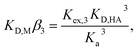image file: c6ra27208h-t7.tif(10)
where KD,M and β3 represent the distribution constant of the neutral Eu(tta)3 chelate and the overall formation constant of a 1[thin space (1/6-em)]:[thin space (1/6-em)]3 chelate in the aqueous phase, respectively. The calculated KD,Mβ3 values are shown in Table 1. The values of both Kex,3 and K′ex,4 in the [Cnmim][Tf2N] systems increase with an increase in IL cation 1-alkyl chain length. This result indicated that the enhanced D values for Eu(III) in [C6mim][Tf2N] and [C8mim][Tf2N] are caused by an increase in the extraction constants of both the neutral and the anionic Eu(III) chelates. The Kex,3 values in the [Cnmim][Tf2N] systems are higher than those in the DIPE, MIBK, benzene, and DCE systems. This finding is ascribed to the large values of KD,MKD,HA−3 in the [Cnmim][Tf2N] system because Kex,3 is described by KD,Mβ3Ka3KD,HA−3 as shown in eqn (10). In a series of [Cnmim][Tf2N], because the KD,HA values are almost independent of the 1-alkyl chain length of the IL cation, the Kex,3 values depend solely on KD,M. Thus, the higher values of Kex,3 in [C6mim][Tf2N] and [C8mim][Tf2N] were attributed to the respective KD,M values. In contrast, the K′ex,4 values were affected by the solubility products (Ksp = [Cnmim+] × [Tf2N−]) of the ILs because K′ex,4 is derived from the anion-exchange extraction constant shown in eqn (6). The Ksp value of [Cnmim][Tf2N] decreased with an increase in the 1-alkyl chain length of the IL cation, i.e., 2.9 × 10−4 > 2.8 × 10−5 > 3.5 × 10−6 mol2 dm−6 for [C4mim][Tf2N], [C6mim][Tf2N], and [C8mim][Tf2N],50 respectively. The distribution of the anionic Eu(tta)4− chelate, K′ex,4, increased with a decrease in Tf2N− concentration in the aqueous phase in accord with the equilibrium shift (Le Chatelier's principle).


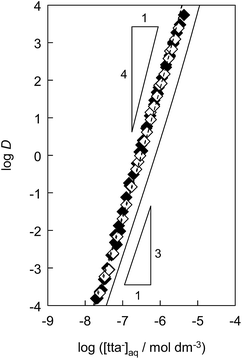image file: c6ra27208h-f2.tif
Fig. 2 Distribution ratio of Eu(III) as a function of tta− concentration in the aqueous phase in the [C4mim][Tf2N]28 (solid line), [C6mim][Tf2N] (♦), and [C8mim][Tf2N] (◇) systems. The triangles express the respective slopes. Initial concentration of Htta was 1.0 × 10−3 to 1.6 × 10−2 mol dm−3. Aqueous phase pH was 2.5–5.4. The dashed lines were obtained by a non-linear least-squares fitting.
Table 1 Extraction constants of Eu(tta)3 and Eu(tta)4−, distribution constants of the enol form of 2-thenoyltrifluoroacetone (Htta), and the two-phase stability constants of Eu(tta)3 in the Eu(III)–Htta–[Cnmim][Tf2N] and –organic solvent systems at 25 °C
Solvent δo/J1/2 cm−3/2 δo,w/J1/2 cm−3/2 log[thin space (1/6-em)]Kex,3 log[thin space (1/6-em)]K′ex,4 log[thin space (1/6-em)]KD,HE log(KD,Mβ3)
a Calculated from standard molar enthalpy of vaporization53 and density.54b Ref. 28.c Ref. 27.d Calculated from standard molar enthalpy of vaporization53 and density.55e Calculated from ref. 46.f Calculated from ref. 47 and 48.g Calculated from ref. 48.h Calculated from ref. 49.
[C4mim][Tf2N] 21.7a 22.0 −5.51b −8.14b 3.04 ± 0.05c 18.3b
[C6mim][Tf2N] 21.3a 21.5 −4.70 ± 0.05 −6.46 ± 0.06 3.22 ± 0.06c 19.3
[C8mim][Tf2N] 20.5d 20.7 −4.68 ± 0.06 −6.24 ± 0.06 3.29 ± 0.08c 19.2
DIPE 14.4 14.5 −5.76e — 3.14e 17.8
MIBK 17.2 17.5 −6.01f — 3.72g 19.9b
Benzene 18.7 18.8 −8.01e — 3.39e 15.8b
DCE 20.0 20.0 −8.33h — 3.48h 15.7b

Evaluation of the KD,M value based on the regular solution theory

The values of KD,Mβ3 obtained for [Cnmim][Tf2N] were close to those obtained for oxygen-containing organic solvents such as MIBK and DIPE (Table 1). Because β3 is independent of the extraction solvents, the effect of ILs on Kex,3 can be discussed using KD,Mβ3. Hence, the order of KD,M values becomes as follows: MIBK > [C6mim][Tf2N] ≈ [C8mim][Tf2N] > [C4mim][Tf2N] > DIPE > benzene ≈ DCE.

Given that β-diketones exist in solution, including IL solutions, as a mixture of the keto and enol forms, the distribution constant of the enol form (KD,HE) as a proton complex in various solvents was calculated27,46,48,49 and used for the discussion. The distribution constant of a solute, expressed on the mole fraction scale 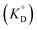image file: c6ra27208h-t8.tif, can be written using a modified equation based on the regular solution theory:51,52

 
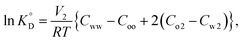image file: c6ra27208h-t9.tif(11)
where V and C are the molar volume and the cohesive energy density, respectively. The subscripts 2, w, and o denote the solute, water, and organic solvent, respectively, and the terms Co2 and Cw2 stand for the cohesive energy density between the solvent and solute molecules. If the interactions between the neutral solute and organic solvent molecules are caused mainly by their dispersion forces, the geometric mean approximation for the solubility parameter (δ) is applicable, i.e., Co2 ≈ δoδ2. Hence, eqn (11) can be rewritten as:
 
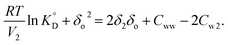image file: c6ra27208h-t10.tif(12)

The solubility parameter of a water-saturated organic solvent (δo,w) was calculated using the conventional solubility parameter for the aqueous solution (δw = 35.8 J1/2 cm−3/2) as follows:

 
δo,w = ϕoδo + ϕwδw, (13)
where ϕ is the volume fraction. Plots of the left-hand side of eqn (12) using δo,w instead of δo versus δo,w are expected to be a straight line. The apparent solubility parameter of the solute (δ2) can be obtained from the slope. The solubility parameters of [Cnmim][Tf2N] (δIL) were calculated from the standard molar enthalpies of vaporization53 and the densities,54,55 and are listed in Table 1. 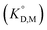The values of image file: c6ra27208h-t11.tif for the enol form of Htta image file: c6ra27208h-t12.tif and Eu(tta)3 image file: c6ra27208h-t13.tif were calculated, and the molar volume of Htta, 160 cm3 mol−1, was taken from the literature.56 The molar volume of the Eu(tta)3 chelate was estimated to be 448 cm3 mol−1 from an empirical relation between that of Htta and Hf(tta)4.57,58

Fig. 3 shows the plots based on eqn (12) for the neutral Eu(tta)3 chelate in [Cnmim][Tf2N] and various organic solvents including benzene, DCE, DIPE, and MIBK46–49,59 along with the enol form of Htta as a proton complex. Because of the lack of a reliable value of β3 for Eu(tta)3, the 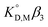image file: c6ra27208h-t14.tif value was used instead of 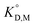image file: c6ra27208h-t15.tif for the subsequent discussion. A linear relationship was observed for the enol of Htta in all of the organic solvents including [Cnmim][Tf2N]. This result indicated that the [Cnmim][Tf2N] solutions of the enol of Htta behave like a regular solution as observed in conventional organic solutions. The same is true for the evaluation of the distribution constant of the enol form of Htta expressed on the molar concentration scale.27 Consequently, the value of δ2 for the enol form of Htta was obtained as 18.6 ± 0.5 J1/2 cm−3/2 from the slope of the straight line.


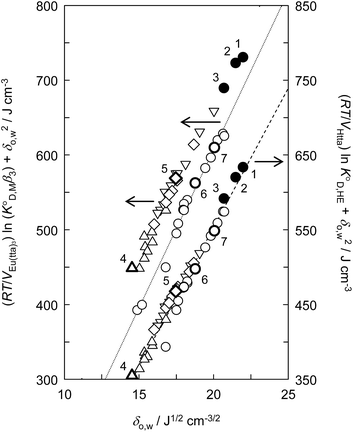image file: c6ra27208h-f3.tif
Fig. 3 Evaluation of the effect on the distribution constant of the neutral Eu(tta)3 chelate and the distribution constant of the enol form of Htta on the basis of the regular solution theory. (●), [Cnmim][Tf2N]; (○), alkanes, aromatic hydrocarbons, and chlorohydrocarbons;46,49 (◇), ketones;47,48 (△), ethers;46 (▽), esters.47,59 (1), [C4mim][Tf2N]; (2), [C6mim][Tf2N]; (3), [C8mim][Tf2N]; (4), DIPE; (5), MIBK; (6), benzene; (7), DCE. The respective straight lines were obtained by a least-squares fitting of the Eu(tta)3 chelate for alkanes, aromatic hydrocarbons, and chlorohydrocarbons (dotted line) and for the enol form of Htta (dashed line).

In contrast to the enol of Htta, the plots for the neutral Eu(tta)3 chelate in [Cnmim][Tf2N] and in oxygen-containing organic solvents such as ketones, ethers, and esters show a large positive deviation from the straight line obtained for alkanes, aromatic hydrocarbons, and chlorohydrocarbons, which are nonpolar or inert solvents. This deviation clearly demonstrates the existence of specific solute–solvent interactions between Eu(tta)3 and [Cnmim][Tf2N], i.e., inner- and/or outer-sphere solvation effects (cf. Fig. S1†). Since such specific interactions with Eu(tta)3 cannot be generated by the inert solvent molecules, it is expected that the slope of the straight line for Eu(tta)3 gives its δ2 value in those inert solvents. The value obtained, 21.1 ± 0.6 J1/2 cm−3/2, which is much larger than that of the enol, reflects the hydrated states of Eu(tta)3 in those solvents as will be discussed later by TRLFS. On the other hand, the values of δ2 for Eu(tta)3 calculated from the linear relationship for ketones, ethers, and esters were 20.3 ± 0.6, 17.8 ± 3.1, and 18.2 ± 0.7 J1/2 cm−3/2, respectively, which are significantly smaller than that in the inert solvents. Although the reliable δ2 value could not be obtained in [Cnmim][Tf2N] because of only 3 plots, the value was estimated to be about 17 J1/2 cm−3/2 and was relatively close to those in the oxygen-containing organic solvents. These results implied that the dehydration of the Eu(tta)3 chelate occurred in the oxygen-containing organic solvents and also [Cnmim][Tf2N].

TRLFS of [Eu(tta)3(H2O)3] in ILs

To clarify such specific solvation effect in ILs, the hydration state in the first coordination sphere of the neutral Eu(III) chelate in [Cnmim][Tf2N] was examined by TRLFS. The fluorescence decay of [Eu(tta)3(H2O)3] dissolved in a series of [Cnmim][Tf2N] (n = 2, 4, 6, 8, and 10) and in [C4dmim][Tf2N] saturated with H2O or D2O was measured by the excitation at 394 nm, along with that in DIPE, MIBK, benzene, and DCE (the fluorescence spectra of [Eu(tta)3(H2O)3] are shown in Fig. S2 and S4† and the fluorescence decay curves are shown in Fig. S3 and S5†). All decay curves were well fitted by a single exponential function as expected. Table 2 shows the mean fluorescence decay constants in those solvents saturated with H2O and D2O (kH2O and kD2O, respectively) and the mean nH2O values, along with the estimated 5D0 radiative decay constants (krad) obtained by summing over the radiative constants krad,0j for each 5D0 → 7Fj transition as described in the ref. 60 and 61. The krad,0j values were calculated from the ratios of the integrated intensities of the 5D0 → 7Fj transitions to that of the 5D0 → 7F1 and the magnetic-dipole transition rate constant, krad,01 = 0.05 ms−1.60 The krad values were less affected by the solvents. In contrast, the kD2O value varies depending on the solvents and is considerably higher than krad, which is consistent with the reported result in the IL.35 There is little change in the fluorescence intensity as well as the fluorescence lifetime and the hydration number of the Eu(tta)3 chelate in each IL for the three measurements. The uncertainty in the decay constants presented in Table 2 is the standard deviation between replicate experiments. Furthermore, the fluorescence lifetime and the hydration number were without dependence on the laser power from 0.005 to 1 mJ per pulse. These demonstrate that the decomposition of the Eu(tta)3 chelate and IL components by the laser irradiation was negligible under the present conditions.
Table 2 Fluorescence decay constants, the number of coordinated water molecules, and radiative decay constants for [Eu(tta)3(H2O)3] dissolved in [Cnmim][Tf2N] and organic solvents saturated with H2O or D2O
Solvent kH2O/ms−1 kD2O/ms−1 nH2O krad/ms−1
a Ref. 28.
[C2mim][Tf2N] 2.05 ± 0.04 2.06 ± 0.04 0 0.56 ± 0.01
[C4mim][Tf2N] 2.25a 2.02a 0.2a 0.75 ± 0.01
[C6mim][Tf2N] 1.89 ± 0.01 1.88 ± 0.01 0 0.68 ± 0.01
[C8mim][Tf2N] 1.88 ± 0.02 1.91 ± 0.01 0 0.60 ± 0.01
[C10mim][Tf2N] 1.87 ± 0.04 1.88 ± 0.03 0 0.60 ± 0.01
[C4dmim][Tf2N] 1.92 ± 0.04 1.92 ± 0.02 0 0.56 ± 0.01
DIPE 3.43 ± 0.06 2.48 ± 0.05 1.0 0.48 ± 0.01
MIBK 3.18 ± 0.03 1.97 ± 0.02 1.3 0.54 ± 0.01
Benzene 6.05a 3.75a 2.4a 0.60 ± 0.02
DCE 5.09a 3.76a 1.4a 0.62 ± 0.01

The [Eu(tta)3(H2O)3] complex was almost completely dehydrated in the series of [Cnmim][Tf2N] and [C4dmim][Tf2N] saturated with water, whereas the hydrated complex was observed in DIPE, MIBK, benzene, and DCE. These results were in agreement with those obtained by TRLFS of the Eu(tta)3 chelate extracted with Htta into the same such solvents.28 In addition, the presence of Cl− had no effect on the dehydration of [Eu(tta)3(H2O)3]. Because the nH2O values in [Cnmim][Tf2N] and [C4dmim][Tf2N] were independent of the 1-alkyl chain length and the type of the IL cation, the cause of the dehydration observed in all of the ILs is ascribed to the common IL anion, Tf2N−. Considering that the coordination number of Eu(III) is usually 8 or 9 in solution, it was, therefore, plausible that the Tf2N− anions could coordinate to the neutral Eu(tta)3 chelate in [Cnmim][Tf2N] and replace the coordinated water molecules of [Eu(tta)3(H2O)3]. Although the donor number of [Cnmim][Tf2N], 7.5–11.2 kcal mol−1,62 is significantly smaller than those of DIPE (19.0 kcal mol−1) and MIBK (16.0 kcal mol−1),63 it should be noted that the pKa value of the conjugate acid of Tf2N−, 1.7,64 is much higher than those of DIPE (−4.30)65 and MIBK. If the dehydrated adduct like [Eu(tta)3(Tf2N)]− is formed in the IL, it may be more stable than the hydrated chelate like [Eu(tta)3(H2O)3] in [Cnmim][Tf2N] because the adduct is more hydrophobic and is one of the IL component.

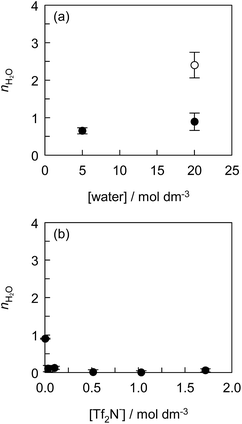
The effect of the water concentration in ILs on the solvation of Eu(tta)3 was investigated using the mixed solvent of [C2mim][Tf2N] with hydrophilic IL, [C2mim][ClO4]. Fig. 4(a) shows the nH2O value as a function of water concentration in [C2mim][Tf2N, ClO4] and [C2mim][ClO4]. The fluorescence spectra, the fluorescence decay curves, and the values of kH2O, kD2O, and nH2O are shown in Fig. S6, S7 and Table S1,† respectively. The Eu(tta)3 chelate exists as di- or tri-hydrates in [C2mim][ClO4] containing 20 mol dm−3 water, indicating that the ClO4− anion does not give rise to the dehydration of Eu(tta)3 in the IL. In contrast, mono-hydrated Eu(tta)3 chelate was formed in [C2mim][Tf2N, ClO4] containing 0.50 mol dm−3 Tf2N− and 20 mol dm−3 water. This means that the Tf2N− anions displaced the coordinated water molecules of [Eu(tta)3(H2O)3]. The nH2O value of Eu(tta)3 in the presence of 0.50 mol dm−3 Tf2N− decreased with a decrease in water concentration in [C2mim][Tf2N, ClO4]. Therefore, these observations prove the ligand displacement between water and Tf2N− molecules in the Eu(tta)3 chelate in ILs.


image file: c6ra27208h-f4.tif
Fig. 4 Effect of water concentration in [C2mim][Tf2N, ClO4] (●) and [C2mim][ClO4] (○) (a) and effect of Tf2N− concentration in DCE (b) on the number of coordinated water molecules (nH2O) of the Eu(tta)3 chelate. (a) Tf2N− concentration in the [C2mim][Tf2N, ClO4] solution was kept constant at 0.50 mol dm−3 and (b) the [C4mim][Tf2N]–DCE solution was saturated with water. The error bars represent the standard deviation of nH2O. Concentration of [Eu(tta)3(H2O)3] was 1.0 × 10−4 mol dm−3.

To make sure of the coordination ability of Tf2N− to Eu(tta)3, the effect of the Tf2N− concentration in DCE containing varying amounts of [C4mim][Tf2N] was investigated, and the results are shown in Fig. 4(b), S8, S9 and Table S2.† The partially-hydrated Eu(tta)3 chelate was found in DCE containing 0.10 vol% [C4mim][Tf2N] (3.4 × 10−3 mol dm−3 Tf2N−) saturated with water (1.3 × 10−1 mol dm−3). It is noteworthy that almost complete dehydration of [Eu(tta)3(H2O)3] was observed even in 1.0 vol% [C4mim][Tf2N] solution (3.4 × 10−2 mol dm−3 Tf2N−) saturated with water (1.3 × 10−1 mol dm−3). Therefore, [Eu(tta)3(H2O)3] was completely dehydrated in the mixed solvents of DCE with more than 3.4 × 10−2 mol dm−3 of Tf2N−. This result reveals that the coordination ability of Tf2N− to Eu(tta)3 is stronger than that of water in non-coordinating solvents in contrast to that of Tf2N− to Eu3+ ion in ILs.35 Jensen et al., reported that the hydrated [Eu(tta)2(H2O)2]+ and dehydrated Eu(tta)3 chelates were extracted from the aqueous phase containing 1 mol dm−3 NaClO4 into the IL, 1-butyl-3-methylimidazolium nonafluoro-1-butanesulfonate ([C4mim][NfO]), phase.66 Since the IL phase contained 10 mol dm−3 H2O and 1.6–2.3 mol dm−3 NfO− anion which is more hydrophobic than the Tf2N− anion, the hydrated chelate cation can be preferentially extracted by the ion-exchange of the IL component.

Assuming that three water molecules of [Eu(tta)3(H2O)3] were released by the coordination of m molecules of Tf2N− in the mixed solvent, the following equation is derived:

 
[Eu(tta)3(H2O)3]mix + mTf2Nmix−⇌ [Eu(tta)3(Tf2N)m]mixm− + 3H2Omix, (14)
where the subscript mix denotes the mixed solvent. The adduct formation constant (βs,m) with Tf2N− can be represented as follows:
 
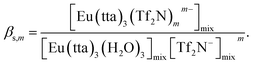image file: c6ra27208h-t16.tif(15)

The concentrations of [Eu(tta)3(Tf2N)]−, [Eu(tta)3(H2O)3], and Tf2N− in the mixed solvent were calculated from the nH2O value of Eu(tta)3 in DCE containing 1.0 and 3.0 vol% [C4mim][Tf2N], and the log[thin space (1/6-em)]βs,1 value was estimated to be 2.7. The βs,1 value obtained was dramatically higher than that of MIBK in chloroform (log[thin space (1/6-em)]βs,1 = 0.9) and carbon tetrachloride (log[thin space (1/6-em)]βs,1 = 1.6).67 The dissociated Tf2N− in solutions effectively coordinates to [Eu(tta)3(H2O)3] and displaces the coordinated water molecules. In the LLD systems, the solubility of Eu(tta)3 is enhanced in hydrophobic ILs by the formation of the hydrophobic anionic chelate resulting from the release of the coordinated water molecules of [Eu(tta)3(H2O)3]. Consequently, the coordination environment of Eu(III) chelates in ILs is quite different from that of Eu(III) ion.35

ESI-MS of [Eu(tta)3(H2O)3] in the presence of [C4mim][Tf2N]

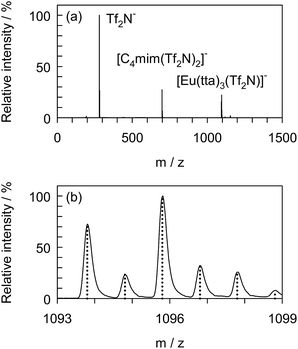
To confirm the formation of the adduct complex, [Eu(tta)3(Tf2N)]−, in the presence of [C4mim][Tf2N], negative ion ESI-MS was undertaken with [Eu(tta)3(H2O)3] dissolved in DCE containing 1.0 vol% [C4mim][Tf2N] serving as the sample solution. Fig. 5 shows the mass spectrum of the sample recorded just after 100-fold dilution with pure DCE. The high resolution mass spectrum covered the m/z range from 1093 to 1099 and the calculated mass spectrum for [Eu(tta)3(Tf2N)]− is represented by the dotted line. The full mass spectrum was normalized using the intensity at m/z of 280. Three clearly distinguishable peaks were observed at m/z of 280, 699, and 1096, which corresponded to Tf2N−, [C4mim(Tf2N)2]−, and [Eu(tta)3(Tf2N)]−, respectively. The experimental m/z and the intensity ratio were consistent with the theoretical values, indicating the existence of [Eu(tta)3(Tf2N)]− as a stable adduct.
image file: c6ra27208h-f5.tif
Fig. 5 Negative ion electrospray ionization mass spectrum of [Eu(tta)3(H2O)3] dissolved in DCE containing [C4mim][Tf2N] (a) and the high resolution mass spectrum (solid line) and the calculated mass spectrum (dotted line) for [Eu(tta)3(Tf2N)]− (b). Sample, 3.0 × 10−4 mol dm−3 [Eu(tta)3(H2O)3], 3.4 × 10−4 mol dm−3 [C4mim][Tf2N].

Conclusions

The special role of the Tf2N− anions in the IL–water distribution of Eu(III)–tta chelates was elucidated in this paper. The equilibrium constants, Kex,3 and K′ex,4 for the distribution of Eu(tta)3 and Eu(tta)4−, respectively, depended on the hydrophobicities of the ILs. The former were attributed only to the distribution constant of Eu(tta)3 (KD,M) while the latter were also affected by the solubility product of the IL in the aqueous phase. The KD,M values in [Cnmim][Tf2N] were significantly enhanced by the specific solvation effect. The TRLFS study indicated that such specific solvation effect in ILs was caused by the replacement of the coordinated water molecules of [Eu(tta)3(H2O)3] with Tf2N−. The coordination ability of Tf2N− toward [Eu(tta)3(H2O)3] was confirmed in DCE. Furthermore, a most probable adduct species, [Eu(tta)3(Tf2N)]−, was found by ESI-MS. Accordingly, the Eu(III) chelates can be present as IL components such as [Eu(tta)3(Tf2N)]−·Cnmim+ and Eu(tta)4−·Cnmim+ in the ILs. In LLD, the hydrophobic metal chelate is effectively formed by the coordination of Tf2N− in water-saturated ILs, resulting in the enhancement in the distribution constant of the neutral chelates. The knowledge obtained in this study can lead to the further progress in the development of IL distribution systems of metal ions.

Acknowledgements

The authors thank Dr Takumi Saito of The University of Tokyo for helping with TRLFS measurements. The Center for Instrumental Analysis at Ibaraki University is acknowledged for the elemental analysis and NMR measurements. This research was supported in part by JSPS KAKENHI Grant Numbers 26810078, 25620108, and 25288064.

Notes and references

  1. M. Petkovic, K. R. Seddon, L. P. N. Rebelo and C. S. Pereira, Chem. Soc. Rev., 2011, 40, 1383–1403 RSC.
  2. M. D. Joshi and J. L. Anderson, RSC Adv., 2012, 2, 5470–5484 RSC.
  3. T. D. Ho, C. Zhang, L. W. Hantao and J. L. Anderson, Anal. Chem., 2014, 86, 262–285 CrossRef CAS PubMed.
  4. A. Rehman and X. Zeng, RSC Adv., 2015, 5, 58371–58392 RSC.
  5. D. R. MacFarlane, J. M. Pringle, P. C. Howlett and M. Forsyth, Phys. Chem. Chem. Phys., 2010, 12, 1659–1669 Search PubMed.
  6. H. Liu, Y. Liu and J. Li, Phys. Chem. Chem. Phys., 2010, 12, 1685–1697 RSC.
  7. M. V. Fedorov and A. A. Kornyshev, Chem. Rev., 2014, 114, 2978–3036 Search PubMed.
  8. J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508–3576 CrossRef CAS PubMed.
  9. S. T. Keaveney, J. B. Harper and A. K. Croft, RSC Adv., 2015, 5, 35709–35729 RSC.
  10. P. N. Reddy, P. Padmaja, B. V. S. Reddy and G. Rambabu, RSC Adv., 2015, 5, 51035–51054 RSC.
  11. J. Estager, J. D. Holbrey and M. Swadźba-Kwaśny, Chem. Soc. Rev., 2014, 43, 847–886 RSC.
  12. E. Santos, J. Albo and A. Irabien, RSC Adv., 2014, 4, 40008–40018 RSC.
  13. K. Goossens, K. Lava, C. W. Bielawski and K. Binnemans, Chem. Rev., 2016, 116, 4643–4807 CrossRef CAS PubMed.
  14. I. Billard, A. Ouadi and C. Gaillard, Anal. Bioanal. Chem., 2011, 400, 1555–1566 CrossRef CAS PubMed.
  15. N. Hirayama, Solvent Extr. Res. Dev., Jpn., 2011, 18, 1–14 CrossRef CAS.
  16. X. Sun, H. Luo and S. Dai, Chem. Rev., 2012, 112, 2100–2128 CrossRef CAS PubMed.
  17. F. Kubota, Y. Baba and M. Goto, Solvent Extr. Res. Dev., Jpn., 2012, 19, 17–28 CrossRef CAS.
  18. Z. Kolarik, Solvent Extr. Ion Exch., 2013, 31, 24–60 CrossRef CAS.
  19. C. Gaillard, M. Boltoeva, I. Billard, S. Georg, V. Mazan and A. Ouadi, RSC Adv., 2016, 6, 70141–70151 RSC.
  20. K. Shimojo, K. Kurahashi and H. Naganawa, Dalton Trans., 2008, 5083–5088 RSC.
  21. A. Rout and K. Binnemans, Dalton Trans., 2015, 44, 1379–1387 RSC.
  22. S. A. Ansari, P. K. Mohapatra, V. Mazan and I. Billard, RSC Adv., 2015, 5, 35821–35829 RSC.
  23. M. P. Jensen, J. Neuefeind, J. V. Beitz, S. Skanthakumar and L. Soderholm, J. Am. Chem. Soc., 2003, 125, 15466–15473 CrossRef CAS PubMed.
  24. K. Kidani, N. Hirayama and H. Imura, Anal. Sci., 2008, 24, 1251–1254 CrossRef CAS PubMed.
  25. K. Shimojo, H. Okamura, N. Hirayama, S. Umetani, H. Imura and H. Naganawa, Dalton Trans., 2009, 4850–4852 RSC.
  26. H. Okamura, N. Hirayama, K. Morita, K. Shimojo, H. Naganawa and H. Imura, Anal. Sci., 2010, 26, 607–611 CrossRef CAS PubMed.
  27. K. Kidani and H. Imura, Talanta, 2010, 83, 299–304 CrossRef CAS PubMed.
  28. H. Okamura, H. Sakae, K. Kidani, N. Hirayama, N. Aoyagi, T. Saito, K. Shimojo, H. Naganawa and H. Imura, Polyhedron, 2012, 31, 748–753 CrossRef CAS.
  29. H. Okamura, A. Ikeda-Ohno, T. Saito, N. Aoyagi, H. Naganawa, N. Hirayama, S. Umetani, H. Imura and K. Shimojo, Anal. Chem., 2012, 84, 9332–9339 CAS.
  30. H. Okamura, H. Takagi, T. Isomura, K. Morita, H. Nagatani and H. Imura, Anal. Sci., 2014, 30, 323–325 CrossRef CAS PubMed.
  31. M. Atanassova and V. Kurteva, RSC Adv., 2016, 6, 11303–11324 RSC.
  32. S. Stumpf, I. Billard, C. Gaillard, P. J. Panak and K. Dardenne, Radiochim. Acta, 2008, 96, 1–10 CrossRef CAS.
  33. J.-C. G. Bünzli, Chem. Rev., 2010, 110, 2729–2755 CrossRef PubMed.
  34. R. N. Collins, T. Saito, N. Aoyagi, T. E. Payne, T. Kimura and T. D. Waite, J. Environ. Qual., 2011, 40, 731–741 CrossRef CAS PubMed.
  35. A. Brandner, T. Kitahara, N. Beare, C. Lin, M. T. Berry and P. S. May, Inorg. Chem., 2011, 50, 6509–6520 CrossRef CAS PubMed.
  36. P. Thakur, J. L. Conca, C. J. Dodge, A. J. Francis and G. R. Choppin, Radiochim. Acta, 2013, 101, 221–232 CrossRef CAS.
  37. S. A. Ansari, L. Liu, P. D. Dau, J. K. Gibson and L. Rao, RSC Adv., 2014, 4, 37988–37991 RSC.
  38. S. A. Ansari, L. Liu and L. Rao, Dalton Trans., 2015, 44, 2907–2914 RSC.
  39. S. A. Ansari, P. K. Mohapatra, W. Verboom, Z. Zhang, P. D. Dau, J. K. Gibson and L. Rao, Dalton Trans., 2015, 44, 6416–6422 RSC.
  40. M. Atanassova, V. Kurteva and I. Dukov, RSC Adv., 2016, 6, 81250–81265 RSC.
  41. W. D. Horrocks Jr and D. R. Sudnick, J. Am. Chem. Soc., 1979, 101, 334–340 CrossRef.
  42. R. M. Supkowski and W. D. Horrocks Jr, Inorg. Chim. Acta, 2002, 340, 44–48 CrossRef CAS.
  43. M. Schmeisser, P. Keil, J. Stierstorfer, A. König, T. M. Klapötke and R. van Eldik, Eur. J. Inorg. Chem., 2011, 4862–4868 CrossRef CAS.
  44. R. G. Charles and R. C. Ohlmann, J. Inorg. Nucl. Chem., 1965, 27, 255–259 CrossRef CAS.
  45. T. Sekine, Y. Hasegawa and N. Ihara, J. Inorg. Nucl. Chem., 1973, 35, 3968–3970 CrossRef CAS.
  46. K. Akiba, Bunseki Kagaku, 1972, 21, 1630–1636 CrossRef CAS.
  47. K. Akiba and T. Kanno, J. Inorg. Nucl. Chem., 1980, 42, 273–276 CrossRef CAS.
  48. T. Wakabayashi, K. Takaizumi, K. Seto, N. Suzuki and K. Akiba, Bull. Chem. Soc. Jpn., 1968, 41, 1854–1858 CrossRef CAS.
  49. Y. Kitatsuji, Y. Meguro, Z. Yoshida, T. Yamamoto and K. Nishizawa, Solvent Extr. Ion Exch., 1995, 13, 289–300 CrossRef CAS.
  50. M. G. Freire, P. J. Carvalho, R. L. Gardas, I. M. Marrucho, L. M. N. B. F. Santos and J. A. P. Coutinho, J. Phys. Chem. B, 2008, 112, 1604–1610 CrossRef CAS PubMed.
  51. H. Imura and N. Suzuki, J. Radioanal. Nucl. Chem., 1985, 88, 63–73 CrossRef CAS.
  52. H. Imura and N. Suzuki, Talanta, 1985, 32, 785–790 CrossRef CAS PubMed.
  53. M. A. A. Rocha, C. F. R. A. C. Lima, L. R. Gomes, B. Schröder, J. A. P. Coutinho, I. M. Marrucho, J. M. S. S. Esperança, L. P. N. Rebelo, K. Shimizu, J. N. C. Lopes and L. M. N. B. F. Santos, J. Phys. Chem. B, 2011, 115, 10919–10926 CrossRef CAS PubMed.
  54. H. Shirota, T. Mandai, H. Fukazawa and T. Kato, J. Chem. Eng. Data, 2011, 56, 2453–2459 CrossRef CAS.
  55. C. Kolbeck, J. Lehmann, K. R. J. Lovelock, T. Cremer, N. Paape, P. Wasserscheid, A. P. Fröba, F. Maier and H.-P. Steinrück, J. Phys. Chem. B, 2010, 114, 17025–17036 CrossRef CAS PubMed.
  56. T. Wakahayashi, S. Oki, T. Omori and N. Suzuki, J. Inorg. Nucl. Chem., 1964, 26, 2255–2264 CrossRef CAS.
  57. E. M. Larsen, G. Terry and J. Leddy, J. Am. Chem. Soc., 1953, 75, 5107–5111 CrossRef CAS.
  58. T. Omori, T. Wakahayashi, S. Oki and N. Suzuki, J. Inorg. Nucl. Chem., 1964, 26, 2265–2270 CrossRef CAS.
  59. N. Suzuki, K. Akiba and T. kanno, Anal. Chim. Acta, 1968, 43, 311–320 CrossRef CAS.
  60. G. F. de Sá, O. L. Malta, C. d. M. Donegá, A. M. Simas, R. L. Longo, P. A. Santa-Cruz and E. F. da Silva Jr, Coord. Chem. Rev., 2000, 196, 165–195 CrossRef.
  61. L. D. Carlos, R. A. S. Ferreira, V. d. Z. Bermudez and S. J. L. Ribeiro, Adv. Mater., 2009, 21, 509–534 CrossRef CAS PubMed.
  62. M. Schmeisser, P. Illner, R. Puchta, A. Zahl and R. van Eldik, Chem.–Eur. J., 2012, 18, 10969–10982 CrossRef CAS PubMed.
  63. Y. Marcus, The Properties of Solvents, Wiley Series in Solution Chemistry, John Wiley & Sons Ltd, Chichester, England, 1998, vol. 4 Search PubMed.
  64. J. Foropoulos Jr and D. D. DesMarteau, Inorg. Chem., 1984, 23, 3720–3723 CrossRef.
  65. E. M. Arnett and C. Y. Wu, J. Am. Chem. Soc., 1962, 84, 1680–1684 CrossRef CAS.
  66. M. P. Jensen, M. Borkowski, I. Laszak, J. V. Beitz, P. G. Rickert and M. L. Dietz, Sep. Sci. Technol., 2012, 47, 233–243 CrossRef CAS.
  67. T. Sekine and D. Dyrssen, J. Inorg. Nucl. Chem., 1967, 29, 1457–1473 CrossRef CAS.

Footnote

† Electronic supplementary information (ESI) available: Fig. S1–S9, Tables S1 and S2. See DOI: 10.1039/c6ra27208h
This journal is © The Royal Society of Chemistry 2017