DFT study of NO adsorption on pristine graphene

Abstract

This study reports in detail the adsorption of NO exhaust gas on pristine graphene by a first-principle. Ten kinds of adsorption configurations were built for three different adsorption sites on graphene. Structure optimization was carried out using different approximation methods; we found that the optimal method was the PBEsol approximation under the GGA approximation, and the orbital cutoff was 6 Å. Optimal parameters were used to calculate the adsorption energy, charge Mulliken, electron density difference, LUMO HOMO, and projected density of states (PDOS) for these ten kinds of adsorption configurations. We found that the adsorption of NO molecules on graphene was a physical adsorption process, and electrons were transferred from graphene to a NO molecule. The optimal adsorption site of graphene indicated the B-site, followed by the T-site, and the least negative adsorbed position was the H-site. Meanwhile, adsorption energy analysis showed that O-end graphene was the most stable adsorption configuration.

---

1. Introduction

Graphene, made up of six-member rings, is a two-dimensional periodic lattice structure. Graphene can be warped into zero-dimensional fullerene, rolled up into one-dimensional carbon nanotubes, and stacked into three-dimensional graphite.^1,2 Ideally, graphene is a monolayer plane with a hexagonal type honeycomb lattice structure, in which carbon (C) atoms have a sp² hybrid orbital, meaning that each C atom has four bonds, and every C atom forms a σ-bond with the nearest neighbor three C atoms. The remaining p electrons, which are perpendicular to the surface of graphene, form π-bonds with the surrounding electrons. Graphene crystallites of high quality were fabricated by Andre G. and Konstantin N., who were awarded the Nobel Prize for Physics in 2010, by using the ‘Scotch-tape’ method, which was invented by Novoselov et al. in 2004.^3–5 Enormous amounts of research have been reported concerning the basic characterization of graphene, which used graphene as a carrier for various modifications.^4,6–9 Graphene, which has a particular nanostructure and excellent physical and chemical properties, has a wide range of applications in electronics, optics, magnetism, biomedicine, catalysis, energy storage, sensors, and other areas. Applications of graphene, especially in areas of environmental protection, have significant practicability and exploitability.

With the enhancement of people's awareness concerning environmental protection, automobile exhaust pollution has become a global issue due to rapid developments in the automobile industry. Automotive exhaust mainly includes hydrocarbons, nitrogen oxide, carbon monoxide, sulfur dioxide, solid suspended particles, etc.^10–12 Graphene as an adsorption material to deal with this exhaust has been confirmed by many experiments and research results.^13–16 From literature concerning graphene as an adsorption material, we found that most research focused on major emissions, such as CO, NO, and NO₂. Liu et al.¹⁷ found that CO adsorption energy could be enhanced by an electric field, and Choudhuri et al.¹⁸ also demonstrated that B–N doped graphene could heighten adsorption of NO, NO₂, CO, and CO₂. Based on our previous work, we used Density Functional Theory (DFT) methods to calculate NO, the main pollution gas from exhaust, on pristine graphene surface in this investigation. We finally pinpointed the stable adsorption sites; meanwhile, this paper provides a detailed analysis on electronic structures of the adsorption configurations. The results of this research can provide theoretical guidance for relevant experimental research.

2. Computational details

Adsorption of NO on pristine graphene was investigated by a first principle using the Dmol³ code. Using computer simulation we chose ten kinds of supercells without vacuum layers including 4 × 4 × 1, 5 × 5 × 1, 6 × 6 × 1, 7 × 7 × 1, 8 × 8 × 1, 9 × 9 × 1, 10 × 10 × 1, 11 × 11 × 1, and 12 × 12 × 1, and tried to determine the most stable supercell system. Furthermore, we carried out an optimization test of functions under the LDA and GGA approximates in the process of geometry optimization, and then chose the optimum one. Orbital cutoffs were also tested by the optimum functional, 0.006 smearing and 5 × 5 × 1 k-points.

In this computer simulation, the length of N–O bond was set as l_N–O = 1.17 Å.¹⁹ For this study, a NO molecule was adsorbed on pristine graphene surface, and the adsorption energy E_ad was defined as:

E_ad = E_total − (E_graphene + E_NO) (1)

where E_total was the total energy of NO adsorbed graphene system, and E_graphene, E_NO represented, respectively, the total energy of the pristine graphene and the free state of the NO molecule.

3. Results and discussion

3.1 Supercell chosen with calculation parameters at software default values

To obtain detailed comprehension of adsorption structures of NO on the graphene layer, it was necessary to perform a study on selection of a supercell. The C–C bond length of a pristine graphene unit cell was 1.42 Å.^20–22

In Table 1, the longest C–C bond lengths for pristine graphene supercells in the surface center region are 1.423, 1.422, 1.418, 1.419, 1.417, 1.416, 1.415, 1.415, and 1.414 Å, respectively. We found that the supercell 7 × 7 × 1 was the most appropriate one and the relative deviation was 0.000704. Meanwhile, a short time was spent on calculations for a hexagonal structure that included 96 atoms.

Table 1 Comparison of C–C bond lengths with experimental values under nine different supercell structures

Supercell	C–C (min.) (Å)	Relative deviation (%)	C–C (max.) (Å)	Relative deviation (%)	Exp. (Å)
4 × 4 × 1	1.418	−0.00141	1.423	0.00211
5 × 5 × 1	1.412	−0.00563	1.422	0.00141
6 × 6 × 1	1.415	−0.00352	1.418	−0.00141
7 × 7 × 1	1.414	−0.00423	1.419	−0.00070
8 × 8 × 1	1.413	−0.00493	1.417	−0.00211	1.420
9 × 9 × 1	1.413	−0.00493	1.416	−0.00282
10 × 10 × 1	1.413	−0.00493	1.415	−0.00352
11 × 11 × 1	1.413	−0.00493	1.415	−0.00352
12 × 12 × 1	1.413	−0.00493	1.414	−0.00423

---

3.2 Select functional and test orbital cutoff

During the process of geometric optimization, LDA and GGA were two kinds of common exchange–correlation energy approximation methods used. The structural optimization of pristine graphene using a 7 × 7 × 1 supercell was conducted by PWC, VWN under LDA, and PW91, BP, PBE, BLYP, BOP, VWN-BP, RPBE, HCTH, and PBEsol under GGA. The computational specific conditions are shown in Table 2.

Table 2 Bond length and energy calculated by different functionals under LDA/GGA and compared with the experimental value for the graphene supercell 7 × 7 × 1

		C–C (Å)	Relative deviation (%)	HOMO^a (eV)	LUMO^b (eV)	Δ^c (eV)
a HOMO: Highest Occupied Molecular Orbital.b LUMO: Lowest Unoccupied Molecular Orbital.c Δ: HOMO − LUMO.
LDA	PWC	1.418	−0.00141	−5.895	−5.738	−0.157
	VWN	1.417	−0.19230	−5.896	−5.739	−0.157
GGA	PW91	1.424	0.00282	−5.813	−5.789	−0.024
	BP	1.425	0.00352	−5.748	−5.721	−0.027
	PBE	1.425	0.00352	−5.786	−5.761	−0.025
	BLYP	1.428	0.00563	−5.596	−5.575	−0.021
	BOP	1.429	0.00634	−5.517	−5.493	−0.0.24
	VWN-BP	1.425	0.00352	−5.749	−5.722	−0.027
	RPBE	1.429	0.00634	−5.784	−5.755	−0.029
	HCTH	1.424	0.00282	−6.145	−6.118	−0.027
	PBEsol	1.423	0.00211	−5.782	−5.758	−0.024

---

By comparing the obtained results with experimental values, we found that LDA approximation methods were more applicable for calculating molecule bond length.^23,24 The C–C bond length was 1.418 Å as calculated by PWC, which was closer to the experimental value (1.420 Å). But, the LDA approximation had strong localization about the electron distributions; moreover, it wasn't suitable for analyzing the absolute value of the forbidden band width and the system binding energy. Generally, the semiconductor band gap computed by GGA was closer to the experimental values than when computed by LDA. Through comprehensive consideration of calculated and experimental values of the lattice constant and energy band gap, we selected the GGA approximation PBEsol functional to proceed with further work.

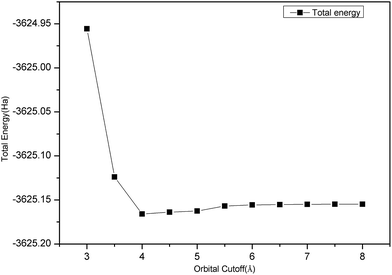
Fig. 1 clearly shows that the convergence test of the orbital cutoff was calculated using a GGA-PBEsol approximation. When orbital cutoff was 4.0 Å, the curve began to appear to converge. When the value of the orbital cutoff was 6.0 Å, then geometry converged very well, so we chose the value of orbital cutoff as 6.0 Å.

Fig. 1 Convergence test image of orbital cutoff.

3.3 NO adsorption on graphene layer

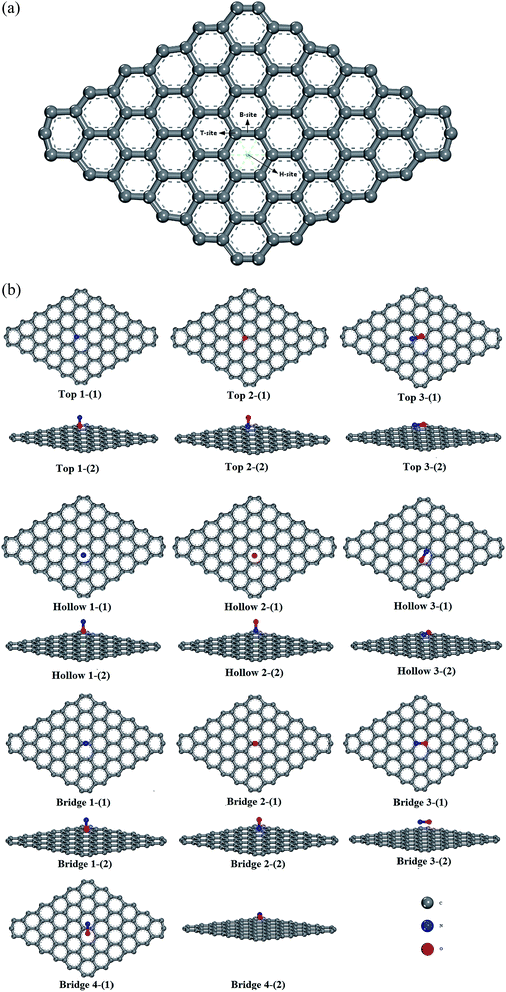
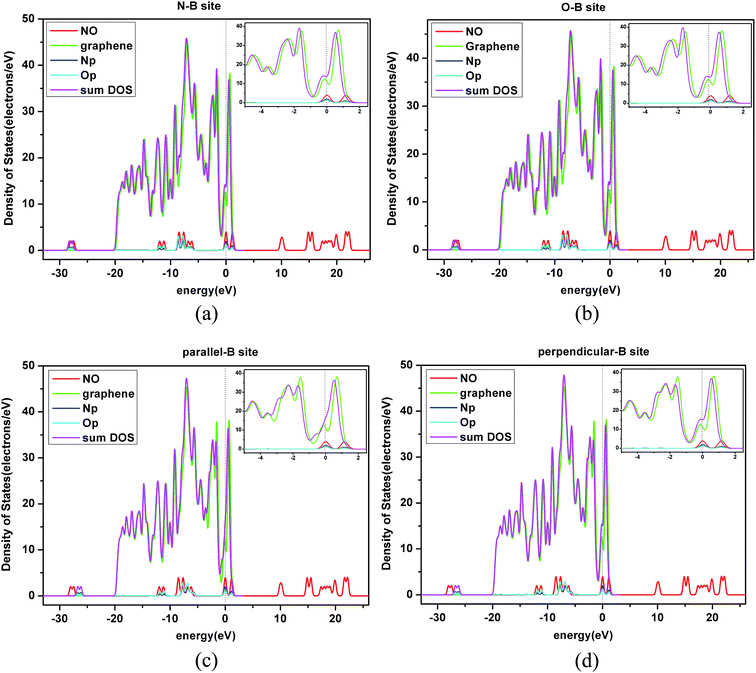
Three sites were considered for NO adsorption on graphene, as shown in Fig. 2(a): bridge site, top site, and hollow site which are abbreviated as B-site, T-site, and H-site, respectively. For the T-site and H-site, three different configurations of NO–graphene were calculated and a N atom, O atom, and N–O bond were placed near adsorption sites, respectively. For the B-site, the N–O bonds placed parallel and perpendicular to the adsorption sites were considered during the adsorption process of the N–O bond. Ten configurations are shown in Fig. 2(b). When NO was adsorbed on three sites of graphene by various adsorption methods, tiny deformations occurred in all graphene layers. The C–C bond length was no longer a fixed value because it changed from 1.242 Å to 1.481 Å. The isolated N–O bond was 1.17 Å and all bond lengths increased after adsorption.

Fig. 2 (a): A total of three adsorption sites on pristine graphene surface. (b): Ten different configurations of three sites on pristine graphene surface: (1) top observation; (2) side observation; (1): O terminal approached graphene; (2): N terminal approached graphene; (3, 4): N–O bond parallel or perpendicular approached graphene.

Based on DFT, adsorption energies, distances of NO to graphene surface, and geometry structures of ten configurations are listed in Table 3.

Table 3 The adsorption energies and adsorption height of the ten adsorption configurations

Configuration		h (Å)	Total energy (eV)	Ead (eV)	C–C (Å)	N–O (Å)	Relative deviation (%)
T-Site	O	3.144	−102498.381	−2.1424	1.242–1.480	1.201	0.02637
	N	3.154	−102498.347	−2.1084	1.242–1.479	1.120	0.02517
	N–O	3.089	−102498.187	−1.9489	1.243–1.479	1.201	0.02626
B-Site	O	2.849	−102498.610	−2.3713	1.243–1.480	1.201	0.02645
	N	3.147	−102498.440	−2.2018	1.243–1.481	1.120	−0.00147
	N–O(Para.)	3.086	−102498.137	−1.8981	1.242–1.481	1.202	0.02742
	N–O(Perp.)	2.839	−102498.565	−2.3266	1.242–1.480	1.200	0.02604
H-Site	O	2.940	−102498.195	−1.9569	1.243–1.480	1.201	0.02645
	N	2.845	−102498.332	−2.0932	1.242–1.481	1.194	0.02043
	N–O	3.101	−102497.984	−1.7453	1.243–1.480	1.201	0.02678

---

A. Adsorption energy. Adsorption energies of all configurations were calculated on the basis of eqn (1) and it can be clearly seen in Table 3 that all the values of adsorption energy were negative, implying that the adsorption structures were stable, and that the adsorption processes were exothermic. At the T-site, the values of the adsorption energies were −2.1424, −2.1084, and −1.9489 eV, respectively, and the values of corresponding bond lengths were 1.201, 1.199, and 1.201 Å, which respectively corresponded to O approaching graphene, N approaching graphene, and N–O parallel approaching graphene. By analysis and comparison, we found that the best adsorption configuration at the T-site was O approaching a graphene sheet. In addition, adsorption energy for N–O parallel to graphene was −1.8981 eV and the adsorption energies of other configurations at the B-site were higher than that of the T-site. The adsorption energies of O approaching graphene, N approaching graphene, and perpendicularly approaching graphene were −2.3713, −2.2018, and −2.3266 eV, respectively. The bond lengths of these four configurations were 1.201, 1.199, 1.202, and 1.200 Å, respectively. This observation showed that adsorption of the B-site was the same as that of the T-site, and O approaching graphene was also the most stable and strongest one. When NO adsorbed on the H-site, the adsorption capacity of NO was not very strong for three adsorption configurations as compared with the T-site and B-site. Adsorption energies of the three configurations were −1.9569, −2.0932, and −1.7453 eV, which correspond to O approaching graphene, N approaching graphene, and N–O parallelly approaching graphene, respectively. For these six different configurations, we found that all distances between adsorbed atoms and the graphene surface were less than 3.76 Å,^25,26 which showed our calculation was reasonable.

Comparing the calculated results, we found that the most favorable adsorption position of NO on a graphene surface was the B-site, which is in accordance with the study reported by Leenaerts.²⁵ But the calculated adsorption energy (−2.4 eV) in our paper is larger than that by Leenaerts²⁵ (29 meV, i.e. 0.029 eV). Therefore, we consulted other literature and found that the adsorption energies of NO on a graphene surface were −0.061 eV by using the DMol³ package by Chen et al.,²⁷ −24 kJ mol⁻¹ (about −0.25 eV) using Grimme's D3 dispersion model by Rad et al.,²⁸ −0.801 eV using SIESTA software code by Balangi et al.,²⁹ −0.14 eV using VASP5.2 by Hou et al.,³⁰ −0.30 eV using CASTEP by Zhang et al.,³¹ and 0.19 eV using DMol³ by Tang,³² respectively. In our previous works, the calculated adsorption energy of NO N-end on Pt_n/γ-Al₂O₃ (ref. 33) using the Dmol³ module in a Materials Studio8.0 package was −1.90 eV. However, the calculated adsorption energy of NO N-end on Pd/γ-Al₂O₃ (ref. 34) using the CASTEP module in a Materials Studio8.0 package was −0.18 eV. The adsorption energies of NO on different catalysts (Al₂O₃, GaAl_IV, GaAl_III) by Liu et al.³⁵ based on the DMol³ module in a Materials Studio package were −1.08 eV, −1.12 eV, and −1.04 eV, respectively. The adsorption energy of NO on pristine graphene using the Atomistix ToolKit package by Aghaei et al.³⁶ was −2.68 eV, but the distance between NO and the surface was 1.73 Å. We also found that the calculated adsorption energy by Zhang et al.³⁷ has a big difference with one by Aghaei et al.,³⁶ although the distance between NO and the surface was similar. By comparing the adsorption energies in the above literature, and checking our work again, we thought that this inconformity may be due to differences in the application of computational software, computational methods, and calculation parameters. Furthermore, for NO adsorption on a pristine graphene sheet in our paper, the calculated adsorption energy of the B-site was the largest, and those of T-site and H-site were similar. This result was consistent with existing research results in the literature.

B. Mulliken charge analysis. After a NO gas molecule was adsorbed on graphene, the original equilibrium charge distribution was broken, and the Mulliken charges were 0.066e and −0.066e for the N atom and O atom in the free state NO. Table 4 shows the gained or lost electrons situation of the N atom and O atom at different adsorption sites, and positive and negative values represent the gained and lost charges, respectively. Meanwhile, the Mulliken charges were calculated for six C atoms located on the hexagon at the adsorption site and marked in Fig. 3. For ten adsorption configurations, Mulliken charges of every N atom were all positive, and so were each O atom. When NO was adsorbed on the T-site, Mulliken charges of the N atom were 0.071, 0.072, and 0.071e, and those of the O atom were −0.075, −0.074, and −0.074e. The electron transfer shows that there are −0.004, −0.002, and −0.003e charge from graphene to NO, so this phenomenon indicates that NO acts as an acceptor. This result coincided well with Tang's, who claimed that the electrons transferred from nitrogen oxides to graphene in the system of nitrogen oxides adsorbed on graphene.³⁸ By comparison, the NO molecule also gave electrons to the graphene sheet, and the charge transfers of these four adsorption configurations were −0.005, −0.001, −0.007, and −0.001e, respectively. Like the T-site and B-site, the values of electrons transferred on the H-site of three adsorption configurations were −0.005, 0.042, and −0.004e. Charge transfers of 0.042e were transferred from NO to the graphene sheet, which indicates that NO acts as a donor to provide electrons. We found electron values on the H-site was positive, which meant electrons transferred from a N atom to the graphene surface for the H-site, because the Mulliken charge was easily affected by the basis set.

Table 4 The Mulliken charge of 6C atoms nearby the adsorption sites, O atoms, and N atoms in ten adsorption configurations

Mulliken
		C1	C2	C3	C4	C5	C6	N	O	Electron transfer
Graphene		0.000	0.009	0.000	0.000	0.009	0.001	—	—	—
NO		—	—	—	—	—	—	0.066	0.066	0.000
T-Site	O	0.001	0.012	0.001	−0.002	0.010	0.003	0.071	−0.075	−0.004
	N	0.000	0.011	0.001	−0.003	0.009	0.002	0.072	−0.074	−0.002
	N–O	−0.020	0.009	0.001	−0.003	0.011	−0.002	0.071	−0.074	−0.003
B-Site	O	0.002	0.012	−0.002	−0.001	0.012	0.002	0.070	−0.075	−0.005
	N	0.001	0.012	−0.001	−0.001	0.012	0.001	0.073	−0.074	−0.001
	N–O(Para.)	−0.019	0.012	0.000	−0.002	0.012	−0.009	0.070	−0.077	−0.007
	N–O(Perp.)	−0.013	0.009	−0.001	−0.001	0.009	−0.013	0.071	−0.072	−0.001
H-Site	O	0.001	0.011	0.001	0.001	0.010	0.002	0.073	−0.078	−0.005
	N	−0.002	0.007	0.000	−0.001	0.007	−0.003	0.087	−0.045	0.042
	N–O	−0.007	0.004	−0.002	−0.004	0.000	−0.009	0.071	−0.075	−0.004

---

Fig. 3 Six C atoms on the hexagon of the three adsorption sites.

Taken together in Table 4, electrons were transferred from a NO molecule to the graphene surface. When a NO molecule is vertical and its O atom is close to the graphene surface, the number order of electrons transferred on different adsorption sites was B-site = H-site > T-site. When a NO molecule is vertical and its N atom is close to the graphene surface, then the number order of electrons transferred on different adsorption sites was H-site > T-site > B-site. When a NO molecule is parallel to the graphene surface, the number order of electrons transferred on different adsorption sites was B-site > H-site > T-site.

Table 4 also shows the effect of the direction for NO adsorption on the graphene surface. The number of electrons transferred is not the same for different directions. The number (0.007e) of electrons transferred for a parallel NO molecule is much larger than that (0.001e) for a perpendicular NO molecule. The H-site has the greatest change attributed to the direction. Therefore, the charge transfer is not only affected by adsorption sites, but also by molecular orientation. We found that the data in Table 5 of Leenaerts et al.²⁵ have the similar rule, but they focused on the role of orientations.

Table 5 The HOMO, LUMO value and HOMO–LUMO of the ten adsorption configurations

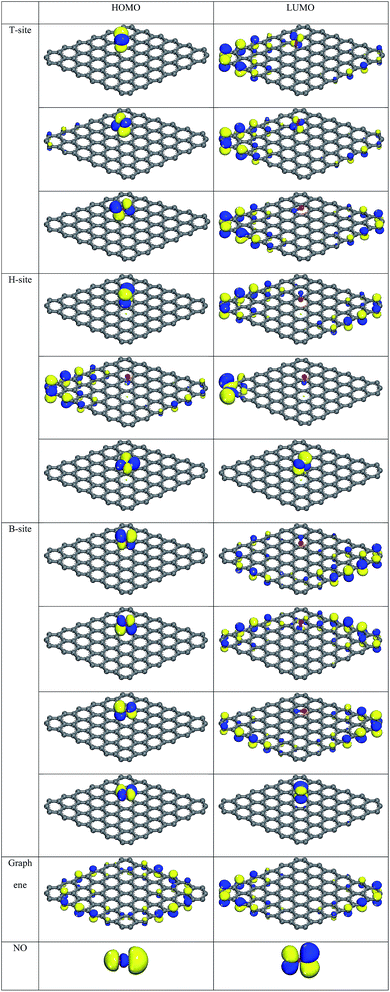
	T-Site			B-Site				H-Site
	O	N	N–O	O	N	N–O(Para.)	N–O(Perp.)	O	N	N–O
HOMO (eV)	−5.437	−5.415	−5.444	−5.394	−5.448	−5.429	−5.469	−5.543	−5.446	−5.447
LUMO (eV)	−5.331	−5.314	−5.201	−5.343	−5.335	−5.276	−5.428	−5.315	−5.443	−5.408
HOMO–LUMO (eV)	−0.106	−1.101	−0.243	−0.051	−0.113	−0.153	−0.041	−0.115	−0.013	−0.039

---

C. Electron density difference. After the adsorption of NO on graphene, the charge of graphene was uniformly distributed in the chemical bond instead of concentrating on a certain atom, thus showing a strong covalent bond. To be more intuitive to analyze the effect of the charge density distribution of NO adsorption on graphene, we made ten sectional views of electron density difference, as shown in Fig. 4. In this section, electron density difference Δρ was defined as follows:

Δρ = ρ_{NO–graphene} − ρ_graphene − ρ_NO (2)

ρ_{NO–graphene}, ρ_graphene, ρ_NO, represents the total electron density of the adsorbed system, the electron density of the pure graphene, and the electron density of free state NO molecule,^39,40 respectively.

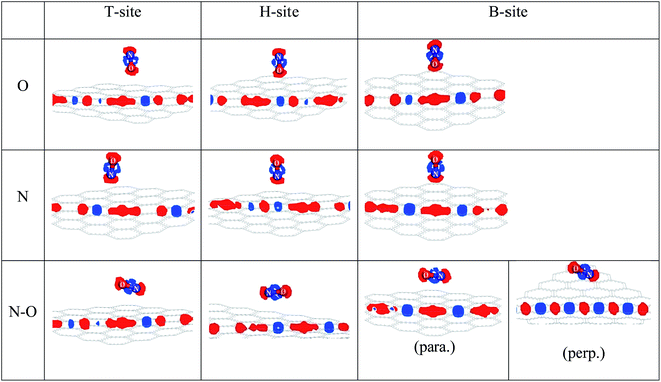Fig. 4 The electron density difference of the ten adsorption configurations. (para.): N–O bond parallel approached graphene, (perp.): N–O bond perpendicular approached graphene.

In the ten sectional views, there were no overlaps of the electron density between a NO molecule and C atom. This also showed that the ten kinds of adsorption configurations in the three sites were physical adsorption, which is consistent with the conclusion of the adsorption part of this paper. The red part represents the gained electrons and the blue part represents the lost electrons in different charge density maps. From Fig. 4, we found that graphene acted as an acceptor, which meant the charge was transferred from a NO molecule to the monolayer graphene, and the gained charge in all systems was mainly derived from the NO molecule that was closest to the C atom. By comparing the size of the red area and blue area, we found that most of the electrons were obtained by the O-end to the graphene B-site, the second was on the T-site, and the least was on the H-site. When N-end to a NO molecule was near three adsorption sites, then the graphene B-site lost the most electronic area, the second was located at the T-site, and the least was at the H-site. When the N–O bond was parallel or perpendicular to the graphene layer, we found that two configurations of the B-site had obvious symmetry, and that most electrons were transferred from the NO molecule to graphene. The electron values that NO lost and gained on the H-site were similar to the T-site. Through the comprehensive comparison of ten configurations gaining and losing of electrons, we found that a NO molecule got its number of electrons from the graphene layer following the order: B-site > T-site > H-site. This conclusion was consistent with our previous conclusion of the adsorption energy discussion.

D. HOMO and LUMO. The Highest Occupied Molecular Orbital is abbreviated as HOMO and Lowest Unoccupied Molecular Orbital is abbreviated as LUMO. They are collectively referred to as FMO (Frontier Molecular Orbital). The HOMO orbital and LUMO orbital are adjacent to the Fermi level, which helped us to understand the information of electron states near the Fermi surface and the information from the transferred electrons. The distribution of the HOMO orbital and LUMO orbital are shown in Fig. 5. We found that the electron cloud distribution in these two orbits was concentrated in the pure graphene edge region, meaning the electron states near the Fermi surface were mainly from the defect location of the C atom on the edge of graphene. Furthermore, we found that the information of the defect was because the p_z orbital of the C atom couldn't be related to the neighbor p_z orbital to constitute π and π* bonds, which eventually became a dangling bond, and non-paired electrons form defect states near the Fermi level. These defect states could capture electrons or lose electrons to form holes. After a NO molecule adsorbed on pure graphene, then the HOMO orbital and LUMO orbital electron clouds had great differences, which represented a significant trend of our regionalization. Observing the HOMO and LUMO of the NO molecule in Fig. 5, we found that LUMO of the free state NO molecule was more distributed on a N atom, which meant that the transfer of electrons was mainly due to the interaction between a N atom and the HOMO orbitals of graphene in the adsorption process. The π* bond electrons on graphene edges were transferred to the anti-bonding orbital of a NO molecule, of which the bond order, which was 2.5 in the original free state, decreased to 2. The stability of the NO molecule was reduced by the electrons filling in the anti-bonding orbital; meanwhile, the bond energy became weak and the length value of the N–O bond lengthened. This result was in accordance with the results of previous adsorption energy calculations. Observe in Table 5 that the HOMO energy of the O terminal approaching the graphene B-site configuration was the highest and the LUMO energy was relatively low. While the higher the electron energy of the HOMO orbital was, the less the bound ability showed; meanwhile, the lower the electron energy of LUMO was, the easier an electron was accepted in the molecule, so we found this configuration was the most stable. From HOMO and LUMO, for ten configurations on three kinds of adsorption sites, we found that the highest probability of electron transition occurred on the T-site, and next was four kinds of adsorption configuration on the B-site. The electronic transition did not easily occur on the H-site. However, through observing HOMO and LUMO energy values of adsorption configurations on the T-site, we found that the HOMO energy of the B-site was larger than that of the T-site, while LUMO energy of the B-site was overall lower than that of the T-site. By comprehensively comparing them, the adsorption of the B-site was more active than that of the T-site and the most inactive was adsorption on the H-site. This result verified our previous conclusion.

Fig. 5 HOMO and LUMO of the ten adsorption configurations, graphene, and NO molecule.

E. Projected density of states. Density of States (DOS) on an optimal adsorption site (B-sites) was also worked out by first-principles calculations for understanding the influence of NO gas on the optimal adsorption sites of a pristine single graphene layer. The DOS and PDOS of a NO molecule, pristine graphene layer, and NO–graphene on B-sites were plotted in Fig. 6. The electron arrangements for C, N, and O were 2s²2p², 2s²2p³, and 2s²2p⁴. The lengths of C–N bond were 1.153, 1.153, 1.202, and 1.200 Å, for O-end to B-site, N-end to B-site, N–O parallel to B-site, and N–O perpendicular to B-site, respectively. This process brought about the activity of the N–O bond; meantime, the change of bond lengths lead to the greater degree of overlap of the electron cloud. The stronger bond led to the greater bond energy. Due to adsorption of the NO molecule, the DOS of pristine graphene sheet which adsorbed NO at the Fermi level moved upward; meanwhile, the electro-conductibility of NO adsorbed on a graphene surface with different directions were slightly higher than that of a single pristine graphene sheet. In Fig. 6(a)–(d), the Fermi level of NO–graphene for four configurations had a little charge transfer, and total electron transfers were 2.444, 2.601, 5.167, and 3.8536 eV from NO anti-bonding to graphene anti-bonding. By analysis, we found the adsorption process was physisorption, which was caused by intermolecular van der Waals forces, through contrasting the distances of a molecule to the graphene surface and the adsorption energies.

Fig. 6 The density of states (DOS) of a NO molecule and graphene sheet. The total density of states (TDOS) of NO adsorbed on the B-site of a pristine graphene layer with the projected density of states (PDOS) for the p state of N and O atoms in four orientations. (a) N-B site: N terminal approaching the B-site; (b) O-B site: O terminal approaching the B-site; (c) parallel-B-site: N–O bond parallel approaching the B-site; (d) perpendicular-B-site: N–O bond perpendicular approaching the B-site.

4. Conclusions

Along with more and more people paying attention to environmental pollution problems, exhaust gas processing has become a key problem for research focus. In this paper, based on previous studies, we studied the adsorption of NO gas on pristine graphene, which is a basic guide for future experiments and the treatment of NO gas under real life situations.

Using DFT computer simulation, we investigated the adsorption of NO on a pristine graphene surface. Through an optimizing test, we selected a PBEsol approximation and GGA approximation to carry out further work. We studied the graphene surface of three adsorption sites, and calculated the adsorption energy, Mulliken charge, electron density difference, and the HOMO, LUMO, and PDOS of these three kinds of adsorption sites. We found that the adsorption process was physical adsorption and the adsorption energies were −2.37 to −1.74 eV. The number of transferred electrons from molecular NO to graphene was −0.007 to −0.001e. Calculated results showed that the largest adsorption energy of NO on the graphene surface was the B-site, followed by the T-site, and finally the H-site. Meanwhile, these results were verified by the analysis of Mulliken charge, electron density difference, HOMO, and LUMO.

Results showed that the graphene played a role in adsorbing NO exhaust gas. When a B-site acted as an adsorption site, the adsorption effect was better. Research results have a certain theoretical support and guidance for future NO exhaust gas treatment.

Acknowledgements

This work was supported by Natural Science Foundation of Xinjiang, China, Grant No. 2016D01A073. This work was also financially supported by Recruitment Program of Global Experts, and the Director Foundation of XTIPC, CAS, Grant No. 2015RC011.

References

1. Z. M. Ao and F. M. Peeters, J. Phys. Chem. C, 2010, 114, 14503–14509.
2. A. Geim and K. Novoselov, R. Swed. Acad. Sci., 2011, 181, 1283.
3. K. S. Novoselov, Int. J. Mod. Phys. B, 2011, 25, 4081–4106.
4. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
5. K. S. Novoselov, D. Jiang, F. Schedin, T. J. Booth, V. V. Khotkevich, S. V. Morozov and A. K. Geim, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10451–10453.
6. W. Wu, Q. Yu, P. Peng, Z. Liu, J. Bao and S.-S. Pei, Nanotechnology, 2012, 23, 035603.
7. T. Gao, S. Xie, Y. Gao, M. Liu, Y. Chen, Y. Zhang and Z. Liu, ACS Nano, 2011, 5, 9194–9201.
8. X. Li, W. Cai, J. An, S. Kim, J. Nah, D. Yang, R. Piner, A. Velamakanni, I. Jung, E. Tutuc, S. K. Banerjee, L. Colombo and R. S. Ruoff, Science, 2009, 324, 1312–1314.
9. M. Liu, Y. Zhang, Y. Chen, Y. Gao, T. Gao, D. Ma, Q. Ji, Y. Zhang, C. Li and Z. Liu, ACS Nano, 2012, 6, 10581–10589.
10. P. S. Arun, B. P. Ranjith and S. M. A. Shibli, Environ. Sci. Technol., 2013, 47, 2746–2753.
11. F. Ahmed, M. K. Alam, A. Suzuki, M. Koyama, H. Tsuboi, N. Hatakeyama, A. Endou, H. Takaba, C. A. Del Carpio, M. Kubo and A. Miyamoto, J. Phys. Chem. C, 2009, 113, 15676–15683.
12. N. Takahashi and H. Imagawa, J. Jpn. Pet. Inst., 2009, 52, 90–101.
13. K. J. Berean, J. Z. Ou, M. Nour, M. R. Field, M. M. Y. A. Alsaif, Y. Wang, R. Ramanathan, V. Bansal, S. Kentish, C. M. Doherty, A. J. Hill, C. McSweeney, R. B. Kaner and K. Kalantar-zadeh, J. Phys. Chem. C, 2015, 119, 13700–13712.
14. E. C. Mattson, K. Pande, M. Unger, S. Cui, G. Lu, M. Gajdardziska-Josifovska, M. Weinert, J. Chen and C. J. Hirschmugl, J. Phys. Chem. C, 2013, 117, 10698–10707.
15. S. C. Xu, S. Irle, D. G. Musaev and M. C. Lin, J. Phys. Chem. B, 2006, 110, 21135–21144.
16. S. Wannakao, T. Nongnual, P. Khongpracha, T. Maihom and J. Limtrakul, J. Phys. Chem. C, 2012, 116, 16992–16998.
17. H. Liu and J. Y. Lee, J. Phys. Chem. C, 2012, 116, 3034–3041.
18. I. Choudhuri, N. Patra, A. Mahata, R. Ahuja and B. Pathak, J. Phys. Chem. C, 2015, 119, 24827–24836.
19. M. P. Jigato, K. Somasundram, V. Termath, N. C. Handy and D. A. King, Surf. Sci., 1997, 380, 83–90.
20. R. Heyrovska, ArXiv08044086 Phys., 2008.
21. E. V. Castro, K. S. Novoselov, S. V. Morozov, N. M. R. Peres, J. M. B. L. dos Santos, J. Nilsson, F. Guinea, A. K. Geim and A. H. C. Neto, J. Phys.: Condens. Matter, 2010, 22, 175503.
22. P. R. Wallace, Phys. Rev., 1947, 71, 622–634.
23. D. Bensaid, J. Mod. Phys., 2011, 2, 642–650.
24. P. Haas, F. Tran, P. Blaha, K. Schwarz and R. Laskowski, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 195109.
25. O. Leenaerts, B. Partoens and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125416.
26. C. Berger, Z. Song, X. Li, X. Wu, N. Brown, C. Naud, D. Mayou, T. Li, J. Hass, A. N. Marchenkov, E. H. Conrad, P. N. First and W. A. de Heer, Science, 2006, 312, 1191–1196.
27. Y. Chen, B. Gao, J.-X. Zhao, Q.-H. Cai and H.-G. Fu, J. Mol. Model., 2012, 18, 2043–2054.
28. A. S. Rad and E. Abedini, Appl. Surf. Sci., 2016, 360, 1041–1046.
29. H. R. Balangi and A. A. Shokri, Phys. E, 2015, 74, 515–526.
30. M. Hou, W. Cen, H. Zhang, J. Liu, H. Yin and F. Wei, Appl. Surf. Sci., 2015, 339, 55–61.
31. Y.-H. Zhang, Y.-B. Chen, K.-G. Zhou, C.-H. Liu, J. Zeng, H.-L. Zhang and Y. Peng, Nanotechnology, 2009, 20, 185504.
32. S. Tang and Z. Cao, J. Chem. Phys., 2011, 134, 044710.
33. H. Gao, RSC Adv., 2016, 6, 102914–102923.
34. H. Gao, Appl. Catal., A, 2017, 529, 156–166.
35. Z. Liu, L. Ma and A. S. M. Junaid, J. Phys. Chem. C, 2010, 114, 4445–4450.
36. S. M. Aghaei, M. M. Monshi and I. Calizo, RSC Adv., 2016, 6, 94417–94428.
37. N. C. Zhang, J. Ren and X. J. Peng, Fullerenes, Nanotubes, Carbon Nanostruct., 2016, 24, 298–304.
38. S. Tang and Z. Cao, J. Chem. Phys., 2011, 134, 044710.
39. Y. Lin and K. A. Fichthorn, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 165303.
40. Y. Dong, D. Tang and C. Li, Sci. China: Technol. Sci., 2014, 57, 2153–2160.

---