Self-assembly of glycine on Cu(001): the effect of temperature and polarity

Abstract

Self-assembly (SA) of molecules on solid surfaces has attracted enormous attention in terms of fundamental interest and a variety of applications. Here glycine on Cu(001) is studied as an example to illustrate the critical role of finite temperature and molecular polarity in the SA of biomolecules at a metal surface. We clarify that the SA structure of a glycine monolayer on Cu(001) is thermodynamically stable as determined by the lowest energy at room temperature, and a p(2 × 4) structure is identified to be the most stable through ab initio molecular dynamics simulations. This unique p(2 × 4) structure is derived based on a full polarity compensation mechanism, and its STM images and anisotropic free-electron-like dispersion are in excellent agreement with experiments. Moreover, the rich self-assembling patterns including the heterochiral and homochiral phases, and their inter-relationships are found to be entirely governed by the same polarity compensation mechanism.

---

I. Introduction

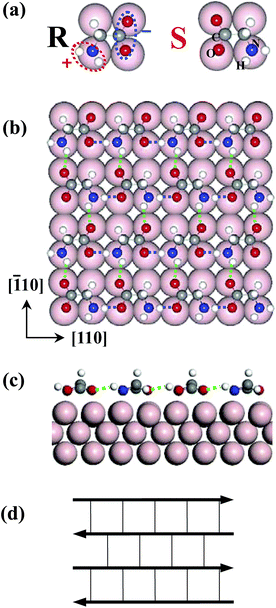
Owing to both fundamental interests in physics, chemistry and biology and potential applications such as the bulk fabrication of nanoscale devices, self-assembled monolayers (SAMs) of molecules on solid surfaces is particularly interesting.^1–22 This approach is a promising route to construct functional systems with nanometre dimensions by autonomous ordering of molecules on atomically well-defined surfaces. Since a common characteristic of self-assembled systems is their thermodynamic stability, most theoretical studies are performed at finite temperature using classical molecular dynamics in literature.^23–25 Since there is a subtle balance between molecule–molecule (M–M) and molecule–surface (M–S) interactions, temperature plays an important role as the third parameter in the molecular self-assembly at surfaces.⁴ Generally, the proposed structure is a ground state obtained from first-principles calculations at 0 K. However, whether this structure at 0 K is the SA structure at finite temperature is an open question. Also is there any difference between SA and adsorption on surface? The answers are not clear and straightforward. Therefore, in order to comprehensively understand the SA mechanism it is necessary to include the temperature effect.

The simplest amino acid, glycine, comprising only an amino group (as the head) and a carboxyl group (as the tail), is one of most fundamental components for biomolecules. Glycine is the only amino acid that does not have chirality, however, by adsorbing on Cu surfaces glycine loses a hydrogen atom and is converted to glycinate. Then, the amino and carboxyl groups of glycinate are strongly positively and negatively polarized, respectively, exhibiting two different chiral configurations upon surface adsorption [see Fig. 1(a)]. In experiments, plenty of structural patterns such as homochiral c(2 × 4) and heterochiral p(2 × 4) phases have been observed for glycine on Cu(001) by scanning tunneling microscopy (STM).²⁶ Meanwhile, in the p(2 × 4) structure scanning tunneling spectroscopy (STS) revealed an anisotropic free-electron-like (FEL) dispersion²⁷ with electron effective mass differing by 10-fold along different directions. Different from organic molecules on metal surfaces where organic molecules are usually planar and rigid, and directly observable with STM,^3–6,11,27 it is difficult to reach atomic resolution in STM images for biomolecules^12–15,26 due to their stereostructures. Thus, building an atomistic model of the glycine monolayer structure has been challenging.

Fig. 1 (a) Adsorbed glycinate molecule (R) and its enantiomeric isomer (S). Two positive sites in the amino group and two negative sites in carboxyl group are circled by red and blue dashed lines, respectively. (b) Top-view for the anti-parallel molecular arrangement of a heterochiral p(2 × 4) structure. Each molecule interacts with four neighbors via HB. (c) The side-view of an SA monolayer on the Cu surface showing a flat adsorbed geometry. (d) Schematic plot of anti-parallel HB ladder-like network. Horizontal bold lines represent strong HB along [110] and vertical thin lines weak HB along [1̄10]. The arrows indicate the directions of strong HBs.

In literature, various structural models have been proposed to interpret experimental observations for glycine on Cu(001).^{12–14,26–30} However, the conformation in these models ignore that SA is a consequence of local interactions among the components themselves and the full intermolecular interactions between the polarized glycine molecules. The internal factors such as intermolecular hydrogen bonding (HB) between glycine molecules would be the intrinsic driving force for SA. Despite many attempts, the SAM structure reproducing the anisotropic electronic behavior and the mechanism governing SA of glycine on Cu surface, which have been a long-term controversy, still remain to be explored.

In this work, we employed first-principles calculations and ab initio molecular dynamics simulations to investigate the SA structure of glycine on Cu(001). Our results indicate that finite temperature and molecular polarity play vital roles in determining the microscopic mechanisms for glycine SA on a metal substrate. The heterochiral p(2 × 4) structure satisfying a full polarity compensation rule, can best reproduce the well-known features observed in experiments including STM images^26,27 and 10-fold anisotropic FEL dispersion.²⁷ The rich self-assembling patterns including the heterochiral and homochiral phases, and their inter-relationships are found to be entirely governed by the polarity compensation mechanism. As a thermodynamically stable state, the unique p(2 × 4) phase has the lowest energy at room temperature (RT), though not at 0 K. The intermolecular hydrogen bonds are determinative forces for glycine self-assembling on Cu surface, which is a unique intrinsic nature of self-assembly in this system.

The paper is organized as follows. The computational methods are described in Section II. We present our results and discussions in Sections III and IV, respectively. Finally, we provide conclusions in Section V.

II. Computational methods

Optimizations were performed within the framework of density functional theory (DFT) using the Vienna ab initio simulation package (VASP),^31–33 in which projector-augmented wave pseudopotentials and generalized gradient approximation³⁴ were chosen. A plane wave basis set was used to expand the Kohn–Sham orbitals with a 400 eV kinetic energy cutoff. Glycinate molecules were placed on a seven-layer Cu(001) slab in a supercell with dimensions of 10.28 Å × 10.28 Å × 25 Å. The Monkhorst–Pack scheme³⁵ was adopted for the Brillouin zone integration, and we have tested that a 4 × 4 × 1 k-point mesh is sufficient to ensure a good convergence in the total energy differences. The atoms in the top four Cu layers were allowed to fully relax until the forces on them were all smaller than 0.03 eV Å⁻¹. Energy convergence for the geometry optimization was better than 0.1 meV per atom. In addition, van der Waals interactions were also included to check the total energy differences by using a van der Waals density functional (vdW-DF). In molecular dynamics simulations, the time step was chosen to be 0.5 fs and all atoms were allowed to move. An equilibration process was first performed by slowly heating the systems from 0 to 310 K. Then we examined thermal oscillations in atomic structure and energy at 310 K in the canonical ensemble using the Nosé–Hoover thermostat to control the temperature.

III. Results

We begin with a single glycinate adsorption case. A single glycinate molecule and its enantiomeric isomer binds to the Cu(001) surface in a tridentate manner through one nitrogen atom and two oxygen atoms on top sites of substrate Cu atoms. Their adsorption geometries are schematically shown in Fig. 1(a). They have the same adsorption energy (2.33 eV) in our first-principles calculations.

A. Full polarity compensation rule

Based on the concept of SA that requires the maximum interaction among molecules, and the special characteristics of the strong polarity of glycinate, we propose a general rule for the construction of glycinate SA structures on a Cu surface. The rule has three elementary components: (i) because of the strong polarity, the positive site of a glycinate interacts with the negative site of another glycinate via hydrogen bonding to form a head-to-tail chain; (ii) the polarity of glycinate also affects its side neighbors, i.e., the positive sites of side neighbors will approach to the negative site of the glycinate, and vice versa. Thus, (i) and (ii) together result in local molecular configurations where the positive site of each glycinate is surrounded by the negative sites of three neighbors, and the negative site is surrounded by the three positive sites; (iii) each glycinate molecule must contribute its all active sites, two positive sites from the amino group and two negative sites from the carboxyl group, to interact with its neighbors via HB. The rule (iii) implies the determination of chirality of structure, an important feature associated with SA. This means glycinate molecules will automatically adjust their chirality to self-organize HB network structures according to the rule (iii). These three principles for constructing glycinate SA are collectively denoted the polarity compensation rule here.

B. The unique heterochiral p(2 × 4) phase

Following the polar compensation rule, we start to construct the atomistic geometry of glycinate SAMs and exclusively reached a heterochiral p(2 × 4) structure of glycinate on Cu(001), as shown in Fig. 1(b). Glycinate molecules arrange themselves into a linear chain via head-to-tail HB along the [110] direction in their own R chirality, due to strong attractions between the positively (amino head) and negatively polarized ends (carboxyl tail). The neighboring chain forms an anti-parallel pattern to eliminate the net polarity of the two-dimensional (2D) island. Moreover, the glycinates in neighboring chains must “turn their heads” to be of S chirality in order to form the HB network connected by weaker HB along the [1̄10] direction. Then all active sites of molecules are fully participating in interaction, as required by the rule (iii) mentioned above. Glycinate molecules automatically alternate their chirality from one chain to the next to make the monolayer structure an integral network, otherwise, less stable and isolated double-rows would form instead of the 2D monolayers as observed experimently.^26,27

Geometry optimization shows that all O⋯H lengths in the HB along [110] are 1.6 Å with a binding energy of 210 meV (indicating a strong HB), whereas those along the [1̄10] direction are 2.0 Å with the energy of only 138 meV (weak HB).³⁶ They are denoted in blue and green dashed lines in Fig. 1(b) and (c), respectively. This anti-parallel HB network is also schematically drawn in Fig. 1(d), to indicate the arrangement of molecular polarity. In this structure each glycinate acts as two HB donors and two HB acceptors, where all its polar sites are fully saturated with HB.³⁷ This is consistent with the general understanding of H-bonding interactions: namely, the selectively, linearity and saturation of H bonds.

Any structures proposed for glycine SA on Cu(001) would have to withstand stringent tests to reproduce properties measured experimentally; our structure model based on the polarity compensation mechanism, shown in Fig. 1, satisfies these tests very well. To confirm it is indeed the one observed experimentally, we compare STM images and electronic band structures from both theory and experiment. Fig. 2(a) shows the simulated STM image for the p(2 × 4) phase, together with the measured image²⁷ in the inset for comparison. The STM image is calculated by integrating local density of states with energy <100 meV below the Fermi level (same as experimental condition²⁷) within the Tersoff–Hamann approximation.³⁸ It displays a pattern of triangular protrusions: triangles slightly tilted to the left are glycinate in S conformation, while those tilted to the right are in R conformation, forming an array of alternating anti-parallel rows along the [1̄10] direction. Experimentally, a pattern of blurred triangles was observed with two opposite orientations, in a very similar manner to the simulated images. In each row along the [110] direction the molecules are close to each other, indicating a stronger interaction within the rows; while there is a larger separation between the rows, suggesting weaker row-to-row interactions. These features are well reproduced and explained by our model.

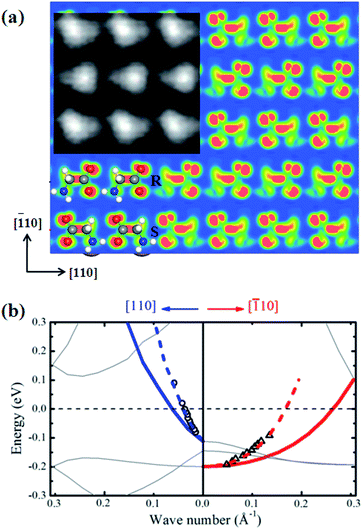Fig. 2 (a) The calculated STM image for the p(2 × 4) structure. The inset is an experimental image from ref. 27 shown for comparison. (b) Energy dispersion relations for the [110] direction in blue and [1̄10] in red, respectively. Solid lines represent our calculated results and dashed lines are rescaled for comparison with experimental results from ref. 27 (dark circles for [110] and dark triangles for [1̄10]). The Fermi energy is indicated by a horizontal dashed line.

A more stringent and more interesting test comes from the 10-fold difference in electron effective mass 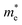for the FEL dispersions along the [110] and [1̄10] directions observed in STS.²⁶ Again this strong anisotropic FEL behavior is obtained for our proposed p(2 × 4) structure. Obviously, the anisotropy originates from the anisotropic geometries of the absorbed glycinate molecules. As in our SA structure model, the glycinate molecules interact with strong HB along the direction [110] and in a sideways interaction with weak HB along [1̄10], forming HB networks as shown schematically in Fig. 1(d), where the bold lines represent strong HB along the glycinate molecular rows. It is noted that the glycinate monolayer is an insulator. Since the Cu surface along the direction [110] is covered by glycinate molecules, the charge density within the monolayer and Cu surface along this direction is much larger than that for [1̄10] and thus the dispersion is stronger in the direction [110]. Furthermore, FEL behavior is a more intrinsic property in this system. In our model the three active sites (one N and both O) in glycinate are saturated with HBs, resulting in a flat absorbed SA monolayer on the Cu surface [see Fig. 1(c)]. Such a saturating and flat SA structure provides a necessary condition for the FEL dispersions produced by the standing wave between the glycine monolayer and the Cu substrate.²⁶ Following the above qualitative picture, we are able to calculate the energy dispersion relations.

Initially, we failed to obtain a 10-fold difference in FEL dispersions along the two directions with several attempts by choosing different Cu layers and k-points. Later, we realized that this strong anisotropic electronic behavior observed in experiment arises from the surface state within the glycine monolayer and the Cu surface. If Cu sublayers are included in the calculation, the contribution of these symmetrical Cu sublayers will diminish the surface anisotropic behavior. Thus, for this reason we calculated the surface band structure of glycinate on a single Cu(001) layer. This approximation neither affects the anisotropic property because the removed Cu atoms are symmetric to the [110] and [1̄10] directions, nor affect the FEL behavior since the dispersion of Cu substrate itself is electronically free. This is a necessary approximation without loss of physical considerations. In this way, a tidy band structure was obtained, as shown in Fig. 2(b). There is only one band across the Fermi surface along both [110] and [1̄10] directions. In Fig. 2(b), the solid lines represent the calculated results. However, a compensation is required for the single Cu layer approximation since a single layer Cu has a much lower charge density than bulk Cu and a scaling constant, which should be larger than 1, is needed to compensate the drawback in our approximation. By comparing with experimental data, curves are multiplied a single constant of 2.46 for both directions as shown by dashed lines in Fig. 2(b). The experimental data now lie exactly on the dashed curves, which show the parabolic FEL dispersions, as well as the 10-fold difference in the effective mass with respect to the [110] and [1̄10] directions.

To interpret their STM observations, Kanazawa et al.^26,27 adopted a structural model consisting of only head-to-tail alignments in the same direction, which is prevailing in literature for glycine SAM on Cu(001)^{12–14,26,28,39} (see Fig. S1 in ESI‡). For convenience of presentation, we denote this structure the head-to-tail (HT) model. This model, however, does not consider the influence of polarity towards side neighbors, or the associated HB network. Thus, neither STM images nor FEL dispersion in experiments were reproduced by the HT model (see Fig. S2 in ESI‡). Moreover, the HBs in the HT structures are unsaturated with consequently stronger bonds to the Cu substrate (see Fig. S3 in ESI‡). For free-standing monolayers, first-principles calculation shows indeed that the HT structure is 76 meV higher per molecule in energy than our structure, indicating that our model is intrinsically more stable for SA than the HT model. In our p(2 × 4) structure glycinate molecules are saturated with H bonds and all H bonds conform the ideality of H bonding interactions such as selectively and linearity, thus its free-standing structure is more stable than the unsaturated HT structure. Note that the electronic dispersion of the SA structures from the other models³⁰ do not show parabolic FEL along the [1̄10] direction.

C. Thermodynamic stability

However, a complexity arises from the subtle balance between the intralayer M–M interactions and the M–S binding, which is a central theme in all SA processes on surface. At 0 K, first-principles calculations give the adsorption energy is 2.69 eV per glycinate in the HT model compared with 2.55 eV in our model, which shows the HT model is lower in total energy by 140 meV per glycinate than that of our structure.⁴⁰ That is, the HT model is the “ground state structure” at 0 K. Then why it is not observed in experiments, which shows very different STM/STS features as to those of the HT structure?⁴¹ This question has concerned us for a long time since in principle the stable structure should be the state with the lowest total energy. After revisiting the concept of SA, we realize that the SA is a thermodynamically stable state whose structure is constructed at a finite temperature. Therefore, the stable SA structure will correspond to the lowest total energy at the finite temperature. To verify this, we then performed ab initio MD simulations to compare the total energies between the HT and our structure model at 310 K. Fig. 3 shows the energy fluctuations as a function of time in an MD run lasting for ∼5 ps after equilibrium, revealing that the energy curve of our model (in red) is below that of the HT model (in black). Further analysis on the energy distributions of the two cases are plotted in the inset of Fig. 3. We calculated their average energies and found that indeed the HT model has a higher energy at 310 K, which is now 75 meV per molecule higher in energy than our model. The difference in energy is coincidental to that for free-standing layers, 76 meV, suggesting that the SA structure at RT is dominated by intermolecular H-bonds, rather than the molecule–substrate bonds as in the case at 0 K. At 0 K the unsaturated HT model has stronger interaction with the substrate compared to our saturated structure. At finite temperature, however, thermal fluctuations weaken glycinate–Cu bonds and result in glycine–Cu interactions of similar strength between the two models. Thus, the self-assembly structures are now determined by the maximum molecular interactions.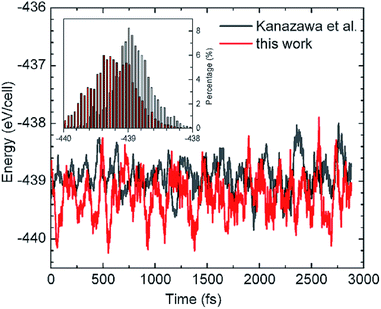

Fig. 3 Energy fluctuations as a function of time in molecular dynamics simulations at 310 K for our structure and that adopted by Kanazawa et al.^26,27 The inset shows the distribution of energies for the two cases.

Therefore, the observed SAM p(2 × 4) structure satisfies both requirements of strong interaction among molecules and the lowest energy at finite temperature, and is the thermodynamically stable state.

D. Mixed heterochiral and homochiral phases

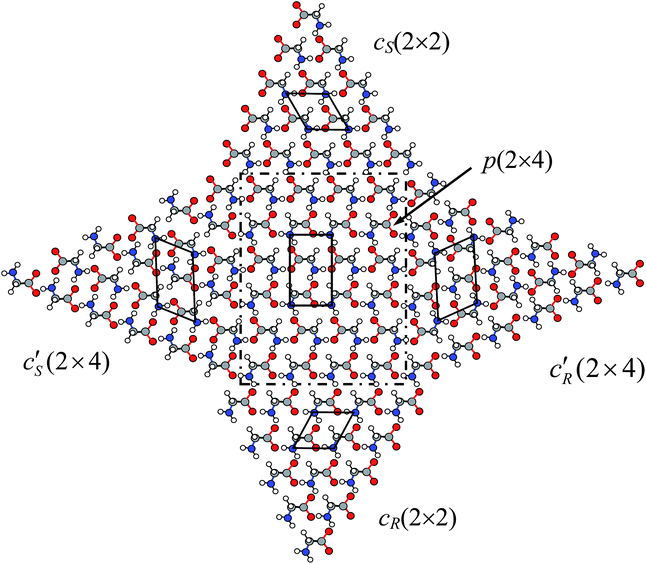
Besides the dominant heterochiral p(2 × 4) phases widely observed in experiments,^12–14,26 homochiral phases were also found by several groups for glycinate SA on Cu(001).^12–14,28 The presence of both heterochiral and homochiral phases induces a variety of SA patterns in STM images, e.g., a homochiral array at the boundary between heterochiral p(2 × 4) phases.²⁶ To reach a unified understanding on these rich SA patterns, we invoke the polarity compensation rule to unravel the underlying mechanism for the formation of different chiral phases.

We first look in Fig. 4 at the boundary between two p(2 × 4) domains, p₁(2 × 4) and p₂(2 × 4), where p₂ is shifted by one lattice of the Cu surface along [1̄10] with respect to p₁. At the boundary, the glycinate with R chirality has to switch its head, turning into S chirality in order to form a strong HB across the boundary and a weak HB with the side neighbor. Thus all molecules at the leftmost column of p₂(2 × 4) become of S chirality, denoted as c′_S(2 × 4) in Fig. 4. Homochiral glycinate arrays must exist between two shifted heterochiral p(2 × 4) domains, offering full HBs to stabilize the boundary and lowering the energy by ∼100 meV per molecule. This explains the well observed homochiral boundary between p(2 × 4) domains in experiment (indicated by white arrows in Fig. 2(e) of ref. 26).

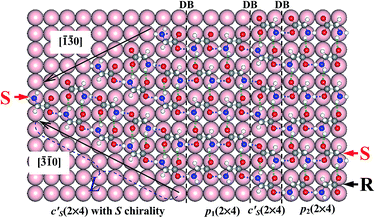Fig. 4 Molecular arrangements for comparing with STM images in ref. 26, which exhibit various structures including the heterochiral p(2 × 4) and homochiral c′_S(2 × 4) domains and their relationship.

The above observation demonstrates how glycinate changes its chirality to interact with its neighbors according to the rule when the molecule shifts along [1̄10] by a Cu atom position. Shifting continuously in this way, all glycinates with R chirality would change to S chirality in order to bond together, so a complete homochiral phase of S chirality is formed. Moreover, this homochiral phase naturally develops a step along the [3̄1̄0] direction, on which all molecules are saturated with HB and the step becomes inactive, shown in the left corner of Fig. 4 and 5. This triangular c′_S(2 × 4) phase is indeed observed by STM, denoted as c(2 × 4) in Fig. 2(e) of ref. 26.

Fig. 5 Panorama of the SA monolayer of glycinate on Cu(001). There are four homochiral phases around the heterochiral phase p(2 × 4). Domain boundaries are represented by the dashed lines, and the unit cell for each phase is denoted by solid lines. For the sake of clarity, the Cu substrate is not shown.

E. Complete SA structures

Since glycinate is enantiomeric, it is expected that an alternative homochiral c′_R(2 × 4) phase with all R chirality also exists. Indeed this homochiral R-phase is formed in the same way at the right side of the p(2 × 4) pattern, illustrated in Fig. 5. Similarly, this phase could also be formed by shifting the glycinate molecules along [11̄0] at the left side of the p(2 × 4) pattern by a Cu position, while the c′_S(2 × 4) phase occurs at the right side (see Fig. S4 in ESI‡). Both c′_S and c′_R phases are composed of hydrogen-bonded twin chains.

Besides the aforementioned homochiral phases, by shifting the glycinate a Cu position along [110] sequentially, two other homochiral phases above and below the p(2 × 4) pattern can also be constructed based on the rule, denoted as c_S(2 × 2) and c_R(2 × 2) in the upper and lower part of Fig. 5, respectively. However, the polarity is not eliminated in the c phases. Thus these phases are less stable than the p phase, and could be formed only in small domains or by some external factors, e.g. steps on surface. The chirality of the outermost glycinate in the p(2 × 4) phase decides the chirality of the c phase. Since each adsorbed glycinate molecule occupies a (2 × 2) Cu surface cell, every possibility for the c′ and c phases by shifting a Cu position along each direction has been completely considered. It should be noted that all the above homochiral phases are different from the c(2 × 4) model adopted by Kanazawa et al.²⁶ (see Fig. S5 in ESI‡).

We have thus considered all possible SA structures of glycinate on Cu(001): a unique heterochiral p(2 × 4) phase and four homochiral phases based on our polarity compensation rule. In particular, the chirality of each phase is automatically determined by the rule (iii). The inter-relationships between various phases are displayed in Fig. 5 where the heterochiral p(2 × 4) phase is surrounded by different homochiral phases in each direction. The reason that we put them together is to emphasize their seamless connections where the boundaries between the hetero- and homo-chiral phases also obey the rule. No matter where a glycinate molecule locates in a single phase or boundary, it fully interacts with the neighbors by two positive sites in the amino group and two negative sites in the carboxyl group via HB without any exceptions. Such a full intermolecular interaction provides a sufficient and necessary condition for the stable SA structure at RT.

To our knowledge, glycine on Cu(001) exhibits the richest 2D SA patterns on a surface, where all SA structures and their inter-relationships can be explained in the same polarity compensation mechanism. Since p(2 × 4) and c′(2 × 4) structures have already been observed in STM experiment,²⁶ searching for other predicted phases experimentally remains a challenge to prove our theory.

IV. Discussion

It might be significant to further discuss the different concepts between SA and adsorption on a surface, as well as the crucial roles of temperature and substrate played during SA process in general.

A. SA on surface vs. adsorption on surface

First, we would like to clarify the difference between SA and adsorption on surface. Since self-assembly leads to a thermodynamically stable state, molecules interact with each other sufficiently with the help of thermal energy during the SA process. In experimental conditions (temperature ∼370 K^26,27 and ∼430 K^12–14), glycinate molecules move around on Cu surface in translational and rotational modes, and interact with each other by HB. The HB would continually break and re-bond, providing sufficient opportunities for molecules to search for stronger intermolecular interactions. This process, together with strong polarity compensation of glycinate, promotes formation of an anti-parallel HB network on Cu(001). Once formed, the structure is trapped as a stable phase even at very low temperatures. The fact that the structure we proposed is observed at a temperature as low as 5 K in experiments, implies that transition from our structure to the “ground-state” HT structure could be blocked by a large energy barrier. One can see that, essentially different from simple adsorption, the SA structures are thermodynamically stable when formed at finite temperature. Therefore, the SA structure is determined by the lowest energy at a finite temperature. Actually, the adsorption structure with the lowest energy at 0 K would not be reached during the SA process. We emphasize that the usual DFT calculations at 0 K is no longer valid for such a system, in other words, stable SA structures are not able to be obtained from the DFT total energy minimum.

B. The temperature effect and weak molecular interaction

In SA on a surface two key factors, temperature and the molecular interactions, combine together to determine the SAM structure. Our MD simulations have demonstrated that the temperature is not merely a third important parameter, but plays a crucial role during the molecular self-assembly at surfaces because the temperature substantially affects the M–S interactions and here reverses the interacting energy in the two structures, where the HT model has the lowest energy at 0 K while our structure has lower energy at RT.

Although the M–S interaction is much stronger than the M–M interaction, the weaker intermolecular interaction plays a dominant role for the glycinate SA arrangements on Cu(001) due to the influence of temperature. The thermal energy breaks the dominant role of the M–S interactions at 0 K and makes M–S strengths almost the same at RT, and then the weaker M–M interaction prevails. The M–S interaction determines the adsorbed glycinate molecular configuration in the tridentate fashion, while the M–M interaction determines the molecular arrangements. Therefore, the SA structure on surfaces at finite temperature are determined by the relatively weaker HB rather than the stronger interfacial interaction.

C. The role of the substrate

Finally, the substrate is crucial for forming a truly 2D SAM. Two conditions are required to be satisfied. One is that the interaction between the molecule and surface should be moderate. The substrate converts glycine to glycinate leading to increased interaction among them to self-organize in defined patterns. However, the interaction is not too strong so as to prevent molecules to move on the surface by thermal energy. Additionally, the surface lattice must match with periodicity of patterns on surface. The Cu(001) surface provides a perfect condition for SA of glycine molecules. Other noble metals, e.g. Au and Ag, are not able to dissociate the glycine molecule. Further, the Cu(001) surface accommodates various SA patterns in a comfortable way with typical lengths of strong and weak HBs.

V. Conclusions

In conclusion, we have clarified for the first time that the SAM on surface is thermodynamically stable which is determined by the lowest energy at finite temperature, and further revealed that the mechanism for self-assembly of glycine on Cu(001) is via molecular polarity implemented in terms of a full polarity compensation rule where its chirality is automatically adjusted. The optimization of the H-bonding environment leads to a unique antiparallel HB network of glycinates in a p(2 × 4) phase. We elucidate that thermal fluctuation at finite temperatures not only provides the mobility for molecules during the SA process, but more importantly it weakens the molecule–substrate interaction and leads the intermolecular interactions to assume a dominant role to orchestrate glycine self-assembly. The long-term controversy about competing phases, i.e., homochiral phase and heterochiral phase, as well as their relationships has been uniformly resolved in the same framework. The present work represents a distinct example that self assembly of molecules is driven by intermolecular interactions themselves, rather than being fixed by interactions with templates, even though the molecule–template interaction is stronger at 0 K. Although demonstrated for a small molecule on a simple surface, the SA mechanism and the rule revealed here are expected to have wider implications in understanding self-assembly of polar molecules with other metal templates^4,5 and of larger biomolecules in biologically relevant environments.

Acknowledgements

We acknowledge the useful discussions with W. S. Yang, I. Stich and Q. M. Zhang. This work was supported by the National Science Foundation of China (Grants No. 10774177, No. 10634070 and No. 11174297), and the National Basic Research Project (Grants No. 2010CB923002 and No. 2011CB922204), and the Fundamental Research Funds for the Central Universities, and the Research Funds of Renmin University of China.

References

1. J. V. Barth, G. Costantini and K. Kern, Nature, 2005, 437, 671.
2. F. Höök, B. Kasemo, M. Grunze and S. Zauscher, ACS Nano, 2008, 2, 2428.
3. M. Böhringer, K. Morgenstern, W. D. Schneider, R. Berndt, F. Mauri, A. De Vita and R. Car, Phys. Rev. Lett., 1999, 83, 324.
4. J. V. Barth, J. Weckesser, C. Cai, P. Günter, L. Bürgi, O. Jeandupeux and K. Kern, Angew. Chem., Int. Ed., 2000, 39, 1230.
5. J. Weckesser, A. DeVita, J. V. Barth, C. Cai and K. Kern, Phys. Rev. Lett., 2001, 87, 096101.
6. A. Kühnle, L. M. Molina, T. R. Linderoth, B. Hammer and F. Besenbacher, Phys. Rev. Lett., 2004, 93, 086101.
7. T. Yokoyama, S. Yokoyama, T. Kamikado, Y. Okuno and S. Mashiko, Nature, 2001, 413, 619.
8. S. Stepanow, M. Lingenfelder, A. Dmitriev, H. Spillmann, E. Delvigne, N. Lin, X. Deng, C. Cai, J. V. Barth and K. Kern, Nat. Mater., 2004, 3, 229.
9. J. A. Theobald, N. S. Oxtoby, M. A. Phillips, N. R. Champness and P. H. Beton, Nature, 2003, 424, 1029.
10. R. Madueno, M. T. Räisänen, C. Silien and M. Buck, Nature, 2008, 454, 618.
11. G. Pawin, K. L. Wong, K. Y. Kwon and L. A. Bartels, Science, 2006, 313, 961.
12. X. Zhao, Z. Gai, R. G. Zhao, W. S. Yang and T. Sakurai, Surf. Sci., 1999, 424, L347.
13. X. Zhao, H. Wang, R. G. Zhao and W. S. Yang, Mater. Sci. Eng., C, 2001, 16, 41.
14. V. Efstathiou and D. P. Woodruff, Surf. Sci., 2003, 531, 304.
15. P. Messina, A. Dmitriev, N. Lin, H. Spillmann, M. Abel, J. V. Barth and K. Kern, J. Am. Chem. Soc., 2002, 124, 14000.
16. R. G. Nuzzo and D. L. Allara, J. Am. Chem. Soc., 1983, 105, 4481.
17. C. D. Bain, E. B. Troughton, Y. T. Tao, J. Evall, G. M. Whitesides and R. G. Nuzzo, J. Am. Chem. Soc., 1989, 111, 321.
18. B. D. Gates, Q. B. Xu, M. Stewart, D. Ryan, C. G. Willson and G. M. Whitesides, Chem. Rev., 2005, 105, 1171.
19. J. C. Love, L. A. Estroff, J. K. Kriebel, R. G. Nuzzo and G. M. Whitesides, Chem. Rev., 2005, 105, 1103.
20. A. V. Zhukhovitskiy, M. G. Mavros, T. Van Voorhis and J. A. Johnson, J. Am. Chem. Soc., 2013, 135, 7418.
21. C. M. Crudden, et al., Nat. Chem., 2014, 6, 409.
22. J. L. Miller, Phys. Today, 2014, 67, 20.
23. E. Lindahl and M. S. P. Sansom, Curr. Opin. Struct. Biol., 2008, 18, 425.
24. T. Carpenter, P. J. Bond, S. Khalid and M. S. P. Sansom, Biophys. J., 2008, 95, 3790.
25. Y. Xue and G. Ali Mansoori, Int. J. Mol. Sci., 2010, 11, 288.
26. K. Kanazawa, A. Taninaka, O. Takeuchi and H. Shigekawa, Phys. Rev. Lett., 2007, 99, 216102.
27. K. Kanazawa, Y. Sainoo, Y. Konishi, S. Yoshida, A. Taninaka, A. Okada, M. Berthe, N. Kobayashi, O. Takeuchi and H. Shigekawa, J. Am. Chem. Soc., 2007, 129, 740.
28. K. Mae and Y. Morikawa, Surf. Sci., 2004, 553, L63.
29. M. S. Dyer and M. Persson, J. Phys.: Condens. Matter, 2008, 20, 312002.
30. Z. X. Hu, W. Ji and H. Guo, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 085414.
31. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter, 1993, 47, 558.
32. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15.
33. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169.
34. Y. Wang and J. P. Perdew, Phys. Rev. B: Condens. Matter, 1991, 44, 13298.
35. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
36. S. Meng, L. F. Xu, E. G. Wang and S. W. Gao, Phys. Rev. Lett., 2002, 89, 176104.
37. J. J. Yang, S. Meng, L. F. Xu and E. G. Wang, Phys. Rev. Lett., 2004, 92, 146102.
38. J. Tersoff and D. R. Hamann, Phys. Rev. B, 1985, 31, 805.
39. N. Nicoara, E. Roman, J. M. Gomez-Rodriguez, J. A. Martin-Gago and J. Mendez, Org. Electron., 2006, 7, 287.
40. We have checked the results by additional calculations that include van der Waals corrections and found the energy in HT model is still lower by 130 meV. The vdW interaction might be significant for the glycine molecule, but not for glycinate here. Thus, the van der Waals corrections do not affect our conclusion in this work.
41. See the ESI for geometries and simulated results.‡.

---

Footnotes

† PACS numbers: 81.16.Dn, 82.30.Rs, 68.43.Bc, 68.43.Hn.

‡ Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra26548k

§ These authors contributed equally.

---