Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Multiple Li+- and Mg2+-decorated PAHs: potential systems for reversible hydrogen storage†
Avik Ghosh,
Tanay Debnath,
Tamalika Ash and
Abhijit K. Das *
*
Department of Spectroscopy, Indian Association for the Cultivation of Science, Jadavpur, Kolkata-700032, India. E-mail: spakd@iacs.res.in
First published on 31st January 2017
Abstract
The hydrogen binding efficiency of multiple metal-ion-(Li+, Mg2+)-decorated small Polycyclic Aromatic Hydrocarbons (PAHs) has been investigated using Density Functional Theory (DFT). The CAM-B3LYP method and 6-311+G(d,p) basis set have been used for the systematic calculation of the interaction energy of the metal ion with the aromatic system (ΔE) and the average binding energy (ΔBE) of the hydrogen molecules to these metal-ion-decorated PAHs. Our results show that the aromatic ring current associated with a PAH can bind at most one pair of metal ions, with the metal ions ensconcing themselves with appreciable values of ΔE both on the same and opposite faces of a PAH with certain preferences. The ΔBE values associated with H2 binding on Li+-decorated systems are found to be almost similar for anthracene and phenanthrene, which are higher in comparison to naphthacene. The Mg2+-decorated counterparts, however, exhibit ΔBE values of around four to five times higher than the Li+-decorated ones. The nature of interaction between hydrogen molecules and metal ions is predicted by the topological analysis of the atoms in molecules formalism (AIM), employing an AIMAll program. The Natural Population Analysis (NPA) method is used for the evaluation of charge distribution between donor hydrogen molecules and acceptor metal ions. The value of charge transfer from H2 to metal ions (ΔECT) is evaluated employing Natural Bond Orbital (NBO) analysis. The charge transfer from the bonding orbital of the hydrogen molecule to the antibonding lone pair orbital of the metal ion is taken into account for stability of the complexes. All the complexes possess high gravimetric storage capacity, and are found to be maximum for Mg2+-decorated anthracene (9.6 wt% H2).
1. Introduction
Fossil fuels, viz., coal, oil and natural gas have bolstered confidence in supplying the vast majority of our needs for years. However, the non-renewable nature of fossil fuels and the increased energy demands have exerted pressure to think about shifting towards alternate renewable sources of power. Hydrogen is considered to be one of the most important alternate energy sources because of its non-polluting and renewable nature. It is found to be the most abundant element in the universe, and contains the highest energy density per unit mass, burns clean, producing only water. However, it should be noted here that practically H2 is not an energy source; rather it is an energy carrier. Due to its diffusive and buoyant nature, the safe and efficient storage of hydrogen is difficult. Therefore, the main challenge lies in designing efficient hydrogen storage systems with high gravimetric and volumetric hydrogen contents. An ideal hydrogen storage system should be lightweight, to which hydrogen can be delivered and can be taken out at moderate temperatures and pressures.1–3 The binding energy of H2 needs to be in the range of 20–40 kJ mol−1.4 The U.S. Department of Energy (DOE) had set a target of 6.0 wt% reversible hydrogen storage by 2010 and 9.0 wt% by 2015.5 Essentially, hydrogen gets adsorbed on materials in three different ways. It may remain in its molecular state with small binding energy value, as in case of physisorption.6,12–15 In chemisorption, the H2 molecule splits into atoms and thus the binding energy is higher.9–11 The third type is quasi-molecular binding, where the binding energy is in between the above two.48,49 The current options for hydrogen storage include metal hydrides (which is basically a ‘chemical’ hydrogen storage system),9,11,47 and porous materials like zeolites, carbon nanotubes,7,8 metal organic framework (MOF)15,52–61 and covalent organic framework (COF) materials,12–14 where physisorption of H2 molecules is observed.Polycyclic Aromatic Hydrocarbons (PAHs), a major component of interstellar dust, have been brought under observation over the years and their aromatic surfaces have been utilized for possible adsorption of molecular hydrogens.50 A number of MOFs have been developed both theoretically and experimentally, where small PAHs are used as organic linkers.43–45 The ligand subunits, by which MOFs are composed of, maintain their precursor (or pre-MOF) structures to a reasonable approximation.64 H2 adsorption or interaction with the naked or decorated organic linkers is a local interaction and depends highly on the local sites where the H2 molecule gets adsorbed. A single such molecule or the cluster model, rather than a continual matrix, should thus provide a reliable description of the quality or extent of interaction. Over the last decade or so, a significant number of studies on such pre-MOF structures have already been done, considering the aromatic surface only.4,21,24,25,62,63 Tran and co-workers first theoretically investigated the physisorption of H2 on the aromatic surfaces provided by ordinary small and large PAHs.51 Alkali metal doping onto the organic linker part of MOFs and on carbon based systems were studied widely in order to increase the binding interactions of the H2 molecules with these systems. Han et al. first proposed the idea of Li-decorated MOFs for reversible hydrogen storage at room temperature.20 Subsequently, a significant number of theoretical works were reported, showing the increase in interaction energies with the incorporation of light weight metal atoms like Li.16–20 Srinivasu et al. theoretically reported the significant increase in hydrogen adsorption ability of organic molecular systems upon decoration with alkali metal ions due to electron transfer from the metal to the carbon surface.21 They also concluded that the strength of interaction of H2 as well as the number of adsorbed H2 molecules increase on a charged surface with a certain degree of curvature, which can be easily achieved by decoration with metal ions. Performing Grand Canonical Monte Carlo (GCMC) simulations, Mavrandonakis et al. concluded that the Li is preferably located on the organic linker part and the Li-decorated MOF provides increased hydrogen uptake compared to undecorated analogue.22 In the same year, Dalach and coworkers reported that the Li+ ion interacts strongly with hydrogen molecules compared to neutral Li atoms.23 But their prediction showed that the Li is getting associated strongly with the metal oxide part and less with the organic linker part. Kolmann et al. investigated the interaction of the three hydrogen molecules with Li+-decorated benzene.4 Chandrakumar et al. studied the interaction of hydrogen molecules with alkali and alkaline earth metal ions in MH16 complexes and showed the interactions are mediated by simple electrostatic interactions.24 In our previous work, we have given the insight into H2 binding affinities of metal-ion-(Li+, Mg2+)-decorated substituted benzene systems.25 Very recently, Armakovic and co-workers have investigated the influence of modifications of sumanene on its hydrogen adsorption properties and reported changes in hydrogen storage properties when the benzylic positions are substituted with boron and nitrogen atoms.26
In the present investigation, we have explored the feasibility of hydrogen adsorption on metal-ion-(Li+, Mg2+)-decorated small Polycyclic Aromatic Hydrocarbons (PAHs). Inspired by the work of Tran and co-workers, we have chosen three small PAHs, namely, anthracene, phenanthrene and naphthacene for this present study and decorated their surfaces with metal ion. As stated by Kolmann et al., Li+-benzene serves a model system for the Li atom decoration of the BDC linker in MOF-5.4 So these PAHs can serve as good model systems for the MOFs where dicarboxylates of anthracene, phenanthrene and naphthacene are used as organic ligands. As evident from Fig. 1, naphthacene (tetracyclic aromatic hydrocarbon), anthracene (tricyclic aromatic hydrocarbon with three linearly fused rings) and phenanthrene (also tricyclic, but thermodynamically more stable isomer, where rings are connected angularly) possess multiple connected aromatic rings, thus providing possible sites for multiple metal decoration on a single adsorbent. The aim of our present work is, therefore, to create charged surface over PAHs by introducing multiple Li+ and Mg2+, predicting all possible sites where multiple Li+ and Mg2+ can be decorated and to check the viability of these decorated sites towards molecular hydrogens. We have carried out DFT calculations to examine the corresponding optimized geometries, atomic charges, interaction energy (ΔE) between metal ion and the rings of PAH and the binding energies (ΔBEs) of the adsorbed hydrogens. The interaction between the metal ion and hydrogen molecules has further been studied critically employing natural bond orbital (NBO) analysis and topological analysis of charge density. The nature of interaction between the metal ion and hydrogen molecule of each optimized structure has been studied using the topological analysis of atoms in molecules (AIM) formalism employing AIMAll program.
2. Computational details
All electronic structure and frequency calculations have been performed using Gaussian 09 (ref. 27) suite of quantum chemistry program. The DFT functionals considered for the systems under investigation are, namely, B3LYP,28,29 and CAM-B3LYP.30 All the complexes have been first optimized using B3LYP and then reoptimized using CAM-B3LYP. The hybrid B3LYP exchange correlation functional is the most widely used density functional, while the CAM-B3LYP functional of Handy and co-workers combines the hybrid B3LYP with the long-range correction (CAM = Coulomb-attenuating method). Grimme's dispersion effect (D3) has also been considered during the optimization process.All ab initio and DFT calculations associated with the binding of one H2 molecule to the metal-decorated PAHs have been carried out using 6-311+G(d,p)31,32 basis set. Frequency calculations have been performed to confirm that the resulting stationary points are real energy minima, without imaginary frequencies in their vibration spectra. The average interaction energy (ΔE) between metal ion pairs and PAH, the binding energy (ΔBE) per molecular hydrogen to the system65 and the successive binding energy (ΔBE(n)) per hydrogen, where in each step hydrogen molecules being added in pair, have been calculated using the following formulae:
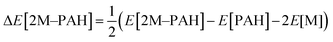 | (1) |
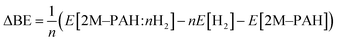 | (2) |
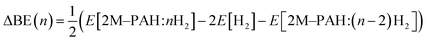 | (3) |
The effect of basis-set superposition error (BSSE) has been taken into account by the counterpoise procedure (CP)33 and the corrected binding energy is given by
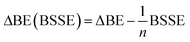 | (4) |
The nature of interaction between hydrogen molecules and metal ions has been predicted using the topological analysis of atoms in molecule formalism employing AIMAll program,34 where the classical definition of a ‘bond’ has been modified in the form of ‘bond path’ which basically indicates a line of maximum electron density linking bonded pairs of atoms in an equilibrium geometry.35,36 According to Bader, every classical structure is mirrored by a molecular graph consisting of bond paths, linking neighbouring atoms.37–39 Interaction of two atoms at a certain distance creates a critical point in the electron density, where the gradient, ∇ρ(r) vanishes, which is termed as bond critical point (BCP). In order to evaluate the strength of the interaction, two important parameters, viz., electron density ρ(r) and its Laplacian (∇2ρ) at the bond critical point (BCP) have been calculated. Electronic energy density [H(r)] is defined as the summation of kinetic energy density, G(r) (always positive) and potential energy density, ∇(r) (always negative), the ratio of which, i.e., −G(r)/V(r) predicts the nature of bond. The interaction is said to be non-covalent if −G(r)/∇(r) > 1 and partly covalent if 0.5 < −G(r)/∇(r) < 1. Negative values of both ∇2ρ and H(r) indicate the interaction to be strong, for medium interaction H(r) is negative but ∇2ρ is positive, and the interactions are weak when both are positive.
A more vivid picture of the nature of interaction is exhibited by employing natural bond orbital (NBO) analysis using NBO 6.0 program,40 which is implemented in Gaussian 09. The donor–acceptor (bond–antibond) charge transfer interaction,41 say i → j, is evaluated by the delocalization correction energy (ΔECT) calculated using second order perturbation theory:
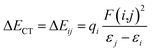 | (5) |
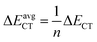 | (6) |
In eqn (5), F(i,j) is the off-diagonal Fock matrix element expressed in the NBO basis, qi is the donor orbital occupancy and εi and εj are the respective orbital energies. Eqn (6) gives the average delocalization correction energy, where n = 2, 4, 6, 8 (the number of hydrogen molecules adsorbed).
Since we are not working on a true MOF surface, but only on a pre-MOF model,64 we have not considered the weight of segments of MOF other than the active site, which is the aromatic surface provided by a PAH along with the metal ions. As the GCMC simulation calculates the weight capacity of the entire MOF, our model using DFT, in this respect, is completely different.
3. Results and discussion
In our recent theoretical study, we have studied the H2 binding affinities of metal-ion-decorated substituted benzene systems, with the special emphasis on hydrogen–metal interaction.25 In the present work, we extended the scope of our previous work by decorating different PAH systems having multiple rings with multiple metal ions, and thereby investigating the capability of hydrogen storage of such multiple metal-decorated PAH systems. Our first motive is to predict the possible number of metal ions that can be decorated and consequently locate their favourable sites over the rings.3.1. Favourable positions of Li+ and Mg2+
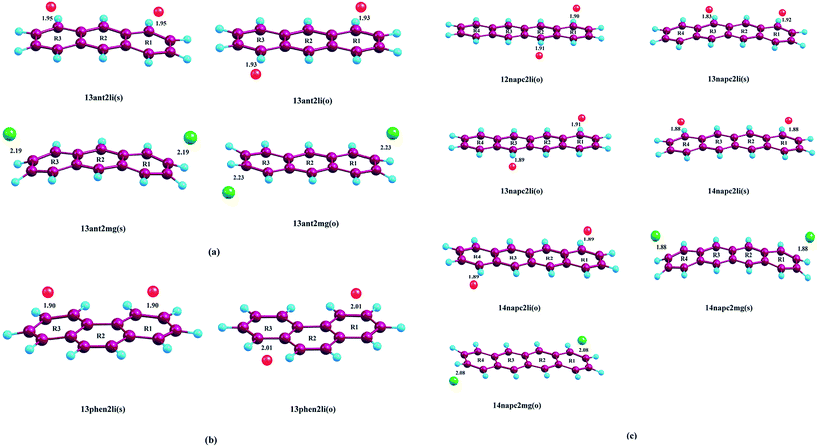
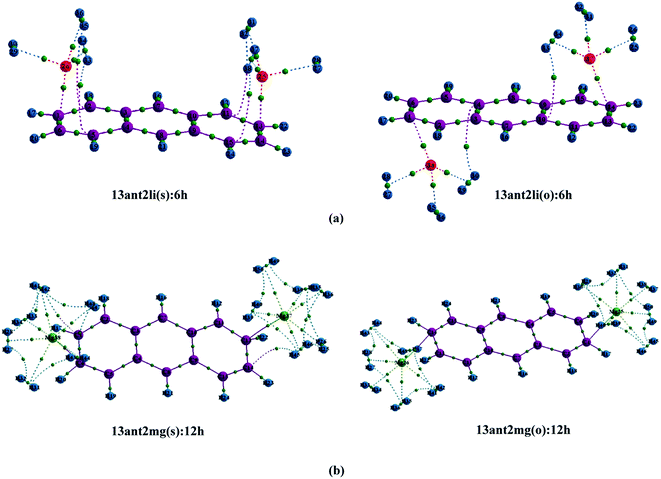
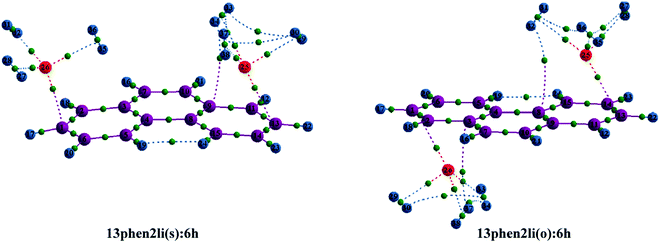
Initially, we have started exploring the property of multiple decorations by incorporating two metal ions on the opposite faces of the same aromatic ring but ended up with a positive value of interaction energy, indicating the process to be implausible. The attempt is also failed when we tried to bind two metal ions over the ‘R1–R2’ position either on the same face or on the opposite. However, interaction energies of −95.1 and −106.3 kJ mol−1, respectively, are observed when 2 Li+ ions are incorporated on the same and opposite faces over R1 and R3 (Table 1) of anthracene. The corresponding lithium-decorated structures are defined as 13ant2li(s) and 13ant2li(o), respectively. As apparent from Table 1, the decoration is more favourable in case of Mg2+ analogue, with interaction energies of −200.9 and −207.8 kJ mol−1, respectively on same and opposite faces, respectively; with the corresponding structures being designated as 13ant2mg(s) and 13ant2mg(o), respectively. Decoration with multiple Mg2+ ion is not possible on phenanthrene. However, for Li+ pairs on R1 and R3 of phenanthrene, the interaction energies are of −90.4 and −105.7 kJ mol−1 for the same and opposite faces respectively and the corresponding structures are defined as 13phen2li(s) and 13phenli(o). In this context, it is important to note that the Li+ ions prefer the centre of rings (ring-over site) while Mg2+ ions prefer the position over C–C bond (bond-over site). Fig. 1 depicts all the possible binding sites of Li+ and Mg2+ onto the small PAHs. The rings corresponding to the binding sites have also been enumerated.| System | ΔE (kJ mol−1) | Mn+-Ring distance (Å) | Charge on metal ion | ||
|---|---|---|---|---|---|
| 13ant2li(s) | −95.1 | 1.95 (R1) | 1.95 (R3) | 0.962 (R1) | 0.962 (R3) |
| 13ant2li(o) | −106.3 | 1.93 (R1) | 1.93 (R3) | 0.963 (R1) | 0.963 (R3) |
| 13ant2mg(s) | −200.9 | 2.19 (R1) | 2.19 (R3) | 1.838 (R1) | 1.838 (R3) |
| 13ant2mg(o) | −207.8 | 2.13 (R1) | 2.13 (R3) | 1.84 (R1) | 1.84 (R3) |
| 13phen2li(s) | −90.4 | 1.90 (R1) | 1.90 (R3) | 0.961 (R1) | 0.961 (R3) |
| 13phen2li(o) | −105.7 | 2.01 (R1) | 2.01 (R3) | 0.963 (R1) | 0.963 (R1) |
| 12napc2li(o) | −108.7 | 1.9 (R1) | 1.91 (R2) | 0.968 (R1) | 0.970 (R2) |
| 13napc2li(s) | −134.0 | 1.92 (R1) | 1.83 (R3) | 0.962 (R1) | 0.965 (R3) |
| 13napc2li(o) | −145.1 | 1.91 (R1) | 1.89 (R3) | 0.964 (R1) | 0.966 (R3) |
| 14napc2li(s) | −173.0 | 1.88 (R1) | 1.88 (R4) | 0.961 (R1) | 0.961 (R1) |
| 14napc2li(o) | −176.9 | 1.89 (R1) | 1.89 (R4) | 0.961 (R1) | 0.961 (R4) |
| 14napc2mg(s) | −411.0 | 1.88 (R1) | 1.88 (R4) | 1.82 (R1) | 1.82 (R1) |
| 14napc2mg(o) | −413.9 | 2.08 (R1) | 2.08 (R4) | 1.821 (R1) | 1.821 (R4) |
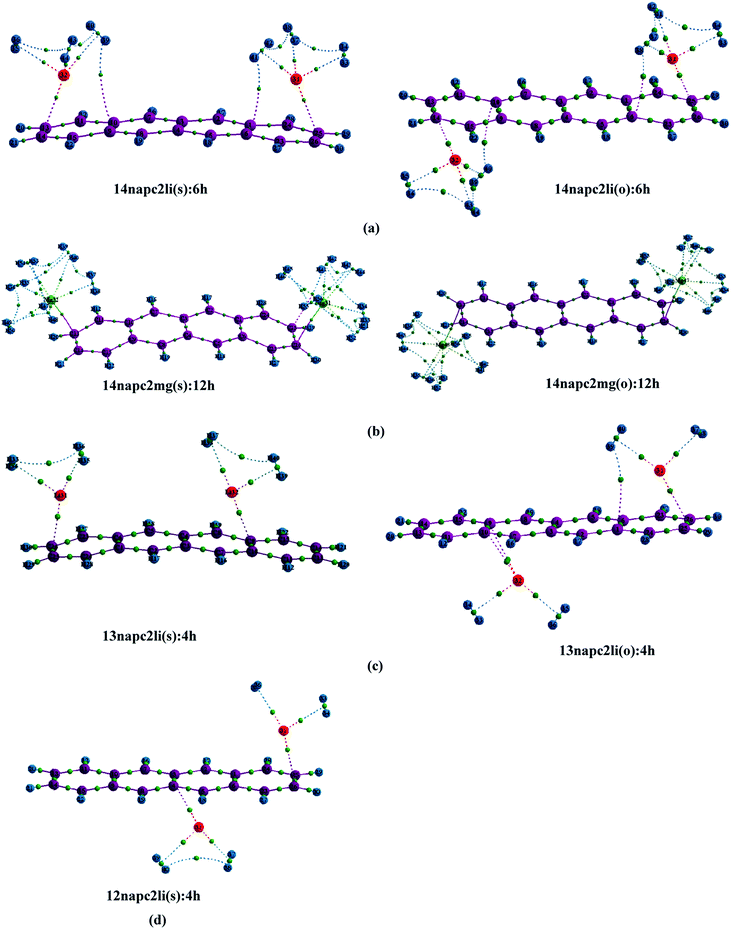
The successful implementation of this idea has encouraged us to work with the higher analogue of PAH, i.e., naphthacene, constituting of four adjacent aromatic rings. On fixing one Li+ ion on terminal ring (ring-1) of naphthacene, we move on to another Li+ from R2 to R3 to R4, placing it on the same and opposite faces to that of the first one. As evident from Fig. 1 and the calculated binding energy values from Table 1, there are three possible sites to posit one Li+ pair in naphthacene: opposite faces of ‘R1 and R2’, [12napc2li(o)], same and opposite faces of ‘R1 and R3’, [13napc2li(s) and 13napc2li(o)], same and opposite faces of ‘R1 and R4’, [14napc2li(s) and 14napc2li(o)]. Two Li+ ions do not ensconce on the same face of ‘R1 and R2’ probably due to electrostatic repulsion in the close vicinity. Mg2+ ion pairs, in fact, do not bind with ‘R1 and R2’ or on ‘R1 and R3’ either in same or opposite faces. However, Mg2+ ion pairs bind with ‘R1 and R4’ with binding energies of −411.0 and −413.9 kJ mol−1 for same and opposite faces, respectively. Thus, we encounter some sharp trends in binding energy values. The larger the size of the PAH or greater the separation between the two ions, higher is the interaction energy. The average interaction energy is also observed to be higher for a pair of divalent cation (Mg2+) compared to monovalent cation (Li+).
We have tried to increase the number of decorated metal ions beyond two in the systems under investigation, but the corresponding structures give positive value of average interaction energy, indicating the endeavour to be implausible.
3.2. Adsorption of molecular hydrogen on Li+ and Mg2+ decorated PAHs
In this section, we are going to discuss the interaction of molecular H2 with Li+ and Mg2+-decorated PAHs, where all the calculations have been performed using CAM-B3LYP functional. Fig. 2–4 depict the complexes with maximum number of H2 molecules for anthracene, phenanthrene and naphthacene respectively and their corresponding binding energy values are listed in Tables 2–4. The intermediate optimized geometries of H2 adsorbed Li+ and Mg2+-decorated PAHs are depicted in Fig. S1–S3 (see ESI†). In this study, each of the two metal centres are first allowed to bind one H2 molecule and the average binding energy (ΔBE) is calculated. Afterward, each metal is allowed to bind with the second molecule of H2 and again the ΔBE value is determined. In doing so, we have observed that a Li+ ion can bind maximum three molecules of H2, whereas for Mg2+ the limit extends up to six. During the H2 adsorption process, the H2 molecules adopt different orientations around the metal centres. When only one H2 molecule binds to the metal centre, it always remains on the top of the metal ion irrespective of the nature of the metal ion. However, when more than one H2 molecules are attached, to avoid the steric hindrance, the H2 molecules reorient themselves around the metal ions, where the axis of H2 molecules get tilted with respect to the plane of the aromatic rings. In the following sections, we are going to elaborate the entire phenomena.| System | ΔBE (kJ mol−1) | Charge on metal ion | ||
|---|---|---|---|---|
| 0 K, 1 atm | 298 K, 700 atm | |||
| 13ant2li(s):2h | −17.2 | −34.2 | 0.922 (R1) | 0.922 (R3) |
| 13ant2li(s):4h | −13.8 | −22.2 | 0.895 (R1) | 0.895 (R3) |
| 13ant2li(s):6h | −11.9 | −17.5 | 0.869 (R1) | 0.869 (R3) |
| 13ant2li(o):2h | −17.7 | −34.7 | 0.924 (R1) | 0.924 (R3) |
| 13ant2li(o):4h | −14.6 | −22.9 | 0.894 (R1) | 0.894 (R3) |
| 13ant2li(o):6h | −12.1 | −17.5 | 0.868 (R1) | 0.868 (R3) |
| 13ant2mg(s):2h | −73.0 | −95.0 | 1.785 (R1) | 1.785 (R3) |
| 13ant2mg(s):4h | −61.7 | −73.0 | 1.731 (R1) | 1.731 (R3) |
| 13ant2mg(s):6h | −55.1 | −62.4 | 1.686 (R1) | 1.686 (R3) |
| 13ant2mg(s):8h | −48.3 | −53.6 | 1.649 (R1) | 1.648 (R3) |
| 13ant2mg(s):10h | −41.6 | −45.9 | 1.618 (R1) | 1.618 (R3) |
| 13ant2mg(s):12h | −36.0 | −39.4 | 1.597 (R1) | 1.596 (R3) |
| 13ant2mg(o):2h | −73.0 | −95.5 | 1.787 (R1) | 1.787 (R3) |
| 13ant2mg(o):4h | −62.3 | −73.7 | 1.731 (R1) | 1.731 (R3) |
| 13ant2mg(o):6h | −55.4 | −62.8 | 1.686 (R1) | 1.686 (R3) |
| 13ant2mg(o):8h | −48.8 | −54.2 | 1.649 (R1) | 1.648 (R3) |
| 13ant2mg(o):10h | −42.2 | −46.5 | 1.618 (R1) | 1.618 (R3) |
| 13ant2mg(o):12h | −36.5 | −31.0 | 1.596 (R1) | 1.596 (R3) |
| System | ΔBE (kJ mol−1) | Charge on metal ion | ||
|---|---|---|---|---|
| 0 K, 1 atm | 298 K, 700 atm | |||
| 13phen2li(s):2h | −16.7 | −34.4 | 0.920 (R1) | 0.920 (R3) |
| 13phen2li(s):4h | −13.0 | −21.8 | 0.890 (R1) | 0.890 (R3) |
| 13phen2li(s):6h | −11.2 | −17.1 | 0.866 (R1) | 0.873 (R3) |
| 13phen2li(o):2h | −17.2 | −35.1 | 0.922 (R1) | 0.922 (R3) |
| 13phen2li(o):4h | −13.7 | −22.6 | 0.893 (R1) | 0.893 (R3) |
| 13phen2li(o):6h | −11.2 | −17.2 | 0.868 (R1) | 0.869 (R3) |
| System | ΔBE (kJ mol−1) | Charge on metal ion | ||
|---|---|---|---|---|
| 0 K, 1 atm | 298 K, 700 atm | |||
| 12napc2li(o):2h | −17.3 | −41.6 | 0.929 (R1) | 0.936 (R2) |
| 12napc2li(o):4h | −14.8 | −27.0 | 0.896 (R1) | 0.900 (R2) |
| 13napc2li(s):2h | −16.1 | −39.9 | 0.923 (R1) | 0.929 (R3) |
| 13napc2li(s):4h | −12.9 | −24.8 | 0.909 (R1) | 0.909 (R3) |
| 13napc2li(o):2h | −16.4 | −40.3 | 0.924 (R1) | 0.929 (R3) |
| 13napc2li(o):4h | −13.7 | −25.6 | 0.893 (R1) | 0.895 (R3) |
| 14napc2li(s):2h | −15.4 | −38.7 | 0.921 (R1) | 0.921 (R4) |
| 14napc2li(s):4h | −11.9 | −23.6 | 0.890 (R1) | 0.89 (R4) |
| 14napc2li(s):6h | −9.6 | −17.4 | 0.865 (R1) | 0.865 (R4) |
| 14napc2li(o):2h | −15.7 | −39.0 | 0.921 (R1) | 0.921 (R4) |
| 14napc2li(o):4h | −12.4 | −24.1 | 0.891 (R1) | 0.891 (R4) |
| 14napc2li(o):6h | −10.0 | −17.8 | 0.865 (R1) | 0.865 (R4) |
| 14napc2mg(s):2h | −65.2 | −94.8 | 1.777 (R1) | 1.777 (R4) |
| 14napc2mg(s):4h | −56.1 | −70.9 | 1.728 (R1) | 1.728 (R4) |
| 14napc2mg(s):6h | −49.4 | −59.3 | 1.689 (R1) | 1.689 (R4) |
| 14napc2mg(s):8h | −43.8 | −51.2 | 1.653 (R1) | 1.653 (R4) |
| 14napc2mg(s):10h | −37.3 | −43.2 | 1.628 (R1) | 1.628 (R4) |
| 14napc2mg(s):12h | −31.9 | −36.9 | 1.609 (R1) | 1.609 (R4) |
| 14napc2mg(o):2h | −65.8 | −95.2 | 1.778 (R1) | 1.778 (R4) |
| 14napc2mg(o):4h | −56.6 | −71.3 | 1.729 (R1) | 1.729 (R4) |
| 14napc2mg(o):6h | −49.9 | −59.7 | 1.688 (R1) | 1.688 (R4) |
| 14napc2mg(o):8h | −44.2 | −51.5 | 1.653 (R1) | 1.653 (R4) |
| 14napc2mg(o):10h | −37.6 | −43.5 | 1.627 (R1) | 1.627 (R4) |
| 14napc2mg(o):12h | −32.2 | −37.1 | 1.609 (R1) | 1.609 (R4) |
Table S1 (in ESI†) depicts the BSSE corrected successive H2 binding energy (ΔBE(n)) of Li+/Mg2+-decorated anthracene, phenanthrene and naphthacene.
3.3. NPA analysis
We have used the Natural Population Analysis (NPA) to evaluate the charge distribution on the metal ion due to the energy transfer occurring between the donor H2 molecules and the acceptor metal ions.42,46 In case of metal-decorated anthracene, the metal ion pairs on ‘R1–R3’ (either in same or in opposite faces) possess identical charges as both of them experience the same ring current from the aromatic substrate. In case of 13ant2li(s), the charge on lithium is 0.962 which decreases to 0.922, 0.895 and 0.869 after the consecutive addition of two, four and six molecules of hydrogen. Before the binding of H2 molecules, the charge on Mg2+ in 13ant2mg(s) is observed to be 1.838 which gradually decreases to 1.785, 1.731, 1.686, 1.648, 1.618 and 1.597 after the addition of two, four, six, eight, ten and twelve H2 molecules. As seen from Table 2, for both 13ant2li(o) and 13ant2mg(o), a trend similar to the above mentioned cases is observed. For 13ant2li(o), the charge of 0.963 on lithium decreases to 0.924, 0.894 and 0.868 after the adsorption of two, four and six molecules of H2; that is found to be 1.787, 1.731, 1.686, 1.649, 1.618 and 1.596 for 13ant2mg(o) after the accumulation of one, two, three, four, five and six pairs of H2 on each Mg, respectively.Like anthracene, a similar trend of NPA charges is observed for phenanthrene, where the metal decoration is restricted to Li+ only. As evident from Table 3, for 13phen2li(s), the NPA charge of 0.961 gets reduced to 0.920, 0.890 and 0.866 after consecutive binding of two, four and six molecular hydrogens. For 13phen2li(o), the calculated value of 0.963 before H2 adsorption decreases to 0.922, 0.893 and 0.868, respectively after adsorption of two, four and six H2 molecules.
Among the three binding sites of the metal ion pairs in naphthacene, i.e., ‘R1–R4’, ‘R1–R3’ and ‘R1–R2’, the charges on metal ions are same for the first one only as both the metal ions are placed under same ring current environment. For the latter two, charges on the two metals vary slightly because of their positions in two different ring current environment. In case of 14napc2li(s) and 14napc2li(o), the charge on both the Li+ ions is found to be 0.961. In 13napc2li(s), the charge on Li decorated on ‘R1’ is 0.962 and that on ‘R3’ is 0.965, while those in case of 13napc2li(o) are 0.964 and 0.966 on the Li ions decorated on ‘R1’ and ‘R3’ respectively, which are slightly higher than the 14napc2li(s) and 14napc2li(o) analogues, but lower than 12napc2li(o) having Li metal ions with charges 0.968 and 0.970 on ‘R1’ and ‘R2’. Hence, it is apparent that the adsorption of H2 molecules on the Li metal ions results in the sharp decrease of electronic charge from 0.921 to 0.891 to 0.865 for both 14napc2li(s) and 14napc2li(o). Similar trend is observed in 13napc2li(s), 13napc2li(o) and 12napc2li(o), as evident from Table 4. For the Mg2+-decorated naphthacene systems, namely, 14napc2mg(s) and 14napc2mg(o), the charges on the metal ions are 1.820 and 1.821, which decrease to 1.777, 1.728, 1.689, 1.653, 1.628 and 1.609 after the adsorption of two, four, six, eight, ten and twelve molecules of H2, respectively.
3.4. NBO analysis
The NBO analysis is an efficient tool for investigating the energy transfer phenomena between the bonding orbital of H2 molecule and the antibonding orbitals of metal ions. In Table 5, we have tabulated all the energy transfer values calculated for all Li+ and Mg2+-decorated PAHs. In case of Li+-decorated anthracenes, the ΔEavgCT values for the first pair of H2 molecules are found to be 51.9 and 53.0 kJ mol−1, respectively for 13ant2li(s) and 13ant2li(o), which increase to 57.2 and 61.8 kJ mol−1 for second and third pair of H2 adsorption in case of 13ant2li(s); while for 13ant2li(o), the respective values become 59.2 and 62.1 kJ mol−1 respectively. In case of the Mg2+ analogues, for 13ant2mg(s), the ΔEavgCT values are 123.1, 132.5, 135.6, 132.9, 121.7 and 107.7 kJ mol−1 after the adsorption of two, four, six, eight, ten and twelve H2 molecules, respectively, whereas for 13ant2mg(o), the corresponding ΔEavgCT values are 123.3, 133.5, 135.7, 133.1, 102.2 and 108 kJ mol−1. For 13phen2li(s), the observed values are 53.2, 57.5 and 60.2 kJ mol−1 for the adsorption of two, four and six H2 molecules, which are 54.3, 58.5 and 60.1 kJ mol−1 for 13phen2li(o). In case of 14napc2li(s) and 14napc2li(o), when the first pair of H2 molecules are adsorbed, the ΔEavgCT values are 51.6 and 52.2 kJ mol−1, respectively. So, with increasing number of adsorbed H2 molecules, the molecules get tilted and the values of ΔEavgCT are found to be increased, as observed in the earlier cases. In 14napc2li(s):6h and 14napc2li(o):6h, the ΔEavgCT values are increased to 59.8 and 60.4 kJ mol−1, respectively. In the Mg2+ analogue, for 14napc2mg(s), the value increases from 115.9 to 128.3 kJ mol−1 with the adsorption of two to six H2 molecules and decreases slightly to 111.5 to 121.7 to 107.7 kJ mol−1 after adsorption of eight to ten to twelve molecules of H2. The corresponding values observed for 14napc2mg(o) are 116.0, 126.7, 129.3, 126.5, 102.2 and 108 kJ mol−1 respectively. 13napc2li(s) gives ΔEavgCT values of 50.5 and 41.5 kJ mol−1 for two and four hydrogen molecules, while 51.2 and 59.4 kJ mol−1 are calculated for 13napc2li(o). Almost similar trend is observed for 12napc2li(o):2h and 12napc2li(o):4h with ΔEavgCT values of 52.2 and 60.1 kJ mol−1 respectively.
| System | ΔECT (kJ mol−1) | System | ΔECT (kJ mol−1) |
|---|---|---|---|
| 13ant2li(s):2h | 51.9 | 14napc2li(s):2h | 51.6 |
| 13ant2li(s):4h | 57.2 | 14napc2li(s):4h | 58.5 |
| 13ant2li(s):6h | 61.8 | 14napc2li(s):6h | 59.8 |
| 13ant2li(o):2h | 53.0 | 14napc2li(o):2h | 52.2 |
| 13ant2li(o):4h | 59.2 | 14napc2li(o):4h | 59.2 |
| 13ant2li(o):6h | 62.1 | 14napc2li(o):6h | 60.4 |
| 13ant2mg(s):2h | 123.1 | 14napc2mg(s):2h | 115.9 |
| 13ant2mg(s):4h | 132.5 | 14napc2mg(s):4h | 126.3 |
| 13ant2mg(s):6h | 135.6 | 14napc2mg(s):6h | 128.3 |
| 13ant2mg(s):8h | 132.9 | 14napc2mg(s):8h | 111.5 |
| 13ant2mg(s):10h | 121.7 | 14napc2mg(s):10h | 121.7 |
| 13ant2mg(s):12h | 107.7 | 14napc2mg(s):12h | 107.7 |
| 13ant2mg(o):2h | 123.3 | 14napc2mg(o):2h | 116 |
| 13ant2mg(o):4h | 133.5 | 14napc2mg(o):4h | 126.7 |
| 13ant2mg(o):6h | 135.7 | 14napc2mg(o):6h | 129.3 |
| 13ant2mg(o):8h | 133.1 | 14napc2mg(o):8h | 126.5 |
| 13ant2mg(o):10h | 122.2 | 14napc2mg(o):10h | 122.2 |
| 13ant2mg(o):12h | 108.0 | 14napc2mg(o):12h | 108.0 |
| 13phen2li(s):2h | 53.2 | 13napc2li(s):2h | 50.5 |
| 13phen2li(s):4h | 57.5 | 13napc2li(s):4h | 41.5 |
| 13phen2li(s):6h | 60.2 | 13napc2li(o):2h | 51.2 |
| 13phen2li(o):2h | 54.3 | 13napc2li(o):4h | 59.4 |
| 13phen2li(o):4h | 58.5 | 12napc2li(o):2h | 12.5 |
| 13phen2li(o):6h | 60.1 | 12napc2li(o):4h | 14.4 |
Thus, in all the three systems, the amount of energy transfer in Mg2+-decorated systems is found to be much higher, about twice, than that in the Li+-decorated systems. The value is independent of whether the metal ions are decorated either in same or opposite faces. In case of Li+-decorated naphthacenes, the value remains almost same for all different binding sites.
3.5. AIM analysis
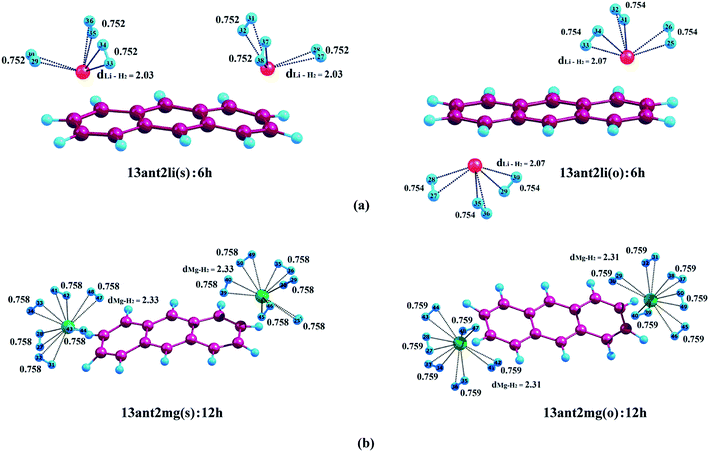
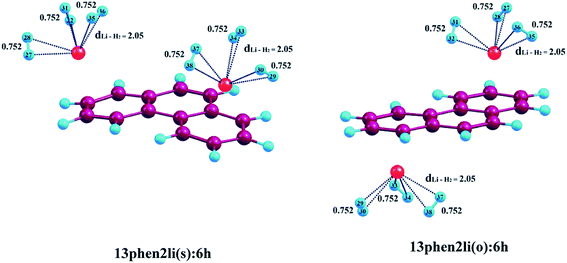
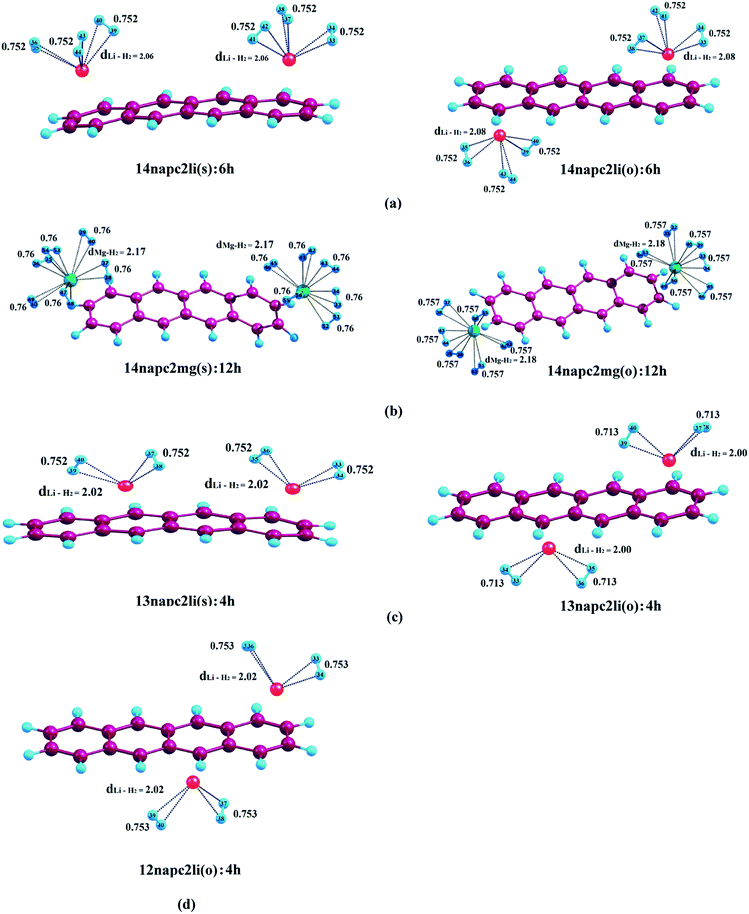
In order to perceive better physical understanding of the H2-metal ion interaction of the Li+ and Mg2+-decorated PAHs, we have opted for AIM analysis. Tables S2–S4† exhibit the electron density and the Laplacian of charge density (∇2ρ) values at the H2–metal ion BCP of the complexes. The molecular graphs of the decorated systems with maximum number of adsorbed hydrogen molecules on them are illustrated in Fig. 5–7. As evident from Tables S2–S4,† positive values of both ∇2ρ and H(r) at the respective BCPs suggest weak interactions between the metal ions and the adsorbed hydrogen molecules. In our systems, the values of charge density and ∇2ρ lie within the range of 0.008–0.013 and 0.043–0.068, respectively for the Li+-decorated systems, and those for Mg2+-decorated systems lie within the range of 0.09–0.019 and 0.028–0.084, respectively, indicating the interaction to be greater than van der Waals interaction in each case. Comparatively higher values of charge density and ∇2ρ indicate stronger charge shift type interactions among H2–Mg2+ complexes than H2–Li+ analogues. Also, the ratio −G(r)/V(r) is greater than 1 in all cases, connoting the non-covalent type of H2–metal ion interactions.4. Conclusion
In the present work, we have explored the possibility of hydrogen adsorption on three Li+ and Mg2+-decorated polycyclic aromatic hydrocarbons (PAHs): anthracene, phenanthrene and naphthacene. The main objective is to decorate the PAHs with multiple metal ions, and we are successful in decorating maximum two metal ions with appreciable interaction energies. All favourable sites for the decoration of metal ion pairs have been investigated for three aromatic systems. The Li+ ions in pairs are found to prefer ring-over site, while bond-over site is observed to be more preferable for Mg2+ ions in pairs. Anthracene is found to bind both Li+ and Mg2+ ions on ‘R1–R3’ positions both at same as well as opposite faces, but phenanthrene binds only Li+ on ‘R1–R3’ position at same and opposite faces, but not Mg2+, probably due to electrostatic repulsion arising when the two Mg2+ ions on terminal rings get too closer. In case of naphthacene, ‘R1–R4’ position is feasible for decoration of both Li+ and Mg2+ on both same and opposite faces. In addition to the terminal rings of naphthacene, decoration of Li+ ion pair is feasible at the same and opposite faces of ‘R1–R3’ and only at the opposite faces of ‘R1–R2’ position. However, two Mg2+ ions could not be decorated on these sites. Each Mg2+ and Li+ ion is found to bind 4 and 3 molecular hydrogens respectively when decorated on the terminal ring, but Li+ ions of 13napc2li(o), 13napc2li(s) and 12napc2li(o) bind only 2 molecular hydrogens. The interaction energy of the metal ions with the aromatic rings increases as the distance between the pairs increases, or on enlarging the aromatic systems. Among the three PAHs, the largest binding energies are noted when anthracene is decorated with Li+ or Mg2+. The binding energy is found to be higher in case of Mg2+-decorated PAHs compared to the Li+ analogues. The gravimetric storage capacity is found to be maximum for the Mg2+-decorated systems of anthracene and naphthacene possessing 9.6 and 8%, respectively, with average binding energies around −36 and −32 kJ mol−1 per hydrogen, that are optimal for reversible hydrogen storage. From the NBO analysis, it is observed that considerable amount of charge transfer occurs from the bonding orbital of hydrogen molecule to the antibonding lone pair orbital of metal ion, which is greater in case of the Mg2+-decorated systems compared to Li+ analogues. We had endeavoured decorating more than two metal ions on pentacene, possessing five fused adjacent aromatic rings, but the attempt was failed. So, decorating only two metal ions on large PAHs would not be a wise attempt as it leads to further decrease in gravimetric storage capacity. Based on our DFT calculations, Mg2+-decorated anthracene can be considered as the best candidate among the small metal ion decorated PAHs for reversible hydrogen storage due to its optimal binding energy and maximum hydrogen binding ability; thus, it can be considered as modified organic linker which may help developing MOFs in future that can entrap and release H2 molecules reversibly at moderate temperature and pressure.Acknowledgements
AG is grateful to the University Grant Commission (UGC), TD and TA are grateful to the Council of Scientific and Industrial Research (CSIR) and, Government of India, for providing them research fellowships. Thanks are due to Tahamida Banu for her assistance and helpful discussions. AKD is grateful to the Council of Scientific & Industrial Research (CSIR), Govt. of India, for a research grant under scheme number: 01(2846)/16/EMR-II.References
- G. W. Crabtree, M. S. Dresselhaus and M. V. Buchanan, Phys. Today, 2004, 57, 39–44 CrossRef CAS.
- M. Felderhoff, C. Weidenthaler, R. von Helmolt and U. Eberle, Phys. Chem. Chem. Phys., 2007, 9, 2643–2653 RSC.
- P. Kowalczyk, R. Holyst, M. Terrones and H. Terrones, Phys. Chem. Chem. Phys., 2007, 9, 1786–1792 RSC.
- S. J. Kolmann, B. Chan and M. J. T. Jordan, Chem. Phys. Lett., 2008, 467, 126–130 CrossRef CAS.
- US Department of Energy, Hydrogen, Fuel Cells and Infrastructure Technologies Program: Multi-year Research, Development, and Demonstration Plan, 2007 Search PubMed.
- S. Hamel and M. Cote, J. Chem. Phys., 2004, 121, 12618–12625 CrossRef CAS PubMed.
- H.-M. Cheng, Q.-H. Yang and C. Liu, Carbon, 2001, 39, 1447–1454 CrossRef CAS.
- F. E. Pinkerton, B. G. Wicke, C. H. Olk, G. G. Tibbetts, G. P. Meisner, M. S. Meyer and J. F. Herbst, J. Phys. Chem. B, 2000, 104, 9460–9467 CrossRef CAS.
- C. Fellay, P. J. Dyson and G. Laurenczy, Angew. Chem., Int. Ed., 2008, 120, 4030–4032 CrossRef.
- S.-I. Orimo, Y. Nakamori, J. R. Eliseo, A. Züttel and C. M. Jensen, Chem. Rev., 2007, 107, 4111–4132 CrossRef CAS PubMed.
- L. K. Wagner, E. H. Majzoub, M. D. Allendorf and J. C. Grossman, Phys. Chem. Chem. Phys., 2012, 14, 6611–6616 RSC.
- F. Li, J. Zhao, B. Johansson and L. Sun, Int. J. Hydrogen Energy, 2010, 35, 266–271 CrossRef CAS.
- E. Klontzas, E. Tylianakis and G. E. Froudakis, Nano Lett., 2010, 10, 452–454 CrossRef CAS PubMed.
- S. S. Han, H. Furukawa, O. M. Yaghi and W. A. Goddard, J. Am. Chem. Soc., 2008, 130, 11580–11581 CrossRef CAS PubMed.
- S. S. Han, W.-Q. Deng and W. A. Goddard, Angew. Chem., Int. Ed., 2007, 46, 6289–6292 CrossRef CAS PubMed.
- M. Barbatti, G. Jalbert and M. A. C. Nascimento, J. Chem. Phys., 2001, 114, 2213–2218 CrossRef CAS.
- G. Mpourmpakis, E. Tylianakis and G. E. Froudakis, Nano Lett., 2007, 7, 1893–1897 CrossRef CAS PubMed.
- Q. Sun, P. Jena, Q. Wang and M. Marquez, J. Am. Chem. Soc., 2006, 128, 9741–9745 CrossRef CAS PubMed.
- G. E. Froudakis, Nano Lett., 2001, 1, 531–533 CrossRef CAS.
- S. S. Han and W. A. Goddard, J. Am. Chem. Soc., 2007, 129, 8422–8423 CrossRef CAS PubMed.
- K. Srinivasu, K. R. S. Chandrakumar and S. K. Ghosh, ChemPhysChem, 2008, 10, 5832–5839 CAS.
- A. Mavrandonakis and W. Klopper, J. Phys. Chem. C, 2008, 112, 11580–11585 CAS.
- P. Dalach, H. Frost, R. Q. Snurr and D. E. Ellis, J. Phys. Chem. C, 2008, 112, 9278–9284 CAS.
- K. R. S. Chandrakumar and S. K. Ghosh, Chem. Phys. Lett., 2007, 447, 208–214 CrossRef CAS.
- T. Banu, D. Ghosh, T. Debnath, K. Sen and A. K. Das, RSC Adv., 2015, 5, 57647–57656 RSC.
- S. Armakovic, S. J. Armakovic, S. Pelemis and D. Mirjanic, Phys. Chem. Chem. Phys., 2016, 18, 2859–2870 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford, CT, USA, 2009.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- A. D. McLean and G. S. Chandler, J. Chem. Phys., 1980, 72, 5639–5648 CrossRef CAS.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- T. A. Keith, AIMAll, 14.06.21, TK Gristmill Software, Overland Park, KS, 2013, http://www.aim.tkgristmill.com Search PubMed.
- R. F. W. Bader, J. Phys. Chem. A, 2007, 111, 7966–7972 CrossRef CAS PubMed.
- F. Weinhold and C. R. Landis, Discovering Chemistry with Natural Bond Orbitals, John Wiley & Sons, Inc., Hoboken, New Jersey, 2012 Search PubMed.
- R. F. W. Bader, J. Phys. Chem. A, 1998, 102, 7314–7323 CrossRef CAS.
- J. Hernández-Trujillo and R. F. W. Bader, J. Phys. Chem. A, 2000, 104, 1779–1794 CrossRef.
- R. F. W. Bader, J. Phys. Chem. A, 2009, 113, 10391–10396 CrossRef CAS PubMed.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO6.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, USA, 2013 Search PubMed.
- F. Weinhold and C. R. Landis, Discovering Chemistry with Natural Bond Orbitals, John Wiley & Sons, Inc., Hoboken, New Jersey, 2012 Search PubMed.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS.
- S. Ma, D. Sun, J. M. Simmons, C. D. Collier, D. Yuan and H.-C. Zhou, J. Am. Chem. Soc., 2008, 130, 1012–1016 CrossRef CAS PubMed.
- I. M. Walton, J. M. Cox, C. A. Benson, D. G. Patel, Y. S. Chen and J. B. Benedict, New J. Chem., 2016, 40, 101–106 RSC.
- R. Warmbier, A. Quandt and G. Seifert, J. Phys. Chem. C, 2014, 118, 11799–11805 CAS.
- F. Maseras and K. Morokuma, Chem. Phys. Lett., 1992, 195, 500–504 CrossRef CAS.
- S.-I. Orimo, Y. Nakamori, J. R. Eliseo, A. Züttel and C. M. Jensen, Chem. Rev., 2007, 107, 4111–4132 CrossRef CAS PubMed.
- Q. Wang and P. Jena, J. Phys. Chem. Lett., 2012, 3, 1084–1088 CrossRef CAS PubMed.
- B. Pathak, K. Pradhan, T. Hussain, R. Ahuja and P. Jena, ChemPhysChem, 2012, 13, 300–304 CrossRef CAS PubMed.
- K. Srinivasu, K. R. S. Chandrakumar and S. K. Ghosh, ChemPhysChem, 2009, 10, 427–435 CrossRef CAS PubMed.
- F. Tran, J. Weber, T. A. Wesolowski, F. Cheikh, Y. Ellinger and F. Pauzat, J. Phys. Chem. B, 2002, 106, 8689–8696 CrossRef CAS.
- J. L. C. Rowsell and O. M. Yaghi, Angew. Chem., Int. Ed., 2005, 44, 4670–4679 CrossRef CAS PubMed.
- A. Kuc, T. Heine, G. Seifert and H. A. Duarte, Chem.–Eur. J., 2008, 14, 6597–6600 CrossRef CAS PubMed.
- G. Garberoglio, A. I. Skoulidas and J. K. Johnson, J. Phys. Chem. B, 2005, 109, 13094–13103 CrossRef CAS PubMed.
- J. L. C. Rowsell, J. Eckert and O. M. Yaghi, J. Am. Chem. Soc., 2005, 127, 14904–14910 CrossRef CAS PubMed.
- O. Hübner, A. Glöss, M. Fichtner and W. Klopper, J. Phys. Chem. A, 2004, 108, 3019–3023 CrossRef.
- Q. Yang and C. Zhong, J. Phys. Chem. B, 2006, 110, 655–658 CrossRef CAS PubMed.
- M. Dincă, A. Dailly, Y. Liu, C. M. Brown, D. A. Neumann and J. R. Long, J. Am. Chem. Soc., 2006, 128, 16876–16883 CrossRef PubMed.
- S. S. Han, H. Furukawa, J. L. Mendoza-Cortes and W. A. Goddard, J. Am. Chem. Soc., 2009, 38, 1460–1476 CAS.
- J. L. C. Rowsell, A. R. Millward, K. S. Park and O. M. Yaghi, J. Am. Chem. Soc., 2004, 126, 5666–5667 CrossRef CAS PubMed.
- J. L. C. Rowsell and O. M. Yaghi, J. Am. Chem. Soc., 2006, 128, 1304–1315 CrossRef CAS PubMed.
- P. Verma, X. Xu and D. J. Truhlar, J. Phys. Chem. C, 2013, 117, 12648–12660 CAS.
- T. A. Maark and S. Pal, Int. J. Hydrogen Energy, 2010, 35, 12846–12857 CrossRef CAS.
- E. Tsivion, J. R. Long and M. H.-Gordon, J. Am. Chem. Soc., 2014, 136, 17827–17835 CrossRef CAS PubMed.
- B. Xu, X. L. Lei, G. Liu, M. S. Wu and C. Y. Ouyang, Int. J. Hydrogen Energy, 2014, 39, 17104–17111 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6ra25746a |
| This journal is © The Royal Society of Chemistry 2017 |