Structural evolution of FeH₄ under high pressure

Abstract

The solid inner core of Earth is mainly composed of an iron-rich alloy with nickel and some lighter elements like hydrogen, carbon, and oxygen, but the exact composition and chemical reactions are still elusive. Hydrogen has been proposed as the main element responsible for the density deficit observed in the Earth’s inner core. Moreover, the solubility of hydrogen in iron increases considerably with increasing pressure. Here, we systematically investigated global energetically stable structures of FeH₄ in the pressure range of 80–400 GPa using a first-principles structural search. A transition from an insulated α-phase to a metallic β-phase and then to a semi-conductive γ-phase was predicted. Interestingly, we find a superconducting state in the β-phase with a transition temperature of 1.70 K at 109.12 GPa. The results are useful for investigating the stable phases and equation of state in the Fe–H system, which are relevant to the Earth’s core.

---

I. Introduction

The determination of the chemical composition of the Earth and other planets has been one of the key issues for geoscientists, physicists, chemists, and materials scientists for several decades. The Earth’s inner core is believed to be composed of iron-based alloys. However, the density of the Earth’s inner core is 2–5% lower than that of pure Fe at relevant pressures and temperatures according to geophysical data.^1–6 To explain these differences, the Earth’s inner core might also contain a certain amount of light elements, where the likeliest candidates are H, C, O, S and Si.⁴ Particularly, hydrogen is the fundamental element of the Earth’s core, and as a consequence, hydrogen could be the main element responsible for the density deficit observed in the Earth’s inner core.

Under pressure experimental studies are scarce because of technical difficulties. Depending on the experimental conditions, FeH has been synthesized into different close-packed phases (dhcp), hcp, and face-centered cubic, and at least up to 80 GPa the most stable phase has the double hexagonal close-packed structure.^7–11 Recently, cubic FeH₃ was observed using X-ray diffraction above 86 GPa.¹² Moreover, the solubility of hydrogen in iron increases considerably with increasing pressure.¹³ In a recent theoretical study, FeH₄ with space group P2₁/m has been proposed in a pressure range of 300–400 GPa.¹³ However, its crystal structure and electronic properties in a broader pressure range need to be confirmed and studied. Therefore, with the help of theoretical calculations, predictions of the possible chemical reactions and structures of the Fe–H system may help to understand the density deficit observed in the Earth’s inner core.

In this work, we present an extensive structure search to identify the crystal structure of FeH₄ by using the developed CALYPSO method, which has succeeded in predicting the crystal structures of various systems. Our work shows that FeH₄ crystallizes in the cubic P2₁3 (α-phase) structure up until 109.12 GPa and undergoes structural transitions to the orthorhombic Imma (β-phase) structure up until 241.72 GPa, then to the monoclinic P2₁m (γ-phase) structure. The phonon-mediated superconducting behavior of the β-phase was revealed by exploring the electron–phonon coupling. We hope that our study provides guidance for experimental groups aiming to synthesize novel crystal stoichiometry under high pressure. The present work establishes the comprehensive understanding of the structures and properties of FeH₄ under the Earth’s core pressure.

II. Computational details

The search for stable high pressure structures of the FeH₄ system was based on the global minimization of free energy surfaces using ab initio total energy calculations and the particle-swarm-optimization scheme as implemented in the CALYPSO (crystal structure analysis by particle swarm optimization) code.^14–19 The method has successfully predicted the high-pressure structures of various systems, ranging from elements to binary and ternary compounds.^20,21 During structure relaxations within CALYPSO simulations, we used homogeneous Monkhorst–Pack²² k-point meshes with a reciprocal-space resolution of 2π × 0.05 Å⁻¹ and Methfessel–Paxton²³ electronic smearing with 0.2 eV. The first-principles energetic calculations were carried out using density functional theory (DFT) with the Perdew–Burke–Ernzerhof exchange–correlation and employing the projector-augmented wave method, using the Vienna ab initio simulation package (VASP).^24–27 For Brillouin zone integration, we used the Monkhorst–Pack scheme and checked the convergence of the ground state calculations with uniformly increasing k-point meshes for each structure.²⁸ We used a cutoff energy of 800 eV for the expansion of the wave function into the plane-wave basis-set. Monkhorst–Pack k-point meshes with a denser sampling of 2π × 0.03 Å⁻¹ were chosen to achieve the total energy convergence of less than 1 meV per atom. The phonon calculations were carried out by using a supercell approach as implemented in the PHONOPY code.²⁹ This method uses the Hellman–Feynman forces calculated from the optimized supercell through VASP.

III. Results and discussion

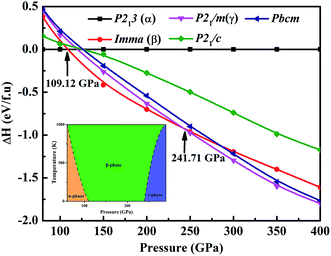
We performed variable-cell structure predictions with a simulation cell size of 2 and 4 formula units at a pressure of 80, 100, 200, 300 and 400 GPa. Under the considered pressure range, three new low-enthalpy structures with space groups cubic primitive P2₁3 (α-phase), orthorhombic Imma (β-phase) and monoclinic P2₁m (γ-phase) were unraveled. Fig. 1 shows the calculated enthalpy per formula unit for the various structures at different pressures. As can be seen from Fig. 1, the α-phase is the most stable structure from 80 to 109.12 GPa, and the β-phase becomes more favorable in the pressure range of 109.12 to 241.71 GPa, and above this the γ-phase is energetically superior to the β-phase up until 400 GPa. No imaginary frequency is observed throughout the Brillouin zones, which indicates that the three novel phases are dynamically stable in the pressure region. We also performed quasi-harmonic free-energy calculations to take into account the temperature effects, with phonon spectra computed using the finite-displacement method. The calculated pressure versus temperature phase diagram is shown in the inset of Fig. 1. From the results in the high-temperature region, the α- and γ-phase have a smaller dynamically stable range, while the β-phase has a larger dynamically stable range. For example, at a temperature of 500 K, the phase transitions from the α-phase to β-phase to γ-phase occur at 89.21 GPa and 255.37 GPa, respectively. Our results established the phase stability at a pressure of 400 GPa and a temperature of 1000 K. The current simulation environment reached the Earth’s internal core pressure (330–364 GPa).

Fig. 1 The calculated enthalpies per formula unit of various structures as a function of pressure with respect to our predicted FeH₄ P2₁3 structure (α-phase). Inset: the calculated pressure versus temperature phase diagram.

The atomic arrangements of the competing structures are shown in Fig. 2. The optimized structure parameters at related pressures are listed in Table 1. The α-phase has a cubic primitive symmetry, with a = b = c = 4.061 Å (Z = 4) at 80 GPa (Fig. 2(a)). Four Fe atoms occupy the Wyckoff 4a site and sixteen H atoms lie in the 4a and 12b sites in the unit cell. In this structure, each Fe atom is coordinated to six H atoms in a trigonal prismatic environment, connected by a hydrogen bridge. The Fe–H distances are 1.587 Å and 1.526 Å at 80 GPa. In the case of the β-phase, it belongs to an orthorhombic space group, with lattice parameters of a = 2.400 Å, b = 3.225 Å, and c = 7.967 Å at 109.12 GPa (Fig. 2(b)). Four Fe atoms occupy the Wyckoff 4e site and six H atoms lie in the 4e, 8h, and 4b sites in the unit cell. Each Fe atom is coordinated to six H atoms in a unit cell. The Fe–H distances are 1.616 Å and 1.628 Å. In the case of the γ-phase, its equilibrium lattice parameters are a = 2.373 Å, b = 3.107 Å, and c = 3.567 Å, and β = 77.772° at 241.71 GPa (Fig. 2(c)). Two Fe atoms occupy the Wyckoff 2e site and eight H atoms lie in 2e, 2c and 4f sites in the unit cell. Each Fe atom is coordinated to seven H atoms in the unit cell. The Fe–H distances are 1.481 Å, 1.568 Å, and 1.543 Å at 109.12 GPa. In these hydrides, the H–H distance diminishes with pressure, from 1.470 Å in the α-phase to 1.442 Å in the β-phase to 1.203 Å in the γ-phase. However, the 1.0 Å H–H distance for metal hydrogen (at P = 450 GPa) does not appear in FeH₄ structures until 400 GPa.²⁸ The coordination number of the Fe atom increases from 4 in the α-and β-phase to 7 in the γ-phase, which is in agreement with the behavior of extended systems under pressure in general. In fact, our simulated γ-phase is consistent with the results in a theoretical study.¹³ Fig. 3 shows the simulated X-ray diffraction data of these structures, indicating that their structures are different from each other.

Fig. 2 Structures of predicted stable FeH₄ for the (a) α-phase, (b) β-phase, and (c) γ-phase at P = 80 GPa, 109.12 GPa, and 241.71 GPa, respectively. The large (brown) and small (pink) spheres are Fe atoms and H atoms, respectively. In the three structures, Fe atoms and H atoms with the same color have an equal bond distance.

Table 1 Lattice parameters and atomic coordinates of the α-, β-, and γ-phases at 80 GPa, 109.12 GPa, and 241.71 GPa, respectively

	Lattice parameters (Å)	Atoms	x	y	z
α-Phase	a = 4.061	Fe (4a)	0.5979	0.5979	0.5979
	b = 4.061	H (4a)	0.2263	0.2263	0.2263
	c = 4.061	H (12b)	0.7776	0.0491	0.1101
β-Phase	a = 2.400	Fe (4e)	1.0000	0.2500	0.1153
	b = 3.225	H (4b)	0.5000	0.0000	0.0000
	c = 7.967	H (8h)	0.0000	0.9680	0.3002
		H (4e)	0.0000	0.7500	0.1019
γ-Phase	a = 2.373	Fe (2e)	0.5516	0.2500	0.2505
	b = 3.107	H (2c)	0.0000	0.0000	0.5000
	c = 3.567	H (2e)	0.4388	0.2500	0.6871
	β = 77.772°	H (4f)	0.8672	0.0324	0.8780

---

Fig. 3 The simulated X-ray diffraction for the (a) α-phase, (b) β-phase and (c) γ-phase.

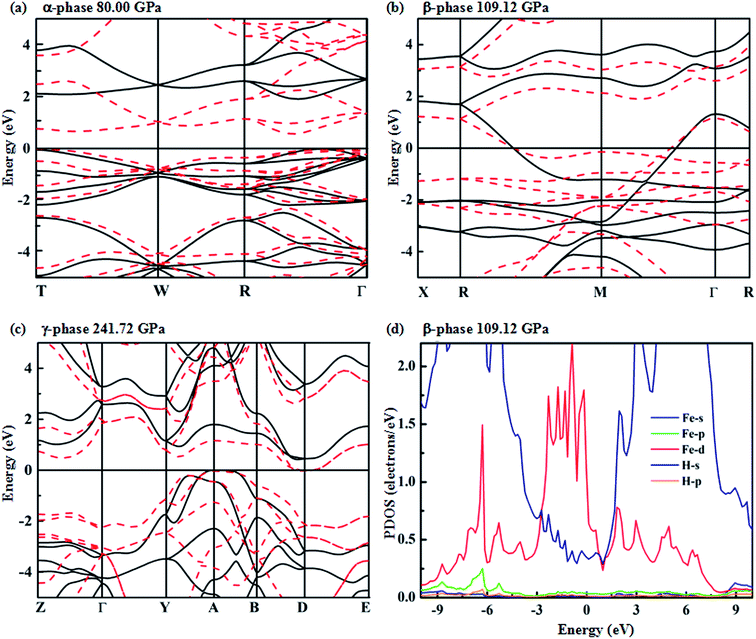
To analyze the electronic properties of the identified stable structures, we calculate their energy band structures considered in the standard PBE-GGA functional for crystalline FeH₄ in Fig. 4(a–c). The calculated PDOSs (projected densities of states) for the β-phase are shown in Fig. 4(d). For the α-phase, it is an insulator with a larger indirect band gap of 2.64 eV. In this structure, the band gaps decrease with increasing pressure when the molar volume decreases – when the van der Waals gap reduces, the orbital overlap across the gap is enhanced and this would reduce the energy separation between bonding and anti-bonding interactions.^30,31 In Fig. 4(d), between −3 to 1.5 eV, a significant hybridization of Fe 3d and H s for the β-phase is shown. It must also be mentioned that H s has been extended ten times. We employ Bader charge analysis, which provides a description of electron transfer, to quantify the amount of charge belonging to each atom at different pressure points. The calculated charge values are 7.1335 (1.2166), 7.228 (1.1921) and 7.2061 (1.1985) electrons for Fe(H) for the α-, β- and γ-phase, respectively. This result reveals that the charge states of Fe and H atoms change with pressure-induced transition. However, the net charges on Fe and H atoms are less than the nominal charges on the ions (+8 for Fe and −1 for H). Accordingly, in FeH₄, the bond between Fe and H atoms shows evident ionic character and a little covalent bond exists between Fe and H atoms at the same time.

Fig. 4 Electronic band structure of Fe atoms and H atoms for the (a) α-phase, (b) β-phase, and (c) γ-phase. The projected electronic DOS for the β-phase (d). Note that H s has been extended ten times. Zero energy is at the Fermi level. The dotted (red) and solid (black) lines in the band structures represent results obtained using the PBE and HSE function, respectively.

The predicted overlap between conduction and valence bands reveals that the β-phase is metallic, while a weak overlap of conduction and valence bands occurs in the γ-phase. It is known that standard PBE-GGA usually underestimates the band gap. Therefore, we have employed the HSE hybrid functional that has been widely considered as providing a better description of the electronic properties (especially the band position).^32–34 For the β structure, the band still crosses over the Fermi level at 109.12 GPa. It is interesting to note that the predicted γ-phase is a semi-conductor, as illustrated by the HSE corrections with a band gap of 0.4 eV.

Metallic high-pressure phases of hydrogen-rich compounds are promising high-temperature superconductors.^35–41 Interestingly, the band structure of the β-phase crossing the Fermi level along the R–M–Γ direction is quite flat, and a narrow energy window located at the Fermi level results in a large electronic density of states near the Fermi energy. The corresponding restricted conduction electrons near the band gap possess a large effective mass with their group velocities approaching zero. Above all, such flat bands with highly mobile and localized electrons should provide the strong electron–phonon coupling necessary for superconductivity. To explore the superconducting properties, we calculated the electron–phonon coupling parameter, λ(ω), the logarithmic average phonon frequency, ω log, and the electronic DOS at the Fermi level, N(E_f), for the β-phase, at 109.12 GPa in Fig. 5. Note that the low-frequency vibrations which are mainly associated with the Fe atoms due to their relatively higher atomic mass, provide a contribution of 25% of the total EPC parameter, while the phonon high-frequencies between 15 and 60 THz associated with the H atoms account for nearly 75% of λ(ω). Therefore, it is suggested that H atoms play a significant role in the superconductivity of FeH₄. According to our calculations, λ(ω) reaches 0.36, and ω log is 756.33 K, so the estimated T_c within the Allen–Dynes modified McMillan equation³⁸ becomes 1.70 K, considering the typical Coulomb pseudopotential parameter, μ* = 0.1. It should be noted that a recent theoretical prediction of GeH₄ and SnH₄ gave a much larger T_c of 102 K and 62 K, respectively, where the “H₂” unit has been suggested to be mainly responsible for the EPC parameter.^42,43 In our predicted structure of FeH₄, the relatively small T_c stems from a missing H₂ unit.

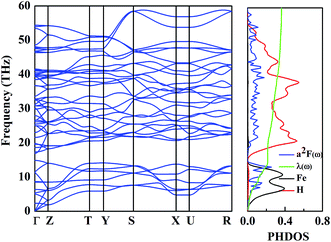Fig. 5 The calculated phonon dispersion (left), Eliashberg phonon spectral function, α²F(ω)/ω, partial electron–phonon integral, λ(ω), and site-projected phonon DOS of the β-phase (right).

IV. Conclusions

In summary, we have determined the high-pressure structural evolution of FeH₄ by using first-principles calculations in combination with a swarm structure search in the pressure range of 80–400 GPa. We predicted three new phases and determined their stable pressure ranges. The α-phase has an insulating electronic state, which is stable from 80 GPa to 109.12 GPa. Furthermore, increasing the pressure to above 109.12 GPa, a metallic β-phase occurs, and then undergoes a structural transition from the metallic β-phase to a weak metallic γ-phase above 241.71 GPa. Moreover, the estimated superconducting critical temperature, T_c, of the β-phase reaches 1.7 K by application of the Allen–Dynes modified McMillan equation. Our results provide insight into the search of hydrogen-rich iron hydrides under the Earth’s core pressure.

Acknowledgements

This work is supported by the National Natural Science Foundation of China under No. 11474125, 51202084, 11404035 and 11504007.

References

1. F. Birch, J. Geophys. Res., 1952, 57, 227.
2. J. P. Poirier, Geophys. J. Int., 2001, 144, 498.
3. F. Birch, J. Geophys. Res., 1964, 69, 4377.
4. D. J. Stevenson, Science, 1981, 214, 611.
5. R. Jeanloz, Annu. Rev. Earth Planet. Sci., 1990, 18, 357.
6. E. I. Isaev, N. V. Skorodumova, R. Ahuja, Y. K. Vekilov and B. Johansson, PNAS, 2007, 104, 9168.
7. J. V. Badding, R. J. Hemley and H.-K. Mao, Science, 1991, 253, 421.
8. M. Yamakata, T. Yagi, W. Utsumi and Y. Fukai, Proc. Jpn. Acad., 1992, 68, 172.
9. Y. Fukai, A. Fukizawa, K. Watanabe and M. Amano, Jpn. J. Appl. Phys., 1982, 21, L318.
10. N. Hirao, T. Kondo, E. Ohtani, K. Takemura and T. Kikegawa, Geophys. Res. Lett., 2004, 31, L06616.
11. E. I. Isaev, N. V. Skorodumova, R. Ahuja, Y. K. Vekilov and B. Johansson, PNAS, 2007, 104, 9168.
12. C. M. Pépin, A. Dewaele, G. Geneste, P. Loubeyre and M. Mezouar, Phys. Rev. Lett., 2014, 113, 265504.
13. Z. G. Bazhanova, A. R. Oganov and O. Gianola, Phys.-Usp., 2012, 55, 489.
14. Y. C. Wang, J. Lv, L. Zhu and Y. Y. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094116.
15. Y. C. Wang, J. Lv, L. Zhu and Y. M. Ma, Comput. Phys. Commun., 2012, 183, 2063.
16. J. Lv, Y. C. Wang, L. Zhu and Y. M. Ma, Phys. Rev. Lett., 2011, 106, 015503.
17. L. Zhu, H. Wang, Y. C. Wang, J. Lv, Y. M. Ma, Q. L. Cui, Y. Y. Ma and G. T. Zou, Phys. Rev. Lett., 2011, 106, 145501.
18. Y. C. Wang, H. Y. Liu, J. Lv, L. Zhu, H. Wang and Y. M. Ma, Nat. Commun., 2011, 2, 1407.
19. G. C. Yang, Y. C. Wang, F. Peng, A. Bergara and Y. M. Ma, J. Am. Chem. Soc., 2016, 138, 4046.
20. Q. Li, D. Zhou, W. T. Zheng, Y. M. Ma and C. F. Chen, Phys. Rev. Lett., 2013, 110, 136403.
21. F. Peng, Y. S. Yao, H. Y. Liu and Y. M. Ma, J. Phys. Chem. Lett., 2015, 6, 2363.
22. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188.
23. M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616.
24. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
25. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 78, 1396.
26. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
27. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
28. H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13, 5188.
29. S. Baroni, P. Giannozzi and A. Testa, Phys. Rev. Lett., 1987, 58, 1861.
30. H. Y. Liu and Y. M. Ma, Phys. Rev. Lett., 2013, 110, 025903.
31. J. C. Jamieson and D. B. McWhan, J. Chem. Phys., 1965, 43, 1149.
32. J. Heyd, J. E. Peralta, G. E. Scuseria and R. L. Martin, J. Chem. Phys., 2005, 123, 174101.
33. B. G. Janesko, T. M. Henderson and G. E. Scuseria, Phys. Chem. Chem. Phys., 2008, 11, 443.
34. J. Heyd and G. E. Scuseria, J. Chem. Phys., 2004, 121, 1187.
35. Z. W. Wang, Y. S. Yao, L. Zhu, H. Y. Liu, L. Toshiaki, H. Wang and Y. M. Ma, J. Chem. Phys., 2014, 140, 124707.
36. G. Y. Gao, A. R. Oganov, A. Bergara, M. M. Canales, T. Cui, T. Iitaka, Y. M. Ma and G. T. Zou, Phys. Rev. Lett., 2008, 101, 107002.
37. G. Y. Gao, R. Hoffmann, N. W. Ashcroft, H. Y. Liu, A. Bergara and Y. M. Ma, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 184104.
38. I. Goncharenko, M. I. Eremets, M. Hanfland, J. S. Tse, M. Amboage, Y. Yao and I. A. Trojan, Phys. Rev. Lett., 2008, 100, 045504.
39. S. T. Zhang, Y. C. wang, J. R. Zhang, H. Y. Liu, X. Zhong, H. F. Song, G. C. Yang, L. J. Zhang and Y. Y. Ma, Sci. Rep., 2015, 5, 15433.
40. P. B. Allen, Phys. Rev. B, 1972, 6, 2577.
41. X. Zhong, H. Wang, J. R. Zhang, H. Y. Liu, S. T. Zhang, H. F. Song, G. C. Yang, L. J Zhang and Y. M. Ma, Phys. Rev. Lett., 2016, 116, 057002.
42. G. Y. Gao, H. Wang, A. Bergara, Y. W. Li, G. T. Liu and Y. M. Ma, Phys. Rev. B, 2011, 84, 064118.
43. G. Y. Gao, A. R. Oganov, P. F. Li, Z. W. Li, H. Wang, T. Cui, Y. M. Ma, A. Bergara, A. O. Lyakhov, T. Iitakaand and G. T. Zou, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 1317.

---