Self-assembly of AB diblock copolymer solutions confined in cylindrical nanopores
Yuping
Sheng
ab,
Yutian
Zhu
*a,
Wei
Jiang
*a and
Zeyuan
Dong
*c
aState Key Laboratory of Polymer Physics and Chemistry, Changchun Institute of Applied Chemistry, Chinese Academy of Sciences, Changchun 130022, People's Republic of China. E-mail: ytzhu@ciac.ac.cn; wjiang@ciac.ac.cn
bAnalytical and Testing Center, Sichuan University of Science and Engineering, Zigong 643000, People's Republic of China
cState Key Laboratory of Supramolecular Structure and Materials, College of Chemistry, Jilin University, 2699 Qianjin Street, Changchun 130012, People's Republic of China. E-mail: zdong@jlu.edu.cn
First published on 23rd August 2016
Abstract
The self-assembly of AB diblock copolymer solutions confined in a cylindrical nanopore is investigated systematically via Monte Carlo simulations. Two types of diblock copolymers, i.e. hydrophobic and amphiphilic AB diblock copolymers, are examined to reveal the effects of the wall surface properties, copolymer concentration, and diameter of the cylindrical nanopore on the self-assembled nanostructures. It was found that the wall surface properties and the nanopore diameters dominate the self-assembled nanostructures, whereas the copolymer concentration has little influence on the resulting nanostructures. Moreover, the contact number and mean-square radius of gyration of hydrophobic polymer segments were used to monitor the evolutions of the chain configurations under cylindrical confinement. It is interesting to note that the polymer chains were more folded when the confinement effect (le/d) exceeded a critical value, thus causing a transition in the self-assembled structures. This result indicates that the block copolymer can automatically adjust its chain configuration to adapt to the strongly confined environment, which provides new opportunities to explore more novel self-assembled nanostructures based on existing block copolymers.
1 Introduction
The confinement effect, which is imposed by boundary surfaces, can effectively frustrate the symmetry of a structure, and thus lead to the formation of some unique structures that cannot be obtained in the unconfined state. In the last decade, the self-assembly of polymer melts confined in the cylindrical nanopores of anodic aluminum oxide (AAO) membranes has attracted intense attention, which has been proven to be a powerful method for the fabrication of one-dimensional nanorods with various ordered structures, including cylindrical barrel structures,1–4 stacked torus-type structures,4,5 helical strings of spherical structures,4 stacked disks,1,5 helical morphologies5,6 and gyroid structures.7 In theoretical studies, various simulation techniques, including Monte Carlo (MC), molecular dynamics (MD), self-consistent field theory (SCFT) and dissipative particle dynamics (DPD) simulations, have been applied to mimic the self-assembly of AB diblock copolymers,8–17 ABA amphiphilic triblock copolymers,18,19 ABC triblock copolymers,20,21 ABC star triblock copolymers,22–24 multiblock copolymers25 and copolymer mixtures26,27 under cylindrical confinement, which predict a large number of novel nanostructures, including concentric lamellae, parallel lamellae, stacked disks, various concentric perforated lamellae-related structures, stacked toroids, multiple straight cylinders and helical structures.On the other hand, the self-assembly of block copolymers in solution has been a hot issue both theoretically and experimentally because block copolymers can spontaneously assemble into various nanostructured micelles.28–33 However, there are very limited works which focus on the self-assembly behavior of polymer solutions confined in a cylindrical nanopore. Due to the confinement effect and template effect, it is expected that block copolymers can aggregate into completely different micellar structures under cylindrical confinement. For instance, Russell and Chen introduced a poly(methyl methacrylate) (PMMA) solution into the nanopores of AAO membranes, which produced a series of well controlled polymer nanospheres, nanorods, nanotubes, and nanorods with periodic encapsulated holes driven by the Rayleigh instability of the nanotubes as the solvent evaporated.34,35 Subsequently, more complex polymer solutions, such as poly(styrene-b-1,4-butadiene) (PS-b-PBD) diblock copolymer solution,36 poly(isoprene-b-styrene-b-2-vinyl pyridine) (PI-b-PS-b-P2VP) triblock copolymer solution,37 as well as polymer blend solutions38,39 were filled into the nanopores of AAO membranes, which fabricated many novel micellar structures, such as vesicles with a mesh-like hydrophobic membrane, nanostructured nanorods, nanopeapods, and core–shell nanospheres. Hou et al. generated spiral or porous block copolymer nanofibers by using the geometric confinement of nanochannels.40 In our previous work, we investigated the self-assembly of polystyrene-b-poly(4-vinylpyridine) (PS-b-P4VP) confined in the nanopores of an AAO template.41 In that work, we observed a series of ordered nanotubes and nanorods induced by the confinement effect and template effect of AAO nanopores. In a theoretical study, Chen and Ruckenstein investigated the nanostructures self-assembled from polymer solutions confined in cylindrical nanopores via Monte Carlo simulation.42 They proposed that the interaction of the segment with the wall is a crucial factor which dominates the resulting nanostructures. Although great progress has been made in this issue, it is unknown thus far how block copolymers aggregate and pack into different nanostructures under the confinement of a cylindrical pore. Moreover, it has been proven that the diameter of the nanopore plays a critical role in the self-assembly of block copolymer melts confined in nanopores.8,27,43 However, it is still not very clear how the size of the confinement space affects the self-assembly of block copolymer solutions.
In the current study, we apply Monte Carlo simulations to investigate the self-assembly of an AB diblock copolymer solution confined in cylindrical nanopores. The influence of the surface properties of the cylindrical pore (neutral, selective, attractive or repulsive surfaces), properties of the block segments (hydrophobic or hydrophilic), sizes of confined spaces (i.e. the diameter of the cylindrical pores) and concentration of the block copolymers on the aggregated nanostructures are systematically examined. Moreover, the contact number between different polymer monomers and mean-square radius of gyration of polymer chains are also calculated to reveal how the block copolymer chains pack and aggregate under different cylindrical confinements.
2 Models and methods
The Lattice Monte Carlo (MC) method is used in this work to study the self-assembly of an AB diblock copolymer solution confined in cylindrical nanopores. All simulations were carried out in the cylindrical boundary (the wall), i.e., both the motions of the polymer beads and solvents were limited in the cylindrical pore. The period boundary condition was imposed in the cylinder axis direction (z axis) and not imposed in the cylindrical boundary direction (x and y axes). When the diameter (d) of the nanopore was increased from 10 to 60, the nanopore length (h) was decreased from 350 to 50 to avoid an apparent increase in computation time. Each polymer bead occupied one lattice site, and the remaining vacancies were regarded as the solvent. The single-site bond fluctuation model44–46 was used in this work, and the bond length was restricted to 1 and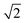 . Therefore each site has 18 nearest neighbor sites in the lattice. Excluded volume interactions were enforced to ensure that no more than one monomer existed at one lattice site. Also, no bond crossing was allowed. The initial state was generated by randomly dispersing a desired number of polymer chains in the cylindrical nanopore. Then, the chain configuration was evolved through the exchange between monomer and vacancy, i.e., a polymer bead was randomly selected to exchange with a bead on one of its 18 nearest neighbors. To improve the computation efficiency, the partial-reptation algorithm47 was used in the simulation. If the selected neighbor bead was a vacancy, the exchange was allowed when it satisfied the excluded volume conditions, no-bond-crossing and bond length restrictions. If the exchange creates a single break in the chain, the vacancy will continue to exchange with the following monomers along the chain until the chain reconnects. The acceptance or rejection of one tentative exchange was further governed by the Metropolis rule.48 The tentative exchange is accepted if the energy change, ΔE, is negative or accepted with a probability of p = exp[−ΔE/kBT], where,
. Therefore each site has 18 nearest neighbor sites in the lattice. Excluded volume interactions were enforced to ensure that no more than one monomer existed at one lattice site. Also, no bond crossing was allowed. The initial state was generated by randomly dispersing a desired number of polymer chains in the cylindrical nanopore. Then, the chain configuration was evolved through the exchange between monomer and vacancy, i.e., a polymer bead was randomly selected to exchange with a bead on one of its 18 nearest neighbors. To improve the computation efficiency, the partial-reptation algorithm47 was used in the simulation. If the selected neighbor bead was a vacancy, the exchange was allowed when it satisfied the excluded volume conditions, no-bond-crossing and bond length restrictions. If the exchange creates a single break in the chain, the vacancy will continue to exchange with the following monomers along the chain until the chain reconnects. The acceptance or rejection of one tentative exchange was further governed by the Metropolis rule.48 The tentative exchange is accepted if the energy change, ΔE, is negative or accepted with a probability of p = exp[−ΔE/kBT], where, 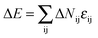 is the energy change in one tentative move; ΔNij is the difference between the number of nearest neighbor pairs of components i and j before and after the movement, i, j = A, B, S (solvent) and W (wall) respectively; εij is the reduced interaction; kB is the Boltzmann constant and fixed to be 1 in this simulation; and T is the reduced temperature.
is the energy change in one tentative move; ΔNij is the difference between the number of nearest neighbor pairs of components i and j before and after the movement, i, j = A, B, S (solvent) and W (wall) respectively; εij is the reduced interaction; kB is the Boltzmann constant and fixed to be 1 in this simulation; and T is the reduced temperature.
Moreover, the annealing method was used in this simulation, which is a well-known procedure for obtaining low-energy stable states in complex systems. The inverse temperature 1/T changes from 0 to a given positive value of 0.07, which represents the system changing from a thermal state to a low temperature state. The annealing rate was set as 0.0002 per step. In each annealing step, 9000 Monte Carlo steps (MCS) were performed. In each MCS, it guarantees that each monomer on average has one attempted exchange move. After 350 annealing steps, the inverse temperature 1/T is kept as 0.07, and other sufficiently long annealing steps are taken to ensure that the final structures are under equilibrium state.
3 Results and discussion
Using the Monte Carlo method, the self-assemblies of hydrophobic–hydrophilic and hydrophobic-hydrophobic AB diblock copolymers confined in cylindrical nanopores were investigated. In all the simulations, the total chain length (le) was fixed at 20. The interaction parameters between the same components were set as εAA = εBB = εSS = 0, and the interaction between different blocks was set as εAB = 2 to mimic the incompatibility between the A and B blocks. The polymer–solvent interaction parameters, εAS and εBS, represent the interactions between the polymers (A or B) and solvents, while the polymer–wall interaction parameters, εAW and εBW, represent the interactions between the polymers (A or B) and the wall surface of the cylindrical pore.3.1 Effect of εAW and εBW on self-assembled nanostructures
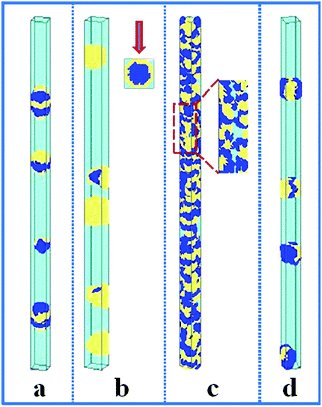
In this section, the property of the wall surface on the self-assembled nanostructures is examined. The copolymer concentration (fAB) and the diameter of the nanopore (d) were fixed, i.e. fAB = 0.1 and d = 16. In Fig. 1, we present a series of nanostructures from the confined self-assembly of hydrophobic A10B10 diblock copolymers with different wall surfaces. Herein, to show a 3D effect, cuboid frames are added to the figures. However, the actual boundaries in all the simulations are the cylinders, which are tangent to the faces of the cuboids. When the wall surface is repulsive to all the blocks (i.e. εAW = εBW = 5), hydrophobic A10B10 diblock copolymers aggregate into compact segmented nanoparticles in the center of the cylinder pore since both the A and B blocks are strongly repelled by the wall surface, as shown in Fig. 1a. Moreover, the A and B blocks have the same hydrophobicity in solution, which results in segmented patterns of nanoparticles. When the wall surface is selective to the B block but repulsive to the A block (i.e. εAW = 5 and εBW = −5), it is observed that the B blocks form a concentric outer lamella and the A blocks form the inner core (Fig. 1b). When both the A and B blocks are attracted to the wall surface (i.e. εAW = εBW = −5), these two blocks are more likely to adhere to the cylindrical surface, which results in the formation of a nanotube, as shown in Fig. 1c. More interesting, it is observed that the nanotube is randomly piled up by pearl-necklace structures with alternating A and B domains, as shown in the sectioned image in Fig. 1c. When the wall surface is neutral, i.e. no interactions between the wall surface and polymer beads, hamburger-like nanoparticles are formed by the A10B10 diblock copolymers (Fig. 1d). Due to the fact that the wall surface is neutral and the hydrophobicities of A and B are the same, either A or B can form the “buns” or the “filling” of the hamburgers, as shown in Fig. 1d. From the nanostructures shown in Fig. 1, it is also observed that the micellar sizes are relatively uniform because of the template effect.In comparison, the confined self-assembly of the asymmetrical hydrophobic A15B5 diblock copolymer is also considered, and the resulting nanostructures as a function of the properties of the wall surfaces are summarized in Fig. 2. When both the A and B blocks are repulsive to the cylindrical wall (i.e. εAW = εBW = 5), the A15B5 diblock copolymers form spherical hamburger-like nanoparticles which are made up of A-type “buns” and B-type “fillings” (Fig. 2a). When εAW = 5 and εBW = −5, i.e., the wall surface is attractive to the B blocks but repulsive to the A blocks, and some short nanorods with a concentric barrel structure are observed. Conversely, A blocks form the outer barrels and B blocks form some ring-structures inside when εAW = −5 and εBW = 5, as shown in Fig. 2c. Fig. 2d shows that the A15B5 diblock copolymers prefer to form a nanotube constructed from alternating A and B domains. Different from the nanostructure shown in Fig. 1c, it seems that the A domains dominate the nanotube surface because the A block is much longer than the B block. When there are no interactions between the blocks and the wall surfaces, some patchy-like nanoparticles are obtained from the confined self-assembly of the A15B5 diblock copolymers, as shown in Fig. 2e. Comparing Fig. 2 with Fig. 1, it seems most of the nanostructures formed by the symmetrical A10B10 diblock copolymers can be reproduced by the asymmetrical A15B5 diblock copolymers. This result implies that the property of the wall surface is more important than the symmetry of the block copolymer when the self-assembly occurs in the cylindrical nanopores.
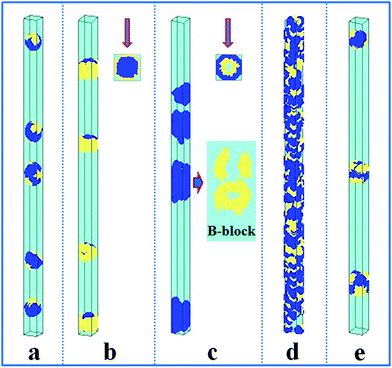 | ||
| Fig. 2 Self-assembled nanostructures of a hydrophobic A15B5 diblock copolymer solution confined in cylindrical nanopores with different wall surfaces. The diameter of the cylindrical pore is fixed at 16. The polymer–solvent interactions are fixed at εAS = εBS = 3. (a) Repulsive surface, i.e. εAW = εBW = 5; (b) selective surface, i.e. εAW = 5 and εBW = −5; (c) selective surface, i.e. εAW = −5 and εBW = 5; (d) attractive surface, i.e. εAW = εBW = −5; and (e) neutral surface, i.e. εAW = εBW = 0. The color codes in the images are the same as that in Fig. 1. Top views are shown in snapshots (b) and (c), and the partial enlargement of B block is also shown on the right of snapshot (c). | ||
The self-assembly of the amphiphilic A15B5 diblock copolymer, which contains a long hydrophobic A block and a short hydrophilic B block, confined in a cylindrical nanopore was also investigated, as shown in Fig. 3. When both the A and B blocks are repelled by the wall surface (εAW = 5), hydrophobic A blocks always aggregate into an inner core, while the hydrophilic B blocks tend to form a hydrophilic shell covering the hydrophobic core. Whereas, when the wall surface is attractive to B blocks but repulsive to A blocks (εAW = 5, εBW = −5), some nanostructures with a concentric barrel structure are observed, as seen in Fig. 3b. When the wall surface is attractive (εAW = −5) or neutral (εAW = 0) to the A block, A15B5 diblock copolymers self-assemble into interesting Janus lamellar nanostructures, i.e., the hydrophobic A blocks form lamellae adhering onto wall surface, while the hydrophilic B blocks form lamellae on the other side of the A lamellae to prevent contact between the hydrophobic A blocks and solvents, no matter the interaction between the hydrophilic B block and wall surface (repulsive surface, i.e. εBW = 5, Fig. 3c; attractive surface, i.e. εBW = −5, Fig. 3d; and neutral surface, i.e. εBW = 0, Fig. 3e). Fig. 3 indicates that the interaction between the hydrophobic block and wall surface dominates the nanostructures, whereas the interaction between the hydrophilic block and wall surface plays a negligible role for the confined self-assembly of the amphiphilic diblock copolymer solution.
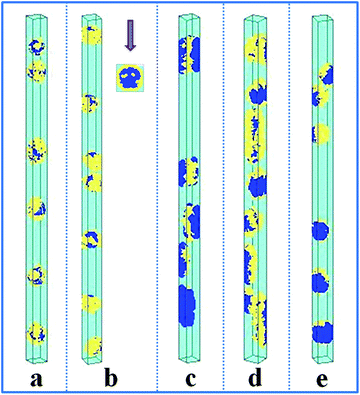 | ||
| Fig. 3 Self-assembled nanostructures of an amphiphilic A15B5 diblock copolymer solution confined in cylindrical nanopores with different wall surfaces. fAB is fixed at 0.1. The diameter of the cylindrical pore is fixed at 16. The polymer–solvent interactions are fixed at εAS = 5 and εBS = −1. (a) εAW = εBW = 5; (b) εAW = 5, εBW = −5; (c) εAW = −5, εBW = 5; (d) εAW = εBW = −5; and (e) εAW = εBW = 0. The color codes in the images are the same as that in Fig. 1. A top view is shown in snapshot (b). | ||
3.2 Effects of the nanopore diameter and copolymer concentration on self-assembled nanostructures
It has been reported that the size of the confined space (i.e. the diameter of the cylindrical pore) plays an important role in the self-assembled nanostructures of polymer melts confined in a cylindrical pore.8,26,43 In Fig. 4a, we present the self-assembled morphologies of a hydrophobic A15B5 diblock copolymer solution confined in a cylindrical pore as a function of copolymer concentration and pore diameter. As the diameter of the nanopore is increased from 10 to 60, it is observed that the aggregated nanostructures of the hydrophobic A15B5 diblock copolymers change from segmented structures to patch-like structures. On the other hand, the micellar shapes transition from small spheres to long rods when the A15B5 concentration is increased from 0.1 to 0.3. This implies that the confined self-assembly of the block copolymer solution get closer to that in the bulk system with an increase in copolymer concentration.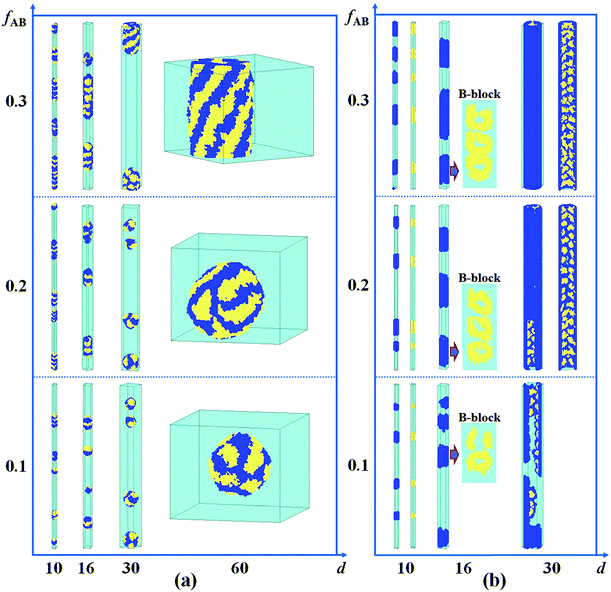 | ||
| Fig. 4 Self-assembled nanostructures of a hydrophobic A15B5 diblock copolymer solution confined in a cylindrical nanopore as a function of d and fAB. (a) εAS = εBS = 3 and εAW = εBW = 5; (b) εAS = εBS = 3 and εAW = −5, and εBW = 5. The color codes in the images are the same as that in Fig. 1. | ||
Subsequently, the influence of fAB and d on the self-assembled nanostructures of hydrophobic A15B5 diblock copolymers confined in selective nanopores (i.e. εAW = −5 and εBW = 5) is also investigated and the results are shown in Fig. 4b. When d is increased from 10 to 30, the self-assembled nanostructures transition from short nanorods with a concentric lamellar structure (d = 10) to short nanotubes with B-type rings inside (d = 20), and then to long nanotubes with ordered B-type lumps inside. When fAB is increased from 0.1 to 0.3, it is also observed that the self-assembled nanostructures remain almost unchanged however the dimension of the nanostructure in the Z direction is increased, which is similar to Fig. 4a.
In Fig. 5, we present a series of self-assembled nanostructures of amphiphilic A15B5 diblock copolymers as a function of d and fAB. It is observed that the self-assembled nanostructures change from hamburger-like nanospheres or segmented nanorods to core–shell nanospheres or nanorods when the diameter of the cylindrical pore increases from 10 to 60. When the copolymer concentration is increased from 0.1 to 0.3, the self-assembled nanostructures transition from small spheres to long rods.
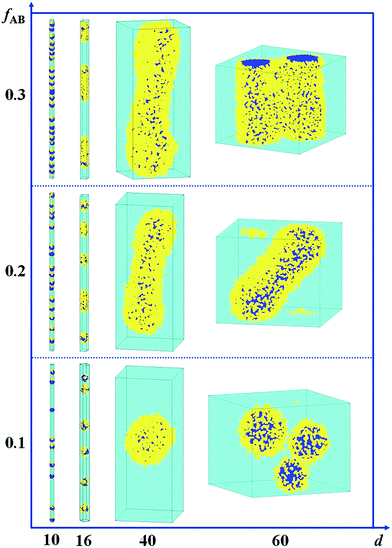 | ||
| Fig. 5 Self-assembled nanostructures of an amphiphilic A15B5 diblock copolymer solution confined in a cylindrical nanopore as a function of diameter of d and fAB. εAS = 5, εBS = −1, and εAW = εBW = 5. The color codes in the images are the same as that in Fig. 1. | ||
For the confined self-assembly of BCPs in a bulk system, the resulting assemblies of BCPs can only be BCP nano-cylinders with various nanostructures, including concentric lamellae, parallel lamellae, stacked disks, helices, and stacked toroids.8–10 However, the self-assembled aggregates of BCP solutions confined in cylindrical nanopores vary from spheres to lamellae, rods to tubes and so on, which are related to the confinement degree, wall surface properties, solvent properties, and BCP concentrations. On the other hand, the self-assembled morphologies of BCP solutions confined in cylindrical pores are more uniform compared with the self-assembly of BCP solutions under the unconfined state because of the template effect. Therefore, the solution self-assembly of BCPs confined in cylindrical pores can be an effective method to fabricate uniform BCP nanoparticles with different nanostructures.
3.3 Chain configurations of block copolymers confined in nanopores
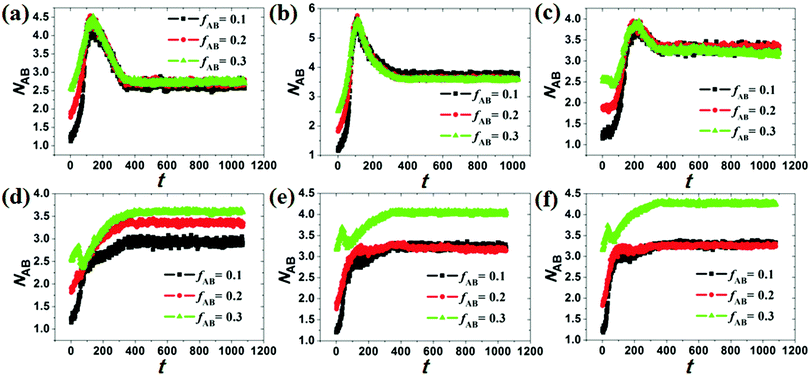
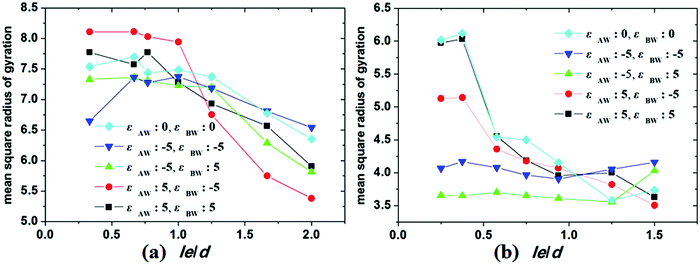
Under cylindrical confinement, the configurations of the block copolymer chains will be adjusted as a change in wall surface properties, solvent properties, copolymer concentration, and pore size to fit the new environment, which result in morphological transitions of the self-assembled nanostructures. Herein, the chain configurations are monitored by the contact numbers and mean-square radius of gyration of the chains. For example, NAB (i.e. the contact number between A and B monomers) is used to reflect the microphase-separation degree between A and B blocks, whereas the mean-square radius of gyration of chains can be used to reveal the stretch degree of the polymer chain. In Fig. 6, the NAB–t curves of different hydrophobic or amphiphilic A15B5 copolymers, different wall surfaces, and different copolymer concentrations are summarized. When hydrophobic A15B5 copolymers are used (Fig. 6a–c), it can be seen that NAB increases at first then decreases, and then remains mostly unchanged after 400 annealing steps, indicating that micellization is finished after 400 annealing steps. This implies that the diblock copolymers aggregate at first, resulting the increase of NAB. Thereafter, microphase separation between A and B occurs, which causes a decrease in NAB. It is also noticed that the NAB–t curves are almost overlapped when fAB is increased from 0.1 to 0.3, which indicates that copolymer concentration has little effect on the confined self-assembly of hydrophobic A15B5 copolymers. For amphiphilic A15B5 copolymers (Fig. 6d–f), their NAB–t curves are more complex. It is observed that NAB is increased at first, and then drops later. Thereafter, NAB increases again, and then remains almost unchanged after t = 400. This indicates that the amphiphilic A15B5 copolymers aggregate rapidly into loose aggregates at the beginning (causes the increase in NAB), and then the hydrophobic A blocks tend to move to the core of the micelles or adhere onto the wall surfaces to avoid contact with the solvents, while the hydrophilic B blocks are more likely to migrate to the micellar surfaces to cover the hydrophobic domains (causes the decrease of NAB). Subsequently, micellization continues and amphiphilic A15B5 copolymers aggregate into tight micelles, which result in the second increase of NAB, as shown in Fig. 6d–f. Moreover, it is also observed that fAB has an effect on the confined self-assembly of amphiphilic A15B5 copolymers, especially when fAB is increased to 0.3.To investigate the stretch degree of the polymer chain under cylindrical confinement, we also calculated the mean-square radius of gyration (Rg2) of the hydrophobic blocks (i.e. AB diblock for the hydrophobic AB copolymer and the hydrophobic A block for the amphiphilic AB copolymer) for different self-assembled nanostructures. In Fig. 7, the variations of Rg2 of hydrophobic blocks with le/d are presented, where le is the length of the hydrophobic blocks and d is the diameter of the cylindrical pore. When le/d increases, i.e., d decreases, this means that the confinement effect is enhanced. For the hydrophobic A15B5 copolymers (Fig. 7a), no distinct change in Rg2 is observed when le/d is less than 1.0. However, it sharply decreases when le/d is greater than 1.0, which indicates that the copolymer chains are more folded under strong confinement. For amphiphilic A15B5 diblock copolymers (Fig. 7b), it is observed that the Rg2 of the A blocks starts to obviously decline when le/d is greater than 0.4, which indicates that the strong confinement causes the A blocks to be highly be folded. Moreover, A blocks possess inferior Rg2 when they are attracted by the wall surfaces. This is because the A blocks are more likely to adhere on the wall surfaces and crowd together to avoid contact with the solution, resulting in a decrease in the Rg2 of the A blocks.
4 Conclusions
In the current study, we investigated the self-assembly of AB diblock copolymer solutions confined in cylindrical pores using the Monte Carlo method. Both hydrophobic and amphiphilic AB diblock copolymers were considered. The effects of the wall surface properties, concentration of the block copolymer, and diameter of the cylindrical pore, on the resulting nanostructures were investigated. The simulation results indicate that the wall surface properties and the diameter of the cylindrical pore dominate the self-assembled structures, whereas the copolymer concentration could only cause an increase in the dimension of the nanostructures in the Z direction. Moreover, the chain configurations of the hydrophobic blocks were examined via the contact number, NAB, and the mean-square radius of gyration of the hydrophobic segments. It is interesting to note that the polymer chain becomes more folded when the confinement effect (le/d) exceeds a critical value, which results in the corresponding morphological transitions of the self-assembled structures.Acknowledgements
This work was financially supported by the National Natural Science Foundation of China for General Program (51373172, 21274051), and Major Program (51433009). The simulations were also supported by High Performance Computing Center, Sichuan University of Science & Engineering.References
- K. Shin, H. Xiang, S. I. Moon, T. Kim, T. J. McCarthy and T. P. Russell, Science, 2004, 306, 76 CrossRef CAS PubMed.
- H. Xiang, K. Shin, T. Kim, S. I. Moon, T. J. McCarthy and T. P. Russell, Macromolecules, 2004, 37, 5660–5664 CrossRef CAS.
- Y. Sun, M. Steinhart, D. Zschech, R. Adhikari, G. H. Michler and U. Gösele, Macromol. Rapid Commun., 2005, 26, 369–375 CrossRef CAS.
- H. Xiang, K. Shin, T. Kim, S. Moon, T. J. McCarthy and T. P. Russell, J. Polym. Sci., Part B: Polym. Phys., 2005, 43, 3377–3383 CrossRef CAS.
- P. Dobriyal, H. Xiang, M. Kazuyuki, J.-T. Chen, H. Jinnai and T. P. Russell, Macromolecules, 2009, 42, 9082–9088 CrossRef CAS.
- H. Xiang, K. Shin, T. Kim, S. I. Moon, T. J. McCarthy and T. P. Russell, Macromolecules, 2005, 38, 1055–1056 CrossRef CAS.
- M. Ma, E. L. Thomas, G. C. Rutledge, B. Yu, B. Li, Q. Jin, D. Ding and A.-C. Shi, Macromolecules, 2010, 43, 3061–3071 CrossRef CAS.
- B. Yu, P. Sun, T. Chen, Q. Jin, D. Ding, B. Li and A.-C. Shi, Phys. Rev. Lett., 2006, 96, 138306 CrossRef PubMed.
- W. Li, R. A. Wickham and R. A. Garbary, Macromolecules, 2006, 39, 806–811 CrossRef CAS.
- J. Feng and E. Ruckenstein, Macromolecules, 2006, 39, 4899–4906 CrossRef CAS.
- P. Chen, X. He and H. Liang, J. Chem. Phys., 2006, 124, 104906 CrossRef PubMed.
- J. Feng, H. Liu and Y. Hu, Macromol. Theory Simul., 2006, 15, 674–685 CrossRef CAS.
- J. Feng and E. Ruckenstein, J. Chem. Phys., 2006, 125, 164911 CrossRef PubMed.
- B. Yu, P. Sun, T. Chen, Q. Jin, D. Ding, B. Li and A.-C. Shi, J. Chem. Phys., 2007, 127, 114906 CrossRef PubMed.
- Y. Han, J. Cui and W. Jiang, Macromolecules, 2008, 41, 6239–6245 CrossRef CAS.
- W. Li and R. A. Wickham, Macromolecules, 2009, 42, 7530–7536 CrossRef CAS.
- M. Pinna, X. Guo and A. V. Zvelindovsky, J. Chem. Phys., 2009, 131, 214902 CrossRef PubMed.
- Z. Wang, B. Li, Q. Jin, D. Ding and A.-C. Shi, Macromol. Theory Simul., 2008, 17, 301–312 CrossRef CAS.
- Z. Wang, B. Li, Q. Jin, D. Ding and A.-C. Shi, Macromol. Theory Simul., 2008, 17, 86–102 CrossRef CAS.
- J. Feng and E. Ruckenstein, J. Chem. Phys., 2007, 126, 124902 CrossRef PubMed.
- P. Chen and H. Liang, J. Phys. Chem. B, 2008, 112, 1918–1925 CrossRef CAS PubMed.
- Y. Xu, W. Li, F. Qiu, Y. Yang and A.-C. Shi, J. Phys. Chem. B, 2009, 113, 11153–11159 CrossRef CAS PubMed.
- J. Song, T. Shi, J. Chen and L. An, J. Phys. Chem. B, 2010, 114, 16318–16328 CrossRef CAS PubMed.
- M. Liu, W. Li and F. Qiu, J. Chem. Phys., 2013, 138, 104904 CrossRef PubMed.
- H. Chen and E. Ruckenstein, Polymer, 2010, 51, 968–974 CrossRef CAS.
- Y. Zhu and W. Jiang, Macromolecules, 2007, 40, 2872–2881 CrossRef CAS.
- J.-H. Huang and X.-Z. Li, Soft Matter, 2012, 8, 5881–5887 RSC.
- L. Zhang and A. Eisenberg, Science, 1995, 268, 1728–1731 CAS.
- D. E. Discher and A. Eisenberg, Science, 2002, 297, 967–973 CrossRef CAS PubMed.
- Y. Sheng, X. Yang, N. Yan and Y. Zhu, Soft Matter, 2013, 9, 6254–6262 RSC.
- Y. Zhu, H. Yu, Y. Wang, J. Cui, W. Kong and W. Jiang, Soft Matter, 2012, 8, 4695–4707 RSC.
- Y. Zhu, X. Yang, W. Kong, Y. Sheng and N. Yan, Soft Matter, 2012, 8, 11156–11162 RSC.
- N. Yan, H. Liu, Y. Zhu, W. Jiang and Z. Dong, Macromolecules, 2015, 48, 5980–5987 CrossRef CAS.
- J.-T. Chen, M. Zhang and T. P. Russell, Nano Lett., 2007, 7, 183–187 CrossRef CAS PubMed.
- C.-W. Lee, T.-H. Wei, C.-W. Chang and J.-T. Chen, Macromol. Rapid Commun., 2012, 33, 1381–1387 CrossRef CAS PubMed.
- D. Chen, W. Zhao, D. Wei and T. P. Russell, Macromolecules, 2011, 44, 8020–8027 CrossRef CAS.
- W. Zhao, D. Chen, Y. Hu, G. M. Grason and T. P. Russell, ACS Nano, 2011, 5, 486–492 CrossRef CAS PubMed.
- J.-T. Chen, T.-H. Wei, C.-W. Chang, H.-W. Ko, C.-W. Chu, M.-H. Chi and C.-C. Tsai, Macromolecules, 2014, 47, 5227–5235 CrossRef CAS.
- H.-W. Ko, M.-H. Chi, C.-W. Chang, C.-W. Chu, K.-H. Luo and J.-T. Chen, ACS Macro Lett., 2015, 4, 717–720 CrossRef CAS.
- P. Hou, H. Fan and Z. Jin, Macromolecules, 2015, 48, 272–278 CrossRef CAS.
- N. Yan, Y. Sheng, H. Liu, Y. Zhu and W. Jiang, Langmuir, 2015, 31, 1660–1669 CrossRef CAS PubMed.
- H. Chen and E. Ruckenstein, Langmuir, 2009, 25, 12315–12319 CrossRef CAS PubMed.
- P. Chen and H. Liang, J. Phys. Chem. B, 2008, 112, 1918–1925 CrossRef CAS PubMed.
- I. Carmesin and K. Kremer, Macromolecules, 1988, 21, 2819–2823 CrossRef CAS.
- R. G. Larson, J. Chem. Phys., 1988, 89, 1642–1650 CrossRef CAS.
- R. G. Larson, J. Chem. Phys., 1992, 96, 7904–7918 CrossRef CAS.
- S. Ji and J. Ding, Langmuir, 2006, 22, 553–559 CrossRef CAS PubMed.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1092 CrossRef CAS.
| This journal is © the Partner Organisations 2017 |