Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Modelling direct DNA damage for gold nanoparticle enhanced proton therapy†
Marios
Sotiropoulos
 *a,
Nicholas T.
Henthorn
*a,
Nicholas T.
Henthorn
 a,
John W.
Warmenhoven
a,
John W.
Warmenhoven
 a,
Ranald I.
Mackay
a,
Ranald I.
Mackay
 b,
Karen J.
Kirkby
b,
Karen J.
Kirkby
 ac and
Michael J.
Merchant
ac and
Michael J.
Merchant
 ac
ac
aDivision of Cancer Sciences, School of Medical Sciences, Faculty of Biology, Medicine and Health, The University of Manchester, Manchester, UK. E-mail: marios.sotiropoulos@manchester.ac.uk
bChristie Medical Physics and Engineering, The Christie NHS Foundation Trust, Manchester, UK
cThe Christie NHS Foundation Trust, Manchester, UK
First published on 17th November 2017
Abstract
Gold nanoparticles have been proven as potential radiosensitizer when combined with protons. Initially the radiosensitization effect was attributed to the physical interactions of radiation with the gold and the production of secondary electrons that induce DNA damage. However, emerging data challenge this hypothesis, supporting the existence of alternative or supplementary radiosensitization mechanisms. In this work we incorporate a realistic cell model with detailed DNA geometry and a realistic gold nanoparticle biodistribution based on experimental data. The DNA single and double strand breaks, and damage complexity are counted under various scenarios of different gold nanoparticle size, biodistribution and concentration, and proton energy. The locality of the effect, i.e. the existence of higher damage at a location close to the gold distribution, is also addressed by investigating the DNA damage at a chromosomal territory. In all the cases we do not observe any significant increase in the single/double strand break yield or damage complexity in the presence of gold nanoparticles under proton irradiation; nor there is a locality to the effect. Our results show for the first time that the physical interactions of protons with the gold nanoparticles should not be considered directly responsible for the observed radiosensitization effect. The model used only accounts for DNA damage from direct interactions, whilst considering the indirect effect, and it is possible the radiosensitization effect to be due to other physical effects, although we consider that possibility unlikely. Our conclusion suggests that other mechanisms might have greater contribution to the radiosensitization effect and further investigation should be conducted.
Introduction
Radiation is commonly implemented as treatment in cancer therapy, in order to control or kill the malignant cells. The effectiveness of the treatment is directly linked to the dose of radiation absorbed by the tumour. In general, the greater the radiation dose in the tumour the higher the tumour control probability. However, for a specific treatment setup, the radiation beam has to pass through normal tissues, depositing unwanted dose. This dose may limit the dose delivered to the tumour, since the normal tissues have a limited tolerance to radiation. Therefore, methods that increase the local dose to the tumour, improving the therapeutic ratio of radiation therapy have recently attracted significant interest.High atomic number materials have been proven to be able to enhance the local dose of radiation, providing radiosensitization capabilities. However, only recently have advances in the manufacturing of nanoparticles lead to the consideration of metallic nanoparticles as a radiosensitizing agent in radiation therapy. In particular, gold nanoparticles (GNP) constitute a very promising radiosensitization agent as they provide high atomic number (Z = 79), one of the highest biocompatibility and low toxicity, ease of fabrication into a range of sizes and shapes, and high surface area. GNPs have demonstrated in vivo and in vitro radiosensitization potential both for photon and ion beams.1–5
The cell nucleus, and more specifically the nuclear DNA, has been established as the main target for radiation damage. Therefore, to understand the GNP radiosensitization the cell survival has been investigated in relation to the dose deposited to the nucleus and the subsequent DNA damage. Dosimetric studies around a GNP revealed highly inhomogeneous dose distributions,6–8 rendering the macroscopic dose an unsuitable predictor of the cell survival. Instead, the local effect model (LEM) was incorporated to account for the high dose gradient.9–11
In the case of photon irradiation, McMahon9 demonstrated a good agreement between the LEM and the data from Jain et al.12 for the MDA-MB-231 cell line when exposed to 160 kVp X-rays and 1.9 nm GNPs. Lechtman et al.10 also found a good agreement between cell survival and their LEM modification for PC-3 human prostate cancer cells treated with 300 kVp X-rays and 30 nm GNPs. Although the LEM linked the dose distributions produced by the GNPs to the cell survival, it renders difficulties in understanding the underlying radiosensitization mechanisms. To further elucidate the physical mechanisms and study the molecular radiosensitization effect in the nucleus, Xie et al.13 implemented the biophysical Monte Carlo code PARTRACK. They showed that for X-rays ranging from 60 to 200 kVp a significant DNA double strand break enhancement is produced only when the GNPs are located on the nucleus surface.
Chithrani et al.2 reported an increase in the γ-H2AX and 53BP1 foci number of 1.84 (1.45), at 4 h, and 1.28 (1.34) at 24 h post-irradiation, when HeLa cells were treated with 220 kVp X-rays and 50 nm GNP. At the same conditions the enhancement ratio (ER), which is the ratio of the survival fraction with and without GNPs at a specific dose and can be calculated from the cell survival curves, was 2.24 at 4 Gy. For A375 melanoma cells treated with 6 MV X-rays and gold nanorods (∼15 nm × 44 nm), a γ-H2AX foci number increase of 2.10 was observed at 2 Gy, while the ER can be calculated from the data reported by Xu et al.14 to be 1.14. In contrast, Jain et al.12 found no significant 53BP1 foci number increase either 1 h or 24 h post irradiation for MDA-MB-231 breast cancer cells exposed to 160 kVp X-rays and 1.9 nm GNPs. For the same conditions the ER was calculated to be 1.22 at 1.5 Gy. In an attempt to understand the variations between theoretical calculations and experimental measurements, McQuaid et al.15 implemented two separate models. The first model accurately predicted the short term DNA damage, while the second model was in good agreement with the long term cell survival. The need for two models suggests that different mechanisms may operate at different timescale. The fact that the DNA damage was not sufficient to account for the cell survival allowed the speculation of other mechanisms.
Polf et al.4 first demonstrated experimentally the radiosensitization effect under proton irradiation. Specifically they showed an ER of 1.12 at 2 Gy when DU145 prostate cancer cells loaded with 44 nm GNPs were exposed in a 160 MeV proton spread out Bragg peak. Liu et al.3 found an ER of 1.06 at 2 Gy for EMT-6 murine breast cancer cells treated with 3 MeV protons and 6.1 nm GNPs. Li et al.16 studied the effect of 1.3 and 4 MeV protons with 5 or 10 nm GNPs to A431 epidermoid carcinoma cells. They found an ER of 1.22–1.43 at 2 Gy for the 1.3 MeV beam depending on the GNP size, but no significant enhancement for the 4 MeV beam. Similarly, Jeynes et al.17 did not see any radiosensitization effect when RT-112 bladder cancer cells were irradiated with 3 MeV protons, although their result may be an outcome of the relatively low GNP concentration used. In spite of the experimental validation of GNP enhanced proton therapy, computational models have suggested a much lower radiosensitization effect. For instance, Lin et al.11 predicted a significant enhancement in the case of proton irradiations only when the GNPs were inserted in the cell nucleus.
The DNA damage induction in the case of GNP enhanced proton therapy has not been systematically investigated, creating a gap between the observed effect and the related mechanisms. In this work we apply Monte Carlo simulations in order to calculate for the first time direct single and double strand break (SSB and DSB) induction and investigate the effect on the damage complexity in the presence of GNPs. A cell model complete with chromosomal territories and detailed nuclear structure are adopted. A realistic GNP distribution is used, arranging the GNP in clusters of vesicles that contain the GNP. The results provide further evidence that the radiosensitization effect in gold nanoparticle enhanced proton therapy should not be attributed, at least exclusively, to the physical interaction mechanisms but alternative or supplementary mechanisms should be considered.
Methods
Monte Carlo simulations
Simulations were performed using the Geant4 toolkit,18,19 version 10.2. Only the physical stage (direct damage) of the radiation–DNA interactions was simulated. The geometry was based on the Geant4 WholeNuclearDNA example20 and consisted of an ellipsoid nucleus, with half axes 11.83 μm × 8.52 μm × 3 μm, containing the DNA structures. More specifically, a total of 6 × 109 base pairs are divided into five different organization levels; DNA double helix (containing the amino bases and the backbone region) representing a B-DNA arrangement, nucleosomes, chromatin fibres, chromatin fibre loops, and chromosomal territories. The nucleus was positioned in a 32 μm × 26 μm × 16 μm water box representing the cytoplasm and the extracellular environment. The cytoplasm was defined as the ellipsoidal area surrounding the nucleus with half axes 13.00 μm × 10.00 μm × 5.00 μm. The geometry is illustrated in Fig. 1. GNPs were distributed inside the cytoplasm as described in the next section.A second geometry consisting of a chromosomal territory of the first geometry was also used to study the effects on a localized area. The chromosomal territory is a cube with an edge of 3.114 μm. In front of the chromosomal territory a box with dimensions 3.114 μm × 3.114 μm and variable length and filled with GNPs (length: 1 μm) or solid gold (length: 0.5 μm) is placed. The chromosomal territory was also filled with GNPs (while the box remained empty) in order to study the effect of the nuclear internalization of the nanoparticles.
A combination of two physics lists was used as follows: for the gold material the “Livermore” models and for the water material constituting the cell and DNA material the Geant4-DNA physics models were implemented. No nuclear interactions were included in the simulations. The “Livermore” physics list was considered more suitable since we expect the GNPs to be situated close enough to the DNA structures.21
In this study the free radical production was not taken into account, scoring DNA damage only from the direct effect. This decision was based on the premise that the free radicals generated are proportional to the secondary electrons produced. Indeed, in the study by Xie et al.13 the inclusion of the free radical production did not change the trends of radiation enhancement but affected only the absolute numbers of single and double strand breaks. We are unable to accurately model the indirect effect at this time, and acknowledge that this limitation prevents prediction of absolute values of radiation enhancement using this simulation.
GNP size and distribution
In a realistic scenario the GNPs are not uniformly distributed inside the cell, but clusters of vesicles containing the GNPs are formed.22–25 In this work, in addition to a uniform distribution, we implemented the GNP distribution measured by Peckys and de Jonge.23 More specifically, the vesicle size was sampled from the vesicle size distribution histogram.23 The number of nanoparticles in a vesicle was calculated from the density of GNPs on the vesicle surface (267 GNP per μm2), multiplied by the occupancy factor (67%). This results to a dependence of the GNP number in a vesicle only from the vesicle radius. Then the GNPs were positioned randomly on the inner surface of the vesicle. Finally, the vesicle was positioned randomly into the cytoplasm.The majority of the formulations available do not allow accumulation of the GNPs into the nucleus. Therefore, we assumed that the gold nanoparticles did not enter the nucleus,15,17 and all the nanoparticles were located in the cytoplasm. The concentration of 0.7% wt/wt gold was used as reference, similar to the concentration achieved in a tumour in a mouse model;1 the effect of higher GNP number was also studied (5×, 10×, 20×, and 100× the reference GNPs at the 0.7% gold wt/wt reference concentration, i.e. about 3.4%, 6.6%, 12%, and 42% gold wt/wt) since large variations in the number of GNP uptake has been observed.26 The GNP sizes of 6, 15, 30 nm were studied, with the number of GNPs used for each size given in Table 1. As some nuclear accumulation has been demonstrated,27,28 the chromosomal territory was filled with 1×, 10×, and 20× the GNP number at the reference concentration in an attempt to address the effect of the nuclear accumulation.
| Radius (nm) | Number of GNPs in cytoplasm |
|---|---|
| 6 | 587![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 200 |
| 15 | 38![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| 30 | 4700 |
Cell irradiation
In order to represent linear energy transfer (LET) values found in clinical proton spread-out Bragg Peak (SOBP), proton energies of 1, 10, and 50 MeV (LET = 26.90, 4.80, 1.30 keV μm−1 respectively) were simulated. In the first geometry the protons entered the simulation from an ellipsoidal surface with half-axes 15 μm and 12 μm, 7 μm away from the cell centre. In the second geometry, the source is placed on the cube's surface. All irradiations were equivalent to a dose of 2 Gy to the cell or chromosomal territory.Scoring process
Due to the complexity of the mechanisms leading to strand breaks and the approximations made on the DNA geometrical representation any ab initio calculation of the strand breaks is not possible. Instead assumptions have to be made to convert energy deposition to strand breaks. In this work it was assumed that any energy deposition inside the DNA material can be converted to a strand break with linear probability. Energy deposition of less than 5 eV was not enough to create a strand break, while 25.0 eV or more would always create a break. As discussed by Pater et al.29 there is large dependence of the SSB and DSB yield on the selection of these values. Our values were selected in such a way to provide better agreement with reference values of SSB and DSB yields (see discussion in section 2 of ESI†). On the other hand the choice of the DNA model does not seem to have major influence on the strand break yields.30 Two or more SSB at a distance of less than 3.3 nm (equivalent to 10 base pairs) and on opposite strands were considered as a DSB. For identifying the DSBs the density-based spatial clustering of applications with noise (DBSCAN) algorithm was incorporated.31 The number of SSBs composing a DSB was defined as the complexity of the damage. In this study we classified DSBs as simple where two SSBs were involved, and complex, where more than two SSBs were involved. The total SSB, DSB numbers and damage complexity for each simulation were scored; and each simulation scenario was repeated 1000 times, to get mean values and the standard error of the mean. The DSB enhancement ratio (ERDSB), defined as the DSB induction at a scenario to the control scenario, was also presented.Results
The SSB, DSB and damage complexity in the case of a cell model with detailed DNA structure were calculated. The study also focused in a smaller region comprising a GNP filled box next to a chromosomal territory to study the effect at a more localized scale.Cell model
The cell model with the detailed nuclear DNA material was used to study the dependence on the SSB and DSB induction, and damage complexity of the GNP size, distribution, and concentration, and proton energy.Dependence on GNP size and distribution
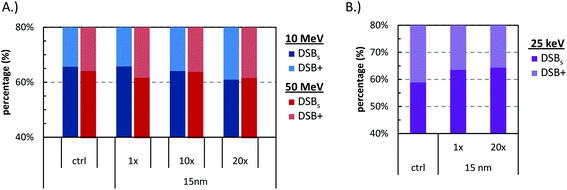
The SSB and DSB absolute yields for 6, 15, and 30 nm GNP size for the uniform and “Peckys” distribution when irradiated with 10 and 50 MeV protons are presented in Fig. 2. Only a small increase in the DSB production is observed for all sizes and distributions, with a direct DSB yield of around 33 and 27 for the 10 and 50 MeV protons respectively. The percentages of the simple and complex DSBs contributing to the DSB yield are shown in Fig. 3. Neither the GNP size nor the distribution has a significant effect on the DSB complexity for both the 10 and 50 MeV irradiation. | ||
| Fig. 3 Percentage of the contribution of the simple (DSBs) and complex (DSB+) double strand breaks for the irradiation conditions described in Fig. 2. | ||
Dependence on GNP concentration
Fig. 4 shows the SSB and DSB yields produced by GNPs of 15 and 30 nm radii, when irradiated with 10 or 50 MeV protons. The reference concentration of 0.7% wt/wt or 5, 10, 20, and 100 times the GNPs at the reference concentration were used. The concentration of the GNP does not seem to have any effect on the SSB and DSB yield independently of the GNP size, or proton energy, although a small increase of the SSBs might be present at the highest concentration.Dependence on proton energy
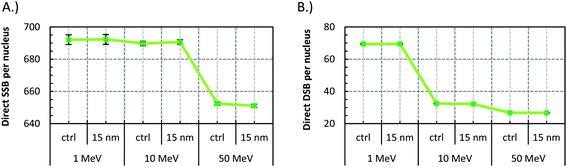
Fig. 5 presents the SSB and DSB yields for a 15 nm GNP when irradiated with 1, 10, and 50 MeV protons. In all cases the ERDSB is close to unity, suggesting no observed increase in the DNA damage (Fig. 6). The 1 MeV protons create a higher number of DSBs and higher complexity, although the presence of the GNPs does not have any influence (Fig. 7).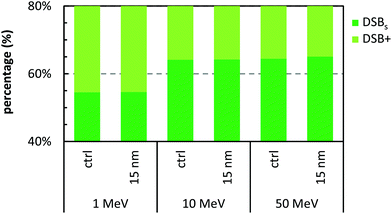 | ||
| Fig. 7 Percentage of the contribution of the simple (DSBs) and complex (DSB+) for the reference concentration (0.7% wt/wt gold) of 15 nm GNP, when irradiated with 2 Gy of 1, 10, and 50 MeV protons. | ||
Chromosomal territory
To further investigate the locality of the effect, the DNA damage to a chromosomal territory was investigated. In the previous results we showed that there is not any increase in the average damage enhancement in the presence of GNPs to a cell nucleus by proton irradiation. However, we suspect that there might be a locality to the effect, since the produced secondary electrons have a limited range.GNP or solid gold filled box close to the chromosomal territory
Fig. 8 and 9 present the SSB and DSB yields produced in the case of the GNP or solid gold filled box impinging the chromosomal territory respectively. When the box is filled with GNPs the SSB and DSB yields have only small variations, independently of the concentration or size. In the case of the solid gold filled box, an increase in the SSBs is observed for both energies, suggesting that more secondary electrons are produced in the presence of the gold, mainly due to the very high interaction probability. On the other hand, the DSB are similar to the control case, suggesting that there is not any clustering of the additional electrons generated.Gold nanoparticles inside the chromosomal territory
Although there is limited availability of formulations that allow the GNPs to enter the nucleus and localize close to the DNA, it is interesting to study this case. Here we should note that the GNPs in our model may enter the nucleus but cannot attach to the DNA, so that the closest proximity to the DNA is about 100 nm.Fig. 10 presents the results for 15 nm GNP at the reference, 10×, and 20× times the GNPs at the reference concentration (0.7% wt/wt), under 10 and 50 MeV proton irradiation. In addition, for the same cases the DNA damage complexity is shown in Fig. 11A. The results show that, under proton irradiation, even when the GNPs are inside the nucleus they do not increase the DNA damage. Although we believe that our model underestimates the strand break yields in the case photons, it is interesting to include a photon irradiation test case. Fig. 10 presents the DSB yield by mono-energetic photon beam of 25 keV, where about a 2, and 25 fold increase in the DSB damage is observed for the 1× and 20× times the reference GNPs, in line with previous findings.11 Notably, for the photon test case, as shown in Fig. 11B higher concentration increases also the damage complexity.
Discussion
We have shown for the first time that the DNA damage enhancement from the physical interactions should not account for the radiosensitization observed under proton irradiations, at least at clinically relevant concentrations. Our results indicate that the DNA DSB number and DSB complexity do not change when GNPs are present in the cytoplasm or chromosomal territory, even when high concentration of GNPs are used. On the other hand considering a control case, when the GNPs are inside the chromosomal territory and irradiated with photons a substantial increase in the DSB formation and complexity is observed.According to our results, the radiosensitization effect under proton irradiation does not depend on the size or distribution of the GNPs. McQuaid et al.,15 for photon irradiation, found a better estimation of the dose enhancement with the local effect model (LEM) when larger GNP were used in the model instead of the nominal value. They attributed this discrepancy to “the aggregation of the gold particles in to clusters and the formation of biological vesicles”. In this study we implemented a realistic distribution allowing GNP to form vesicles (“Peckys” distribution) and we did not find any difference in the DSB induction between the uniform distribution and the formation into vesicles, independently of the GNP size or proton energy. The introduction of a higher amount of gold, even at unrealistic concentrations, did not increase the DNA damage. Interestingly, we found no dependence on the DNA damage enhancement to the proton energy or LET values studied. We suspect that the number and range of the electrons produced are not enough to create a measurable effect.
Since we expect the number and range of the produced secondary electrons to be limited, we hypothesize that the effect may be localized in regions close to the GNP distribution. Therefore, the effect may average over the whole nucleus making the identification of the DNA damage enhancement more difficult. To study the locality of the effect the damage to a chromosomal territory by a GNP or solid gold filled box was investigated. In the case of the GNP filled box impinging the chromosomal territory, no substantial increase in SSB or DSB was observed. We attribute the effect mainly to the low geometrical interaction probability. It is worth noting that although for the high concentration of 100 times the reference GNPs we have 42% gold wt/wt, only 3.7% of the cytoplasm volume is actually gold. When the box is filled with gold, we observe an increase in the SSB for both irradiation energies, but the DSB yield does not increase. This indicates that not only the increase of ionizations is important but the spatial distribution as well. Indeed, the SSBs are directly linked to the ionization number but the DSBs are related to the spatial distribution of the ionizations through the clustering of the SSBs.
Relative to the previous claim is the suitability of dose enhancement as an index of the damage enhancement. In previous works, the macroscopic quantity of dose deposition has been utilized to compare the damage enhancement at the micro-scale, in the presence of the GNPs. We suggest that dose enhancement might have limited applicability when we focus our interest to cell fate; similar to the need for accounting for the relative biological effectiveness in ion therapy.
Unlike photon irradiations, in a proton irradiation a small number of protons are needed to deliver a clinically relevant dose. As a result, the geometrical interaction probability of a proton with a GNP might be extremely low. In addition, not every particle that crosses the GNP will interact with it. This makes the production of secondary electrons a very rare process. To further support our findings we calculated (see section 1 at the ESI†) the (i) geometrical, and (ii) physical interaction probability in the case of the GNP filled box impinging the chromosomal territory. We estimate that 0.5 and 1.7 protons will cross a GNP on average, while 9 and 1.4 more electrons with range higher than 100 nm will be generated for the 10 and 50 MeV proton irradiation respectively, at the dose of 2 Gy. As a result we believe that in the case of proton irradiation the physical contribution to the DNA damage is expected to be very low. Indeed, Martínez-Rovira and Prezado32 with Monte Carlo simulations, and Cho et al.33 with experimental and Monte Carlo calculations studied the physical dose distribution produced by GNPs irradiated with protons and showed that there is no, or very little, physical contribution to the radiosensitization effect, a conclusion that we also see when considering the strand break yields. The absence of DNA damage from the physical interactions of the protons with the GNPs points out to the presence of chemical or biological factors.
In our simulations we took into account only damage resulting from direct interactions of radiation with DNA only, i.e. the free radical production was not simulated. We expect our observations to be similar when the free radical production is taken into account. It has been demonstrated34 under ion irradiation that the inclusion of free radicals mainly affects the absolute numbers of single and double SBs, with minimal effect in the damage complexity. Similar observation can be made on Xie et al.,13 where the inclusion of free radicals resulted to similar trends in the observed single and double SBs. Regardless, since in the case of proton irradiation the probability of an electron generated by the physical interactions with the gold to reach the nucleus is very low, much lower than the case of photon irradiation, we believe that the inclusion of the free radicals might not have a strong effect. Free radicals, on the other hand, might play an important role in the radiosensitization properties of the GNPs which do not relate with DNA damage. Nonetheless, the inclusion of the indirect damage could shed some additional light into the chemical pathway of the radiosensitization, especially when combined with a model of free radical–GNP coating reaction. Sicard-Roselli et al.35 showed that the free radicals react with the GNP coating and produce even more free radicals, with the possibility of contributing to the oxidative stress.
As has been mentioned in the scoring process section and discussed in more detail in section 2 of the ESI† (dependence of the clustering algorithm to the energy threshold values), there is a high sensitivity of the predicted SSB and DSB to the threshold values selected, the conversion scheme, and in particular DNA geometry. This dependence on the parameters and assumptions made in each model has resulted in different threshold values being used between different models. The parameters are optimized in a way that consistency is achieved when compared with well-established experimental values. Our model was mainly developed for proton irradiation, therefore was optimized to achieve consistent yields under protons. Under photon irradiation of the GNP filled chromosomal territory a substantial underestimation of the SSB and DSB yields is observed, implying a track structure dependence of the model. While under photon irradiation our model requires further optimization to ensure agreement with experimental yields, those results provide an indirect validation that our model is sensitive enough to account for the increased DNA damage observed in the presence of GNPs. We expect that a conversion scheme based on the accumulation of energy deposition, rather than the conversion of the energy deposition events at the sugar-phosphate group will produce a more consistent model at a wider radiation quality range.
Since the GNP radiosensitization effect under proton irradiation has been experimentally established in vivo and in vitro,4,5,16 it is interesting to speculate possible mechanisms that might be responsible for the effect. Our work and previous studies32,33 make clear that the radiosensitization under proton irradiations, unlike photon irradiations where physical interactions can also contribute to the effect, is highly unlikely to originate from direct or indirect damage to the DNA. As a result, the alternative or supplementary mechanisms that have been proposed for photon irradiations, such as increased oxidative stress, mitochondria function disruption,36,37 and lysosomal rupture,38 might be more important in the case of proton irradiations, and ultimately the key to understanding radiosensitization with heavy metal nanoparticles bombarded with ions.
Conclusion
A cell model with detailed DNA structure and realistic GNP distribution was implemented to study the DNA damage under proton irradiation. We showed that independently of the proton energy, and GNP size, concentration and distribution the DNA damage from the physical interactions is very low to account for the radiosensitization effect. This is an important addition to a growing body of evidence supporting that cytoplasm mediated radiosensitization may exist. We expect our findings to support the identification of new mechanisms of radiosensitization, away from the well-established pathway of radiation induced direct DNA damage.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by Marie Curie Actions – Initial Training Networks (ITN) as an Integrating Activity Supporting Postgraduate Research with Internships in Industry and Training Excellence (SPRITE) under EC contract no. 317169.Notes and references
- J. F. Hainfeld, D. N. Slatkin and H. M. Smilowitz, Phys. Med. Biol., 2004, 49, N309–N315 CrossRef CAS PubMed.
- B. D. Chithrani, S. Jelveh, F. Jalali, M. van Prooijen, C. Allen, R. G. Bristow, R. P. Hill and D. A. Jaffray, Radiat. Res., 2010, 173, 719–728 CrossRef PubMed.
- C. J. Liu, C. H. Wang, S. T. Chen, H. H. Chen, W. H. Leng, C. C. Chien, C. L. Wang, I. M. Kempson, Y. Hwu, T. C. Lai, M. Hsiao, C. S. Yang, Y. J. Chen and G. Margaritondo, Phys. Med. Biol., 2010, 55, 931–945 CrossRef CAS PubMed.
- J. C. Polf, L. F. Bronk, W. H. P. Driessen, W. Arap, R. Pasqualini and M. Gillin, Appl. Phys. Lett., 2011, 98, 3–5 CrossRef PubMed.
- J.-K. Kim, S.-J. Seo, H.-T. Kim, K.-H. Kim, M.-H. Chung, K.-R. Kim and S.-J. Ye, Phys. Med. Biol., 2012, 57, 8309–8323 CrossRef PubMed.
- E. Lechtman, N. Chattopadhyay, Z. Cai, S. Mashouf, R. Reilly and J. P. Pignol, Phys. Med. Biol., 2011, 56, 4631–4647 CrossRef CAS PubMed.
- C. Wälzlein, E. Scifoni, M. Krämer and M. Durante, Phys. Med. Biol., 2014, 59, 1441–1458 CrossRef PubMed.
- Y. Lin, S. J. McMahon, M. Scarpelli, H. Paganetti and J. Schuemann, Phys. Med. Biol., 2014, 59, 7675–7689 CrossRef PubMed.
- S. J. McMahon, W. B. Hyland, M. F. Muir, J. a. Coulter, S. Jain, K. T. Butterworth, G. Schettino, G. R. Dickson, A. R. Hounsell, J. M. O'Sullivan, K. M. Prise, D. G. Hirst and F. J. Currell, Sci. Rep., 2011, 1, 1–9 CrossRef PubMed.
- E. Lechtman, S. Mashouf, N. Chattopadhyay, B. M. Keller, P. Lai, Z. Cai, R. M. Reilly and J.-P. Pignol, Phys. Med. Biol., 2013, 58, 3075–3087 CrossRef CAS PubMed.
- Y. Lin, S. J. McMahon, H. Paganetti and J. Schuemann, Phys. Med. Biol., 2015, 60, 4149–4168 CrossRef PubMed.
- S. Jain, J. a. Coulter, A. R. Hounsell, K. T. Butterworth, S. J. McMahon, W. B. Hyland, M. F. Muir, G. R. Dickson, K. M. Prise, F. J. Currell, J. M. O'Sullivan and D. G. Hirst, Int. J. Radiat. Oncol., Biol., Phys., 2011, 79, 531–539 CrossRef PubMed.
- W. Z. Xie, W. Friedland, W. B. Li, C. Y. Li, U. Oeh, R. Qiu, J. L. Li and C. Hoeschen, Phys. Med. Biol., 2015, 60, 6195–6212 CrossRef CAS PubMed.
- W. Xu, T. Luo, B. Pang, P. Li, C. Zhou, P. Huang, C. Zhang, Q. Ren and S. Fu, Nano Biomed. Eng., 2012, 4, 6–11 CAS.
- H. N. McQuaid, M. F. Muir, L. E. Taggart, S. J. McMahon, J. A. Coulter, W. B. Hyland, S. Jain, K. T. Butterworth, G. Schettino, K. M. Prise, D. G. Hirst, S. W. Botchway, F. J. Currell, A. Jonathan, W. B. Hyland, S. Jain, K. T. Butterworth, G. Schettino, M. Prise, D. G. Hirst, S. W. Botchway, F. J. Currell, J. A. Coulter, W. B. Hyland, S. Jain, K. T. Butterworth, G. Schettino, K. M. Prise, D. G. Hirst, S. W. Botchway and F. J. Currell, Sci. Rep., 2016, 6, 19442 CrossRef CAS PubMed.
- S. Li, S. Penninckx, L. Karmani, A.-C. Heuskin, K. Watillon, R. Marega, J. Zola, V. Corvaglia, G. Genard, B. Gallez, O. Feron, P. Martinive, D. Bonifazi, C. Michiels and S. Lucas, Nanotechnology, 2016, 27, 455101 CrossRef PubMed.
- J. C. G. Jeynes, M. J. Merchant, a. Spindler, a.-C. Wera and K. J. Kirkby, Phys. Med. Biol., 2014, 59, 6431–6443 CrossRef CAS PubMed.
- S. Agostinelli, J. Allison, K. Amako, J. Apostolakis, H. Araujo, P. Arce, M. Asai, D. Axen, S. Banerjee, G. Barrand, F. Behner, L. Bellagamba, J. Boudreau, L. Broglia, a. Brunengo, H. Burkhardt, S. Chauvie, J. Chuma, R. Chytracek, G. Cooperman, G. Cosmo, P. Degtyarenko, a. Dell'Acqua, G. Depaola, D. Dietrich, R. Enami, a. Feliciello, C. Ferguson, H. Fesefeldt, G. Folger, F. Foppiano, a. Forti, S. Garelli, S. Giani, R. Giannitrapani, D. Gibin, J. J. Gomez Cadenas, I. Gonzalez, G. Gracia Abril, G. Greeniaus, W. Greiner, V. Grichine, a. Grossheim, S. Guatelli, P. Gumplinger, R. Hamatsu, K. Hashimoto, H. Hasui, a. Heikkinen, a. Howard, V. Ivanchenko, a. Johnson, F. W. Jones, J. Kallenbach, N. Kanaya, M. Kawabata, Y. Kawabata, M. Kawaguti, S. Kelner, P. Kent, a. Kimura, T. Kodama, R. Kokoulin, M. Kossov, H. Kurashige, E. Lamanna, T. Lampen, V. Lara, V. Lefebure, F. Lei, M. Liendl, W. Lockman, F. Longo, S. Magni, M. Maire, E. Medernach, K. Minamimoto, P. Mora de Freitas, Y. Morita, K. Murakami, M. Nagamatu, R. Nartallo, P. Nieminen, T. Nishimura, K. Ohtsubo, M. Okamura, S. O'Neale, Y. Oohata, K. Paech, J. Perl, a. Pfeiffer, M. G. Pia, F. Ranjard, a. Rybin, S. Sadilov, E. di Salvo, G. Santin, T. Sasaki, N. Savvas, Y. Sawada, S. Scherer, S. Sei, V. Sirotenko, D. Smith, N. Starkov, H. Stoecker, J. Sulkimo, M. Takahata, S. Tanaka, E. Tcherniaev, E. Safai Tehrani, M. Tropeano, P. Truscott, H. Uno, L. Urban, P. Urban, M. Verderi, a. Walkden, W. Wander, H. Weber, J. P. Wellisch, T. Wenaus, D. C. Williams, D. Wright, T. Yamada, H. Yoshida and D. Zschiesche, Nucl. Instrum. Methods Phys. Res., Sect. A, 2003, 506, 250–303 CrossRef CAS.
- J. Allison, K. Amako, J. Apostolakis, H. Araujo, P. A. Dubois, M. Asai, G. Barrand, R. Capra, S. Chauvie, R. Chytracek, G. a P. Cirrone, G. Cooperman, G. Cosmo, G. Cuttone, G. G. Daquino, M. Donszelmann, M. Dressel, G. Folger, F. Foppiano, J. Generowicz, V. Grichine, S. Guatelli, P. Gumplinger, a. Heikkinen, I. Hrivnacova, a. Howard, S. Incerti, V. Ivanchenko, T. Johnson, F. Jones, T. Koi, R. Kokoulin, M. Kossov, H. Kurashige, V. Lara, S. Larsson, F. Lei, F. Longo, M. Maire, a. Mantero, B. Mascialino, I. McLaren, P. M. Lorenzo, K. Minamimoto, K. Murakami, P. Nieminen, L. Pandola, S. Parlati, L. Peralta, J. Perl, a. Pfeiffer, M. G. Pia, a. Ribon, P. Rodrigues, G. Russo, S. Sadilov, G. Santin, T. Sasaki, D. Smith, N. Starkov, S. Tanaka, E. Tcherniaev, B. Tomé, a. Trindade, P. Truscott, L. Urban, M. Verderi, a. Walkden, J. P. Wellisch, D. C. Williams, D. Wright, H. Yoshida and M. Peirgentili, IEEE Trans. Nucl. Sci., 2006, 53, 270–278 CrossRef.
- M. Dos Santos, C. Villagrasa, I. Clairand and S. Incerti, Nucl. Instrum. Methods Phys. Res., Sect. B, 2013, 298, 47–54 CrossRef CAS.
- M. Sotiropoulos, M. J. Taylor, N. T. Henthorn, J. W. Warmenhoven, R. I. Mackay, K. J. Kirkby and M. J. Merchant, Biomed. Phys. Eng. Express, 2017, 3, 25025 CrossRef.
- E. Sadauskas, N. R. Jacobsen, G. Danscher, M. Stoltenberg, U. Vogel, A. Larsen, W. Kreyling and H. Wallin, Chem. Cent. J., 2009, 3, 16 CrossRef PubMed.
- D. B. Peckys and N. de Jonge, Nano Lett., 2011, 11, 1733–1738 CrossRef CAS PubMed.
- D. B. Peckys and N. De Jonge, Microsc. Microanal., 2014, 20, 189–197 CrossRef CAS PubMed.
- L. Stefančíková, E. Porcel, P. Eustache, S. Li, D. Salado, S. Marco, J.-L. Guerquin-Kern, M. Réfrégiers, O. Tillement, F. Lux and S. Lacombe, Cancer Nanotechnol., 2014, 5, 6 CrossRef PubMed.
- J. C. G. Jeynes, C. Jeynes, M. J. Merchant and K. J. Kirkby, Analyst, 2013, 138, 7070–7074 RSC.
- S. Huo, S. Jin, X. Ma, X. Xue, K. Yang, A. Kumar, P. C. Wang, J. Zhang, Z. Hu and X. J. Liang, ACS Nano, 2014, 8, 5852–5862 CrossRef CAS PubMed.
- C. Yang, J. Uertz, D. Yohan and B. D. Chithrani, Nanoscale, 2014, 6, 12026–12033 RSC.
- P. Pater, J. Seuntjens, I. El Naqa and M. A. Bernal, Med. Phys., 2014, 41, 121708 CrossRef PubMed.
- N. T. Henthorn, J. W. Warmenhoven, M. Sotiropoulos, R. I. Mackay, K. J. Kirkby and M. J. Merchant, Radiat. Res., 2017, RR14755.1 CrossRef PubMed.
- Z. Francis, C. Villagrasa and I. Clairand, Comput. Methods Programs Biomed., 2011, 101, 265–270 CrossRef PubMed.
- I. Martínez-Rovira and Y. Prezado, Med. Phys., 2015, 42, 6703 CrossRef PubMed.
- J. Cho, C. Gonzalez-Lepera, N. Manohar, M. Kerr, S. Krishnan and S. H. Cho, Phys. Med. Biol., 2016, 61, 2562–2581 CrossRef CAS PubMed.
- V. A. Semenenko and R. D. Stewart, Phys. Med. Biol., 2006, 51, 1693–1706 CrossRef CAS PubMed.
- C. Sicard-Roselli, E. Brun, M. Gilles, G. Baldacchino, C. Kelsey, H. McQuaid, C. Polin, N. Wardlow and F. Currell, Small, 2014, 1–9 Search PubMed.
- L. E. Taggart, S. J. McMahon, K. T. Butterworth, F. J. Currell, G. Schettino and K. M. Prise, Nanotechnology, 2016, 27, 1–11 CrossRef PubMed.
- M. Ghita, S. J. McMahon, L. E. Taggart, K. T. Butterworth, G. Schettino and K. M. Prise, Sci. Rep., 2017, 7, 44752 CrossRef PubMed.
- L. Štefančíková, S. Lacombe, D. Salado, E. Porcel, E. Pagáčová, O. Tillement, F. Lux, D. Depeš, S. Kozubek and M. Falk, J. Nanobiotechnol., 2016, 14, 63 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7nr07310k |
| This journal is © The Royal Society of Chemistry 2017 |