Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ion transport in gel and gel–liquid systems for LiClO4-doped PMMA at the meso- and nanoscales†
Timothy
Plett
a,
Mya Le
Thai
b,
Josslyn
Cai
a,
Ivan
Vlassiouk
c,
Reginald M.
Penner
b and
Zuzanna S.
Siwy
 *abd
*abd
aDepartment of Physics and Astronomy, University of California, Irvine, California 92697, USA. E-mail: zsiwy@uci.edu; Fax: +1 949-824-2174; Tel: +1 949-824-8290
bDepartment of Chemistry, University of California, Irvine, California 92697, USA
cOak Ridge National Laboratory, 1 Bethel Valley Road, Oak Ridge, TN 37831, USA
dDepartment of Biomedical Engineering, University of California, Irvine, California 92697, USA
First published on 9th October 2017
Abstract
Solid and gel electrolytes offer significant advantages for cycle stability and longevity in energy storage technologies. These advantages come with trade-offs such as reduced conductivity and ion mobility, which can impact power density in storage devices even at the nanoscale. Here we propose experiments aimed at exploring the ion transport properties of a hybrid electrolyte system of liquid and gel electrolytes with meso and nanoscale components. We focus on single pore systems featuring LiClO4-propylene carbonate and LiClO4-PMMA gel, which are model electrolytes for energy storage devices. We identified conditions at which the systems considered featured rectifying current–voltage curves, indicating a preferential direction of ion transport. The presented ion current rectification suggests different mechanisms arising from the unique hybrid system: (i) PMMA structure imposing selectivity in fully immersed systems and (ii) ionic selectivity linked to ion sourcing from media of different ionic mobility. These mechanisms were observed to interplay with ion transport properties linked to nanopore structure i.e. cylindrical and conical.
Introduction
Energy harvesting and storage make up a significant portion of current electrochemical research. A class of energy storage devices which appears most promising in both research and industry are high-performance lithium ion batteries,1 which predominantly utilize organic solvent-based electrolyte.2–4 One of the challenges limiting further optimization of this technology is degradation and breakdown phenomena.3,5 Several groups have performed studies on degradation, focusing on different electrolyte solutions,3,5 electrode material and construction,3,6 and cycling rate5 to determine what factors significantly affect a device's lifetime. Common factors leading to degradation are fast cycling rates,2 water contamination,3 electrode fracture,5 and dendrite formation7 causing short-circuits8 in the battery system. Most recently, research into nanofabricated battery components has revealed an additional challenge as delamination5 has been observed due strong electric fields and mechanical factors. All these factors can limit capacitance and ultimately lifetime in such energy storage devices.Recently, however, a study by Le Thai et al. demonstrated a model electrochemical cell design using ultra-long δ-MnO2 mesowires exhibiting cycling stability up to 200k cycles,5,9 several times better than anything reported previously in the literature. A key innovation in the previous study was the inclusion of a gel-based electrolyte, composed of LiClO4/propylene carbonate (PC) solution and poly(methyl) methacrylate (PMMA). SEM images of the gel-based cell alongside a liquid cell after several thousand cycles revealed that the gel imparted mechanical stability to the MnO2 wire structures, preventing their delamination from the metal core.5
Electrochemical properties of the LiClO4/PMMA gel were previously studied only in the bulk, where its conductance was reported to be similar to the bulk conductivity of LiClO4 in propylene carbonate.10,11 The purpose of our manuscript is to probe ionic transport of the PMMA/LiClO4 electrolyte system on meso- and nanoscales, which so far have not been explored in detail. Ionic transport in confined geometries has been mostly examined in aqueous salt solutions12 and only a few studies have been reported on transport properties of electrolytes in organic solvents, or in water/organic solvent mixtures.13–17 Understanding ionic transport through PMMA gel would be important for fundamental studies of electrochemistry in this usual electrolyte as well as could potentially help the energy storage research, which employs gel electrolytes. Moreover, it has been demonstrated that nanoscale architectures, such as conical nanopores, have the ability to modulate ionic concentrations inside their structure due to the nanoscale and surface charge properties.18–27 Since δ-MnO2 is formed of several tendril-like structures and layers,10,28,29 synthetic meso- and nanopores could provide insight on the ionic transport properties of LiClO4/PMMA gel in such structures. It has been confirmed through experiment that drop-cast deposition of PMMA-based gels on both sides of cylindrical and conical nanopores in polyethylene terephthalate (PET) films result in a complete filling of the nanopore.30,31 It has also been shown that the gel can pass both ionic and electronic currents,32–34 and that the conical geometry leads to rectification phenomena of the ionic transport.31
Here we disclose a series of experiments utilizing cylindrical and conically shaped single polymer meso and nanopores implanted with LiClO4/PMMA gel to understand the transport response of the gel when in contact with a compatible electrolyte i.e. LiClO4/propylene carbonate (PC). We selected polyethylene terephthalate (PET) pores because they have shown robustness in recent experiments involving the LiClO4/PMMA gel and have already demonstrated ion transport properties such as rectification in gel-only systems.31 Our experimental approach allows us to test interfacial characteristics between the gel and liquid electrolyte in micro and nanoconfinement, the ion transport properties of gel–liquid electrolyte systems, and also whether gel systems are permeable to liquid electrolyte exposure.
Materials and procedure
Chemicals and materials
Lithium perchlorate (99.0%, Sigma-Aldrich, St Louis, MO) was dissolved in propylene carbonate (PC, 99.7% and dried over 5 Å sieves for at least 24 hours). 5 mL aliquots of dry 0 mM, 100 mM, 250 mM, and 1 M LiClO4/PC solution and poly(methyl) methacrylate PMMA were mixed at 115 °C to make gels of PMMA (by w/w % mass, 2.0 g for 25% PMMA and 2.6 g for 30% PMMA) and then allowed to cool, forming the gel. The gels were then drop-cast onto PET nanopores at 75–90 °C and allowed to set in air overnight before experimenting. PET nanopores were studied in aqueous KCl (99.0%, Macron, Center Valley, PA) solutions without gel-coating, as well as PC solutions of LiClO4, with and without gel-coating. Electrodes used in the current–voltage (I–V) measurements were AgCl-coated Ag wire and pellet electrodes.Preparation of cylindrical and conical nanopores
Single pores were prepared in 12 μm thick films of polyethylene terephthalate (PET) using the track-etching technique.35 First, films were bombarded with a single U or Au ion accelerated to 11.4 MeV/u at the UNILAC linear accelerator of the GSI Helmholtzzentrum fur Schwerionenforschung in Darmstadt, Germany.36 Irradiated films were then subjected to wet chemical etching. In order to obtain a cylindrical geometry,37 irradiated PET films were immersed in aqueous solutions of 5 M NaOH at 50 °C, 2 M NaOH at 60 °C, or 0.5 M NaOH at 70 °C. All these conditions were shown to lead to cylindrical pores whose diameter increases with the etching time in a linear fashion. For the conical PET pores, 9 M NaOH was used as an etchant along with an acidic stopping medium (1 M formic acid, 1 M KCl), where the etchant was introduced to one side of the membrane and the stopping medium placed on the other;21 the etching process occurred at room temperature. Such a procedure has been extensively studied before and results in conically shaped nanopores.18,20,21,24Characterization of cylindrical and conical nanopores via current–voltage recordings
We used a Keithley 6487 picoammeter/voltage source (Keithley Instruments, Cleveland, OH) to record all current–voltage curves. Two Ag/AgCl electrodes were used to apply transmembrane potentials and record currents for all measurements, which also utilized symmetric electrolyte configurations. Polymer pores were sized after exhibiting stable current–voltage responses over the tested voltage window (−2 V to +2 V) in aqueous 1 M KCl. For cylindrical pores, size was calculated based on a direct calculation of conductance, yielding sizes from 400–1100 nm in diameter. Conical nanopores assumed the pore shape to be that of a truncated cone. Diameters of pores used in this study were 5–50 nm and 340–1500 nm for small (tip) and large opening (base), respectively. After characterization in KCl, current–voltage (I–V) curves were recorded in solutions of LiClO4 (10 mM–1 M) in propylene carbonate. Fig. S1† gives example I–V curves for both as prepared cylindrical and conical pores. This was done for comparison with the pore after it had been filled with gel and subjected to identical tests.Results and discussion
Experiments with single cylindrical pores and 25% (by wt) PMMA gel
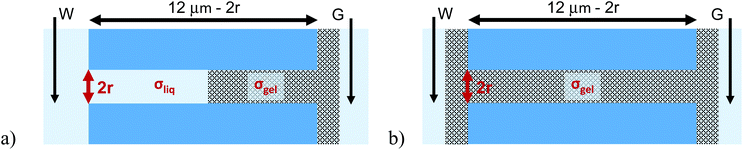
An important question to answer regards whether PMMA gel matrix at the sub-micron scale can ‘hold’ its initial doping concentration in the presence of liquid LiClO4-PC electrolyte. A simple experiment to examine this property is a one-sided drop-cast on a membrane followed by probing ionic current in a liquid electrolyte system. Fig. 1 shows a schematic of the planned experiment. Even though, in the one-sided drop-cast experiment, the depth of the gel penetration into the pore is not known, we expect it to be at least half of the pore length. It is because our previous experiments with samples subjected to drop-casting on both sides of the membrane provided evidence that the whole pore volume became filled with the gel.31 The previous work was performed without the liquid electrolyte and allowed us to examine the combination of ionic and electronic conductivity through the gel.Experiments with cylindrical pores entirely filled with gel, via double-sided gel casting, were performed as well (Fig. 1b). These samples were used in control experiments to observe change of the pore resistance before and after exposing it to the liquid electrolyte. We expected that if the gel was unaffected by the liquid electrolyte, I–V measurements would be similar in the immersed and gel-only cases, and would show no dependence based on the concentration of the liquid electrolyte. Experiments were performed with PMMA doped with 100 mM LiClO4 as well as undoped PMMA gel. The bulk solution was LiClO4 in propylene carbonate; the salt concentration was varied between 10 mM and 1 M.
At first we checked the stability of PMMA gel in contact with solutions of LiClO4 in propylene carbonate. The gel was deposited on a glass slide and observed using a microscope and camera before and after exposing the gel to propylene carbonate (Fig. S2†). These experiments were aimed at understanding the possibility of our gel spreading since propylene carbonate is known to be a PMMA gel plasticizer.38 Indeed, the gel did spread after exposure to the solvent, however the gel layer remained continuous. In order to assure that the mesoscopic structure of the gel quickly equilibrates when exposed to liquid PC and does not change during measurements, current–voltage curves were recorded using the following order. We started with 100 mM LiClO4 in PC, followed by probing lower concentrations down to 10 mM, we re-measured the 100 mM conditions and finally increased the salt concentration to 1 M LiClO4. For some samples, after the set of measurements was completed we checked the currents at 100 mM LiClO4 one more time. The three sets of 100 mM salt would not typically differ more than 10%, providing evidence for a stable structure of the PMMA gel in contact with PC. Each set of current–voltage curves was recorded after ∼1 minute equilibration of the system with a given salt concentration, four scans were performed at each concentration; the reported I–V curves are the average of the last three scans.
The polymer samples with PMMA gel were visually examined after I–V recordings. As in the case of the glass side, the gel spreading on the polymer surface was evident as well, and we confirmed lack of visible loss of the gel. For pores entirely filled with the gel, we expected no loss of gel from the inside of the pore, since the gel in the pore was protected via the thick layers on the polymer surfaces.
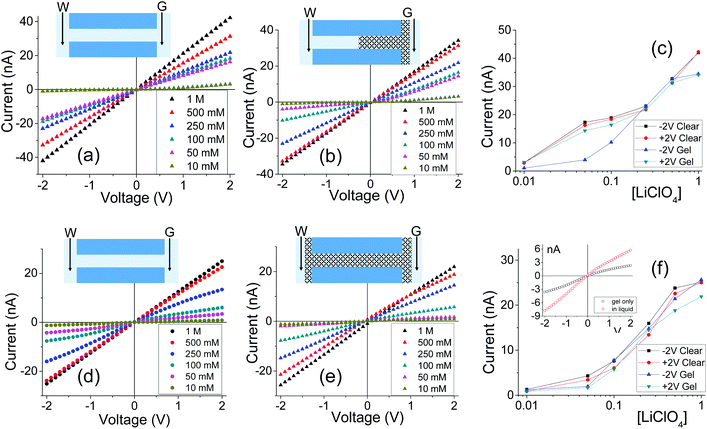
Fig. 2 shows I–V curves recorded for two samples with single pores, subjected to PMMA gel casting and exposed to bulk electrolyte of LiClO4 in PC. The salt concentration of the liquid electrolyte was varied between 10 mM and 1 M. One sample (Fig. 2a–c) was subjected to PMMA gel drop-cast on one side only, and the gel was undoped. The second sample (Fig. 2d–f) was entirely filled with gel, which had been doped with 100 mM LiClO4 during its preparation. The first feature of the two single pore membranes is a clear dependence of the I–V curves on the salt concentration in the bulk, regardless of gel doping: higher currents were recorded for higher concentrations of the salt in the liquid electrolyte. In the samples subjected to gel casting on one side of the membrane, concentration dependence is expected since the gel infiltration may not be through the entirety of the pore. However for the pores that were entirely filled with PMMA, the presence of a clear concentration dependence of the current gives the first evidence that the ion transport properties of the gel do not remain unaffected by the liquid electrolyte. Similar values of pore conductance before and after gel infiltration, independent of whether the pore was subjected to drop-casting with an undoped gel or with PMMA that contained LiClO4, constitute the most surprising finding. This observation also suggests that once a PMMA gel is immersed in the liquid electrolyte, its conductivity becomes dominated by the bulk solution. This finding is further corroborated by data in Fig. S3,† showing ion current through a pore containing the gel in the absence of a liquid electrolyte i.e. with electrodes placed directly into the gel. The gel-only measured conductance was significantly lower compared to the recordings obtained after introducing liquid electrolyte on both sides of the membrane.31
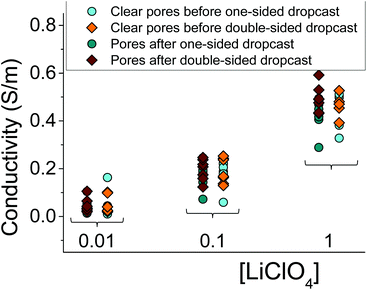
Fig. 3 summarizes several tested single cylindrical pores (n = 10) and their ionic conductivities before and after gel deposition in three standard concentrations (1 M, 100 mM, and 10 mM) of LiClO4/PC. Ionic conductivities were calculated by assuming the pore geometry to be cylindrical and relating the pore resistance (obtained from I–V curves) with its diameter and length, leaving conductivity as the only unknown. The figure shows a spread of conductivities, with no clear groupings to distinguish one-sided or double-sided samples or doping concentration in the PMMA. The data also highlight the statistical similarity between clear and gel-deposited cases when in contact with liquid electrolyte on both sides. This, along with the dependence of recorded current on concentration of the bulk electrolyte (Fig. 2), suggests the PMMA gel is highly permeable to the liquid electrolyte.
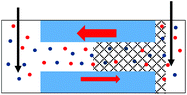
Additional evidence of PMMA affecting ion transport was observed in one-sided drop-cast samples as ion current rectification (Fig. 2b and Fig. S4†). The rectification direction observed is consistent with the gel acting as an ion selective porous39 medium with effective positive surface charges in the PMMA gel voids and on the pore walls. Higher currents in our electrode configuration correspond to anions moving from the gel side to the open pore entrance (not covered with gel). The presence of positive charges was previously suggested by our experiments with conical nanopores utilizing LiClO4/PC and LiClO4/PMMA gels;13,31 the excess charge could originate from adsorption of lithium ions as well as propylene carbonate molecules, whose high dipole moment can impart effective charge.40,41 The system rectifies, because the part of the pore filled with the gel is anion selective; the remaining part of the pore, even though containing charges on the walls, has too large diameter to cause a significant modulation of ionic concentrations thus it can be considered neutral. A pore subjected to a one-sided gel cast could be therefore considered similar to a system of a unipolar ionic diode,42–44 which contains a junction between a zone filled with one type of ions, and a zone that is filled with bulk solution.
Note that the highest degrees of rectification were recorded at intermediate concentrations of salt in the liquid electrolyte; this finding is in agreement with earlier observations and modeling of ionic transport through unipolar diodes and conically shaped pores with finite surface charges.18–20,25,26,45–47 As mentioned above, the side with the gel deposited could be considered equivalent to a charged zone of a unipolar diode. Ion current rectification occurs due to voltage modulations of ionic concentrations. For the voltage polarity, which sources counterions from the charged/ion selective side (side with the gel), concentrations of both counterions and co-ions increase above the bulk; for the opposite voltage polarity, a depletion zone is formed, leading to lower currents.45,47 In low salt concentrations, an overlap of the electrical double-layer makes the channel filled primarily with counterions and hinders the extent of the voltage-induced modulations of ionic concentrations. For high salt concentrations, such as 1 M, the charges are screened and the pore is filled with the bulk solution independently of the applied voltage.
Thus, the rectifying I–V curves of pores with PMMA also support our hypothesis that, while the PMMA gel is permeable to the liquid electrolyte, its porosity39 and effective surface13,31 charge can still have an impact on the ionic current if the ionic strength of the electrolyte fails to screen surface charges.
Note that the ion current rectification observed in pores that were only partially filled with PMMA, is reminiscent of a previously reported rectifying system of the same type of cylindrical pores containing a porous MnO2 rod.48 The rod contained negative surface charges due to the presence of hydroxyl groups, and the rectification properties were modulated by intercalated lithium ions.49
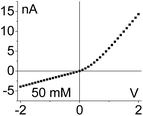
Further tests were conducted to determine if exposing pores with PMMA gel to a liquid electrolyte only from one side is sufficient to observe an enhanced ionic transport. The schematic in Fig. 4a illustrates how this would be accomplished for a one-sided gel deposition: one electrode was secured in the gel-cast side, while the open end was exposed to a reservoir of LiClO4 electrolyte with the electrode freely suspended in the liquid. For a gel sample subjected to gel casting on both sides, the only difference would be the pore being completely filled with gel and one side being exposed to liquid electrolyte (Fig. 4b). This set of tests will be referred to as a Gel–Liquid-Interface (GLI) experiment, and the results are shown in Fig. 4c–h. We found that conductance of nanopore membranes subjected to a one-sided gel drop-cast is less sensitive to the salt concentration in the liquid electrolyte, and lower than when the pores were exposed to liquid electrolyte on both sides. A similar qualitative conclusion can be drawn from the data recorded for samples subjected to the gel drop-cast on both sides, with exception that in this case rectification of ion currents was observed.
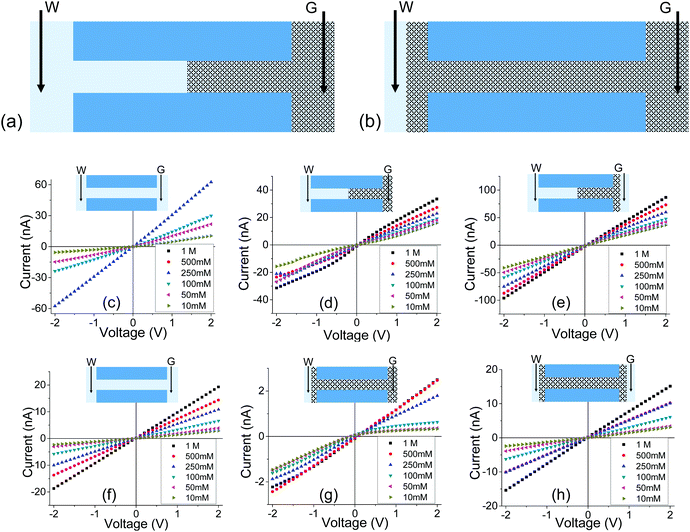 | ||
| Fig. 4 (a, b) Schematics of an experiment, called GLI, in which one side of the membrane was exposed to solution. Two electrodes were used in the measurements: one was embedded in the gel, the other one was located in the liquid. (c–e) Results for a cylindrical pore with an opening of 1060 nm in diameter subjected to gel deposition on one side; (c) recordings before depositing the gel; (d) measurements in the GLI mode, and (e) data obtained when both sides of the pore were placed in contact with a liquid electrolyte. (f–h) recordings performed with a 440 nm in diameter pore filled with PMMA gel doped with 100 mM LiClO4. Additional set of data with independently prepared pores is shown in Fig. S5.† | ||
Another difference between the one-side and double-sided casted membranes considers the magnitude of current decrease in the GLI mode when compared to an empty pore. In the former case, at 1 M LiClO4 the current dropped from ∼60 nA for the open pore to ∼30 nA after gel casting. For a pore entirely filled with the gel, the current in the GLI mode dropped ten-fold compared to the value before gel deposition. We believe that once a pore is filled with PMMA, even with only one electrode placed in the gel, the system conductance becomes limited by the conductivity of the gel, which is lower than the conductivity of the liquid electrolyte. It is also possible that the liquid electrolyte at the GLI mode does not have access to the whole volume of the PMMA in the pore, which would explain why the conductance of the system in Fig. 4a is higher than the conductance of the system in Fig. 4b.
The lower magnitude of ionic conductivity of the PMMA based gel electrolyte as well as the possibility of an incomplete infiltration of the liquid electrolyte into the gel would also explain the effect of ion current rectification seen with pores filled with the gel. It is because, when the membrane is in contact with liquid on one side only, at opposite voltage polarities ions are sourced from media of different conductivities. The effect is similar to the previously reported finding of ion current rectification induced in geometrically symmetric silica nanochannels placed in contact with a salt gradient in aqueous conditions.50 The key requirement for the silica channel and our systems is the presence of surface charges and nano-confinement, which make the pores at least partly ion selective. For one voltage polarity, the majority carriers are sourced from the side of the pore in contact with a medium of lower conductivity i.e. lower salt concentration in the silica channel system,50 and gel electrolyte in our case. For the opposite voltage polarity, majority carriers are sourced from the opposite side of the membrane in contact with a medium of higher conductivity. The effect of ion current rectification observed in pores filled with PMMA gel provides yet more evidence that the gel contains interconnected voids with excess positive surface charges.
Experiments with single conical pores and 30% (by wt) PMMA gel
Experiments with cylindrical pores allowed us to verify that PMMA gel is permeable to ions from the interfacing liquid electrolyte and carries net positive surface charge. A conical geometry of pores offers an easy access to nanoscale, and enables one to probe effects the gel exerts on ion transport when placed on the narrow and/or wide opening.51 For conical nanopores, stable ion current signals were observed after increasing the weight percent of PMMA to 30%. As demonstrated before, this PMMA concentration allowed full infiltration of the gel into the pore, so that the whole volume of conical nanopores was filled with the gel.31 As with cylindrically shaped pores, experiments with one-sided and double-sided gel casting were performed, using doped and blank PMMA gels.In our previous study we reported that conical nanopores filled with gel and studied as an ionics solid system without liquid electrolyte, function as an ionic rectifier.31 In addition, as shown in Fig. S1,† an as prepared nanopore filled with liquid PC based electrolyte rectifies the current as well.13 Thus, we expected conical nanopores with PMMA gel (drop cast on one side or two-sides) and in contact with liquid electrolyte would also rectify however with degree that is modulated by the gel placement. Previous studies in aqueous KCl solutions indeed revealed that rectification of conical nanopore membranes was sensitive to the placement of agar hydrogels on one or two membrane surfaces.51 In contrast to the previous report, the gel in our samples infiltrated the pores changing the overall nanostructure of the system, and we operate in entirely non-aqueous conditions. Fig. 5 shows representative samples of conically shaped nanopores after drop cast on the tip (and base) side only, as well as a nanopore filled with the gel entirely. The PMMA used was doped with 100 mM LiClO4, and all samples were placed in contact with liquid electrolyte on both sides. Comparison with conductance of the clear pore, i.e. before gel deposition, is also shown.
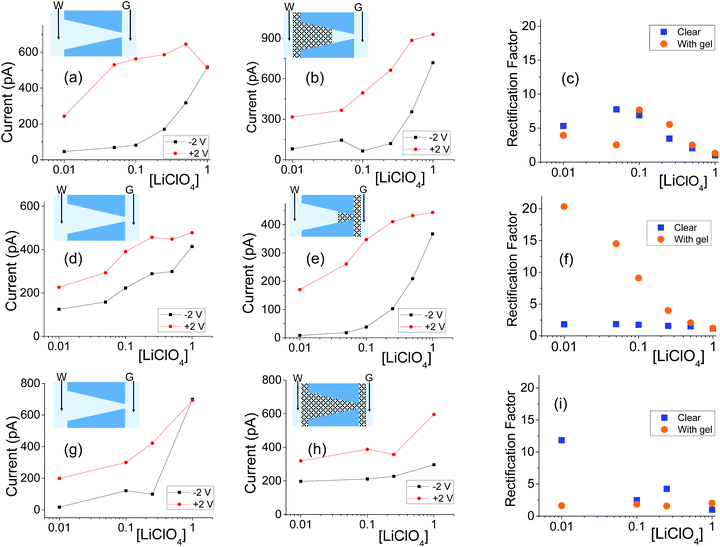 | ||
| Fig. 5 (a, b) Recordings with a single conical nanopore with opening diameters of 440 nm (base) and 55 nm (tip) subjected to gel drop-casting on the base side; the gel was doped with 100 mM LiClO4. (d, e) Results from a pore with dimensions of 808 nm (base) and 18 nm (tip) subjected to one-sided casting of blank (undoped) gel. (g, h) Measurements for a pore with dimensions 354 nm (base) and 44 nm (tip) filled with doped gel (100 mM LiClO4). (c, f, i) Rectification degrees calculated as a ratio of currents at +2 V and −2 V for pores before and gel deposition in each case. Another set of data obtained with independently prepared pores in shown in Fig. S6.† | ||
All conical nanopores examined exhibited the effect of ion current rectification with the currents for positive voltages higher than currents for negative voltages. This observation is in agreement with the existence of effective positive surface charges in the gel, as evidenced by our earlier experiments,31 measurements with cylindrical pores shown in the previous section, as well as literature data.52,53 The enhancement of ionic concentrations in the pore and an ‘on’ state of the system occurred when anions were sourced from the tip side (positive voltages); a depletion zone was formed for the opposite voltage polarity, which sourced the anions from the base side. The highest degrees of rectification were observed for pores subjected to drop-casting of the gel only on the tip side of the pore, similar to the observations with the agar hydrogel system.51 The gel on the tip side could lead to effective diminishing of the pore opening diameter as well as an increase of local surface charge densities; both these effects would lead to ion current rectification.18,19,21,45,47
Note that we observed significant differences in the rectification degrees exhibited by various pores before gel deposition, even for pores with similar tip diameters but different base openings (Fig. 5a and g). This variability in rectification of independently prepared nanopores is an accordance with earlier reports showing that ion current rectification on nanoscale is very sensitive to differences in pore geometry, effective length, and possible inhomogeinities in local surface charge.18,46,54–57 Even though the as prepared pores exhibited very different rectification degrees, filling them entirely or partly with the gel led to qualitatively reproducible changes in current–voltage curves. As an example, the pore shown in Fig. 5a exhibited the highest rectification before the gel deposition; after placing the gel on the base side, the rectification became the lowest out of the three pores shown in Fig. 5b, e and h.
The dependence of rectification on salt concentration for conically shaped pores with the gel is more complex than what was observed for cylindrical pores (Fig. 2 and Fig. S4†). Some pores exhibited the highest rectification degrees for intermediate concentrations (Fig. 5c and S6i†), while for others, rectification degree would decrease monotonically with the increase of salt concentration (Fig. 5f, 6f and S6c†). We do not have yet explanation for the results. We hypothesize that the differences in transport properties might arise from possible differences in the local structure of the gel, which are expected to influence transport properties at the nanoscale to a larger degree than at the mesoscale. The gel structure and charge characteristics can also be dependent on the salt concentration.
In terms of system conductance for an immersed sample before and after gel deposition, a large number of samples (n = 8) for one-sided pores and (n = 15) double-sided pores exhibited a reduced conductivity. Because of the rectification in samples, quantitative tracking of conductance shall be left to ESI (Fig. S8†).
We also performed GLI experiments in conical pores in the following configurations: (i) one-sided gel drop cast on the tip side, and (ii) pores filled with the gel in which the tip or base side was exposed to liquid electrolyte. Fig. 6 details the findings and compares the GLI experiment to the immersed case and tracks rectification.
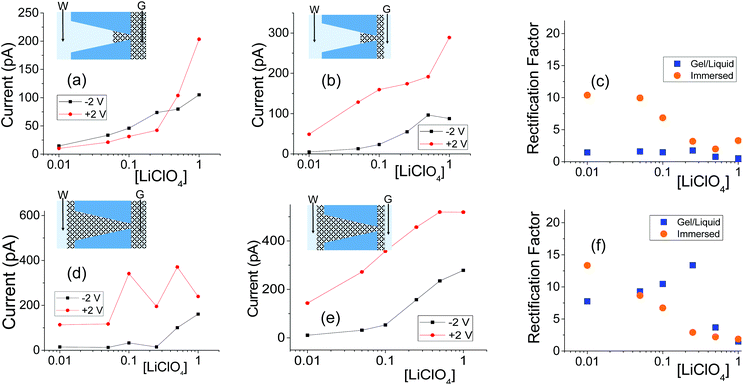 | ||
| Fig. 6 (a, b) Recordings with a single conical nanopore with opening diameters of 515 nm (base) and 16 nm (tip); this pore was subjected to one-sided drop cast of PMMA gel doped with 100 mM LiClO4. (d, e) Measurements from another conical nanopore (1080 nm (base) and 18 nm (tip)), filled with PMMA gel. The base side was initially exposed to liquid electrolyte for the GLI test. Another set of data obtained with independently prepared pores in shown in Fig. S7.† | ||
The GLI experimental results follow the pattern shown in cylindrical pores as they all exhibit lower system conductance as compared to the immersed condition. This GLI experimental set-up also allowed us to probe the interplay of the two mechanisms for ion current rectification originating from (i) geometrical asymmetry of a nanopore with excess surface charges,18–26 and (ii) asymmetry in medium conductivities on both sides of the membrane.50
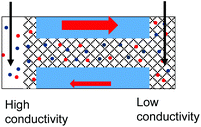
Let's first analyze the results obtained in the GLI mode with conical nanopores that were entirely filled with the gel. These experiments (Fig. 6d–f) suggest that the rectification properties of this system are dominated by the structural asymmetry of the pore. The dominant role of the conical shape is especially evident in recordings in which the base side of the pore was in contact with liquid electrolyte, and the other electrode was placed directly in the gel on the tip side (Fig. 6d). In our electrode configuration, for positive voltages the majority carriers – anions – are sourced from the tip side, thus from a medium with lower conductivity, and yet, positive currents are higher than negative currents. Thus the conical geometry imparts the opposite asymmetry of ionic transport: a higher current is observed when ions are sourced from the gel.
Conical nanopores subjected to one-sided gel deposition on the tip side exhibit a more complex rectification behavior. At lower concentrations of LiClO4, these pores feature a nearly ohmic behavior (currents at −2 V and +2 V in Fig. 6a are nearly the same) that is reminiscent of a linear character of current–voltage curves of cylindrical pores subjected to a single-sided gel casting and examined in the GLI mode (Fig. 4d). Surprisingly, however, significant rectification properties emerged at high salt concentrations of 500 mM and 1 M; this rectification has the same direction as exhibited by the entirely filled pores studied in the GLI mode (Fig. 6d) and when placed in contact with a liquid electrolyte on both sides (Fig. 5h and 6e). We do not have yet an explanation for the results. One possible mechanism behind the emergence of rectification properties at high salt concentrations could be a possibility of lithium ions adsorption into the gel structure,52 causing a higher effective positive surface charge of the gel at higher lithium concentrations. Enhancement of rectification in high salt concentrations in the GLI mode was also observed with one conical pore subjected to double-sided gel casting (Fig. S7d†).
In order to understand differences in rectification properties of conical nanopores subjected to one-sided and double-sided gel casting in the GLI mode, we hypothesize that the current–voltage character might be influenced by the location of the gel/liquid interface51,58 (Fig. 7). If the interphase between liquid and the gel occurs inside the pore, the zone of the pore with gel will be shorter than the length of the whole conical pore. This shorter gel zone is placed in contact with a conductivity gradient, higher (lower) on the liquid (gel) side. Rectification of conical pores is known to decrease with the decrease of pore length,56 thus with a partial gel infiltration, the influence of the geometry-induced rectification can be expected to be less dominant compared to a pore entirely filled with the gel.
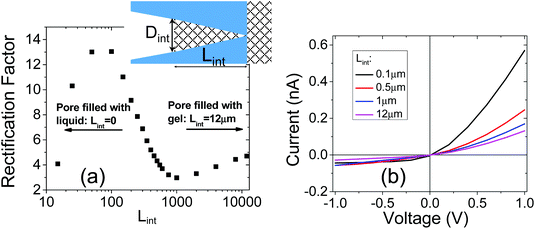
In order to illustrate the interplay of the two mechanisms, geometric26 and asymmetric conductivity,50 the system of a single nanopore in contact with two media that differ in conductivity was subjected to numerical modeling based on the Poisson–Nernst–Planck equations.47,59 Details of the model together with boundary conditions are given in ref. 31. Lint is the length of the pore infiltrated with the gel (Fig. 7a and b); this parameter was changed from 0 to 12 μm. Due to axial symmetry of the system, 1D model along the pore axis, z, was considered. Presence of gel in the part of conical nanopore filled with PMMA was captured via introduction of space charges, ρ(z), added to the Poisson equation, as reported before:31
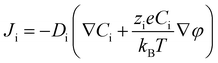 | (1a) |
| ∇·Ji = 0 | (1b) |
| ε0εΔφ = −[e(C+ − C−) + ρ(z)] | (1c) |
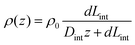 | (2) |
Fig. 7a shows how the rectification factor calculated as I(+1 V)/I(−1 V) depends on Lint. The modeling confirmed that as in the case of a conical pore in contact with liquid and containing two zones with different surface characteristics,18,42–44 rectification is the strongest for a Lint below 500 nm.60 Note, however, that the modeling predicted a dominant role of the geometric asymmetry over the mobility differences in the gel and liquid electrolyte, so that even for very short infiltration lengths, Lint, the rectification with higher positive currents was observed. The nearly linear I–V curve observed in our experiments (Fig. 6a) suggests that the gel placed on the tip side infiltrated the pore at the depth of at least a micrometer.
Conclusions
Experiments with meso and nanopores containing PMMA gel revealed that ionic conductivity of the gel became dominated by the salt concentration in the liquid bulk solutions in contact with the pores. Even a pore filled with an undoped gel placed in contact with liquid salt solution on both sides exhibited conductances comparable to these in a control experiment of the same pore performed before gel infiltration. The effect of the gel on ionic transport was clearly observed via ion current rectification consistent with a model of a porous structure of the gel39 with effective positive charges.One of the most important contributions of this manuscript is reporting measurements of ion current through such hybrid gel/liquid electrolyte system at the meso- and nanoscales. Our previous manuscript dealt with the pores behavior without any liquid electrolyte,31 but it is indeed possible that some applications of the gel electrolyte in energy-storage devices will require an interface with liquid. The systems presented in this manuscript also provide a unique platform to investigate different mechanisms of ion current rectification. Breaking symmetry of electrochemical potential has been previously shown via surface charge patterns,18,42–44 asymmetry in ionic concentrations/ionic conductivity in nanoscale channels,50 and in conically shaped pores with finite surface charges.18,19–26 The interplay between the conductivity and geometric asymmetries could be observed when the samples were examined in the GLI mode i.e. when one electrode was placed in the liquid electrolytes, and the other one was inserted directly into the gel.
Table 1 summarizes all pore geometries considered with single or double-sided gel casting that allowed us to consider contribution of conductivity or/and geometrical asymmetry to the rectification. (case 1) A cylindrical pore partly filled with the gel could be understood using similar physical concepts as done in ionic unipolar diodes.18,42–44 (cases 2, 3) A cylindrical pore studied in the GLI mode rectifies due to the asymmetry of conductivity of the two media placed on both sides of the membrane;50 higher currents were observed if the majority carriers were sourced from the higher conductivity – liquid electrolyte. The experiments with cylindrical pores subjected to single and double-sided gel casting point to the influence of the length of the pore containing gel on the pore transport properties. Only pores entirely filled with the gel were found to rectify the current. (case 4) Conical nanopores filled with the gel and placed in contact with liquid electrolyte provide a model of a system, which rectifies due to the pore geometrical asymmetry; larger currents occur when the anions are sourced from the tip side. (cases 5, 6) A conical nanopore filled with gel and studied in the GLI mode such that the liquid electrolyte is placed only on the base side allows us to study how the asymmetry induced by the geometry is counteracted by the conductivity asymmetry. Again, the pore has to be filled with the gel entirely to lead to a significant ion current rectification to occur.
| Experimental setup | I–V curves recorded | |
|---|---|---|
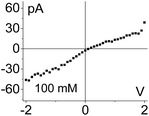
| 1. Asymmetry in ionic concentrations in the pore is analogous to the system of ionic unipolar diodes.42–44 The part of the pore with the gel is filled predominantly with anions, the remaining part of the pore is filled with the bulk solution. I–V curve from Fig. 2b is shown. |
|
|
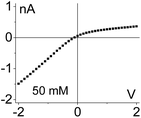
| 2. The system exhibits conductivity asymmetry only,50 so that lower currents are observed when counterions are sourced from the gel side that is not exposed to the liquid electrolyte. I–V curve from Fig. 4d is shown. |
|
|
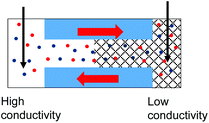
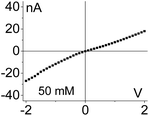
| 3. Asymmetry in conductivity is superimposed on the asymmetry in ionic concentrations as shown in case (1). These two effects act against each other. I–V curve from Fig. 4g is shown. |
|
|
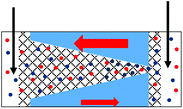
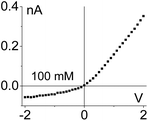
| 4. Geometrical asymmetry together with charges on the pore walls and in the gel lead to rectification. Higher currents are observed when counterions are sourced from the tip side. Data from the pore shown in Fig. 6e is shown. |
|
|
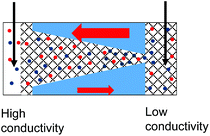
| 5. Combined geometrical and conductivity asymmetries acting against each lead to rectification if the pore is entirely filled with the gel. The asymmetry stemming from the pore geometry and presence of charges dominates. Data from the pore shown in Fig. 6d is shown. |
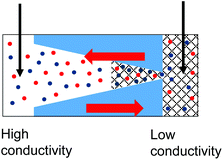
|
|
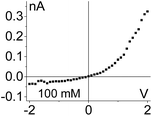
| 6. Combined geometrical and conductivity asymmetries acting against each other produce a linear current–voltage curve. Data from the pore shown in Fig. 6a is shown. |
|
|
Our results indicate that some mechanisms of ionic transport identified in aqueous conditions could be applied to understand, at least qualitatively, transport properties in non-aqueous electrolytes. Some observations, however, including emergence of rectification at high salt concentrations, could not be explained using models applied to aqueous solutions. Our results also point to the various mechanisms that lead to preparation of rectifying systems in organic and solid electrolytes.
The manuscript contributes to the understanding of ionic transport in non-aqueous PMMA-based electrolytes, an area of research, which has so far been underexplored. Non-aqueous based electrolytes at the meso- and nanoscale are however important for energy-storage systems as well as possibility of performing separations of organic molecules, among other applications. The manuscript shows complexity of such electrolytes, which change when in contact with liquid electrolytes. Future areas of research will include other gel and solid state electrolytes at nano- and mesoconfinement.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Nanostructures for Electrical Energy Storage (NEES), an Energy Frontier Research Center funded by the US Department of Energy, Office of Science, Office of Basic Energy Sciences under Award Number DESC001160. We also acknowledge GSI Helmholtzzentrum für Schwerionenforschung in Darmstadt, Germany for providing irradiated membranes. We thank especially Dr Phil Collins of UC Irvine and Dr Charles Martin of University of Florida for valuable conversations during the course of the research.References
- M. S. Whittingham, Proc. IEEE, 2012, 100, 1518–1534 CrossRef CAS.
- K. Xu, Chem. Rev., 2004, 104, 4303–4418 CrossRef CAS PubMed.
- P. Voelker, Trace Degradation Analysis of Lithium-Ion Battery Components, R&D Magazinde, (April 2014) http://www.rdmag.com/articles/2014/04/trace-degradation-analysislithium-ion-battery-components Search PubMed, (accessed August 2015).
- M. Y. Saidi, C. Scordilis-Kelley and J. Barker, Stabilized Electrochemical Cell, US Patent, 5869207A, 1999 Search PubMed.
- M. L. Thai, G. T. Chandran, R. K. Dutta, X. Li and R. M. Penner, ACS Energy Lett., 2016, 1, 57–63 CrossRef.
- A. C. Kozen, A. J. Pearse, C. F. Lin, M. Noked and Gary W. Rubloff, Chem. Mater., 2015, 27, 5324–5331 CrossRef CAS.
- I. Yoshimatsu, T. Hirai and J. Yamaki, J. Electrochem. Soc., 1988, 135, 2422–2427 CrossRef CAS.
- K. M. Abraham, J.S. Foos and J. L. Goldman, J. Electrochem. Soc., 1984, 131, 2197–2199 CrossRef CAS.
- W. Yan, M. L. Thai, R. Dutta, X. Li, W. Xing and R. M. Penner, ACS Appl. Mater. Interfaces, 2014, 6, 5018–5025 CAS.
- Z. Osman, M. I. Mohd Ghazali, L. Othman and K. B. Md Isa, Results Phys., 2012, 2, 1–4 CrossRef CAS.
- A. M. M. Ali, M. Z. A. Yahya, H. Bahron, R. H. Y. Subban, M. K. Harun and I. Atan, Mater. Lett., 2007, 61, 2026–2029 CrossRef CAS.
- R.B. Schoch, J. Han and P. Renaud, Rev. Mod. Phys., 2008, 80, 839–883 CrossRef CAS.
- T. Plett, W. Shi, Y. Zeng, W. Mann, I. Vlassiouk, L.A. Baker and Z. S. Siwy, Nanoscale, 2015, 7, 19080–19091 RSC.
- X. Yin, S. Zhang, Y. Dong, S. Liu, J. Gu, Y. Chen, X. Zhang, X. Zhang and Y. Shao, Anal. Chem., 2015, 87, 9070–9077 CrossRef CAS PubMed.
- G.B. Westermann-Clark and C.C. Christoforou, J. Membr. Sci., 1984, 20, 325–339 CrossRef CAS.
- E.C. Yusko, R. An and M. Mayer, ACS Nano, 2010, 4, 477–487 CrossRef CAS PubMed.
- L. Luo, D.A. Holden, W.J. Lan and H.S. White, ACS Nano, 2012, 6, 6507–6514 CrossRef CAS PubMed.
- Z. S. Siwy and S. Howorka, Chem. Soc. Rev., 2010, 39, 1115–1132 RSC.
- C. Wei, A. J. Bard and S. W. Feldberg, Anal. Chem., 1997, 69, 4627–4633 CrossRef CAS.
- Z. Siwy and A. Fulinski, Phys. Rev. Lett., 2002, 89, 198103 CrossRef CAS PubMed.
- P. Y. Apel, Y. E. Korchev, Z. Siwy, R. Spohr and M. Yoshida, Nucl. Instrum. Methods Phys. Res., Sect. B, 2001, 184, 337–346 CrossRef CAS.
- Z. Siwy, D. Dobrev, R. Neumann, C. Trautmann and K. Voss, Appl. Phys. A, 2003, 76, 781–785 CrossRef CAS.
- P. Y. Apel, I. V. Blonskaya, O. L. Orelovitch, P. Ramirez and B. A. Sartowska, Nanotechnology, 2011, 22, 175302 CrossRef PubMed.
- C. C. Harrell, Z. S. Siwy and C. R. Martin, Small, 2005, 2, 194–198 CrossRef PubMed.
- M. Ali, P. Ramirez, S. Mafé, R. Neumann and W. Ensinger, ACS Nano, 2009, 3, 603–608 CrossRef CAS PubMed.
- Z. S. Siwy, Adv. Funct. Mater., 2006, 16, 735–7 CrossRef CAS.
- E. R. Cruz-Chu, A. Aksimentiev and K. Schulten, J. Phys. Chem. C, 2009, 113, 1850–1862 CAS.
- S. Devaraj and N. Munichandraiah, J. Phys. Chem. C, 2008, 112, 4406–4417 CAS.
- O. Ghodbane, J. L. Pascal and F. Favier, ACS Appl. Mater. Interfaces, 2009, 1, 1130–1139 CAS.
- S. Vorrey and D. Teeters, Electrochim. Acta, 2003, 48, 2137–2141 CrossRef CAS.
- T. S. Plett, W. Cai, M. Le Thai, I. Vlassiouk, R. M. Penner and Z. S. Siwy, J. Phys. Chem. C, 2017, 121, 6170–6 CAS.
- Z. Osman, M. I. Mohd Ghazali, L. Othman and K. B. Md Isa, Results Phys., 2012, 2, 1–4 CrossRef CAS.
- A. M. M. Ali, M. Z. A. Yahya, H. Bahron, R. H. Y. Subban, M. K. Harun and I. Atan, Mater. Lett., 2007, 61, 2026–2029 CrossRef CAS.
- C. M. Mathew, K. Kesavan and S. Rajendran, Int. J. Electrochem., 2015, 2015, 494308 Search PubMed.
- R. L. Fleischer, P. B. Price and R. M. Walker, Nuclear Tracks in Solids: Principles and Applications, University of California Press, Berkeley, CA, 1975 Search PubMed.
- R. Spohr, Methods and Device to Generate a Predetermined Number of Ion Tracks, German Patent, DE2951376C2, 1983 Search PubMed; R. Spohr, Methods and Device to Generate a Predetermined Number of Ion Tracks, US Patent, 4369370, 1983 Search PubMed.
- S. Müller, C. Schötz, O. Picht, W. Sigle, P. Kopold, M. Rauber, I. Alber, R. Neumann and M. E. Toimil-Molares, Cryst. Growth Des., 2012, 12, 615–621 Search PubMed.
- C.-W. Kuo, W.-B. Lin, P.-R. Chen, J.-W. Liao, C.-G. Tseng and T.-Y. Wu, Int. J. Electrochem. Sci., 2013, 8, 5007–502 CAS.
- C. Svanberg, W. Pyckhout-Hintzen and L. Börjesson, Electrochim. Acta, 2006, 51, 4153–4156 CrossRef CAS.
- M.L. Belaya, M.V. Feigel'man and V.G. Levadny, Langmuir, 1987, 3, 648–654 CrossRef CAS.
- M. Belaya, V. Levadny and D.A. Pink, Langmuir, 1994, 10, 2010–2014 CrossRef CAS.
- R. Karnik, C. Duan, K. Castelino, H. Daiguji and A. Majumdar, Nano Lett., 2007, 7, 547–551 CrossRef CAS PubMed.
- I. Vlassiouk, S. Smirnov and Z.S. Siwy, ACS Nano, 2008, 2, 1589–1602 CrossRef CAS PubMed.
- G. Nguyen, I. Vlassiouk and Z.S. Siwy, Nanotechnology, 2010, 21, 265301 CrossRef PubMed.
- J. Cervera, B. Schiedt and P. Ramirez, Europhys. Lett., 2005, 71, 35–41 CrossRef CAS.
- J. Cervera, B. Schiedt, R. Neumann, S. Mafe and P. Ramirez, J. Chem. Phys., 2006, 124, 104706 CrossRef PubMed.
- H.S. White and A. Bund, Langmuir, 2008, 24, 2212–2218 CrossRef CAS PubMed.
- T. Gamble, E. Gillette, S.B. Lee and Z.S. Siwy, J. Phys. Chem. C, 2013, 117, 24836–24842 CAS.
- T. Plett, T. Gamble, E. Gillette, S.B. Lee and Z.S. Siwy, J. Mater. Chem. A, 2015, 3, 12858–12863 CAS.
- L. J. Cheng and L.J. Guo, Nano Lett., 2007, 7, 3165–3171 CrossRef CAS PubMed.
- L. Wang, H. Zhang, Z. Yang, J. Zhou, L. Wen, L. Li and L. Jiang, Phys. Chem. Chem. Phys., 2015, 17, 6367–6373 RSC.
- J. Y. Wang, W. Chen and T. P. Russell, Macromolecules, 2008, 41, 4904–4907 CrossRef CAS.
- H. Falahati, L. Wong, L. Davarpanah, A. Garg, P. Schmitz and D. P. J. Barz, Electrophoresis, 2014, 35, 870–882 CrossRef CAS PubMed.
- B. Yameen, M. Ali, R. Neumann, W. Ensinger, W. Knoll and O. Azzaroni, J. Am. Chem. Soc., 2009, 131, 2070–2071 CrossRef CAS PubMed.
- M. Ali, P. Ramirez, S. Mafé, R. Neumann and W. Ensinger, ACS Nano, 2009, 3, 603–608 CrossRef CAS PubMed.
- J.-F. Pietschmann, M.-T. Wolfram, M. Burger, C. Trautmann, G. Nguyen, M. Pevarnik, V. Bayer and Z. S. Siwy, Phys. Chem. Chem. Phys., 2013, 15, 16917–16926 RSC.
- P. Ramirez, P.Y. Apel, J. Cervera and S. Mafe, Nanotechnology, 2008, 19, 315707 CrossRef PubMed.
- F. Maletzki, H. -W. Rosler and E. Staude, J. Membr. Sci., 1992, 71, 105–116 CrossRef CAS.
- I. Vlassiouk, S. Smirnov and Z. S. Siwy, Nano Lett., 2008, 8, 1978–1985 CrossRef CAS PubMed.
- I. Vlassiouk, T.R. Kozel and Z.S. Siwy, J. Am. Chem. Soc., 2009, 131, 8211–8220 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7nr06719d |
| This journal is © The Royal Society of Chemistry 2017 |