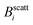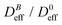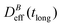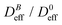Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reversible and irreversible aggregation of magnetic liposomes†
Sonia
García-Jimeno
 a,
Joan
Estelrich
a,
Joan
Estelrich
 a,
José
Callejas-Fernández
a,
José
Callejas-Fernández
 b and
Sándalo
Roldán-Vargas
b and
Sándalo
Roldán-Vargas
 *c
*c
aSecció de Fisicoquímica, Facultat de Farmàcia i Ciències de l'Alimentació, Universitat de Barcelona, Avda. Joan XXIII 17-31, E-08028, Barcelona, Catalonia, Spain
bGrupo de Física de Fluidos y Biocoloides, Departamento de Física Aplicada, Facultad de Ciencias, Universidad de Granada, E-18071, Granada, Spain
cMax Planck Institute for the Physics of Complex Systems, D-01187, Dresden, Germany. E-mail: sandalo@pks.mpg.de
First published on 26th September 2017
Abstract
Understanding stabilization and aggregation in magnetic nanoparticle systems is crucial to optimizing the functionality of these systems in real physiological applications. Here we address this problem for a specific, yet representative, system. We present an experimental and analytical study on the aggregation of superparamagnetic liposomes in suspension in the presence of a controllable external magnetic field. We study the aggregation kinetics and report an intermediate time power law evolution and a long time stationary value for the average aggregate diffusion coefficient, both depending on the magnetic field intensity. We then show that the long time aggregate structure is fractal with a fractal dimension that decreases upon increasing the magnetic field intensity. By scaling arguments we also establish an analytical relation between the aggregate fractal dimension and the power law exponent controlling the aggregation kinetics. This relation is indeed independent on the magnetic field intensity. Despite the superparamagnetic character of our particles, we further prove the existence of a population of surviving aggregates able to maintain their integrity after switching off the external magnetic field. Finally, we suggest a schematic interaction scenario to rationalize the observed coexistence between reversible and irreversible aggregation.
I. Introduction
In recent times, the ad hoc design of novel mesoscopic particles has opened new research avenues and brought several promising applications. Significant examples of this bottom-up design appear in material science,1–3 biotechnology,4,5 and nanomedicine.6,7 Indeed, the highly versatile functionality of these new primary constituents relies on our efficacy to control the distinct interactions governing their dynamic and structural properties.A notable family among these new primary components is that constituted by those nano- and meso-sized particles able to respond to an external magnetic field. These “magnetic nanodevices” are usually categorized according to their remanent magnetization at a given temperature after having been exposed to an external magnetic field.8 Thus mesoscopic particles consisting of single magnetic domains9 can behave as permanent magnets due to their remanent (or even spontaneous) magnetization in the absence of an external magnetic field. This phenomenon is known as stable ferromagnetism.8 However, if thermal energy is able to cause the random orientation of the different single magnetic domains, the particle remanent magnetization after removing the external magnetic field will be negligible. These particles, which present no magnetic hysteresis, are known as superparamagnetic particles.8,10 These two behaviors (ferromagnetic and superparamagnetic) are nowadays exploited in several consolidated research lines with a special emphasis in nanomedical applications.11–19
Among the distinct mesoscopic particles, liposomes, i.e. mesosized lipid vesicles, have been recognized by their singular capabilities (e.g. as drug nanocarriers) due to their synthetically controllable size, surface electric charge, membrane elastic properties, and encapsulation efficiency.20–22 The superparamagnetic version of these highly tuneable particles results from our ability to encapsulate in their interior small (single domain) magnetite grains.23–30 These are the so-called magnetic liposomes. Thus these systems combine biocompatibility and vesicular structure31 with their superparamagnetic character, therefore being magnetically controllable agents with no side-effects on the organism. Fruitful applications using these systems are already amenable to experimentation covering specific areas in therapy and diagnostics such as chemotherapy,17,32 hyperthermia,33–37 magnetic resonance imaging,24,38,39 magnetic cell targeting,40–42 or magnetically driven delivery.30,43
Reaching an efficient functionality for these vesicular systems (and other magnetic nanoparticles) depends on our understanding of the distinct particle interactions. This understanding is intrinsically connected with those mechanisms controlling stabilization and aggregation. Indeed, magnetically induced aggregation not only provides us with an implicit understanding on the particle interactions but it is explicitly manifested in real applications. For instance, aggregates of superparamagnetic particles present an enhanced heating efficiency in hyperthermia as compared to that corresponding to non-aggregated samples.44–46 The presence of aggregates can also increase the sensitivity of some detection techniques such as Surface-Enhanced Raman Scattering (SERS), leading to a significant increase of the Raman intensity.47 Irreversible aggregates can also influence the system functionality when their size is comparable to those length scales defining the targeted microenvironment, e.g. in Enhanced Permeability and Retention (EPR)15,48 or in the subsequent particle excretion from the body.49 These functional implications demand a comprehensive study on the still poorly understood mechanisms controlling aggregation in magnetic nanoparticle systems. In this work we present such a study for a system of magnetic vesicles.
So far, magnetically induced aggregation has been experimentally investigated but being focused on the study of non-encapsulating superparamagnetic particles. For instance, light scattering has been used to probe aggregation kinetics and/or aggregate structure50–56 whereas two-dimensional microscopy images have been analyzed to look into the cluster morphology.51,52,55–58 Apart from studies on real systems, simulations and analytical approaches have also been proposed to rationalize the aggregation of ferro- and superpara-magnetic particles where magnetic interaction is treated in terms of a dipolar hard-sphere like model.59–63
Here we present a detailed study on the aggregation of magnetic liposomes in suspension in the presence of a controllable external magnetic field. By Dynamic Light Scattering (DLS) we explore the aggregation kinetics and find an intermediate time regime where the aggregate diffusion coefficient presents a power law evolution. This evolution, which can be controlled by changing the magnetic field intensity, reaches at sufficiently long times a stationary value as a result of a competition between cluster formation and fragmentation. This final steady-state of the diffusion coefficient allows us to investigate the aggregate structure by Static Light Scattering (SLS). This structure is fractal and results in increasingly linear aggregates upon increasing the magnetic field intensity. Interestingly, we can appeal to scaling arguments and establish a relation between the aggregate fractal dimension and the power law exponent governing the aggregation kinetics. With this analytical approach we create a link between structure and dynamics in our system. To extend the aggregate characterization, we directly observe the system by Transmission Electron Microscopy (TEM) and report a coexistence between reversible and irreversible aggregates (i.e. aggregates that survive despite switching off the external magnetic field). Finally, this coexistence is discussed in terms of an interplay between interactions of different origin. Our results and the general picture we offer are of particular interest for predicting and controlling those time and length scales that play a relevant role in real physiological applications.
The rest of the paper is organized as follows: in section II we introduce the system and present our methodologies. In section III we show and discuss our results on stabilization, aggregation kinetics, aggregate structure, and aggregate reversibility. Finally, in section IV we summarize our main findings and present our conclusions.
II. Materials and methods
The protocol for synthesizing the magnetic liposomes used in this work as well as part of the liposome characterization have been presented in a previous study.30 Here we summarize the previous methodologies and include the protocol to obtain our dynamic and static light scattering results as well as the methodology to acquire the TEM micrographs. Additional information on the characterization of the magnetic liposomes such as their zeta-potential at different salt concentrations or their encapsulation efficiency can be consulted in Ref. 30A. Synthesis of magnetic liposomes
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 molar ratio) dissolved in chloroform/methanol (2
20 molar ratio) dissolved in chloroform/methanol (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, v/v) are placed in a round-bottom flask and dried in a rotary evaporator under reduced pressure at 40 °C to form a thin film on the inner surface of the flask. The film is hydrated with 9 ml of diethyl ether and 3 ml of an aqueous dilution of FerroTec, resulting in a final concentration of 1.86 g l−1 of magnetite. The mixture is then sonicated for 5 min in a bath sonicator (Transsonic Digital Bath sonifier, Elma, Germany) at 0 °C. Once the emulsion has been formed, it is placed in a round-bottom flask and the organic solution is removed under a pressure range of 420–440 mmHg at room temperature. The emulsion becomes a gel and, finally, this gel transforms into a suspension of liposomes. Once the liposome suspension is obtained we add 1 ml of water, rotating the suspension at 760 mmHg to remove the ether. Liposomes are then diluted with water until obtaining a final PC concentration of 16 mmol l−1. Liposome are then extruded both ways at room temperature into a Liposofast device (Avestin, Canada) through two polycarbonate membrane filters of 200 nm pore size and for at least 9 times.65 Separation of non-encapsulated ferrofluid from magnetic liposomes is performed by size exclusion chromatography (Sephacryl S-400 HR, GE Healthcare, Uppsala, Sweden). The iron content of the purified magnetic liposomes is determined by atomic absorption spectrophotometry (UNICAM PU 939 flame absorption spectrometer) giving an average value of 180 μg ml−1. PC was determined by colorimetry.66 Both determinations allow obtaining the Fe3+/PC ratio which resulted in an average value of 45 g mol−1.
1, v/v) are placed in a round-bottom flask and dried in a rotary evaporator under reduced pressure at 40 °C to form a thin film on the inner surface of the flask. The film is hydrated with 9 ml of diethyl ether and 3 ml of an aqueous dilution of FerroTec, resulting in a final concentration of 1.86 g l−1 of magnetite. The mixture is then sonicated for 5 min in a bath sonicator (Transsonic Digital Bath sonifier, Elma, Germany) at 0 °C. Once the emulsion has been formed, it is placed in a round-bottom flask and the organic solution is removed under a pressure range of 420–440 mmHg at room temperature. The emulsion becomes a gel and, finally, this gel transforms into a suspension of liposomes. Once the liposome suspension is obtained we add 1 ml of water, rotating the suspension at 760 mmHg to remove the ether. Liposomes are then diluted with water until obtaining a final PC concentration of 16 mmol l−1. Liposome are then extruded both ways at room temperature into a Liposofast device (Avestin, Canada) through two polycarbonate membrane filters of 200 nm pore size and for at least 9 times.65 Separation of non-encapsulated ferrofluid from magnetic liposomes is performed by size exclusion chromatography (Sephacryl S-400 HR, GE Healthcare, Uppsala, Sweden). The iron content of the purified magnetic liposomes is determined by atomic absorption spectrophotometry (UNICAM PU 939 flame absorption spectrometer) giving an average value of 180 μg ml−1. PC was determined by colorimetry.66 Both determinations allow obtaining the Fe3+/PC ratio which resulted in an average value of 45 g mol−1.
B. Transmission electron microscopy
To obtain the TEM micrographs of section III.E, we placed a drop of an initially stable aqueous suspension of magnetic liposomes at room temperature on a microscope slide covered with parafilm. The water used for sample dilution was purified by inverse osmosis using Millipore equipment. To induce aggregation we placed at both sides of the microscope slide two Neodymium–Iron–Boron (Nd2Fe12B) magnets (Halde GAC, Barcelona, Spain). The magnetic field intensity created by the magnets in the space where the sample was placed is B = 80 mT. After 15 min of exposure to the magnetic field, a 400-mesh copper grid coated with a carbon film with a Formvar membrane was placed on the sample for 5 min. After this time (20 min in total), the magnets were removed and a drop of water was added to the grid for washing the sample. This washing step was repeated once more. Then a drop containing a 2% of uranyl acetate was added and, after 1 min, the excess of staining solution was removed. The sample was allowed to dry in air for several minutes before observation. The observation was performed by transmission electron microscopy using an EFTEM (EM902 Zeiss, Carl Zeiss Jena, Germany) operating at 105 V. In addition, TEM micrographs for non-aggregated samples were routinely used within this work for control purposes by using a transmission electron microscope Jeol 1010 (Jeol, Japan) operating at 8 × 104 V, recording the images by a Megaview III camera. The acquisition was accomplished with Soft-Imaging software (SIS, Germany).C. Magnetization of magnetic liposomes
Magnetization curves of purified aqueous suspensions of magnetic liposomes as a function of the applied external magnetic field were obtained in a SQUID Quantum Design MPMS XL magnetometer. The probed external magnetic field ranged from −600 mT to +600 mT. Measurements were taken at room temperature.D. Light scattering experiments
The protocol we use to probe aggregation kinetics and aggregate structure under the influence of an external magnetic field by light scattering is partially similar to that reported in ref. 53–55 to study the aggregation of magnetic polystyrene particles. Here we present separately the experimental protocol to perform our measurements and a succinct theoretical background to interpret our measurements in terms of appropriate dynamic and static observables.For both aggregating and non-aggregating samples we used purified aqueous suspensions of magnetic liposomes where the presence of salt in the medium was prevented by inverse osmosis using Millipore equipment. We prepared sufficiently diluted suspensions at 0.1% liposome volume fraction. This concentration avoids the effect of long-range interactions between liposomes in case of non-aggregating samples (section III.A) and gives us an optimal aggregation time for the magnetically induced aggregating samples. This time is sufficiently long compared with that needed for computing 〈I(θf;t)I(θf;t + τ)〉 (2 orders of magnitude greater) but sufficiently short to follow the complete aggregation process. We ensured statistical reliability by performing at least 10 independent experimental realizations of each DLS and SLS measurement for both aggregating and non-aggregating samples. In all the light scattering experiments temperature was kept constant at 25 °C.
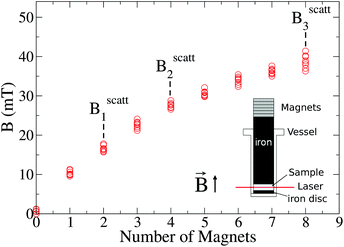
The experimental set-up to induce liposome aggregation by means of an external magnetic field deserves further explanation. Fig. 1 shows a schematic view of this experimental set-up where the magnetic field intensity is controlled by adding or removing Nd2Fe12B magnets on the top of the scattering vessel containing the sample. To enhance the magnetic field intensity acting on the sample, we insert between the pile of magnets and the sample a cylindrical iron bar to promote magnetic field line confinement. Thus, the direction of the magnetic field is essentially perpendicular to the scattering plane. Fig. 1 also shows the magnetic field intensity acting on the sample as a function of the number of neodymium magnets. We see how upon increasing the number of magnets the magnetic field intensity increases, leading to an intensity field saturation which imposes an upper threshold for the magnetic field intensity of about 40 mT. Accordingly we performed DLS and SLS experiments for magnetically induced aggregating samples at Bscatt = 16.6(±0.7), 27.5(±0.7), and 38.8(±0.6) mT. No aggregation was detected for B < 16.6 mT.
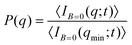 | (1) |
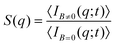 | (2) |
Aggregates with fractal structure (section III.C) present a power law behavior for S(q) within an intra-aggregate spatial scale which is constrained by the typical linear size of the aggregates and the linear size of the monomers (i.e. the liposomes) constituting the aggregates:69–71
| S(q) ∼ q−df ; 1/Ragg ≪ q ≪ 1/ā | (3) |
Dynamics in aggregating and non-aggregating samples is probed by DLS experiments through the intensity autocorrelation function 〈I(q;t)I(q;t + τ)〉 at a fixed q. This autocorrelation function provides us with the corresponding electric field autocorrelation function, gE(τ), by means of Siegert relation.72 In its turn, gE(τ) is expanded into cumulants and interpreted in terms of a sample probability distribution of diffusion coefficients.72,73 The first cumulant, μ1, represents an inverse relaxation time containing both translational and rotational diffusive contributions:54,74
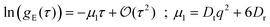 | (4) |
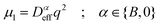 | (5) |
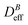 (D0eff) is the effective diffusion coefficient of an aggregating (non-aggregating) sample which essentially contains a translational contribution. More details on this approach as well as on more sophisticated treatments can be found in ref. 52 and 54. One final consideration should be taken into account in those cases where the magnetic field is present. Our DLS measurements are analyzed according to a diffusive interpretation of gE(τ). However magnetic nanoparticles immersed in a magnetic field could in principle present a non-diffusive drift, manifested by a uniform motion, due to the balance between the magnetic force acting on the particles77 and the friction coming from the interaction between the particles and the surrounding fluid. However, as shown in the supplementary material, this effect is negligible in all the DLS experiments performed in the present work.
(D0eff) is the effective diffusion coefficient of an aggregating (non-aggregating) sample which essentially contains a translational contribution. More details on this approach as well as on more sophisticated treatments can be found in ref. 52 and 54. One final consideration should be taken into account in those cases where the magnetic field is present. Our DLS measurements are analyzed according to a diffusive interpretation of gE(τ). However magnetic nanoparticles immersed in a magnetic field could in principle present a non-diffusive drift, manifested by a uniform motion, due to the balance between the magnetic force acting on the particles77 and the friction coming from the interaction between the particles and the surrounding fluid. However, as shown in the supplementary material, this effect is negligible in all the DLS experiments performed in the present work.
III. Results
A. Characterization of magnetic liposomes
SLS measurements at B = 0 allow us to prove the stabilization of the non-aggregating samples and permit a characterization of the individual magnetic liposomes in terms of their shape, average size, and size polydispersity. In this respect, Fig. 2(a) shows the experimental form factor, P(q), of a diluted sample of magnetic liposomes at B = 0 (eqn (1)). The experimental P(q) is here rationalized by means of a solid sphere model in the context of the Rayleigh–Gans–Debye (RGD) theory74 (solid line in Fig. 2(a)). In particular, size polydispersity is introduced in the model by assuming a three-modal distribution whose first five moments are distributed according to a Schulz distribution.69 This distribution has shown its efficiency to describe the size distribution of polydisperse systems of mesosized particles coming from different synthesis protocols.78,79 Indeed, with this procedure, based on a SLS measurement, we avoid those systematic errors due to a plausible wide spectrum of relaxation modes not discriminated by a DLS measurement80 (see ESI†). As a result, we obtain an average liposome diameter![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) = 2ā ≅ 180 nm and a diameter polydispersity of 0.2 (relative standard deviation). This
= 2ā ≅ 180 nm and a diameter polydispersity of 0.2 (relative standard deviation). This ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) value is in agreement with that obtained from the same sample by DLS experiments, where D0eff (eqn (5)) is interpreted in terms of the Stokes–Einstein relation.74 Moreover, liposomes observed by TEM micrographs30 (e.g. inset in Fig. 2(a)) seem to present by simple inspection a size which is, roughly speaking, compatible with the
value is in agreement with that obtained from the same sample by DLS experiments, where D0eff (eqn (5)) is interpreted in terms of the Stokes–Einstein relation.74 Moreover, liposomes observed by TEM micrographs30 (e.g. inset in Fig. 2(a)) seem to present by simple inspection a size which is, roughly speaking, compatible with the ![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) obtained by P(q).
obtained by P(q).
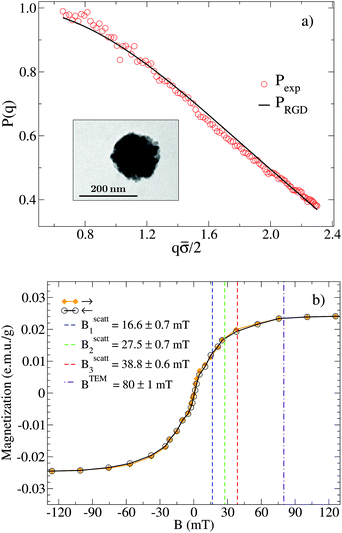 | ||
Fig. 2 (a) Form factor, P(q), of a diluted (non-aggregating) sample of magnetic liposomes. Circles stand for the experimental values as obtained from a SLS measurement at B = 0 whereas solid line represents a fit according to a solid sphere RGD model and assuming a pseudo-Schulz distribution. Inset: TEM micrograph of a single magnetic liposome encapsulating a core of magnetite grains.30 (b) Magnetization as a function of the magnetic field intensity, B. Solid line with solid diamonds (empty circles) stands for the forward (backward) magnetization path. Both paths collapse into a single curve as a manifestation of no magnetic hysteresis. Dashed vertical lines signal the different field intensities (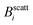 , i ∈ {1,2,3}, see also Fig. 1) at which light scattering experiments were performed (sections III. B and C) whereas the dotted-dashed vertical line indicates the high magnetic field intensity applied to the sample before obtaining the TEM micrographs of section III.E. , i ∈ {1,2,3}, see also Fig. 1) at which light scattering experiments were performed (sections III. B and C) whereas the dotted-dashed vertical line indicates the high magnetic field intensity applied to the sample before obtaining the TEM micrographs of section III.E. | ||
At this point, one might ask for the repulsive interactions avoiding aggregation at B = 0. In this respect, two main interactions for stabilizing these and other lipid vesicle suspensions have been presented in the literature: Coulombic and hydration repulsions. On one hand, Coulombic repulsion, which is the main ingredient for stabilization in DLVO theory,81,82 seems to be present in our system despite the non-polar nature of PC as accounted for by the weak but still non-negligible liposome zeta-potential.30 On the other hand, short-range repulsive hydration forces have been associated to these and other lipid vesicles leading to stabilization even when Coulombic repulsion is not present.70,83–88 Nevertheless, we should stress that the repulsive interactions stabilizing the system in the absence of an external magnetic field do not create long-range structural correlations between the liposomes for the probed dilution as manifested through P(q) (which only contains correlations at the single particle level).
To place the magnetic field intensities at which we perform our light scattering experiments and obtain our TEM micrographs for the aggregating samples, we present in Fig. 2(b) the magnetization, M, of the magnetic liposomes as a function of B (see section II.C). A previous characterization of the liposome magnetization was already presented in ref. 30. We see how the forward and backward magnetization paths essentially collapse into a single curve: the magnetic liposomes do not present hysteresis. The absence of hysteresis represents a manifestation of the superparamagnetic nature of the magnetic liposomes which are indeed lipid vesicles encapsulating single-domain magnetite grains (linear size ≅10 nm) which recover their random field orientation as soon as the magnetic field is switched off.10 As also shown in Fig. 2b), magnetization saturates around ±100 mT. In this respect, we see how our light scattering experiments (sections III.B and C) are performed below the saturation threshold whereas the TEM micrographs obtained for the aggregating samples (section III.E) correspond to an almost magnetically saturated sample. We also note that the different magnetic fields at which we perform our experiments for the aggregating samples do not present a significant difference in magnetization. However, the potential magnetic energy between magnetic liposomes could be significantly different for the different magnetic fields shown in Fig. 2(b). In general, the potential magnetic energy between two magnetic particles (here liposomes) depends on the product of the dipole magnetic moments of the two particles, where each dipole magnetic moment is proportional to the particle magnetization.89–92 Therefore a given ratio between two different generic magnetizations, M1/M2, in Fig. 2(b) will in general re-scale the potential magnetic energy between two magnetic particles by a factor (M1/M2)2.
B. Aggregation kinetics
In this section we discuss the liposome aggregation dynamics under the influence of an external magnetic field by DLS measurements. Contrary to previous works on the aggregation of magnetic polystyrene particles,51,52,54 aggregation is here induced by the external magnetic field with no added electrolyte. This is possible due to the weak Coulombic repulsive interaction between magnetic liposomes (see section III.A).
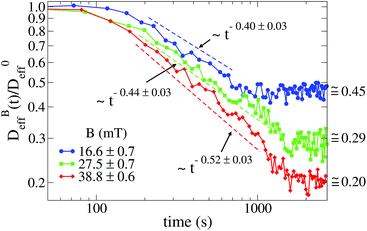
Fig. 3 shows the time evolution of  at different magnetic field intensities (eqn (5)). At short times
at different magnetic field intensities (eqn (5)). At short times  : our aggregation process starts from a monomeric initial condition. At intermediate times
: our aggregation process starts from a monomeric initial condition. At intermediate times 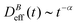 , where α is a B-dependent kinetic exponent which increases upon increasing magnetic field intensity. Finally, at long times
, where α is a B-dependent kinetic exponent which increases upon increasing magnetic field intensity. Finally, at long times 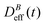 reaches a plateau with a final stationary value,
reaches a plateau with a final stationary value, 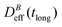 , which decreases upon increasing magnetic field intensity (from
, which decreases upon increasing magnetic field intensity (from 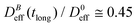 at B = 16.6 mT to
at B = 16.6 mT to 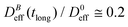 at B = 38.8 mT).
at B = 38.8 mT).
The intermediate time power law behavior 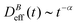 is a common feature in aggregation of mesoscopic particles which has been rationalized by different analytical approaches93,94 being usually expressed in terms of the average aggregate size evolution Ragg(t) ∼ tα. Depending on the system, this power law evolution will in principle continue without reaching a final stationary value69,95,96 or it will present (like in our system) a final constant value for
is a common feature in aggregation of mesoscopic particles which has been rationalized by different analytical approaches93,94 being usually expressed in terms of the average aggregate size evolution Ragg(t) ∼ tα. Depending on the system, this power law evolution will in principle continue without reaching a final stationary value69,95,96 or it will present (like in our system) a final constant value for 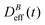 (or Ragg(t)) at sufficiently long times.52,54,59 This second case has in general been interpreted as a balance between aggregation and fragmentation where the sample reaches a steady-state for the cluster-size distribution.97,98
(or Ragg(t)) at sufficiently long times.52,54,59 This second case has in general been interpreted as a balance between aggregation and fragmentation where the sample reaches a steady-state for the cluster-size distribution.97,98
Balance between aggregation and fragmentation in magnetically induced aggregation processes has been discussed in terms of the so-called magnetic coupling parameter, Γ, defined as the ratio (competition) between magnetic dipole–dipole potential energy (which helps to retain particle bonds) and thermal energy (which tends to break particle bonds):59
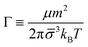 | (6) |
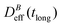 . When comparing in our system two different magnetizations (associated to two different magnetic field intensities, Fig. 2(b)), with their corresponding
. When comparing in our system two different magnetizations (associated to two different magnetic field intensities, Fig. 2(b)), with their corresponding 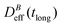 we find:
we find: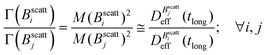 | (7) |
Thus, at constant temperature, re-scaling particle magnetization by a factor γ will re-scale the final stationary diffusion coefficient by a factor 1/γ2, therefore connecting an individual particle property, M, with the final aggregate stability given by 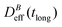 . For instance, (M(B3scatt)/M(B1scatt))2 ≅ (1.55)2 (Fig. 2(b)) to be compared with
. For instance, (M(B3scatt)/M(B1scatt))2 ≅ (1.55)2 (Fig. 2(b)) to be compared with 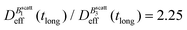 (Fig. 3). This result, however, is satisfied by our system due to the low particle concentration where the influence of the liposome packing fraction is negligible.59
(Fig. 3). This result, however, is satisfied by our system due to the low particle concentration where the influence of the liposome packing fraction is negligible.59
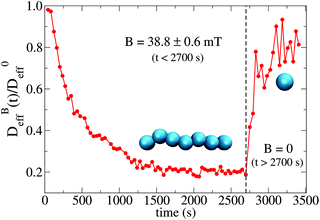
To conclude this section we briefly anticipate the discussion on aggregation reversibility in our system when the magnetic field is switched off. Fig. 4 shows the time evolution of 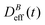 at B = 38.8 mT (i.e. the highest field intensity in our DLS experiments) for times smaller than 2700 s and at B = 0 for times greater than 2700 s. Contrary to Fig. 3 where B is maintained, Fig. 4 shows how, as soon as the magnetic field is unplugged,
at B = 38.8 mT (i.e. the highest field intensity in our DLS experiments) for times smaller than 2700 s and at B = 0 for times greater than 2700 s. Contrary to Fig. 3 where B is maintained, Fig. 4 shows how, as soon as the magnetic field is unplugged, 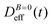 tends to D0eff as a manifestation of aggregation reversibility where the sample almost recovers its initial monomeric condition. However, for this magnetic field intensity, we cannot exclude by our DLS measurements and TEM micrographs the presence of some small surviving aggregates after switching off the magnetic field (note that
tends to D0eff as a manifestation of aggregation reversibility where the sample almost recovers its initial monomeric condition. However, for this magnetic field intensity, we cannot exclude by our DLS measurements and TEM micrographs the presence of some small surviving aggregates after switching off the magnetic field (note that 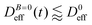 ). We will come back to this point in sections III.E and F.
). We will come back to this point in sections III.E and F.
C. Aggregate structure
We now proceed with the structural description of the liposome aggregates by SLS for those magnetic field intensities for which we already discussed the aggregation kinetics by DLS in the previous section. We stress that our SLS measurements are here performed in the presence of the magnetic field and for those (long) times at which the aggregate diffussion coefficient is already stabilized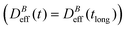 . For this time regime we see no time evolution of the aggregate structure factor, S(q) (eqn (2)).
. For this time regime we see no time evolution of the aggregate structure factor, S(q) (eqn (2)).
Fig. 5 shows the structure factor, S(q), for the aggregated samples at different magnetic field intensities. We see how the different S(q)'s present a power law fractal behavior within a certain intra-aggregate q-range according to eqn (3). On one hand this range is right-side limited by the monomer (liposome) linear size, where q < 2/![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) . On the other hand we need an a priori estimation for the left-side limit based on the linear size of the aggregates given by Ragg (eqn (3)). To estimate the left-side limit we consider Stokes–Einstein relation
. On the other hand we need an a priori estimation for the left-side limit based on the linear size of the aggregates given by Ragg (eqn (3)). To estimate the left-side limit we consider Stokes–Einstein relation 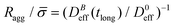 , where here Ragg is, formally speaking, the average hydrodynamic aggregate radius.
, where here Ragg is, formally speaking, the average hydrodynamic aggregate radius.
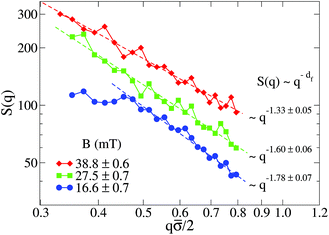 | ||
Fig. 5 Log–log plot of the Structure Factor, S(q), of an aggregated sample for different magnetic field intensities. Measurements are performed at long times, that is, when 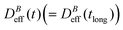 is already stationary (see Fig. 3). Dashed interpolation lines represent the expected fractal behavior, S(q) ∼ q−df, for the different field intensities. is already stationary (see Fig. 3). Dashed interpolation lines represent the expected fractal behavior, S(q) ∼ q−df, for the different field intensities. | ||
Apart from using an interpolation range based on the average liposome and aggregate radii, we should also consider the size polydispersity of the liposomes forming the aggregates as well as the aggregate size polydispersity. Concerning the liposome polydispersity, our q interpolation range defines a length scale which is larger than all the liposome length scales (radii) associated to the populations obtained from our characterization of P(q) (see ESI†). Indeed, with this q constraint previous studies both theoretical and experimental have shown no effect on the aggregate fractal dimension due to the primary particle polydispersity.99,100 Large aggregate size polydispersity could also lead to spurious values of the measured fractal dimensions.101 However aggregation processes mainly controlled by diffusive motion such as that presented here (see ESI†) show a uniform aggregate distribution.96 This aggregate uniformity seems indeed to be present in the TEM micrographs that we will discuss in section III.E.
At low magnetic field intensities (B = 16.6 mT), the small aggregate linear size significantly restricts our q-range (see Fig. 5). Thus for q![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif) /2 ≲ 0.5 we already start to abandon the typical aggregate scale entering into the Guinier regime,71 therefore losing the details of the intra-aggregate structure whose spatial scale would be smaller than our q−1 observational window. Although not reliable, the fractal dimension (df ≊ 1.78) of the small aggregates at B = 16.6 mT would be compatible with that expected from a Diffusion Limited Cluster Aggregation (DLCA).96
/2 ≲ 0.5 we already start to abandon the typical aggregate scale entering into the Guinier regime,71 therefore losing the details of the intra-aggregate structure whose spatial scale would be smaller than our q−1 observational window. Although not reliable, the fractal dimension (df ≊ 1.78) of the small aggregates at B = 16.6 mT would be compatible with that expected from a Diffusion Limited Cluster Aggregation (DLCA).96
Once we increase the magnetic field intensity the power law fractal behavior extends to smaller q values due to the increasing aggregate size, therefore permitting a more reliable estimation of df. The effect is apparent: df decreases upon increasing the magnetic field intensity. Thus, the increasing magnetic field intensity induces a highly directional magnetic liposome interaction which results in more linear fractal structures (df → 1). In particular, we see how at B = 38.8 mT the resulting fractal dimension is df = 1.33. This value, which is far from the typical ramified aggregates reported in DLCA processes, is comparable with those obtained for magnetic polystyrene particles in the presence of a magnetic field with added electrolyte51,52 and compatible with simulations of dipolar hard-sphere fluids.102,103 Finally, we conclude this section by addressing the following question: how is the kinetic exponent, α, connected with the aggregate fractal dimension, df?
D. Kinetic exponent and fractal dimension
Irreversible aggregation in diluted suspensions (like those studied here at intermediate times, Fig. 3) can be understood in terms of a schematic binary reaction mechanism104 of the form Ai + Aj → Ai+j, where Ai represents an aggregate constituted by i monomers (here liposomes). In this context, scaling arguments can be applied to the rate coefficients, ki,j, for the reaction between Ai and Aj aggregates:105,106kai,aj = aλki,j ; ∀i,j ; a∈![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) ; λ∈ ; λ∈![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) | (8) |
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) (t):105
(t):105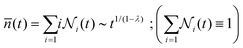 | (9) |
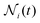 is the relative frequency of aggregates constituted by i monomers at time t. If we now incorporate the fractal scaling of the aggregates according to their fractal dimension,
is the relative frequency of aggregates constituted by i monomers at time t. If we now incorporate the fractal scaling of the aggregates according to their fractal dimension, ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) (t) ∼ Ragg(t)df (previous section), and assume Stokes–Einstein relation,
(t) ∼ Ragg(t)df (previous section), and assume Stokes–Einstein relation, 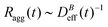 , we reach:
, we reach: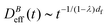 | (10) |
Table 1 shows the homogeneity parameter, λ, for the different magnetic field intensities at which we previously discussed the aggregation kinetics and the aggregate structure (included in the table are α, Fig. 3, and df, Fig. 5). It is interesting to note from the table how λ is almost independent (λ ≅ −0.4) on the applied magnetic field intensity. As a result, here all the aggregation processes at intermediate times present a connection between their corresponding α and df values which leads to a common ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) (t) behavior given by eqn (9). According to our previous discussion, we can reach a physical intuition for the negative λ value by considering that the decreasing aggregate diffusivity is not compensated by the increasing aggregate collision cross section as
(t) behavior given by eqn (9). According to our previous discussion, we can reach a physical intuition for the negative λ value by considering that the decreasing aggregate diffusivity is not compensated by the increasing aggregate collision cross section as ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) (t) increases. Indeed, the very geometry of the magnetic field lines around an aggregate results in an almost constant (elongated) cross section which will not depend on
(t) increases. Indeed, the very geometry of the magnetic field lines around an aggregate results in an almost constant (elongated) cross section which will not depend on ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) (t).57 However, diffusivity will decrease upon increasing
(t).57 However, diffusivity will decrease upon increasing ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) (t) with an expected power law evolution.57 These scaling behaviors therefore lead to a more efficient reaction between small–small aggregates as compared with that between large–large aggregates.
(t) with an expected power law evolution.57 These scaling behaviors therefore lead to a more efficient reaction between small–small aggregates as compared with that between large–large aggregates.
| B (mT) | 16.6 ± 0.7 | 27.5 ± 0.7 | 38.8 ± 0.6 |
| λ | −0.40 ± 0.12 | −0.42 ± 0.11 | −0.45 ± 0.10 |
| α | 0.40 ± 0.03 | 0.44 ± 0.03 | 0.52 ± 0.03 |
| d f | 1.78 ± 0.07 | 1.60 ± 0.06 | 1.33 ± 0.05 |
E. TEM micrographs
We now proceed to discussing the TEM micrographs obtained from the magnetic liposome suspensions after applying an intense magnetic field of B = 80 mT (see section II.B and Fig. 2(b) in section III.A). This magnetic field intensity is much higher than that applied during our light scattering experiments and almost corresponds to the liposome magnetic saturation (Fig. 2(b)). It is important to stress that before capturing our TEM micrographs, the sample first aggregates according to the protocol described in section II.B and then, after being exposed to the magnetic field, the magnetic field is removed leaving the sample to evolve for several minutes (this time is indeed significantly greater than that needed to recover the almost monomeric state reported in Fig. 4). The discussion we present here is based on a simple observational inspection of the TEM micrographs.Fig. 6 shows different TEM micrographs of the liposome suspension for different control regions within the sample and different magnifications. The first message is obvious: despite having evolved without the presence of an external magnetic field, the sample shows the existence of several surviving aggregates (Fig. 6(b)). From now on we will refer to these aggregates as irreversible aggregates. Despite we cannot discard the existence of small surviving aggregates after applying lower magnetic field intensities, the presence of these irreversible aggregates seems to contrast with the almost complete reversible aggregation reported at the end of section III.B (Fig. 4). Micrographs also support a second structural message: irreversible aggregates show an almost linear structure (Fig. 6(a), (c), (d) and (f)) compatible with the fractal dimension (df → 1) that would be expected after having aggregated under the influence of an intense magnetic field (see section III.C). Indeed, the only non-linear (branched) structures we see (albeit scarce) correspond to “Y-like” shaped aggregates where one of the liposomes acts as a junction point between two branches (Fig. 6(e)).62
 | ||
| Fig. 6 TEM micrographs of a sample of magnetic liposomes which was first exposed to an intense magnetic field of B = 80 mT. The sample then evolved for several minutes without the presence of an external magnetic field before capturing the images (see sections II.B and III.A, and Fig. 2b). The micrographs correspond to different control regions and different magnifications. | ||
We now discuss some specific but still significant details. On one hand, aggregate size polydispersity seems to be rather low (with an average number of liposomes per aggregate of the order of 10). On the other hand, irreversible aggregates seem to be constituted by rather monodisperse liposomes, that is, the size polydispersity of the liposomes forming the irreversible aggregates seems to be lower than that corresponding to the whole sample (section III.A). This rather monodisperse aggregate composition is compatible with theoretical predictions for chain-like aggregates in polydisperse ferrofluids where the presence of small magnetic particles as part of the aggregates is not favorable.107,108 On this theoretical basis, we could understand the presence of small magnetite spots in our TEM micrographs as a manifestation of small dried magnetic liposomes which were not able of being part of the irreversible aggregates.
Aggregate shape also deserves further discussion. Magnetic particles with remanent magnetization in the absence of an external magnetic field can in principle self-assemble into closed aggregates. In particular, computational studies on dipolar hard-spheres61 and experimental investigations with microscopic ferromagnetic particles109 show the emergence of ring shaped aggregates. However, our irreversible aggregates do not show (at least from the current TEM micrographs) ring structures. The absence of rings (whose presence is expected for particles with a high remanent magnetization) can represent a manifestation of the superparamagnetic nature of the magnetic liposomes for which no magnetic hysteresis was detected (Fig. 2(b)). In this respect, and giving that we cannot appeal to particle remanent magnetization, what is the interaction mechanism responsible for maintaining the integrity of our irreversible aggregates in the absence of an external magnetic field?
F. Liposome interactions
Reaching a precise quantitative answer to the previous question needs further systematic investigation, specially focused on the empirical phenomenology associated to the different interactions governing aggregation and stabilization in our system. Instead, here we address this question by briefly discussing a plausible schematic picture based on purely heuristic arguments.Coexistence between reversible and irreversible aggregation in mesoscopic particle systems has been rationalized by the existence of primary and secondary minima of the particle potential energy.110 Thus, when aggregation is promoted by a certain mechanism (e.g. here by applying an external magnetic field), particles can in principle aggregate in a permanent (irreversible) state which is associated to a primary minimum where the aggregated state will be maintained despite canceling the mechanism provoking aggregation (e.g. by switching off the external magnetic field). However, particles can also aggregate in a secondary minimum being restored to their non-aggregated state as soon as the mechanism promoting aggregation is canceled.
The idea of an interaction mechanism based on the existence of primary and secondary minima to understand irreversible and reversible aggregation is schematically presented in Fig. 7 for a magnetically induced aggregation process. Thus, in the presence of an external magnetic field (blue line) some particles (purple) aggregate in a permanent (irreversible) primary minimum whereas other (blue particles) aggregate in a (reversible) secondary minimum. When the external magnetic field is switched off (red line), particles aggregating in the secondary minimum become separated. Theoretical approximations based on this underlying picture have been proposed in the past to understand the aggregation of superparamagnetic colloidal latex particles.110–112 In this context, the emergence of primary and secondary minima results from the interplay (or competition) between Coulombic repulsion (treated by a linear superposition approximation), London-van der Waals attraction (Derjaguin approach), and magnetic dipole–dipole attraction. This approach has indeed shown to be successful for predicting and controlling magnetic flocculation to concentrate or remove ultrafine magnetic particles (linear size smaller than 5 μm).113
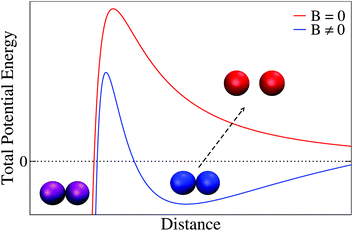 | ||
| Fig. 7 Sketch of the total potential energy between two magnetic particles (here liposomes) based on the theoretical approximation of ref. 110–112. Blue line represents the total potential energy in the presence of an external magnetic field where particles can become stuck in a primary (purple particles) or in a secondary (blue particles) minimum. In the absence of an external magnetic field (red line) those particles that were in a secondary minimum become separated (reversible aggregation, red particles) whereas particles that were in a primary minimum retain their aggregated state (irreversible aggregation, purple particles). Distance can here be interpreted as the separation distance between the external surface of the particles (i.e. the distance between the external surface of two liposome membranes). Separation between particle sketches is merely illustrative in the figure: thus separation between non-aggregated particles (red) has been enhanced whereas that corresponding to the aggregated particles (blue and purple) has been intentionally reduced. | ||
These interactions110–112 (i.e. DLVO and magnetic dipole–dipole interactions) seem to play, a priori, a significant role by governing stabilization–aggregation in our magnetic liposome system. Thus, Coulombic repulsion is present in our system as manifested by the non-negligible zeta-potential30 whereas London-van der Waals interaction has been identified as the main short range attraction between lipid membranes.114 In addition, a non-DLVO ingredient widely reported in the liposome literature should presumably be considered to reach a complete theoretical description for the magnetic liposome aggregation mechanism: short range hydration repulsion.70,83–88
To calibrate whether or not this complete approach is consistent with a primary–secondary minimum scenario in the present system, additional experiments should be performed. In particular, a more refined control of the magnetic field intensity would help us to better quantify the emergence of primary and secondary minima. Moreover, further experiments in the presence of added electrolyte could also help us to judiciously manipulate Coulombic and hydration repulsions,70 therefore providing valuable quantitative information on the interplay between attractive and repulsive interactions. In the meantime, we are led to speculate on the primary–secondary minimum picture as a plausible mechanism to explain irreversibility–reversibility in our system suggesting future systematic experimental work to resolve this issue further.
IV. Summary and conclusions
We have presented a comprehensive study on the aggregation of superparamagnetic liposomes in solution under the influence of a controllable external magnetic field. We have investigated the liposome aggregation kinetics, the aggregate structure, and the coexistence between reversible and irreversible aggregation by Dynamic and Static Light Scattering (DLS and SLS), and by images obtained from Transmission Electron Microscopy (TEM).Aggregation kinetics has been probed by DLS and followed by the time evolution of the aggregate diffusion coefficient. For a constant magnetic field intensity, the aggregate diffusion coefficient shows a stationary value at sufficiently long times which decreases upon increasing the external magnetic field intensity. We have proven how this stationary value, which is here interpreted as a balance between liposome cluster aggregation and fragmentation, scales with the inverse of the square of the liposome magnetization. Before reaching its stationary value, the diffusion coefficient follows a time dependent power law behavior with a kinetic exponent, α, which increases upon increasing magnetic field intensity. As a manifestation of aggregation reversibility, we have further shown how liposomes aggregating under the influence of a low magnetic field intensity (<40 mT) almost recover their initial (non-aggregated) state when the external magnetic field is switched off.
We have taken advantage of the long time stationary value of the liposome aggregate diffusion coefficient to probe the aggregate structure by SLS through the aggregate structure factor. Thus we have proven the aggregate structure to be fractal and shown how the fractal dimension, df, decreases upon increasing the external magnetic field intensity, resulting in the emergence of almost linear aggregate structures (df → 1). We have finally shown how structure and dynamics are connected in our system by finding a scaling relation between the kinetic exponent, α, and the aggregate fractal dimension, df, which allows us to understand aggregation kinetics and aggregate structure in terms of a single homogeneity parameter.
By TEM micrographs we have also shown the existence of irreversible liposome aggregates which result from an aggregation process in the presence of an intense external magnetic field (80 mT). These irreversible aggregates show an open linear structure and survive despite switching off the external magnetic field. To rationalize the coexistence between reversible and irreversible aggregates, we have suggested a schematic picture based on the existence of primary and secondary minima of the liposome potential energy.
In conclusion, we have revealed the rich interaction scenario involved in the magnetically induced aggregation of superparamagnetic liposomes in suspension. Understanding the mechanisms controlling the aggregation of these (and other) biocompatible magnetic nanodevices is a cornerstone for exploiting their singular capabilities as functional agents in promising medical and biotechnological applications.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Miguel Hernández-Díaz, Fernando Vereda, Miguel Peláez-Fernández, Daniel Aguilar-Hidalgo, and Judit Clopés-Llahí for their valuable technical assistance. We also thank the scientific-technical services of the University of Granada and the University of Barcelona for their support and assistance with the TEM micrographs. Particle sketches in Fig. 4 and 7 were made with VMD software support (VMD is developed with NIH support by the Theoretical and Computational Biophysics group at the Beckman Institute, University of Illinois at Urbana-Champaign). J. C.-F. acknowledges support from Ministerio de Economía y Competitividad (MINECO), Plan Nacional de Investigación, Desarrollo e Innovación Tecnológica (I + D + i), Project FIS2016-80087-C2-1-P. We would like to express our gratitude to Fernando Martínez-Pedrero, Lorenzo Rovigatti, Izaak Neri, and Jakob Löber for the critical reading of this manuscript and their valuable comments. Open Access funding provided by the Max Planck Society.References
- Z. Nie, A. Petukhova and E. Kumacheva, Nat. Nanotechnol., 2010, 5, 15 CrossRef CAS PubMed.
- Janus Particles Synthesis, Self-Assembly, and Applications, RSC Smart Materials, ed. S. Granick and S. Jiang, RCS Publishing, London, 2012 Search PubMed.
- Y. Wang, Y. Wang, D. Breed, V. Manoharan, L. Feng, A. Hollingsworth, M. Weck and D. Pine, Nature, 2012, 491, 51 CrossRef CAS PubMed.
- A. Condon, Nat. Rev. Genet., 2006, 7, 565 CrossRef CAS PubMed.
- N. Seeman, Nature, 2003, 421, 427 CrossRef PubMed.
- A. Wilczewska, K. Niemirowicz, K. Markiewicz and H. Car, Pharmacol. Rep., 2012, 64, 1020 CrossRef CAS PubMed.
- N. Tran and T. Webster, J. Mater. Chem., 2010, 20, 8760 RSC.
- W. Brown Jr., Phys. Rev., 1963, 130, 1677 CrossRef.
- W. Brown Jr., Magneto-static Principles in Ferronzagnetism, North-Holland Publishing Company, Amsterdam, 1962, ch. 6 Search PubMed.
- V. Cabuil, Preparation and Properties of Magnetic Nanoparticles, in Encyclopedia of Surface and Colloid Science, Marcel Dekker, 2000 Search PubMed.
- G. Reiss and A. Hutten, Nat. Mater., 2005, 4, 725 CrossRef CAS PubMed.
- Q. Pankhurst, J. Connolly, S. Jones and J. Dobson, J. Phys. D: Appl. Phys., 2003, 36, R167 CrossRef CAS.
- P. Tartaj, M. del Puerto Morales, T. Veintemillas-Verdaguer, S. González-Carreño and C. Serna, J. Phys. D: Appl. Phys., 2003, 36, R182 CrossRef CAS.
- A. Roca, R. Costo, A. F. Rebolledo, S. Veintemillas-Verdaguer, P. Tartaj, T. González-Carreño, M. Morales and C. Serna, J. Phys. D: Appl. Phys., 2009, 42, 224002 CrossRef.
- M. Arruebo, R. Fernández-Pacheco, M. Ibarra and J. Santamaría, Nanotoday, 2007, 2, 22 CrossRef.
- C. Sun, J. Lee and M. Zhang, Adv. Drug Delivery Rev., 2008, 60, 1252 CrossRef CAS PubMed.
- M. Mahmoudi, S. Sant, B. Wang, S. Laurent and T. Sen, Adv. Drug Delivery Rev., 2011, 63, 24 CrossRef CAS PubMed.
- J. Chomoucka, J. Drbohlavova, D. Huska, V. Adam, R. Kizek and J. Hubalek, Pharmacol. Res., 2010, 62, 144 CrossRef CAS PubMed.
- L. Hu, R. Zhang and Q. Chen, Nanoscale, 2014, 6, 14064 RSC.
- D. Lasic, Liposomes: From Physics to Applications, Elsevier, Amsterdam, 1993 Search PubMed.
- D. Lasic, Handbook of Biological Physics, ed. R. Lipowsky and E. Sackmann, Elsevier, Amsterdam, 1995, ch. 10, vol. 1 Search PubMed.
- Medical Applications of Liposomes, ed. D. D. Lasic and D. Papahadjopoulos, Elsevier, Amsterdam, 1998 Search PubMed.
- M. De Cuyper and M. Joniau, Eur. Biophys. J., 1988, 15, 311 CrossRef CAS PubMed.
- M. Martina, J. Fortin, C. Ménager, O. Clément, G. Barratt, C. Grabielle-Madelmont, F. Gazeau, V. Cabuil and S. Lesieur, J. Am. Chem. Soc., 2005, 127, 10676 CrossRef CAS PubMed.
- R. Sabaté, R. Barnadas-Rodríguez, J. Callejas-Fernández, R. Hidalgo-Álvarez and J. Estelrich, Int. J. Pharm., 2008, 347, 156 CrossRef PubMed.
- V. Plassat, M. Martina, G. Barratt, C. Ménager and S. Lesieur, Int. J. Pharm., 2007, 344, 118 CrossRef CAS PubMed.
- J. Pereira da Silva Gomes, A. Rank, A. Kronenberger, J. Fritz, M. Winterhalter and Y. Ramaye, Langmuir, 2009, 25, 6793 CrossRef PubMed.
- Y. Chen, A. Bose and G. Bothun, ACS Nano, 2010, 4, 3215 CrossRef CAS PubMed.
- S. Nappini, M. Bonini, F. Baldelli Bombelli, F. Pineider, C. Sangregorio, P. Baglioni and B. Nordèn, Soft Matter, 2011, 7, 1025 RSC.
- S. García-Jimeno, E. Escribano, J. Queralt and J. Estelrich, Int. J. Pharm., 2011, 405, 181 CrossRef PubMed.
- Y. Barenholz, Curr. Opin. Colloid Interface Sci., 2001, 6, 66 CrossRef CAS.
- A. Hervault and N. Thanh, Nanoscale, 2014, 6, 11553 RSC.
- M. Safarikova and I. Safarik, Magn. Electr. Sep., 2001, 10, 223 CrossRef CAS.
- S. Hamaguchi, I. Tohnai, A. Ito, K. Mitsudo, T. Shigetomi, M. Ito, H. Honda, T. Kobayashi and M. Ueda, Cancer Sci., 2003, 94, 834 CrossRef CAS PubMed.
- A. Ito, Y. Kuga, H. Honda, H. Kikkawa, A. Horiuchi, Y. Watanabe and T. Kobayashi, Cancer Lett., 2004, 212, 167 CrossRef CAS PubMed.
- M. Gonzales and K. Krishnan, J. Magn. Magn. Mater., 2005, 293, 265 CrossRef CAS.
- G. Béalle, R. Di Corato, J. Kolosnjaj-Tabi, V. Dupuis, O. Clément, F. Gazeau, C. Wilhelm and C. Ménager, Langmuir, 2012, 28, 11834 CrossRef PubMed.
- J. Bulte and M. De Cuyper, Methods Enzymol., 2003, 373, 175 CAS.
- B. Du, S. Han, H. Li, F. Zhao, X. Su, X. Cao and Z. Zhang, Nanoscale, 2015, 7, 5411 RSC.
- S. Dandamudi and R. Campbell, Biochim. Biophys. Acta, 2006, 1768, 427 CrossRef PubMed.
- M. Martina, C. Wilhelm and S. Lesieur, Biomaterials, 2008, 29, 4137 CrossRef CAS PubMed.
- S. Soenen, A. Brisson, E. Jonckheere, N. Nuytten, S. Tan, U. Himmelreich and M. De Cuyper, Biomaterials, 2011, 32, 1748 CrossRef CAS PubMed.
- F. Benyettou, I. Chebbi, L. Motte and O. Seksek, J. Mater. Chem., 2011, 21, 4813 RSC.
- S. Saville, R. Woodward, M. House, A. Tokarev, J. Hammers, B. Qi, J. Shaw, M. Saunders, R. Varsani and T. St Pierre, et al. , Nanoscale, 2013, 5, 2152 RSC.
- S. Saville, B. Qi, J. Baker, R. Stone, R. Camley, K. Livesey, L. Ye, T. Crawford and O. Mefford, J. Colloid Interface Sci., 2014, 424, 141 CrossRef CAS PubMed.
- E. Myrovali, N. Maniotis, A. Makridis, A. Terzopoulou, V. Ntomprougkidis, K. Simeonidis, D. Sakellari, O. Kalogirou, T. Samaras and R. Salikhov, et al. , Sci. Rep., 2016, 6, 37934 CrossRef CAS PubMed.
- B. Jun, G. Kim, J. Baek, H. Kang, T. Kim, T. Hyeon, D. Jeong and Y. Lee, Phys. Chem. Chem. Phys., 2011, 13, 7298 RSC.
- Y. Matsumura and H. Maeda, Cancer Res., 1986, 46, 6387 CAS.
- V. Mody, A. Cox, S. Shah, A. Singh, W. Bevins and H. Parihar, Appl. Nanosci., 2014, 4, 385 CrossRef CAS.
- P. Licinio and F. Frézard, Braz. J. Phys., 2001, 31, 356 CrossRef CAS.
- F. Martínez-Pedrero, M. Tirado-Miranda, A. Schmitt and J. Callejas-Fernández, Colloids Surf., A, 2005, 270, 317 CrossRef.
- F. Martínez-Pedrero, M. Tirado-Miranda, A. Schmitt and J. Callejas-Fernández, J. Chem. Phys., 2006, 125, 084706 CrossRef PubMed.
- F. Martínez-Pedrero, M. Tirado-Miranda, A. Schmitt and J. Callejas-Fernández, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2007, 76, 011405 CrossRef PubMed.
- F. Martínez-Pedrero, M. Tirado-Miranda, A. Schmitt and J. Callejas-Fernández, Colloid Interface Sci., 2008a, 318, 23 Search PubMed.
- F. Martínez-Pedrero, M. Tirado-Miranda, A. Schmitt and J. Callejas-Fernández, Langmuir, 2009, 25, 6658 CrossRef PubMed.
- P. Domínguez-García and M. Rubio, Colloids Surf., A, 2010, 358, 21 CrossRef.
- F. Martínez-Pedrero, A. El-Harrak, J. Fernández-Toledano, M. Tirado-Miranda, J. Baudry, A. Schmitt, J. Bibette and J. Callejas-Fernández, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2008b, 78, 011403 Search PubMed.
- P. Domínguez-García, S. Melle and M. Rubio, J. Colloid Interface Sci., 2009, 333, 221 CrossRef PubMed.
- J. S. Andreu, J. Camacho and J. Faraudo, Soft Matter, 2011, 7, 2336 RSC.
- G. Bertoni, B. Torre, A. Falqui, D. Fragouli, A. Athanassiou and R. Cingolani, J. Phys. Chem. C, 2011, 115, 7249 CAS.
- L. Rovigatti, J. Russo and F. Sciortino, Phys. Rev. Lett., 2011, 107, 237801 CrossRef PubMed.
- T. Tlusty and S. A. Safran, Science, 2000, 290, 1328 CrossRef CAS PubMed.
- J. Cerdà, S. Kantorovich and C. Holm, J. Phys.: Condens. Matter, 2008, 20, 204125 CrossRef PubMed.
- F. Szoka and D. Papahadjopoulos, Proc. Natl. Acad. Sci. U. S. A., 1978, 75, 4194 CrossRef CAS.
- R. C. MacDonald, R. I. MacDonald, B. P. Menco, K. Takeshita, N. K. Subbarao and L. R. Hu, Biochim. Biophys. Acta, 1991, 1061, 297 CrossRef CAS.
- J. C. Steward-Marshall, Anal. Biochem., 1980, 104, 10 CrossRef.
- P. Pusey, Liquids, Freezing and Glass Transition, Lecture Notes for Les Houches, Session LI, Part 2, Course 10: Colloidal Suspensions, North Holland, Amsterdam, 1989 Search PubMed.
- P. Pusey, Introduction to scattering experiments, in Neutrons, X-rays and light: scattering methods applied to soft condensed matter, North Holland, Elsevier, Amsterdam, 2002 Search PubMed.
- S. Roldán-Vargas, A. Martín-Molina, M. Quesada-Pérez, R. Barnadas-Rodríguez, J. Estelrich and J. Callejas-Fernández, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2007, 75, 021912 CrossRef PubMed.
- S. Roldán-Vargas, R. Barnadas-Rodríguez, M. Quesada-Pérez, J. Estelrich and J. Callejas-Fernández, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2009a, 79, 011905 Search PubMed.
- C. Sorensen, Aerosol Sci. Technol., 2001, 35, 648 CrossRef CAS.
- B. Berne and R. Pecora, Dynamic Light Scattering With Applications to Chemistry, Biology, and Physics, Dover Publications, Mineola, New York, 2000 Search PubMed.
- D. Koppel, J. Chem. Phys., 1972, 57, 4814 CrossRef CAS.
- J. Dhont, An Introduction to Dynamics of Colloids, Elsevier, Amsterdam, 1996 Search PubMed.
- S. Roldán-Vargas, M. Quesada-Pérez and J. Callejas-Fernández, J. Chem. Phys., 2009b, 131, 034509 Search PubMed.
- I. Morrison, E. Grabowski and C. Herb, Langmuir, 1985, 1, 496 CrossRef CAS.
- S. Shevkoplyas, A. Siegel, R. Westervelt, M. Prentiss and G. Whitesides, Lab Chip, 2007, 7, 1294 RSC.
- B. D'Aguanno and R. Klein, J. Chem. Soc., Faraday Trans., 1991, 87, 379 RSC.
- B. D'Aguanno and R. Klein, Phys. Rev. A, 1992, 46, 7652 CrossRef.
- H. Schnablegger and O. Glatter, Appl. Opt., 1991, 30, 4889 CrossRef CAS PubMed.
- B. V. Derjaguin and L. Landau, Acta Physicochim. URSS, 1941, 14, 633 Search PubMed.
- E. Verwey and J. Overbeek, Theory of the Stability of Lyophobic Colloids, Elsevier, Amsterdam, 1948 Search PubMed.
- T. J. McIntosh, Chem. Phys. Lipids, 1996, 81, 117 CrossRef CAS PubMed.
- J. Israelachvili and H. Wennerstrom, Nature, 1996, 379, 219 CrossRef CAS PubMed.
- D. Petsev and P. Vekilov, Chem. Phys. Lett., 2000, 84, 1339 CAS.
- S. Marcella, Phys. Rev. Lett., 1976, 42, 129 Search PubMed.
- S. Ohki and K. Arnold, Colloids Surf., B, 2000, 18, 83 CrossRef CAS.
- D. LeNeveu, P. Rand and V. Parsegian, Nature, 1976, 259, 601 CrossRef CAS PubMed.
- Y. Chan, D. Henderson, J. Barojas and A. Homola, IBM J. Res. Dev., 1985, 29, 11 CrossRef.
- J. Promislow and A. Gast, J. Chem. Phys., 1995, 102, 5942 CrossRef.
- C. Tsouris and T. Scott, J. Colloid Interface Sci., 1995, 171, 319 CrossRef CAS.
- S. Chikazumi, Physics of Magnetism, Wiley, New York, 1964 Search PubMed.
- F. Leyvraz, Phys. Rep., 2003, 383, 95 CrossRef CAS.
- M. Kolb, Phys. Rev. Lett., 1984, 53, 1653 CrossRef.
- D. Weitz and J. Huang, Self-Similar Structures and the Kinetics of Aggregation of Gold Colloids, Elsevier Science, New York, 1984 Search PubMed.
- M. Y. Lin, H. M. Lindsay, D. A. Weitz, R. Klein, R. C. Ball and P. Meakin, J. Phys.: Condens. Matter, 1990, 2, 3093 CrossRef.
- P. van Dongen and M. Ernst, J. Stat. Phys., 1984, 37, 301 CrossRef.
- F. Family, P. Meakin and J. Deutch, Phys. Rev. Lett., 1986, 57, 727 CrossRef CAS PubMed.
- G. Bushell and R. Amal, J. Colloid Interface Sci., 1998, 205, 459 CrossRef CAS PubMed.
- M. Tence, J. Chevalier and R. Jullien, J. Phys., 1986, 47, 1989 CAS.
- J. Martin, J. Wilcoxon, D. Schaefer and J. Odinek, Phys. Rev. A, 1990, 41, 4379 CrossRef CAS.
- L. Rovigatti, J. Russo and F. Sciortino, Soft Matter, 2012, 8, 6310 RSC.
- P. J. Camp and G. N. Patey, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 5403 CrossRef CAS.
- M. Brodie, Experimental study of aggregation kinetics: dynamic scaling of measured Cluster-Size Distributions, PhD. thesis, Massachusetts Institute of Technology, 1981 Search PubMed.
- P. van Dongen and M. Ernst, Phys. Rev. Lett., 1985, 54, 1396 CrossRef CAS PubMed.
- P. van Dongen and M. Ernst, J. Stat. Phys., 1988, 50, 295 CrossRef.
- S. Kantorovich and A. O. Ivanov, J. Magn. Magn. Mater., 2002, 252, 244 CrossRef CAS.
- A. O. Ivanov and S. Kantorovich, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2004, 70, 021401 CrossRef PubMed.
- F. Martínez-Pedrero, A. Cebers and P. Tierno, Phys. Rev. Appl., 2016, 6, 034002 CrossRef.
- C. Chin, S. Yiacoumi and C. Tsouris, Langmuir, 2001, 17, 6065 CrossRef CAS.
- S. Yiacoumi, D. Rountree and C. Tsouris, J. Colloid Interface Sci., 1996, 184, 477 CrossRef CAS PubMed.
- C. Chin, S. Yiacoumi and C. Tsouris, J. Colloid Interface Sci., 1998, 206, 532 CrossRef CAS PubMed.
- L. Luo and A. V. Nguyen, Sep. Purif. Technol., 2017, 172, 85 CrossRef CAS.
- J. Israelachvili, Intermolecular and Surface Forces, Academic Press, London, 1991 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/C7NR05301K |
| This journal is © The Royal Society of Chemistry 2017 |