Self-texturizing electronic properties of a 2-dimensional GdAu₂ layer on Au(111): the role of out-of-plane atomic displacement

Abstract

Here, we show that the electronic properties of a surface-supported 2-dimensional (2D) layer structure can self-texturize at nanoscale. The local electronic properties are determined by structural relaxation processes through variable adsorption stacking configurations. We demonstrate that the spatially modulated layer-buckling, which arises from the lattice mismatch and the layer/substrate coupling at the GdAu₂/Au(111) interface, is sufficient to locally open an energy gap of ∼0.5 eV at the Fermi level in an otherwise metallic layer. Additionally, this out-of-plane displacement of the Gd atoms patterns the character of the hybridized Gd-d states and shifts the center of mass of the Gd 4f multiplet proportionally to the lattice distortion. These findings demonstrate the close correlation between the electronic properties of the 2D-layer and its planarity. We demonstrate that the resulting template shows different chemical reactivities which may find important applications.

---

Tuning the electronic properties of two-dimensional (2D) layers is a current focus of interdisciplinary investigation fields dealing with fundamental aspects of science at the nanoscale and aiming to promote nanotechnological applications.^1,2 At present, one of the most promising expectations arises from the departure of the 2D layer from the perfect crystallographic flatness, typical of graphene. The emergence of new physical and chemical properties is expected from the out-of-plane displacement of the atoms in the layer and its modified orbital hybridization.^3–10 Atomic-buckling is, therefore, the fundamental parameter to tailor the electronic layer properties. In this contest, an elegant solution to template the electronic structure at nanoscale is the formation of interfaces with variable atomic stacking registry, as those observed in lattice mismatched layers leading to Moiré superstructures. Notwithstanding that these Moiré superstructures are quite commonly observed at the interface of 2D-materials, little attention has been paid on the buckling-induced texturization of their electronic properties. In this work, we address the role of the out-of-plane displacement characterizing the electronic properties of a lattice-mismatched 2D-layer. We consider a 2D layer forming a Moiré superstructure and demonstrate the spontaneous patterning of the electronic properties upon the formation of the interface. We will rationalize in terms of layer buckling and structural relaxations, the observed spatially-periodic energy shifts of the electronic structures. We will show that this variable interface coupling paves an ideal and viable route to engineer the characteristics of the 2D-layer at the nanoscale leading to space modulated electronic properties and to a chemical-reaction template.

Specifically, we characterize a bi-metallic monolayer alloy, namely GdAu₂, obtained upon evaporation of gadolinium atoms on the annealed Au(111) surface^11,12 (see also ESI S1†), which results in a weakly interacting Moiré superstructure. Previous studies have focused on the occupied band structure of the alloy layer, characterized by photoemission experiments and Density Functional Theory (DFT) calculations.¹² In those studies, the GdAu₂ monolayer on Au(111) was approximated as a coherent interface, neglecting the lattice-mismatch with the supporting substrate and its spatially-dependent structural relaxations. Recently, we have shown that in a similar structure, the GdAg₂/Ag(111), this assumption underestimates the role of the stacking geometry and that interesting electronic and magnetic effects emerge when the interface coupling is taken into account.¹³

Here, we combine spectroscopic techniques as scanning tunneling spectroscopy (STS), ultraviolet and inverse photoemission (UPS and IPES), with DFT calculations to achieve a precise characterization of the interface between GdAu₂ layers supported on Au(111), both in the occupied and unoccupied density of states. We will show that the density of states of the alloy layer is modulated on the whole energy range with the nanoscale periodicity of the Moiré superstructure. We observe: (i) the opening of a gap at the Fermi level at well-defined surface positions, (ii) a change in the energetic ordering of the hybridized Gd d electrons, and (iii) a space-dependent energy shift of the Gd 4f multiplet-states linearly proportional to the out-of-plane lattice distortions. The DFT simulations support these findings and assist the interpretation of the measured spectroscopic features.

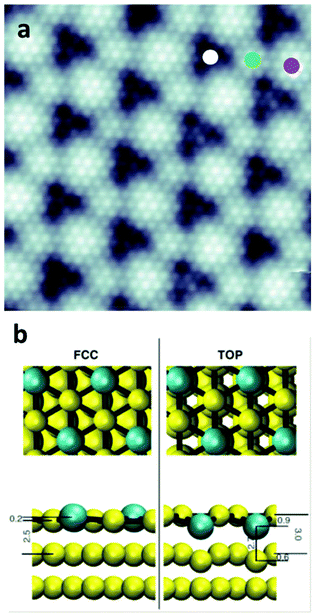
In Fig. 1, we report a topographic STM image of the GdAu₂/Au(111) surface showing a Moiré superlattice superposed on the atomically-resolved alloy structure. The apparent sequence of minima and maxima of the Moiré pattern reflects the variation of the vertical stacking sequence characteristics of the superposition of layers with different lattice constants. The GdAu₂ structure, its adsorption configurations and electronic features of the adsorbed layer have been calculated using DFT calculations. In particular, we used periodic spin-orbit coupling applied to the Au atoms and a Hubbard U correction (U = 6 eV) to the Gd f states (computational details are given in the ESI†).²⁵ Note that the large periodicity of the superlattice prevents its direct DFT simulation because this would require exceedingly large periodic supercells. Following previous studies, to keep the cost of the DFT simulations tractable, we modelled the GdAu₂/Au(111) system as a coherent interface [lattice parameter 5.11 Å, surface periodicity (√3 × √3)R30°] and considered three different stacking registries of the GdAu₂ layer with respect to the underlying Au surface. The latter was modelled with five atomic layers. These models provide realistic representations of specific Moiré regions, namely the one in which the Gd atom is on top of a Au atom (denoted as TOP), and in the high symmetry hpc/fcc hollow sites of the Au(111) surface (denoted as HPC and FCC, respectively).

Fig. 1 Structural characterization of GdAu₂/Au(111). (a) Topographic image of GdAu₂/Au(111) (12 nm × 12 nm). (b) Calculated equilibrium geometries of the GdAu₂/Au(111) interfaces in the FCC and TOP regions. Gd and Au atoms are represented by cyan and yellow colors. Only the two outermost Au(111) layers are displayed. The numbers report selected vertical distances (in Å) that characterize the interface distortions. The dots indicated in panel (a) refer to 3 different regions TOP, hollow FCC and HCP stacking positions of the Moiré superstructure (see the text).

In Fig. 1b, two of the possible adsorption configurations, namely the TOP and FCC, are reported. The latter is almost indistinguishable from the HCP one (see ESI-4†). These results, obtained by relaxing the coordinates of the outermost three layers, predict that in the region of the superlattice in which the Gd atoms are on top of the substrate Au atoms, the interface structure undergoes significant buckling and deformations involving both the Gd atoms in the alloy and Au(111) surface atoms. In this configuration, the Gd atom displaces inward with respect to the alloy Au atoms by 0.9 Å. Consequently, this pushes the underlying surface Au atoms towards the bulk shifting them by 0.6 Å. Instead, in the hollow configurations, the structural distortions are minor and the planarity of the GdAu₂ layer is largely preserved with the Gd atoms being higher than the Au atoms of the layer by only 0.2 Å (Fig. 1b). Further details are given in the ESI.†

The inward displacement of the Gd and of the underlying Au atoms suggests that the TOP position corresponds to the “dark” areas of the topographic images in analogy to the GdAg₂/Ag(111) case.¹³ This assignment will be further corroborated by the spectroscopic characterization of the Moiré superstructure described below. As predicted by theory, the two hollow positions are, instead, very similar topographically and spectroscopically and do not allow a clear identification in the topographic image.

The atomic structural relaxation of the TOP regions are reflected in the interfacial binding energy, which our DFT simulations predict to be larger (i.e. more bound) in the hollow regions than in the top regions by ∼11% (0.087, 0.097, 0.096 eV Å⁻² for the TOP, FCC, and HCP, respectively). Topographic images, showing a partial coverage of the GdAu₂ on Au(111), support this theoretical prediction (see also the ESI†). Indeed, the borders of GdAu₂ islands are always formed exclusively by an alloy in a hollow configuration, i.e. the dark regions of the Moiré superstructure are never observed at the domain border, confirming their structural unfavorable energetics. Despite the small energy difference between the TOP and the hollow configurations, an extended continuous alloy layer leading to a Moiré superlattice forms, where TOP, FCC, and HCP regions coexist.

In Fig. 2, the local density of states, measured at the TOP and hollow positions of the Moiré superstructure, as indicated by the color-coded circles in Fig. 1a, is shown. The spectra present a similar number of electronic features, although local energy shifts and intensity variations, observable in the whole energy range, suggest that the density of states is position-dependent. The localization of the density of states at specific surface positions is confirmed by surface energy maps shown in the ESI.† A remarkable difference that clearly distinguishes the TOP configuration (black line) from the two hollow geometries (green and red lines) is visible at a low energy. Specifically, the TOP regions are characterized by a decrease in the density of states at the Fermi level, which appears depopulated over an energy range of ∼0.5 eV (see also the inset in panel a). The opening of this gap characterizes the TOP regions, as a finite density of states can be observed at the hollow positions. A peak in the unoccupied energy range is observed at ∼700 meV in all Moiré regions although it broadens and splits into two small maxima only in the TOP case. Although comparable in energy, the peak measured at the hollow and TOP position has a different orbital nature as suggested by their distinct temperature behavior (shown in ESI-12†) and substantiated in the following by theoretical calculations demonstrating the mutual dependence of the electronic structure and the stacking-registry. This highlights that the substrate-induced layer buckling induces a reordering of the orbital character along the Moiré superlattice as well as a band-gap opening in the TOP regions.

Fig. 2 Local spectroscopy at different positions on the Moiré superstructure. The spectra have been measured at the 3 characteristic positions of the Moiré pattern according to the colour coded circles indicated in Fig. 1a. These are shown in separated windows to highlight the low energy contributions, which have a small intensity. The inset in panel a shows the density of states at the Fermi energy level.

In order to provide insight into the measured local electronic structure and to understand its dependence on the crystalline environment, we plot in Fig. 3 the calculated total and atom-projected density of states (DOS and PDOS) for the FCC (panel a–c) and TOP (d–f) interface geometries. Furthermore, we calculate the DOS components at the Γ point (Γ-DOS) of the Brillouin zone for the two configurations to reproduce the electron density of states probed by STS. In panel b and e of Fig. 3, the gray area marks the total DOS, while the yellow, cyan, and red colors mark the Au, Gd, and Gd-f Γ-PDOS components, respectively.

Fig. 3 DFT electronic structure of GdAu₂/Au(111) in FCC (left) and TOP (right) configurations. (a, d) Total and atom-projected density of states (DOS and PDOS). (b, e) DOS components at the Γ point of the Brillouin zone (Γ-DOS). (c, f) Orbital analysis and charge density (insets) corresponding to the states labelled with numbers.

The most evident difference in these calculated DOS of the TOP and FCC configurations occurs at the Fermi level, where a gap of ∼0.5 eV opens in the TOP configuration (Fig. 3f), and reaches zero in the FCC configuration (Fig. 3c). This is in agreement with the STS measurements, where a gap is observed only in the “dark” areas of the Moiré superstructure, which are therefore associated with the TOP configuration. Furthermore, we observe that in the low energy window [−1.5 eV, 1.5 eV], the electron states at Γ have dominant Gd-pd and Au-p orbital components (see S7.1–3†), despite the orbital ordering and character differs in the TOP and FCC interfaces.

We relate the gap opening and these differences in the local electronic structure to the out-of-plane displacement of the Gd atoms induced by the adsorption position along the Moiré superlattice. To support this claim we have calculated the electronic structure of free standing GdAu₂ layers having the exact distorted structure taken from the TOP and FCC GdAu₂/Au(111) calculations. The corresponding Γ-PDOS are displayed in Fig. 4. When compared to the Γ-PDOS and DOS of a free-standing perfectly-flat GdAu₂ layer (see ESI-7.1†), it is evident that the buckled TOP geometry opens a gap of ∼0.25 eV around the Fermi energy level, while the gap is not present in the almost flat FCC configuration. This demonstrates that although the gap size decreases by a factor of two, the gap persists in the distorted TOP geometry even in the absence of the Au(111) substrate. The same analysis also demonstrates that the out-of-plane Gd buckling changes the hybridization of the Gd-pd and Au-sp orbitals having energy close to the Fermi level. In the FCC geometry, the occupied states between −1 eV and the Fermi level are dominated by Gd-pd orbitals while the first two unoccupied states are primarily Au-p states (see ESI-7†). The buckled geometry of the TOP configuration leads to a totally different ordering and character of the electron states between −0.5 eV and 0.5 eV, involving the Au-sp and Gd-pd orbital hybridization (see Fig. 4b, d and ESI†).

Fig. 4 Effects of buckling on the electronic structure. Calculated DOS and Γ-PDOS for free-standing GdAu₂ layers with structural distortions as in the FCC (left) and TOP (right) supported configurations.

This different orbital ordering near the Fermi level, which is clearly controlled by the out-of-plane position of the Gd atom (as confirmed by the free standing calculations), is observed also in the surface-supported TOP and FCC GdAu₂ layers. We report in the insets above Fig. 3(c) and (f) the integrated electron density of states labeled with numbers in the Γ-PDOS plots. In the FCC configuration (Fig. 3c), the Gd-d state 1 is occupied and state 2 is partly occupied. Both of them have clear planar orbital character, which persist up to state 3. The first electron state with a substantial out-of-plane orbital component is state 4. Instead, in the TOP configuration, the corresponding Gd-d states are all unoccupied. State 1′, the analogue of the occupied state 1 in the FCC configuration, is shifted above the Fermi level at 0.25 eV. In the TOP configuration, states 2′ and 3′ have a marked out-of-plane orbital component. This reordering of the orbital-sequence results from the different valence Gd-pd and Au-sp hybridization that occur when the Gd atoms displace out of the layer plane.

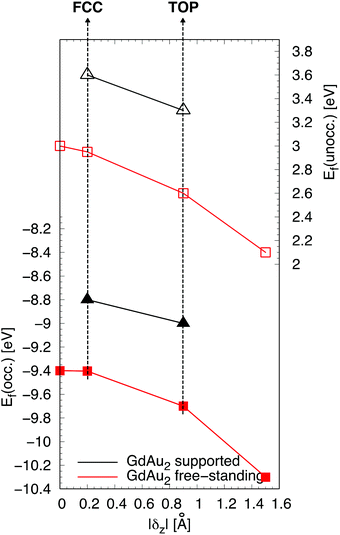
Quite interestingly, the layer buckling also controls the energy of the occupied and unoccupied Gd-f states (see the PDOS of Fig. 3 and Table SI-5.2 in the ESI†). In the supported GdAu₂ layer, the occupied Gd-f band center of mass lowers by ∼0.25 eV going from the FCC to the TOP geometry. This results in a dependence of the energy of the f multiplet according to the adsorption configurations as highlighted in Fig. 5. Here, we plot the energy E_f of the Gd-f states, calculated as a weighted average from the PDOS, as a function of the structural parameter δz, i.e. the out-of-plane position of the Gd atoms. Values of |δz| equal to 0, 0.2 Å and 0.9 Å correspond to the geometry of a perfectly flat, and of the buckled FCC and TOP GdAu₂ layers. To further corroborate our claim, for the free-standing case we calculated an additional geometry displacing the Gd atom by |δz| = 1.5 Å. The data for the supported layer (black symbols and lines) demonstrate that the energy shift E_f is proportional to |δz| and therefore it is controlled by the layer buckling. It is worth noting that the data for the corresponding free-standing distorted configurations (red symbols and lines) follow the same trend. Moreover, this also demonstrates that the relative energy difference of the Gd-f states between the TOP and FCC configurations is induced by the layer buckling while the coupling to the supporting Au crystal induces an almost rigid shift of 0.6–0.8 eV of the Gd-f states in both the TOP and FCC configurations.

Fig. 5 Induced energy shift of the center of mass of the Gd 4f multiplet states as a function of the Gd atom inward displacement in GdAu₂ layers. Filled and empty symbols represent occupied states (left energy scale) and unoccupied states (right energy scale).

The spatial modulation of the f states can indeed be clearly observed in the experimental measurements. In Fig. 6, we compare the density of states of the monolayer GdAu₂ on Au(111) measured with space averaging techniques, as Ultra-Violet Spectroscopy (UPS) and Inverse Photoemission Spectroscopy (IPES), with local spectroscopic measurements. The most distinguishing feature that characterizes the occupied electron states of the supported GdAu₂ from the Au(111) electronic density of states (panel a, blue and yellow lines, respectively) is a peak visible at about 10 eV below the Fermi level, which corresponds to the Gd 4f electron state.^14,15 The features of the IPES spectrum measured on the GdAu₂/Au(111) interface are clearly distinguishable from the ones measured on the clean Au(111) substrate (panel b) and closely resemble the one observed in the dI/dV curves (Fig. 2). In Fig. 6b, the arrow highlights the highest energy feature of the IPES spectrum, which corresponds to the photon emission from the unoccupied Gd 4f multiplet states (see also the ESI†). Summarizing, both occupied and unoccupied Gd 4f states are observed at comparable energies to the ones reported for the Gd and GdAu₂ bulk materials. These features are, however, considerably broadened.^14,16–19 In a previous work, we have reported that the formation of the GdAu₂ alloy does not change the occupancy of the 4f multiplet with respect to the Gd bulk, which remains half occupied.¹² This confirms the expected low reactivity of the 4f electrons, which do not participate directly in chemical bonding and are shielded by the more delocalized s and d electrons. Despite this, the structural changes and re-hybridisation of the d orbitals previously described can cause small perturbations to the 4f multiplet even if their occupation number is unaffected.

Fig. 6 Spectroscopic measurements of the Gd 4f multiplet on the GdAu₂/Au(111) interface. (a) Occupied density of states (HeII) and coverage 0.6 ML; (b) unoccupied density of states (IPES) and coverage 0.9 ML; (c) local spectroscopic measurements of the unoccupied 4f density of states at the indicated position on the Moiré superstructure. The spectra are displaced for better visualization. The arrows indicate the onset of the 4f multiplet and the onset of the Au(111) bulk band (ref. 21), respectively.

In order to clarify this we have probed locally the energy region of the unoccupied 4f electrons, which is energetically accessible by scanning tunneling spectroscopy (STS). The highly localized nature and the small radial expansion of the 4f electrons result, however, in a rather weak dI/dV signal.²⁰ The spectra recorded at the various positions of the Moiré superstructure are reported in Fig. 6c. For the sake of completeness, in panel c, we also report the STS spectrum measured on the Au(111) surface. The small feature measured on this surface coincides with the reported onset of the Au bulk empty states,²¹ which is not visible on the alloy overlayer. The onset of the f states, indicated by arrows, shifts of about 0.2–0.3 eV from the TOP to the hollow position, being the first the lowest in energy. This result, which is in full agreement with the predictions shown in Fig. 3 and 5, suggests that energy-shifted contributions sum up in the UPS-IPES spectra leading to their broadening.

The shift of the 4f states of Gd should not be surprising. Indeed, although these states do not participate directly in chemical bonding, they are sensitive to the chemical environment through the screening effect of the valence band electrons as observed in pure Gd in PES and IPES spectra.^{14,16–18,22} In DFT+U calculations, the chemical composition and the crystalline environment are accounted by the parameter U, whose value influences the computed energy of the f states. In our calculations, in order to disentangle the effect of the layer buckling on the Gd-f energy shift, we followed previous studies and set the value of U_eff for the GdAu₂ alloy equal to that suggested for the Gd bulk.^23,24 The value of U_eff reflects the on-site Coulomb interaction of the localized f electrons, which is likely to be different in the GdAu₂ alloy and in Gd bulk. As a consequence, comparing the absolute position of the f states in Gd bulk and in the alloy is not meaningful in our DFT+U approach. The relative Gd-f energy shifts arising from the out-of-plane GdAu₂ distortions should instead be well captured by the calculations. As shown in ESI-6,† using larger values of this on-site parameter (U_eff ∼7 eV), corresponding to higher Gd-f electron Coulomb repulsion in the GdAu₂ layer than in Gd bulk, would shift the energy of the Gd-f states to lower energies, in better agreement with the measured absolute energies of the occupied states ∼−10 eV (see below).

We can discard the contribution of charge-transfer effects from the observed energy shift according to the results of the Bader charge analysis (see ESI-8†). This shows that, with respect to isolated atoms, the charge rearrangement occurs almost exclusively between the Gd atom and the Au atoms of the alloy layer, reducing the 28e in the elemental bulk Gd, to 26.9e and to 26.8e in the free standing and supported GdAu₂ monolayers, respectively. The supported GdAu₂ layer is slightly positive but its overall charge is basically preserved with respect to the free-standing value while the alloy layer has a partial ionic character. Therefore, we conclude that the physical origin of the predicted and experimentally observed energy shift of the 4f-states across the Moiré lattice is not induced by charge transfer effects but by the structural layer buckling experienced by the Gd atoms at the different adsorption positions.

The present work provides valuable insights into the correlation between the electronic properties of 2D layers and their planarity. The stacking configuration and the structural relaxation prompt, despite their relatively weak interaction, a considerable local atomic buckling in the GdAu₂ superstructure on the Au(111) surface and consequently a clear patterning of the electronic density of states with a nanoscale spatial periodicity.

Given the described modulation of the electronic properties, it can be expected that this layer acts as a chemical template. To test this hypothesis, we have performed a set of preliminary calculations by adsorbing a probe H atom on the top of Au and Gd atoms of the TOP and FCC configurations of the Au(111)-supported GdAu₂ system. Indeed, these calculations demonstrate the patterning of the surface reactivity, with a preferential binding of H to the Au atoms of the FCC superlattice regions with respect to the Au atoms of the TOP regions. Despite the high H coverage used in these model simulations, the difference in the calculated adsorption energies for the different supercell regions is larger than 0.3 eV per atom. These findings therefore provide valuable insights into the correlation between the electronic properties of 2D layers and their planarity and a perspective for controlling the electronic, magnetic and reactivity properties in atomically-thin layers.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

This project is partially funded by the EU-H2020 research and innovation programme under grant agreement no. 654360, NFFA-Europe and the Spanish Ministry of Economy (MAT2013-46593-C6-4-P and MAT2016-78293-C6-5-R).

We are grateful to Prof. S. Modesti (CNR-IOM) for his support with the electronics. Federico Salvador and Andrea Martin are acknowledged for technical assistance.

Notes and references

1. D. Jariwala, T. J. Marks and M. C. Hersam, Mixed-dimensional van der Waals heterostructures, Nat. Mater., 2017, 16, 170–181.
2. Q. A. Vu, J. H. Lee, V. L. Nguyen, Y. S. Shin, S. C. Lim, K. Lee, J. Heo, S. Park, K. Kim, Y. H. Lee and W. J. Yu, Tuning Carrier Tunneling in van der Waals Heterostructures for Ultrahigh Detectivity, Nano Lett., 2017, 17, 453–459.
3. M. Zhou, Z. Liu, W. Ming, Z. Wang and F. Liu, sd2 Graphene: Kagome Band in a Hexagonal Lattice, Phys. Rev. Lett., 2014, 113, 236802.
4. L. Meng, Y. Wang, L. Zhang, S. Du, R. Wu, L. Li, Y. Zhang, G. Li, H. Zhou, W. A. Hofer and H.-J. Gao, Buckled Silicene Formation on Ir(111), Nano Lett., 2013, 13, 685.
5. P. M. Sheverdyaeva, S. K. Mahatha, P. Moras, L. Petaccia, G. Fratesi, G. Onida and C. Carbone, Electronic States of Silicene Allotropes on Ag(111), ACS Nano, 2017, 11, 975.
6. O. O. Brovko, D. Bazhanov, H. L. Meyerheim, D. Sander, V. S. Stepanyuk and J. Kirschner, Effect of mesoscopic misfit on growth,morphology,electronic properties and magnetism of nanostructures at metallic surfaces, Surf. Sci. Rep., 2014, 69, 159.
7. A. Correa, B. Xu, M. J. Verstraete and L. Vitali, Strain-induced effects in the electronic and spin properties of a monolayer of ferromagnetic GdAg2, Nanoscale, 2016, 8, 19148.
8. A. Molle, J. Goldberger, M. Houssa, Y. Xu, S.-C. Zhang and D. Akinwande, Buckled two-dimensional Xene sheets, Nat. Mater., 2017, 16, 163–169.
9. S. Cahangirov, M. Topsakal, E. Akturk, H. Sahin and S. Ciraci, Two- and One-Dimensional Honeycomb Structures of Silicon and Germanium, Phys. Rev. Lett., 2009, 102, 236804.
10. L. Li, S.-Z. Lu, J. Pan, Z. Qin, Y.-Q. Wang, Y. Wang, G.-Y. Cao, S. Du and H.-J. Gao, Buckled Germanene Formation on Pt(111), Adv. Mater., 2014, 26, 4820.
11. Y. Lu, W. Xu, M. Zeng, G. Yao, L. Shen, M. Yang, Z. Luo, F. Pan, K. Wu, T. Das, P. He, J. Jiang, J. Martin, Y. P. Feng, H. Lin and X.-S. Wang, Topological Properties Determined by Atomic Buckling in Self-Assembled Ultrathin Bi(110), Nano Lett., 2015, 15, 80.
12. L. Fernández, M. Blanco-Rey, M. Ilyn, L. Vitali, A. Magaña, A. Correa, P. Ohresser, J. E. Ortega, A. Ayuela and F. Schiller, Co Nanodot Arrays Grown on a GdAu₂ Template: Substrate/Nanodot Antiferromagnetic Coupling, Nano Lett., 2014, 14, 2977.
13. M. Ormaza, L. Fernández, M. Ilyn, A. Magaña, B. Xu, J. M. Verstraete, M. Gastaldo, M. A. Valbuena, P. Gargiani, A. Mugarza, A. Ayuela, L. Vitali, M. Blanco-Rey, F. Schiller and J. E. Ortega, High Temperature Ferromagnetism in a GdAg2 Monolayer, Nano Lett., 2016, 16, 4230.
14. J. Szade and M. Neumann, J Electronic structure investigation of Gd intermetallics, J. Phys.: Condens. Matter, 1999, 11, 3887.
15. H.-G. Zimmer and A. Goldmann, Surface- atom valence-band photoemission from Au (111) and Au(100)∼(5×20), Surf. Sci., 1986, 176, 115.
16. E. Weschke and G. Kaindl, 4f- and. surface-electronic structure of lanthanide metals, J. Electron Spectrosc. Relat. Phenom., 1995, 75, 233.
17. M. Alden, B. Johansson and H. L. Skriver, Surface shift of the occupied and unoccupied 4f levels of the rare-earth metals, Phys. Rev. B: Condens. Matter, 1995, 51, 5386.
18. O. Rader and A. M. Shikin, An Elastic “Sieve” to Probe Momentum Space: Gd Chains on W(110), Phys. Rev. Lett., 2004, 93, 256802.
19. A. V. Fedorov, E. Arenholz, K. Starke, E. Navas, L. Baumgarten, C. Laubschat and G. Kaindl, Surface Shifts of 4f Electron-Addition and Electron-Removal States in Gd(0001), Phys. Rev. Lett., 1994, 73, 601.
20. L. Vitali, S. Fabris, A. Mosca Conte, S. Brink, M. Ruben, S. Baroni and K. Kern, Electronic Structure of Surface-supported Bis(phthalocyaninato) terbium(III) Single Molecular Magnets, Nano Lett., 2008, 8, 3364.
21. D. P. Woodruff, W. A. Royer and N. V. Smith, Empty surface states, image states, and band edge on Au(111), Phys. Rev. B: Condens. Matter, 1986, 34, 764.
22. G. Kaindl, Bulk and surface electronic structure of lanthanide metals, J. Alloys Compd., 1995, 223, 265–273.
23. Ph. Kurz, G. Bihlmayer and S. Blügel, Magnetism and electronic structure of hcp Gd and the Gd(0001) surface, J. Phys.: Condens. Matter, 2002, 14, 6353–6371.
24. M. Petersen, J. Hafner and M. Marsman, Structural, electronic and magnetic properties of Gd investigated by DFT+U methods: bulk, clean and H-covered (0001) surfaces, J. Phys.: Condens. Matter, 2006, 18, 7021–7043.
25. P. Giannozzi, et al. QUANTUM ESPRESSO: a Modular and Open-source Software Project for Quantum Simulations of Materials, J. Phys.: Condens. Matter, 2009, 21, 395502.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7nr04699e

---