Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Drastic difference between hole and electron injection through the gradient shell of CdxSeyZn1−xS1−y quantum dots†
Mohamed
Abdellah
*ab,
Felipe
Poulsen
 c,
Qiushi
Zhu
a,
Nan
Zhu
de,
Karel
Žídek
f,
Pavel
Chábera
a,
Annamaria
Corti
g,
Thorsten
Hansen
c,
Qijin
Chi
c,
Qiushi
Zhu
a,
Nan
Zhu
de,
Karel
Žídek
f,
Pavel
Chábera
a,
Annamaria
Corti
g,
Thorsten
Hansen
c,
Qijin
Chi
 d,
Sophie E.
Canton
*hi,
Kaibo
Zheng
d,
Sophie E.
Canton
*hi,
Kaibo
Zheng
 *aj and
Tõnu
Pullerits
*a
*aj and
Tõnu
Pullerits
*a
aDivision of Chemical Physics and NanoLund, Lund University, Box 124, 22100, Lund, Sweden. E-mail: tonu.pullerits@chemphys.lu.se; kaibo.zheng@chemphys.lu.se; mohamed.qenawy@kemi.uu.se
bDepartment of Chemistry, Qena Faculty of Science, South Valley University, 83523 Qena, Egypt
cDepartment of Chemistry, University of Copenhagen, DK 2100 Copenhagen, Denmark
dDepartment of Chemistry, Technical University of Denmark, Kemitorvet Building 207, DK-2800 Kongens Lyngby, Denmark
eZhang Dayu School of Chemistry, Dalian University of Technology, Dalian, 116024, China
fRegional Centre for Special Optics and Optoelectronic Systems (TOPTEC), Institute of Plasma Physics, Academy of Sciences of the Czech Republic, Za Slovankou 1782/3, 182 00 Prague 8, Czech Republic
gÅngström Laboratory, Department of Chemistry, Uppsala University, Box 523, 75120 Uppsala, Sweden
hAttosecond Science group, Deutsches Elektronensynchrotron DESY, Notkestrasse 85, D-22607 Hamburg, Germany. E-mail: secanton2012@gmail.com
iELI-ALPS, ELI-HU Non-Profit Ltd., Dugonics ter 13, Szeged 6720, Hungary
jGas Processing Center, College of Engineering, Qatar University, P.O. Box 2713, Doha, Qatar
First published on 9th August 2017
Abstract
Ultrafast fluorescence spectroscopy was used to investigate the hole injection in CdxSeyZn1−xS1−y gradient core–shell quantum dot (CSQD) sensitized p-type NiO photocathodes. A series of CSQDs with a wide range of shell thicknesses was studied. Complementary photoelectrochemical cell measurements were carried out to confirm that the hole injection from the active core through the gradient shell to NiO takes place. The hole injection from the valence band of the QDs to NiO depends much less on the shell thickness when compared to the corresponding electron injection to n-type semiconductor (ZnO). We simulate the charge carrier tunneling through the potential barrier due to the gradient shell by numerically solving the Schrödinger equation. The details of the band alignment determining the potential barrier are obtained from X-ray spectroscopy measurements. The observed drastic differences between the hole and electron injection are consistent with a model where the hole effective mass decreases, while the gradient shell thickness increases.
Introduction
Colloidal quantum dots (QDs) form an important family of materials for third-generation solar cells. They have high extinction coefficient, size-tunable optical band gap, and show multiple exciton generation opening the possibility to break the Shockley–Queisser limit.1–8 Recently, Sargent and co-workers have achieved ∼11% solar power conversion efficiency using PbS/ZnO QDs via solvent-polarity-engineered halide passivation.9,10 The long-term photo-stability of the QDs is a critical precondition for their photovoltaic applications.11–13 By growing a wider band gap semiconductor shell around the core, these so called core–shell QDs (CSQDs) can be protected against possible surface traps and degradation.14–16 Generally, we can produce two types of distinct CSQDs, i.e. (i) step-like CSQDs, in which the composition-change from the core to the shell materials is sharp15 and (ii) alloyed CSQDs, where the change in compositions is gradual.14 The second approach to growing the shell can minimize the interfacial defects, enhances the photoluminescence (PL) quantum yield (QY), and reduces the unwanted Auger recombination process.17,18 In our previous work, we have studied the electron injection from the optically active core through the gradient shell to the n-type metal oxide (MO), represented by the CdxSeyZn1−xS1−y CSQDs/ZnO system.19 We found that electron injection is optimal for a ∼1.3 nm shell thickness showing good surface passivation, while keeping the injection rate still sufficiently high.QDs can also be utilized for sensitizing p-type solar cells. Here, the holes are injected from the valence band of the QDs to the p-type MO acceptor because the process is energetically favorable, while the electrons can be scavenged by the redox couples.20,21 Hole injection from neat colloidal CdSe QDs to p-type MO was reported with a low incident photon-to-current conversion efficiency (17%) due to the strong competition between hole injection and surface hole trapping.20 However, our preliminary results have shown that the core–shell structure can passivate such surface traps and consequently enhance the hole injection efficiency.22
In this work, we systematically study the hole injection from gradient CSQDs (CdxSeyZn1−xS1−y) to NiO mesoporous film by time-resolved photoluminescence (TRPL) and transient absorption (TA) spectroscopies. We find that the hole injection rate for the thinner shells is relatively slow compared to the corresponding electron injection rate. At the same time, the hole injection exhibits much less dependence on the shell thickness than the previously reported electron injection in the n-type system (e.g. CSQDs/ZnO). In order to better understand such qualitative differences, we performed theoretical modelling for the electronic probability densities of a carrier to be outside the gradient CSQDs based on the band alignment and energies determined from synchrotron-based X-ray experiments. The experimental results are consistent with the modelling, suggesting that the hole effective mass is much smaller in the gradient shell of the CSQDs than in the conventional bulk materials. In this case, the wave-function of the holes extends more easily through the shell barrier than the wave-function of the electrons, leading to the lower sensitivity of the hole transfer rate to the shell thickness. Such unexpected results provide a novel reference for future design and fabrication of p-type QD solar cells.
Results and discussion
The chemical reactivity of the cations plays a critical role in synthesis of gradient CSQDs. Due to the higher chemical reactivity of Cd-oleate compared to Zn-oleate at the reaction temperature, the Cd-rich core forms within the first 5 seconds of the reaction, then the alloyed shell grows in the epitaxial direction to the outer layer (Zn-rich shell). Fig. 1A presents the steady-state absorption and emission spectra for as-prepared oleic acid capped CSQDs in toluene with different shell thicknesses. The 1S exciton peak is well distinguishable for all samples.19 The QDs extracted within the initial 5 seconds of the growth are taken as the “core” for our CSQDs and are defined as the “0” nm sample (i.e. without the shell). Increasing the shell thickness results in a red shift of the 1S exciton peak due to the increase in the effective size and leakage of the exciton wave function into the shell material similarly to the step-like CSQDs of the same materials.15 The core of our CSQDs is ternary CdSexS1−x alloy evidenced by energy-dispersive X-ray spectroscopy (EDX) analysis in TEM of our previous work.19 The possibility of ion diffusion during the QD growth at high temperature has been observed in other analogous systems.23–25 In the present case, however, XPS measurements with different incident photon energies (hence probing a different escape depths for the photoelectrons) unambiguously demonstrate that the electronic structure of the CSQDs varies radially (for details, see ESI†). This means that the synthesized CSQDs have a gradient core–shell and not a homogeneous alloy structure.The diameter of the core size was estimated from the HR-TEM images to be 3.0 nm as reported in our previous work.19,26 The shell thickness was determined to be 0.6, 1.3, 1,6, 1.9, and 2.3 nm by comparing the HR-TEM images of the core (“0” nm) and the CSQDs collected at different synthesis times.15Fig. 1A also shows the steady-state emission for the CSQDs together with the “0” nm shell QDs. The relatively narrow emission bands (∼33 nm FWHM) observed for all the samples confirm the small size distribution (<15%) of our QDs as estimated from HR-TEM images.19
The as-prepared QDs were initially capped with the long-chain oleic acid, which is a one-terminal capping agent and is not suitable to anchor the QDs to the MO surface.14 Therefore, the bifunctional short-chain linker molecule, mercaptopropionic acid (MPA) was used to replace the oleic acid.5,22,27 However, such ligand exchange can induce numerous surface states acting as hole traps.22,28 Indeed, a drastic decrease in the PL QY of the core QDs was observed after ligand exchange due to the quenching by the surface hole traps.16 However, the PL QY decreased significantly less if the shell is coated well around the core (see the inset in Fig. 1B), confirming the good passivation of the surface traps by the shell.
Besides passivation, the shell also acts as a barrier for the hole injection from the valence band of the QDs to NiO. Fig. 1B shows the absorption spectra of QDs attached to NiO. After attachment to the NiO, the 1S exciton peak of the QDs is (indicate red/blue) slightly shifted, while the neat NiO has no spectral features in this wavelength range (see Fig. 1B, black line). The overall collection efficiency of the photo-generated charges by the MO depends both on the surface passivation and the hole injection process.20 In our previous work, we confirmed the existence of hole injection from CdxSeyZn1−xS1−y gradient CSQDs to NiO in the CSQD/NiO system.22 Here, we aim at obtaining further insight into the dependence of the hole injection dynamics on the gradient shell thickness. Generally speaking, various methods such as TA and TRPL can be utilized to probe the charge transfer dynamics.29,30 However, the density of excited hole states at the band edge in the QDs is significantly higher than that of the excited electron states. Consequently, the TA signal in the visible range is not very sensitive to holes (see Fig. S1†).22,31,32 Therefore, TRPL spectroscopy has been preferentially used to monitor the hole injection dynamics.
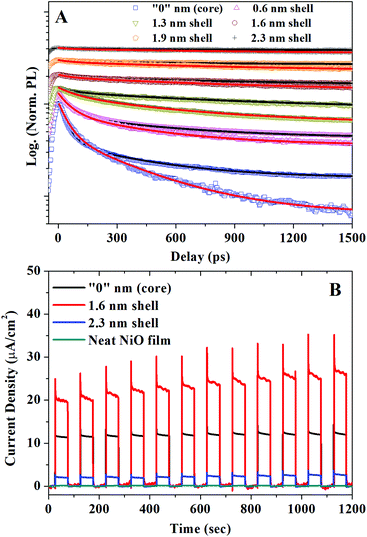
Fig. 2A presents the normalized PL decay kinetics for CSQDs with different shell thickness deposited on glass or attached to a NiO film. Comparing the TRPL kinetics for these two categories of QDs provides a clear evidence that a new hole depopulation pathway is introduced by attaching QDs to NiO. It should be noted here that the electron depopulation can be unambiguously excluded by TA measurements as no electron depopulation related bleach kinetics can be observed (for the details see ESI†). Multiple exciton recombination can also be ruled out since a very low excitation fluence (1.1 × 1012 ph per cm2 per pulse) was used, corresponding to a mean excitation density per QD much below 1 (0.001 ph per QD).22 In order to verify that the depopulation of excited holes is indeed due to the hole injection from the QDs into NiO, we conducted photocurrent measurements using CSQD–NiO as photocathodes, shown in Fig. 2B. The significantly enhanced photocurrent through the CSQDs–NiO compared to the neat NiO film photocathodes clearly demonstrates the hole transfer from CSQDs to NiO.30 Thereby, we can assign the hole depopulation probed by TRPL to the hole injection from QDs to NiO. We point out that CSQDs with shell thickness of 1.6 nm exhibited the highest photocurrent. This is due to the optimized surface trap passivation versus charge transfer efficiency in this particular thickness discussed in our previous study.19
In the next step, we extracted the hole injection rates in the CSQDs–NiO from the PL kinetics. All measured PL kinetics can be well fitted as biexponential decays as summarized in the Table 1. For the QDs deposited on glass, we obtain time constants τ1 = 60–160 ps and τ2 = 1.5–12 ns. For QDs attached to NiO film, τ1 is almost the same (70–160 ps), while τ2 = 0.7–3.0 ns shows a shell-thickness dependence. According to our previous study, the common component (τ1) can be attributed to the hole trapping in QDs by volume defect states, which is slower than conventional surface trapping while the shortening of the shell-thickness dependent component τ2 is related to the hole injection.22 Since the trapping is much faster than the lifetime of the slow component (τ2), the contribution of the QDs with traps to the hole injection is negligible and is not considered in the following discussion. The slow component represents the intrinsic excitation lifetime of the QDs which have no traps. The rate constants of the slow components in CSQDs/NiO (τ2-QDs/NiO) correspond to the sum of the decay of the neat MPA capped CSQDs on glass (1/τ2-QDs/glass) and the hole injection rates to NiO. Thereby we can express the hole injection rate as:
 | (1) |
| Sample | A 1 (%) | τ 1 (ps) | A 2 (%) | τ 2 (ps) | k h-inj. (10−4 ps−1) |
|---|---|---|---|---|---|
| “0” nm/glass | 65 | 60 ± 5 | 35 | 2200 ± 40 | 8.4 |
| “0” nm/NiO | 70 | 80 ± 5 | 30 | 780 ± 10 | |
| 0.6 nm/glass | 65 | 90 ± 5 | 35 | 1500 ± 20 | 6.6 |
| 0.6 nm/NiO | 65 | 90 ± 10 | 35 | 760 ± 10 | |
| 1.3 nm/glass | 60 | 160 ± 10 | 40 | 2710 ± 40 | 4.8 |
| 1.3 nm/NiO | 50 | 165 ± 5 | 50 | 1180 ± 10 | |
| 1.6 nm/glass | 60 | 80 ± 10 | 40 | 3660 ± 50 | 3.1 |
| 1.6 nm/NiO | 3 | 110 ± 10 | 97 | 1690 ± 20 | |
| 1.9 nm/glass | 10 | 170 ± 15 | 90 | 5000 ± 200 | 2.8 |
| 1.9 nm/NiO | 3 | 110 ± 10 | 97 | 2070 ± 25 | |
| 2.3 nm/glass | 5 | 120 ± 20 | 95 | 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 ± 800 800 ± 800 |
2.5 |
| 2.3 nm/NiO | 2 | 80 ± 10 | 98 | 3000 ± 40 |
Fig. 3A presents the hole injection rates to NiO as a function of shell thickness (blue). For comparison, the electron injection rates (black) to n-type ZnO using the same CSQDs system has also been plotted.19 Even though there are exceptions,33 the charge transfer rates between donors and acceptors generally follow the exponential dependence k(d) ∝ e−βd, where β expresses the distance dependence of the transfer rates and d is the donor–acceptor distance.15,34 In conventional dye or polymer systems, the donor and acceptor are usually separated by organic linker molecules whose length defines d.35 In core–shell QD systems, the initial excitons are mainly generated within the core materials. Therefore, we can simplify the model by assuming that the electrons/holes excited in the core are separated from the MO acceptor by the shell barrier. In this case, d denotes the thickness of the shell (i.e. the distance from the edge of the core to the acceptor). In the CSQDs-MO system, β represents the characteristics of the shell barrier affecting the charge transfer.15 By fitting the experimental kh-inj.vs. shell thickness shown in Table 1, we obtain a β value for hole injection of 0.06 ± 0.01 A−1 (Fig. 3A, blue) which is much lower than the one for electron injection in n-type system (β = 0.51 ± 0.01 A−1, Fig. 3A, black).19 This implies a substantially lower shell thickness dependence for the hole transfer compared to electron transfer.
 | ||
| Fig. 3 (A) Electron injection (black) and hole injection rate (blue) as a function of shell thickness. The black and blue lines are the exponential fitting of the electron and hole injection rates as a function of the shell thickness, respectively. (B) The change of CBM and VBM with the growth of the gradient shell obtained from X-ray data. The CBM/VBM of the MOs are obtained from the literature.22,27 The solid side lines extended from the experimental data points mean that the measured “CBM” and “VBM” are the average values within such depth from the surface (<1 nm). (C) Calculated probability of being outside of the quantum dot for the electron (black) and the hole (blue). | ||
In order to understand the origin for the drastic difference between the electron and hole injection rates we build and test a model for the dependence of the charge transfer dynamics on shell thickness. The model is based on Fermi's Golden rule:
k ∝ |〈i|![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) |f〉|2 ≅ |〈i|f〉|2 ∝ Poutside |f〉|2 ≅ |〈i|f〉|2 ∝ Poutside | (2) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) |f〉, where
|f〉, where ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) is the constant perturbing potential. We assume that the perturbing potential is slowly varying in the overlap region, which justifies the second equality. Then the absolute square of this expression should be positively correlated to the probability of finding the particle outside the QD, Poutside. These probability densities for the electron and hole (Poutside electron and Poutside hole) were obtained numerically by integrating the Schrödinger equation using a fourth order Runge–Kutta method:36
is the constant perturbing potential. We assume that the perturbing potential is slowly varying in the overlap region, which justifies the second equality. Then the absolute square of this expression should be positively correlated to the probability of finding the particle outside the QD, Poutside. These probability densities for the electron and hole (Poutside electron and Poutside hole) were obtained numerically by integrating the Schrödinger equation using a fourth order Runge–Kutta method:36 | (3) |
The potential profile of the barriers in the CSQDs/MO system is given by the relative positions of the valence band minima (VBM) and the conduction band maxima (CBM) of the core and the shell of the CSQDs. Such information can be reliably extracted from X-ray absorption spectroscopy (XAS) and X-ray photoelectron emission spectroscopy (XPS) of the QDs. The extensive strategy for homogeneous QDs system has been presented in previous study.37 For CSQDs, the X-ray photons with low energy (130 eV) enable a surface sensitive characterization (escape depth ∼0.7 nm) of the electronic structure of the QDs. In this scenario, we can evaluate the band alignment for the outer part of the CSQDs. By combing the measurements of CSQDs with different shell thickness, we can build up the corresponding energy barrier for the charge carrier injection as shown in Fig. 3B. Note that in the experimental measurements the band energies are obtained as an average over the X-ray probe depth (0.7 nm). Therefore, the precision of the CB and VB energies can be limited (for details see ESI†).
Finally, the potential after the shell (i.e. the terminal point of the barrier potential profile) is determined by the HOMO and LUMO energies of the ligand attached to the QD surface.33 We have positioned the HOMO and LUMO energies symmetrically with respect to the core bandgap.
The other essential parameter entering the model is the charge carrier effective mass in the CSQDs. Using the ratio of Cd to Zn obtained from the energy dispersive X-ray analysis as a function of shell thickness,19 we can construct the effective mass profiles for the six samples. These profiles are based on the assumption that the effective mass of both electrons and holes scales linearly with the ratio of the composite materials taking the known effective mass of pure CdSe and ZnS as a reference.38 Interestingly, our initial trial using the conventional effective mass of bulk CdSe 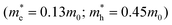 and ZnS
and ZnS 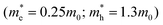 led to a shell dependence of the injection rate opposite to the experimental results (i.e. the electron injection exhibited less shell-dependence than the hole injection, for details see ESI†). The best simulation was achieved when much lower hole effective mass of the outer layer has been imposed
led to a shell dependence of the injection rate opposite to the experimental results (i.e. the electron injection exhibited less shell-dependence than the hole injection, for details see ESI†). The best simulation was achieved when much lower hole effective mass of the outer layer has been imposed  as shown in Fig. 3C (for details of simulation see ESI†). The basic physics here is intuitive. If the effective hole mass of the shell is lowered, the hole is more delocalized, and has a greater probability to be found outside. If the effective hole mass decreases in the outward radial direction, then as the shell thickness is increased, the increase in Poutside-hole from this contribution competes with the decrease of Poutside resulting from the increased shell thickness. In this way, the injection rate appears less sensitive to the shell thickness. On the other hand, if the effective electron mass increases in the outward radial direction, this contribution complements the decrease in Poutside-electron, hence, the injection rate appears to be very sensitive to the shell thickness.
as shown in Fig. 3C (for details of simulation see ESI†). The basic physics here is intuitive. If the effective hole mass of the shell is lowered, the hole is more delocalized, and has a greater probability to be found outside. If the effective hole mass decreases in the outward radial direction, then as the shell thickness is increased, the increase in Poutside-hole from this contribution competes with the decrease of Poutside resulting from the increased shell thickness. In this way, the injection rate appears less sensitive to the shell thickness. On the other hand, if the effective electron mass increases in the outward radial direction, this contribution complements the decrease in Poutside-electron, hence, the injection rate appears to be very sensitive to the shell thickness.
The effective mass approximation is developed for bulk material and its validity for nano-scale objects might be questionable. Still, our approach does explain the basic trends in the photophysics. For the thin shell the electron and hole transfer rates are very different, whereas for the thicker shell the rates are more or less the same. This trend is captured by simulations that have a radially decreasing/increasing effective hole/electron mass in the shell. Therefore, we suggest that the behaviour of the hole injection rate is due to a gradual decrease of an effective hole mass in the CdSe/ZnS alloy as the concentration of ZnS increases. We point out, though, that some deviations between the theoretical calculations and experimental data can be due to other factors that could influence the charge transfer. One of them is the possible intermediate charge transfer states within the gradient shell, which could modulate the electron and hole injection.35 Furthermore, because of the possible ion diffusion (especially for Zn ion), the electronic structure of the inner part of the CSQDs could be slightly changed while the outer shell builds up. In this scenario, the actual VBM and CBM radial profiles within the CSQDs could deviate somewhat from the simple illustration shown in Fig. 3B where only the thickness of 0.7 nm to the surface has been probed by the X-ray characterization with XPS. Nevertheless, the qualitative agreement between the experimental and the modeled rates argues favorably for the validity of the interpretation for the present CSQDs.
Conclusions
We have studied the hole injection from gradient CSQD to a common p-type MO, NiO. Compared to step-like CSQDs, gradient CSQDs have less interface defects owing to a smooth change in the chemical composition from the core to the shell materials. Compared to the electron injection in n-type solar cells, the hole injection rates are slower but with significantly weaker shell thickness dependence. By theoretical modelling based on the band alignment of the VB and CB in the CSQDs/MOs system, we attribute this phenomenon to the reduced hole effective mass of the shell compared with the core materials. Our results indicate a great potential for such CSQDs in both n-type and p-type solar cell applications and provide novel reference for band engineering in CSQD solar cells.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was made possible by NPRP Grant # NPRP7-227-1-034 from the Qatar National Research Fund (a member of the Qatar Foundation). The statements made herein are solely the responsibility of the authors. Financial support from KWA, Swedish Research Council, and STINT (CH2015-6232) is acknowledged. The ELI-ALPS project (GINOP-2.3.6-15-2015-00001) is supported by the European Union and co-financed by the European Regional Development Fund. Q.C. acknowledges the financial support by the Danish Council for Independent Research for Natural Science (DFF-FNU). We are dedicating this work to the soul of Prof. Ahmed Zewail.Notes and references
- A. J. Nozik, Nano Lett., 2010, 10, 2735–2741 CrossRef CAS PubMed.
- P. V. Kamat, J. Phys. Chem. Lett., 2013, 4, 908–918 CrossRef CAS PubMed.
- P. V. Kamat, J. Phys. Chem. C, 2008, 18737–18753 CAS.
- N. Guijarro, J. M. Campiña, Q. Shen, T. Toyoda, T. Lana-Villarreal and R. Gómez, Phys. Chem. Chem. Phys., 2011, 13, 12024–12032 RSC.
- K. Zídek, K. Zheng, M. Abdellah, N. Lenngren, P. Chábera and T. Pullerits, Nano Lett., 2012, 12, 6393–6399 CrossRef PubMed.
- O. E. Semonin, A. J. Nozik and M. C. Beard, Science, 2011, 334, 1530–1533 CrossRef CAS PubMed.
- K. J. Karki, K. Zheng, K. Zidek, A. Mousa, M. A. Abdellah, M. E. Messing, L. R. Wallenberg, A. Yartsev and T. Pullerits, Sci. Rep., 2013, 3, 2287 CrossRef PubMed.
- K. J. Karki, J. R. Widom, J. Seibt, I. Moody, M. C. Lonergan, T. Pullerits and A. H. Marcus, Nat. Commun., 2014, 5, 5869 CrossRef CAS PubMed.
- X. Lan, O. Voznyy, F. P. Garcia De Arquer, M. Liu, J. Xu, A. H. Proppe, G. Walters, F. Fan, H. Tan, M. Liu, Z. Yang, S. Hoogland and E. H. Sargent, Nano Lett., 2016, 16, 4630–4634 CrossRef CAS PubMed.
- Z. Jin, M. Yuan, H. Li, H. Yang, Q. Zhou, H. Liu, X. Lan, M. Liu, J. Wang, E. H. Sargent and Y. Li, Adv. Funct. Mater., 2016, 26, 5284–5289 CrossRef CAS.
- A. Makhal, H. Yan, P. Lemmens and S. K. Pal, J. Phys. Chem. C, 2010, 114, 627–632 CAS.
- C.-H. M. Chuang, P. R. Brown, V. Bulović and M. G. Bawendi, Nat. Mater., 2014, 13, 796–801 CrossRef CAS PubMed.
- C. V. V. M. Gopi, M. Venkata-Haritha, S.-K. Kim and H.-J. Kim, Dalton Trans., 2015, 44, 630–638 RSC.
- W. Bae, K. Char, H. Hur and S. Lee, Chem. Mater., 2008, 20, 531–539 CrossRef CAS.
- H. Zhu, N. Song and T. Lian, J. Am. Chem. Soc., 2010, 132, 15038–15045 CrossRef CAS PubMed.
- P. Reiss, M. Protière and L. Li, Small, 2009, 5, 154–168 CrossRef CAS PubMed.
- A. M. Smith and S. Nie, Acc. Chem. Res., 2010, 43, 190–200 CrossRef CAS PubMed.
- G. E. Cragg and A. L. Efros, Nano Lett., 2010, 10, 313–317 CrossRef CAS PubMed.
- M. Abdellah, K. Zidek, K. Zheng, P. Chabera, M. E. Messing and T. Pullerits, J. Phys. Chem. Lett., 2013, 4, 1760–1765 CrossRef CAS PubMed.
- I. Barceló, E. Guillén, T. Lana-villarreal, R. Gómez and I. Universitari, J. Phys. Chem. C, 2013, 117, 22509–22517 Search PubMed.
- Z. Wang, A. Shakya and J. Gu, J. Am. Chem. Soc., 2013, 135, 9275–9278 CrossRef CAS PubMed.
- K. Zheng, K. Zidek, M. Abdellah, W. Zhang, P. Chábera, N. Lenngren, A. Yartsev, T. T. Pullerits, P. Chabera, N. Lenngren, A. Yartsev and T. T. Pullerits, J. Phys. Chem. C, 2014, 118, 18462–18471 CAS.
- E. Groeneveld, L. Witteman, M. Lefferts, X. Ke, S. Bals, G. Van Tendeloo and C. de Mello Donega, ACS Nano, 2013, 7, 7913–7930 CrossRef CAS PubMed.
- S. Maiti, T. Debnath, P. Maity and H. N. Ghosh, J. Phys. Chem. C, 2016, 120, 1918–1925 CAS.
- T. Debnath, K. Parui, S. Maiti and H. N. Ghosh, Chem. – Eur. J., 2017, 23, 3755–3763 CrossRef CAS PubMed.
- M. Abdellah, R. Marschan, K. Žídek, M. E. Messing, A. Abdelwahab, P. Chábera, K. Zheng and T. Pullerits, J. Phys. Chem. C, 2014, 118, 25802–25808 CAS.
- K. Zídek, K. Zheng, C. S. Ponseca, M. E. Messing, L. R. Wallenberg, P. Chábera, M. Abdellah, V. Sundström, T. Pullerits, K. Žídek, K. Zheng, C. S. Ponseca, M. E. Messing, L. R. Wallenberg, P. Chábera, M. Abdellah, V. Sundström, T. Pullerits, K. Zídek, K. Zheng, C. S. Ponseca, M. E. Messing, L. R. Wallenberg, P. Chábera, M. Abdellah, V. Sundström, T. Pullerits and K. Žídek, J. Am. Chem. Soc., 2012, 134, 12110–12117 CrossRef PubMed.
- B. Omogo, J. F. Aldana and C. D. Heyes, J. Phys. Chem. C, 2013, 117, 2317–2327 CAS.
- P. V. Kamat, Acc. Chem. Res., 2012, 45, 1906–1915 CrossRef CAS PubMed.
- K. Zheng, K. Zidek, M. Abdellah, M. Torbjornsson, P. Chabera, S. Shao, F. Zhang and T. Pullerits, J. Phys. Chem. A, 2012, 117, 5919–5925 CrossRef PubMed.
- V. Klimov, Annu. Rev. Phys. Chem., 2007, 58, 635–673 CrossRef CAS PubMed.
- A. V. Malko, A. A. Mikhailovsky, M. A. Petruska, J. A. Hollingsworth and V. I. Klimov, J. Phys. Chem. B, 2004, 108, 5250–5255 CrossRef CAS.
- T. Hansen, K. Zidek, K. Zheng, M. A. Abdellah, P. Chabera, P. Persson and T. Pullerits, J. Phys. Chem. Lett., 2014, 5, 1157–1162 CrossRef CAS PubMed.
- L. Dworak and V. Matylitsky, J. Phys. Chem. C, 2011, 115, 3949–3955 CAS.
- C. Deibel, Adv. Mater., 2010, 22, 4097–4111 CrossRef CAS PubMed.
- A. D. Alhaidari, Phys. Rev. A, 2002, 66, 42116 CrossRef.
- R. Meulenberg, J. Lee and A. Wolcott, ACS Nano, 2009, 3, 325–330 CrossRef CAS PubMed.
- C. S. Wang and B. M. Klein, Phys. Rev. B: Condens. Matter, 1981, 24, 3393–3416 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details, detailed TA results, and results of the theoretical simulation with different effective mass used. See DOI: 10.1039/c7nr04495j |
| This journal is © The Royal Society of Chemistry 2017 |