Chirality-dependent growth of single-wall carbon nanotubes as revealed inside nano-test tubes

Abstract

Growth dynamics of single-wall carbon nanotubes (SWCNTs) have been studied with nickelocene as a precursor encapsulated in the interior of template SWCNTs. By means of multi-laser Raman spectroscopy, growth curves of nine different SWCNTs, (8,8), (12,3), (13,1), (9,6), (10,4), (11,2), (11,1), (9,3) and (9,2), have been determined upon in situ annealing at various temperatures. The data reveal that the nanotubes grow through fast and slow reaction pathways with high and low activation energies, respectively. While the activation energy of the slow growth is independent of the nanotube's chiral vector, that of the fast growth exhibits a monotonic increase as the tube diameter reduces from ∼1.1 down to 0.8 nm and no dependency on the chiral angle, which can be attributed to the size-dependent properties of catalyst clusters. The chirality dependent catalytic growth properties exploited in this study provide the basis for a large-scale synthesis of single-chiral vector SWCNTs.

---

1 Introduction

The exceptional properties of single-wall carbon nanotubes (SWCNTs)¹ can find applications in various fields.^2,3 Although progress made thus far on the synthesis of SWCNTs and post-synthesis purification techniques^4–8 is remarkable with regard to large yield and high purity, it remains a challenge to synthesize single-chiral vector nanotubes on a bulk scale.^9–13 The chemical vapor deposition (CVD) method has shown potential for chirality control as a greater abundance of large chiral angle SWCNTs was observed with this method.^14,15 Chirality control at the nucleation stage was demonstrated based upon the catalyst composition and structure.^9,10,16

In situ observations on the growth of SWCNT forests by means of optical absorption spectroscopy,^17,18 optical imaging¹⁹ and Raman spectroscopy^20–22 have led to improved understanding of the growth mechanism. A laser-induced cold-wall CVD in situ growth was observed by Raman spectroscopy^23,24 and vapour phase epitaxy (VPE) (or cloning) was observed by scanning electron microscopy.²⁴ It was demonstrated that the rate of individual SWCNT growth increased proportionally with the chiral angle, in agreement with theoretical predictions based on the dislocation mechanism of SWCNT growth.^25,26

It was reported that the CVD growth rate for carbon filaments and nanotubes could be limited by diffusion and mass transfer in the gas phase, surface reactions on the catalyst, or carbon diffusion through the catalyst bulk or over the catalyst surface.²⁷ In many works, the bulk carbon diffusion was suggested to be the growth rate limiting process for carbon filaments,^28–31 multi-wall carbon nanotubes (MWCNTs)^27,32–36 and SWCNTs.^18,19 In contrast, the surface diffusion was reported to be rate limiting for carbon filaments³⁷ and MWCNTs.^32,38–41 In ref. 21 and 41–47, the surface reaction on the catalyst was suggested to be rate limiting for MWCNTs^41–45 and SWCNTs.^21,46,47

The activation energy is evaluated from the exponential temperature dependence of the growth rate. Besides a large variety in activation energy reported for carbon filaments (0.23–1.68 eV)^28–31,37 and MWCNTs (0.23–2.09 eV),^{27,32–36,38–45,48} those for SWCNTs fall in the range of 0.38–2.8 eV.^{18,19,21,46,47,49,50} The reported values vary with the type of catalyst and carbon feedstock, the definition of the growth rate and the temperature region where the activation energy is evaluated. Accordingly, suggested rate-limiting processes are very different. A comprehensive understanding of microscopic reaction processes is a prerequisite towards a better controlled bulk synthesis of SWCNTs.

To the best of our knowledge, there are no experimental reports on the activation energy of SWCNTs for a given chiral vector, due to complexities in the bulk synthesis. In the present work, we use SWCNTs as template nano-reactors in which small diameter tubes grow from precursor nickelocene (NiCp₂) under ultra clean conditions.^51,52 This method allows as precise as possible control over the nanotube diameter and chemical composition of the catalyst and carbon feedstock without deactivations. From in situ Raman spectroscopy, growth dynamics of nine different SWCNTs, (8,8), (12,3), (13,1), (9,6), (10,4), (11,2), (11,1), (9,3) and (9,2), with diameters in the range of ∼0.8 to 1.1 nm, have been revealed on a much longer time scale (several minutes to tens of hours) at much lower temperatures (480–600 °C), compared to those for the conventional CVD synthesis. The growth curves are decomposed into two exponential growth functions with fast and slow growth rates, both of which increase exponentially with the temperature, from which two activation energies are determined. It is found that the higher activation energy for the fast growth decreases monotonically with the tube diameter, while the lower activation energy shows no clear dependency. The former is attributed to the size-dependent catalytic activity of encapsulated carbide clusters. As a consequence, small-diameter SWCNTs can grow at temperatures as low as 400 °C so that no vacuum would be required. This provides facile means towards post-synthesis tuning of SWCNT's electronic properties.

2 Experimental section

2.1 Preparation of SWCNT films

SWCNTs synthesized by the enhanced direct injection pyrolytic synthesis (e-DIPS) method were used as a starting material.⁵³ Thin films were made as follows. Typically, 3 mg of the as-grown SWCNT material were dispersed in 20 ml of toluene (≥99.5%, Carl Roth GmbH+Co. KG) by bath ultrasonication for 1 h and then filtered through a 4.7 cm diameter cellulose filter membrane with a pore diameter of 0.2 μm (Millipore) using a vacuum filtration setup. The SWCNT film on the membrane was dispersed in 45 ml of methanol (≥99.5%, Carl Roth GmbH+Co. KG) by ultrasonication for a few minutes. After the membrane was removed, the methanol solution of the SWCNT was further ultrasonicated for 30 min. 9 ml of the prepared solution was filtered through a 2.5 cm diameter cellulose filter membrane with a pore diameter of 0.2 μm (Millipore). As soon as the methanol was evaporated, the SWCNT film (a mass of about 0.6 mg and a diameter of 1 cm) was peeled off the membrane.

2.2 Filling of SWCNT films with nickelocene

Prior to the filling, the nanotube films were oxidized in air at 500 °C for 1 h. Nickelocene in a vacuum starts to sublime at 50 °C above which it also decomposes. The vapor transfer method described in the following allowed SWCNT films to be exposed to a nickelocene vapour without being contaminated with decomposed materials. A borosilicate glass tube (outer diameter 6 mm, inner diameter 3 mm, length ∼10 cm) containing nickelocene powder (99%, Strem Chemicals Inc.) at its closed end and a oxidized SWCNT film in the middle of the tube was evacuated with a vacuum chamber equipped with a turbomolecular pump (Pfeiffer vacuum) to a vacuum pressure better than 10⁻⁶ mbar and then sealed with a blow torch. One side of the sealed glass tube including the nickelocene powder and SWCNT film was wrapped with a heating wire (Thermocoax heating element with a Ni–Cr alloy core, MgO insulant and stainless steel sheath) connected to a laboratory power supply (Heinzinger or TDK-Lambda). Maintained at 50 °C, the nickelocene slowly sublimes and deposits at the cold end of the glass ampoule. Typically after 12–24 hours, all metallocene was transferred to the cold end. Then, the ampoule was flipped and the other side was heated. This procedure was repeated 5–10 times. Finally, the ampoule was opened in a glove box.

2.3 Transmission electron microscopy

The nickelocene-filled SWCNT samples for high-resolution transmission electron microscopy (HR-TEM) and annular dark field (ADF) scanning TEM (STEM) imaging were dispersed in n-hexane by ultrasonication and dropped onto molybdenum microgrids coated with holey amorphous carbon films. JEOL JEM-2100F and ARM-200F microscopes were operated at electron accelerating voltages of 60 and 80 kV, respectively. Each sample was maintained at 200 °C inside the microscope to prevent contamination during (S)TEM observation.

2.4 In situ Raman spectroscopy

A metallocene-filled SWCNT film (about 3 mm × 3 mm) was placed in between two quartz plates inside a flat quartz tube (QSIL GmbH) closed at one end. Then, the quartz tube was evacuated with a turbomolecular pump (Pfeiffer vacuum) that provided a vacuum pressure better than 10⁻⁶ mbar and placed so that the nanotube film was positioned under an objective (50×) of a Raman spectrometer (Horiba Jobin Yvon LabRAM HR800). A section of the quartz tube including the nanotube film was heated with a home-built heating tube made out of a resistive heating wire connected to a power supply (Xantrex) with a temperature controller (Eurotherm). The temperature was measured on the quartz tube next to the sample with a thermocouple (type K) made from Ni–Cr and Ni–Al alloy wires (Omega Resistance Wire). The sample was heated sequentially for periods of time t = 2 + 2ⁿ (min), where n = 1, 2, 3, …, 12. The first term is the time required for heating the sample up to a set temperature. After every annealing step was finished, the heater was slid off the quartz tube and Raman measurements were carried out on the sample at room temperature. Seven different samples were used for the measurements at seven different temperatures of 480, 500, 520, 540, 560, 580 and 600 °C.

Raman spectroscopy was performed with a Horiba Jobin Yvon LabRAM HR800 spectrometer adapted for multifrequency measurements, as described in ref. 54. The system was equipped with an internal He–Ne laser operated at a wavelength of 633 nm (an energy of 1.96 eV) and an external tunable Ar–Kr mixed gas laser (Coherent Innova 70c) operated at a wavelength of 568 nm (an energy of 2.18 eV). These laser wavelengths were chosen for two reasons. Firstly, inner tubes with chiral vectors of our interest are in resonance. Secondly, the radial breathing mode (RBM) frequencies of the inner tubes in resonance to each laser are well separated from one another. RBM peaks were fitted with Voigtian functions using PeakFit v4.12. All Raman spectra were normalized to the area intensity of the G-band (1350–1700 cm⁻¹).

3 Results

3.1 Transmission electron microscopy

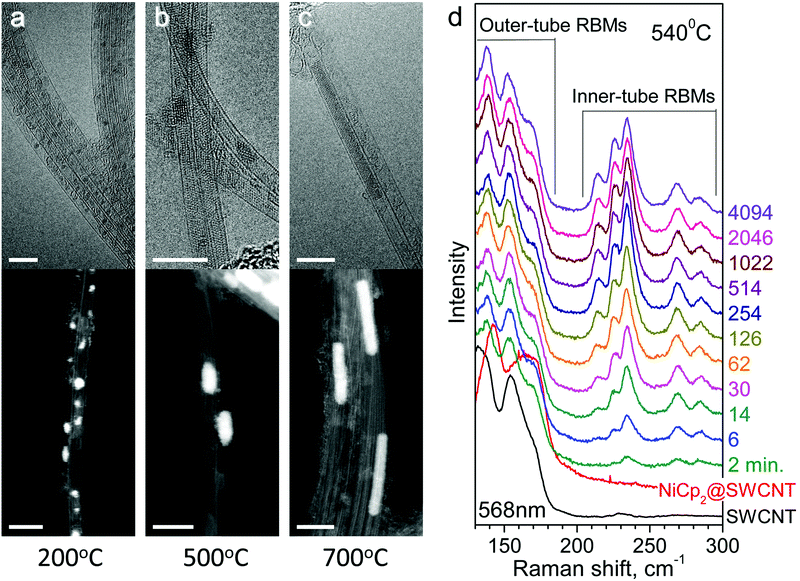
Nickelocene-filled SWCNTs (NiCp₂@SWCNT) were characterized by means of TEM to evaluate the effect of annealing on the inner structures. Fig. 1 shows the HR-TEM and ADF-STEM images of the annealed samples. Nickel clusters derived from nickelocene inside SWCNTs by annealing give a dark and a bright contrast in the HR-TEM and ADF-STEM images, respectively. Fig. 1a shows that small nickel clusters with diameters of around 1 nm are formed inside SWCNTs by in situ annealing at 200 °C. Pre-annealing of the nickelocene-filled SWCNTs at higher temperatures yields larger nickel clusters with cylindrical shapes, as shown in Fig. 1b and c. Also, paired parallel line contrasts extend from one end of the clusters, visualising inner tubes rooting from the metal catalysts. The lengths of typical nickel clusters found inside SWCNTs pre-annealed at 500 and 700 °C are 3–5 and 10–20 nm, respectively. This indicates that the reaction volume per inner tube increases with temperature. Continuous exposure of the cylindrical nickel clusters to electron beam irradiation causes their transformation and migration to the outside of SWCNTs (see ESI Fig. S1†).

Fig. 1 (Top) HR-TEM and (bottom) ADF-STEM images of nickel clusters derived from nickelocene inside SWCNTs by (a) in situ annealing at 200 °C, (b, c) pre-annealing at (b) 500 °C and (c) 700 °C, respectively. Scale bars, 5 nm. (d) The temporal evolution of the RBM peaks of the nickelocene-filled SWCNTs upon in situ annealing at 540 °C for 2–4094 min, measured at a laser wavelength of 568 nm.

3.2 In situ Raman spectroscopy

Fig. 1d shows the temporal evolution of the Raman spectra of NiCp₂-filled SWCNTs in the RBM region upon vacuum annealing at 540 °C for 2–4094 minutes. The RBM frequency is scaled inversely by the tube diameter. The outer-tube RBM lines are observed at frequencies lower than 185 cm⁻¹, which are upshifted by up to 10 cm⁻¹ upon filling with nickelocene, commonly observed for molecule-filled SWCNTs.⁵¹ Upon annealing, the outer-tube RBM peaks are shifted back to the original frequencies of the pristine SWCNTs, and new RBM peaks corresponding to inner-shell SWCNTs appear at frequencies in the range of 205–295 cm⁻¹. Note that the smaller diameter tubes grow faster than the larger ones, indicating diameter-dependent growth dynamics (see ESI Fig. S2 and S3†).

In Fig. 2, the individual inner-tube RBM components are singled out by fitting the spectra acquired with 568 and 633 nm lasers with Voigtian functions, labeled with the chiral vectors and diameters assigned according to the Kataura plot that correlates the RBM frequency and optical transition energy of SWCNTs.^55–57 We identify nine different SWCNTs, (8,8), (12,3), (13,1), (9,6), (10,4), (11,2), (11,1), (9,3) and (9,2), with diameters in the range of 0.8–1.1 nm. See Table S1† summarizing the chiral vector assignments.

Fig. 2 The RBM peaks of SWCNTs formed inside template NiCp₂-filled SWCNTs by annealing at 540 °C for 514 minutes, acquired at laser wavelengths of 568 nm (a) and 633 nm (b), fitted with Voigtian functions labeled with the assigned chiral vectors.

In Fig. 3, the normalized area intensities of the nine RBM peaks are plotted against annealing time at 540 °C. We see that the (12,3) and (13,1) tubes grow fast within 514 minutes and a slow growth continues at further annealing steps. The growth of the (8,8), (9,6), (10,4) and (11,2) tubes are completed after 514 minutes, the (11,1) tube – after 254 minutes, the (9,3) and (9,2) tubes – after 126 minutes. These observations demonstrate that the inner-shell carbon nanotubes grow initially fast and then a slow growth takes place over a longer period of time. Also, smaller diameter tubes grow faster. The same trends are observed in growth curves obtained at other temperatures, see ESI Fig. S4.†

Fig. 3 The normalised RBM area intensity versus annealing time for the (8,8), (12,3), (13,1), (9,6), (10,4), (11,2), (11,1), (9,3) and (9,2) inner tubes formed in NiCp₂-filled SWCNTs at 540 °C. The solid curves are fits using eqn (4).

3.3 Modeling and evaluation of growth rates

Apparently, the observed growth curves do not follow a self-exhausting growth model that was frequently adapted for the catalyst lifetime-limited SWCNT growth by the conventional CVD method,^{18,19,21,23,24,47,50} with the temporal evolution expressed by C(t) = γ₀τ(1 − e^−t/τ), where γ₀ is the initial growth rate and τ is the lifetime.

Here, we model the SWCNT growth with two different growth rates α and β. α determines the fast growth at the beginning and β determines the slow growth over longer annealing hours. The set of first order linear differential equations is given in eqn (1)–(3). The signs are chosen in a way that meaningful α and β are always positive. The initial amount of carbon that can be transformed into SWCNTs is given by A₀ (at t = 0). A part A_α0 = χA₀ of this carbon is processed at the growth rate α and the remaining part A_β0 = (1 − χ)A₀ of the carbon is processed at the growth rate β (0 ≤ χ ≤ 1). The amount of carbon in the form of SWCNTs is given by C(t):

The solution of the system may be readily found by an exponential ansatz:

C(t) = A₀(1 − χe^−αt − (1 − χ)e^−βt). (4)

This model fits well the experimental growth curves, as shown in Fig. 3, allowing growth rates α and β to be evaluated. Fig. 4a and b summarize α and β for the (8,8), (12,3), (13,1), (9,6), (10,4), (11,2), (11,1), (9,3) and (9,2) tubes upon annealing at temperatures ranging from 480 up to 600 °C. See Table S2 and Fig. S5 in the ESI.† For all identified nanotubes, α is on average 16 times larger than β. Both diagrams show clearly two general trends: both growth rates are greater (i) for small diameter tubes and (ii) at higher temperatures.

Fig. 4 Column bar diagrams summarizing evaluated growth rates α (a) and β (b) of the (8,8), (12,3), (13,1), (9,6), (10,4), (11,2), (11,1), (9,3) and (9,2) inner tubes at different annealing temperatures. At every annealing temperature, the column bars of the smallest diameter tubes are placed at the leftmost side and the ones of the largest diameter tubes – at the rightmost side. The column bars are color-coded: different shades of blue reflect the chiral angles of inner tubes. The lightest shade of blue belongs to the smallest chiral angle and the darkest – to the biggest chiral angle of inner tubes. (c) Logarithmic growth rates α and β versus inverse annealing temperature for the (13,1) inner tube, fit to eqn (6) with activation energies of E_α = 2.36 ± 0.16 eV and E_β = 1.53 ± 0.21 eV, respectively.

Studies on the CVD growth of nanotubes reported that the diameter was defined by the size of catalyst particles.^{32,38,58–62} Reducing the size of catalyst particles or grains led to higher growth rates of carbon filaments and nanotubes, regardless of the type of catalyst,^{58,59,63–66} and smaller diameter nanotubes exhibited higher growth rates.^58,59 This was explained by the increased catalytic activity of smaller diameter particles due to their larger specific surface area, larger curvature of surface and, consequently, greater number of active sites,^67,68 increased carbon solubility,^64,69 shortened diffusion length of carbon atoms to arrive at the growth site,⁵⁹ and modified electronic structure.⁶⁷ In the present case, the catalyst particle is confined inside the template SWCNTs. The diameter of the growing inner tube is optimally defined by the diameter of the outer nanotube and the van der Waals distance between the outer and inner graphene layers of double-wall carbon nanotubes (DWCNTs) (0.67 nm).⁵¹ In analogy to the CVD process, the increased growth rates for smaller diameter tubes can be attributed to the increased catalytic activity of smaller metallic particles.⁵²

It should be noted that although the correlation between the growth rate and the chiral angle was reported in the CVD synthesis of SWCNTs,^23,24 the present results show no clear dependence on the chiral angle, see ESI Fig. S5.† This indicates that diameter control by encapsulation has no selectivity towards smaller or bigger chiral angles.

3.4 Activation energy

Fig. 4a and b show an exponential increase of growth rates α and β for all assigned nanotubes with increasing annealing temperature. The same trend was observed for the CVD growth of carbon filaments^29–31,63 and nanotubes,^{32,38,41,46,47,50,70} and it indicates that the catalytic nanotube growth is a thermally-activated process in which the growth rate versus temperature obeys the Arrhenius equation:⁷¹where γ is the growth rate of nanotubes, E_a is the activation energy of the nanotube growth, k_B is the Boltzmann constant, T is the absolute temperature and B is a proportionality coefficient.

Eqn (5) is also written as:

highlighting the linear dependence of the logarithmic growth rate ln(γ) on the inverse temperature 1/T.

In Fig. 4c, logarithmic growth rates α and β for the (13,1) tube are plotted against inverse annealing temperature. The plots for other inner tubes are presented in Fig. S6 in the ESI.† Every point in these plots corresponds to a data bar as shown in Fig. 4a and b. The data fit well with linear functions (Fig. 4c and S6†) so that E_α and E_β for all nanotubes can be determined, as summarized in Table S3 in the ESI.†

In Fig. 5, E_α and E_β are plotted against the tube diameter (a) and chiral angle (b). Panel (a) demonstrates that E_α (2.02–2.57 eV) is higher than E_β (1.23–1.84 eV), and E_α increases monotonically with increasing the diameter while E_β is constant within the limits of experimental accuracy. Panel (b) certifies that both activation energies are independent of the chiral angle.

Fig. 5 Activation energies E_α and E_β for the growth of the inner tubes with chiral vectors of (8,8), (12,3), (13,1), (9,6), (10,4), (11,2), (11,1), (9,3) and (9,2) plotted versus the tube diameter (a) and chiral angle (b). The dashed line is the linear regression line.

4 Discussion

After an initial burst, the growth of inner tubes continues for hours. Considering the stoichiometry of 1 : 10 (Ni : C) in NiCp₂, there should be a major excess of carbon as nanotubes start to grow. In contrast, in the CVD synthesis, SWCNTs usually stop growing after several tens of minutes due to the deactivation of the catalyst (the encapsulation of the catalyst particle by a passivating carbon layer) and diffusion limitation of the gaseous carbon precursor. The key difference of the inner tube growth to the CVD growth is the well-shielded inner space of the host SWCNTs where the formation of inner tubes takes place in an undisturbed manner and the growth continues until no more carbon is available.

The first part of excess carbon is processed rapidly at the beginning and forms the inner tube at rate α. The other part of carbon is transformed slower into the inner tube at rate β. Two different activation energies E_α and E_β should be attributed to different rate-limiting mechanisms.

4.1 Rate-limiting process

The activation energy reported previously for the growth of SWCNTs is typically in the range of 1–3 eV for both the initial growth and inverse lifetime (catalyst decay rate), which in some cases depends strongly on the temperature range.

Generally, energies above 2 eV could be attributed to the reaction at the gaseous carbon source–catalyst interface,^21,43,46,47 while those below 1 eV to the surface diffusion of carbon on the catalyst.^32,37–41

The E_β values of 1.23–1.84 eV fit well into the energy range of 1.43–1.74 eV reported for solid-state carbon diffusion through face-centered cubic (fcc) nickel,^67,72–78 and for carbon solubility,⁷⁹ yet the uniformity of E_β for different diameters indicates another limiting mechanism for the slow growth such as feedstock diffusion resistance or carbon transport through the interior of nanotubes to reach metals as well as mobile metal clusters that could merge with one another to extend in length as they heal already made inner tubes.

In contrast, the monotonic increase of E_α with the SWCNT diameter suggests the catalytic activity of the clusters as its origin. The decomposition of precursors and surface reactions can be eliminated. It also suggests that the catalyst sustains its solid state to some extent as carbon diffusion through liquid metal is less likely to exhibit the size effect. However, the values of 2.02–2.57 eV are much higher than 1.43–1.74 eV for solid-state carbon diffusion through face-centered cubic (fcc) nickel.

Generally, the activation barrier of carbon diffusion through metal carbides is higher than through the pure metal.^67,80–82 Nickel carbides are known to be metastable⁸³ and decompose at temperatures higher than 400 °C.^84–86 A recent X-ray photoelectron spectroscopy (XPS) and TEM study on nickelocene-filled SWCNTs elucidated that nickel carbide (Ni₃C) clusters are formed after annealing at 250–400 °C and only metallic nickel after annealing at temperatures above 450 °C.⁸⁷ Considering that the concentration of carbon is very high as most of the inner tubes grow, so that Ni₃C is most likely the major component of the catalyst clusters in action. Thus, the high values of E_α can be attributed to the activation energy of solid-state carbon diffusion through Ni₃C.

Note that the diffusion of carbon through carbides is no longer interstitial, but it is mediated by thermal vacancies in the metal and carbon sub-lattices.^67,88 This would further increase the energy barrier.

4.2 Size effect

The thermodynamic properties of clusters are altered as their sizes reduce to the nanoscale. For instance, the Ni–C phase diagram is largely size dependent. The eutectic point of nickel drops with the cluster size.⁸⁹ The melting point of metallic nanoparticles can be significantly reduced by the size effect^{52,69,90–92} and carbon incorporation.^67,91,93 The depletion can be inversely proportional to the particle size. All these could result in lowered activation barrier for the growth of smaller-diameter SWCNTs as we observe here. The important finding is that in the interior of SWCNTs, the catalyst can be thermally activated at unconventionally low temperatures. We have observed that some inner tubes can be formed even at 400 °C at which template SWCNTs survive in air, see ESI Fig. S7.†

5 Conclusions

We have shown that in the interior of template nanotubes, SWCNT growth is controlled at an unprecedented level so that its activation energies could be determined for nine different chiral vectors. Provided that sophisticated single-chirality separation,⁸ inner-tube extraction⁹⁴ and cloning²⁴ techniques are available, the monotonic diameter dependence of the activation energy found in this study would pave the way towards synthesis of single-chiral vector SWCNTs on a bulk scale. Also, DWCNTs with defined inner-tube chiral vectors serve as templates for the synthesis of one-dimensional atom chains.^95–97 In addition, one immediate application of the encapsulated nanotube growth would be the formation of SWCNTs in air. Our preliminary result demonstrates that this is indeed possible for the (7,6) and (10,2) tubes, see ESI Fig. S7.† Combined with binary metal alloys with even lower eutectic points to be sought, our method would allow template nanotube networks on electronics to be tuned with regard to their optical and electrical transport properties without pricey vacuum chambers and other means like focused ion/electron beams. Patterned formation of inner tubes could also be possible by means of focused laser annealing in air.

Acknowledgements

The work was supported by the Austrian Science Fund (FWF), project P27769-N20. M. V. K. acknowledges the Austrian Academy of Sciences for DOC-fFORTE fellowship. Y. S. and K. S. acknowledge financial support from JSPS KAKENHI grant numbers JP16K05948 and JP16H06333, respectively.

References

1. R. Saito, G. Dresselhaus and M. S. Dresselhaus, Physical properties of carbon nanotubes, Imperial College Press, London, 1998.
2. P. M. Ajayan and O. Z. Zhou, Applications of carbon nanotubes, in Carbon nanotubes: Topics in Applied Physics, ed. M. S. Dresselhaus, G. Dresselhaus and A. Avouris, Springer, Berlin, 2001, vol. 80, pp. 391–425.
3. M. Endo, M. S. Strano and P. M. Ajayan, Potential applications of carbon nanotubes, in Carbon nanotubes: Topics in Applied Physics, ed. A. Jorio, G. Dresselhaus and M. S. Dresselhaus, Springer, Berlin, 2008, vol. 111, pp. 13–61.
4. R. Krupke, F. Hennrich, H. von Lohneysen and M. M. Kappes, Science, 2003, 301, 344–347.
5. M. Zheng, A. Jagota, M. S. Strano, A. P. Santos, P. Barone, S. G. Chou, B. A. Diner, M. S. Dresselhaus, R. S. Mclean, G. B. Onoa, G. G. Samsonidze, E. D. Semke, M. Usrey and D. J. Walls, Science, 2003, 302, 1545–1548.
6. M. S. Strano, C. B. Huffman, V. C. Moore, M. J. O'Connell, E. H. Haroz, J. Hubbard, M. Miller, K. Rialon, C. Kittrell, S. Ramesh, R. H. Hauge and R. E. Smalley, J. Phys. Chem. B, 2003, 107, 6979–6985.
7. K. Arnold, F. Hennrich, R. Krupke, S. Lebedkin and M. M. Kappes, Phys. Status Solidi B, 2006, 243, 3073–3076.
8. H. P. Liu, D. Nishide, T. Tanaka and H. Kataura, Nat. Commun., 2011, 2, 309.
9. W. H. Chiang and R. M. Sankaran, Nat. Mater., 2009, 8, 882–886.
10. A. R. Harutyunyan, G. G. Chen, T. M. Paronyan, E. M. Pigos, O. A. Kuznetsov, K. Hewaparakrama, S. M. Kim, D. Zakharov, E. A. Stach and G. U. Sumanasekera, Science, 2009, 326, 116–120.
11. H. Omachi, T. Nakayama, E. Takahashi, Y. Segawa and K. Itami, Nat. Chem., 2013, 5, 572–576.
12. M. S. He, H. Jiang, B. L. Liu, P. V. Fedotov, A. I. Chernov, E. D. Obraztsova, F. Cavalca, J. B. Wagner, T. W. Hansen, I. V. Anoshkin, E. A. Obraztsova, A. V. Belkin, E. Sairanen, A. G. Nasibulin, J. Lehtonen and E. I. Kauppinen, Sci. Rep., 2013, 3, 1460.
13. F. Yang, X. Wang, D. Q. Zhang, J. Yang, D. Luo, Z. W. Xu, J. K. Wei, J. Q. Wang, Z. Xu, F. Peng, X. M. Li, R. M. Li, Y. L. Li, M. H. Li, X. D. Bai, F. Ding and Y. Li, Nature, 2014, 510, 522–524.
14. S. M. Bachilo, L. Balzano, J. E. Herrera, F. Pompeo, D. E. Resasco and R. B. Weisman, J. Am. Chem. Soc., 2003, 125, 11186–11187.
15. Y. H. Miyauchi, S. H. Chiashi, Y. Murakami, Y. Hayashida and S. Maruyama, Chem. Phys. Lett., 2004, 387, 198–203.
16. Y. Y. Liu, A. Dobrinsky and B. I. Yakobson, Phys. Rev. Lett., 2010, 105, 235502.
17. A. A. Puretzky, D. B. Geohegan, S. Jesse, I. N. Ivanov and G. Eres, Appl. Phys. A, 2005, 81, 223–240.
18. E. Einarsson, Y. Murakami, M. Kadowaki and S. Maruyama, Carbon, 2008, 46, 923–930.
19. P. Vinten, J. Lefebvre and P. Finnie, Chem. Phys. Lett., 2009, 469, 293–297.
20. S. Chiashi, Y. Murakami, Y. Miyauchi and S. Maruyama, Chem. Phys. Lett., 2004, 386, 89–94.
21. M. Picher, E. Anglaret, R. Arenal and V. Jourdain, Nano Lett., 2009, 9, 542–547.
22. A. Li-Pook-Than, J. Lefebvre and P. Finnie, J. Phys. Chem. C, 2010, 114, 11018–11025.
23. R. Rao, D. Liptak, T. Cherukuri, B. I. Yakobson and B. Maruyama, Nat. Mater., 2012, 11, 213–216.
24. B. L. Liu, J. Liu, X. M. Tu, J. L. Zhang, M. Zheng and C. W. Zhou, Nano Lett., 2013, 13, 4416–4421.
25. F. Ding, A. R. Harutyunyan and B. I. Yakobson, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 2506–2509.
26. H. Dumlich and S. Reich, Phys. Rev. B: Condens. Matter, 2010, 82, 085421.
27. C. T. Wirth, C. Zhang, G. F. Zhong, S. Hofmann and J. Robertson, ACS Nano, 2009, 3, 3560–3566.
28. R. T. K. Baker, M. A. Barber, R. J. Waite, P. S. Harris and F. S. Feates, J. Catal., 1972, 26, 51.
29. R. T. K. Baker, P. S. Harris, R. B. Thomas and R. J. Waite, J. Catal., 1973, 30, 86–95.
30. R. T. K. Baker, J. J. Chludzinski, N. S. Dudash and A. J. Simoens, Carbon, 1983, 21, 463–468.
31. R. T. K. Baker, J. J. Chludzinski and C. R. F. Lund, Carbon, 1987, 25, 295–303.
32. C. Ducati, I. Alexandrou, M. Chhowalla, G. A. J. Amaratunga and J. Robertson, J. Appl. Phys., 2002, 92, 3299–3303.
33. Y. T. Lee, J. Park, Y. S. Choi, H. Ryu and H. J. Lee, J. Phys. Chem. B, 2002, 106, 7614–7618.
34. M. Perez-Cabero, E. Romeo, C. Royo, A. Monzon, A. Guerrero-Ruiz and I. Rodriguez-Ramos, J. Catal., 2004, 224, 197–205.
35. K. E. Kim, K. J. Kim, W. S. Jung, S. Y. Bae, J. Park, J. Choi and J. Choo, Chem. Phys. Lett., 2005, 401, 459–464.
36. S. K. Pal, S. Talapatra, S. Kar, L. Ci, R. Vajtai, T. Borca-Tasciuc, L. S. Schadler and P. M. Ajayan, Nanotechnology, 2008, 19, 045610.
37. S. Hofmann, G. Csanyi, A. C. Ferrari, M. C. Payne and J. Robertson, Phys. Rev. Lett., 2005, 95, 036101.
38. M. Chhowalla, K. B. K. Teo, C. Ducati, N. L. Rupesinghe, G. A. J. Amaratunga, A. C. Ferrari, D. Roy, J. Robertson and W. I. Milne, J. Appl. Phys., 2001, 90, 5308–5317.
39. S. Hofmann, C. Ducati, J. Robertson and B. Kleinsorge, Appl. Phys. Lett., 2003, 83, 135–137.
40. W. H. Chiang and R. M. Sankaran, Appl. Phys. Lett., 2007, 91, 121503.
41. Y. van de Burgt, Y. Bellouard and R. Mandamparambil, Phys. Chem. Chem. Phys., 2014, 16, 5162–5173.
42. K. Liu, K. L. Jiang, C. Feng, Z. Chen and S. S. Fan, Carbon, 2005, 43, 2850–2856.
43. L. B. Zhu, J. W. Xu, F. Xiao, H. J. Jiang, D. W. Hess and C. P. Wong, Carbon, 2007, 45, 344–348.
44. E. R. Meshot, D. L. Plata, S. Tawfick, Y. Y. Zhang, E. A. Verploegen and A. J. Hart, ACS Nano, 2009, 3, 2477–2486.
45. G. D. Nessim, M. Seita, K. P. O'Brien, A. J. Hart, R. K. Bonaparte, R. R. Mitchell and C. V. Thompson, Nano Lett., 2009, 9, 3398–3405.
46. J. B. In, C. P. Grigoropoulos, A. A. Chernov and A. Noy, ACS Nano, 2011, 5, 9602–9610.
47. G. H. Chen, R. C. Davis, H. Kimura, S. Sakurai, M. Yumura, D. N. Futaba and K. Hata, Nanoscale, 2015, 7, 8873–8878.
48. K. Bartsch, K. Biedermann, T. Gemming and A. Leonhardt, J. Appl. Phys., 2005, 97, 114301.
49. A. Gorbunov, O. Jost, W. Pompe and A. Graff, Carbon, 2002, 40, 113–118.
50. S. Yasuda, D. N. Futaba, T. Yamada, M. Yumura and K. Hata, Nano Lett., 2011, 11, 3617–3623.
51. H. Shiozawa, T. Pichler, A. Gruneis, R. Pfeiffer, H. Kuzmany, Z. Liu, K. Suenaga and H. Kataura, Adv. Mater., 2008, 20, 1443–1449.
52. H. Shiozawa, C. Kramberger, R. Pfeiffer, H. Kuzmany, T. Pichler, Z. Liu, K. Suenaga, H. Kataura and S. R. P. Silva, Adv. Mater., 2010, 22, 3685–3689.
53. T. Saito, S. Ohshima, T. Okazaki, S. Ohmori, M. Yumura and S. Iijima, J. Nanosci. Nanotechnol., 2008, 8, 6153–6157.
54. G. Fabian, C. Kramberger, A. Friedrich, F. Simon and T. Pichler, Rev. Sci. Instrum., 2011, 82, 023905.
55. H. Kataura, Y. Kumazawa, Y. Maniwa, I. Umezu, S. Suzuki, Y. Ohtsuka and Y. Achiba, Synth. Met., 1999, 103, 2555–2558.
56. W. Plank, R. Pfeiffer, C. Schaman, H. Kuzmany, M. Calvaresi, F. Zerbetto and J. Meyer, ACS Nano, 2010, 4, 4515–4522.
57. R. Pfeiffer, F. Simon, H. Kuzmany and V. N. Popov, Phys. Rev. B: Condens. Matter, 2005, 72, 161404.
58. C. Bower, O. Zhou, W. Zhu, D. J. Werder and S. H. Jin, Appl. Phys. Lett., 2000, 77, 2767–2769.
59. Y. C. Choi, Y. M. Shin, Y. H. Lee, B. S. Lee, G. S. Park, W. B. Choi, N. S. Lee and J. M. Kim, Appl. Phys. Lett., 2000, 76, 2367–2369.
60. Z. P. Huang, D. Z. Wang, J. G. Wen, M. Sennett, H. Gibson and Z. F. Ren, Appl. Phys. A, 2002, 74, 387–391.
61. M. Chen, C. M. Chen, S. C. Shi and C. F. Chen, Jpn. J. Appl. Phys., 2003, 42, 614–619.
62. M. Lin, J. P. Y. Tan, C. Boothroyd, K. P. Loh, E. S. Tok and Y. L. Foo, Nano Lett., 2006, 6, 449–452.
63. R. T. K. Baker, Carbon, 1989, 27, 315–323.
64. W. H. Chiang and R. M. Sankaran, Diamond Relat. Mater., 2009, 18, 946–952.
65. S. P. Patole, H. Kim, J. Choi, Y. Kim, S. Baik and J. B. Yoo, Appl. Phys. Lett., 2010, 96, 094101.
66. F. Cervantes-Sodi, T. P. McNicholas, J. G. Simmons, J. Liu, G. Csanyi, A. C. Ferrari and S. Curtarolo, ACS Nano, 2010, 4, 6950–6956.
67. V. Jourdain and C. Bichara, Carbon, 2013, 58, 2–39.
68. G. A. Somorjai, Introduction to surface chemistry and catalysis, Wiley, New York, 1994.
69. M. Diarra, A. Zappelli, H. Amara, F. Ducastelle and C. Bichara, Phys. Rev. Lett., 2012, 109, 185501.
70. Y. T. Lee, N. S. Kim, J. Park, J. B. Han, Y. S. Choi, H. Ryu and H. J. Lee, Chem. Phys. Lett., 2003, 372, 853–859.
71. I. Chorkendorff and J. W. Niemantsverdriet, Concepts of Modern Catalysis and Kinetics, Wiley-VCH, 2nd edn, 2007.
72. A. D. Le Claire, Diffusion in solid metals and alloys, in Landolt-Börnstein: Numerical data and functional rerelationships in science and technology, Springer-Verlag, Berlin, 1990, vol. 26, p. 471.
73. R. Sharma, S. W. Chee, A. Herzing, R. Miranda and P. Rez, Nano Lett., 2011, 11, 2464–2471.
74. J. Xu and M. Saeys, J. Phys. Chem. C, 2008, 112, 9679–9685.
75. J. J. Lander, H. E. Kern and A. L. Beach, J. Appl. Phys., 1952, 23, 1305–1309.
76. S. Diamond and C. Wert, Trans. Metall. Soc. AIME, 1967, 239, 705.
77. A. Rinaldi, J. P. Tessonnier, M. E. Schuster, R. Blume, F. Girgsdies, Q. Zhang, T. Jacob, S. B. A. Hamid, D. S. Su and R. Schlogl, Angew. Chem., Int. Ed., 2011, 50, 3313–3317.
78. A. Wiltner, C. Linsmeier and T. Jacob, J. Chem. Phys., 2008, 129, 084704.
79. L. Baraton, Z. B. He, C. S. Lee, C. S. Cojocaru, M. Chatelet, J. L. Maurice, Y. H. Lee and D. Pribat, EPL, 2011, 96, 46003.
80. B. Ozturk, V. L. Fearing, J. A. Ruth and G. Simkovich, Solid State Ionics, 1984, 12, 145–151.
81. A. Schneider and G. Inden, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2007, 31, 141–147.
82. F. J. J. Vanloo and G. F. Bastin, Metall. Trans. A, 1989, 20, 403–411.
83. N. Greenwood and A. Earnshaw, Chemistry of the elements, Elsevier, 2nd edn, 1997.
84. Y. G. Leng, H. Y. Shao, Y. T. Wang, M. Suzuki and X. G. Li, J. Nanosci. Nanotechnol., 2006, 6, 221–226.
85. S. Sinharoy and L. L. Levenson, Thin Solid Films, 1978, 53, 31–36.
86. G. J. Kovacs, I. Bertoti and G. Radnoczi, Thin Solid Films, 2008, 516, 7942–7946.
87. M. V. Kharlamova, M. Sauer, T. Saito, Y. Sato, K. Suenaga, T. Pichler and H. Shiozawa, Nanoscale, 2015, 7, 1383–1391.
88. R. Andrievsky and K. Gurov, Fiz. Met. Metalloved., 1968, 26, 818–822.
89. Y. Magnin, A. Zappelli, H. Amara, F. Ducastelle and C. Bichara, Phys. Rev. Lett., 2015, 115, 205502.
90. A. Moisala, A. G. Nasibulin and E. I. Kauppinen, J. Phys.: Condens. Matter, 2003, 15, S3011–S3035.
91. F. Ding, K. Bolton and A. Rosen, J. Vac. Sci. Technol., A, 2004, 22, 1471–1476.
92. Y. Qi, T. Cagin, W. L. Johnson and W. A. Goddard, J. Chem. Phys., 2001, 115, 385–394.
93. C. T. Wirth, S. Hofmann and J. Robertson, Diamond Relat. Mater., 2009, 18, 940–945.
94. Y. Miyata, M. Suzuki, M. Fujihara, Y. Asada, R. Kitaura and H. Shinohara, ACS Nano, 2010, 4, 5807–5812.
95. T. Fujimori, A. Morelos-Gomez, Z. Zhu, H. Muramatsu, R. Futamura, K. Urita, M. Terrones, T. Hayashi, M. Endo, S. Y. Hong, Y. C. Choi, D. Tomanek and K. Kaneko, Nat. Commun., 2013, 4, 2162.
96. R. Senga, H. P. Komsa, Z. Liu, K. Hirose-Takai, A. V. Krasheninnikov and K. Suenaga, Nat. Mater., 2014, 13, 1050–1054.
97. L. Shi, P. Rohringer, K. Suenaga, Y. Niimi, J. Kotakoski, J. C. Meyer, H. Peterlik, M. Wanko, S. Cahangirov, A. Rubio, Z. J. Lapin, L. Novotny, P. Ayala and T. Pichler, Nat. Mater., 2016, 15, 634–639.

---

Footnote

† Electronic supplementary information (ESI) available: Raw Raman spectra and additional TEM images, together with the further steps of data analysis: Raman peak intensities as a function of time and temperature, growth rates as a function of diameter and chiral angle, and Arrhenius plots for different chiralities of nanotubes. See DOI: 10.1039/C7NR01846K

---