Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ultrafast pressure sensing with transient tunnelling currents†
Ashok S.
Chauhan
,
Isaac
Taylor-Harrod
,
Samuel D.
Littlejohn
and
Alain
Nogaret
 *
*
Department of Physics, University of Bath, Bath, BA2 7AY, UK. E-mail: A.R.Nogaret@bath.ac.uk
First published on 15th March 2017
Abstract
We report and systematically study large amplitude piezoresistance spikes in thin composite films under stress. These spikes are characterized by a unique double exponential decay which we demonstrate to be the signature of transient tunnelling currents. We establish an expression that predicts the dynamic conductivity of the composite with only three material parameters and use it to infer the magnitude of applied stress from resistance spikes, thus achieving quasi-instantaneous readout unhindered by viscoelastic relaxation. We demonstrate the proof of principle of ultrafast mechanoreceptors based on this effect by making a sensor array which images pressure at close to cinematic speeds with a sensitivity of 50 Pa.
Introduction
Mimicking the human touch with fast sensitive sensors is important for making intelligent human-machine interfaces,1 biometric identification and pattern recognition systems,2–4 biomimetic sensors,5,6 biomedical implants,7,8 and artificial skins that increase aerodynamic efficiency through active flow control.9 Mechanoreceptors embedding graphitic nanoparticles,10,11 carbon nanotubes,12 graphene platelets,13–15 in flexible polymer matrices rely on piezoresistance,12,16–21 capacitance,22,23 or piezoelectric24 transduction to sense pressure. The viscoelastic nature of strain relaxation however severely limits the response times of organic conductors as internal stresses and strains stabilize long after deformation has been applied.25,26 While nanoscale engineering helps reduce viscoelastic delays,12 the short range intermolecular forces responsible for viscous relaxation can never be completely eliminated. This unavoidably hinders efforts to reduce the response time of pressure sensing polymers.27,28Here, we demonstrate a dynamic method which makes constructive use of the instantaneous response of organic conductors to read strain and pressure on ultra-short time scales with high sensitivity. We establish the principle of this approach by interrogating an array of 64 × 64 sensors at a rate of 8 images per second with pressure resolution down to 50 Pa. The method relies on the formation of resistance spikes in organic films under stress. The spikes occur symmetrically during loading–unloading stress cycles. After each spike, the resistance recovers according to a double exponential decay which we demonstrate to be the signature of transient tunnelling currents. We perform a rigorous experimental and theoretical study of this effect in composites of highly oriented pyrolytic graphite (HOPG) nanoparticles in a polydimethylsiloxane (PDMS) matrix. By treating stress as a perturbation of sequential quantum tunnelling in the percolation network, we obtain a universal analytical formula which successfully predicts the dynamic piezoresistance with only three material parameters and which we use to rapidly and accurately infer stress from piezoresistance spikes.
Results and discussion
We performed time resolved electrical transport measurements in thin composite films. Our composites were prepared by mixing HOPG nanoparticles, of diameter dHOPG = 450 nm in PDMS with volume filling fractions ranging from p = 22% to 34.2%. The composites were moulded and cured on cellulose acetate substrates to obtain conductive films 100 μm thick. Gold ohmic contacts were evaporated on the 8.0 mm long and 1.5 mm wide active region. The composite was incrementally stressed by bending the substrate with two purpose made stepper benches (ESI, sections 1 and 2†). The 4-terminal resistance was measured at a sampling rate of 20 kHz. Following a cycle of stress loading and stress unloading (Fig. 1a), the film resistance exhibits a series of sharp spikes followed by rapid recovery. After compression, the resistance decays towards a lower baseline which characterizes the partial recovery behaviour of non-ideal viscoelastic solids. Shortening the duration of individual stress steps from τ = 30 min to τ = 5 min changes the resistance profile from V-shaped (Fig. 1a) to M-shaped (Fig. 1b). The dynamic piezoresistance we observe is always positive when loading or unloading the composite. The rise time of piezoresistance spikes is of the order of the millisecond and their amplitude is reproducible within 8% for strain steps of small magnitude (<0.5%). After each spike, the resistance recovers according to a double exponential time dependence, of the form R(t) ∝ exp[exp(−t/τc)] (Fig. 1c). The fit of the resistance decay in films with p = 28% filling fraction (resp. p = 31%) gives decay time τc = 240 ± 25 s (resp. 175 ± 25 s). The I–V curves of the bilayer are linear (Fig. S6†). Their d.c. conductivity at zero-bias was plotted as a function of HOPG filling fraction in Fig. 1d (symbols). One verifies that the conductivity increases as a power law of the HOPG filling fraction, σ = σ0(p − pc)α, which characterizes percolation transport (full line). The fit to the data gives a percolation threshold: pc = 22.5%, α = 4.7, and σ0 = 2 × 106 S m−1.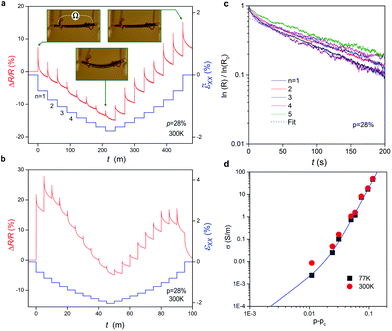 | ||
| Fig. 1 Transient piezoresistance of composite thin films. (a) V-shaped resistance of thin films of HOPG–PDMS (red line) obtained by applying stress steps at intervals of τ = 30 min. During a compression–release cycle the cumulative strain (blue line) is calculated from incremental changes in the curvature radius (Table S5†). Inset: composite-acetate bilayer. (b) M-shaped resistance observed for τ = 5 min long intervals. (c) Decay of the thin film resistance in individual steps n = 1, 2, …, 6 for HOPG filling fraction p = 28% (full lines). The decay is fitted with R(t) ∝ exp(exp(−t/τc)) using creep time τc = 240 s as the adjustment parameter (p = 28%) (dashed line). (d) Dependence of the percolation conductivity as a function of the HOPG filling fraction at 77 K (blue hollow squares) and 300 K (red dots). Data fitted using σ = 20(p − pc)2 + 2 × 106(p−pc)4.7 give a percolation threshold pc = 22.5%. | ||
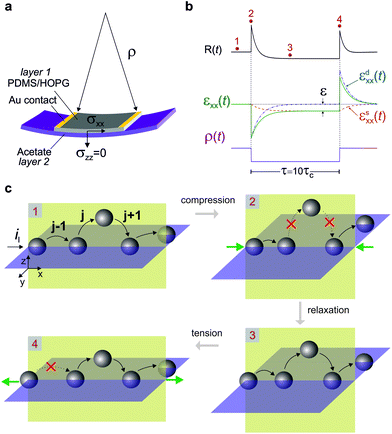
In order to describe the piezoresistance spikes, we model percolation transport by calculating the sequential tunnelling current through percolation bonds randomly oriented in the strain field generated by substrate bends. This picture follows from the observation of a double exponential decay law (Fig. 1c). The first exponential is associated with the dependence of the tunnelling current on the tunnelling barrier width in percolation links which undergo maximum elongation during elastic deformation. The second exponential arises from the exponential time dependence of the tunnelling bond length during the viscous recovery phase. Our theory goes beyond static effective medium approaches27,28 by describing for the first time the dynamic conductivity of the viscoelastic solid. We begin by establishing the exact 3D stress and strain tensors induced by bending the substrate. Changing the radius of curvature of the substrate from ρn−1 to ρn applies biaxial stress (Δnσxx,Δnσyy,0) in the plane (Fig. 2a). The magnitude of the nth stress increment is proportional to Δn(1/ρ) = ρn−1 − ρn−1−1. This stress induces a strain field (Δnεxx,Δnεyy,Δnεzz) in the composite which is transmitted to HOPG nanoparticles via the instantaneous elastic action of viscoelastic coupling. Assuming the mechanical coupling between HOPG nanoparticles is described by a spring-dashpot model,30 it follows that stress and strain will decay exponentially with respective time constants τR (stress relaxation time) and τc (creep time). Because the deformations involved are small (<0.5%), strain may be calculated analytically within the linear response.29 The strain tensor was calculated by solving the equations of linear viscoelasticity in the dynamic regime.30 After the Nth change in curvature radius, the principal components of strain are:
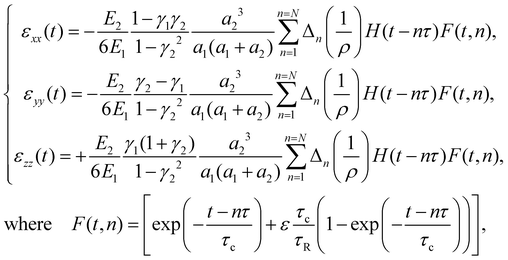 | (1) |
Next, the dynamic piezoresistance is calculated by considering stress as a perturbation of the steady state resistance of the percolation network. The amplitude of stress steps (Table S5†) is small enough that stress does not change the topology of the percolation network. The effect of stress is only to change the length of tunnelling bonds depending on their orientation relative to the strain field of eqn (1). The low bias tunnelling current density through bond j of percolation line l (Fig. 2c) is given by Simmons31 as  where V0 is the height of the PDMS potential barrier, bjl is the barrier width and
where V0 is the height of the PDMS potential barrier, bjl is the barrier width and  . We obtain the resistance of the composite film by applying Kirchhoff's voltage law to voltages Vjl dropped across the bonds of current line l, and Kirchhoff's current law to all current lines through the composite. We make the assumption that, at rest, all tunnelling bonds have equal length bjl = b0. It may be shown that the most conductive (hence likeliest) percolation path is the one for which all connections have lengths equal to the tunnelling length b0 = κ−1. When stress is applied, incomplete viscoelastic relaxation – under the effect of εμμs(t) – changes the average bond length from b0 to b. In addition, the εμμd(t) term induces a relative change in bond length Δbjl. Δbjl depends on the orientation of bonds in the strain field which is random hence can be positive or negative. We calculated the dynamic resistance perturbatively by substituting b0 with b + Δbjl in the resistance of the composite. Retaining the first order terms in Δbjl, the dynamic resistance may be written as the product of two terms: a slowly varying resistance term, R0(t), associated with viscoelastic relaxation of the tunnelling barrier average b; and a rapidly varying term accounting for direction dependent changes in tunnelling probabilities. The second term is responsible for the resistance spikes. Due to the large number of bonds (∼104) in a percolation path, one may write the sum over bonds bjl as a continuous sum over the 4π solid angle to obtain the time dependent resistance:
. We obtain the resistance of the composite film by applying Kirchhoff's voltage law to voltages Vjl dropped across the bonds of current line l, and Kirchhoff's current law to all current lines through the composite. We make the assumption that, at rest, all tunnelling bonds have equal length bjl = b0. It may be shown that the most conductive (hence likeliest) percolation path is the one for which all connections have lengths equal to the tunnelling length b0 = κ−1. When stress is applied, incomplete viscoelastic relaxation – under the effect of εμμs(t) – changes the average bond length from b0 to b. In addition, the εμμd(t) term induces a relative change in bond length Δbjl. Δbjl depends on the orientation of bonds in the strain field which is random hence can be positive or negative. We calculated the dynamic resistance perturbatively by substituting b0 with b + Δbjl in the resistance of the composite. Retaining the first order terms in Δbjl, the dynamic resistance may be written as the product of two terms: a slowly varying resistance term, R0(t), associated with viscoelastic relaxation of the tunnelling barrier average b; and a rapidly varying term accounting for direction dependent changes in tunnelling probabilities. The second term is responsible for the resistance spikes. Due to the large number of bonds (∼104) in a percolation path, one may write the sum over bonds bjl as a continuous sum over the 4π solid angle to obtain the time dependent resistance:
 | (2) |
and:
Setting the weight function as w(θ, φ) = 1 models random hopping whereas w(θ, φ) = 2sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ models directional hopping driven by bias along the x-direction. Random hopping correctly predicts the symmetric piezoresistance observed in Fig. 1 over a loading–unloading cycle (ESI, Fig. S7†). In contrast, an asymmetric piezoresistance is observed when directional hopping is considered (ESI, Fig. S7†). This argument indicates that percolation proceeds by random hopping through the isotropic network.
φ models directional hopping driven by bias along the x-direction. Random hopping correctly predicts the symmetric piezoresistance observed in Fig. 1 over a loading–unloading cycle (ESI, Fig. S7†). In contrast, an asymmetric piezoresistance is observed when directional hopping is considered (ESI, Fig. S7†). This argument indicates that percolation proceeds by random hopping through the isotropic network.
We now validate the theory by comparing its predictions to the experiment. Eqn (2) demonstrates that the double exponential decay of the piezoresistance (Fig. 1c) arises from exponential relaxation of PDMS bond lengths over time, combined with the exponential dependence of tunnelling on bond length. Eqn (2) was used in Fig. 3a (dashed lines) to fit the amplitudes of resistance spike n = 1 for different HOPG filling fractions. These fits give the values of material parameters V0 = 247 ± 21 meV, ε = 0.15 and τc = 240 s. Incorporating these parameters into eqn (2) allows us to predict the dependence of the resistance spike amplitude (dynamic piezoresistance) when a strain step is applied (Fig. 3b, red line). The theoretically predicted piezoresistance is in good agreement with experimental observation (symbols). Therefore eqn (2) may be used to accurately infer strain from the amplitude of resistance spikes in sensor devices. At low values of strain, Δ1εxx< 0.2%, a gauge factor of 8 may be inferred from the linear dependence of the piezoresistance on strain. Discrepancies between experiment and theory at higher strain may be ascribed to a limitation of our perturbative approach which gives the highest accuracy at small strains. Fig. 3c plots time resolved measurements of the rising front of the n = 1 resistance spike. The piezoresistance rise time is found to be Trise ≈ 1 ms for p = 28%. The dependence of Trise on the filling fraction is shown in Fig. 3d where Trise increases when p decreases. The other parameters, V0, τc, and ε are, within experimental error, all independent of the HOPG filling fraction, as expected from intrinsic material parameters. Eqn (2) further correctly explains the M- and V-shapes of the piezoresistance in Fig. 1a & b. The M-shape arises from incomplete stress relaxation over stress steps of shorter duration τ ≤ τc (ESI, Fig. S8†). Eqn (2) also explains the effect of material parameters V0, τc, and ε on the piezoresistance (ESI, Fig. S9–11†) which allow our findings to be generalized to other composite materials. There is no optimum filling fraction for sensing because the piezoresistance depends very little on p. This is shown experimentally in Fig. 3a and c and theoretically in Fig. S9.† The choice of HOPG filling fractions in the 25.6%–34.2% range happens to be practical. 34% is the threshold of miscibility of HOPG in PDMS. Above this level, the mixture forms lumps. Below 25.6% the resistance of the composite increases in the MΩ range (Fig. S6†) which increases the signal-to-noise ratio of the sensor.
 | ||
| Fig. 3 Experimental results. (a) Dependence of the resistance spike amplitude on the HOPG filling fraction (full lines) and theoretical fits with eqn (2) (dotted lines). (b) Dependence of the spike amplitude on applied strain: experiment (square symbols) theoretical prediction (red line). (c) Time resolved response of the spike rise time. (d) Dependence of the tunnelling barrier height V0 and the rise time of the piezoresistance Trise on the HOPG filling fraction. The former is fitted from panel (a), the latter from panel (c). | ||
To demonstrate pressure imaging with the dynamic piezoresistance, we have built the sensor of Fig. 4a which integrates spikes over a time window comparable to the composite rise time, Trise. A 64 × 64 sensor array (Fig. 4b; ESI,† section 6) was built to construct pixelated images of the pressure field with 0.1 inch spatial resolution. The 64 sensors in each row were scanned in parallel by a bank of 64 integrators which allowed the array to be interrogated at a frequency of up to 8 images per second. The array was used to visualize a pressure imprint in Fig. 4c. The pressure detection threshold was accurately estimated by immersing one sensor in water tank and applying acoustic pulses (3.5 MHz) of calibrated amplitude. The change in resistance observed near the pressure detection threshold is shown in Fig. 4d. The pressure sensitivity threshold is found to be ∼50 Pa. This limit is set by instrument noise.
Conclusions
In summary, we have systematically studied the transient piezoresistance of thin composite films and found that strain and pressure may be reliably deduced from the amplitude of resistance spikes. We have derived the theoretical relationship between piezoresistance and stress that correctly predicts the experimental piezoresistance. This allows ultrafast pressure sensors to be made and calibrated. We demonstrated the feasibility of this approach by imaging time dependent pressure fields at close to cinematic speeds with a 4096 sensor array. The proposed sensing method may be extended to other conductive elastomers by using appropriate values for V0, ε, τc.Experimental
Material preparation
The composites were prepared by mixing HOPG nanoparticles (450 nm NanoAmor) in dimethylpolysiloxane (Alchemie RTV137) in volume fractions ranging from 22% to 34.2% (Fig. S13†). Once the mixture became homogeneous, after 15 min of continuous mixing with pestle and mortar, catalyst C137 was added. The mixture was coated on cellulose acetate substrate to form thin strips (100 μm thick, 5 mm wide, 8 mm long) and left to cure for 96 hours at room temperature (Fig. S14†). Au contacts were thermally evaporated at the ends of the strip (Fig. S15†). The contact resistance (∼15 Ω) was negligible compared to the resistance of the composite which varied between 1 kΩ and 50 kΩ depending of the HOPG volume filling fraction. Labelling the composite film as layer 1 and the acetate substrate as layer 2 (Fig. S3†), the bilayer has the following parameters: thickness a1 = 100 μm (a2 = 100 μm); Young's modulus, E1 = 1.8 ± 0.05 MPa (E2 = 41 ± 11 MPa); Poisson ratio, γ1 = 0.4999 ± 0.0001 (γ2 = 0.391 ± 0.008).Experimental setup
Acknowledgements
This work has been supported by DSTL under grants CDE 32154 and CDE 28143 and EPSRC DTA studentships (ITH & SDL). We thank Prof. C. R. Bowen for the loan of piezoceramic actuators.Notes and references
- Y. Zhang, F. Zhang, C.-A. Di and D. Zhu, Mater. Horiz., 2015, 2, 140 RSC.
- R. A. Potyrailo and A. M. Leach, Appl. Phys. Lett., 2006, 88, 134110 CrossRef.
- X. Wang, Y. Gu, Z. Xion, Z. Cui and T. Zhang, Adv. Mater., 2014, 26, 1336–1342 CrossRef CAS PubMed.
- J. W. Wang, Z. S. Yao, T. Lei and A. W. Poon, Sci. Rep., 2014, 4, 7528 CrossRef CAS PubMed.
- D. Kang, P. V. Pikhitsa, Y. W. Choi, C. Lee, S. S. Shin, L. Piao, B. Park, K.-Y. Suh, T.-I. Kim and M. Choi, Nature, 2014, 516, 222 CrossRef CAS PubMed.
- S. Littlejohn, A. Nogaret, G. M. Prentice and G. D. Pantoş, Adv. Funct. Mater., 2013, 23, 5398 CrossRef CAS.
- M. S. Humayun, J. D. Weiland, G. Y. Fuji, R. Greenberg, R. Williamson, J. Little, B. Mech, V. Cimmarusti, G. Van Boemel, G. Dagnelie and E. de Juan Jr., Vision Res., 2003, 43, 2573 CrossRef PubMed.
- B. Olshansky, M. Richards, A. Sharma, N. Wold, P. Jones, D. Perschbacher and B. L. Wilkoff, Circ.: Arrhythmia Electrophysiol., 2016, 9(8) Search PubMed , e003806.
- M. Gad El Hak, Act. Flow Control, 2007, 95, 1 Search PubMed.
- T. Someya, T. Sekitani, S. Iba, Y. Kato, H. Kawaguchi and T. Sakurai, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 9966 CrossRef CAS PubMed.
- T. Someya, Y. Kato, T. Sekitani, S. Ina, Y. Noguchi, Y. Murase, H. Kawaguchi and T. Sakurai, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 12321 CrossRef CAS PubMed.
- D. J. Lipomi, M. Vosgueritchian, B. C. T. Tee, S. Hellstrom, J. A. Lee, C. H. Fox and Z. Bao, Nat. Nanotechnol., 2011, 6, 788 CrossRef CAS PubMed.
- C. You, T. Huang, H. Wang, H. Yu, Q. Zhang and Y. Yaogang, Sci. Rep., 2013, 3, 3138 Search PubMed.
- L. Chen, G. Chen and L. Lu, Adv. Funct. Mater., 2007, 17, 898 CrossRef CAS.
- T. Ramanathan, A. A. Abdala, S. Stankovich, D. A. Dikin, M. Herrera-Alonso, R. D. Piner, D. H. Adamson, H. C. Schniepp, X. Chen, R. S. Ruoff, S. T. Nguyen, I. A. Aksay, R. K. Prudhomme and L. C. Brinson, Nat. Nanotechnol., 2008, 3, 328 CrossRef PubMed.
- M. Ying, A. P. Bonifas, N. Lu, Y. Su, R. Li, H. Cheng, A. Ameen, Y. Huang and J. A. Rogers, Nanotechnology, 2012, 23, 344004 CrossRef PubMed.
- S. Littlejohn, A. Nogaret and S. Crampin, Adv. Mater., 2011, 23, 2815 CrossRef CAS PubMed.
- X. Wang, Y. Gu, Z. Xiong, Z. Cui and T. Zhang, Adv. Mater., 2013, 26, 1336 CrossRef PubMed.
- K. Takei, T. Takahashi, J. C. Ho, H. Ko, A. Gillies, P. Leu, R. S. Fearing and A. Javey, Nat. Mater., 2012, 7, 825 Search PubMed.
- S.-E. Zhu, M. Krishna Ghatkesar, C. Zhang and G. C. A. M. Janssen, Appl. Phys. Lett., 2013, 102, 161904 CrossRef.
- W. Wu, X. Wen and Z. Li Wang, Science, 2014, 340, 952 CrossRef PubMed.
- S. C. B. Mannsfeld, B. C.-K. Tee, R. M. Stoltenberg, C. V. H.-H. Chen, S. Barman, B. V. O. Muir, A. N. Sokolov, C. Reese and Z. Bao, Nat. Mater., 2010, 9, 859 CrossRef CAS PubMed.
- J. Kim, T. Nga Ng and W. Soo Kim, Appl. Phys. Lett., 2012, 101, 103308 CrossRef.
- T. Q. Trung, N. T. Tien, Y. G. Seol and N.-E. Lee, Org. Electron., 2012, 13, 533 CrossRef CAS.
- Y. Ishigure, S. Iijima, H. Ito, T. Ota, H. Unuma, M. Takahashi, Y. Hikichi and H. Suzuki, J. Mater. Sci., 1999, 34, 2979 CrossRef CAS.
- S. Stassi, V. Cauda, G. Canavese and C. F. Pirri, Sensors, 2014, 14, 5296 CrossRef CAS PubMed.
- D. A. G. Bruggeman, Ann. Phys., 1935, 24, 636 CrossRef CAS.
- R. Landauer, J. Appl. Phys., 1952, 23, 779 CrossRef CAS.
- M. Ohring, in Materials Science of Thin films, ed. M. Ohring, Academic Press, 2002, pp. 711–781 Search PubMed.
- S. C. Hunter, Mechanics of Continuous Media, John Wiley, ch. 15, 1976 Search PubMed.
- J. G. Simmons, J. Appl. Phys., 1963, 34, 238 CrossRef; J. G. Simmons, J. Appl. Phys., 1963, 34, 1793 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7nr01214d |
| This journal is © The Royal Society of Chemistry 2017 |