Colloidal joints with designed motion range and tunable joint flexibility

Abstract

The miniaturization of machines towards the micron and nanoscale requires the development of joint-like elements that enable and constrain motion. We present a facile method to create colloidal joints, that is, anisotropic colloidal particles functionalized with surface mobile DNA linkers that control the motion range of bonded particles. We demonstrate quantitatively that we can control the flexibility of these colloidal joints by tuning the DNA linker concentration in the bond area. We show that the shape of the colloidal joint controls the range of motion of bonded particles through a maximisation of the bond area. Using spheres, cubes, and dumbbells, we experimentally realize spherical joints, planar sliders, and hinges, respectively. Finally we demonstrate the potential of the colloidal joints for programmable bottom-up self-assembly by creating flexible colloidal molecules and colloidal polymers. The reconfigurability and motion constraint offered by our colloidal joints make them promising building blocks for the development of switchable materials and nanorobots.

---

Introduction

Macroscopic machines transform an input signal from an actuator into a defined motion pattern. They rely on stiff structural elements called links connected by components that allow and constrain their movement, known as joints. Depending on their design, joints enable angular (hinges), linear (sliders), or spherical motion. More complex 3D motion and thus functionality can be achieved by combining multiple types of joints. Replicating these pivotal objects on the nano and micrometer scale will not only facilitate the assembly of functional materials with novel phase behavior not observed for rigid building blocks,^1–6 but also be a crucial step for the development of nanorobotics, biosensors and drug delivery devices.^7–10

On the nanometer scale, DNA origami has recently been used to fabricate joints, hinges, crank-sliders and Bennett linkages, which facilitated angular and linear motion, coupled rotational and linear motion, and a complex 3D motion pattern, respectively.^7,11 On the colloidal scale, however, only one mechanism of a lock-and-key type has been reported so far. This lock-and-key mechanism consists of particles with dimples, the “locks”, that flexibly connect spheres, the “keys”, by exploiting a shape specific attraction imposed by depletion interactions.^4,12–14 The number of locks per particle sets the branching of the final structure and enables the assembly of colloidal polymers¹⁵ and porous liquid phases.¹⁶ However, these colloidal ball bearings rely on the presence of a depletant, constrain the angular motion range of the “key” particles bonded to the “locks” and do not provide any specificity for assembly other than the shape recognition. Ideally, colloidal joints should feature strong and specific bonding to direct their position within a desired structure, while allowing flexibility and different types of motion constraints.

Here, we present an experimental realization of colloidal joints with controllable joint flexibility by employing colloidal particles with surface mobile DNA linkers. We show that the particle shape can be used to control the range of motion, and thereby experimentally realize micron-sized spherical joints, hinges, and planar sliders. This fascinatingly simple reconfiguration mechanism relies on the accumulation of DNA linkers in the bond area, which allows us not only to control the motion range of the colloidal joints but also their flexibility. We demonstrate the potential of our colloidal joints by assembling two reconfigurable structures: flexible colloidal molecules and colloidal polymers.

Experimental section

Materials

The lipids 1,2 dioleoyl-sn-glycero-3-phosphocholine (DOPC), 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-[methoxy(polyethylene glycol)-2000](ammonium salt) (DOPE-PEG₂₀₀₀), 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-(lissamine rhodamine B sulfonyl) (ammonium salt) (DOPE-Rhodamine), 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-(carboxyfluorescein) (ammonium salt) (DOPE-Fluorescein) and Ganglioside GM1 (Ovine Brain) were obtained at >99% purity from Avanti Polar Lipids, Inc. The different DNA strands used (Eurogentec) had the following sequences: (a) the A strand: anchor-spacer-5′-TTT-ATC-GCT-ACC-CTT-CGC-ACA-GTC-AAT-CTA-GAG-AGC-CCT-GCC-TTA-CGA-GTA-GAA-GTA-GG-3′-6FAM, (b) the B strand: anchor-spacer-5′-TTT-ATC-GCT-ACC-CTT-CGC-ACA-GTC-AAT-CTA-GAG-AGC-CCT-GCC-TTA-CGA-CCT-ACT-TCT-AC-3′-Cy3 and (c) the C strand: anchor-spacer-3′-TTT-TAG-CGA-TGG-GAA-GCG-TGT-CAG-TTA-GAT-CTC-TCG-GGA-CGG-AAT-GC-5′. As anchors, we used cholesterol and stearyl groups. The A and B strands have 11 base pair long complementary sticky ends at the 3′ ends (denoted by italic characters) and are labelled with a green fluorescent dye 6-FAM, i.e. 6-carboxyfluorescein (excitation: 488 nm, emission: 521 nm) and the red Cy3 dye (excitation: 561 nm, emission: 570 nm), respectively. For the particles with surface bound DNA linkers, the two DNA strands used were (a) the D strand: 5′-CGT-AAG-GCA-GGG-CTC-TCT-AGA-TTG-ACT-GTG-CGA-AGG-GTA-GCG-ATT-TT-3′-TEG-Biotin and (b) the E strand: 5′-Cy3-TTT-ATC-GCT-ACC-CTT-CGC-ACA-GTC-AAT-CTA-GAG-AGC-CCT-GCC-TTA-CGA-CCT-ACT-TCT-AC-3′.

Particle synthesis

Silica spheres of 1.15 ± 0.05 μm diameter both undyed and dyed with fluorescein isothiocyanate were synthesized using a modified Stöber method.¹⁷ Commercial silica spheres were purchased from Microparticles GmbH (2.06 ± 0.05 μm, 3.0 ± 0.25 μm). Hollow silica cubes with rounded edges and an edge length of 1.24 ± 0.08 μm were synthesized by coating haematite cubes made by a sol–gel method¹⁸ with silica¹⁹ and dissolving the haematite cores in HCl.¹⁹ Silica dumbbells were obtained from aggregated 2 μm silica colloids. Polystyrene spheres of 1.05 ± 0.02 μm diameter containing carboxylic acid surface groups were synthesized following a surfactant free radical polymerization protocol.²⁰ The spheres were coated with neutravidin by adding 8 μL of 5 g L⁻¹ neutravidin and 10 μL of freshly dissolved 1 g L⁻¹ EDC to a suspension of 1 mg particles in 500 μL MES buffer (10 mM MES, 10 mM NaCl, 0.5 wt% Pluronic F-127, pH = 4.7).³⁶ The coupling reaction was allowed to proceed on the vortex mixer for 120 min at room temperature and washed three times.

Functionalization of colloidal particles with mobile linkers

For functionalization with surface mobile DNA linkers, we adapted a protocol from ref. 5. For the spherical colloidal joints, small unilamellar lipid vesicles (SUVs) were prepared from mixtures of DOPC and DOPE-PEG₂₀₀₀ in a 90 : 10 molar ratio in chloroform. If necessary, 0.001% mole fraction of DOPE-Rhodamine or DOPE-Fluorescein was added to increase fluorescence. After desiccation in vacuum, the lipids were re-suspended in HEPES buffer (10 mM HEPES, 47 mM NaCl, 3 mM NaN3, pH = 7.01) for 30 min to obtain a 3 g L⁻¹ solution. Then the lipid mixture was extruded 21 times through two stacked polycarbonate filters (Whatman) with 30 nm pore size to obtain SUVs. For the functionalization of the hollow silica cubes, a composition of 58.6% DOPC, 6.9% DOPE-PEG₂₀₀₀ and 34.5% GM1 (by mole-fraction) was used. We hybridized 50 μM solutions of the A or B DNA strand with the C strand in a 1 : 1.5 volume ratio by heating the solution to 90 °C and cooling down at 1 °C min⁻¹. The hybridized strands consisted of a 47 base pair long double-stranded central part, with double cholesterol/stearyl anchors connected through TEG (triethylene glycol)/DEG (diethylene glycol) spacers at one end and an 11 base-pair long single-stranded sticky part at the other end which could bind to a complementary sticky end. S′ strand is obtained by hybridizing A and C and S strand by hybridizing B and C. For particles with surface bound linkers, the E strand and the biotinylated D strand were hybridized separately under similar conditions.

The SUVs were added to an equal volume of 5 g L⁻¹ colloidal silica solution and put on a rotating tumbler for 40 min at 9 rotations per min to prevent sedimentation by gravity. After that the particles were centrifuged for 5 min at 494 rcf and washed with HEPES. Appropriate amounts of DNA were added to the SUV encapsulated particles and the resulting solution was again kept on the tumbler for 1 hour. Finally the particles were washed three times in HEPES by centrifugation to remove excess dye and lipids.

Functionalization of colloidal particles with bound linkers

For producing the colloids with surface bound linkers, 50 μl of 5 g L⁻¹ neutravidin coated polystyrene particles were incubated with appropriate amounts of 2.08 μM pre-hybridized biotinylated DNA in PBS buffer. The sample was incubated at 55 °C for 30 minutes, cooled to room temperature and washed 3 times.

Functionalization of hollow silica cubes with mobile linkers

The hollow silica cubes were at first injected onto a cleaned glass cover slip and the PVP layer on the cubes was decomposed at 500° C for 30 min. The cover-slip containing the dried cubes was introduced into a microscope sample holder and 600 μl of HEPES was added. 150 μl SUVs composed of DOPC, DOPE-PEG₂₀₀₀ and GM1 were mixed with 2 μl of Choleratoxin Alexa Fluor 488 dye and 10 μl of 4.34 μM hybridized DNA with 6-FAM and incubated for 1 day. The SUVs were then added to the cubes and the final solution in the sample holder was heated for 30 min.

Imaging and tracking

Particles were imaged in sample holders having a hydrophobized and passivated glass as the bottom surface. Hydrophobization of the glass surface was done using Surfasil (a siliconizing agent), followed with passivation by adding 5% w/v Pluronic F-127 to the holder, storing it for 30 min and rinsing with water. Imaging was done using an inverted Nikon TI-E A1 confocal microscope with 8 kHz resonant scanner and 100x objective lens (NA 1.4). Particle tracking was done using Trackpy,²¹ an open source Python based implementation of the Crocker and Grier algorithm.²²

Measurement of linker density

Linker densities on the colloidal particles were measured in a comparative way: first, we estimated the linker density of a highly fluorescent reference sample. To this end, we quantified the amount of fluorescent DNA linkers left in the supernatant after particle functionalization (collected from three washing cycles) using a Cary Eclipse fluorometer calibrated with a known concentration of DNA linkers. The DNA linker density on the reference colloids was obtained by subtracting the DNA left in the supernatant from the amount of added DNA. We then obtained the linker density of all other colloids by comparison of their fluorescence intensity collected in the photomultiplier tubes of the confocal microscope to this reference sample, using identical conditions of laser power and gain in the linear response regime.

For the polystyrene particles with surface bound linkers, we measured the amount of neutravidin on the polystyrene particles to be ∼10⁵ molecules per particle following Kada et al.²³ Assuming that all the biotinylated DNA linkers are bound to neutravidin molecules at a low DNA density (∼10³ linkers per μm²), we can approximate the number of surface bound linkers per polystyrene particle to be equal to the number of added linkers per particle. By comparing the fluorescence intensity of samples with higher linker densities with this reference sample using confocal microscopy as outlined above, we estimated the approximate linker density on all other samples.

To determine the DNA linker density in the bond area, we measured the fluorescence signal of the patch area using confocal microscopy and compared it with the fluorescence signal of the non-patch area. Assuming that the fluorescence intensity varies linearly with the number of linkers and using the patch geometry as input (see ESI†), we could estimate the number of linkers in the bond area for samples with high surface densities of DNA linkers.

Results and discussion

We realize colloidal joints by coating colloidal silica particles of various diameters (1.15 ± 0.05 μm, 2.06 ± 0.05 μm, 3.0 ± 0.25 μm) with a lipid bilayer consisting of DOPC and 10 mol% DOPE-PEG₂₀₀₀ by addition of small unilamellar lipid vesicles (SUVs). We functionalize these particles by adding DNA strands with hydrophobic double cholesterol or stearyl anchors which insert spontaneously into the lipid bilayer.⁵ Unless specifically noted otherwise, it is to be understood that all DNA linkers are connected to double cholesterol anchors. The other end of the hybridized DNA strands features an unpaired sticky end of 11 base pairs and projects outwards into solution, which enables strong and specific binding to particles functionalized with the complementary sequence. See Experimental section for details. At room temperature, the lipid bilayer is in the liquid phase since the transition temperature T_m of DOPC is −17 °C.²⁴ Therefore, both the lipids and the DNA linkers can diffuse freely in the lipid bilayer while being confined to the particle surface. The presence of DNA on the particle surface is visualized by fluorescence or confocal microscopy through fluorescent markers (6-FAM or Cy3) attached to the 3′ end after the sticky sequence. This particle functionalization scheme, shown in Fig. 1a and b, enables strong and specific binding by the DNA sticky ends while allowing motion of bonded particles with respect to each other – the crucial ingredients for colloidal joints.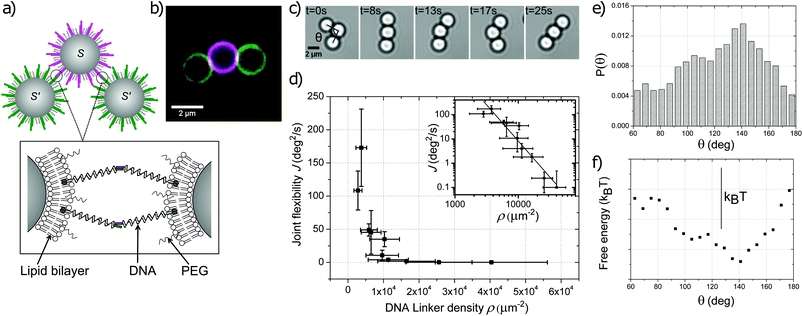

Fig. 1 A spherical colloidal joint. (a) Schematic diagram of the experimental particle configuration and surface functionalization. Green (S′) and magenta (S) coloring is used to indicate the functionalization and fluorescence of the two complementary sticky ends. (b) Confocal microscopy image of a colloidal joint with two bonded silica spheres functionalized with complementary DNA linkers. The white patches indicate the bond areas. (c) Time lapse sequence of a string of three particles showing full angular motion. The angle θ is defined as the angle enclosed by the lines connecting the center of the middle particle with the centers of the two outer particles. (d) The joint flexibility J= 〈(θ(t + Δt) − θ(t))²〉/Δt decreases with increasing DNA linker density ρ as J∝ρ^{−(2.9±0.3)}. The inset shows the data in a log–log plot together with the least squares fit. (e) The probability density of the opening angle θ averaged from 24 colloidal joints with J > 70 deg² s⁻¹ shows an average angle at 140°. (f) The free energy landscape was calculated from the probability assuming Boltzmann energy weighting (scale bar indicates an energy scale of k_BT).⁷

We first demonstrate that spherical colloids functionalized with mobile DNA linkers can act as flexible joints and measure their joint flexibility. To this end, we mix two batches of spheres functionalized with complementary DNA linkers S and S′ and quantify the relative motion of the particles in a string of three spheres using particle tracking. Indeed, we find that two particles with linkers S′ bonded to a central sphere with complementary linkers S can explore the full angular range from θ = [60°, 300°] with respect to each other, indicating that the central sphere acts as a spherical joint. See Fig. 1c. The two limits of the opening angle are set by the steric constraint originating from the non-zero radius of the spheres. We note that the motion of the here employed silica particles is essentially confined to the glass plane due to the small gravitational height of the particles.

We characterize the mobility or “joint flexibility” J of such a colloidal joint by measuring the change in the angle θ, which is enclosed by the lines connecting the center of the middle particle with the centers of the two outer particles, over time. We define the joint flexibility J as the slope of the mean square displacement (MSD) of this relative angle θ versus time, that is, J = 〈(θ(t + Δt) − θ(t))²〉/Δt. An exemplary MSD plot is given in ESI Fig. S1.† The value of the joint flexibility of the colloidal joint in Fig. 1c is 200 deg² s⁻¹, which relates to an effective diffusion constant of D_joint = 0.03 μm² s⁻¹ through: D_joint = d²J/8, where d is the particle diameter. For comparison, unbounded 2 μm silica particles in our experiments exhibit a diffusion constant of D_free = 0.044 μm² s⁻¹. This is lower than the expected diffusion constant from the Einstein–Smoluchowski equation, D_ES = 0.24 μm² s⁻¹, possibly due to friction with the Pluronic F-127 polymer coating on the glass surface required to prevent particle adhesion (see Experimental section). The bonding with the colloidal joint slows down the thermal motion of the particles even more, likely due to viscous forces that hinder the motion of the linkers through the lipid membrane. A larger number of linkers participating in the bond should then decrease the diffusion constant more strongly and may provide a handle to tune the joint flexibility.

To test this idea, we study the effect of the linker surface density ρ on the joint flexibility J by preparing colloidal samples with different linker densities. We estimate the linker density by comparison of the fluorescent signal emitted by the DNA linkers of a given sample with the signal of particles with a known quantity of fluorescent DNA linkers. See Experimental section for details. This allows us to investigate the dependence of the joint flexibility on the linker density as shown in Fig. 1d. All linker densities were measured in the absence of bonding, since bonding quickly leads to an increase of the concentration of the linkers in the bond area as indicated by the appearance of a bright fluorescent patch, see Fig. 1b and ESI Fig. S2† for the corresponding single channel images. We therefore measured the bond flexibility 1 hour after mixing of particles with complementary linker functionalization. An alternative way to restrict the linker density at the bond area is to bond particles with surface bound DNA linkers to colloidal joints.

Our first observation is that the spread in the linker density within a sample is rather broad, likely due to the random distribution of cholesterol anchors over the particles in a sample. At very low linker densities below 10³ linkers per μm², the probability for bonding between particles with complementary linkers drops significantly and we do not observe bond formation within 3 hours. At linker densities above (3.8 ± 1.5) × 10³ linkers per μm² we find that the joints gradually stiffen up with increasing linker density. A least square fit of the experimental data with a power law function yields J∝ρ^{−(2.9±0.3)}. Above a critical linker density of (1.1 ± 0.6) × 10⁴ linkers per μm² the motion of the particles essentially arrests and the joint functionality is lost. Thus, the optimal linker density in which binding occurs sufficiently rapidly while providing adequate bond flexibility lies roughly between 10³–10⁴ linkers per μm², at least for our 2 μm silica particles. We observed the threshold values to depend on the particle size and surface properties, but more systematic results are required to establish a conclusive trend. Other than the effect of the global linker density, in the bond area, the local linker concentration may be higher due to linker accumulation. For colloidal joints with a high linker concentration ((2.6 ± 0.9) × 10⁴ linkers per μm²), we could estimate the linker density in the patch area by measuring the fluorescence signal of the patch area relative to the signal of the non-patch particle surface and assuming that the bonded linkers spread out over the maximum bond area, A_p = 2πrL (see ESI for calculation and Fig. S3†). Taking the particle radius r = 1 μm and the DNA linker length L = 20 nm, we found that the linker density in the bond area had increased by (8.4 ± 3.1) × 10³ linkers per μm².

Various effects may cause this loss of mobility at high linker densities: firstly, a larger number of bonded linkers increases the viscous drag of the bond patch through the lipid bilayer and therefore hinders the diffusion of the particles relative to each other. While the maximum patch area A_p within which complementary linkers can bond is only determined by geometric factors, a higher linker density does enable the formation of more bonded DNA linkers and thus increased friction between bonded particles. We could corroborate that this effect plays an important role by employing polystyrene spheres with known densities of surface-bound DNA linkers. Using different linker densities on the polystyrene spheres and binding them to a colloidal joint, we observed a transition from high to intermediate flexibility and to immobility for (0.9 ± 0.2) × 10³ linkers per μm², (1.8 ± 5.7) × 10³ linkers per μm², and (10.6 ± 3.8) × 10³ linkers per μm², respectively. While the overall patch size remained constant, the joint flexibility decreased with increasing linker density.

Secondly, a straightening of the membrane in the patch area by stretching and flattening of the membrane similar to what has been observed in giant unilamellar vesicles²⁵ would increase the translational and combinatorial entropy^25,26 of the bonded linkers while simultaneously increasing the friction between the membrane in the centre of the bond area and the particle surface. The translational entropic cost for confining a linker to the patch area can be estimated as 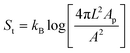, where A is the total surface area of the colloidal joint.²⁵ The combinatorial entropy gain of the bonded linkers can be calculated as S_c = k_B log[N] where N is the number of possible linkages a single DNA linker can form. Taking L = 20 nm and r = 1 μm, we find TS_t = −13k_BT and TS_c = 12.7k_BT for a typical value of N = 3.2 × 10⁵. Entropic forces may thus impact the joint flexibility as well.

Thirdly, a higher linker concentration implies high concentrations of cholesterol anchors in the bond area. Cholesterol is known to decrease the lateral diffusivity in DOPC bilayers in the liquid disordered phase²⁷ and in the extreme case may locally induce a phase transition towards a liquid ordered phase, which would drastically inhibit the bond mobility.²⁸ By conducting similar experiments with DNA linkers having double stearyl (C₁₈) anchors instead of double cholesterol anchors, we could exclude that the increased cholesterol concentration is causing the decreased mobility. While the time scale for bonding was much larger than for particles functionalized with cholesterol anchors, we again observed that high linker densities led to an increase in the joint stiffness and the formation of fractal aggregates, while low linker densities ensured mobility (see ESI Fig. S4†). The above experiments on polystyrene spheres with surface bound DNA linkers further support this: the concentration of cholesterol only increases in the patch area with increasing linker density on the polystyrene spheres and remains almost constant outside. Thus, while the concentration of cholesterol may contribute to a higher joint stiffness, the viscous drag and entropic effects seem to play a more important role.

The translational and rotational entropy of the colloidal joint with bonded spheres may also lead to a preference in the opening angle θ. We test this by plotting the probability density of the opening angle averaged from 24 colloidal joints with J > 70 deg² s⁻¹, see Fig. 1e. We find that a flexible cluster consisting of three equal sized spheres exhibits an angular preference at 140°. This average angle is significantly larger than the ones found for revolute joints made from DNA origami,⁷ which were around 60–80°. This larger average angle probably originates from the unconstrained motion of the DNA linkers on the surface of the colloidal joint, which is also in line with the non-zero probability outside the peak area. Assuming a Boltzmann energy weighting,⁷ we can deduce the free energy landscape and find a minimum of about 0.9k_BT (Fig. 1f). This minimum in the free energy is likely induced by the angle-dependant rotational and translational entropy, which favours asymmetric configurations.²⁹ Close to the lower limit of 60°, the diffusion of the colloid is likely also affected by the proximity of the second bonded particle, similar to diffusion close to a wall.

The formation of a patch of bonded linkers allows us furthermore to exploit the particle shape of the colloidal joint to constrain the range of motion. By choosing the appropriate shape (Fig. 2a–d), different types of joints, similar to the ones available in macroscopic machines, could be created (Fig. 2e–h). As shown above, a spherical colloidal joint allows the full 2π radians motion of bonded particles that move in quasi 2D due to their low gravitational height (see Fig. 2i, j and ESI movie S1†). Bonding lighter polystyrene spheres 1 μm in diameter lifts this constraint and we can observe the full 4π steradians range of motion in 3D, see Fig. 2k, l and ESI movie S2.† A spherical particle with surface mobile linkers therefore acts like a perfect ball and socket or spherical joint. Unlike a mechanical or colloidal ball and socket joint¹² where the ball fits into the groove of the socket for multidirectional movement, these colloidal analogues allow unrestricted continuous movement over the entire surface.

Fig. 2 The shape of the colloidal joint determines the range of motion. (a)–(d) Scanning electron micrograph (SEM) of a 2 μm silica sphere, 1 μm silica particle, hollow 1 μm silica cube and dumbbell composed of 2 μm silica particles respectively. (e)–(h) Schematic diagrams of a spherical colloidal joint with (e) planar and (f) with 3D mobility, (g) a planar slider joint and (h) a colloidal hinge. (i) Still images from ESI movie S1† showing a spherical colloidal joint with 2π radians motion in 2D composed of 2 μm silica particles with mobile linkers. (j) The trajectory of the two bonded particles in (i) with respect to the central colloidal joint. (k) Time lapse of a spherical joint exhibiting 4π steradian motion in 3D composed of a 2 μm silica particle with mobile linkers and 1 μm polystyrene spheres with surface bound DNA linkers (ESI movie S2†). (l) Schematic showing that the patch areas for spherical joints are uniform on the surface. (m) A planar slider type joint between a 1 μm silica sphere and a hollow 1 μm silica cube both with mobile DNA linkers (ESI movie S3†). (n) The trajectory of the silica particle (magenta) in (l) shows motion only on one face of the cube. (o) Schematic diagram to illustrate that the bond patch area for a sphere at the corner of the cube is much more compact than that for a sphere on one face of the cube. This makes crossing of the corners entropically unfavorable. (p) A colloidal hinge formed from a silica dumbbell of 2 μm spheres restricts the motion of two 1 μm polystyrene particles along the neck of the dumbbell (ESI movie S4†). (q) Schematic showing the double bond areas for a sphere constrained to move along the neck of the dumbbell while a sphere on the positive curvature side has only one bonding patch.

In contrast, colloidal joints with regions of different curvature (positive, flat or negative) can restrict the motion to areas with a sufficiently lower curvature. Once a particle has formed multiple links with a colloidal joint, the linkers will be distributed in a patch area that is set by the particle's geometry and the maximum distance over which two linkers can still be tethered (see ESI†). To diffuse into a region of higher positive curvature, this bond area needs to adapt to the new geometric situation by compacting. However, a compaction to half of the patch radius, for example, would require an entropy increase per linker of 1.4k_B for 2 μm spherical silica particles and 20 nm DNA linker length, neglecting any crowding or multi-linker effects.^25,26 Diffusion into regions of lower curvature is permitted, but once the bond area has extended, a return to regions of significantly higher curvature becomes unlikely. Thus, the patch of linkers guides and confines the bonded particle to regions of lowest curvature on the colloidal joint and allows us to constrain the range of motion.

We demonstrate this effect by utilizing cubic silica colloids with round edges fixed to a glass cover-slip and functionalized with strand S′, and dispersed silica spheres with strand S. After binding to the cubic colloid, the spherical particle freely diffuses on one side of the cube as revealed by particle tracking, but it does not move to another side, see Fig. 2m and ESI movie S3.† While the flat side of the cube allows motion without any restrictions, diffusion over the more strongly curved edges or corners is prohibited due to the significantly smaller patch size in these regions, see Fig. 2n and o. The cubic particles therefore act as planar sliders. The motion of bonded spheres with a low gravitational height may further be restricted to essentially one dimension, thereby rendering the cube a true colloidal slider with one degree of translational motion. From the trajectory of the bonded silica particle (Fig. 2n), we extracted a diffusion constant of 0.08 μm² s⁻¹. Again, one may define a joint flexibility by relating this value to the diffusion constant of freely diffusing particles (0.48 μm² s⁻¹ for 1 μm silica particles) as J_cube = D_meas/D_free = 1/6.

Besides confinement to entropically preferred regions, particles can also be restricted to certain areas of a colloidal joint by binding to multiple, disconnected locations. For example, colloidal dumbbells topologically constrain bonded spheres to their waist by forming two patches on either lobe of the dumbbell. A colloidal dumbbell thereby only allows angular motion around its waist, essentially acting as a colloidal hinge (Fig. 2p, q and ESI movie S4†).

Finally, we demonstrate the potential of these colloidal joints for creating reconfigurable structures by assembling two exciting objects: flexible colloidal molecules and colloidal polymers. To obtain colloidal polymers, we mix 2 μm silica particles with mobile DNA linkers and 1 μm polystyrene particles with surface-bound DNA linkers (linker density 884 ± 248 μm⁻²) in a ratio of 1 : 3. This size and number ratio produced a mixture of chains and clusters, roughly 40% chains and 60% clusters. The colloidal polymer, shown in Fig. 3a and ESI movie S5,† is a floppy chain which can fully reconfigure and even fold onto itself. The very low persistence length of our colloidal polymers which is essentially equal to the size of the constituent spheres is in contrast to previous realizations of flexible 1 D structures from gold nanorods³⁰ and dimpled spheres.¹² This opens up the possibility to use these linear chains in a hierarchical folding scheme. The eventual collapse into a dense structure due to unconnected DNA linkers on the particle surface may be prevented using hairpin loops,³¹ a more complex sequence of DNA linkers,³² or by saturation of the remaining linkers with complementary oligomers after assembly. Encoding additional information in the form of multiple types of DNA linkers into the sequence of the individual joint elements will allow subsequent assembly and the formation of complex 3D architectures analogous to protein folding.³² The yield of colloidal polymers could be increased by choosing a size ratio that geometrically restricts bonding of only two larger particles to one smaller one, or by using external fields to align the particles before linking.³³

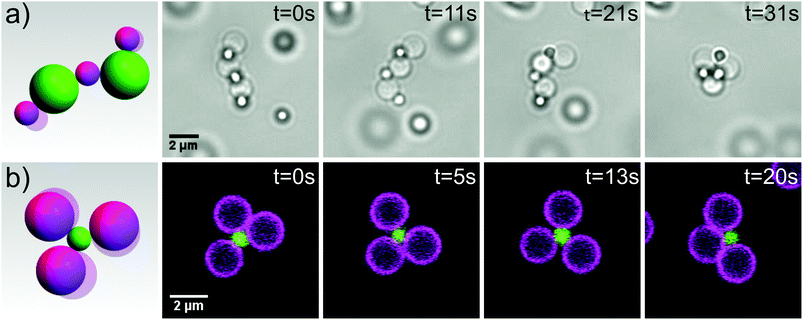Fig. 3 Self-assembly of reconfigurable structures. (a) A floppy colloidal polymer consisting of 2 μm silica spheres with mobile DNA linkers and 1 μm polystyrene with surface bound DNA linkers reconfigures and folds onto itself. Images were taken by light microscopy. See also corresponding movie S5. (b) A flexible colloidal molecule composed of 2 μm (magenta) and 1 μm (green) silica spheres with mobile DNA linkers imaged by confocal microscopy. See also corresponding movie S6.†

At more extreme number ratios, for example by mixing 1 μm and 2 μm silica with complementary mobile DNA linkers in a ratio of 1 : 8, the formation of clusters is favoured.³⁴ Due to the colloidal joints at the centers, these colloidal clusters exhibit mobility of the outer spheres, essentially forming flexible colloidal molecules, see Fig. 3b and ESI movie S6.† We obtained yields of 70% of one type of colloidal molecule by simply adjusting the size and number ratio of the constituent spheres. By tuning the size ratio, various types of colloidal molecules may be assembled³⁵ and used as flexible building blocks to study novel crystal structures¹ and phase behaviour.³ These simple yet exciting objects are just one example of the wide variety of reconfigurable structures that come within reach through the use of colloidal joints.

Conclusions

In summary, flexible colloidal joints were produced by embedding DNA linkers in lipid bilayers encapsulating micrometer-sized silica particles. The formation of a dense patch of linkers in the bond area leads to control over the flexibility of the joint and the range of motion for different particle shapes. We quantified the joint flexibility using particle tracking and observed that the joint flexbility depends on the linker density in the bond area. Controlling the maximum linker density by using colloids with surface bound linkers in combination with the colloidal joints thereby allows selection of the bond flexiblity. The finite patch size furthermore allows the restriction of motion on the particle surface by implementing joints with different local curvatures. Regions that allow expansion of the patch area act as sinks for the particles, thereby enabling the realization of spherical joints, hinges and planar sliders on the colloidal scale. We demonstrated the potential of colloidal joints by assembling flexible colloidal polymers and colloidal molecules. In combination with actuatable components, for example colloidal particles with a magnetic core or with the ability to self-propel, the controlled joint stiffness and motion range provided by the colloidal joints could be exploited for the development of reconfigurable materials and nanorobots.

Acknowledgements

This work was financially supported by the Netherlands Organisation for Scientific Research (NWO) through VENI grant 680-47-431 and as part of Frontiers of Nanoscience program (NWO/OCW). We thank Stef van der Meulen and Mirjam Leunissen for introducing us to the functionalization protocol published in ref. 5 and Melissa Rinaldin for help with the functionalization of the cubic colloids.

References

1. D. Ortiz, K. L. Kohlstedt, T. D. Nguyen and S. C. Glotzer, Soft Matter, 2014, 10, 3541–3552.
2. C. L. Phillips, E. Jankowski, B. J. Krishnatreya, K. V. Edmond, S. Sacanna, D. G. Grier, D. J. Pine and S. C. Glotzer, Soft Matter, 2014, 10, 7468–7479.
3. F. Smallenburg and F. Sciortino, Nat. Phys., 2013, 9, 554–558.
4. S. Sacanna, D. J. Pine and G.-R. Yi, Soft Matter, 2013, 9, 8096–8106.
5. S. A. J. van der Meulen and M. E. Leunissen, J. Am. Chem. Soc., 2013, 135, 15129–15134.
6. F. Smallenburg, L. Filion and F. Sciortino, Nat. Phys., 2014, 10, 653–657.
7. A. E. Marras, L. Zhou, H.-J. Su and C. E. Castro, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 713–718.
8. S. M. Douglas, I. Bachelet and G. M. Church, Science, 2012, 335, 831–834.
9. G. J. Lavella, A. D. Jadhav and M. M. Maharbiz, Nano Lett., 2012, 12, 4983–4987.
10. W. Shu, D. Liu, M. Watari, C. K. Riener, T. Strunz, M. E. Welland, S. Balasubramanian and R. A. McKendry, J. Am. Chem. Soc., 2005, 127, 17054–17060.
11. L. Zhou, A. E. Marras, H. J. Su and C. E. Castro, ACS Nano, 2014, 8, 27–34.
12. S. Sacanna, W. T. M. Irvine, P. M. Chaikin and D. J. Pine, Nature, 2010, 464, 575–578.
13. S. H. Kim, A. D. Hollingsworth, S. Sacanna, S.-J. Chang, G. Lee, D. J. Pine and G.-R. Yi, J. Am. Chem. Soc., 2012, 134, 16115–16118.
14. L. Colón-Meléndez, D. J. Beltran-Villegas, G. van Anders, J. Liu, M. Spellings, S. Sacanna, D. J. Pine, S. C. Glotzer, R. G. Larson and M. J. Solomon, J. Chem. Phys., 2015, 142, 174909.
15. D. J. Ashton, R. L. Jack and N. B. Wilding, Soft Matter, 2013, 9, 9661–9666.
16. D. J. Ashton, R. L. Jack and N. B. Wilding, Phys. Rev. Lett., 2015, 114, 237801.
17. K. Nozawa, H. Gailhanou, L. Raison, P. Panizza, H. Ushiki, E. Sellier, J. P. Delville and M. H. Delville, Langmuir, 2005, 21, 1516–1523.
18. T. Sugimoto, M. M. Khan and A. Muramatsu, Colloids Surf., A, 1993, 70, 167–169.
19. L. Rossi, S. Sacanna, W. T. M. Irvine, P. M. Chaikin, D. J. Pine and A. P. Philipse, Soft Matter, 2011, 7, 4139–4142.
20. J. Appel, S. Akerboom, R. G. Fokkink and J. Sprakel, Macromol. Rapid Commun., 2013, 34, 1284–1288.
21. D. Allan, T. Caswell, N. Keim and C. van der Wel, Trackpy v0.3.0, Zenodo, 2015, 34028. URL http://zenodo.org/record/34028.
22. J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298–310.
23. G. Kada, H. Falk and H. J. Gruber, Biochim. Biophys. Acta, Gen. Subj., 1999, 1427, 33–43.
24. D. Marsh, Handbook of lipid bilayers, CRC Press, Florida, USA, 2013.
25. L. Parolini, B. M. Mognetti, J. Kotar, E. Eiser, P. Cicuta and L. Di Michele, Nat. Commun., 2015, 6, 5948.
26. M. E. Leunissen and D. Frenkel, J. Chem. Phys., 2011, 134, 084702.
27. A. Filippov, G. Orädd and G. Lindblom, Biophys. J., 2003, 84, 3079–3086.
28. L.-L. Pontani, M. F. Haase, I. Raczkowska and J. Brujic, Soft Matter, 2013, 9, 7150–7157.
29. G. Meng, N. Arkus, M. P. Brenner and V. N. Manoharan, Science, 2010, 327, 560–563.
30. Z. Nie, D. Fava, E. Kumacheva, S. Zou, G. C. Walker and M. Rubinstein, Nat. Mater., 2007, 6, 609–614.
31. M. E. Leunissen, R. Dreyfus, F. C. Cheong, D. G. Grier, R. Sha, N. C. Seeman and P. M. Chaikin, Nat. Mater., 2009, 8, 590–595.
32. L. Cademartiri and K. J. M. Bishop, Nat. Mater., 2015, 14, 2–9.
33. H. R. Vutukuri, A. F. Demirörs, B. Peng, P. D. J. Van Oostrum, A. Imhof and A. Van Blaaderen, Angew. Chem., Int. Ed., 2012, 124, 11411–11415.
34. F. M. Hecht and A. R. Bausch, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8577–8582.
35. D. B. Miracle, W. S. Sanders and O. N. Senkov, Philos. Mag., 2003, 83, 2409–2428.
36. C. van der Wel, et al. , Sci. Rep., 2016, 6, 32825.

---

Footnote

† Electronic supplementary information (ESI) available: Calculations, Fig. S1, S2 and movies S1–S6. See DOI: 10.1039/c6nr08069c

---