 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Protein corona composition of poly(ethylene glycol)- and poly(phosphoester)-coated nanoparticles correlates strongly with the amino acid composition of the protein surface†
Giovanni
Settanni
 *ab,
Jiajia
Zhou
a,
Tongchuan
Suo
a,
Susanne
Schöttler
cd,
Katharina
Landfester
c,
Friederike
Schmid
*a and
Volker
Mailänder
*cd
*ab,
Jiajia
Zhou
a,
Tongchuan
Suo
a,
Susanne
Schöttler
cd,
Katharina
Landfester
c,
Friederike
Schmid
*a and
Volker
Mailänder
*cd
aInstitute of Physics, Johannes Gutenberg University Mainz, Germany. E-mail: settanni@uni-mainz.de; friederike.schmid@uni-mainz.de
bMax Planck Graduate Center with the Johannes Gutenberg University Mainz, Germany
cMax Planck Institute for Polymer Research, Mainz, Germany. E-mail: mailaend@mpip-mainz.mpg.de
dUniversity Medical Center, Dermatology Clinic, Johannes Gutenberg University Mainz, Germany
First published on 5th January 2017
Abstract
Extensive molecular dynamics simulations reveal that the interactions between proteins and poly(ethylene glycol) (PEG) can be described in terms of the surface composition of the proteins. PEG molecules accumulate around non-polar residues while avoiding the polar ones. A solvent-accessible-surface-area model of protein adsorption accurately fits a large set of data on the composition of the protein corona of poly(ethylene glycol)- and poly(phosphoester)-coated nanoparticles recently obtained by label-free proteomic mass spectrometry.
Nanoparticles are being intensively investigated as possible drug carriers due to their ability to load drugs, and potentially deliver them selectively to the target (e.g. the cancer cells or tissues), opening the way to highly effective therapies with reduced side effects.1 As soon as the nanoparticles come into contact with the blood stream they are covered by plasma proteins, forming the “protein corona”. Numerous studies have demonstrated that the nature and composition of the protein corona determines the most important characteristics of the nanoparticles, for example, their ability to be taken up by cells or to stimulate an immune response, or their toxicity.2,3 The composition of the protein corona can be measured experimentally, for example by liquid chromatography/mass spectrometry.4,5 However many other features, like the orientation of the adsorbed proteins and the degree of exposure of the proteins’ functional epitopes are more difficult to access.6 These features, as well as the determinants of the protein corona composition, are particularly important as they help to understand how the corona will interact with the host organism.
Poly(ethylene glycol) (PEG) has a wide variety of applications, which often involve its capacity to limit protein adsorption. PEG, immobilized to surfaces, greatly retards protein adsorption7 and shows antifouling activity.8 PEGylation of drugs and nanocarriers leads to an increase of their circulation half-lives, not only by increasing their hydrodynamic radius or thermal stability, but also by decreasing their susceptibility to phagocytosis.9 These properties of PEG – often subsumed under the name of the “stealth” effect – are essential for the effective targeting of nanocarriers.10 The stealth effect has been generally explained by the large hydrophilicity of PEG which leads to the formation of a thick hydration layer that hinders interactions with the surrounding proteins. Notwithstanding its “stealth” properties, PEG is not totally inert. Indeed, several proteins have been detected in protein coronas of PEGylated nanocarriers after incubation in serum or plasma.11 Recent data from label-free proteomic mass spectrometry of PEG-coated nanoparticles,5 show that their coronas have a very specific protein composition, which is significantly different from the one observed in plasma. These data suggest that PEG may not limit uniformly the adsorption of proteins, but it may do so in a protein-dependent manner, with few proteins showing a highly preferential binding affinity for PEG-coated nanoparticles. The possible reasons of the observed preferential binding are not well understood yet.
Molecular dynamics (MD) simulations have been extensively used to describe protein/peptide adsorption on several different surfaces as recently reviewed in ref. 12 and 13. Protein adsorption on surfaces coated with hydrophilic polymers like PEG provide a further challenge due to their brush structure. In this case, depending on their size, the proteins may partially or completely penetrate into the polymer brush formed on the coated surface.14 Herein, we evaluate the possible origin of the selective adsorption of proteins on the surface of PEG-coated nanoparticles and show how it can be related to and predicted by the amino acid composition of the protein surface. We address the problem by performing atomistic MD simulations of selected plasma proteins immersed in PEG–water mixtures characterized by different PEG lengths and concentrations. These simulations help us understand how PEG molecules distribute on the surface of the proteins and relate PEG distribution to protein surface properties. From the simulation results we infer the possible relationship between the concentration of proteins in the nanoparticle corona and the amino acid composition of their surface. Finally we verify the inferred relationship on a large dataset of proteins, using only the available structural information without performing further simulations.
The simulations were prepared by immersing selected plasma proteins into periodic simulation boxes filled with pre-equilibrated PEG/water mixtures at physiological ionic strength (0.15 M [NaCl]). The simulations were carried out using the program NAMD15 and the charmm27 force field16,17 including parameters for PEG.18 Tip3p19 was used as a model for the explicit treatment of water. Further details about the simulations and the data analysis are provided in the ESI.† In the course of the MD simulations, all the particles (water, PEG, ions and protein) can diffuse freely, thus allowing for the PEG molecules to probe many possible binding modes with the protein surface. This approach has been successfully used in the context of drug design to identify druggable cavities in proteins20,21 and also to study protein–polymer interactions including PEG.22,23 It is justified by the fact that PEG is not assumed to induce large conformational changes in the protein conformation.24 We have purposely used short PEG chains (4 and 7 monomers), which diffuse fast, and allow for the fast sampling of the possible binding modes. Given the very short persistence length of PEG (0.38 nm) which is comparable with the distance between the adjacent monomers, even the short PEG chains capture the flexibility of the longer PEG chains used in the experiments. Thus, in the polymer conformations bound to the protein surface the monomers are expected to occupy similar positions either if they belong to long or short PEG chains. If non-negligible interactions are formed between the protein (or parts of it) and PEG molecules, the concentration of PEG atoms in the vicinity of the protein (or the selected parts) will differ from the value in the bulk. Thus, we measure the ratio between the number of PEG atoms (excluding hydrogen atoms) and water molecules present within a certain distance (0.5 nm) from the protein (or the selected parts). A PEG/water ratio larger than the bulk values would indicate the presence of effective attractive interactions between PEG and protein (or the selected parts). We have analyzed 3 plasma proteins, human serum albumin (HSA), transferrin (TRF), and complement Cq1 subcomponent subunit C(CQ1C). These proteins were selected based on several criteria including the availability of the crystallographic structure and either high (CQ1C) or low (HSA, TRF) experimentally observed concentration in the protein corona of PEG-coated nanoparticles.5 We have also analyzed the possible effects of PEG concentration (from 0.04 to 0.12 g ml−1) and length (4 or 7 monomers), as well as simulation box size. A list of all the simulated systems including the number and length of runs is provided in Table S1 in the ESI.† The length of the simulations (200 ns) is sufficient to reach statistical convergence of the PEG–protein interactions (see the ESI†). The simulations show that (i) the analyzed proteins have different affinity for PEG molecules, consistent with the experimental observation of the protein concentration in the nanoparticle corona; (ii) PEG molecules do not distribute uniformly on the protein surfaces. Instead, they tend to accumulate in specific regions (Fig. 1a–c).
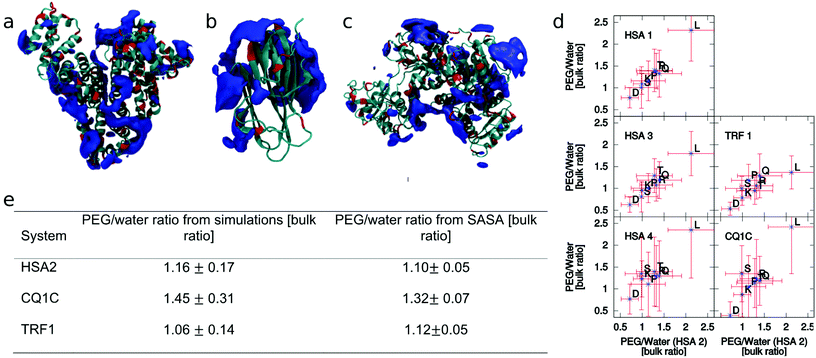 | ||
| Fig. 1 Cartoons of HSA (a), C1qC (b), and TRF (c) highlighting the regions (dark blue) with an average PEG density twice as large as in the bulk. These regions are not uniformly distributed on the protein surface. They tend to be located away from negatively charged residues (red). (d) The residue-specific PEG/water ratios measured in several simulated systems and plotted versus those obtained for simulation HSA2 (see the ESI†) on the x axis to highlight the correlation. Only the amino acid types which contribute at least 3% of the solvent accessible surface area in each of the simulated system are considered. The correlation coefficients measured between each possible simulation pair are equal to or larger than 0.7. The dependence of the PEG/water ratios on PEG concentration, density or box size (left column) is weak. The impact of the simulated protein on the PEG/water ratios (right column) is also limited. The error bars correspond to the standard deviations measured along the trajectories of each simulation. (e) The PEG/water ratio in the 0.5 nm region around the protein averaged over the simulations (left column) and approximated using eqn (1) (right column). | ||
We assumed that these observations might reflect the heterogeneous amino acid composition of the protein surface in the analyzed proteins. Thus, we measured the residue specific affinity for PEG in all the simulations, i.e. the PEG/water ratio in the vicinity of each amino acid type, and normalized it to the bulk PEG/water ratio. It turns out that these values are surprisingly similar across the different proteins and simulation conditions, especially for the most solvent exposed residue types (Fig. 1d) (for the less exposed residue types the statistical noise is large).
This finding led us to propose a simple model to describe PEG–protein interactions, based on few assumptions. The first assumption is that the total PEG/water ratio (in the vicinity) of a protein P can be approximated as the sum of the contributions coming from each residue type weighted by the corresponding solvent-accessible surface area.
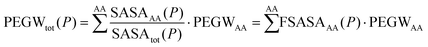 | (1) |
We tested this assumption by taking the PEGWAA averaged over different simulations (weighting the simulations according to the solvent-exposed-surface area of the amino acid type) and computing the approximated PEGWtot(P) with eqn (1) for each of the simulated proteins. We then compared this number with the actual PEGWtot(P) measured directly in the simulations. The comparison (Fig. 1e) shows that the approximation reproduces within the error, the affinity of the protein for PEG (measured with the PEG/water ratio) for the three simulated proteins.
The second assumption that we make is that the average adhesion force FA between a protein and a PEG-coated nanoparticle is a function of the PEG/water ratio.
| FA = FA(PEGWtot(P)) | (2) |
In other words, a high PEG/water ratio of the protein would result in a strong adhesion force, due to the large amount of PEG molecules per unit area that are attracted in the vicinity of the protein. Although the core of the PEGylated nanoparticle may have an influence on the nature and quantity of the adsorbed proteins,11 at this point we are neglecting it. The adsorption free energy of each protein can be written as:
ΔGads(P) = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log([P]np/[P]plasma) log([P]np/[P]plasma) | (3) |
 | (4) |
 | (5) |
In the following, we prove the validity of eqn (5) using the available experimental data.
To test eqn (5) we obtained the protein concentrations [P]np and [P]plasma from proteomic mass spectrometry experiments,5 where the amount of different plasma proteins was measured both on PEG-coated nanoparticles and in plasma (see the ESI† for details). Then, if available, the structures of the proteins adsorbing on the nanoparticles were collected either from the Protein Data Bank (PDB) or from the homology model database.25 This resulted in a database of 36 plasma proteins (Table S2 in the ESI†). Then, we computed the solvent exposed surface area of each residue type in each protein using VMD,26 which provided the FSASAAA(P) data in eqn (5) (see Table S3 in the ESI†).
Using, in eqn (5), the PEGWAA determined with the simulations, we already observed a significant correlation coefficient (r = 0.55, p < 0.001, df = 36)27 between the left and the right hand side of the equation (Fig. 2a and Table S2 in the ESI†). On the other hand, the values obtained from the simulations may be biased by several factors including the short length of the PEG molecules, the approximate nature of the force field, the limited number of simulated proteins and the low statistical accuracy for the less exposed amino acids. For these reasons, starting from the average values obtained from the simulations, we optimized the PEGWAA to maximize the correlation coefficient between the left- and right-hand side of eqn (5) using a bootstrap approach. Details about the fitting procedure are provided in the ESI.† The resulting model shows a very high correlation coefficient (r = 0.85) with the available data (Fig. 2b and Table S2 in the ESI†). We proved the statistical significance of this correlation by generating a thousand artificial datasets, where the FSASAAA were randomized across the proteins, and applying the same bootstrap procedure to each set. Only 1.4% of the random datasets led to correlation coefficients higher than the one measured on the original data, proving the statistical significance of the observed correlation. This fact supports the validity of eqn (5).
 | ||
| Fig. 2 The logarithm of the protein concentration ratio on the nanoparticle corona and in plasma (measured experimentally) is plotted versus the PEG/water ratios (r.h.s. of eqn (5)) of the plasma proteins, estimated using (a) the PEGWAA from the simulations (Table 1 third column), i.e. with no fitted parameter, and (b) the PEGWAA obtained by fitting r.h.s. of eqn (5) to the experimental data (Table 1, second column) through the bootstrap procedure (see the ESI†). The blue line represents the best linear fit and the correlation coefficients (r) are reported in the upper left corner of the respective box. In (a) the error bars are obtained by propagating the error on the PEGWAA. In (b) the error bars report the standard deviations measured over all the bootstrap sets. Each protein is indicated with its gene name. See Table S2 in the ESI.† | ||
As exposed more diffusely in the ESI,† the bootstrap procedure used for fitting the experimental data involves, fitting the parameters to a subset of the proteins in the original data set (training set) and then using the fitted parameters also to predict the protein concentration of the remaining proteins (test set, see Fig. S1 in the ESI† for an example). This is repeated for many different random choices of the training and test set. Thus, the results presented here, which are averages over many choices of training and test sets show that the model is predictive and the high correlation coefficient provides an assessment for this.
The PEGWAA values obtained from the fit and reported in Table 1 (which do not deviate strongly from the average values obtained from the simulations, with a correlation coefficient of 0.69, see Fig. S2 in the ESI†), provide a measure of the relative affinity of each residue type for PEG. They show, for example, that the negatively charged residues tend to repel PEG, as expected by the presence of a negative partial charge concentrated on the oxygen atoms in PEG. Unexpectedly, however, also positively charged lysine, which generally provides the largest fraction of the solvent-accessible surface to the analyzed proteins, shows the tendency to have a lower density of PEG in its vicinity than in the bulk. A possible explanation of this phenomenon could be related to the large charge density of lysine. According to the CHARMM force field lysine's charge is concentrated on the zeta-nitrogen (NZ) and epsilon-carbon (CE) atoms (and bound hydrogen atoms), while, as a comparison, arginine's charge is spread over 5 heavy atoms (and bound hydrogen atoms). The large charge density may favor interactions with water over PEG, which has a smaller polarity.
| Amino acid | PEGWAA fit [bulk ratio] | PEGWAA sim. [bulk ratio] |
|---|---|---|
| S | 0.50 ± 0.17 | 1.07 ± 0.15 |
| D | 0.66 ± 0.22 | 0.59 ± 0.10 |
| E | 0.82 ± 0.11 | 0.69 ± 0.07 |
| P | 0.82 ± 0.22 | 1.16 ± 0.13 |
| W | 0.87 ± 0.26 | 1.73 ± 0.97 |
| N | 0.89 ± 0.23 | 0.94 ± 0.12 |
| K | 0.89 ± 0.15 | 1.31 ± 0.22 |
| T | 0.98 ± 0.22 | 1.17 ± 0.14 |
| A | 1.00 ± 0.23 | 1.61 ± 0.35 |
| L | 1.00 ± 0.23 | 1.79 ± 0.37 |
| G | 1.02 ± 0.22 | 1.49 ± 0.45 |
| Q | 1.07 ± 0.21 | 1.27 ± 0.12 |
| Y | 1.11 ± 0.19 | 1.34 ± 0.42 |
| C | 1.15 ± 0.18 | 1.47 ± 0.17 |
| H | 1.17 ± 0.23 | 1.10 ± 0.22 |
| R | 1.29 ± 0.18 | 1.17 ± 0.16 |
| F | 1.53 ± 0.23 | 1.94 ± 0.41 |
| V | 1.55 ± 0.26 | 1.82 ± 0.40 |
| I | 1.56 ± 0.23 | 1.57 ± 0.48 |
| M | 2.11 ± 0.23 | 2.00 ± 0.95 |
On the other hand, the data show that PEG interacts in general more favorably with hydrophobic residues compared to polar or hydrophilic residues. This is in agreement with previously published simulations of CI2 in PEG4 water mixtures22 which showed the formation of a larger number of contacts between PEG and atoms with small partial charges compared to atoms with large partial charges. It has also been shown that PEG may penetrate the membrane of PEGylated liposomes.28 Similarly, sum frequency generation vibrational spectroscopy experiments29 showed that the addition of free PEG in solution reduced the number of strong hydrogen bonds between lysozyme and water indicating the formation of interactions between PEG and the hydrophobic parts of the protein. However, it has been shown that free PEG and surface-bound PEG as found on nanoparticles may affect the protein hydration shell differently.29 The discrepancy was attributed to the expected burial of the CH2 groups of PEG in the surface film but it may also be related to the interactions of the protein with the core of the nanoparticle. Indeed, it has been shown that, although providing qualitatively similar protein adsorption patterns, differences in the core of PEGylated nanoparticles may result in differences in the amount and type of the adsorbed proteins.11 This may explain the partial discrepancy between the PEG/water ratio measured in the simulations and those obtained by fitting the experimental data.
The model proposed here is based on the assumption that the proteins in contact with the nanoparticle surface retain their structure, including the solvent exposed surface area of their amino acids. This assumption was verified experimentally for some of the proteins.30 In addition, the simulated proteins did not show relevant conformational changes during the simulations with PEG. The Cα root mean square deviation from the crystallographic structures averaged across the simulation runs remained below 0.2, 0.35 and 0.5 nm for C1QC, HSA and TRF, respectively, compatible with native state fluctuations for proteins of that size. However, if the proteins underwent unfolding upon adsorption, a better determinant for their adsorption properties could be their amino acid sequence composition. Then, eqn (5) could be modified by replacing the FSASAAA of the amino acids with their relative abundance in the sequence. We fitted this sequence-based model to the experimental data using the same bootstrap procedure used above and we obtained a correlation coefficient of 0.79 with the experimental data, which is lower than what was obtained using the solvent exposed surface area. This indicates that, on average, the fraction of the solvent exposed surface area is a better predictor of protein adsorption on nanoparticles, and lets us conclude that the majority of the proteins examined here remain folded upon adsorption. However, we cannot exclude that some of the proteins may undergo unfolding upon adsorption.
The adsorbed-protein concentration data used in eqn (5) were obtained on PEG44-coated polystyrene nanoparticles (PS-PEG44). To assess the selectivity of our method for PEG we have first calculated the correlation coefficient between the values of the l.h.s. of eqn (5) measured for PS-PEG44 nanoparticles with the same values measured for other nanoparticles reported in our previous studies5,31 including those coated with poly(ethyl ethylene phosphate) (PEEP) a polymer proposed as an alternative to PEG to provide stealth properties to nanocarriers. The analyzed nanoparticles include PEG110-coated polystyrene (PS-PEG110), PEEP49-coated polystyrene (PS-PEEP49), PEEP92-coated polystyrene (PS-PEEP92), amino-functionalized polystyrene (PS-NH2), Lutensol-stabilized polystyrene (PS-LUT) and Lutensol-stabilized amino-functionalized polystyrene (PS-LUT-NH2) nanoparticles (see ESI Table S2†). The correlation is high for PEG and PEEP coated nanoparticles (correlation coefficients equal to or larger than 0.9) while low for the other nanoparticles (correlation coefficient equal to or lower than 0.7). This demonstrates that there is a large similarity between the protein corona of PEG and PEEP coated nanoparticles but not between PEG-coated and PS-NH2, PS-LUT or PS-LUT-NH2 nanoparticles. The similarity can be related to the chemical structure of the two coating polymers which both have an electronegative part (the oxygen atom in PEG and the phosphate group in PEEP) alternating with mostly neutral/hydrophobic parts (the ethyl groups in both PEG and PEEP) in similar proportions (in Lutensol-stabilized nanoparticles, Lutensol is used as a surfactant in the preparation of the nanoparticles and then it is mostly removed so that the amount of the residual surfactant is less than 0.1% of the polymer in the nanoparticles).
Given the similarity in the composition of the corona of PEG- and PEEP-coated nanoparticles, it is expected that the PEG/water ratio estimated using our method, would also predict the composition of PEEP-coated nanoparticles but not that of the other nanoparticles. This is actually the case: the correlation coefficient of the estimated PEG/water ratios with the l.h.s. of eqn (5) computed using the data for PS-PEEP49 and PS-PEEP92 particles is 0.82 in both cases, similar to 0.85 measured for PS-PEG44 nanoparticles used in the fit and to 0.77 measured for PS-PEG110. This correlation drops to values equal to or lower than 0.5 for PS-NH2, PS-LUT and PS-LUT-NH2 nanoparticles. A similar trend is observed when using the PEG/water ratios estimated using the simulation data as in Fig. 2a: in this case the correlations with protein concentrations on PEG- and PEEP-coated nanoparticle are between 0.5 and 0.6, while with PS-NH2, PS-LUT and PS-LUT-NH2 nanoparticles they drop to below 0.2. The fact that the correlation of PEG/water ratios with the fitted data is not significantly higher than that with similar data not used in the fit but it is low with not similar data confirms that the method used to fit the data has successfully reduced the overfitting.
The PEG- and PEEP-coated nanoparticles showing a similar corona composition differ by several other aspects: for example, PS-PEG44 and PS-PEG110 have on average 3500 and 2900 grafted chains per particle, a size of 117 nm and 119 nm, and a zeta-potential of 15 mV and 8 mV, respectively and the total adsorbed proteins varied significantly in the two cases (0.77 mg m−2 and 1.24 mg m−2, respectively). Although these examples do not cover all the possible variations of PEGylated nanoparticles, however, the similarity in their corona composition, represented by the quantity we have identified (log([P]np/[P]plasma)), suggests that this is only weakly dependent on the characteristics of the PEGylated nanoparticle. In particular, the reported grafting density of PS-PEG44 and PES-PEG1105 (3.0 and 3.8 nm2 per PEG chain, respectively) indicates that PEG chains form a dense brush.32,33 The protein adsorption pattern of PEGylated nanoparticles do not change significantly above a certain PEG density,11 thus the analysis presented here is possibly valid for PEGylated nanoparticles with similar or higher PEG densities than those analyzed here.
Although the main contribution (about 60%) to the PEG/water ratio in the vicinity of the protein comes from the most exposed amino-acids, we found that the FSASAAA(P) of few specific amino acid types correlate particularly strongly with the left hand side of eqn (5). One striking example is methionine. Indeed, the FSASAMET(P) alone shows a correlation of 0.62 with the left hand side of eqn (5), suggesting that proteins where methionine amino acids expose the largest fraction of the surface area may more likely adsorb on PEG-coated nanoparticles. This also explains why methionine is the amino acid with the largest PEGWAA in both the fitted parameters and those derived from the simulations (see ESI Fig. S2†). The analysis of the trajectories shows an accumulation of PEG in the vicinity of exposed methionine side-chains (ESI Fig. S3†). Interestingly, clusterin, which is the protein that adsorbs most abundantly on the PEG-coated nanoparticles analyzed here, but is not part of our data set as it has not been structurally characterized yet, has a very high percentage of methionine amino acids in its sequence (3.5%) compared to the other proteins in the data set. A higher percentage of methionine is found only in the fibrinogen beta chain (3.7%) and the complement C1q subcomponent B subunit (3.6%), which also adsorb abundantly on the nanoparticle surface.
Conclusions
The simulations presented here show that PEG–protein interactions can be described using a simple model based on the solvent-accessible surface area exposed by each amino acid type on the protein surface. The model has been applied to provide a simple and accurate description of the adsorption process of plasma proteins on the surface of PEGylated nanoparticles. The model, however, is not necessarily limited to plasma proteins and may be applicable to protein–PEG interactions occurring in other body fluids, as long as the main solvent is water. The model allows for making predictions on how PEG will interact with specific proteins, and is not necessarily limited to the corona of PEGylated nanoparticles. For example, it may allow for predicting which parts of the protein will be buried by PEG, or which binding epitopes will remain available for receptor binding. In turn, this may allow for a fast evaluation of the consequences of PEGylation in relation to the substrate-specific targeting needs. Although, very well-established as a drug modifier, PEG has several shortcomings including interfering with the cellular uptake and triggering immune response.34 Alternatives to PEG are being investigated by several groups.5,34 As demonstrated for PEEP-coated nanoparticles above, we expect our approach to be transferable to the description of other protein–nanocarrier interactions.Author contributions
GS, FS, KL and VM conceived and designed the research, GS, JZ and TS performed the simulations, GS analyzed the data, SS, KL and VM provided the experimental data, GS, FS and VM wrote the manuscript.Acknowledgements
GS acknowledges support from the Max Planck Graduate Center (MPGC). We gratefully acknowledge support with computing time from HPC facility Mogon at the University of Mainz, and the High Performance Computing Center Stuttgart (ACID 44059). This work was supported by the DFG/SFB1066 (‘Nanodimensionale polymere Therapeutika fuer die Tumortherapie’, project Q1). Open Access funding provided by the Max Planck Society.Notes and references
- K. Cho, X. Wang, S. Nie, Z. (Georgia) Chen and D. M. Shin, Clin. Cancer Res., 2008, 14, 1310–1316 CrossRef CAS PubMed.
- M. P. Monopoli, C. Åberg, A. Salvati and K. A. Dawson, Nat. Nanotechnol., 2012, 7, 779–786 CrossRef CAS PubMed.
- A. Lesniak, F. Fenaroli, M. P. Monopoli, C. Åberg, K. A. Dawson and A. Salvati, ACS Nano, 2012, 6, 5845–5857 CrossRef CAS PubMed.
- S. Tenzer, D. Docter, J. Kuharev, A. Musyanovych, V. Fetz, R. Hecht, F. Schlenk, D. Fischer, K. Kiouptsi, C. Reinhardt, K. Landfester, H. Schild, M. Maskos, S. K. Knauer and R. H. Stauber, Nat. Nanotechnol., 2013, 8, 772–781 CrossRef CAS PubMed.
- S. Schöttler, G. Becker, S. Winzen, T. Steinbach, K. Mohr, K. Landfester, V. Mailänder and F. R. Wurm, Nat. Nanotechnol., 2016, 11, 372–377 CrossRef PubMed.
- P. M. Kelly, C. Åberg, E. Polo, A. O'Connell, J. Cookman, J. Fallon, Ž. Krpetić and K. A. Dawson, Nat. Nanotechnol., 2015, 10, 472–479 CrossRef CAS PubMed.
- Y. Mori, S. Nagaoka, H. Takiuchi, T. Kikuchi, N. Noguchi, H. Tanzawa and Y. Noishiki, Trans. – Am. Soc. Artif. Intern. Organs, 1982, 28, 459–463 CAS.
- J. L. Dalsin and P. B. Messersmith, Mater. Today, 2005, 8, 38–46 CrossRef CAS.
- D. E. Owens and N. A. Peppas, Int. J. Pharm., 2006, 307, 93–102 CrossRef CAS PubMed.
- B. Kang, P. Okwieka, S. Schöttler, S. Winzen, J. Langhanki, K. Mohr, T. Opatz, V. Mailänder, K. Landfester and F. R. Wurm, Angew. Chem., Int. Ed., 2015, 54, 7436–7440 CrossRef CAS PubMed.
- R. Gref, M. Lück, P. Quellec, M. Marchand, E. Dellacherie, S. Harnisch, T. Blunk and R. H. Müller, Colloids Surf., B, 2000, 18, 301–313 CrossRef CAS PubMed.
- H. Heinz and H. Ramezani-Dakhel, Chem. Soc. Rev., 2016, 45, 412–448 RSC.
- M. Ozboyaci, D. B. Kokh, S. Corni and R. C. Wade, Q. Rev. Biophys., 2016, 49, e4 CrossRef PubMed.
- A. Halperin, Langmuir, 1999, 15, 2525–2533 CrossRef CAS.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, J. Comput. Chem., 2005, 26, 1781 CrossRef CAS PubMed.
- A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef CAS PubMed.
- A. D. Mackerell, M. Feig and C. L. Brooks, J. Comput. Chem., 2004, 25, 1400–1415 CrossRef CAS PubMed.
- H. Lee, R. M. Venable, A. D. Mackerell and R. W. Pastor, Biophys. J., 2008, 95, 1590–1599 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- N. Basse, J. L. Kaar, G. Settanni, A. C. Joerger, T. J. Rutherford and A. R. Fersht, Chem. Biol., 2010, 17, 46–56 CrossRef CAS PubMed.
- J. Seco, F. J. Luque and X. Barril, J. Med. Chem., 2009, 52, 2363–2371 CrossRef CAS PubMed.
- Q. Shao, Y. He, A. D. White and S. Jiang, J. Chem. Phys., 2012, 136, 225101 CrossRef PubMed.
- E. D. Musselman, Master thesis, University of Iowa, 2010.
- S. N. Timasheff, Adv. Protein Chem., 1998, 51, 355–432 CrossRef CAS PubMed.
- J. Haas, S. Roth, K. Arnold, F. Kiefer, T. Schmidt, L. Bordoli and T. Schwede, Database Oxf., 2013, 2013, bat031 Search PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33 CrossRef CAS PubMed.
- R. A. Fisher, Biometrika, 1915, 10, 507–521 Search PubMed.
- M. Stepniewski, M. Pasenkiewicz-Gierula, T. Róg, R. Danne, A. Orlowski, M. Karttunen, A. Urtti, M. Yliperttula, E. Vuorimaa and A. Bunker, Langmuir, 2011, 27, 7788–7798 CrossRef CAS PubMed.
- C. Leng, H.-C. Hung, S. Sun, D. Wang, Y. Li, S. Jiang and Z. Chen, ACS Appl. Mater. Interfaces, 2015, 7, 16881–16888 CAS.
- J. Wu, C. Zhao, W. Lin, R. Hu, Q. Wang, H. Chen, L. Li, S. Chen and J. Zheng, J. Mater. Chem. B, 2014, 2, 2983–2992 RSC.
- K. Mohr, M. Sommer, G. Baier, S. Schöttler, P. Okwieka, S. Tenzer, K. Landfester, V. Mailänder, M. Schmidt and R. Meyer, J. Nanomed. Nanotechnol., 2014, 05 Search PubMed.
- J. L. Perry, K. G. Reuter, M. P. Kai, K. P. Herlihy, S. W. Jones, J. C. Luft, M. Napier, J. E. Bear and J. M. DeSimone, Nano Lett., 2012, 12, 5304–5310 CrossRef CAS PubMed.
- V. B. Damodaran, C. J. Fee, T. Ruckh and K. C. Popat, Langmuir, 2010, 26, 7299–7306 CrossRef CAS PubMed.
- Z. Amoozgar and Y. Yeo, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2012, 4, 219–233 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the methodology used for the simulations and the analysis of the data including three supplementary figures and three supplementary tables. See DOI: 10.1039/c6nr07022a |
| This journal is © The Royal Society of Chemistry 2017 |
