Direct observation of site-selective hydrogenation and spin-polarization in hydrogenated hexagonal boron nitride on Ni(111)

Abstract

We report the structural analysis and spin-dependent band structure of hydrogenated boron nitride adsorbed on Ni(111). The atomic displacement studied by using the normal incidence X-ray standing wave (NIXSW) technique supports the H–B(fcc):N(top) model, in which hydrogen atoms are site-selectively chemisorbed on boron atoms and N atoms remain on top of Ni atoms. The distance between the Ni plane and nitrogen plane did not change after hydrogenation, which implies that the interaction between Ni and N is 3d–π orbital mixing (donation and back-donation) even after hydrogenation of boron. The remaining π* peaks in near-edge X-ray absorption fine structure (NEXAFS) spectra are a manifestation of the rehybridization of sp² into sp³ states, which is consistent with the N–B–N bonding angle derived from NIXSW measurement. The SPMDS measurement revealed the spin asymmetry appearing on hydrogenated h-BN, which was originated from a π related orbital with back donation from the Ni 3d state. Even though the atomic displacement is reproduced by the density functional theory (DFT) calculation with the H–B(fcc):N(top) model, the experimental spin-dependent band structure was not reproduced by DFT possibly due to the self-interaction error (SIE). These results reinforce the site-selective hydrogenation of boron and pave the way for efficient design of BN nanomaterials for hydrogen storage.

---

Introduction

While hexagonal boron nitride (h-BN) is now widely used as an ideal substrate material for graphene-based electronics and spintronic devices,^1–4 the hetero-polar bonding in hexagonal boron nitride makes it also promising for applications such as light emitting diodes,⁵ catalysis supports⁶ and hydrogen storage materials.⁷ Large hydrogen uptakes as large as 4.2 wt% and 2.3 wt% are reported for h-BN nanotubes⁸ and porous microbelts,⁹ respectively, which are larger than that of a carbon nanotube (<1 wt%).^10,11 It is theoretically reinforced that boron nitride nanotubes are preferable to carbon nanotubes for hydrogen storage, partially due to the strong interaction between physisorbed H₂ and heteropolar B–N bonding.^12–14 In the case of carbon nanotubes, the key to improve the hydrogen uptake is to make the best use of chemisorption. Li et al. reported a very small physisorption energy of hydrogen molecules at room temperature,¹⁵ while it is predicted that chemisorbed hydrogen on all carbon atoms can realize a quite large hydrogen uptake (7.7 wt%).^15,16 A similar strategy would be effective for h-BN as well. The strong physisorption together with saturated chemisorption on h-BN can make the hydrogen uptake of the material even higher than that of the carbon materials.

For the chemisorption site of atomic hydrogen on h-BN, however, a couple of theoretical results are presented, which are apparently contradictory to each other. While some researchers claim that hydrogen atoms are site-selectively chemisorbed on electron-deficient boron atoms,^17–19 others claim N site-selectivity,²⁰ no site-selectivity,^21,22 or H cluster formation after B–H bond formation.²³ For experimental results, it is claimed that high energy plasma treatment or accelerated ion irradiation results in both B–H and N–H formation,^24,25 while the selective formation of the B–H bond was claimed by Koswattage et al. upon atomic hydrogen exposure.²⁶ Additional experimental results, such as structural analysis, are necessary to figure out the chemisorption site of hydrogen.

One of the consequences of hydrogen chemisorption on h-BN is the magnetic moment formation. While a couple of reports have been made upon the magnetic moment in graphane (hydrogenated graphene),²⁷ no experimental reports have been made on the magnetic moment of the hydrogenated h-BN to the best of our knowledge. We have previously reported the spin-resolved band structure of monolayer h-BN on Ni(111).^28–30 In order to elucidate the induced spin-polarization on the monolayer material independently from strong Ni signals, we employed spin-polarized metastable helium de-excitation spectroscopy (SPMDS).³¹ The extreme surface sensitivity of the method revealed that the π–d orbital mixing between topmost Ni and N induces spin-polarized in-gap states on h-BN. In the present research, the spin-resolved band structure of the hydrogenated h-BN monolayer on Ni(111) is evaluated using surface-sensitive SPMDS. The structural modification upon hydrogenation is also studied by means of low energy electron diffraction (LEED) and normal incidence X-ray standing wave (NIXSW) method. Even though the atomic coordinates of the H–B bonding model derived from density functional theory (DFT) match our experimental results rather well, spin-polarization was not reproduced by DFT. By referring to the previous reports on hydrogenated graphene,³² we assume that the discrepancy is due to the self-interaction error (SIE).^33,34 Our structural and spin-resolved analysis presents concise and conclusive evidence that atomic hydrogen is site-selectively chemisorbed on the boron site.

Experimental

The substrate is a W(110) single crystal which is cleaned by using standard oxygen roasting and flash annealing procedures³⁵ in an ultra-high vacuum chamber with a base pressure of 3.0 × 10⁻⁸ Pa. The ∼10 nm thick epitaxial film of Ni(111) is grown on W(110) by molecular beam epitaxy (MBE). The epitaxial monolayer of h-BN is then grown on Ni(111) by a UHV-CVD technique with a borazine precursor as described in our previous report.²⁹ After cooling down to room temperature, the atomic hydrogen was exposed to h-BN/Ni(111) using a homemade source equipped with a tungsten filament.³⁶ Since the dissociation efficiency has not been evaluated so far, the partial pressure of hydrogen detected at the ion gauge is used as a relative measure in the following discussion. All samples were fabricated in the same chamber. The SPMDS, ultra-violet photoemission spectroscopy (UPS) and LEED measurements were performed in situ, and the near-edge X-ray absorption fine structure (NEXAFS) and NIXSW measurements were performed ex situ after transferring into air.

Before SPMDS measurement, the sample was pulse-magnetized in-plane along the [11̄0] easy axis of magnetization of an Ni(111) thin film. The magnetic saturation is confirmed using the in situ magneto-optical Kerr effect, and SPMDS measurement was carried out in remanence. The probe of SPMDS is metastable triplet He* impinging on the surface with thermal velocity. The weak magnetic field (∼0.1 G), which is too weak to flip sample magnetization but strong enough to align triplet He*, is applied around the sample. By exchanging spins with evanescent states, the He* atoms are de-excited via resonant ionization followed by the Auger neutralization (RI + AN) process on h-BN/Ni(111). Since the He* polarized parallel to the sample magnetization can obtain minority spins of the sample exclusively, the energy spectra of Auger electrons emitted upon the AN process with He* parallel and anti-parallel to the sample magnetization are a manifestation of the minority and majority spin density of states of the sample, respectively. The detailed experimental setup and the de-excitation mechanism of SPMDS can be found in our previous publications.^29,37

The atomic and electronic structure of a set of hydrogenated h-BN/Ni heterostructures with different mutual configurations of hydrogenated h-BN and Ni(111) fragments was calculated by a GGA PBE approach, plane wave (PW) basis sets and ultrasoft Vanderbilt-type pseudopotentials (PP) under Periodic Boundary Conditions (PBC) using the VASP code.^38,39 For the sake of comparison the h-BN/Ni(111) heterostructure was calculated as well using the same approach. For all calculations the cutoff energy (E_cutoff) was equal to 286 eV. The geometry of the structures was optimized until residual forces became less than 0.01 eV Å⁻¹. The Γ-centered Monkhorst–Pack⁴⁰ (21 × 21 × 1) k-point Brillouin zone sampling scheme was used.

The pristine Ni plates constituted by 9 atomic layers with two symmetrically equivalent fcc (111) surfaces, pristine h-BN and hydrogenated h-BN sheets were calculated as the reference structures. The thickness of the Ni plate was adjusted by preliminary electronic structure calculations and it was found that the surface energy of the Ni plate reveals no change after 9 Ni(111) atomic layers. The rectangular Ni plate supercell consisted of 9 Ni atoms with a and b translational vectors equal to 2.444 and 4.226 Å, respectively. The Ni–Ni interlayer distances were in the range of 1.963–1.995 Å depending on the position of the layers with respect to the plate surfaces. The h-BN/Ni(111) and hydrogenated h-BN/Ni(111) supercells contained one Ni(111) fragment with 9 Ni atoms and either one h-BN (2 atoms, B and N, respectively) or hydrogenated h-BN (3 atoms: B, N and H) fragments due to the close structural parameters of pristine h-BN and Ni(111). To avoid the artificial interaction of the supercell partner images in the z direction, the length of the c translation vector was equal to 40.8 Å.

Results and discussion

The in situ LEED analysis revealed contraction of the in-plane lattice upon hydrogenation. The electron beam energy dependence of the spot distances is shown in Fig. 1(a). The horizontal direction of LEED patterns (Fig. 1(a), lower inset) is parallel to the [11̄0] direction of the tungsten substrate. The sharp hexagonal LEED patterns indicating high crystallinity are confirmed in all samples. The mismatch δ between h-BN, hydrogenated h-BN and Ni(111) is evaluated by extracting the spot distance from the cross section profile of the LEED patterns and Gaussian fitting to the spots. The monolayer h-BN lattice is relaxed on Ni(111)/W(110) with a mismatch as large as ∼0.7% as previously reported by Usachov et al.⁴¹ Upon hydrogenation, however, the lattice is contracted and matches the lattice of Ni(111).

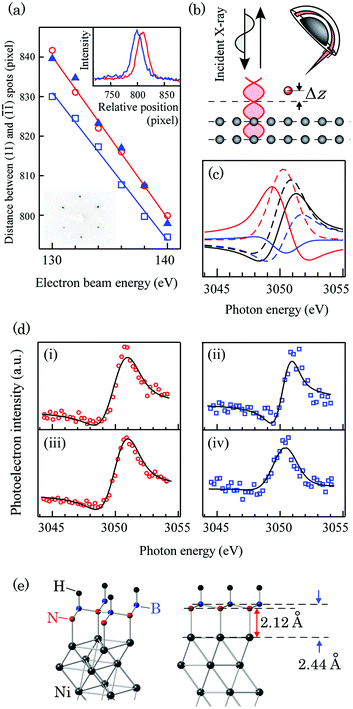Fig. 1 (a) The electron beam energy dependence of the distance between the (11) and (1̄1̄) spots in the LEED patterns. The red open circles, blue open squares, and blue triangles represent the spot distances in pristine Ni(111)/W(110), monolayer (ML) h-BN/Ni(111)/W(110), and hydrogenated h-BN/Ni(111)/W(110) samples, respectively. The inset (upper panel) is the relative cross section profile of the (11) spots in Ni(111)/W(110) (red) and ML h-BN/Ni(111)/W(110) (blue) samples. The acceleration voltage of the electron beam was 138 eV. The horizontal axis is aligned with respect to the (1̄1̄) spots. The other inset (lower panel) is the LEED pattern of the hydrogenated h-BN/Ni(111)/W(110) sample. The acceleration voltage of the electron beam is 140 eV. (b) The schematic diagram of the NIXSW experimental setup. (c) The simulated NIXSW profile of atoms on the Ni(111) surface with atomic displacement Δz = 0 Å (black solid line), 0.2 Å (black dashed line), 0.5 Å (red dashed line), 1.0 Å (red solid line), 1.5 Å (blue solid line), and 1.8 Å (blue dashed line). (d) The experimental NIXSW profiles of (i) N 1s and (ii) B 1s photoemission lines of pristine monolayer h-BN/Ni(111), and (iii) N 1s and (iv) B 1s of hydrogenated h-BN/Ni(111). The red circles and blue rectangles are experimental data and the black solid line is the fit using eqn (1) to the data. (e) The atomic geometry of the H–B(fcc):N(top) model derived from NIXSW analysis.

The displacement perpendicular to the sample surface upon hydrogenation is studied by NIXSW at BL-27A of the Photon Factory, KEK (KEK-PF). This spectroscopy utilizes an X-ray standing wave formed when the sample is irradiated by X-ray around the Bragg conditions. While the single scattering theory assumes that the standing wave appears only when the Bragg conditions are satisfied, multiple scattering theories with forward scattering give finite, but high reflectivity over a finite range of the incidence conditions, with a node and an antinode displaced accordingly. The profile of the core-level photoemission intensity by the X-ray standing wave is modulated depending on the relative atomic position with respect to the node and antinode, which allows us to element-specifically determine the vertical distances of the constituent atoms with respect to the X-ray scattering plane in the substrate. The detailed numerical description of the NIXSW method can be found elsewhere.⁴² The formula (14) in ref. 42 is used to simulate the XSW intensity I as follows:

where E is the photon energy, R(E) is the reflectivity of the substrate, δ is the energy-dependent phase modulation caused by the X-ray standing wave, f_co is the structure factor, d_H is the separation of coherent planes, and Δz is the displacement of the target atom from atomic scattering planes.

Fig. 1(b) and (c) show the schematic diagram of the NIXSW setup and simulated NIXSW profile for Ni(111) single crystals, respectively. The intensity of photoelectrons emitted upon B and N 1s core-excitation is recorded using a hemi-spherical electron analyzer. Fig. 1(d) shows the NIXSW profiles for (i) N 1s, (ii) the B 1s photoemission line of monolayer h-BN/Ni(111), and (iii) N 1s and (iv) B 1s of the hydrogenated sample, respectively. The black solid lines in the figure are the fits to the data. The displacement Δz evaluated from the fit is (i) 2.13(2) Å, (ii) 1.98(3) Å, (iii) 2.12(1) Å, and (iv) 2.44(2) Å, respectively. The observed displacement for monolayer h-BN/Ni(111) matches well with the values predicted by DFT calculation at the LDA level (2.118 Å for d_Ni–N and 2.007 Å for d_Ni–B)²⁸ and values derived from LEED I–V measurement (2.22(7) Å for d_Ni–N and 2.04(7) Å for d_Ni–B)⁴³ within the error bar. The corrugation value of the B–N framework in pristine h-BN/Ni(111) derived from our measurement is 0.15(4) Å, which is slightly larger but agrees within the error with the X-ray photoelectron diffraction (XPD) results.⁴⁴ After hydrogenation, the vertical separation between Ni and B planes (d_Ni–B) was significantly stretched while the vertical separation between Ni and N planes (d_Ni–N) did not change. The stretch of d_Ni–B is one piece of evidence showing that the hydrogen is mainly adsorbed on boron atoms. The constant d_Ni–N indicates that the interaction between Ni and N, which is orbital mixing (donation of the N 2p electron and back-donation of the Ni 3d electron) in pristine h-BN/Ni(111),^28–30,45 does not change.

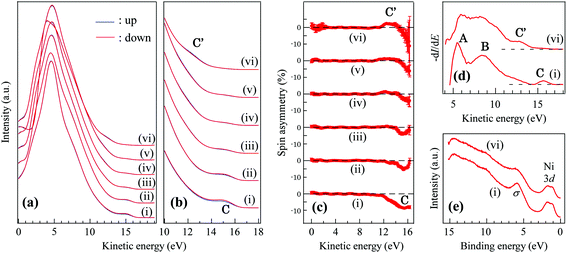
The adsorption of atomic hydrogen and the overhang of boron atoms toward the outer surface induce a prominent change in the electronic structure. Fig. 2 shows the NEXAFS spectra of hydrogenated h-BN/Ni(111) and the same sample after 500 °C annealing, which are taken by a sample current method at BL-7A (KEK-PF).⁴⁶ It was confirmed from SPMDS measurement that 500 °C annealing desorbed hydrogen, and the SPMDS spectrum of h-BN/Ni(111) was recovered, as described later. The features in the spectra of pristine h-BN/Ni(111) are assigned as follows:⁴⁷ A (excitation of the 1s electron to π*), B and C (1s to σ*), A′ (1s to mid-gap states induced by 3d–π orbital mixing), and A′′ (1s to the interlayer band). There are some notable changes in the spectra upon hydrogenation. First, a sharp peak (A* in Fig. 2(b)) appeared in the lower photon energy side of N K-edge absorption, which means the extra mid-gap state formation in the π–π* band gap. Second, the 1s to σ* peaks (B and C) of the B K-edge are developed into a new peak B′, while the other peaks, especially the 1s to σ* and π* peaks of the N K-edge and the 1s to the π* peak of the B K-edge, are not largely affected. The modification of the 1s to the σ* peak is another clear implication of the σ bond formation on boron. Finally, the A′′ peak appeared as a sharp peak, which was a broad peak in the previous reports of pristine h-BN/Ni(111).⁴⁷ This sharp A′′ peak, however, was not recovered by 500 °C annealing. The reason for the irreversible change is an open question, but probably associated with a localized interlayer band caused by the shrinkage of h-BN grains upon hydrogenation.

Fig. 2 (a) B K-edge and (b) N K-edge NEXAFS spectra of (i) hydrogenated h-BN/Ni(111) and (ii) the same sample after 500 °C annealing. The incidence angle of X-ray is 50° from the sample normal.

Fig. 3(a–c) show the series of the SPMDS spectra and spin asymmetry upon atomic hydrogen exposure. The de-excitation process of He* is examined by the He* survival probability as described in our publication,²⁹ and determined to be the Auger neutralization (AN) process both before and after hydrogenation, which indicates that the sample has metallic density of states. Since the SPMDS spectra are the self-convolution of the density of states in the case of the AN process, the first derivatives of the spectra are also shown in Fig. 3(d) in order to assign each feature to the density of states. There are three prominent peaks in Fig. 3(d), which are labeled A–C. In our previous study, it was revealed that the surface sensitive SPMDS spectrum of monolayer h-BN/Ni(111) does not have features directly derived from Ni(111). The peaks A and B are derived from σ and π bands of h-BN. The peak C is the manifestation of the π–d orbital mixing between nitrogen and Ni atoms, which induce spin-polarized in-gap states in the case of pristine h-BN/Ni(111). As the sample is exposed to atomic hydrogen, the peak C disappears and the new peak labeled C′ appears with a kinetic energy of 12–14 eV (binding energy of 2–4 eV). In the UPS spectra (hν = 21.2 eV), the intensity of the σ band peak⁴⁸ is decreased (Fig. 3(e)), which is derived from the new B–H σ band formation. For spin asymmetry, the peak C′ is spin-polarized parallel to the minority spin of Ni(111) with an asymmetry of ∼2%, which is opposite to the spin asymmetry of the peak C (Fig. 3(c) (i, vi)). As the metastable He* of SPMDS exchange electrons several angstroms above the topmost surface, the method is especially sensitive to the orbitals distributed perpendicular to the surface, such as π and π*. Therefore, we assume that the peak C′ (Fig. 3(d)) is derived from the π or π* related orbital with back-donation from the Ni 3d state. This assignment is reinforced by the previously-reported DFT-GGA results for semi-hydrogenated (hydrogen selectively chemisorbed on boron sites) h-BN with a free-standing geometry,⁴⁹ in which the magnetic moment is mainly possessed by unpaired N 2p_z electrons.

Fig. 3 (a–c) The overall SPMDS spectra, the magnified spectra, and the spin asymmetry of each spectrum of h-BN/Ni(111) with atomic hydrogen exposure. As mentioned in the Experimental section, the partial pressure of hydrogen (1 × 10⁻⁶ Pa) detected at the ion gauge is used as a relative measure. The dosage duration is (i) 0 s, (ii) 25 s, (iii) 120 s, (iv) 180 s, (v) 240 s, and (vi) 600 s, respectively. (d) The first derivative of the SPMDS spectra before and after hydrogenation. The atomic hydrogen dosage is the same as the captions in (a–c). (e) The UPS spectra of h-BN/Ni(111) before and after hydrogenation.

The sharp peak A* appearing at the N K-edge NEXAFS spectrum is accordingly assigned to the empty part of the spin-down N p_z band. The π* band peak of NEXAFS remaining after hydrogenation is a manifestation of the re-hybridization of the sp² state to the sp³ state of h-BN. The bonding angle of the N–B–N frame evaluated from experimental atomic coordinates is 115.4°, which is the intermediate angle between sp² and sp³, and support re-hybridization. The change induced by hydrogenation in the SPMDS spectra was persistent when annealed up to 400 °C, which implies that atomic hydrogen atoms are not simply physisorbed on the surface. After 500 °C annealing, the original SPMDS spectrum of h-BN/Ni(111) was recovered.

In our first-principles simulation, all possible configurations of mutually hydrogenated h-BN/Ni(111), namely top:N/fcc:BH (shown for example in Fig. 1(e)), top:NH/fcc:B, top:B/fcc:NH and top:BH/fcc:N were examined (Table 1). Here top: position denotes the coordination of an atom (N or B) or a group (BH or NH) to a Ni atom of the Ni(111) surface, and fcc: position denotes the coordination of either an atom or a group of atoms by fcc: position of the Ni(111) surface. Partial hydrogenation of the h-BH fragment atop the Ni(111) plate leads to structural corrugation of a perfectly planar h-BN sheet with a 0.32 Å separation of N and B sublattices in the vertical direction. The distances between the Ni plane and B plane (d_Ni–B) and the Ni plane and the N plane (d_Ni–N) were 2.395 Å and 1.917 Å, respectively, which are slightly underestimated but match well with the values of 2.44(2) Å and 2.12(1) Å observed in our NIXSW measurement. The PDOSs (Fig. S2(b)†) reveal a visible amount of an uncompensated spin located on a hydrogenated h-BN fragment, equal to −0.040 μ per unit cell.

Table 1 Relative energies of the hydrogenated h-BN/Ni(111) interfaces

Interface configuration	top:N/fcc:BH	top:NH/fcc:B	top:B/fcc:NH	top:BH/fcc:N
Relative energy	0.0 eV	0.04983	0.43919	0.71512

---

On the other hand, none of the mutual configurations match well with our experimental spin-dependent band structure. As is the case for the density of states (DOS) of the parent h-BN/Ni(111), the total density of states (TDOS) of the top:N/fcc:BH configuration is mostly determined by the Ni(111) substrate with some differences in the region of −1 to −3 eV (Fig. S2†). In particular, the formation of new B–H bonds leads to the 3 eV red shift of the leading intensity peak in both spin-up and spin-down partial DOS (PDOS) channels of the h-BNH fragment (Fig. S1 and S2†) due to the rehybridization of the π-system of the parent h-BN. This red shift, however, was not observed in neither of SPMDS, NEXAFS, nor UPS. No spin-polarized states corresponding to the peak C′ in our SPMDS spectra were observed.

The possible reason for the discrepancy is the self-interaction error (SIE). It was previously suggested that the SIE, especially the delocalization error, is particularly severe in hydrogenated graphene.³² The detailed mechanism of how the SIE misleads the results in the case of h-BN hydrogenation is an open question, but it should be noted that the nearly-degenerate sp³-like state in the B atoms of hydrogenated h-BN (H on B sites) is always fractionally occupied, which is a trigger for the SIE. Moreover, the SIE will be particularly severe as the size of the system expands from free-standing h-BN to h-BN/Ni(111). For a comprehensive understanding of hydrogenated h-BN/Ni(111), methods completely free from SIE are strongly awaited.

Conclusions

In summary, the atomic coordinate and spin-dependent band structure of hydrogenated h-BN adsorbed on Ni(111) was examined by means of NIXSW, LEED, UPS, NEXAFS and SPMDS. The vertical atomic displacement derived from NIXSW indicates that hydrogen atoms are site-selectively adsorbed on boron sites. The re-hybridization of σ and π orbitals together with back-donation from Ni 3d creates a magnetic moment on hydrogenated h-BN. The ferromagnetic density of states of hydrogenated h-BN/Ni(111) was confirmed by means of surface sensitive SPMDS. The adsorbed atomic hydrogen was persistent up to 400 °C, which implies that the adsorption mechanism is not simple physisorption. While the NIXSW result suggests that atomic hydrogen is chemisorbed on boron atoms, which is in good agreement with atomic coordinates of DFT-GGA calculation, the DFT-GGA, however, failed to reproduce the spin-dependent band structure probably because fractional charges appearing in partially-sp³-like boron cause SIE. These experimental results reinforce the chemisorption of hydrogen atoms on boron atoms in the case of h-BN and raise the possibility for SIE in the first-principles studies of hydrogenated h-BN.

Acknowledgements

This work is supported by the Grants-in-Aid for Scientific Research (Grant Numbers 23860067, 24760033 and 16H03875) from the Japan Society for the Promotion of Science (JSPS). A part of this work is performed under the approval of the Photon Factory Advisory Committee (PF PAC No. 2010G660, 2012G741 and 2015G110) of KEK, Japan. The Russian Science Foundation (Grant No. 14-13-00139) supported the work of the Russian team.

References

1. J. M. Xue, J. Sanchez-Yamagishi, D. Bulmash, P. Jacquod, A. Deshpande, K. Watanabe, T. Taniguchi, P. Jarillo-Herrero and B. J. Leroy, Nat. Mater., 2011, 10, 282–285.
2. T. Yamaguchi, Y. Inoue, S. Masubuchi, S. Morikawa, M. Onuki, K. Watanabe, T. Taniguchi, R. Moriya and T. Machida, Appl. Phys. Express, 2013, 6, 073001.
3. R. Decker, Y. Wang, V. W. Brar, W. Regan, H.-Z. Tsai, Q. Wu, W. Gannett, A. Zettl and M. F. Crommie, Nano Lett., 2011, 11, 2291–2295.
4. C. R. Dean, A. F. Young, I. Meric, C. Lee, L. Wang, S. Sorgenfrei, K. Watanabe, T. Taniguchi, P. Kim, K. L. Shepard and J. Hone, Nat. Nanotechnol., 2010, 5, 722–726.
5. K. Watanabe, T. Taniguchi and H. Kanda, Nat. Mater., 2004, 3, 404–409.
6. T. Ohashi, Y. Wang and S. Shimada, J. Mater. Chem., 2010, 20, 5129–5135.
7. P. Wang, S. Orimo, T. Matsushima, H. Fujii and G. Majer, Appl. Phys. Lett., 2002, 80, 318–320.
8. C. Tang, Y. Bando, X. Ding, S. Qi and D. Golberg, J. Am. Chem. Soc., 2002, 124, 14550–14551.
9. Q. Weng, X. Wang, C. Zhi, Y. Bando and D. Golberg, ACS Nano, 2013, 7, 1558–1565.
10. A. W. C. van den Berg and C. O. Arean, Chem. Commun., 2008, 668–681,  10.1039/B712576N.
11. A. Lan and A. Mukasyan, J. Phys. Chem. B, 2005, 109, 16011–16016.
12. G. Mpourmpakis and G. E. Froudakis, Catal. Today, 2007, 120, 341–345.
13. S.-H. Jhi and Y.-K. Kwon, Phys. Rev. B: Condens. Matter, 2004, 69, 245407.
14. S. H. Lim, J. Luo, W. Ji and J. Lin, Catal. Today, 2007, 120, 346–350.
15. J. Li, T. Furuta, H. Goto, T. Ohashi, Y. Fujiwara and S. Yip, J. Chem. Phys., 2003, 119, 2376–2385.
16. A. Nikitin, X. Li, Z. Zhang, H. Ogasawara, H. Dai and A. Nilsson, Nano Lett., 2008, 8, 162–167.
17. B. Mårlid, K. Larsson and J. O. Carlsson, J. Phys. Chem. B, 1999, 103, 7637–7642.
18. J.-F. Jia, H. Wang, X.-Q. Pei and H.-S. Wu, Appl. Surf. Sci., 2007, 253, 4485–4489.
19. Z. Zhou, J. Zhao, Z. Chen, X. Gao, T. Yan, B. Wen and P. v. R. Schleyer, J. Phys. Chem. B, 2006, 110, 13363–13369.
20. N. Koi and T. Oku, Sci. Technol. Adv. Mater., 2004, 5, 625.
21. X. Wu, J. Yang, J. G. Hou and Q. Zhu, J. Chem. Phys., 2004, 121, 8481–8485.
22. S. S. Han, S. H. Lee, J. K. Kang and H. M. Lee, Phys. Rev. B: Condens. Matter, 2005, 72, 113402.
23. P. F. Weck, E. Kim, S. H. Lepp, N. Balakrishnan and H. R. Sadeghpour, Phys. Chem. Chem. Phys., 2008, 10, 5184–5187.
24. V. V. Khvostov, I. Y. Konyashin, E. N. Shouleshov, V. G. Babaev and M. B. Guseva, Appl. Surf. Sci., 2000, 157, 178–184.
25. R. Checchetto, A. Miotello and R. S. Brusa, J. Phys.: Condens. Matter, 2001, 13, 5853.
26. K. R. Koswattage, I. Shimoyama, Y. Baba, T. Sekiguchi and K. Nakagawa, J. Chem. Phys., 2011, 135, 014706.
27. C. N. R. Rao, H. Matte, K. S. Subrahmanyam and U. Maitra, Chem. Sci., 2012, 3, 45–52.
28. P. V. Avramov, A. A. Kuzubov, S. Sakai, M. Ohtomo, S. Entani, Y. Matsumoto, H. Naramoto and N. S. Eleseeva, J. Appl. Phys., 2012, 112, 114303–114310.
29. M. Ohtomo, Y. Yamauchi, A. A. Kuzubov, N. S. Eliseeva, P. V. Avramov, S. Entani, Y. Matsumoto, H. Naramoto and S. Sakai, Appl. Phys. Lett., 2014, 104, 051604.
30. X. Sun, A. Pratt, Z. Y. Li, M. Ohtomo, S. Sakai and Y. Yamauchi, J. Appl. Phys., 2014, 115, 17C117.
31. M. Onellion, M. W. Hart, F. B. Dunning and G. K. Walters, Phys. Rev. Lett., 1984, 52, 380–383.
32. S. Casolo, E. Flage-Larsen, O. M. Løvvik, G. R. Darling and G. F. Tantardini, Phys. Rev. B: Condens. Matter, 2010, 81, 205412.
33. A. J. Cohen, P. Mori-Sánchez and W. Yang, Science, 2008, 321, 792–794.
34. A. J. Cohen, P. Mori-Sánchez and W. Yang, Chem. Rev., 2011, 112, 289–320.
35. R. Cortenraad, S. N. Ermolov, V. N. Semenov, A. W. D. van der Gon, V. G. Glebovsky, S. I. Bozhko and H. H. Brongersma, J. Cryst. Growth, 2001, 222, 154–162.
36. M. Kurahashi, X. Sun and Y. Yamauchi, Phys. Rev. B: Condens. Matter, 2010, 81, 193402.
37. M. Kurahashi, T. Suzuki, X. Ju and Y. Yamauchi, Phys. Rev. B: Condens. Matter, 2003, 67, 024407.
38. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter, 1994, 49, 14251–14269.
39. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169–11186.
40. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter, 1976, 13, 5188–5192.
41. D. Usachov, V. K. Adamchuk, D. Haberer, A. Grueneis, H. Sachdev, A. B. Preobrajenski, C. Laubschat and D. V. Vyalikh, Phys. Rev. B: Condens. Matter, 2010, 82, 075415.
42. D. P. Woodruff, Rep. Prog. Phys., 2005, 68, 743–798.
43. Y. Gamou, M. Terai, A. Nagashima and C. Oshima, Sci. Rep. Res. Inst., Tohoku Univ., Ser. A, 1997, 44, 211–214.
44. W. Auwarter, T. J. Kreutz, T. Greber and J. Osterwalder, Surf. Sci., 1999, 429, 229–236.
45. N. Joshi and P. Ghosh, Phys. Rev. B: Condens. Matter, 2013, 87, 235440.
46. K. Amemiya, H. Kondoh, T. Yokoyama and T. Ohta, J. Electron Spectrosc. Relat. Phenom., 2002, 124, 151–164.
47. A. Preobrajenski, A. Vinogradov and N. Mårtensson, Phys. Rev. B: Condens. Matter, 2004, 70, 165404.
48. M. Corso, W. Auwärter, M. Muntwiler, A. Tamai, T. Greber and J. Osterwalder, Science, 2004, 303, 217–220.
49. J. Zhou, Q. Wang, Q. Sun and P. Jena, Phys. Rev. B: Condens. Matter, 2010, 81, 085442.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6nr06308j

‡ Present address: Fujitsu Laboratories Ltd, Atsugi, Kanagawa 243-0197, Japan. E-mail: ohtomo.manabu@jp.fujitsu.com.

§ Present address: Comprehensive Research Organization for Science and Society, Tokai, Ibaraki 319-1106, Japan.

---