Open Access Article
Open Access ArticlePotentiometric sensing of nucleic acids using chemically modified nanopores†
István
Makra
a,
Alexandra
Brajnovits
a,
Gyula
Jágerszki
b,
Péter
Fürjes
c and
Róbert E.
Gyurcsányi
*a
aMTA-BME “Lendület” Chemical Nanosensors Research Group, Department of Inorganic and Analytical Chemistry, Budapest University of Technology and Economics, Szt. Gellért tér 4, 1111 Budapest, Hungary. E-mail: robertgy@mail.bme.hu
bMTA-BME Research Group of Technical Analytical Chemistry, Budapest University of Technology and Economics, Szt. Gellért tér 4, 1111 Budapest, Hungary
cMTA Centre for Energy Research - Institute of Technical Physics and Materials Science, Konkoly-Thege str. 29-33, H-1121 Budapest, Hungary
First published on 30th November 2016
Abstract
Unlike the overwhelming majority of nanopore sensors that are based on the measurement of a transpore ionic current, here we introduce a potentiometric sensing scheme and demonstrate its application for the selective detection of nucleic acids. The sensing concept uses the charge inversion that occurs in the sensing zone of a nanopore upon binding of negatively charged microRNA strands to positively charged peptide-nucleic acid (PNA) modified nanopores. The initial anionic permselectivity of PNA-modified nanopores is thus gradually changed to cationic permselectivity, which can be detected simply by measuring the nanoporous membrane potential. A quantitative theoretical treatment of the potentiometric microRNA response is provided based on the Nernst–Planck/Poisson model for the nanopore system assuming first order kinetics for the nucleic acid hybridization. An excellent correlation between the theoretical and experimental results was observed, which revealed that the binding process is focused at the nanopore entrance with contributions from both in pore and out of pore sections of the nanoporous membrane. The theoretical treatment is able to give clear guidelines for further optimization of potentiometric nanopore-based nucleic acid sensors by predicting the effect of the most important experimental parameters on the potential response.
Introduction
Nanopore-based electrochemical sensors emerged as a versatile platform1 to detect and characterize, without external labels and amplification, nanoparticles,2–5 and macromolecules6 (most often nucleic acids).7–10 The detection mechanism is dominantly based on monitoring the electrical conductivity changes of the extremely small volume defined by a nanopore upon individual species of comparable size passing through or residing in the nanopore. These changes are generally detected by measuring the current induced by an external transpore potential in a setup that consists of two electrically connected electrolyte compartments separated by a membrane integrating a single nanopore or a nanopore array. Despite the wealth of information (e.g., size,5,11 charge,12,13 shape,14etc.) and excellent size resolution15 that this technique can provide on single species, complex samples generally require the use of selective receptors either immobilized to the nanopore environment16–22 or added to the sample23,24 to generate responses that can be selectively distinguished from the background. As the target species become smaller, the nanopore diameters need to be decreased, which requires the accurate assessment of extremely small currents and current changes (pA or fA) often at high time resolution. This makes the current measurement, e.g., resistive pulse sensing, very demanding in terms of instrumentation and noise reduction25,26 which may be limiting for genuine sensing applications. Therefore, we were interested to explore potentiometric readout,27 which only requires, instrumentation-wise, a high input impedance voltmeter, as a more practical electrochemical transduction approach for nanopore-based chemical sensors. Permselective, charged nanopore membranes were shown to generate a potential response either for cations or anions depending on the charge sign of the nanopore surface.28 This response was found to be described by the Nernst–Planck/Poisson model for water permeable charged pores, which approaches ideal Nernstian behavior as the pore diameter is reduced to the range of the Debye layer thickness.29 While such permselective pores exhibit no selectivity among ions of the same charge sign30 we have shown that additional chemical modifications of the permselective nanopores with a hydrophobic compound to exclude water from the pores and a selective ion complexing agent can turn nanopores into ion-selective channels.27 By employing gold coated track-etched membranes with such chemical modification and using a Ag+-selective ligand we were able to develop potentiometric nanopore-based Ag+-selective electrodes in a solvent-free all-solid state design with a nanomolar limit of detection.27 Although direct potentiometric detection is applicable in principle for any ion, its simple extension to polyions such as nucleic acids is rendered unpractical by the very small theoretical sensitivity, i.e. the slope of the Nernstian response scales inversely with the charge of the ion. This problem has been solved for conventional liquid membrane-based potentiometric polyion electrodes by employing non-equilibrium phase boundary potential measurements, as demonstrated for heparin.31,32However, these polymeric ion-exchanger membranes do not provide enough selectivity to extend the potentiometric method for the determination of other polyions such as nucleic acids at low concentrations. In this paper we address this problem by proposing a new potentiometric sensing scheme based on equilibrium potential response which exploits the “charge inversion”20,33 phenomena occurring in peptide nucleic acid (PNA)-modified nanopores upon selective binding of complementary nucleic acids (NAs).
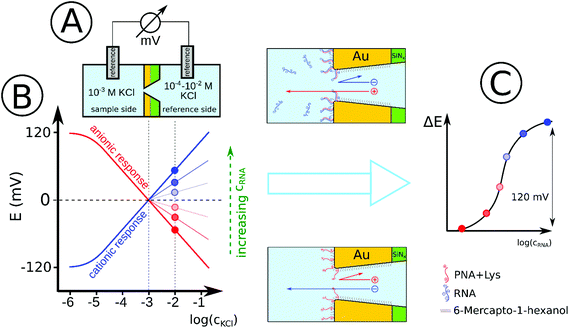
For the proof of principle we used gold nanopore arrays consisting of 7 hexagonally arranged pores (Fig. S1, ESI†)34 modified with positively charged thiol labeled PNA strands for the detection of a 22-mer microRNA (miRNA) as a model for conserved short length single stranded nucleic acids.35 Our hypothesis was that such membranes exhibit anionic permselectivity which upon selective binding of the negatively charged complementary microRNA strands is switched to cationic permselectivity in a concentration dependent manner and the associated potential increase can be used for quantitation (Scheme 1). We were further interested to determine the concentration dependence of this process and to theoretically describe the response mechanism considering for the first time the surface density of the PNA probe and its deployment in the nanopore environment.
Experimental
Reagents and solutions
Solid-state gold nanopore structures were fabricated using a combination of silicon based 3D MEMS/NEMS technology and focused ion beam (FIB) etching. In essence, 380 μm thick Si wafers with three subsequent layers of non-stoichiometric silicon nitride (SiNx), Ti oxide adhesion layer and gold with thicknesses of 205, 5 and 150 nm, respectively, were subjected to anisotropic etching of the Si layer to reveal a SiNx/Au membrane of 700 × 700 μm2. In this membrane 7 conical nanopores (solid angle of 9.2°) of equal tip diameters in the range of 30–80 nm were drilled by FIB using Ga+ ions (Fig. S1, ESI†).34,36 The gold surfaces were modified using thiol terminated 18-mer PNA (N′-Lys-GCTTTTTGCTCGTCTTAT-AEEA-C6-SH-C′), where C6 is (CH2)6 spacer and AEEA 2-(2-aminoethoxy)ethoxyacetic acid (Eurogentec Seraing, Belgium). 22-mer microRNA (5′-AUAAGACGAGCAAAAAGCUUGU-3′) or its DNA analog was used as the target while a similar length random sequence (5′-AGUACUAAUUCGUCUCUGUUCU-3′) was used as the negative control (NC DNA). The PNA strands were immobilized to the gold nanopore in a prehybridized form with a short complementary 7-mer DNA oligo (5′-AAGACGA-3′) to ensure a self-controlled surface density optimal for target hybridization.37 The immobilization was performed in 3× saline-sodium-citrate (SSC) buffer. The buffer components, inorganic salts and nucleic acid strands were purchased from Sigma and aqueous solutions were prepared with 18.2 MΩ × cm resistivity deionized water (Millipore, Bedford, MA).Modification of the gold nanopore array
Before modification, the nanoporous membranes were submerged in 1 ml piranha solution (96% H2SO4 + 35% H2O2 in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, cooled to room temperature) for 15 minutes, then cleaned with copious amount of DI water (Caution: the piranha solution reacts violently with most organic materials and must be handled with extreme care). The gold surface of the chip was modified with the prehybridized PNA–DNA duplex by placing a 10 μl drop on each side of the nanoporous membrane from a SSC solution containing 5–5 μM PNA and 7-mer DNA and was incubated at 4 °C for 12 h. After washing with copious amounts of DI water, the chip was submerged in 1 mL 1 mM water based 6-mercapto-1-hexanol (MH) solution for 30 min to block the remaining gold surface. The PNA–DNA duplex was dehybridized by gentle mixing in 100 mM NaOH for 15 min at 35 °C, then in the same solution at 25 °C for 30 min. Finally the chips were conditioned in 10−3 M KCl + 10−4 M HCl for 15 min at room temperature.
1 ratio, cooled to room temperature) for 15 minutes, then cleaned with copious amount of DI water (Caution: the piranha solution reacts violently with most organic materials and must be handled with extreme care). The gold surface of the chip was modified with the prehybridized PNA–DNA duplex by placing a 10 μl drop on each side of the nanoporous membrane from a SSC solution containing 5–5 μM PNA and 7-mer DNA and was incubated at 4 °C for 12 h. After washing with copious amounts of DI water, the chip was submerged in 1 mL 1 mM water based 6-mercapto-1-hexanol (MH) solution for 30 min to block the remaining gold surface. The PNA–DNA duplex was dehybridized by gentle mixing in 100 mM NaOH for 15 min at 35 °C, then in the same solution at 25 °C for 30 min. Finally the chips were conditioned in 10−3 M KCl + 10−4 M HCl for 15 min at room temperature.
Potentiometric measurements
The chips were secured in a transport cell to separate two compartments, each accommodating a double junction Ag/AgCl electrode (No. 60729.100; Metrohm AG, Switzerland), with 3 M KCl as inner and 1 mM KCl as outer filling solution. The transpore potential was measured under continuous stirring by connecting the electrodes to a high-input impedance (1015 Ω) 16-channel pH meter (Lawson Labs, Inc., Malvern, PA, USA). For off-line detection of the NA binding, the nanopore membranes were incubated outside of the transport cell by placing a drop of the nucleic acid sample (10−7–10−6 M) in SSC at 4 °C to avoid evaporation. After rinsing with SSC and DI water the membrane was mounted in the transport cell. The potential response indicating the type and magnitude of the permselectivity was measured by filling the sample compartment with 10−3 M KCl and measuring the potential change upon increasing the KCl concentration from 10−4 M to 10−2 M in the reference compartment (facing the SiNx layer of the nanoporous membrane). For on-line measurements the same cell setup was used as above but the reference compartment was filled with 10−2 M KCl and the nucleic acid samples were added directly into the sample compartment (facing the tip of the conical nanopore) and the potential change was measured in real-time (at 10−11–10−7 M miRNA concentrations).Simulations
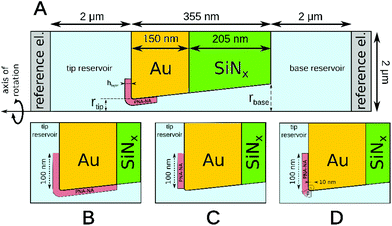
Finite element simulations based on the Poisson and Nernst–Planck equations were performed using Comsol Multiphysics 4.2 software. The simulated geometry consisted of two electrolyte reservoirs connected by a single conical nanopore, which approximates the average behavior of the seven nanopores used in the measurements (Fig. 1). An axisymmetric geometry was used where the axis of the nanopore is the axis of rotation. The implemented conical nanopore geometry was determined by Scanning Electron Microscopy (dtip = 29.3 nm, dbase = 142.8 nm). The PNA strands and PNA–NA hybrids were modeled as a 8.7 nm thick layer adjacent to the gold surface. This length was approximated as the sum of the lengths of a 18-base PNA–DNA double helix (18 × 0.34 = 6.12 nm), twice the radius of gyration of a 4-base ssDNA (2 × 0.7 = 1.4 nm) and twice the radius of gyration of a 3-base nucleic acid considering steric effects only (neglecting electrostatic effects) which approximates the length of the AEEA and C6-SH linkers (2 × 0.584 = 1.168 nm). We used the values for the radius of gyration reported by Sim et al.38 Although the thickness of this layer may depend on the PNA surface density, ionic strength and the state of hybridization, the simulations showed that the variation of layer thickness in a realistic range (4–9 nm) will change the results to only a minor extent, i.e., causing less than 7% error.During simulations the ϕ electric potential satisfied Poisson's equation is:
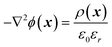 | (1) |
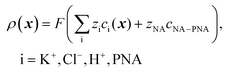 | (2) |
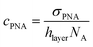 and cNA−PNA are the effective PNA and NA–PNA hybrid concentrations in the PNA layer,
and cNA−PNA are the effective PNA and NA–PNA hybrid concentrations in the PNA layer, 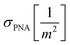 is the surface density of the PNA strands, hlayer is the thickness of the PNA layer, NA is the Avogadro constant, zPNA and zNA are the charge numbers of the PNA and NA strands. In the simulations we assumed first order Langmuir type hybridization kinetics with the reaction rate of the hybridization reaction given in eqn (3).39
is the surface density of the PNA strands, hlayer is the thickness of the PNA layer, NA is the Avogadro constant, zPNA and zNA are the charge numbers of the PNA and NA strands. In the simulations we assumed first order Langmuir type hybridization kinetics with the reaction rate of the hybridization reaction given in eqn (3).39| rhybr = kon(cPNA − cNA−PNA)cNA − koffcNA−PNA | (3) |
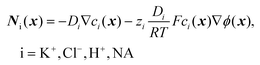 | (4) |
| ∇Ni(x) = 0, i = K+, Cl−, H+, NA | (5) |
The axis of the nanopore (along the z axis) bears an axial symmetry boundary condition. The reference electrode in the base reservoir was grounded (ϕ = 0) while the remaining boundaries were treated as uncharged walls (−∇ϕ·n = 0), where n is the normal unit vector of the given surface. At the two reference electrodes we assumed the same ion concentrations as in the bulk of the solution in the respective compartments. The remaining boundaries were impermeable to ions (Ni·n = 0).
According to the measurement conditions, the simulations assumed a pH of 4.2 where the charge of the nucleic acids was calculated based on their nucleotide and lysine content and the nucleotide pKs43,44 with the use of the Henderson–Hasselbalch equation (see ESI†). The parameters used for the simulation are summarized in Table 1.
| Constants/parameters | Values | Details |
|---|---|---|
| D K + | 1.957 × 10−9 [m2 s−1] | Diffusion constant of K+ |
| D Cl − | 2.032 × 10−9 [m2 s−1] | Diffusion constant of Cl− |
| D H + | 9.31 × 10−9 [m2 s−1] | Diffusion constant of H+ |
| D NA | 9.35 × 10−11 [m2 s−1] | Diffusion constant of 22-mer microRNA45 |
| z PNA | 5.75 | Charge number of 18-mer ssPNA with terminal lysine (at pH 4.2) |
| z NA | −12.7 | Charge number of 22-mer microRNA (at pH 4.2) |
| σ PNA | 5.4 × 1011–7.5 × 1013 [cm−2] | Surface density of PNA |
| K d | 10−9–10−8 [mol l−1] | Dissociation constant of the PNA–NA complex, Kd = koff/kon |
| k on | 104–105 [l (mol s)−1] | Association rate constant of the PNA–NA complex |
| k off | 10−4–10−3 [s−1] | Dissociation rate constant of the PNA–NA complex |
| c NA | 10−11–10−7 [mol l−1] | Concentration of microRNA in the sample |
The fitting of the kinetic data was done with the cma 1.1.06 python package which uses a Covariance Matrix Adaptation Evolution Strategy (CMA-ES) for non-linear numerical optimization. CMA-ES is a stochastic derivative-free method46 that uses only the ranking between candidate solutions and is useful to avoid noise stemming from derivation. To facilitate the comparative overview of the experimental data and their theoretical fitting, the results were plotted as potential change (ΔE), i.e. by shifting the curves to have zero potential when no NA is hybridized to the PNA-modified nanopores.
Results and discussion
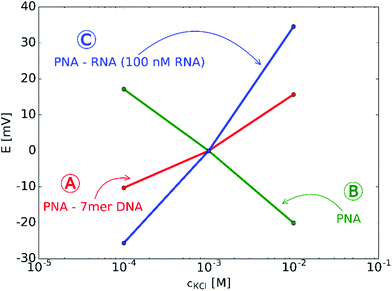
The starting premises of the work was to exploit the charge change that occurs upon selective binding of negatively charged miRNAs to a positively charged PNA-modified nanopore. However, since PNAs are neutral at physiological pH a positively charged, lysine terminated 18-mer PNA strand was custom-synthesized and used. This ensured anion permselectivity indicated by a negative slope of the transmembrane potential as a result of increasing the KCl concentration on the reference side of the nanopore. However, we found that the anionic response is more robust if the positive charge of the PNA was further increased by lowering the pH of the solutions, i.e., by using 0.1 mM HCl as background (actual pH was 4.2). This pH was selected after calculating the net charges of the miRNA and PNA strands as a function of the pH. The calculation took into account their exact sequence as the net charge of PNA and NAs can vary in a large extent as a function of their nucleotide composition (Fig. S2, ESI†).The direct immobilization of PNA for optimal hybridization efficiency is rendered difficult on planar gold surfaces by the strong nonspecific adsorption of the PNA strands and we found this to be even more critical within a nanoconfinement with curved surface. To overcome this problem the thiol-terminated PNA strands were immobilized in a prehybridized form with a short 7-mer complimentary DNA strand that we found earlier by surface plasmon resonance (SPR) to self-regulate the surface density of immobilized strands for optimal hybridization efficiency without the need of lengthy optimization experiments37 and also to reduce the extent of non-specific adsorption.34 After immobilization of the prehybridized strand we observed a cationic response that could be turned into an anionic response by removing the weakly bound short DNA strand with 0.1 M NaOH (Fig. 2). The anionic response could be then reverted back to cationic upon contact with the complementary NA (the larger slope than for the 7-mer PNA–DNA complex is due to the larger negative charge of the 22-mer RNA strand). Despite of the subnernstian responses, the potential stability at each KCl level was found to be remarkably stable (Fig. S3 and S4, ESI†). Of note, voltammetric experiments may also be used to investigate the surface charge of nanopores as showed very early by Bard47 through their current rectification properties. However, to exhibit current rectification the nanopores should feature a marked geometrical or charge distribution asymmetry.48 In principle such asymmetries are not required for potentiometric detection (i.e., even cylindrical nanopores can be used)29 and no external perturbation is needed, which in case of current rectification often manifests in hysteresis and scan-rate dependence.49
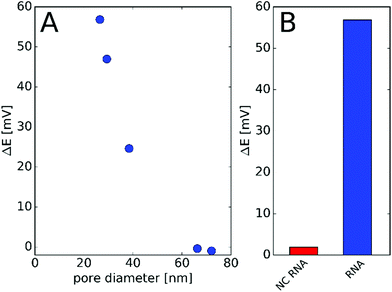
The effect of the nanopore diameter on the observed potential response was studied using nanopores with various diameters down to 26 nm. After modification with PNA, the nanopores were challenged with 1 μM NA and the potential change before and after incubation was determined. We found that the nanopore with the smallest restriction gave the largest potential response while pores with diameters exceeding 60 nm show practically no response (Fig. 3A). These findings are in agreement with our previous study on the effect of the diameter and surface charge density of the nanopores on their permselectivity.29 The potential response was selective for the ca. 26 nm diameter nanopore array, i.e., the response for NC NA remained under 5 mV (Fig. 3B). A similarly small non-specific response was found earlier by SPR,37 which indicates that the detected response for the NC NA reflects the selectivity of the PNA probe rather than being a deficiency of the nanopore sensing. For the following investigations we used membranes with 7 nanopores of diameters between 26 and 30 nm. This size range was a compromise rather than an optimum as the fabrication of smaller diameter pores by FIB would have been possible at much lower yields and higher geometrical uncertainty.
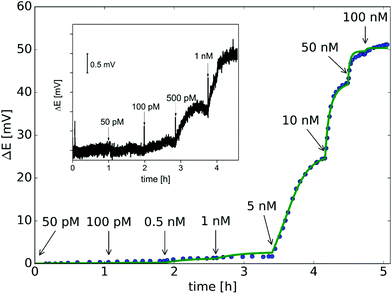
Quantitative measurements involving complementary miRNA (Fig. 4) indicates that a significant potential response is elicited from 0.1 nM that reaches saturation at around 50 nM and follows a sigmoidal shape. Interestingly, the same sigmoidal response with narrow dynamic range is also characteristic for potentiometric polyelectrolyte measurements that use polymeric ion exchanger membrane-based electrodes,50 but their detection limit is ca. an order of magnitude higher.
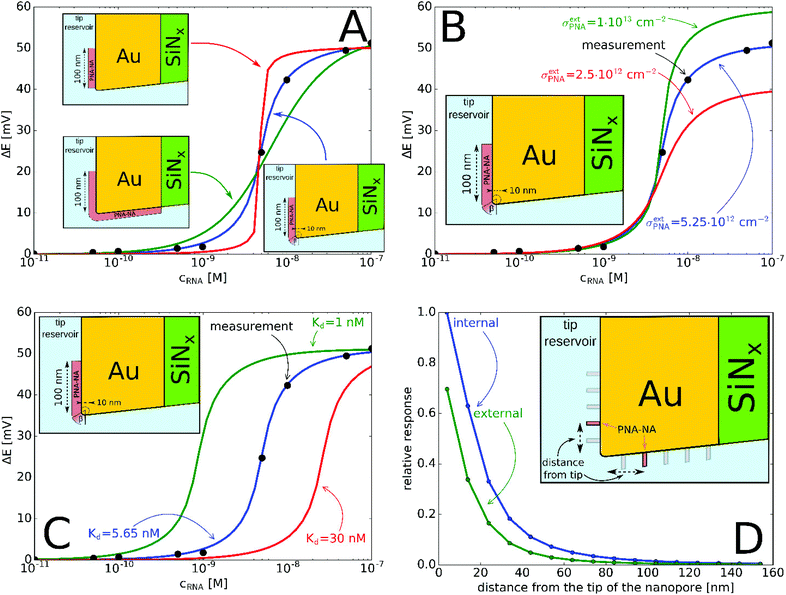 | ||
| Fig. 4 (A) Experimental and simulated potential response of the PNA-modified nanopore sensor as a function of miRNA concentration. The simulated responses considered: (A) different locations of the active PNA layer according to Fig. 1B–D. (The PNA surface density is σPNA = 5.7 × 1011 cm−2 (green), σPNA = 8 × 1013 cm−2 (red), σextPNA = 5.25 × 1012 cm−2 with γ = 2.44 (blue) and Kd = 5.65 nM.) (B) Different PNA surface densities at the outer membrane surface, σextPNA (Kd = 5.65 nM and the PNA layer is the same as on the inset with γ = 2.44); (C) different Kd values (σextPNA = 5.25 × 1012 cm−2 and the PNA layer is the same as on the inset with γ = 2.44). (D) Simulation of the relative potential response upon PNA–NA hybridization as a function of the PNA location from the nanopore tip (see inset). Simulations were made by moving a PNA layer of 2 nm width (in 3D corresponds to a PNA “ring”) independently, both along the external and internal gold surface and calculating the relative potential change in response to 100 nM complementary NA. | ||
The potential span for the whole miRNA concentration range is ca. 50 mV, which is intriguing given that switching from an ideal anionic to an ideal cationic Nernstian response should result in ca. 120 mV potential difference (Scheme 1) in the setup we used, i.e. 10−3 and 10−2 M KCl at the sample and reference side of the nanoporous membrane respectively. The reason is that neither the PNA-modified nor the miRNA saturated nanopores show ideal permselectivity, i.e., there is a mixed ionic transport with either anionic or cationic transport dominating, respectively, but without full exclusion of the oppositely charged ions from the nanopore. The non-ideal permselectivity of such diameter nanopores may be explained either by a low surface charge density and/or that the binding may not occur along the full length of the nanopore. The simulations have shown that with this nanopore geometry it is impossible to match the experimental results at physically meaningful Kd and surface density values by assuming a homogeneous PNA surface density both inside the pore and on the exterior gold surface. Similarly, if we assumed that a homogeneous PNA layer covers only outside the exterior membrane surface, the resulting PNA surface densities needed to generate a match for the experimental results was significantly higher than the (2–4) × 1013 cm−2 maximal values reported in the literature for the surface density of NAs.51,52 After a systematic simulation study we come to the conclusion that the best fit is obtained for a PNA distribution which is homogenous on the external gold surface with a surface density (σextPNA) that gradually falls to zero around the tip of the nanopore, as described by a power function 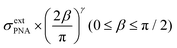 where β is the angle as seen on Fig. 1D and the exponent γ is an additional fitting parameter. To reach this response the PNA surface density on the external gold surface was an experimentally perfectly feasible value (σextPNA = 5.25 × 1012 cm−2). By fitting we obtained a Kd of 5.65 nM and an exponent γ = 2.44. The simulations are very robust as the three main fitting parameters: the location of the PNA layer, the surface density of the PNA layer and the equilibrium dissociation constant of the hybridization have distinguishable influences on the shape of the miRNA calibration curve:
where β is the angle as seen on Fig. 1D and the exponent γ is an additional fitting parameter. To reach this response the PNA surface density on the external gold surface was an experimentally perfectly feasible value (σextPNA = 5.25 × 1012 cm−2). By fitting we obtained a Kd of 5.65 nM and an exponent γ = 2.44. The simulations are very robust as the three main fitting parameters: the location of the PNA layer, the surface density of the PNA layer and the equilibrium dissociation constant of the hybridization have distinguishable influences on the shape of the miRNA calibration curve:
(i) the location of the PNA layer influences the steepness of the calibration (Fig. 4A), i.e., if the PNA layer is confined solely to the outer surface then the dynamic range decreases, while it increases if the in-pore PNA layer dominated the response;
(ii) the surface density of the PNA layer determines the magnitude of the potential response (Fig. 4B) as an increased surface density of both the PNA and PNA–miRNA layers increases the charge density on the nanopore which leads to increased anionic and cationic permselectivity, respectively;
(iii) finally, the Kd determines the concentration corresponding to the inflection point of the sigmoidal curve (Fig. 4C) with a smaller Kd shifting the curve horizontally towards lower concentrations, i.e., toward lower limit of detection.
Thus contrary to the general belief that the immobilization of nucleic acids occurs in a straightforward manner within nanopores of only few tens of nm diameter, these results show that this may not be always the case. At this stage the exact reason for the deficient in-pore immobilization is not known, however, we assume that the access of larger polyectrolytes solely by diffusion in the nanopores is hindered by both entropic and charge repulsion effects. The latter means that since already small ions are excluded from the permselective nanopores, the binding of charged species in the vicinity of the smallest restriction may effectively hinder the access of similar charge-sign polyelectrolytes even at the relatively high ionic strength employed during immobilization.
Given the slightly conical shape of the nanopores made by FIB, the chemical environment of the smallest restriction of the nanopore (smaller diameter entrance) that includes both the outer membrane surface and the inner pore surface in its close vicinity should have the largest effect on the potential response. Systematic simulations were performed to better quantify the relative contribution of the in-pore and outer pore contributions to the potential response. Fig. 4D shows that the closer the PNA layer is located to the pore entrance the larger the potential response, however this vanishes when the PNA layer is further apart than ca. 100 nm from the tip entrance. Interestingly, while the PNA layer in the pore has a larger contribution to the response, as expected, at sufficiently small distances from the entrance (in this case ca. 30 nm) the response starts to be more equally influenced by the outer and inner PNA layers, i.e., the slope of the relative responses as function of the distance from the tip becomes comparable. Similar gating effects were observed with glass nanopore electrodes where the chemical modification of the external glass surface had a marked effect on the accessibility of redox mediators to recessed nanodisk electrodes.53 Overall, however, the contribution of the PNA layer on the outer membrane surface may not exceed ca. 70% of the PNA layer in the pore at the same distance from the entrance. Certainly, the results are valid for the particular pore geometry used in this study but it is easy to foresee that conical pores with larger solid angles will increase the contribution of the outer membrane surface to the overall response.
While the off-line measurement of nucleic acids was made only to be able to independently assess the permselectivity of the nanopores at different hybridization stages, this is not a practical scheme for nucleic acid analysis. Therefore, we pursued the real time detection of complementary nucleic acids by adding the nucleic acid samples directly into the sample compartment and recording the resulting potential changes. The results confirmed that the miRNA binding can be followed label-free in real-time until the equilibrium is reached, which reveals the kinetics of the binding process. The implementation of a time-dependent model, as opposed to the steady state approach, allowed to determine the association kon and dissociation koff rate constants by fitting the model to the potential-time trace obtained during miRNA calibration (Fig. 5). The validity of the theoretical model is further supported by the excellent fit obtained for the whole microRNA concentration range. Although an exact comparison is difficult because of the different experimental parameters and different NAs used but the kon, koff, and Kd obtained in this study are in agreement with the range of data previously reported for PNA–NA hybridization on planar surfaces.40,42,54–59 It is important to note that under the experimental conditions used only the miRNA bound to the sensing zone of the nanopore influences the potential signal and therefore the unbound target strands in the sample bulk do not need to be removed. This is a clear advantage of the proposed potentiometric label-free sensing principle compared with conventional heterogeneous phase hybridization assays based on labels and end-point detection. Furthermore the time-dependent model enables the determination of the kinetic parameters without regeneration between subsequent miRNA additions.
The theoretically achievable LOD based on the standard deviation of the potential signal in the blank solution (σ = 0.08 mV) was estimated to ca. 100 pM, which is in good agreement with the experimentally detected NA concentration (Fig. 5 inset). While the present study focused on the fundamental understanding and demonstration of potentiometric signal transduction mechanism for nanopore-based nucleic acid, this non-optimized setup already provides better LOD than we obtained with SPR measurements (ca. 800 pM),37 the golden standard method for studying biomolecular interaction kinetics.
Conclusion
The results support the feasibility of using potentiometric transduction for the selective detection of nucleic acids exploiting the charge change that occurs in positively charged PNA modified nanopores upon hybridization with negatively charged complementary nucleic acid strands. We were able to describe the sigmoidal shaped response curves and based on that, reveal the most probable location of the PNA layer in the nanopore environment. Moreover, we were able to model not only the steady state response but also the real-time potential-time response during complementary nucleic acid additions, which is unprecedented. Through the corroborative use of the experimental data and the theoretical model we have estimated the association and dissociation rate constants of the miRNA hybridization in the nanopore environment. Even this “simplified” model that neglects the electrostatic and steric effects posed by hybridization proved to be very useful in understanding the potentiometric response of nanopore sensors. The LOD compares favorably with other nanopore-based nucleic acid sensing principles without amplification (typically with LODs between ca. 0.1 nM and 1 nM)20,60,61 but lags behind methods using salt gradient amplification.62 However, we believe that the simple detection methodology that this potentiometric sensing concept offers is very appealing compared to the complexity of resistive pulse sensing, which generally requires pores of less than 5 nm in diameter for direct detection of NAs. The optimization of the nanopore geometry and modification along the directions determined in this study may further improve the analytical performance. Moreover, the proposed potentiometric scheme might be readily adapted for detection of other polyions with great practical importance, such as heparin.Acknowledgements
This work was supported by the “Lendület” Program of the Hungarian Academy of Sciences (LP2013-63). Further support from NKFIH and ENIAC JU via ENIAC CAJAL4EU project (KMR-12-1-2012-0107) as well as NKFIH NN 117637 is acknowledged.References
- S. Majd, E. C. Yusko, Y. N. Billeh, M. X. Macrae, J. Yang and M. Mayer, Curr. Opin. Biotechnol., 2010, 21, 439–476 CrossRef CAS PubMed.
- R. W. DeBlois and C. P. Bean, Rev. Sci. Instrum., 1970, 41, 909–916 CrossRef.
- P. Terejánszky, I. Makra, P. Fürjes and R. E. Gyurcsányi, Anal. Chem., 2014, 86, 4688–4697 CrossRef PubMed.
- R. R. Henriquez, T. Ito, L. Sun and R. M. Crooks, Analyst, 2004, 129, 478–482 RSC.
- R. Vogel, G. Willmott, D. Kozak, G. S. Roberts, W. Anderson, L. Groenewegen, B. Glossop, A. Barnett, A. Turner and M. Trau, Anal. Chem., 2011, 83, 3499–3506 CrossRef CAS PubMed.
- H. Bayley and C. R. Martin, Chem. Rev., 2000, 100, 2575 CrossRef CAS PubMed.
- J. J. Kasianowicz, E. Brandin, D. Branton and D. W. Deamer, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 13770–13773 CrossRef CAS.
- N. An, A. M. Fleming, H. S. White and C. J. Burrows, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 11504–11509 CrossRef CAS PubMed.
- H. Bayley, Clin. Chem., 2015, 61, 25–31 CAS.
- B. M. Venkatesan and R. Bashir, Nat. Nanotechnol., 2011, 6, 615–624 CrossRef CAS PubMed.
- Y. Wang, K. Kececi, M. V. Mirkin, V. Mani, N. Sardesai and J. F. Rusling, Chem. Sci., 2013, 4, 655–663 RSC.
- T. Ito, L. Sun and R. M. Crooks, Anal. Chem., 2003, 75, 2399–2406 CrossRef CAS PubMed.
- R. Vogel, W. Anderson, J. Eldridge, B. Glossop and G. Willmott, Anal. Chem., 2012, 84, 3125–3131 CrossRef CAS PubMed.
- Y. Qiu, P. Hinkle, C. Yang, H. E. Bakker, M. Schiel, H. Wang, D. Melnikov, M. Gracheva, M. E. Toimil-Molares, A. Imhof and Z. S. Siwy, ACS Nano, 2015, 9, 4390–4397 CrossRef CAS PubMed.
- S. R. German, T. S. Hurd, H. S. White and T. L. Mega, ACS Nano, 2015, 9, 7186–7194 CrossRef CAS PubMed.
- S. Howorka, L. Movileanu, O. Braha and H. Bayley, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 12996–13001 CrossRef CAS PubMed.
- P. Kohli, C. C. Harrell, Z. Cao, R. Gasparac, W. Tan and C. R. Martin, Science, 2004, 305, 984–986 CrossRef CAS PubMed.
- Z. Siwy, L. Trofin, P. Kohli, L. A. Baker, C. Trautmann and C. R. Martin, J. Am. Chem. Soc., 2005, 127, 5000–5001 CrossRef CAS PubMed.
- S. M. Iqbal, D. Akin and R. Bashir, Nat. Nanotechnol., 2007, 2, 243–248 CrossRef CAS PubMed.
- G. Jágerszki, R. E. Gyurcsányi, L. Höfler and E. Pretsch, Nano Lett., 2007, 7, 1609–1612 CrossRef PubMed.
- L. Movileanu, S. Howorka, O. Braha and H. Bayley, Nat. Biotechnol., 2000, 18, 1091–1095 CrossRef CAS PubMed.
- S. Ding, C. Gao and L.-Q. Gu, Anal. Chem., 2009, 81, 6649–6655 CrossRef CAS PubMed.
- J. D. Uram, K. Ke, A. J. Hunt and M. Mayer, Angew. Chem., Int. Ed., 2006, 45, 2281–2285 CrossRef CAS PubMed.
- Q. Zhao, G. Sigalov, V. Dimitrov, B. Dorvel, U. Mirsaidov, S. Sligar, A. Aksimentiev and G. Timp, Nano Lett., 2007, 7, 1680–1685 CrossRef CAS PubMed.
- R. M. M. Smeets, U. F. Keyser, N. H. Dekker and C. Dekker, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 417–421 CrossRef CAS PubMed.
- I. Makra and R. E. Gyurcsányi, Electrochem. Commun., 2014, 43, 55–59 CrossRef CAS.
- G. Jágerszki, A. Takács, I. Bitter and R. E. Gyurcsányi, Angew. Chem., Int. Ed., 2011, 50, 1656–1659 CrossRef PubMed.
- M. Nishizawa, V. P. Menon and C. R. Martin, Science, 1995, 268, 700–702 CrossRef CAS PubMed.
- I. Makra, G. Jágerszki, I. Bitter and R. E. Gyurcsányi, Electrochim. Acta, 2012, 73, 70–77 CrossRef CAS.
- E. Grygolowicz-Pawlak, G. A. Crespo, M. Ghahraman Afshar, G. Mistlberger and E. Bakker, Anal. Chem., 2013, 85, 6208–6212 CrossRef CAS PubMed.
- B. Fu, E. Bakker, J. H. Yun, V. C. Yang and M. E. Meyerhoff, Anal. Chem., 1994, 66, 2250–2259 CrossRef CAS PubMed.
- S. C. Ma, V. C. Yang and M. E. Meyerhoff, Anal. Chem., 1992, 64, 694–697 CrossRef CAS PubMed.
- M. Ali, R. Neumann and W. Ensinger, ACS Nano, 2010, 4, 7267–7274 CrossRef CAS PubMed.
- G. Lautner, M. Plesz, G. Jágerszki, P. Fürjes and R. E. Gyurcsányi, Electrochem. Commun., 2016, 71, 13–17 CrossRef CAS.
- G. Lautner and R. E. Gyurcsányi, Electroanalysis, 2014, 26, 1224–1235 CrossRef CAS.
- P. Fürjes, Z. Fekete, L. Illés, A. L. Tóth, G. Battistig and R. E. Gyurcsányi, 26th European Conference on Solid-State Transducers, Eurosensor, 2012, 47, pp. 684–687.
- L. Simon, G. Lautner and R. E. Gyurcsányi, Anal. Methods, 2015, 7, 6077–6082 RSC.
- A. Y. L. Sim, J. Lipfert, D. Herschlag and S. Doniach, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2012, 86, 021901 CrossRef PubMed.
- I. Y. Wong and N. A. Melosh, Biophys. J., 2010, 98, 2954–2963 CrossRef CAS PubMed.
- D. Kambhampati, P. E. Nielsen and W. Knoll, Biosens. Bioelectron., 2001, 16, 1109–1118 CrossRef CAS PubMed.
- D. Yao, J. Kim, F. Yu, P. E. Nielsen, E.-K. Sinner and W. Knoll, Biophys. J., 2005, 88, 2745–2751 CrossRef CAS PubMed.
- H. Park, A. Germini, S. Sforza, R. Corradini, R. Marchelli and W. Knoll, Biointerphases, 2007, 2, 80–88 CrossRef CAS PubMed.
- CRC Handbook of Chemistry and Physics, CRC Press, Boca Raton, FLa, 90th edn, 2009 Search PubMed.
- V. Verdolino, R. Cammi, B. H. Munk and H. B. Schlegel, J. Phys. Chem. B, 2008, 112, 16860–16873 CrossRef CAS PubMed.
- A. E. Nkodo, J. M. Garnier, B. Tinland, H. Ren, C. Desruisseaux, L. C. McCormick, G. Drouin and G. W. Slater, Electrophoresis, 2001, 22, 2424–2432 CrossRef CAS PubMed.
- N. Hansen, in Towards a New Evolutionary Computation: Advances in the Estimation of Distribution Algorithms, ed. J. A. Lozano, P. Larrañaga, I. Inza and E. Bengoetxea, Springer, Berlin, Heidelberg, 2006, pp. 75–102 Search PubMed.
- C. Wei, A. J. Bard and S. W. Feldberg, Anal. Chem., 1997, 69, 4627–4633 CrossRef CAS.
- Z. S. Siwy, Adv. Funct. Mater., 2006, 16, 735–746 CrossRef CAS.
- D. Momotenko and H. H. Girault, J. Am. Chem. Soc., 2011, 133, 14496–14499 CrossRef CAS PubMed.
- M. E. Meyerhoff, B. Fu, E. Bakker, J. H. Yun and V. C. Yang, Anal. Chem., 1996, 68, A168–A175 CrossRef.
- T. Goda, A. B. Singi, Y. Maeda, A. Matsumoto, M. Torimura, H. Aoki and Y. Miyahara, Sensors, 2013, 13, 2267–2278 CrossRef CAS PubMed.
- A. N. Rao and D. W. Grainger, Biomater. Sci., 2014, 2, 436–471 RSC.
- G. Wang, B. Zhang, J. R. Wayment, J. M. Harris and H. S. White, J. Am. Chem. Soc., 2006, 128, 7679–7686 CrossRef CAS PubMed.
- K. K. Jensen, H. Ørum, P. E. Nielsen and B. Nordén, Biochemistry, 1997, 36, 5072–5077 CrossRef CAS PubMed.
- J. Liu, S. Tian, P. E. Nielsen and W. Knoll, Chem. Commun., 2005, 2969–2971 RSC.
- H. Park, A. Germini, S. Sforza, R. Corradini, R. Marchelli and W. Knoll, Biointerphases, 2006, 1, 113–122 CrossRef CAS PubMed.
- Y. Sato, K. Fujimoto and H. Kawaguchi, Colloids Surf., B, 2003, 27, 23–31 CrossRef CAS.
- T. Uno, H. Tabata and T. Kawai, Anal. Chem., 2007, 79, 52–59 CrossRef CAS PubMed.
- F. Xu, A. M. Pellino and W. Knoll, Thin Solid Films, 2008, 516, 8634–8639 CrossRef CAS.
- M. Wanunu, T. Dadosh, V. Ray, J. M. Jin, L. McReynolds and M. Drndic, Nat. Nanotechnol., 2010, 5, 807–814 CrossRef CAS PubMed.
- K. Tian, Z. He, Y. Wang, S.-J. Chen and L.-Q. Gu, ACS Nano, 2013, 7, 3962–3969 CrossRef CAS PubMed.
- Y. Wang, D. Zheng, Q. Tan, M. Wang and L.-Q. Gu, Nat. Nanotechnol., 2011, 6, 668–674 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c6nr05886h |
| This journal is © The Royal Society of Chemistry 2017 |