Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Rational design of potential spin qubits manipulated by the valence tautomerism mechanism: quantum-chemical modeling of the trinuclear transition metal complexes with bischelate linkers†
A. A.
Starikova
 and
V. I.
Minkin
and
V. I.
Minkin
 *
*
Institute of Physical and Organic Chemistry at Southern Federal University, Stachka Avenue 194/2, Rostov-on-Don, 344090, Russian Federation. E-mail: minkin@ipoc.sfedu.ru; Fax: +7 863 243 4700
First published on 1st June 2017
Abstract
A new series of transition metal coordination compounds capable of manifesting the properties of logical elements of quantum computers has been computationally designed using the DFT UB3LYP*/6-311++G(d,p) calculations. The trinuclear 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 adducts formed by CuII and CoII acetylacetonates functionalized with di-o-quinone moieties and CoII diketonates have been shown to meet the principal requirements (well-defined and weakly coupled paramagnetic centers) for the compounds with the potential of spin qubits and also have properties, such as thermodynamic stability, low energy gap between electromeric forms and thermally overcoming energy barriers to their spin state switching transition, ensuring the occurrence of valence tautomeric rearrangements as an additional means for modulation of magnetic characteristics of the designed trinuclear complexes.
2 adducts formed by CuII and CoII acetylacetonates functionalized with di-o-quinone moieties and CoII diketonates have been shown to meet the principal requirements (well-defined and weakly coupled paramagnetic centers) for the compounds with the potential of spin qubits and also have properties, such as thermodynamic stability, low energy gap between electromeric forms and thermally overcoming energy barriers to their spin state switching transition, ensuring the occurrence of valence tautomeric rearrangements as an additional means for modulation of magnetic characteristics of the designed trinuclear complexes.
Introduction
The search for molecular systems suitable for operating in quantum information processing has currently become an actively developing area of metal coordination chemistry.1–6 It has been shown that polynuclear transition and lanthanide metal complexes with weakly coupled paramagnetic centers can find an application in the design of spin qubits.7–12 Another approach based on the use of vanadium(IV) compounds13,14 represents experimental evidence of the importance of the rigidity of the molecular structure for the enhancement of quantum coherence. In a more recent paper15 the correlation between low energy vibration modes and quantum coherence was clearly demonstrated.In the development of these studies, we have assumed and computationally justified16–18 that the dinuclear complexes designed on the basis of redox-active (non-innocent19) ligands capable of undergoing thermally or photochemically initiated reversible intramolecular rearrangements caused by electron transfer between the metal and ligand centers (valence tautomerism VT20–25) can acquire useful properties of controllable switching of their spin states allowing additional manipulation by spin qubits. The involvement in the spin exchange processes of paramagnetic centers located on the organic moieties is an important distinction of the dinuclear complexes with redox-active ligands from the weakly coupled metal complexes in which spin densities are concentrated at the metal ions. The key structural parameter controlling the degree of coupling between paramagnetic sites of the complexes with expectable spin qubit properties is a linker group separating these centers. By means of DFT calculations it was predicted that 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
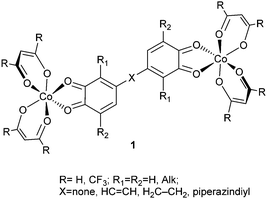
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adducts 1 of cobalt diketonates with redox-active di-o-quinones can undergo two-step VT rearrangements preserving the characteristics of spin qubit species as required by the DiVincenzo criteria26 on the condition of correctly choosing hydrocarbon linker groups X bridging quinone fragments and also the R substituents in the diketone ligand systems.
1 adducts 1 of cobalt diketonates with redox-active di-o-quinones can undergo two-step VT rearrangements preserving the characteristics of spin qubit species as required by the DiVincenzo criteria26 on the condition of correctly choosing hydrocarbon linker groups X bridging quinone fragments and also the R substituents in the diketone ligand systems.
The goal of the present study is to explore the properties of another group of di-o-quinone adducts of cobalt diketonates 2, in which the paramagnetic metal and redox-active ligand centers are divided by a diketonate transition metal linker group. The linker of this type can perform a dual function: separation of paramagnetic centers, and also enrichment of the system with an additional paramagnetic center (M = Co, HSNi, Cu). Preparation of a series of magnetically active ring-like structures on the basis of bischelate metal complexes by linking several heterometallic antiferromagnetic rings has recently been described as a way to synthesize compounds with possible properties of spin qubits.11 Synthesis of the metal diketonates functionalized by two di-o-quinone moieties serving as the donor components of adducts 2 seems to be a feasible procedure accounting for the information on the successful preparation of 3-(4′,5′-dihydroxy-3′,6′-dimethyl)phenylacetylacetone.27
Whereas weak coupling of well-defined paramagnetic centers remains the general and most important condition to be met by any molecular system designed to act as a 2-qubit quantum gate, the complexes formed as the adducts of type 1 and 2 impregnated with thermally regulated VT properties must also comply with the following requirements: (1) sufficient stability of the adduct with respect to dissociation into the components, (2) energy preference of the low-spin (LS) electronic state over the high-spin (HS) state with a relatively low energy gap between the isomers and (3) thermally achievable energy barriers to the LS ⇌ HS VT rearrangements.16 To find within the series of the transition metal complexes 2 the compounds with the potential of spin qubits and also prone to the thermally driven VT rearrangements, i.e. satisfying the above requirements (1)–(3), we have studied the effects of various structural parameters (the nature of the central metal atom M in the bischelate linker, ring centers X and substituents R in the bischelate cobalt moieties) exerted on the magnetic and thermodynamic properties of the complexes. With this purpose detailed density functional theory (DFT) calculations have been performed first on the model complexes featuring certain structural parameters and then on the most prospective complexes 2.
Computational details
The DFT calculations in vacuo were performed using the Gaussian09 program package28 with the UB3LYP* functional29 and the 6-311++G(d,p) basis set. This methodology has been shown to accurately reproduce geometry characteristics of valence-tautomeric complexes,30,31 and also energy parameters of a variety of intramolecular spin-forbidden rearrangements of transition metal complexes.32–36 The stationary points on the potential energy surfaces (PESs) were located by full geometry optimization and checked for the stabilities of the DFT wave function. Exchange coupling of unpaired electrons in the paramagnetic centers was estimated using the “broken symmetry” (BS) formalism.37 There are several approaches to the estimation of exchange interactions (Model Dimer Approach, Doped Cluster Approach and Minimal Cluster Approach).38,39 In the present study, exchange spin coupling constants (J, cm−1) were calculated using the generalized spin projection (GSP) method developed by Yamaguchi et al.40,41 For the search of all possible spin state isomers the Gaussian 09 procedure (Guess = Fragment = N) has been employed. This approach implies a possibility of assuming spin states and signs along with charges for separate parts of a molecule on the stage of generation of the initial guess. Mechanisms of VT rearrangements have been studied by means of calculation of the minimum energy crossing point (MECP) – the point having minimum energy on the seam lying on the crossing point of two corresponding PESs – by implementation of the program code developed by Harvey et al.42 Structural visualizations presented in Fig. 1–3 were prepared using the program suite ChemCraft43 with the calculated atomic coordinates as the input parameters. | ||
| Fig. 2 Optimized geometries of the electromeric forms of adducts 2 (M = Cu; X = O; R = CF3) and structures MECPs calculated by the DFT B3LYP*/6-311++G(d,p) method. | ||
 | ||
| Fig. 3 Optimized geometries of the electromeric forms of adducts 2 (M = HSCo; X = O; R = CF3) calculated by the DFT B3LYP*/6-311++G(d,p) method. | ||
Results and discussion
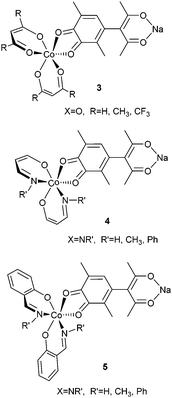
In order to study the effects of the ring center X and substituents R, R′ in the bischelate cobalt fragments of 2 on the stability of adducts and their ability to exhibit VT properties, the calculations have been performed on the abridged dinuclear complexes 3–5 (X = O, NR′, R = H, CH3, CF3, R′ = H, CH3, Ph) with only one bischelate (diketonate, aminovinylketonate and salicylaldiminate) cobalt fragment.The results of the calculations (presented in the ESI,† Fig. S1–S3 and Tables S1–S3) have shown that the insertion of electron-withdrawing trifluoromethyl groups R increases the stability of the mixed-ligand complexes 3 (X = O; R = H, CH3, CF3) and narrows the energy gap between the low-spin (LSCoIII–SQ) and the high-spin (HSCoII–Q) isomers, thus making these compounds appropriate for the occurrence of thermally initiated VT rearrangements. Phenyl substituents at nitrogen atoms of the azomethine cobalt complexes stabilize adducts 4 and 5 (X = NR′; R′ = H, CH3, Ph), while methyl groups decrease their stability with respect to dissociation. The significant energy preference of the electromers (electronic isomers44) LSCoIII–SQ comprising trivalent cobalt ions in the LS state and redox-active ligands in semiquinonate (SQ) form with respect to the HSCoII–Q electromers (>12 kcal mol) points to the low probability of VT rearrangements in the adducts with bis-aminovinylketonates and bis-salicylaldiminates. Thus, the calculations of model systems 3–5 (X = O, NR′; R = H, CH3, CF3, R′ = H, CH3, Ph) allow one to expect that the most suitable cobalt bischelate fragments in the trinuclear adducts 2 (M = Co, Ni, Cu, Zn; X = O, NR′; R = H, CH3, CF3; R′ = H, CH3, Ph) capable of undergoing two-step VT rearrangements should be represented by the diketonates (X = O, R = CH3, CF3).
The influence of the nature of the metal center M and geometry of the coordination site of the bischelate linker on the strength and character of exchange interactions between spins of unpaired electrons of semiquinonate fragments can be studied on the basis of model trinuclear compounds 6 (M = Co, Ni, Cu, Zn) formed by combination of two redox-active 3-(4′,5′-dihydroxy-3′,6′-dimethyl)phenylacetylacetones with double-charged metal ions (Co2+, Ni2+, Cu2+, Zn2+).
Our preliminary DFT UB3LYP*/6-311++G(d,p) calculations45 of complexes 6 have shown significant dependence of their magnetic properties on the type of metal M of the bischelate linker. Complexes comprising zinc and low-spin nickel (which is energetically more favorable than that with HSNi) ions are characterized by triplet biradicaloid electronic configurations and the absence of exchange interactions between spins of the unpaired electrons of semiquinone fragments. Compounds 6 (M = Co) demonstrate weak antiferromagnetic exchange between paramagnetic centers localized at the metal ion and semiquinone moiety. Ferromagnetic ordering between SQ and M is predicted only for the copper complex 6 (M = Cu), which due to small values of exchange spin coupling parameter can serve as the potential basis for spin qubits. In conjunction with the favorable effects of substituents R = CF3 and ring centers X = O elucidated by the study of compounds 3–5 and the results of the calculations performed on complexes 6 it can be inferred that adducts 2 (M = Cu; X = O; R = CH3, CF3) can combine the ability to undergo two-step VT rearrangements (Scheme 1) with weak exchange interactions between their paramagnetic centers as the prerequisite of the necessary quantum entanglement. To justify this assumption we have carried out calculations on the trinuclear complexes 2 (M = Cu; X = O; R = CH3, CF3).
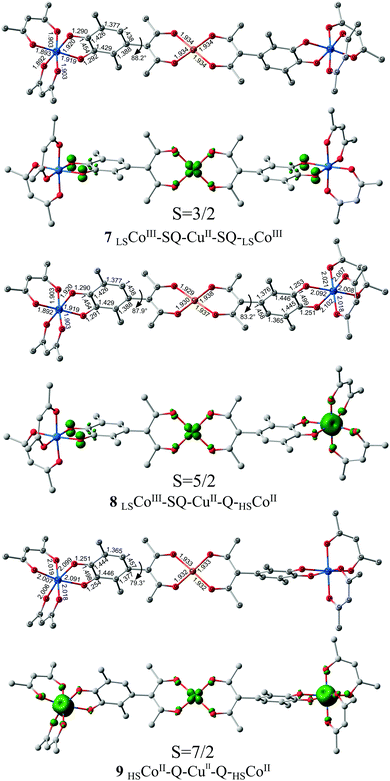
According to the calculations, adducts 2 (M = Cu; X = O; R = CH3, CF3) are stable against dissociation into isolated molecules.46 Electromers LSCoIII–SQ–CuII–SQ–LSCoIII comprising two semiquinone fragments and trivalent cobalt ions in the low-spin state correspond to the ground state of the considered compounds (Fig. 1 and 2). This finding indicates that the adduct formation results in the electron transfer from the metal ions to the di-o-quinone ligand. Estimation of the exchange interactions between paramagnetic centers of the most stable isomer 7LSCoIII–SQ–CuII–SQ–LSCoIII of adducts 2 (M = Cu; X = O; R = CH3) predicts weak antiferromagnetic coupling spins of unpaired electrons of the redox-active ligands and copper (JSQ–Cu = −22 cm−1) and the absence of exchange interactions between semiquinonate moieties (Table 1).
| Structure | S | Estaba | ΔE | ΔH298 | JCu–SQ | J Cu–Co | |
|---|---|---|---|---|---|---|---|
| a Stabilization energies were calculated relative to the isolated molecules of cobalt bischelate and redox-active ligand molecules (see the ESI, Tables S4 and S7). b Exchange interactions between semiquinone (SQ) fragments in the electromers LSCoIII–SQ–CuII–SQ–LSCoIII, between cobalt ion (HSCoII) and semiquinone (SQ) moiety in the electromers LSCoIII–SQ–CuII–Q–HSCoII, and between cobalt ions (HSCoII) in the electromers HSCoII–Q–CuII–Q–HSCoII are absent, therefore constants JSQ–SQ, JSQ–Co and JCo–Co, equal to zero, are not given in the table. | |||||||
| R = CH3 | 7 LSCoIII–SQ–CuII–SQ–LSCoIII | 3/2 | 41.3 | 0.0 | 0.0 | −22 | — |
| 8 LSCoIII–SQ–CuII–Q–HSCoII | 5/2 | 27.2 | 14.0 | 12.0 | −24 | 5 | |
| 9 HSCoII–Q–CuII–Q–HSCoII | 7/2 | 12.9 | 28.3 | 25.5 | — | 4 | |
| R = CF3 | 10 LSCoIII–SQ–CuII–SQ–LSCoIII | 3/2 | 43.4 | 0.0 | 0.0 | −32 | — |
| 11 LSCoIII–SQ–CuII–Q–HSCoII | 5/2 | 40.3 | 3.0 | 2.0 | −31 | 2 | |
| 12 HSCoII–Q–CuII–Q–HSCoII | 7/2 | 36.2 | 7.2 | 5.0 | — | 2 | |
| 13 MECP | 31.4 | 12.0 | |||||
| 14 MECP | 30.2 | 13.1 | |||||
Electromer 8LSCoIII–SQ–CuII–Q–HSCoII with nonequivalent quinone fragments is energy disfavored relative to 7 by 14.0 kcal mol−1 which exceeds the values, typical for VT rearrangements of cobalt complexes47,48 and makes thermally initiated intramolecular redox-process improbable. The calculated parameter JSQ–Cu is equal to −24 cm−1, which is close to that found for electromer 7; exchange between two metal centers bears weak ferromagnetic character (JCu–Co = 5 cm−1). The highest-spin isomer 9HSCoII–Q–CuII–Q–HSCoII represents a molecular complex, in which spin density is localized at the metal centers (Fig. 1). The predicted values of exchange interaction parameters correspond to weak ferromagnetic coupling of spins of unpaired electrons of copper and cobalt (JCu–Co = 4 cm−1) and the absence of exchange interactions between cobalt ions (Table 1). Significant destabilization (ΔE = 28.3 kcal mol−1) of the structure 9HSCoII–Q–CuII–Q–HSCoII with respect to the ground state 7LSCoIII–SQ–CuII–SQ–LSCoIII points to that it cannot be thermally attained. The calculated energy characteristics of electromeric forms of adducts 2 (M = Cu; X = O; R = CH3) clearly indicate strong stabilization of the low-spin state LSCoIII–SQ–CuII–SQ–LSCoIII over a wide temperature range.
It has been earlier shown that insertion of strong electron-withdrawing groups into the diketone fragment of adducts of cobalt diketonates with o-benzoquinones narrows the energy gap between the low-spin and the high-spin electromers.49 The calculations of complex 2 (M = Cu, X = O, R = CF3) with cobalt bis-hexafluoroacetylacetonate fragments (Fig. 2 and Table 1) have shown, indeed, that replacement of methyl groups in the terminal diketonate fragments by trifluoromethyl ones substantially stabilizes the electromers with high-spin divalent cobalt ions (Estab = 36.2 kcal mol−1) and leads to lowering of the relative energies of other electromeric forms 11 and 12 with HSCoII centers. The energy gaps between electromers 11LSCoIII–SQ–CuII–Q–HSCoII and 12HSCoII–Q–CuII–Q–HSCoII and the ground state form 10LSCoIII–SQ–CuII–SQ–LSCoIII are equal to 3.0 and 7.2 kcal mol−1, respectively, and fall into the range of values permissible for the occurrence of thermal VT transformations of cobalt complexes.47,48 Rising the temperature leads to narrowing of the energy gaps between the electromeric forms to facilitate their VT rearrangements (ΔH298 values, Table 1).
To evaluate the energy barriers against the VT rearrangements 10 ⇌ 11 and 11 ⇌ 12 we have calculated the corresponding values of MECPs determining the highest limits of the energy barriers of spin-forbidden reactions. The relative energies of the located structures of MECPs 13 and 14 corresponding to the intersections of the quartet and sextet (13 MECP), and also sextet and octet (14 MECP) potential energy surfaces are equal to 12.1 and 13.0 kcal mol−1, respectively. These values fit well to the conditions for possible occurrence of thermally induced two-step intramolecular electron transfer in adducts 2 (M = Cu; X = O; R = CF3).
The exchange interactions between unpaired electrons of the semiquinone fragments and copper ions in electromers 10LSCoIII–SQ–CuII–SQ–LSCoIII and 11LSCoIII–SQ–CuII–Q–HSCoII bear weak antiferromagnetic character (JSQ–Cu = −31, −32 cm−1), small exchange is predicted between the spins of unpaired electrons of metal centers (JCu–Co = 2 cm−1) in structures 11LSCoIII–SQ–CuII–Q–HSCoII and 12HSCoII–Q–CuII–Q–HSCoII. The calculated values are compatible with those experimentally determined in a number of works aimed at the search for molecules with properties of spin qubits50,51 and close to the results obtained for adducts with cobalt bis-acetylacetonate 2 (M = Cu; X = O; R = CH3) (Table 1), which points to the insignificant influence of CF3-groups on the character and strength of exchange interactions between paramagnetic centers of trinuclear adducts 2.
Therefore, it may be concluded that adducts 2 (M = Cu; X = O; R = CF3) meet the principal requirements (well-defined and weakly coupled paramagnetic centers) imposed on the compounds designed as spin qubit candidates and are also endowed with the properties (thermodynamic stability, low energy gap between the electromers and thermally overcoming energy barrier to their spin state switching rearrangement) that create additional conditions for modulation of magnetic characteristics of this trinuclear complex.
In order to elucidate the effects of the nature of the metal atom M in the bischelate linker group of complexes and also stereochemistry of the coordination site of the linker on energy characteristics of the trinuclear adducts of cobalt bis-hexafluoroacetylacetonate 2 we have performed calculations on complexes 2 (M = HSCo, LSNi, Zn; X = O; R = CF3) with central Co, Ni and Zn atoms. Following the results presented in Tables 1, 2 and Tables S5, S6 (ESI†), the stability and relative energies of electromers of complexes 2 (M = HSCo, LSNi, Zn; X = O; R = CF3) are very close to those calculated for the adduct with copper linker 2 (M = Cu; X = O, R = CF3): the ground states of all complexes are represented by the LSCoIII–SQ–MII–SQ–LSCoIII electromers which are energy preferable compared to electromers LSCoIII–SQ–MII–Q–HSCoII and HSCoII–Q–MII–Q–HSCoII by 3.0–3.2 and 7.2–7.3 kcal mol−1, respectively, and the stabilization energies of the adducts fall in the range of 36.0–36.2 kcal mol−1. These results indicate that the energy characteristics of the electromeric forms of trinuclear adducts 2 are slightly affected by the nature of the central metal atom M. The calculations reveal the absence of the exchange interactions in the compounds with diamagnetic zinc and low-spin spin nickel linkers (Table S6 and Fig. S4, S5, ESI†), which is in accord with the results of the studies of model trinuclear complexes 6 (M = Be, LSNi, Zn).45 At the same time weak exchange interactions were found in adducts 3 (M = HSCo; X = O; R = CF3) with the central high-spin cobalt ion (Fig. 3 and Table 2). This finding makes it possible to regard this compound as having properties of a potential spin qubit.
| Structure | S | Estaba | ΔE | ΔH298 | JCu–SQ | J Cu–Co | |
|---|---|---|---|---|---|---|---|
| a Stabilization energies were calculated relative to the isolated molecules of cobalt bischelate and redox-active ligand molecules (see the ESI, Tables S5 and S7). b Exchange interactions between semiquinone (SQ) fragments in the electromers LSCoIII–SQ–HSCoII(linker)–SQ–LSCoIII, between cobalt ion (HSCoII) and semiquinone (SQ) moiety in the electromers LSCoIII–SQ–HSCoII(linker)–Q–HSCoII, and also between cobalt ions (HSCoII) in the electromers HSCoII–Q–HSCoII(linker)–Q–HSCoII are absent, therefore constants JSQ–SQ, JSQ–Co and JCo–Co, equal to zero, are not presented in the table. | |||||||
| R = CF3 | 15 LSCoIII–SQ–HSCoII(linker)–SQ–LSCoIII | 5/2 | 43.3 | 0.0 | 0.0 | −11 | — |
| 16 LSCoIII–SQ–HSCoII(linker)–Q–HSCoII | 7/2 | 40.1 | 3.2 | 2.1 | −9 | 1 | |
| 17 HSCoII–Q–HSCoII(linker)–Q–HSCoII | 9/2 | 36.0 | 7.2 | 5.1 | — | 1 | |
Conclusions
An expedient way for elucidation of effects of structural parameters on the energy and magnetic properties of adducts 2 involves studying model systems 3–5 (X = O, NR′; R = H, CH3, CF3; R′ = H, CH3, Ph) and 6 (M = Co, Ni, Cu, Zn). The calculations of complexes 4 and 5 on the basis of cobalt bischelates with azomethine ligands revealed the low stability of these compounds. For instance, the high-spin electromeric forms of CoII bis-aminovinylketonate adducts 5 (X = NR′; R′ = H, CH3, Ph) are destabilized with respect to dissociation into the initial components. Annulation of six-membered cycles enhances the stability of complexes 5 (X = NR′; R′ = H, CH3, Ph), and also sharply increases (>11 kcal mol−1) the energy gap between the low-spin LSCoIII–SQ and high-spin HSCoII–Q structures, which excludes the occurrence of redox-processes in the mixed-ligand complexes 2 on the basis of cobalt bis-salicylaldiminates. Insertion of electron-withdrawing groups R = CF3 stabilizes the high-spin electromers 3 (X = O; R = CF3) and narrows the energy gap between the LS and HS electromeric forms to the values typical for the VT rearrangements. The study of model compounds 6 (M = Co, Ni, Cu, Zn) helped to understand the influence of the metal center M in the bischelate linker exerted on the exchange interactions between organic SQ radical-anions in adducts 2. No coupling between the spins of unpaired electrons of the semiquinone fragments was found in the complexes comprising diamagnetic Zn and LSNi ions, whereas weak exchange coupling in complexes 6 with HSCo and Cu central ions allows one to expect spin qubit properties of complexes 2 (M = HSCo, Cu). In summary, analysis of the results obtained makes it possible to reveal the following regularities: functionalization of terminal cobalt complexes allows controlling the energy characteristics of the electromers, while fine tuning of the exchange interactions between paramagnetic centers can be reached via variation of the metal center in the bischelate linker. Being guided by the results of calculations of the model systems 3–6, we could rationally design the trinuclear adducts 2 (M = HSCo, Cu; X = O; R = CF3), potentially capable of undergoing two-step VT rearrangements accompanied by migration of weakly coupled paramagnetic centers.To sum up, the DFT B3LYP*/6-311++G(d,p) calculations performed on a broad series of electrically neutral adducts of CoII diketonates with the functionalized redox-active di-o-quinones 2 (M = Co, Ni, Cu, Zn; X = O, NR′; R = H, CH3, CF3; R′ = H, CH3, Ph) and model compounds 3–6 allowed uncovering of two groups of complexes 2 (M = Cu and Co; X = O; R = CF3) that may potentially have the properties of molecular spin qubits, magnetic characteristics of which can be additionally tuned through the occurrence of low-energy barrier VT rearrangements. The results of the calculations extend the approach17,18,52 to the application of the mechanism of valence tautomerism for the design of molecular 2-qubit quantum gates to trinuclear metal complexes with transition metal containing linker groups.
Acknowledgements
This work has been supported by the Russian Foundation for Basic Research (grant no. 16-33-60019 mol_a_dk).References
-
M. A. Nielsen and I. L. Chuang, Quantum computation and quantum information, Cambridge University Press, Cambridge, 2000 Search PubMed
.
-
D. C. Marinescu, Classical and Quantum Information, Academic Press, 2011 Search PubMed
.
-
Spin-Crossover Materials: Properties and Applications, ed. M. A. Halcrow, John Wiley & Sons, Chichester, 2013 Search PubMed
.
-
G. Aromí, P. Gamez and O. Roubeau, in Spin States in Biochemistry and Inorganic Chemistry: Influence on Structure and Reactivity, ed. M. Swart and M. Costas, John Wiley & Sons, 2016, pp. 263–296 Search PubMed
.
- P. C. E. Stamp and A. Gaita-Arino, J. Mater. Chem., 2009, 19, 1718 RSC
.
- G. Aromí, D. Aguilà, P. Gamez, F. Luis and O. Roubeau, Chem. Soc. Rev., 2012, 41, 537 RSC
.
- M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789 CrossRef CAS PubMed
.
- G. A. Timco, S. Carretta, F. Troiani, F. Tuna, R. J. Pritchard, C. A. Muryn, E. J. L. McInnes, A. Ghirri, A. Candini, P. Santini, G. Amoretti, M. Affronte and R. E. P. Winpenny, Nat. Nanotechnol., 2009, 4, 173 CrossRef CAS PubMed
.
- L. A. Barrios, D. Aguila, O. Roubeau, P. Gamez, J. Ribas-Arino, S. J. Teat and G. Aromí, Chem. – Eur. J., 2009, 15, 11235 CrossRef CAS PubMed
.
- F. Troiani and M. Affronte, Chem. Soc. Rev., 2011, 40, 3119 RSC
.
- G. A. Timco, T. B. Faust, F. Tuna and R. E. P. Winpenny, Chem. Soc. Rev., 2011, 40, 3067 RSC
.
- G. A. Craig, J. Sanchez Costa, D. Aguila, L. A. Barrios, O. Roubeau, S. J. Teat and G. Aromí, New J. Chem., 2011, 35, 1202 RSC
.
- M. Atzori, E. Morra, L. Tesi, A. Albino, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 11234 CrossRef CAS PubMed
.
- L. Tesi, E. Lucaccini, I. Cimatti, M. Perfetti, M. Mannini, M. Atzori, E. Morra, M. Chiesa, A. Caneschi, L. Sorace and R. Sessoli, Chem. Sci., 2016, 7, 2074 RSC
.
- M. Atzori, L. Tesi, S. Benci, A. Lunghi, R. Righini, A. Taschin, R. Torre, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2017, 139, 4338 CrossRef CAS PubMed
.
- V. I. Minkin and A. A. Starikova, Mendeleev Commun., 2015, 25, 83 CrossRef CAS
.
- V. I. Minkin, A. A. Starikova and A. G. Starikov, Dalton Trans., 2015, 44, 1982 RSC
.
- V. I. Minkin, A. G. Starikov and A. A. Starikova, Dalton Trans., 2015, 44, 17819 RSC
.
- Chr. K. Jørgensen, Coord. Chem. Rev., 1966, 1, 164 CrossRef
.
- R. M. Buchanan and C. G. Pierpont, J. Am. Chem. Soc., 1980, 102, 4951 CrossRef CAS
.
- C. G. Pierpont, Coord. Chem. Rev., 2001, 216–217, 99 CrossRef CAS
.
-
D. A. Shultz, in Magnetism: Molecules to Materials II, ed. J. S. Miller and M. Drillon, Wiley, New York, 2001, pp. 281–306 Search PubMed
.
- D. N. Hendrickson and C. G. Pierpont, Top. Curr. Chem., 2004, 234, 63 CrossRef CAS
.
- E. Evangelio and D. Ruiz-Molina, C. R. Chim., 2008, 11, 1137 CrossRef CAS
.
- T. Tezgerevska, K. G. Alley and C. Boskovic, Coord. Chem. Rev., 2014, 268, 238 CrossRef
.
- D. Loss and D. P. Di Vincenzo, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 57, 120 CrossRef CAS
.
- N. O. Druzhkov, M. V. Arsenyev, S. A. Chesnokov, V. K. Cherkasov and G. A. Abakumov, private communication.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 (Revision E.01), Gaussian, Inc., Wallingford CT, 2013 Search PubMed
.
- M. Reiher, O. Salomon and B. A. Hess, Theor. Chem. Acc., 2001, 107, 48 CrossRef CAS
.
- D. Sato, Y. Shiota, G. Juhász and K. Yoshizawa, J. Phys. Chem. A, 2010, 114, 12928 CrossRef CAS PubMed
.
- V. V. Koval, A. G. Starikov, R. M. Minyaev and V. I. Minkin, Dokl. Chem., 2010, 435, 319 CrossRef CAS
.
- O. Salomon, M. Reiher and B. A. Hess, J. Chem. Phys., 2002, 117, 4729 CrossRef CAS
.
- Y. Shiota, D. Sato, G. Juhász and K. Yoshizawa, J. Phys. Chem. A, 2010, 114, 5862 CrossRef CAS PubMed
.
- S. Ye and F. Neese, Inorg. Chem., 2010, 49, 772 CrossRef CAS PubMed
.
- A. G. Starikov, V. I. Minkin, R. M. Minyaev and V. V. Koval, J. Phys. Chem. A, 2010, 114, 7780 CrossRef CAS PubMed
.
- Y. Qu, Int. J. Quantum Chem., 2013, 113, 943 CrossRef CAS
.
- L. Noodleman, J. Chem. Phys., 1981, 74, 5737 CrossRef CAS
.
- A. Bencini, C. Carbonera and F. Totti, Chem. – Eur. J., 2004, 10, 1472 CrossRef CAS PubMed
.
- A. Bencini and F. Totti, J. Chem. Theory Comput., 2009, 5, 144 CrossRef CAS PubMed
.
- K. Yamaguchi, Y. Takahara, T. Fueno and K. Nasu, Jpn. J. Appl. Phys., 1987, 26, L1362 CrossRef CAS
.
- M. Shoji, K. Koizumi, Y. Kitagawa, T. Kawakami, S. Yamanaka, M. Okumura and K. Yamaguchi, Chem. Phys. Lett., 2006, 432, 343 CrossRef CAS
.
- J. N. Harvey, M. Aschi, H. Schwarz and W. Koch, Theor. Chem. Acc., 1998, 99, 95 CrossRef CAS
.
- Chemcraft: http://www.chemcraftprog.com.
- T. Bally, Nat. Chem., 2010, 2, 165 CrossRef CAS PubMed
.
- A. A. Starikova and V. I. Minkin, Mendeleev Commun., 2016, 26, 423 CrossRef CAS
.
- A. A. Starikova and V. I. Minkin, Dokl. Chem., 2017, 473, 57 CrossRef CAS
.
- C. G. Pierpont and O. S. Jung, Inorg. Chem., 1995, 34, 4281 CrossRef CAS
.
- A. Caneschi, A. Cornia and A. Dei, Inorg. Chem., 1998, 37, 3419 CrossRef CAS
.
- V. I. Minkin, A. A. Starikova and R. M. Minyaev, Dalton Trans., 2013, 42, 1726 RSC
.
- E. C. Sañudo, T. Cauchy, E. Ruiz, R. H. Laye, O. Roubeau, S. J. Teat and G. Aromí, Inorg. Chem., 2007, 46, 9045 CrossRef PubMed
.
- L. A. Barrios, D. Aguila, O. Roubeau, P. Gamez, J. Ribas-Arino, S. J. Teat and G. Aromí, Chem. – Eur. J., 2009, 15, 11235 CrossRef CAS PubMed
.
- V. I. Minkin, A. A. Starikova and A. G. Starikov, Dalton Trans., 2016, 45, 12103 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the DFT calculations, including the results of computational modeling of complexes 3–5 (X = O, NR′; R = H, CH3, CF3; R′ = H, CH3, Ph) (Tables S1–S3 and Fig. S1–S3), total energies, expectation values of the spin-squared (S2) operator (Tables S4–S6) and optimized geometries (Fig. S4 and S5) of the electromeric forms of adducts 2 (M = HSCo, LSNi, Cu, Zn; X = O; R = CH3, R = CF3), and total energies of cobalt bischelates and redox-active ligands (Table S7). See DOI: 10.1039/c7nj01071k |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2017 |