Deeper insight into the properties of the newly synthesized macrocycles as drug receptors – some preliminary quantum chemical studies

Abstract

The article presents the results of our more extended studies performed on one of the carbohydrate derivatives of azacrown ethers that were recently synthesized in our laboratory. An attempt is made to explain the interactions between 1,10-N,N′-bis-(β-D-ureidocellobiosyl)-4,7,13-trioxa-1,10-diazacyclopentadecane (host) and the aspirin molecule using theoretical methods. The structure and other properties of the complex formed by the two molecules revealed by NMR, IR spectrometry and microanalysis are compared to the results of quantum calculations performed with the semiempirical and density functional methods for several selected geometries.

---

Introduction

The study of synthetic macrocyclic compounds has been a significant area in chemistry since Pedersen discovered the complexing properties of crown ethers.¹ Supramolecular chemistry examines weak non-covalent interactions between guest and host molecules. These forces include hydrogen bonding, aromatic–aromatic π-stacking and electrostatic or hydrophobic forces.² Derivatives of crown and azacrown ethers are a very useful class of receptors which form stable complexes with numerous metal cations,³ anions⁴ and neutral molecules.⁵ Carbohydrates, because of their natural genesis, low price, optical purity and excellent water solubility, are particularly handy in planning and executing the synthesis of many chiral receptors. Crown ethers containing various carbohydrate moieties have received much attention in recent years.⁶ The sugar moieties can be directly incorporated into the crown macrocycle itself or grafted as pendant arms.

In this paper, we briefly review derivatives of carbohydrate azacrown ethers that we had described before.^5c–e This work also describes assessment of the strength of interaction between the receptor that contains in its structure two units of saccharides and one molecule of azacrown ether (host) and the aspirin molecule, using theoretical methods.

Carbohydrate derivatives of urea – review of earlier achievements

Marsura and co-workers developed a rapid and efficient method for the preparation of carbohydrate derivatives of urea. Staudinger–aza-Wittig reaction (SAW) of saccharide azide with azacrown ether was central to this achievement.⁷ This reaction corresponds to the nitrogen analog of the Wittig olefination process and involves the reaction of an iminophosphorane intermediate with carbon dioxide in the presence of a nitrogen nucleophile.⁸

We have had the opportunity to demonstrate new ligand 1 (Fig. 1) in which the 4,7,13,16-tetraoxa-1,10-diazacyclooctadecane was substituted by two cellobiosyl units.^5c This water soluble new receptor has been obtained by the tandem SAW reaction in high yield. It was established experimentally that the podand 1 interacts efficiently both with busulfan (1,4-butanediol-dimethylsulfonate), a powerful antitumor drug in leukemia, and with basic amino acids (L-lysine and L-arginine) to form 1 : 1 supramolecular species.

Fig. 1 Derivatives of carbohydrate azacrown ethers 1–5.

The stoichiometries of the complexes were established on the basis of the Job plot method (also known as continuous variation method). Our studies showed two kinds of interactions between ligand 1 and busulfan (as guest): (1) van der Waals forces between lipophilic alkyl chain protons of the guest and azacrown protons; (2) hydrogen bonds between sulphonic groups and urea bridges.

Then we decided to obtain new macrocycles in which 4,7,13,16-tetraoxa-1,10-diazacyclooctadecane was replaced with 1,4,10-trioxa-7,13-diazacyclopentadecane.^5d The received receptors include two cellobiosyl or two glucosyl units that are connected by urea linkers to the diazacrown ether platform (compounds 2 and 3 in Fig. 1). The binding studies allowed us to determine experimentally that such derivatives can form when dissolved in water host–guest type complexes with aromatic guests (aspirin and paracetamol). The complexation behaviors of receptors 2 and 3 towards neutral molecules were explored by ¹H NMR spectroscopy in the mixture D₂O/pyridine-d₅ at 293 K. The molar ratio of the host/guest can be 1 : 1 or 2 : 1 and is dependent on the structures of the guest and the host.

We have also demonstrated how the solvent and the size of the ether cavity affect the stability of the host:guest type complexes.^5e We have used receptors 1–5 as hosts and p-toluenesulfonamide as the guest molecule. Compounds 2 and 3 have been applied as model ligands to study the solvent effect on chemical shifts for the selected proton signals in the ¹H NMR spectrum. The biggest chemical shifts have been observed in the mixture D₂O/pyridine-d₅ for the cellobiose derivative 2 and in the mixture CD₃OD/pyridine-d₅ for the glucose derivative 3. Therefore we have studied the stoichiometry of compounds 3, 5/p-toluenesulfonamide in CD₃OD/pyridine-d₅ and 1, 2, 4/p-toluenesulfonamide complexes in D₂O/pyridine-d₅. The macrocycles 1, 2, 4, and 5 are able to complex with one molecule of the guest. Only ligand 3 formed the complex in 2 : 1 stoichiometry (host/guest). The most stable complex has been obtained for receptor 2. We have confirmed that the supramolecular species are formed through weak non-covalent interactions.

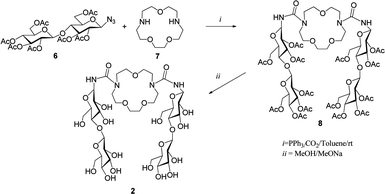
In the present article we focus on the complex formed by cellobiose derivative 2 with aspirin. The host molecule 2 was synthesized in a high yield of 92% from per-O-acetyl-azido-β-D-cellobiose 6 and aza-crown ether 7 over two steps via a tandem Staudinger–aza-Wittig reaction, as shown in Scheme 1.^5d

Scheme 1 Synthesis of the host molecule 2.

The host–guest properties of receptor 2 toward aspirin (Fig. 2) were explored by ¹H and ¹³C NMR spectroscopy in D₂O at 293 K. On the basis of the Job plot method the stoichiometry of the complex was established to be 1 : 1. It was not possible to determine experimentally the exact structures of either the host molecule or its complex with aspirin because we did not obtain single crystals of them to perform X-ray diffraction analysis. Therefore, to expand the knowledge of these compounds, we have decided to use quantum methods. The theoretical approach allows one to explore various properties of chemical systems at the molecular level and also provides some values that can be compared to experimental data.

Fig. 2 Complexation of aspirin by molecular receptor 2.

Methods

Experimental

All solvents and reagents were purchased from Sigma Aldrich Poland. The NMR spectra for the host molecule and for the 2/aspirin complex were recorded in D₂O on Bruker Avance III (600 MHz for ¹H NMR, 150 MHz for ¹³C NMR). The IR spectra were recorded on a Mattson 1000 ATI Unicam FT-IR spectrometer in KBr discs.

Theoretical calculations

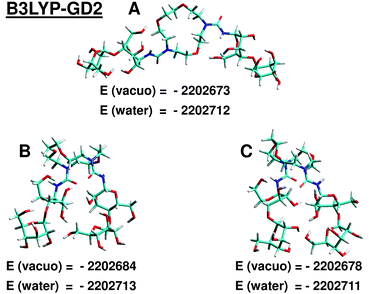
To evaluate the interaction between 1,10-N,N′-bis-(β-D-ureidocellobiosyl)-4,7,13-trioxa-1,10-diazacyclopentadecane and the aspirin molecule we used several semi-empirical methods, as well as the density functional theory. The following procedure was applied: first we constructed models of both molecules using the Hyperchem program,⁹ and their further optimization was performed at the PM6 level using the MOPAC program.¹⁰ The initial structure of the aspirin molecule was adjusted to the conformer reported in the work of Yurtsever et al.¹¹ as the most stable form in the gas phase from the density functional theory (DFT) and MP2 calculations.

As no information is available about the structure of the host 2, it would be desirable to find the ground state of this molecule. However, this would require very extended studies, which we intend to perform in future. For our preliminary tests we have considered just three different types of possible structures. In model A the two cellobiosyl fragments are stretched away, so no hydrogen bonds can be formed between them. In the second model (model B) the cellobiosyl tails are oriented such that some interaction occurs between them, but they do not come very close. The third model (model C) mimics the very close proximity of the cellobiosyl parts and significant deformation of the azacrown ring in comparison to model A. Each structure was first optimized at the PM6 level, and then used as a starting point in the molecular dynamics conformational search combined with the PM6 method. The goal of this stage was to allow the molecule to adopt the geometry more stable in terms of energy, but still resembling the initial structure. The conformational search was performed using the tool available in the program Gabedit¹² combined with the MOPAC program. We used the Stochastic Dynamics method via the Verlet algorithm. In each simulation the conformational space was explored at T = 1000 K during the period of 10 ps with a time step 1 fs. From the trajectory 30 lowest energy conformations were selected and subsequently optimized at the PM6 level. As a result we obtained three different low energy conformers A, B, C of the host molecule, which are shown in Fig. 6 in the Results section.

These structures were used in our further evaluation of the complexation energy in the host:guest complex. The number of significantly different structures of the complex is very large; therefore we limited our search to the cases where the aspirin molecule can interact with both the azacrown and cellobiosyl fragments. Several orientations of the aspirin molecule with respect to the host structures A, B, C were considered; for each the conformational search (using the same method as for the host molecule) was performed. The complexation enthalpy was then calculated as the difference between the standard heats of formation of the optimized products and substrates: ΔH_compl = H^X_f(host–guest) − H_f(host) − H_f(guest). Here X stands for A′, B′ or C′ – the type of the complex structure, similar to those shown in Fig. 7. The reference level was always the same, i.e. H_f(host) is the lowest value found from our tests for the heat of formation of the host molecule (for example, in the case of PM6 calculations this was structure C in Fig. 6).

The structures obtained from the PM6 tests served as starting configurations for calculations performed with two other semiempirical methods, PM6-DH2 and PM7, as well as with the hybrid density functional B3LYP-GD2 method. The latter is the standard B3LYP functional¹³ including the Grimme empirical pair-wise long range corrections.¹⁴ These calculations were performed with the 6-31G(d,p) basis set and the ultrafine integration grid using the Gaussian 09 program.¹⁵

In the case of PM7 and B3LYP-GD2 for each system full optimization (no constrains) was performed, while the PM6-DH2 energies were obtained from the single point SCF calculations, according to the strategy suggested by the authors of the MOPAC program. The DFT complexation energies were obtained using the same strategy as in semiempirical calculations; at this stage additionally the basis set superposition errors were calculated using the counterpoise correction (CP).¹⁶

For the structures optimized with the DFT method we have performed the vibrational analysis, which confirmed the stationary points to be true minima. Additionally, for all compounds the H and C NMR shielding tensors were calculated using the B3LYP/6-31++G(d,p) and the GIAO method. The H and C NMR chemical shifts δ (relative to TMS) were calculated using the procedure proposed by Tantillo¹⁷ according to the formula δ_X = (I_X − σ_X)/(−S_X), where X denotes H or C and σ represents the computed isotropic values. S and I are scaling factors defined as the slope and intercept of the line obtained for a given computational method from the linear regression analysis of experimental and computed chemical shift values. It was shown in a series of articles¹⁸ that such empirical scaling allows one to correct for systematic errors present in chemical shifts obtained from quantum calculations and achieve high-accuracy results. Using the files provided by Tantillo in ref. 17 for the test set of molecules we calculated the scaling factors for the methods we used (optimization with B3LYP-GD2/6-31G(d,p), followed by GIAO NMR calculations with B3LYP/6-31++G(d,p)). The following parameters were obtained in vacuo: S_H = −1.0412, I_H = 31.7502, S_C = −0.9428, I_C = 188.8146; and in water (PCM): S_H = −1.0567, I_H = 31.6557, S_C = −0.9687, I_C = 189.8139.

Results and discussion

NMR and IR experimental spectra

The host 2 was prepared by a two step procedure (Scheme 1).^5d,e The compounds per-O-acetyl-1-azido-1-deoxy-β-D-cellobiose and triphenylphosphine in anhydrous toluene were stirred for 1 h at room temperature. Then, diazacrown ether was added and the mixture was stirred for 24 h under CO₂ bubbling conditions. Next it was concentrated and the residue was purified on a silica gel column. Finally, deacetylation of compound 8 under Zemplén conditions provided the final macrocycle 2. The host–guest properties of the host 2 towards aspirin were analyzed by ¹H NMR spectroscopy in D₂O at 293 K.

In our previous work^5d some chemical shifts were given only in groups, without exact identification. In Table 1 we list chemical shifts we managed to assign to specific atoms of the host molecule. Together with other values from ref. 5d they constitute the data for comparison with computed results. In Fig. 3 the numbering of atoms used in assignment of chemical shifts is shown, while in Fig. 4 the overlapped NMR spectra for aspirin, 1,10-N,N′-bis-(β-D-ureidocellobiosyl)-4,7,13-trioxa-1,10-diazacyclopentadecane molecule (host 2) and their complex are presented. Signs of interaction were first detected by the chemical-induced shifts (CIS) of protons of the guest signals as compared to those of the free compound in D₂O. The signals of both aromatic and methyl protons of aspirin are upfield shifted (lower ppm values) as shown in Fig. 4a. The anomeric (H-1), H-1′ and H-6 protons of the host are also shifted in the direction of lower ppm values (Fig. 4b). The values of changes in chemical shifts for selected atoms of the 2/aspirin complex are given later, in Table 3, together with the results of our quantum calculations. We had published before that in D₂O/pyridine-d₅ (9 : 1) compound 2 formed the complex with aspirin also in 1 : 1 stoichiometry, but the signals of both aromatic and methyl protons of aspirin were downfield shifted.^5d

Table 1 Experimental ¹³C and ¹H NMR chemical shifts (δ in ppm) for the host molecule^a

^13C	C1	C2	C3	C4	C5	C6	C1′	C2′	C3′	C4′	C5′	C6′
a Other δ values:^5d^1H NMR: 3.82–3.30 (crown CH2); ^13C NMR: 159.88 (C=O), 69.55 and 48.95 (C crown).
δ	81.5	71.8	75.3	78.7	76.0	60.2	102.6	73.2	76.2	69.5	75.6	60.7

---

^1H	H-1	H-2	H-3	H-4	H-5	H-6a	H-6b	H-1′	H-2′	H-3′	H-4′	H-5′	H-6′a	H-6′b
δ	4.87	3.47	3.51	3.64	3.59	3.95	3.75	4.52	3.33	3.49	3.43	3.53	3.92	3.79

---

Fig. 3 Atom numbering used in the NMR analysis of the host molecule (a) and aspirin (b).

Fig. 4 Overlapped ¹H NMR spectra of the (a) complex [2/aspirin] and aspirin (zoom views of aromatic and methyl protons of the aspirin); (b) complex [2/aspirin] and host (zoom views of H-1, H-1′ and H-6 protons of the host) at 600 MHz in D₂O.

Fig. 5 presents the IR spectrum obtained for the host molecule. The lines for ν = 3420 and 1636 cm⁻¹ were assigned to vibrations of O–H and C=O bonds, respectively. More detailed assignment of other lines observed will be made on the basis of theoretical results.

Fig. 5 Experimental IR spectrum recorded in the KBr pellet.

Quantum calculations – structures and energies

In Fig. 6–9 the final structures of the host molecule and the complex obtained from the semiempirical PM6 and density functional B3LYP-GD2 calculations are presented. The B3LYP-GD2 structures are generally similar to the PM6 geometries, although some differences can be observed when comparing Fig. 8 and 9 to Fig. 6 and 7, respectively. The corresponding PM6, PM6-DH2 and PM7 binding enthalpies (semiempirical) and B3LYP-GD2 energies are given in Table 2.

Fig. 6 Three structures of the 1,10-N,N′-bis-(β-D-ureidocellobiosyl)-4,7,13-trioxa-1,10-diazacyclopentadecane molecule in vacuo obtained from the PM6 configurational search and used in further tests of the host–guest complexes. The corresponding structures in water do not differ significantly, so they are not shown. The heats of formation (in kcal mol⁻¹) in vacuo and in water are also given for each structure.

Fig. 7 Structures of the host–guest complexes obtained as the lowest energy forms from the PM6 simulations. The corresponding structures in water do not differ significantly, so they are not shown. The heats of formation for each structure in vacuo and in water are in kcal mol⁻¹.

Fig. 8 Three structures of the 1,10-N,N′-bis-(β-D-ureidocellobiosyl)-4,7,13-trioxa-1,10-diazacyclopentadecane molecule obtained from the B3LYP-GD2/6-31G(d,p) optimization in vacuo. For each structure the total energies in vacuo and the corresponding results in water are given. All values are in kcal mol⁻¹. The structures optimized in water do not differ significantly, so they are not shown.

Fig. 9 Structures of the host–guest complexes optimized in vacuo using the B3LYP-GD2/6-31G(d,p) method. The corresponding structures in water are very similar. The total energies (without BSSE corrections) obtained from the optimization in vacuo and in water are given below. All values are in kcal mol⁻¹. The dotted lines mark hydrogen bonds.

Table 2 Comparison of PM6, PM6-DH2 and PM7 complexation enthalpies ΔH_compl (semiempirical) and B3LYP-GD2/6-31G(d,p) energies ΔE_compl (DFT values include the basis set superposition error (BSSE) corrections) of the 1 : 1 complexes A′, B′, C′ (Fig. 7 and 9) calculated in vacuo and in water (semiempirical: COSMO model, DFT: PCM model). In all cases the complexation energy was calculated with respect to the lowest energy structures of the host indicated by the given method: in vacuo – C (PM6, PM6-DH2) or B (PM7, B3LYP-GD2); in water – A (PM6, PM7) or B (B3LYP-GD2). All values are in kcal mol⁻¹

	In vacuo				In water
Type	PM6	PM6-DH2	PM7	B3LYP-GD2	PM6	PM7	B3LYP-GD2
A′	−17.65	−29.84	−25.32	−17.44	−5.10	−17.00	−22.59
B′	−12.42	−27.74	−33.13	−42.05	8.15	−6.98	−38.24
C′	−17.72	−37.01	−30.80	−28.79	10.07	−4.50	−26.60

---

Table 3 Average values of changes Δδ in ¹H scaled chemical shifts [ppm] for selected atoms of aspirin and host molecules upon formation of complex 1 : 1 obtained from DFT calculations in water and from experiment in D₂O. The changes are calculated as Δδ = δ_complex(X′) − δ_substrate(X), where X = A, B, C

Aspirin	Calc. Δδ (A′-asp.)	Calc. Δδ (B′-asp.)	Calc. Δδ (C′-asp.)	Exp. Δδ
H-3as	−0.0078	−0.0116	1.1655	−0.0206
H-4as	−0.0811	−0.0528	0.4452	−0.0333
H-5as	−0.0929	0.6640	−0.0300	−0.0206
H-6as	−0.4869	−0.0618	−0.5812	−0.0490
H-9as (CH3)	0.0929	0.3636	−0.2964	−0.0107

---

Host	A′–A	B′–B	C′–C
H-1	−0.1396	0.2854	0.2444	−0.0022
H-1′	0.0074	−0.4668	0.0908	−0.0031
H-6a	0.0278	−0.1147	−0.1282	−0.0020
H-6b	0.0046	0.0186	0.0117	−0.0020

---

As can be seen, the results are very inconsistent, even within the set obtained with semiempirical methods. Both PM6 and PM6-DH2 methods indicate that the most stable structures are the host and complex structures C and C′, while the lowest PM7 heats of formation are obtained for B and B′. The binding enthalpies obtained with PM6-DH2 and PM7 methods are much higher than the PM6 values. Obviously the results strongly depend on the method used.

The results obtained in vacuo at the highest computational level used in the present work, B3LYP-GD2/6-31G(d,p), corroborate the PM7 predictions, indicating conformers B and B′ (Fig. 8 and 9) as the lowest energy structures, but the agreement is only qualitative. When comparing values obtained with different methods one should remember that semiempirical methods are parametrized so as to give heats of formation at 298 K, while the DFT results are total energies corresponding to the temperature 0 K. The DFT complexation energy in B′ appears to be much higher than for two other structures.

The interaction between the host and guest molecules in the liquid phase will be certainly perturbed by the presence of solvent molecules. Therefore the PM6 and PM7 optimized structures were re-optimized in the presence of water modelled with the Conductor-like Screening Model (COSMO) using the values of 78.39 and 1.3 Å for the dielectric constant and the effective radius, respectively. The results differ significantly from those obtained in vacuo. First of all, both methods PM6 and PM7 predict the host conformer A (and also the complex A′) to be much more stable in water. According to the PM6 results in solution only formation of the complex A′ appears to be profitable; for the two other forms ΔH_compl values are positive. The complexation enthalpy of A′ in water is much smaller than that in vacuo. The PM7 method predicts much larger complexation energies than PM6, but substantially smaller than the corresponding values in vacuo. Both semiempirical methods predict the same trend in the complexation energies: A′ > B′ > C′, suggesting that in aqueous solutions the more “open” structure A′ is expected to be formed.

These findings were further verified at the DFT level. The starting structures obtained in vacuo with the B3LYP-GD2 method were re-optimized in the presence of water that was described by the polarizable continuum model (PCM) of solvent. The DFT results disagree with the semiempirical predictions. As in vacuo, also in water the host molecule B appears to have the lowest total energy, but among the three conformers studied the energy differences are much less pronounced than in vacuo (∼1–2 kcal mol⁻¹).

For the complex the DFT results in aqueous solution again indicate the structure B′ to be the most stable, similar to the one in vacuo. The presence of water affects the total energies of the complexes A′, B′ and C′, and ΔE_compl in solution appears to be less differentiated than in the gas phase. In all structures studied the complex formation involves various interactions, among them there is always formation of some hydrogen bonds between aspirin and the cellobiosyl fragments. As shown in Fig. 9, in B′ three hydrogen bonds between aspirin and the host are observed, while there are only two in C′ and one in A′.

Of course, the continuum solvent model is very approximate and accounts basically for electrostatic interactions between the system and the solvent. Also, we used rather a modest level of theory. Inclusion of diffuse functions into the basis set at the optimization stage may affect the total and complexation energies. The reader should also remember that all the results presented above refer to some arbitrarily chosen structures, and thus should be treated as rather qualitative evaluation of binding energies in these complexes. The configurational space of such systems is vast, and therefore much more extended studies are necessary to determine the lowest energy structures for both the host molecule and the host–guest complex.

Computed IR spectra – comparison with experimental data

The conclusions drawn from the quantum calculations about the structures energetically favored can be at least partially verified by comparing the computed IR spectra to the measured ones. The spectra presented in Fig. 10 were obtained from the B3LYP-GD2/6-31G(d,p) harmonic vibrations using the Gabedit program; we applied a convolution using Lorentzian line shapes with the half-width 10. For qualitative comparison the spectrum obtained experimentally is also included.

Fig. 10 IR spectra obtained from the B3LYP-GD2/6-31G(d,p) calculations (Lorentzian convolution and the original lines, frequencies scaled by 0.961) for the three structures (A, B, C) of the host molecule in vacuo. For qualitative comparison, the experimental curve is superimposed on the computed spectra. The symbols indicate the stretching modes of the corresponding bonds.

As can be seen in Fig. 10A–C, no exact match is observed for any of the conformers, although all exhibit some qualitative agreement. A closer resemblance seems to appear for the more compact structures B and C, except for the C=O stretching mode in B, which corresponds to two lines separated by 55 cm⁻¹.

The computed frequencies and intensities can be used to assign particular peaks to vibrational modes and this is partially done in Fig. 10. More details can be found in Table S1 in the ESI,† where vibrations corresponding to the highest (locally) intensities are listed. The vibrations quite often have a complex character, so the specified frequency corresponds to several different vibrations. In the area of low frequencies the dominant motion is the torsion of the CCOH angle, accompanied by the out-of-plane NH bend and various CH bending deformations. The higher intensity peak, covering the range 1028–1166 cm⁻¹, corresponds to combined vibrations: mainly CC and CO stretches, coupled to COH and CCH bending. The next part of the spectrum, from 1288 to 1458 cm⁻¹, covers again combined modes, in which prevail the COH and CCH bending modes. The peak at 1541 cm⁻¹ refers to the CNH and NCH bending modes, while the next one refers mainly to the C=O stretch, coupled however to the CNH and NCH bending. In this region are also present scissor modes of CH₂ groups belonging to the azacrown fragment. The higher frequency modes are less complex and easier to assign: the CH stretch (2881, 2920 cm⁻¹), the OH (strong) and NH (much weaker) stretches (broad peak around 3420 cm⁻¹).

Calculated NMR chemical shifts

In Fig. 11 the calculated averaged values of chemical shifts δ for the three structures A, B, C of the host molecule are compared to the experimental data (from Table 1). The averaging was done over δ values of atoms having the same number in both cellobiosyl units. For all three structures most carbon shifts (Fig. 11a) appear close to the measured values. The coefficients of determination R² in the linear regression analysis for the calculated vs. experimental values are 0.958 (A), 0.975 (B) and 0.980 (C). The largest deviations with respect to the experimental data are as follows: for A 14.7% (Cb crown), for B 14.2% (C6) and for C 11.9% (C5′). As can be seen in Fig. 11b, the agreement for the ¹H chemical shifts is much worse, especially for the most stable conformer B. The R² for structures A, B, C are, respectively, 0.730, 0.281 and 0.596, and the corresponding maximum deviations are 16.1 (H-4′), 33.7 (H-2) and 19.2% (H-3). The general trend is best reproduced for the conformer A, suggesting that structures of more “open” geometry may dominate in solution. Indeed, a somewhat better fit, with R² = 0.773, is obtained when the averaged chemical shifts are composed as a sum of δ values of A, B and C multiplied respectively by their contributions of 0.6, 0.1 and 0.3. However, this approach is highly speculative, considering the very limited number of conformers tested.

Fig. 11 C (a) and H (b) computed averaged scaled chemical shifts for 3 host structures in water. H-6a and H-6b (H-6a′ and H-6b′) denote averages over two higher and two lower δ values obtained for each pair of H-6 and H-6′ atoms; Ca and Cb crown denote averages over 6 higher and 4 lower δ values for C in the crown. The horizontal black bars mark experimental values in D₂O.

We also made an attempt to compare the changes in ¹H chemical shifts obtained from the DFT calculations in water with the available experimental estimates in D₂O. The DFT values presented in Table 3 are computed from δ averaged over atoms identified in measurements. A more detailed version of Table 3, with values for individual atoms in vacuo and in water, is given in Table S2 in the ESI.† Because in real solution different conformers can be present in various fractions, the change Δδ for a given complex X′ (X = A, B, C) was calculated with respect to the corresponding host structure X.

According to the experimental data the complex formation in D₂O causes relatively small signal shifts toward smaller δ for both aspirin and host atoms. The calculated Δδ are in most cases larger and often have an opposite sign. Only the complex A′ gives Δδ < 0 for all aromatic H of aspirin, but the shift of the H-6_as signal is too large. No agreement is found for aspirin CH₃ and also selected H of the host molecule, the smallest discrepancy appearing again for A′, but the experimental Δδ are much smaller and are expected to be sensitive to subtle changes in the system.

There may be several sources of large discrepancy between experimental and computed NMR values. First of all, our theoretical study probes just a few structures of a certain type. The measured δ and Δδ values certainly depend on the equilibrium between various host and complex structures present in real solution. Another source of disagreement can be the implicit solvent model used in our calculations. An inclusion of specific interactions with neighboring water molecules and possible hydrogen bonds formed are also expected to affect the results. Additionally, unlike the calculated results, the experimental values are obtained for the deuterated host molecule. The isotope effect on chemical shifts is discussed in a number of works (e.g.ref. 19) and has been shown to be important in the systems containing hydrogen bonds, but mainly for substituted hydrogens or heavy atoms.

Conclusions

In this article we made an attempt to deepen our knowledge about the recently synthesized compound that is a potential drug receptor. More detailed experimental data are provided along with results of some preliminary theoretical calculations. We found discrepancies between our semiempirical and DFT results, and thus the application of the former results to similar systems should be done with caution. The B3LYP-GD2/6-31G(d,p) calculations (highest level of theory used in this work) predict that both in vacuo and in aqueous solution the structure B is more stable than A and C. The corresponding energy differences in vacuo are equal to 10.4 and 5.6 kcal mol⁻¹, while in water they are much smaller: 1 and 2 kcal mol⁻¹, respectively. Among the three structures of the aspirin–host complex, the form B′ is found to be energetically most stable due to the formation of three hydrogen bonds between the two molecules. Both in vacuo and in water the host–guest complexation energies follow the order B′ > C′ > A′. However, the comparison of experimental and computed NMR spectra for the azacrown ether suggests that in water the “more open” structures of type A dominate, but in fact no satisfactory agreement between calculated and measured chemical shifts was achieved. The significant discrepancy between computed and experimental δ and complexation Δδ values clearly indicates that more extended study is necessary and we intend to perform such calculations in future.

References

1. C. J. Pedersen, J. Am. Chem. Soc., 1967, 89, 7017.
2. (a) D. J. Cram and J. M. Cram, Acc. Chem. Res., 1978, 11, 8; (b) J. M. Lehn, Pure Appl. Chem., 1978, 50, 871; (c) J. M. Lehn, Science, 1985, 227, 849.
3. (a) H. Takemura, H. Nakamichi and K. Sako, Tetrahedron Lett., 2005, 46, 2063; (b) S. Jarosz and B. Lewandowski, Carbohydr. Res., 2008, 343, 965; (c) A. Späth and B. König, Beilstein J. Org. Chem., 2010, 6, 32; (d) M. Suchý, M. Milne, A. X. Li, N. McVicar, D. V. Dodd, R. Bartha and R. H. E. Hudson, Eur. J. Org. Chem., 2011, 6532; (e) T. Niittymäki, E. Burakova, E. Laitinen, A. Leisvuori, P. Virta and H. Lönnberg, Helv. Chim. Acta, 2013, 96, 31.
4. (a) E. Graf and J. M. Lehn, J. Am. Chem. Soc., 1976, 98, 6403; (b) M. Chmielewski and J. Jurczak, Tetrahedron Lett., 2004, 45, 6005; (c) E. Kleinpeter and A. Holzberger, Tetrahedron, 2006, 62, 10237; (d) R. Chakrabarty, P. S. Mukherjee and P. J. Stang, Chem. Rev., 2011, 111, 6810; (e) T. Guchhait and G. Mani, J. Org. Chem., 2011, 76, 10114; (f) X. Yan, X. Chi, P. Wei, M. Zhang and F. Huang, Eur. J. Org. Chem., 2012, 6351; (g) C. L. Do-Thanh, N. Khanal, Z. Lu, S. A. Cramer, D. M. Jenkins and M. D. Best, Tetrahedron, 2012, 68, 1669.
5. (a) F. Vogtle and W. M. Muller, J. Inclusion Phenom., 1984, 1, 369; (b) S. Menuel, J. P. Joly, B. Courcot, J. Elysee, N. E. Ghermani and A. Marsura, Tetrahedron, 2007, 63, 1707; (c) S. Porwański, F. Dumarcay-Charbonnier, S. Menuel, J.-P. Joly, W. Bulach and A. Marsura, Tetrahedron, 2009, 65, 4196; (d) M. Pintal, B. Kryczka, A. Marsura and S. Porwański, Carbohydr. Res., 2014, 386, 18; (e) M. Pintal, B. Kryczka and S. Porwański, Heteroat. Chem., 2015, 26, 161.
6. (a) J. Xie and N. Bogliotti, Chem. Rev., 2014, 114, 7678; (b) M. Pintal, F. Charbonniere-Dumarcay, A. Marsura and S. Porwański, Carbohydr. Res., 2015, 414, 51.
7. S. Porwański and A. Marsura, Eur. J. Org. Chem., 2009, 2047.
8. A. Scondo, F. Dumarcay-Charbonnier, A. Marsura and D. Barth, J. Supercrit. Fluids, 2009, 48, 41.
9. HyperChem(TM) Professional 8.0.10, Hypercube, Inc., 1115 NW 4th Street, Gainesville, Florida 32601, USA, 2011.
10. (a) MOPAC2012, J. J. P. Stewart, Stewart Computational Chemistry, version 15.027W, web: http://OpenMOPAC.net; (b) J. D. C. Maia, G. A. U. Carvalho, C. P. Mangueira, S. R. Santana, L. A. F. Cabral and G. B. Rocha, J. Chem. Theory Comput., 2012, 8, 3072.
11. Z. Yurtsever, B. Erman and E. Yurtsever, Turk. J. Chem., 2012, 36, 383.
12. Gabedit 2.4.9, A. R. Allouche, J. Comput. Chem., 2011, 32, 174.
13. (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
14. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
15. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013.
16. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553.
17. D. J. Tantillo, Chemical Shifts Repository, http://cheshirenmr.info/Instructions.htm.
18. (a) M. W. Lodewyk, M. R. Siebert and D. J. Tantillo, Chem. Rev., 2012, 112, 1839; (b) M. W. Lodewyk, C. Soldi, P. B. Jones, M. M. Olmstead, J. R. Larrucea, J. T. Shaw and D. J. Tantillo, J. Am. Chem. Soc., 2012, 134, 18550; (c) M. W. Lodewyk and D. J. Tantillo, J. Nat. Prod., 2011, 74, 1339; (d) T. Bally and P. R. Rablen, J. Org. Chem., 2011, 76, 4818; (e) R. J. Jain, T. Bally and P. R. Rablen, J. Org. Chem., 2009, 74, 4017; (f) P. R. Rablen, S. A. Pearlman and J. Finkbiner, J. Phys. Chem. A, 1999, 103, 7357.
19. (a) P. E. Hansen, J. Labelled Compd. Radiopharm., 2007, 50, 967; (b) S. Bolvig and P. E. Hansen, Curr. Org. Chem., 2000, 4, 19.

---

Footnote

† Electronic supplementary information (ESI) available: More detailed analysis of vibrations observed in theoretical and experimental IR spectra; computed changes in chemical shifts upon complex formation. See DOI: 10.1039/c6nj03089k

---