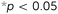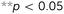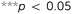Open Access Article
Open Access ArticleRationally designed meta-implants: a combination of auxetic and conventional meta-biomaterials†
Helena M. A.
Kolken
 *a,
Shahram
Janbaz
a,
Sander M. A.
Leeflang
a,
Karel
Lietaert
b,
Harrie H.
Weinans
ac and
Amir A.
Zadpoor
a
*a,
Shahram
Janbaz
a,
Sander M. A.
Leeflang
a,
Karel
Lietaert
b,
Harrie H.
Weinans
ac and
Amir A.
Zadpoor
a
aDepartment of Biomechanical Engineering, Delft University of Technology, Delft, The Netherlands. E-mail: h.m.a.kolken@tudelft.nl; Tel: +31-653258953
b3D Systems – LayerWise NV, Leuven, Belgium
cDepartment of Orthopedics and Department of Rheumatology, University Medical Centre Utrecht, 3584 CX Utrecht, The Netherlands
First published on 18th October 2017
Abstract
Rationally designed meta-biomaterials present unprecedented combinations of mechanical, mass transport, and biological properties favorable for tissue regeneration. Here we introduce hybrid meta-biomaterials with rationally-distributed values of negative (auxetic) and positive Poisson's ratios, and use them to design meta-implants that unlike conventional implants do not retract from the bone under biomechanical loading. We rationally design and additively manufacture six different types of meta-biomaterials (three auxetic and three conventional), which then serve as the parent materials to six hybrid meta-biomaterials (with or without transitional regions). Both single and hybrid meta-biomaterials are mechanically tested to reveal their full-field strain distribution by digital image correlation. The best-performing hybrid meta-biomaterials are then selected for the design of meta-implants (hip stems), which are tested under simulated-implantation conditions. Full-field strain measurements clearly show that, under biomechanical loading, hybrid meta-implants press onto the bone on both the medial and lateral sides, thereby improving implant–bone contact and potentially implant longevity.
Conceptual insightsIn this manuscript, the concept of hybrid meta-biomaterials has been demonstrated to improve implant–bone contact in off-axially loaded ‘meta-implants’ (hip stems). A combination of negative and positive Poisson's ratio structures has been shown to create compression on either side of the meta-implant, decreasing the chance of bone–implant interface failure (Hoffman's criterion), minimizing the chance of wear particles entering the enclosed space and improving implant fixation by mechanically stimulating bone growth. While mechanical meta-materials have been studied for a while now, especially auxetic mechanical metamaterials, special combinations of metamaterials are rarely explored. This study highlights the effectiveness of creating hybrid meta-biomaterials, which can be designed to exhibit specific mechanical properties (such as a hybrid Poisson's ratio). Furthermore, this study covers the complete research trajectory from mechanical-biomaterials to their final hybrid application in ‘meta-implants’. It therefore demonstrates a proof-of-concept of applying rational design and meta-biomaterials to improve implant longevity. The significance of combining specific mechanical metamaterials has been proven, and with the recent advances in additive manufacturing this opens up an interesting field of research. |
The emerging concept of metamaterials offers a promising route to the development of materials with unusual or unprecedented properties and advanced functionalities.1,2 Metamaterials aimed for use in biomedical applications may be called ‘meta-biomaterials’.3,4 The small-scale topology of meta-biomaterials is rationally designed so as to obtain the desired combination of mechanical (i.e. negative Poisson's ratio2), mass transport (e.g. permeability, diffusivity) and biological properties (e.g. tissue regeneration performance).5 Meta-biomaterials could therefore be considered multi-physics metamaterials.4 To date, promising meta-biomaterials include those based on triply periodic minimal surfaces, which due to their mean curvature of zero resemble the curvature of trabecular bone.5,6 Furthermore, the elastic and mass transport properties of pentamode meta-biomaterials can be independently tailored to enhance tissue regeneration.7
Here we introduce the concept of meta-implants, which is the first-ever application of meta-biomaterials for improving the longevity of orthopedic implants. The meta-implants developed here are topologically designed and additively manufactured to take advantage of the unusual mechanical properties that auxetic mechanical metamaterials (metamaterials with a negative Poisson's ratio (NPR)2) have to offer. Moreover, we combine auxetic materials with conventional materials (i.e. positive Poisson's ratio) and rationally distribute the auxetic and conventional parts in the implant to improve implant–bone contact, thereby enhancing implant fixation and, thus, implant longevity.
The meta-implants developed here are aimed for applications in total hip replacement (THR) surgeries, which are among the most common orthopedic procedures carried out to date.8 THR implants have a limited lifetime, with the greatest failure mode being aseptic loosening.9–11 Aseptic loosening refers to the mechanical failure of the implant–bone interface.9,12 The femoral part of the THR (i.e. hip stem) is repeatedly loaded under bending for around 2 million cycles per year,13 which creates tensile loading and compression on either side of the neutral axis of the implant. According to Hoffman's failure criterion, the implant–bone interface is more susceptible to failure when subjected to tension as compared to compression.14 Moreover, bone exhibits higher mechanical strength in compression than in tension.15 If the Poisson's ratio is constant throughout the implant, there will always be one side of the stem that retracts from the bone, while the other side is compressed against the bone. According to the Hoffman's criterion and given the different mechanical strengths of bone in tension and compression, the side that experiences tension (i.e. retracts from the bone) is more susceptible to interface failure. Furthermore, retraction of the implant allows wear particles to enter the space between the implant and the bone, eliciting the foreign body response of the patient's immune system leading to inflammatory bone loss.9,12,16 It is therefore important to maximize the implant–bone contact such that wear particles cannot enter the enclosed cavity. Finally, compression of the implant will improve implant fixation through mechanically stimulated bone ingrowth (Wolff's law).17 All the presented arguments point towards the same direction: the necessity to design an implant that creates compression on both sides of its neutral axis.
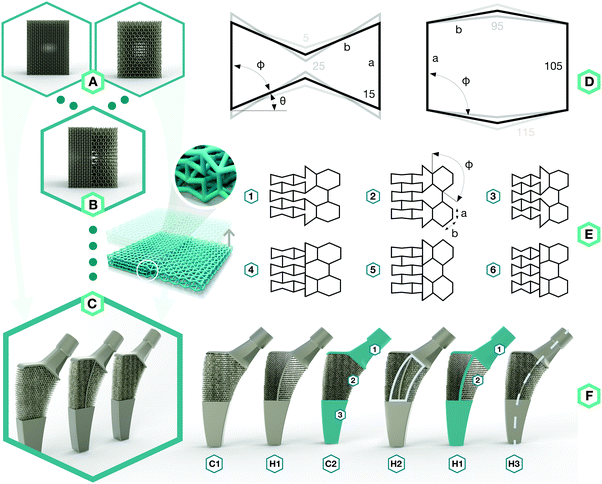
To approach the above-mentioned design challenge, we started by designing two types of meta-biomaterials with either a negative Poisson's ratio (i.e. auxetic) or a positive Poisson's ratio (i.e. conventional) (Fig. 1A). We then combined both types of meta-biomaterials to create a hybrid meta-biomaterial with different values of the Poisson's ratio (Fig. 1B). The meta-implants were then designed using these combined meta-biomaterials, in which the Poisson's ratio of the meta-biomaterials changed around the neutral axis to compress the implant against the bone on both sides (Fig. 1C).
The topological design of the meta-biomaterials was based on the re-entrant hexagonal honeycomb, because they are the most versatile in terms of the mechanical properties they could achieve.2 Six different internal angles (Φ) were used to design the topology of three auxetic (A1–A3) and three conventional (C1–C3) meta-biomaterials (Fig. 1D and Table S1 in the ESI†). The relative density (5–8%) and strut diameter (350 μm) were chosen to be as small as possible to push the limits of the additive manufacturing process and obtain the lowest mechanical properties possible. It is worth noting that a low relative density (high porosity) allows for maximal bone ingrowth, while decreasing the mechanical properties to avoid the stress shielding phenomenon. Moreover, increasing the relative density, strut diameter, and thus, mechanical properties, is relatively easy, while the opposite is technically challenging. Meta-biomaterials or, as they are sometimes called, ‘designer biomaterials’ offer a powerful approach for attaining bone-mimicking mechanical properties, which enables decreasing the mechanical mismatch between the implant and the surrounding bone (i.e. the stress shielding phenomenon). There is a mathematical proof18 showing that any thermodynamically admissible elasticity tensor could be obtained through specific classes of metamaterials, such as pentamode metamaterials. We have recently manufactured pentamode metamaterials from metals and have shown their potential for enhancing tissue regeneration.7 Meta-biomaterials therefore offer a flexible route to the design of implants such that the adverse effects of stress shielding are minimized, while simultaneously satisfying other requirements regarding topological features (e.g. curvature) and mass transport properties (e.g. permeability). Subsequently, re-entrant and conventional hexagonal unit cells were combined to form hybrid meta-biomaterials (Fig. 1E and Table S2 in the ESI†). When designing the hybrid meta-biomaterials, three different combinations of unit cells were considered either with (1–3) or without a transitional region (4–6) (Fig. 1E). Based on the mechanical properties of the (hybrid) meta-biomaterials, a specific combination of unit cells was chosen (hybrid meta-biomaterial Type 6) and was used in the design of the meta-implants (Fig. 1F). A 50/50 cell division around the neutral axis resulted in the first hybrid meta-implant (H1). Two control meta-implants were designed using only conventional (C1) and only auxetic (C2) meta-biomaterials (Fig. 1F). Two additional hybrid meta-implants were added to explore the effects of a solid core, around the neutral axis, on the behavior of the meta-implants (H2) as well as the effects of displacing the division line (70/30 instead of 50/50) between both types of meta-biomaterials (H3) (Fig. 1F). An additive manufacturing technique, namely selective laser melting (SLM), was used to manufacture the specimens from the biomedical-grade titanium alloy Ti6Al4V-ELI. After manufacturing, the samples were removed from the build plate, submerged in 96% ethanol, and ultrasonically cleaned for 10 minutes to remove excess powder.
Four specimens from all six types of meta-biomaterials were compressed up to 10 mm using a static test machine (Zwick GmbH & Co. KG, Ulm, Germany, load cell = 20 kN), applying a constant deformation rate of 1 mm min−1. During the compression tests, the digital image correlation (DIC) technique was used for full-field measurement of the strains on the front surface of the specimens. DIC images were acquired by two 4-Megapixel digital cameras (Limess, Krefeld, Germany) at 1 Hz and were analyzed using VicSnap and Vic-3D (Correlated Solutions Inc., Irmo, USA). The speckle patterns required for DIC measurements were created by initially painting the specimens in black, then applying a white paint on the front surface of the specimens, and ultimately spraying random black dots (Fig. 2A). The vertices of eight centrally located unit cells were marked with a red pixel (one image every five seconds, Fig. 2A-4) to track the strains and calculate the Poisson's ratio using a Matlab code.
Four specimens from each design of hybrid meta-biomaterials were loaded under bending by applying an off-axis compression force (until 2 mm displacement) using the same mechanical testing protocol (Fig. 3A). Four additional specimens from each design of hybrid meta-biomaterials were covered by a self-vulcanizing tape, which was stretched around the specimens to form a tight and continuous outer layer (Fig. 3A-2). A speckle pattern was applied on this layer to enable DIC measurements. To evaluate the bilateral expansion of the hybrid mechanical metamaterials, thirty data points were plotted in Vic-3D (Fig. 3A-3) to retrieve their individual displacements.
To evaluate the performance of the meta-implants (Fig. 4A and B), we designed a test setup that simulated the implant–bone contact after surgery (Fig. 4C). In this setup, bone-mimicking material (Sawbones Europe AB, Malmö, Sweden) enclosed the meta-implants on the medial and lateral sides, while the tip of the implants was clamped in an aluminum plate (Fig. 4C). Two acrylic plates covered the setup on the front and back sides. A static test machine (Zwick GmbH & Co. KG, Ulm, Germany, load cell = 10 kN) was used to apply a maximum deformation of 1.5 mm to the femoral head, at a rate of 0.5 mm min−1. The bone-mimicking materials were covered with speckle patterns as well to enable DIC measurements.
The stress–strain curves of the meta-biomaterials were consistent with the failure of entire layers, causing the stress values to drop to very low values before recovering, as other layers took over (Fig. 2B). The highest pre-fracture stress peaks were found for the auxetic meta-biomaterials, corresponding to a higher ultimate compressive strength as compared to the conventional meta-biomaterials (Fig. 2C). The elastic modulus and the NPR of the auxetic meta-biomaterials increased with re-entrant angle (θ), whereas the elastic modulus and the positive Poisson's ratio of the conventional meta-biomaterials increased with the internal angle (Φ) (Fig. 2C). Pushing the limits of the additive manufacturing process resulted in elastic moduli in the MPa range, whereas the stiffness of bone generally ranges between 1 and 20 GPa.19 To obtain higher values of the mechanical properties, the strut thickness could be increased in the design of the auxetic and conventional unit cells. It is, however, worth noting that in a patient-specific approach to the topological design of implants, the stiffness of the implant does not necessarily need to be uniform. Meta-biomaterials with a lower elastic modulus could therefore be applied in areas where a lower stiffness is required. Moreover, it has been shown that the static and fatigue properties of porous titanium structures increase once bone tissue regeneration has taken place.20 It is therefore still unclear to what extent the initial stiffness of the implant should mimic that of the native bone tissue. It should be noted that the auxetic meta-biomaterials have a higher relative density, which means the conventional meta-biomaterials have a higher stiffness to weight ratio. As expected, the auxetic meta-biomaterials showed lateral shrinkage upon compression, while conventional meta-biomaterials exhibited lateral expansion. We compared the Poisson's ratios measured for the presented meta-biomaterials with those reported in the literature21 and found them to be in good agreement. The above described trends were also similar to those found in the literature (Fig. 2C).21
All hybrid meta-biomaterials showed clear medial compressions, especially types 2 and 5 (Fig. 3B). The lateral sides of the hybrid types 1, 2, 4, and 5 almost entirely exhibited negative strains, while the negative strains found in the hybrid types 3 and 6 were mostly limited to the central area (Fig. 3B). A continuous positive strain profile was found along the lateral border of the type 6 specimens (Fig. 3B). The mean maximum expansion was calculated for each of the data points along the lateral and medial borders of the specimens (Fig. 3C). For types 1, 2, 4, and 5, the maximum expansion on the medial side was more than five times larger than the maximum expansion on the lateral side (Fig. 3C). In contrast, the medial expansion in types 3 and 6 was only four and 1.5 times larger, respectively (Fig. 3C). Furthermore, the expansion on the lateral side occurred along the complete height of the specimens, whereas P29 (Fig. 3A-3) did not seem to expand at all (Fig. 3C). The transitional region enhanced medial expansion, while its absence increased lateral expansion (Fig. 3C).
Hybrid meta-biomaterial type 6 is the design showing the most consistent profile of bilateral compression extending along both borders. The biggest lateral expansion was expected in hybrid meta-biomaterial types 3 and 6 because of their high NPR as compared to the other designs. Hybrid meta-biomaterial types 3 and 6 do, however, differ in that one includes a transitional region while the other does not. Our experimental results showed that the presence of a transitional region adversely affects the performance of the meta-biomaterials by making them less resistant against bending. The absence of a transitional region seems to enhance the bending stiffness of hybrid meta-biomaterial type 6, resulting in a more evenly distributed bilateral expansion. Overall, the hybrid meta-biomaterial type 6 significantly outperformed other designs in terms of bilateral expansion and was therefore selected for implementation in the design of the meta-implants (Fig. 3C).
While all meta-implants exhibited compressive strains on the medial side, only hybrid meta-implants, combining auxetic and conventional meta-biomaterials, showed compression at the lateral implant–bone interface (Fig. 4D). All meta-implants exhibited positive strains on the medial side, which was not expected for C2. Due to its NPR, the medial side was expected to experience negative strains, but instead it showed the same deformation profile as C1. This is probably due to the high level of shear forces that were caused by off-axis bending, which this re-entrant structure could not withstand. The meta-implants incorporating hybrid meta-biomaterials exhibited compression on both medial and lateral sides. There were, however, clear differences between the performances of the different designs. The solid core located around the neutral axis seemed to amplify the expansion created by the unit cells, likely due to its effect on the stiffness of the meta-implants. Among the different designs of the meta-implants considered here, H2 outperformed the others by creating a consistent compression profile along both lines defining the implant–bone interface (Fig. 4D).
The presented results clearly show that meta-implants in general, and the design H2 in particular, compress against the bone under repetitive loads that are applied during gait and other daily activities. According to the Hoffman's failure criterion, this combination of compression and shear is less deleterious than tension and shear.14 Moreover, compression on both sides ensures that bone is not loaded in tension, which is not the usual mode of bone loading and would normally lead to pre-mature failure. Furthermore, the enhanced implant–bone contact decreases the chance of wear particles entering the space between the implant and the bone. Moreover, repetitive loading of the bone surrounding such fully porous implants acts as a mechanical stimulus for bone growth and will most likely improve implant fixation.17 These concepts will contribute to an improved interaction of the implant with the surrounding bone and could potentially improve implant longevity. We have introduced a new generation of implants with advanced functionalities that could be designed using the unusual properties that meta-biomaterials have to offer. The performance of any such design should be evaluated using animal models and clinical trials. The current proof-of-concept study, nevertheless, demonstrates the feasibility of applying rational design and metamaterials for the development of the next generation of medical devices.
In summary, we rationally designed and additively manufactured auxetic and conventional meta-biomaterials as well as hybrid meta-biomaterials incorporating both auxetic and conventional meta-biomaterials. These novel meta-implant designs were found to create compression on both sides of their contact lines with the surrounding bone, thereby decreasing the chance of bone–implant interface failure (Hoffman's criterion), preventing wear particles from entering the interface space, lowering stress-shielding, and improving bone ingrowth.
Conflicts of interest
There are no conflicts to declare.References
- A. A. Zadpoor, Mater. Horiz., 2016, 3, 371–381 RSC.
- H. Kolken and A. Zadpoor, RSC Adv., 2017, 7, 5111–5129 RSC.
- S. A. Yavari, S. Ahmadi, R. Wauthle, B. Pouran, J. Schrooten, H. Weinans and A. Zadpoor, J. Mech. Behav. Biomed. Mater., 2015, 43, 91–100 CrossRef PubMed.
- A. A. Zadpoor, Int. J. Mol. Sci., 2017, 18, 1607 CrossRef PubMed.
- F. Bobbert, K. Lietaert, A. Eftekhari, B. Pouran, S. Ahmadi, H. Weinans and A. Zadpoor, Acta Biomater., 2017, 53, 572–584 CrossRef CAS PubMed.
- A. A. Zadpoor, Biomater. Sci., 2015, 3, 231–245 RSC.
- R. Hedayati, A. Leeflang and A. Zadpoor, Appl. Phys. Lett., 2017, 110, 091905 CrossRef.
- U. N. D. O. Economic, S. Affairs and P. Division, Working Paper, No. ESA/P/WP. 241, 2015.
- S. J. MacInnes, A. Gordon and J. M. Wilkinson, J. Pain, 2012, 2, 29 Search PubMed.
- J.-L. Prudhon, R. Desmarchelier, M. Hamadouche, C. Delaunay and R. Verdier, Int. orthop., 2015, 1–5 Search PubMed.
- K. J. Bozic, S. M. Kurtz, E. Lau, K. Ong, T. P. Vail and D. J. Berry, J. Bone Jt. Surg., Am. Vol., 2009, 91, 128–133 CrossRef PubMed.
- Y. Abu-Amer, I. Darwech and J. C. Clohisy, Arthritis Res. Ther., 2007, 9, S6 Search PubMed.
- M. Silva, E. F. Shepherd, W. O. Jackson, F. J. Dorey and T. P. Schmalzried, J. Arthroplasty, 2002, 17, 693–697 CrossRef PubMed.
- N. Verdonschot and R. Huiskes, Clin. Orthop. Relat. Res., 1996, 329, 326–336 Search PubMed.
- T. M. Keaveny, E. F. Wachtel, C. M. Ford and W. C. Hayes, J. Biomech., 1994, 27, 1137–1146 CrossRef CAS PubMed.
- M. Sundfeldt, L. V. Carlsson, C. B. Johansson, P. Thomsen and C. Gretzer, Acta Orthop., 2006, 77, 177–197 CrossRef PubMed.
- A. Chamay and P. Tschantz, J. Biomech., 1972, 5, 173–180 CrossRef CAS PubMed.
- G. W. Milton and A. V. Cherkaev, J. Eng. Mater. Technol., 1995, 117, 483–493 CrossRef.
- J.-Y. Rho, L. Kuhn-Spearing and P. Zioupos, Medical Engineering & Physics, 1998, 20, 92–102 CAS.
- R. Hedayati, S. Janbaz, M. Sadighi, M. Mohammadi-Aghdam and A. Zadpoor, J. Mech. Behav. Biomed. Mater., 2017, 65, 831–841 CrossRef CAS PubMed.
- D. Yang, S. Lee and F. Huang, Finite elements in analysis and design, 2003, 39, 187–205 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7mh00699c |
| This journal is © The Royal Society of Chemistry 2018 |