An introduction to ratchets in chemistry and biology
Bryan
Lau†
ab,
Ofer
Kedem†
 a,
James
Schwabacher
a,
James
Schwabacher
 ab,
Daniel
Kwasnieski
ab and
Emily A.
Weiss
ab,
Daniel
Kwasnieski
ab and
Emily A.
Weiss
 *ab
*ab
aCenter for Bio-Inspired Energy Science, Northwestern University, 303 E. Superior Street, 11th Floor, Chicago, Illinois 60611-3015, USA. E-mail: e-weiss@northwestern.edu
bDepartment of Chemistry, Northwestern University, 2145 Sheridan Rd., Evanston, IL 60208-3113, USA
First published on 17th February 2017
Abstract
This article is an accessible introduction to ratchets and their potential uses. A ratchet can dramatically improve directional transport of classical or quantum particles in systems that are dominated by random diffusion. The key idea is that ratchets do not overcome poor conductivity with strong gradients, but rather use non-directional sources of energy like heat or chemical energy to power unidirectional transport, making the ratchet a Maxwell's demon. We introduce the ratchet concept and its inspiration from biology, discuss the terminology used in the field, and examine current progress and ideas in ratcheting electrons and classical particles.
Prologue
We tend to consider motion to be a deliberate action, such as produced by an internal-combustion motor or a hydraulic piston that achieves a well-defined displacement and moves a load. These macroscopic machines, whose motions are the sum of microscopic collisions by molecules on the container walls, tightly couple the expenditure of energy and the produced work, because the kinetic energy of these molecules, derived from the oxidation of gasoline or the mechanical pressure in hydraulics, is many orders of magnitude greater than the rate at which thermal energy is exchanged with the environment.An internal-combustion engine on the highway (100 km h−1) with a fuel efficiency of 8 L/100 km, or a fuel consumption rate of 10 mmol s−1, produces 104 W, far more than thermal noise (10−9 W) at a typical environmental collision rate of 1013 s−1 from vibrations or solvent/solute collisions. However, the molecular machines that make up our muscles contend with low energy input on a per-motor and per-unit time basis. A single molecular motor consumes ATP (hydrolysis of ATP produces about 50 kJ mol−1)1 at a rate of about 300–400 Hz, for a time-averaged power input of about 10−18 W2,3 that is easily overwhelmed by thermal noise, yet a muscle is still able to accomplish work. Despite the mechanistic contrasts between a motor and muscle, they are both able to achieve directed, macroscopic motion, with the molecular motor doing so without any significant backsteps (for a certain range of load weight) as the muscle contracts.
How does the muscle accomplish such a task? Instead of simply converting energy to pressure, molecular motors use energy to rectify the random motion that is induced by the thermal fluctuations of their surroundings. At equilibrium, a molecular motor cannot transform the random thermal energy in its surroundings into directed motion, or else it would spontaneously decrease the entropy of its environment, in violation of the second law of thermodynamics. A proposed violator was Maxwell's demon,4 a creature that could increase the temperature of a gas in one side of a container by only opening a door when he sees a high energy gas molecule approaching from the other side. The apparent paradox presented by Maxwell's demon was eventually resolved by the observation that the demon would have to pay energy to measure the kinetic energy of an incoming gas molecule, such that the entropy of the combined box-demon system would increase. A molecular motor that could accomplish such a feat would eventually heat up internally, increasing its chances of going backwards.5 Likewise, an electrical diode cannot rectify the thermal noise in a circuit, as the spontaneous rectification eventually builds up an opposing electric field.6 The second law, however, is a statement of the time-averaged entropy increase – since entropy depends on the system size and the degrees of freedom, on short time scales and small system sizes, such as a molecular motor head fluctuating in space while confined to a linear substrate, spontaneous decreases in entropy can occur, with the probability given by the fluctuation theorem: 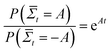 , where
, where 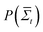 is the probability of a time-averaged irreversible entropy production A. The motor protein exploits this spontaneous reduction of entropy by using energy to couple an action, such as release from a substrate, to a desired state, such as a forward fluctuation. For instance, a forward fluctuation can expose an ATP binding site that causes a conformational change in the head, which leads to dissociation from a substrate. Therefore, just as Maxwell's demon must pay energy to know when to open the shutter, energy is paid to know when the motor head spontaneously flexes and pulls a load.
is the probability of a time-averaged irreversible entropy production A. The motor protein exploits this spontaneous reduction of entropy by using energy to couple an action, such as release from a substrate, to a desired state, such as a forward fluctuation. For instance, a forward fluctuation can expose an ATP binding site that causes a conformational change in the head, which leads to dissociation from a substrate. Therefore, just as Maxwell's demon must pay energy to know when to open the shutter, energy is paid to know when the motor head spontaneously flexes and pulls a load.
Biological motors
Let us examine the mechanism of motion in biological motors a little more closely. The motion in these motors is generally characterized by a series of ATP-catalyzed conformational changes, which strongly constrain the possible motion at every step. In the constrained state, the motor protein relies on thermal energy (Brownian motion) to explore the space, and perform the next step in its movement cycle. The consumption of ATP is necessary for, but is not always strongly coupled with, the conformational changes.7 One well-studied example is kinesin-1 – a two headed motor protein, which transports cargo by “walking” along a microtubule inside the cell. At least one of the heads remains connected to the microtubule, and the protein advances via a hand-over-hand mechanism, where the heads alternate in the lead.8–10 Each head has two binding sites – one for the microtubule, and another for ATP. One ATP molecule is consumed per step, which advances kinesin's center-of-mass by 8.3 nm. The binding of ATP triggers a conformational change in the protein's structure, which allows for the release of the trailing head. The now-free head swings forward and uses the thermal energy to explore the space, until binding to the microtubule in a somewhat strained conformation,9,11 whereupon the cycle begins anew, and the trailing head swings forward for the next step. Though the process is biased in favor of forward steps, backward steps are possible, and occur with increasing frequency for stronger load forces.9 A similar protein, myosin V, transports cargo along actin filaments in the cell, and progresses using a similar hand-on-hand mechanism, Fig. 1; the movement of myosin V was even imaged using high-speed atomic force microscopy.12 In either case, allostery (in the context of enzymes, when binding at one site of the enzyme effects a conformational change, regulating the activity in another site) is used to gate the motion – conformational changes at each step of the process bias the overall motion in one direction. Astumian argues these conformational changes primarily block backward steps, rather than directly produce forward steps.13 The series of conformational changes can be described as a potential energy surface with asymmetric gradients. Here we see a combination of asymmetric energy surfaces, energy input to maintain an out-of-equilibrium state, and the use of thermal energy to allow for diffusion while exploring the space.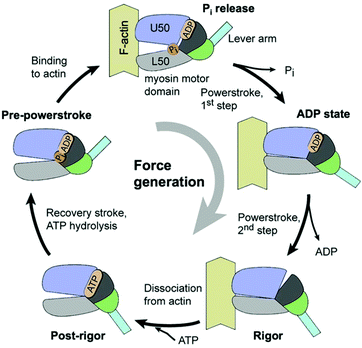 | ||
| Fig. 1 The actomyosin ATPase cycle, showing the binding and unbinding of a myosin head to the actin fiber, in conjunction with conformational changes and ATP consumption (reproduced with permission from ref. 15). The force generation can either come from a direct translation of ATP to motion, or the rectification of thermal motion – experiments suggest the latter, as the consumption of ATP is not correlated with a motor step.2 | ||
Hoffmann's recently published review discusses the journey to understanding biological motors, their properties, and some proposed models;2 a review by Chowdhury provides a thorough introduction to the kinetics of molecular motors;14 and a review by Wang et al. provides specific details about the inner workings of kinesin-1.11
Introducing: the ratchet
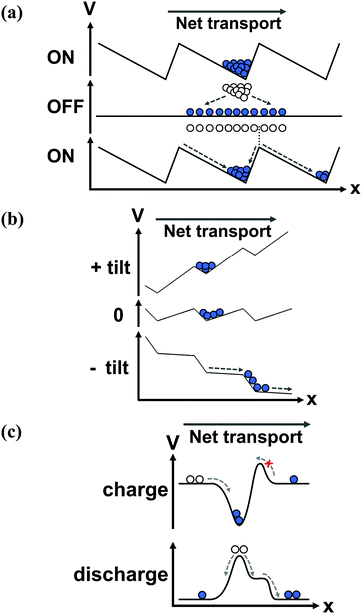
The principle by which the motor protein works has been coined a “ratchet”, a micro-mechanical version of Maxwell's demon, proposed by Lippmann,16 then studied by Smoluchowski17 and Feynman.18 The ratchet was originally proposed to demonstrate how equilibrium fluctuations could not give rise to spontaneous current, and was adapted in the late 20th century to explain the mechanism behind molecular motors.19,20 The ratchet comprises a potential energy surface that is periodic and asymmetric – the paradigmatic example is the 1D sawtooth potential, Fig. 2a. Each period of the potential has a local minimum that is offset from the midpoint of the period. If the potential is static, the motor protein fluctuates in space around the minimum, and no net transport results. However, energy can be used to switch between two modes of transport – diffusive and directed, mediated by the ratchet potential. By switching the potential off (e.g., freeing the protein from the substrate by ATP hydrolysis), the random forces from the environment cause the motor head to diffuse through space. The offset of its starting point, with respect to the midpoint of the potential, leads to an increased likelihood of diffusing to the closer adjacent period, Fig. 2a. As the motor dissipates energy, if it moves to the closer adjacent period it will relax to the next minimum, leading to a net unidirectional current. Formally, a ratchet produces current by using energy to break the symmetries of motion in space and time (see references at the end of this section). In a closed system where energy is conserved, the time evolution of the system is indistinguishable if time is reversed. This time reversal symmetry is commonly broken by the environment, which dissipates energy and exerts a random force that causes diffusion. The spatial symmetry is broken by the ratchet potential that leads to directed motion. Using local symmetry breaking, a ratchet will produce current in the absence of an overall bias along the direction of transport, and it can perform work against an electrical or mechanical load, i.e., against a bias.Ratchets can be used to transport classical and quantum objects, with some caveats. The operation of Maxwell's demon is thermodynamically allowed if it pays a price for the information it collects – the kinetic energy of the gas particle – so it knows when to open and close the shutter between the two chambers. When it can check each particle individually, the energy is used very efficiently; in a way, each biological motor has a Maxwell's demon built into its machinery, and is able to convert ATP to forward motion with nearly no backward steps.9 However, what if we could not access information about the individual particles in the system – in other words, what if Maxwell's demon could only measure the average properties of an ensemble of particles inside a ratchet? The ratchet would still work, but at a lower efficiency. Since the particles diffuse randomly and are independent of each other, a single switching frequency of the potential cannot move all particles in one direction – some will stay in the same period that they started in, and some will even move backwards. It would be as if ATP, which unbinds the motor head from the filament, arrived at the same time for all of the proteins, instead of each protein unbinding only when it flexes forward. Particle–particle interactions change the behavior of the system,22,23 but the fundamental limitation still exists. The oscillation frequency of a multi-particle, single-potential ratchet can be optimized,24 and feedback schemes can be used to improve the efficiency,25 but the oscillations can never be optimal for every particle of an ensemble. The requirement for the ratcheted entities to travel a certain distance per oscillation (to the next potential well) results in a strong dependence of the transport on the oscillation frequency, Fig. 3. As the mobility of particles depends on their size, mass, charge and so on, ratchets can be used to sort particles, using different oscillation frequencies to differentiate between the particles.
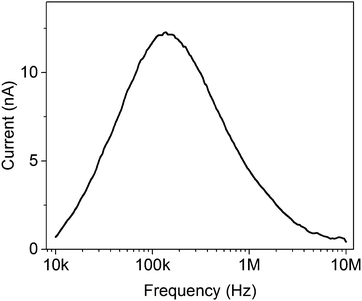 | ||
| Fig. 3 Ratchet current vs. oscillation frequency for a flashing electron ratchet of the type detailed in ref. 21. The current approaches zero for both low and high frequencies. | ||
Ratchets can be useful when a potential energy gradient does not induce significant current, which is the case when the forces from the gradient are small relative to those from the randomizing environment. For example, strong electrical or chemical gradients that could induce drift are not accessible in biological systems; in colloidal or nanostructured systems, such as organic electronics or quantum dot films, electric fields can be screened by electric double layers or mobile charge carriers.26,27 Nanostructured materials have a very high density of interfaces, and charge carriers in polymers are trapped by temperature-induced dynamic disorder,28 both of which reduce the conductivity of the system. Ratchets evolved in nature to improve transport in systems where diffusion dominates over drift, and are able to achieve this enhancement without applying a bias along the direction of transport. They may see future uses in low-power electronics, photovoltaics, and light-driven logic, where charge carriers diffuse to the electrodes.
For detailed discussion of ratcheting principles and examples, the reader is referred to, for example, reviews by Reimann,29 Astumian,30 and by Hänggi and Marchesoni.31 Symmetry breaking underlies the ratchet principle, but a deeper discussion of symmetry lies beyond the scope of this work; the interested reader is referred to work by Denisov et al.32
Ratchet, rectifier, pump? Sorting out the terminology
A flashing, or pulsating, ratchet switches between two states of the potential (usually where the potential is on and off), either through directly changing the potential or giving energy to the particles, Fig. 2a.29 In a tilting, or rocking, ratchet, the potential shape remains constant in time, but is tilted by an oscillating force, applied across the system (along the direction of transport), Fig. 2b. In a flashing ratchet, the net bias between contacts along the direction of transport always remains zero, while in a tilting ratchet, the time-averaged net bias is zero.The main difference between a flashing and tilting ratchet is their response to asymptotic oscillation frequencies. Unlike a flashing ratchet, a tilting ratchet produces current when the oscillation frequency is infinitely slow, since an infinitely slow oscillation is merely a constant bias across the device (e.g., a DC voltage). Neither type will produce current if the oscillation frequency is faster than the system's timescales of motion, as the potential will appear static. The flashing or tilting effect can be stochastic (“noise driven”), which better approximates biological systems, as the arrival of energy (i.e., via ATP hydrolysis) is not regularly spaced in time. A third driving variant is the peristaltic, or travelling wave, ratchet, where the potential is translated in space with time.
A single period of a ratchet is sometimes called a pump, Fig. 2c.33,34 In this configuration, the asymmetry is used to preferentially accumulate particles inside the pump from one reservoir, and then expel it into another reservoir.
Ratchets are usually studied in the overdamped regime. An overdamped system has no inertia – its velocity is purely a function of the ratchet potential, friction, and the fluctuating environmental forces. Underdamped particles have inertia, and can resist having their velocity randomized by the environment. In the study of quantum ratchets, ratchets that work in the coherent, or dissipation-less regime, can be called ballistic (or drift),35 inertial, or Hamiltonian36 ratchets, but are not ratchets in the traditional definition, in that they do not use energy to rectify the random motion induced by the environment.
When discussing molecular motors, two main models were proposed, with either weak or strong (also loose or tight) mechano-chemical coupling, between the expenditure of or energy and the motor's function (linear motion, transport). Strong coupling, where energy expenditure directly triggers forward motion, is also commonly termed a powerstroke model, likening the motor to artificial mechanical motors.2 Even in weakly coupled motors, individual sub-steps in the motor's cycle can be strongly coupled with ATP hydrolysis, or the release of Pi (inorganic phosphate) or ADP.15,37 On/off ratchets are a good example of a weakly coupled motor – energy is used to release particles from their trapped state, but they accomplish the bulk of their motion when they diffuse to the next period and roll down to the next minimum.
Particle ratchets
One of the earliest artificial implementations of the ratchet principle was in transporting or sorting microscopic particles, using the flashing, on/off ratchet scheme, which operates by switching the particle between diffusive and directed transport. In the first implementation, Rousselet et al. used the ratchet to transport polystyrene spheres,38 and later work transported DNA39 and lipids40 in solutions. Since the particles are not attached to a load or a bundle of fibers, their motion is unrestricted, and their lack of internal structure means that there is no Maxwell's demon that can measure the direction it is going – the asymmetry must be provided externally, and therefore is the same for every particle. The ensemble nature of transporting particles means that there can be a significant number of particles that move backwards, decreasing the efficiency of the ratchet.The ratchet potential can be introduced through electric fields,38,39,41–43 magnetic fields,44,45 optical tweezers,46–48 physical barriers,40 and pumped liquid in shaped channels.49,50 The typical case of an electric field utilizes pairs of electrodes, buried inside an insulating layer and at different polarities, to apply a ratchet potential to a transport layer above the insulating layer, Fig. 4.
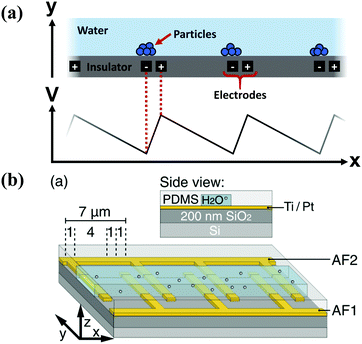 | ||
| Fig. 4 (a) Schematic drawing of the geometry (top) and applied field (bottom) in a typical particle ratchet, using pairs of electrodes (black) inside an insulator layer (grey) to apply an asymmetric electric potential in a transport layer (teal) above. (b) Geometry of an experimental dielectrophoretic ratchet, showing the two interdigitated electrodes under the transport layer (reproduced with permission from ref. 63). | ||
Transport in on/off ratchets is highly sensitive to the frequency of the applied field, and more particularly, the duration of the ‘off’ periods. These periods must be long enough to allow particles to diffuse to the nearest potential well, but not so long as to allow them to arrive at other, farther wells, thereby losing the asymmetry. The diffusion coefficient of the particles depends on their mass and size, and so different oscillation frequencies will optimize transport for different particles, allowing ratchets to sort particles by size or mass.
The necessity of a diffusional step in these system limits the maximum transport velocity they can achieve. The upper limit for this type of system is discussed in detail by Linke et al.,51 and the maximal velocity for one simplified case is derived to be 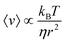 , where kB is the Boltzmann constant, T is the temperature, η is the viscosity of the medium, and r is the particle's radius. The predicted maximum velocity thus ranges from over 100 μm s−1 for 10 nm particles, to 10−5 μm s−1 for 100 μm particles. Some studies propose avoiding the rate-limiting diffusional step by continuously driving the system. A 1998 theoretical study by Tarlie and Astumian concluded that a square wave (with a duty ratio other than 50%) produces superior transport to an on/off drive.52 However, the authors did not examine the impact of a continuous drive on the ability of the ratchet to separate particles. An experimental study switching between spatially offset ratchet potentials53 did find different velocities for latex spheres of different sizes.
, where kB is the Boltzmann constant, T is the temperature, η is the viscosity of the medium, and r is the particle's radius. The predicted maximum velocity thus ranges from over 100 μm s−1 for 10 nm particles, to 10−5 μm s−1 for 100 μm particles. Some studies propose avoiding the rate-limiting diffusional step by continuously driving the system. A 1998 theoretical study by Tarlie and Astumian concluded that a square wave (with a duty ratio other than 50%) produces superior transport to an on/off drive.52 However, the authors did not examine the impact of a continuous drive on the ability of the ratchet to separate particles. An experimental study switching between spatially offset ratchet potentials53 did find different velocities for latex spheres of different sizes.
One way to optimize the transport is by using feedback loops. Instead of oscillating the potential in some pre-set manner, one can use information about the current state of the particles in the system, and then decide when to switch the potential on (or otherwise change its state).25,54 These ‘feedback ratchets’ can be experimentally applied for cases where the particles can be observed and their locations determined in real-time, such as microscopic spheres.55 Feedback protocols maximizing velocity do not necessarily maximize energy efficiency.56
Following work on microscopic particles and molecules, the ratchet concept was expanded to transport electrons. Early work focused on manipulating electrons confined to two dimensions in thin layers of semiconductors, i.e., a 2-dimensional electron gas (2DEG). In the case of ballistic electron ratchets, the semiconductor sheet was patterned with arrays of asymmetric holes (“anti-dots”) spaced closer than the mean free path of the electron. When an oscillating force was applied (using electrodes or microwave radiation) perpendicular to the direction of transport, current was produced;57,58 these systems are sometimes called drift ratchets. In tunneling ratchets, patterning a series of asymmetric constrictions into a 2DEG ribbon created a ratchet potential energy surface, and applying an oscillating bias parallel to the direction of transport also produced current, where tunneling was responsible for current reversals.59
Later, the flashing ratchet concept was also applied to electrons and holes, using pairs of electrodes to apply asymmetric potentials to a 2DEG,60 and to an organic semiconductor;61 and using flat asymmetric electrodes on a 2DEG nanowire.62 We have recently constructed an electron ratchet using electrodes with an asymmetric thickness profile, to transport thermally- and photogenerated carriers in an organic semiconductor.21
Quantum effects in ratchets
Applying ratchets to quantum objects, like cold atoms and electrons, begs the question of how the wave-particle duality, tunneling, and coherence affect the magnitude and direction of the ratchet current. Research in “quantum” ratchets has largely remained theoretical: experimental realizations are few, and are split between cold atoms in optical lattices36 and electron ratchets.59,61,62 Flashing electron ratchets have been demonstrated in a few systems, with organic61 and inorganic60,62 semiconductors, but the electrons can be modeled both quantum-mechanically64 and classically,61,62 depending on the length scales of the experimental devices.Tunneling is a signature of quantum transport, and its effect on the ratchet current depends on the method of modulating the potential. In tilting ratchets, tunneling enhances the ratchet current, as the barriers heights are different during each direction of tilting.59,65,66 In a flashing ratchet, the shape of the potential remains the same while the amplitude is changed, and tunneling introduces an isotropic leakage current that decreases the average current; for a one-dimensional quantum flashing ratchet, the potentials that produce the highest current classically confine the wavefunction to prevent tunneling.64 Exhaustive comparisons between the quantum and classical currents in a delta-kicked flashing ratchet revealed that the quantum current is lower, but more studies are needed with different schemes of potential modulation.67
Interference effects, such as cancellation of current when two transport paths are out of phase,68,69 are the second major signature of quantum transport. Interference effects are important when there is little to no decoherence, and the resulting ratchet current is very dependent on the initial conditions, the shape of the confining potential,70 and the effect of the source and drain electrodes, similar to classical chaos. However, in most quantum systems connected to a bath, such as biological chromophores, the decoherence rate is fast enough such that coherence plays no role in transport,71 leaving us with a picture of a wavepacket with damped oscillations. The ‘sloshing’ of the wavepacket inside a time-dependent potential can lead to resonances that enhance transport,64 an effect that depends on the wave-particle duality but not coherence.
In summary, the role of quantum effects in ratchets will depend on how strongly the quantum system is connected to its surroundings. The strength of dissipation determines whether we can think of the quantum system as under or overdamped, which respectively lead to increased and decreased sensitivity to changes in the ratchet parameters.
Artificial molecular motors
As our understanding of biological motors deepens, so does our desire to utilize the same principles in artificial systems. At one end of the spectrum, one can directly modify a biological system, to impart some new functionality or level of control to the naturally occurring mechanism. In one particularly fascinating example, myosin and kinesin motors were modified with light-sensitive protein domains, which allowed researchers to repeatedly switch the motors' velocity, and even direction, using light to induce a conformational change in the motor's structure.72 At the other end, we find fully artificial motors, typically based on small molecules with functional groups able to produce a structural or conformational change in response to external stimuli. Synthetic molecular motors are still much less capable than their biological counterparts. Biological motors continuously perform useful work (unidirectional motion or rotation) and do so in response to local chemical signals, such as the concentration of ATP, thus allowing for control loops. The components needed to make equally capable synthetic motors are: (i) movable molecular motifs; (ii) elements responsive to local chemical signals; and (iii) control loops, components able to modulate multiple chemical signals for controlling motors and other elements, to allow for regulated activity of complex systems.The very first step to building synthetic molecular motors involved topological entanglement – mechanically linked molecular assemblies, first proposed in the 1950s, and synthesized in the 1960s. These assemblies comprised two main types – catenanes, based on two interlocking rings, and rotaxanes, based on a ring molecule threaded over an axle, with bulky groups at both ends of the axle holding the assembly together. The 1983 publication of a template synthesis route by Sauvage and co-workers offered a relatively simple and high-yield approach, and invigorated the field;73,74 they were later able to demonstrate reversible changes in the shape of catenanes upon ion complexation, providing a response to a chemical signal.75 The rotaxane molecular shuttle, introduced in 1991 by Stoddart and co-workers involved a ring molecule switching between two binding sites on a molecular axle using thermal energy,76 and later modified to allow for controlled switching.77 Like the molecular shuttle, most of the molecular motors studied in the 1990s and 2000s were actually switches, rather than motors; resetting the switch to its initial state also undid the work it had accomplished, so that these implementations were incapable of performing work cumulatively.78 Feringa and co-workers demonstrated the first motor able to perform work in 1999; their motor was based on a central isormerizable bond, and on the steric hindrance between substituent groups.79 The motor rotates in a single direction, prompted by UV-irradiation and heat. The two parts of the molecule rotate about the central double-bond in direct response to irradiation (strong coupling), followed by a thermally-activated (weak coupling) inversion of the helicity of the molecule. Though this system can perform work, its reliance on large-scale signals prevents it from being integrated into larger mechanisms, where it would need to respond to local signals, as is the case in biological motors.80 In 2016, Wilson et al. introduced the first synthetic small-molecule motor, able to produce continuous directional motion using chemical fuel, in the form of a ring molecule continuously and unidirectionally transported around a cyclical track.81 The ring moves around the track using Brownian motion from its surroundings, but the direction of motion is controlled by the raising and lowering of energetic barriers, in the form of bulky groups binding to the track.
A possible route for useful synthetic motors could be protein engineering – proteins offer a variety of movable units, levers, bridges and springs, and can react to local chemical signals. We are still unable to predict the way a primary structure (amino-acid chain) will fold, much less solve the inverse problem of predicting which amino acid sequence will produce a desired structure. Advances in our understanding of protein folding, prompted by increasing computational resources, could have profound impact on the production of artificial molecular motors.
There are many excellent sources of information about molecular motors; in particular, a review by Erbas-Cakmak et al.,82 an essay by Kay and Leigh,78 and a Focus by Michl and Sykes83 are launching points for further study.
Active matter ratchets
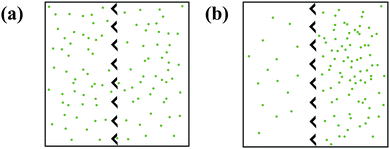
Active matter ratchets are a new class of rectification systems that contain self-propelled particles and, unlike the other ratchets introduced in this text, do not require external driving forces for rectification. Active particle populations (known as active matter) keep the system far-from equilibrium by converting stored or ambient energy into motion.84 Biological active particles, like swimming bacteria, convert chemical energy stored within the cell into motion. Synthetic active particles, such as gold–silica Janus particles, convert light into thermophoretic motion.85 An active particle's direction of motion is set by the anisotropy of its propulsion at short times, but its motion can become random with an enhanced diffusion coefficient component at longer times.86Since active particles drive themselves away from equilibrium, they only need a source of asymmetry to direct their motion, Fig. 5. In an important example, Galajda et al. induced rectification of Escherichia coli bacteria using only an array of asymmetric funnels.87 Removing asymmetry (by making barriers symmetric) or self-propulsion (by restricting the motility of the bacteria) inhibits ratcheting. Wan et al. modeled the bacteria as points moving in straight lines, before randomly changing direction.88 Rectification only arises, however, when run lengths are long enough to allow asymmetric barriers to direct bacteria motion before the next reorientation event occurs. The interplay between the force of an active particle colliding with a wall and the repulsive steric force that drives the particle away from the wall directs the particle motion parallel to the boundary. Either reorientation at the collision site redirects particle motion along the wall, or the collision's net tangential force directs the particle along the boundary.89
While active particles do not need to interact with one another for rectification to occur, particle–particle interactions produce novel macroscopic properties that affect rectification. When interparticle interactions are employed in the Wan et al. ballistic simulations, rectification decreases.88 In general, complex effects like current reversals are observed when collective particle–particle interactions are significant.90 Flocking, jamming, and packing of active particles have been identified as causes of the observed reversals, though, similar to current reversals in externally-driven ratchets, the mechanism varies between systems.
Ratcheting can also occur when passive particles are placed in active baths. Active baths are excess self-propelled synthetic particles or concentrated bacterial solutions that can collectively interact with a few passive particles to induce transport. In contrast to thermal baths, active baths are expected to produce non-Gaussian fluctuations in their coupled systems, creating a far-from equilibrium environment where the rectification of passive particles can occur.89 Self-propelled bath particles, for instance, can collect in the inner corners of a saw-toothed wheel's teeth, creating a net torque that rotates the passive gear in one direction.91,92 Passive colloids, similarly, can be directed over asymmetric barriers by interacting with swimming bacteria.93 Active baths ultimately allow for rectifying passive particle motion without applying the asymmetric external driving force required in externally-driven ratchet systems.
The interface between theory and experiment
The vast majority of publications concerning ratchets explore the topic using theory and simulation, with only a small minority describing experimental systems. The disparity is a direct result of the great difficulty involved in reliably implementing and detecting ratcheting mechanisms. In general, constructing a ratchet is straightforward, as long as time and space symmetry is broken – a reality expressed by the oft-cited Curie's principle, which holds that where a phenomenon is not ruled out by symmetries, it will generally occur.29 However, the relatively lax requirements lead to complex behavior: the ratchet current is very sensitive to the variation of any parameter, and can outright reverse its direction over small variations. Nearly every theoretical and experimental realization of a ratchet thus behaves differently, and predicting the current by simply inspecting a ratchet potential and experimental parameters such as bath temperature and oscillation frequency is very difficult. The lack of intuitive understanding, or rules-of-thumb for predicting ratchet behavior (except in certain limits), make the design of experimental systems, and the interpretation of the resulting data, a serious challenge.Theoretical systems are typically highly simplified, neglecting many types of interactions (e.g., particle–particle interactions; hydrodynamic forces; localized heating), due to computational limitations or analytical intractability. Thus, the theorized systems are rarely directly implementable in experiment. One conspicuous example is dimensionality – while virtually all theoretical systems involve transport along a single dimension (1D), most experimental systems include a 2D or 3D transport layer, with exceptions for cold-atom optical traps36 and transport along nanowires.62
While a theoretical system can be perfectly defined, an experimental one is always subject to deviations from the design – electrodes are slightly misaligned; layers are not uniform; applied fields deviate from the intended shape, magnitude, or timing. Typically, such deviations are not addressed in theoretical studies, which feature perfectly defined systems. The deviations from the design create two separate issues. First, small deviations might be enough to destroy the sensitive ratchet mechanism, so that no transport is observed; experimenters lack guidance about the robustness of the proposed mechanisms. For example, we have recently addressed the issue of potential shape, and showed that even small changes to the shape can result in a reversal, or complete loss, of the current.64 Second, these deviations can result in alternative ratcheting mechanisms. Such “unintended ratcheting” makes it difficult to implement proper controls – is the observed current due to the intended mechanism, or due to some other asymmetry? Large sample sizes can overcome the confounding effect of some accidental asymmetries, but the difficulties in device fabrication often limit the number of tested devices.
The above discussion implies three main challenges for theoretical studies: (i) study and define the robustness of proposed ratchet mechanisms with respect to structural and chemical non-idealities of the system; (ii) examine a large parameter space to find general behaviors, and (iii) propose experimental ways to identify the effects of alternative mechanisms (e.g., via the dependence of current on driving parameters such as frequency). These steps, resulting in closer theory-experiment collaboration, will benefit the development of better models as well, providing experimental tests for the (unavoidable) multitude of simplifications in theoretical works.
Our previous discussion of biological motors does raise an interesting question, which we cannot answer at this time – if ratchet mechanisms are so sensitive to environmental parameters, how does nature utilize them so successfully? Is it that biological ratchets are so exquisitely evolved to their purpose, and a small change will destroy their effectiveness? Or is it that biological systems operate in more forgiving regimes (high dissipation decreases a ratchet's sensitivity to many parameters)?
Summary and outlook
We have discussed the biological foundation of the ratchet as a Maxwell's demon. The demon expends energy to oscillate the object of interest between diffusive and trapped states, where asymmetry is used to bias the object's motion as it relaxes into the trapped state. We connect the concept of a biological ratchet to particle ratchets, which have the potential to enhance transport in systems dominated by diffusive transport.The ratchet effect is easily manifested, and therefore sensitive to variations of any parameters of the system. This sensitivity has led to an abundance of theoretical studies, but a relative paucity of experimental implementations. It remains to be seen whether a unifying theoretical perspective on ratchets will emerge, which will only be possible with more data, complete studies of parameter spaces (in theory and experiment), and an open exchange of information between those who predict, simulate, and model and those who build and characterize ratchets. Efforts to produce better defined and controlled experimental systems on the one hand, and to account for experimental limitations and uncertainties in theoretical models on the other hand, could lead to significant returns in our understanding and advancement of the field.
Acknowledgements
This work was supported as part of the Center for Bio-Inspired Energy Science, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences under Award # DE-SC0000989. JCS thanks the National Science Foundation for support through a Graduate Research Fellowship.References
- C. Bergman, Y. Kashiwaya and R. L. Veech, J. Phys. Chem. B, 2010, 114, 16137–16146 CrossRef CAS PubMed.
- P. M. Hoffmann, Rep. Prog. Phys., 2016, 79, 032601 CrossRef PubMed.
- R. D. Astumian and P. Hänggi, Phys. Today, 2002, 55, 33–39 CrossRef.
- J. C. Maxwell, Theory of Heat, Longmans Green, New York, 1902 Search PubMed.
- R. P. Feynman, R. B. Leighton and M. Sands, The Feynman lectures on physics, Vol. I: The new millennium edition: mainly mechanics, radiation, and heat, Basic Books, New York, NU, 2015, vol. 1 Search PubMed.
- L. Brillouin, Phys. Rev., 1950, 78, 627–628 CrossRef.
- Y. Ishii, S. Esaki and T. Yanagida, Appl. Phys. A: Mater. Sci. Process., 2002, 75, 325–330 CrossRef CAS.
- C. L. Asbury, A. N. Fehr and S. M. Block, Science, 2003, 302, 2130–2134 CrossRef CAS PubMed.
- N. J. Carter and R. A. Cross, Nature, 2005, 435, 308–312 CrossRef CAS PubMed.
- A. Yildiz, M. Tomishige, R. D. Vale and P. R. Selvin, Science, 2004, 303, 676–678 CrossRef CAS PubMed.
- W. Wang, L. Cao, C. Wang, B. Gigant and M. Knossow, Protein Sci., 2015, 24, 1047–1056 CrossRef CAS PubMed.
- N. Kodera, D. Yamamoto, R. Ishikawa and T. Ando, Nature, 2010, 468, 72–76 CrossRef CAS PubMed.
- R. D. Astumian, Nat. Nanotechnol., 2012, 7, 684–688 CrossRef CAS PubMed.
- D. Chowdhury, Phys. Rep., 2013, 529, 1–197 CrossRef CAS.
- S. F. Wulf, V. Ropars, S. Fujita-Becker, M. Oster, G. Hofhaus, L. G. Trabuco, O. Pylypenko, H. L. Sweeney, A. M. Houdusse and R. R. Schröder, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E1844–E1852 CrossRef CAS PubMed.
- G. Lippmann, Rapp. Congr. Int. Phys., 1900, 1, 546–550 Search PubMed.
- M. Smoluchowski, Vorträge über die Kinetische Theorie der Materie und der Elektrizität, 1914, 89–121 Search PubMed.
- R. P. Feynman, R. B. Leighton and M. Sands, The Feynman Lectures on Physics, Addison-Wesley, Reading, MA, 1963, vol. 1, pp. 46.1–46.9 Search PubMed.
- M. O. Magnasco, Phys. Rev. Lett., 1993, 71, 1477–1481 CrossRef PubMed.
- P. Reimann, Phys. Rep., 1997, 290, 149–155 CrossRef.
- O. Kedem, B. Lau and E. A. Weiss, submitted.
- Y. Aghababaie, G. Menon and M. Plischke, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1999, 59, 2578–2586 CrossRef CAS.
- C. C. de Souza Silva, J. Van de Vondel, M. Morelle and V. V. Moshchalkov, Nature, 2006, 440, 651–654 CrossRef CAS PubMed.
- L. Machura, M. Kostur, P. Talkner, J. Łuczka, F. Marchesoni and P. Hänggi, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 061105 CrossRef CAS PubMed.
- F. Cao, L. Dinis and J. M. R. Parrondo, Phys. Rev. Lett., 2004, 93, 040603 CrossRef PubMed.
- M. Kiguchi, M. Nakayama, K. Fujiwara, K. Ueno, T. Shimada and K. Saiki, Jpn. J. Appl. Phys., Part 2, 2003, 42, 1408–1410 CrossRef.
- M. Raja and B. Eccleston, J. Appl. Phys., 2011, 110, 114524 CrossRef.
- A. Troisi, Chem. Soc. Rev., 2011, 40, 2347–2358 RSC.
- P. Reimann, Phys. Rep., 2002, 361, 57–265 CrossRef CAS.
- R. D. Astumian, Phys. Chem. Chem. Phys., 2007, 9, 5067–5083 RSC.
- P. Hänggi and F. Marchesoni, Rev. Mod. Phys., 2009, 81, 387–442 CrossRef.
- S. Denisov, S. Flach and P. Hänggi, Phys. Rep., 2014, 538, 77–120 CrossRef.
- O. V. Mikhnenko, S. D. Collins and T.-Q. Nguyen, Adv. Mater., 2015, 27, 2007–2012 CrossRef CAS PubMed.
- H. Linke, T. E. Humphrey, P. E. Lindelof, A. Löfgren, R. Newbury, P. Omling, A. O. Sushkov, R. P. Taylor and H. Xu, Appl. Phys. A: Mater. Sci. Process., 2002, 75, 237–246 CrossRef CAS.
- A. M. Song, Appl. Phys. A: Mater. Sci. Process., 2002, 75, 229–235 CrossRef CAS.
- T. Salger, S. Kling, T. Hecking, C. Geckeler, L. Morales-Molina and M. Weitz, Science, 2009, 326, 1241–1243 CrossRef CAS PubMed.
- J. A. Spudich, Nat. Rev. Mol. Cell Biol., 2001, 2, 387–392 CrossRef CAS PubMed.
- J. Rousselet, L. Salome, A. Ajdari and J. Prost, Nature, 1994, 370, 446–448 CrossRef CAS PubMed.
- J. S. Bader, R. W. Hammond, S. A. Henck, M. W. Deem, G. A. McDermott, J. M. Bustillo, J. W. Simpson, G. T. Mulhern and J. M. Rothberg, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 13165–13169 CrossRef CAS.
- A. van Oudenaarden and S. G. Boxer, Science, 1999, 285, 1046–1048 CrossRef CAS PubMed.
- L. P. Faucheux and A. Libchaber, J. Chem. Soc., Faraday Trans., 1995, 91, 3163–3166 RSC.
- L. Gorre-Talini, S. Jeanjean and P. Silberzan, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 2025–2034 CrossRef CAS.
- W. C. Germs, E. M. Roeling, L. J. van Ijzendoorn, R. A. J. Janssen and M. Kemerink, Appl. Phys. Lett., 2013, 102, 073104 CrossRef.
- A. Auge, A. Weddemann, F. Wittbracht and A. Hütten, Appl. Phys. Lett., 2009, 94, 183507 CrossRef.
- P. Tierno, P. Reimann, T. H. Johansen and F. Sagués, Phys. Rev. Lett., 2010, 105, 230602 CrossRef PubMed.
- L. P. Faucheux, L. S. Bourdieu, P. D. Kaplan and A. J. Libchaber, Phys. Rev. Lett., 1995, 74, 1504–1507 CrossRef CAS PubMed.
- S.-H. Lee, K. Ladavac, M. Polin and D. G. Grier, Phys. Rev. Lett., 2005, 94, 110601 CrossRef PubMed.
- S.-H. Wu, N. Huang, E. Jaquay and M. L. Povinelli, Nano Lett., 2016, 16, 5261–5266 CrossRef CAS PubMed.
- K. Loutherback, J. Puchalla, R. H. Austin and J. C. Sturm, Phys. Rev. Lett., 2009, 102, 045301 CrossRef PubMed.
- S. Matthias and F. Müller, Nature, 2003, 424, 53–57 CrossRef CAS PubMed.
- H. Linke, M. T. Downton and M. J. Zuckermann, Chaos, 2005, 15, 26111 CrossRef PubMed.
- M. B. Tarlie and R. D. Astumian, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 2039–2043 CrossRef CAS.
- L. Gorre-Talini, J. P. Spatz and P. Silberzan, Chaos, 1998, 8, 650–656 CrossRef CAS PubMed.
- L. Dinis, J. M. R. Parrondo and F. J. Cao, Europhys. Lett., 2005, 71, 536–541 CrossRef CAS.
- B. J. Lopez, N. J. Kuwada, E. M. Craig, B. R. Long and H. Linke, Phys. Rev. Lett., 2008, 101, 220601 CrossRef PubMed.
- S. Roychowdhury, G. Saraswat, S. Salapaka and M. Salapaka, J. Process Control, 2015, 27, 76–86 CrossRef CAS.
- A. Lorke, S. Wimmer, B. Jager, J. P. Kotthaus, W. Wegscheider and M. Bichler, Physica B, 1998, 249–251, 312–316 CrossRef CAS.
- A. M. Song, P. Omling, L. Samuelson, W. Seifert, I. Shorubalko and H. Zirath, Appl. Phys. Lett., 2001, 79, 1357 CrossRef CAS.
- H. Linke, T. E. Humphrey, A. Löfgren, A. O. Sushkov, R. Newbury, R. P. Taylor and P. Omling, Science, 1999, 286, 2314–2317 CrossRef CAS PubMed.
- T. Müller, A. Würtz, A. Lorke, D. Reuter and A. D. Wieck, Appl. Phys. Lett., 2005, 87, 042104 CrossRef.
- E. M. Roeling, W. C. Germs, B. Smalbrugge, E. J. Geluk, T. de Vries, R. A. J. Janssen and M. Kemerink, Nat. Mater., 2011, 10, 51–55 CrossRef CAS PubMed.
- T. Tanaka, Y. Nakano and S. Kasai, Jpn. J. Appl. Phys., 2013, 52, 06GE07 CrossRef.
- W. C. Germs, E. M. Roeling, L. J. van Ijzendoorn, B. Smalbrugge, T. de Vries, E. J. Geluk, R. A. J. Janssen and M. Kemerink, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 041106 CrossRef PubMed.
- B. Lau, O. Kedem, M. A. Ratner and E. A. Weiss, Phys. Rev. E, 2016, 93, 062128 CrossRef PubMed.
- P. Reimann, M. Grifoni and P. Hänggi, Phys. Rev. Lett., 1997, 79, 10–13 CrossRef CAS.
- I. Goychuk, M. Grifoni and P. Hänggi, Phys. Rev. Lett., 1998, 81, 649–652 CrossRef CAS.
- L. Ermann and G. G. Carlo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 010903 CrossRef PubMed.
- A. Aviram and M. A. Ratner, Chem. Phys. Lett., 1974, 29, 277–283 CrossRef CAS.
- G. C. Solomon, D. Q. Andrews, T. Hansen, R. H. Goldsmith, M. R. Wasielewski, R. P. Van Duyne and M. A. Ratner, J. Chem. Phys., 2008, 129, 054701 CrossRef PubMed.
- H. Linke, W. Sheng and A. Löfgren, Europhys. Lett., 1998, 44, 341–347 CrossRef CAS.
- P. Rebentrost, M. Mohseni, I. Kassal, S. Lloyd and A. Aspuru-Guzik, New J. Phys., 2009, 11, 033003 CrossRef.
- M. Nakamura, L. Chen, S. C. Howes, T. D. Schindler, E. Nogales and Z. Bryant, Nat. Nanotechnol., 2014, 9, 693–697 CrossRef CAS PubMed.
- C. O. Dietrich-Buchecker, J. P. Sauvage and J. M. Kern, J. Am. Chem. Soc., 1984, 106, 3043–3045 CrossRef CAS.
- C. O. Dietrich-Buchecker, J. P. Sauvage and J. P. Kintzinger, Tetrahedron Lett., 1983, 24, 5095–5098 CrossRef CAS.
- M. Cesario, C. O. Dietrich-Buchecker, J. Guilhem, C. Pascard and J. P. Sauvage, J. Chem. Soc., Chem. Commun., 1985, 244–247 RSC.
- P. L. Anelli, N. Spencer and J. F. Stoddart, J. Am. Chem. Soc., 1991, 113, 5131–5133 CrossRef CAS PubMed.
- R. A. Bissell, E. Córdova, A. E. Kaifer and J. F. Stoddart, Nature, 1994, 369, 133–137 CrossRef CAS.
- E. R. Kay and D. A. Leigh, Angew. Chem., Int. Ed., 2015, 54, 10080–10088 CrossRef CAS PubMed.
- N. Koumura, R. W. Zijlstra, R. A. van Delden, N. Harada and B. L. Feringa, Nature, 1999, 401, 152–155 CrossRef CAS PubMed.
- W. R. Browne and B. L. Feringa, Nat. Nanotechnol., 2006, 1, 25–35 CrossRef CAS PubMed.
- M. R. Wilson, J. Solà, A. Carlone, S. M. Goldup, N. Lebrasseur and D. A. Leigh, Nature, 2016, 534, 235–240 CrossRef CAS PubMed.
- S. Erbas-Cakmak, D. A. Leigh, C. T. McTernan and A. L. Nussbaumer, Chem. Rev., 2015, 115, 10081–10206 CrossRef CAS PubMed.
- J. Michl and E. C. H. Sykes, ACS Nano, 2009, 3, 1042–1048 CrossRef CAS PubMed.
- M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143–1189 CrossRef CAS.
- H.-R. Jiang, N. Yoshinaga and M. Sano, Phys. Rev. Lett., 2010, 105, 268302 CrossRef PubMed.
- J. R. Howse, R. A. L. Jones, A. J. Ryan, T. Gough, R. Vafabakhsh and R. Golestanian, Phys. Rev. Lett., 2007, 99, 048102 CrossRef PubMed.
- P. Galajda, J. Keymer, P. Chaikin and R. Austin, J. Bacteriol., 2007, 189, 8704–8707 CrossRef CAS PubMed.
- M. B. Wan, C. J. Olson Reichhardt, Z. Nussinov and C. Reichhardt, Phys. Rev. Lett., 2008, 101, 018102 CrossRef CAS PubMed.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- C. J. O. Reichhardt and C. Reichhardt, Annu. Rev. Condens. Matter Phys., 2017, 8 DOI:10.1146/annurev-conmatphys-031016-025522.
- C. Maggi, J. Simmchen, F. Saglimbeni, J. Katuri, M. Dipalo, F. De Angelis, S. Sanchez and R. Di Leonardo, Small, 2016, 12, 446–451 CrossRef CAS PubMed.
- A. Sokolov, M. M. Apodaca, B. A. Grzybowski and I. S. Aranson, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 969–974 CrossRef CAS PubMed.
- N. Koumakis, A. Lepore, C. Maggi and R. Di Leonardo, Nat. Commun., 2013, 4, 2588 CAS.
Footnote |
| † Equal contribution. |
| This journal is © The Royal Society of Chemistry 2017 |