Inverting the design path for self-assembled block copolymers
Karim R.
Gadelrab
 a,
Adam F.
Hannon†
a,
Adam F.
Hannon†
 *ab,
Caroline A.
Ross
a and
Alfredo
Alexander-Katz
*a
*ab,
Caroline A.
Ross
a and
Alfredo
Alexander-Katz
*a
aDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA. E-mail: aalexand@mit.edu
bMaterials Science and Engineering Division, National Institute of Standards and Technology, 100 Bureau Drive, Gaithersburg, MD 20899, USA
First published on 9th October 2017
Abstract
Recent success of inverse design methodologies in the realm of self-assembled materials has allowed us to envision an inverse path of discovery where we go from a desired target function to building blocks. In this review we examine recent advances of such inverse design methods in soft materials containing block copolymers, colloids, or DNA. By combining well-developed theoretical models with advanced inverse search algorithms, the design of such systems has been dramatically enhanced over the past decade. Advantages and disadvantages of the most prominent inverse search algorithms are discussed in the context of block copolymer directed self-assembly inverse design. The success of these methodologies in such systems shows great promise for the future of self-assembling materials, particularly for applications where the desired structure and properties of the system needed for a functional device are known.
Design, System, ApplicationThe progress in understanding the underlying physics governing materials behavior enables designing materials with new and improved properties. This advancement relies on a strong theoretical and computational effort to make informed experimental decisions. While the theoretical and computational investigations systematically explore a parameter space, this parameter space is guided by what is experimentally known in what can be considered a forward type of analysis. However, the ideal role of theoretical and computational work is to provide scientists and engineers with the right starting conditions that would lead to a particular outcome. This inverse approach resembles an optimization problem that needs to be efficiently solved. We discuss several areas within the self-assembly materials community where inverse design strategies have been successfully applied with emphasis on directed self-assembly of block copolymers using topographical template. These strategies share a common theme of defining a target property or structure, translating this output into an objective function, selecting a computational technique that can probe this output for a given parameter space, and finally running an inverse optimization scheme that finds the best set of parameters to yield the desired output. We believe that the pressing need of new advanced materials will push the field of materials design to rely on such inverse design approaches as the parameter space become practically unsearchable. |
Main text
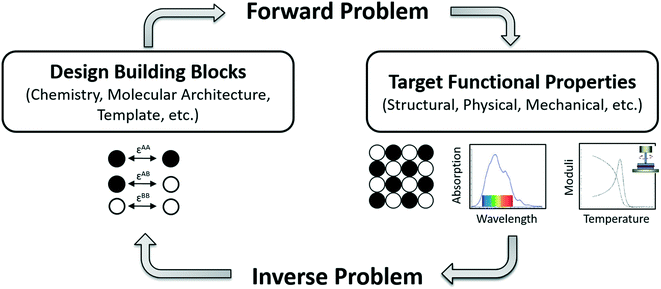
The ability to define the structural basis for materials behavior lies at the core of materials design.1 The advancement of our understanding of materials structure and the capability to control that structure has unlocked the potential for new properties and applications.2–5 This progress in the engineering of materials is facilitated through a strong theoretical and computational effort to make informed experimental decisions.6 Theoretical and computational efforts typically start with a given model parameter space that is systematically explored to predict real material behavior. The selected parameter space is guided by what is experimentally known. This forward type of analysis has been commonly adapted, and successfully contributed to the understanding of the underlying physics of a given problem.7 However, scientists and engineers ideally want to find the right starting conditions that would lead to a desired outcome using the target end results as the search input. Such an approach resembles the inverse nature of optimization problems, where numerical parameters normally utilized in theory and simulations are functionally related to the measurable physical quantities.8A general flow diagram of how the material design process takes place is shown in Fig. 1. The forward design approach starts from hypothesizing candidate building blocks (chemistry, molecular architecture, guiding template, etc.) that are expected to result in target functional properties (structural, physical, mechanical, etc.). The dependence of the outcome on these input blocks can be quickly assessed in a direct fashion using computer simulations. Hence, the target properties are realized through an exhaustive search of the input parameter space. On the contrary, the inverse design method sets the target property as a goal that needs to be achieved through search and optimization techniques. This method's success depends on finding the right set of input design parameters that would produce the closest output to the target goal. In particular, the target application is used to define an objective function of a metric to be optimized by the inverse methodology. Simulations are then performed, seeded with random parameters based on the experimental bounds of the problem, using a given structure model for the system. The structure model simulation results are used with the objective function to compute a goodness of fit for the target metric. The model parameters are updated using an inverse search algorithm or optimization routine of choice. The new parameters are then used to perform new forward simulations and the process is reiterated until a satisfactory solution is found. Using this general methodology, a given problem can be solved by defining the simulation technique and structure model, objective function and data model, and inverse search algorithm. The objective function is usually dependent on the data used for the target metric and can take many forms such as a simple mathematical function from statistical theory (χ2-function), mean-absolute error function, a log-normal function, or, if possible, can be derived from the Hamiltonian describing the physics of the system.9 Particularly, in the field of block copolymer self-assembly, a number of increasingly sophisticated algorithms and strategies have now been proposed for inverse design, starting from pioneering work using simple Monte-Carlo based optimization processes,10,11 to evolutionary computation9,12–15 and swarm-based approaches.16,17
Inverse design has gained much attention in the field of materials self-assembly.15,18 Self-assembly is the process through which a collection of simple units spontaneously form larger complex structures.19,20 The inherent ability of these units to morph into specific patterns provides a valuable tool for materials fabrication, as it has the potential to produce intricate features at the smallest of length scales.21–27 The possible outcomes from a variety of self-assembly processes have been explored experimentally. For example, block copolymers (BCPs) can self-assemble into various periodic structures (spheres, cylinders, lamellae, etc.) that can be used for surface patterning,22–29 battery electrolytes,30 light polarizers,31 photonic crystals,32,33 and optoelectronics.34 DNA origami uses the information encoded via DNA synthesis for self-assembly into almost arbitrarily programmable shapes.35–38 Furthermore, in DNA-mediated assembly, colloidal nanoparticles functionalized with single strand DNA can be used to self-assemble into a variety of crystal structures.39–41
The theoretical perspective for the problem of self-assembly depends mostly on the system of interest. In the case of colloids, the shape of the force profile surrounding a suspended particle has been studied to correlate the self-assembled pattern of the colloid with the strength of the attraction and repulsion components of the field.42–44 Attempts to solve the colloid inverse problem were based on statistical mechanics techniques where a functional form was proposed for the isotropic pair potential. The parameters of the function that gave the desired crystal structure were estimated through an optimization process for an objective function describing structural stability.45–47 A counterintuitive outcome of these studies is that radially symmetric force fields can produce ground state crystals with low symmetry. Low symmetry structures such as 2D rectangular,48,49 hexagonal,49 and diamond crystal43 were achieved through monotonic and convex-repulsive potential expressions that could be experimentally realized.42,43
Inverse search approaches are found in other disciplines including spectroscopy and scattering where instead of trying to design a target structure, an intensity measurement is made by a technique such as transmission scattering,50 reflectivity,51,52 or spectroscopic ellipsometry53 and the resulting data are fit using an inverse algorithm. In this case, the measured data set is an intensity signal that is produced from the path taken by the radiation used to interact with the material medium. This path is generally dependent on the initial conditions of the radiation and the sample material properties. Many of the radiation characteristics are lost in the intensity measurement such as the phase of the radiation. Thus, while there are many processes where the forward calculation of the measured intensity is well understood, in practice one is always solving the inverse problem starting with the measured intensity and having to calculate the material structure and the conditions of radiation. A general inverse methodology for finding the material structure required to produce a given X-ray scattering pattern for periodic nanogratings was shown by Hannon et al.54 using a shape based model and by Khaira et al.55 using a physics-based model. These studies both use a similar inverse methodology analogous to a general inverse materials design approach where the measured intensity data replace the target structure metric. The methodology by Hannon et al. obtained the shape profile of a periodic nanograting from scattered X-ray intensity data via a trapezoid stack model and compared three different inverse search algorithms: Markov chain Monte Carlo, differential evolution, and covariance matrix adaptation evolutionary strategy (CMA-ES). The results of that study suggested that CMA-ES is one of the best inverse search methods for such scattering data and shape models in terms of both speed and consistent convergence to the global minimum solution. The study by Khaira et al. used the CMA-ES algorithm with a more complex physics-based model that not only gives the resulting periodic structure from the scattering data, but also thermodynamic processing and property information of the system studied. Future work in materials inverse design should explore new avenues using this inverse search paradigm with indirect experimental measuring techniques to access the real material structure and properties of the system with physics-based models.56
One of the most prominent self-assembling soft materials that inverse design has recently been applied to are BCPs, which self-assemble through a free energy minimization process known as microphase separation.57 The immiscibility of the constituent polymers in each block promotes phase separation that reduces interfacial contact between the blocks, while the arrangement of different blocks within the same molecule limits the extent of the spatial separation resulting in a periodic pattern rather than macroscale phase separation.58 The critical dimensions of the ordered morphology are on the order of a few nm to 100 s of nm depending on the chain length and chemistry which makes BCPs a very attractive tool for producing complex nanoscale structures, for example in microelectronic device fabrication.58–62 Functional devices have been fabricated successfully through patterning based on BCP thin films, such as quantum dots,63,64 FinFET logic circuits,65 memory devices,66 magnetic storage media,67,68 and semiconductor capacitors.69,70
The spontaneous microphase separation of BCPs typically produces regions (grains) of microdomains with short range order resembling a polycrystalline structure, each grain having a different orientation and localized defects.71 However, many device applications of BCPs require defect-free extended areas of periodic BCP microdomains, in some cases with controlled aperiodic features. This can be accomplished by guiding the self-assembly of a BCP film through a chemical and/or topographical template formed on the substrate, a process known as directed self-assembly (DSA).22–29,31,72–74 Defect annealing and pattern alignment are defined by the template based on factors such as preferential surface wetting and the commensurability between the BCP period and the period of the template.75
Computational modeling of BCP DSA has proved valuable in determining the effects of different parameters such as film thickness, polymer–substrate interactions, and geometrical confinement have on the self-assembly process.76,77 However, transitioning BCP DSA to a commercial manufacturing technique requires implementation of an inverse design method to predict the structure of a template that will yield a desired self-assembled BCP pattern. In applications where a complex pattern needs to be manufactured, the role of inverse design is to start from the target structure pattern and determine the optimum directing template design as well as the polymer composition and processing conditions.8–11,13–16,78
Liu and Lai et al.79,80 incorporated DSA with computational lithography (CL) to implement patterns relevant to circuit design. The inverse design flow works iteratively to optimize the photo-mask for lithography. The role of BCP DSA can be handled through models of varying complexity such as theoretically informed coarse-grained (TICG) Monte Carlo (MC),81 dissipative particle dynamics (DPD),82 and self-consistent field theory (SCFT).83 A phenomenological 2D Cahn–Hilliard (CH) model proved to be a fast and practical alternative from full field analysis.80 Furthermore, a very fast DSA model (orders of magnitude faster compared to 3D MC simulations) was developed specifically to target vertical via interconnects where it was very suitable for inverse analysis and optimizing guiding patterns.80 While the details of this simulator were not explicitly revealed, it is described to be empirical, requiring calibration when processing conditions change, and is not transferable to other DSA processes. Nevertheless, the framework was successfully verified on designing FinFET logic circuit elements and a complex set of via patterns. The integrated process of DSA-CL achieved a high enough computation speed to be incorporated in full scale lithography mask design.79,80,84
In order to achieve a reliable inverse design of BCP patterns through DSA, a significantly large parameter space has to be explored. In addition to materials related parameters, DSA process related ones such as the number, size, and shape of guiding elements, element locations, and surface functionalization also have to be defined.10,11 Optimum guiding templates should generally be sparse (i.e. fewer patterned features per unit area than the target BCP pattern), taking advantage of feature density multiplication in order to achieve short fabrication time and high cost efficiency.22–24 Hence, the inverse design problem is generally ill-posed, and reaching the optimum set of parameters demands an efficient optimization algorithm.9,12–17,85
Meta-heuristic algorithms86 provide an attractive approach to solve the inverse problem. They have been used to obtain global or near-global optimum solution due to their capability of finding promising regions in the search space within a reasonable computational time87 by combining rules and randomness to imitate nature.88 Paradiso et al.17 employed the particle swarm optimization (PSO) to generate elaborate structures of multiblock copolymer blends using SCFT (see Fig. 2a). In the implementation of PSO, a set of randomly generated solutions (swarm) propagates in the design space towards the optimum solution over a number of iterations based on the information gathered from the design space and shared by all the members of the swarm.89 The moves of the swarm are controlled by inertia and drag forces to minimize a simple error function. The algorithm successfully optimized the blend composition, and cell size. The adaptation of PSO for BCP inverse design is in its early stage, however, the technique has the potential to comply with more demanding applications.17
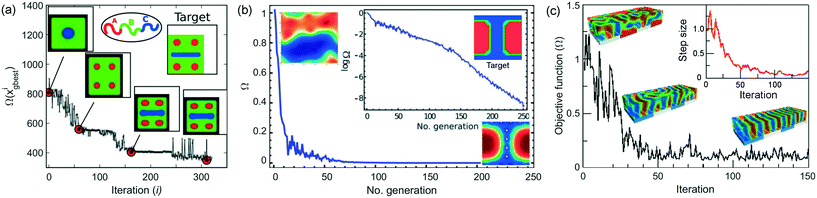 | ||
| Fig. 2 Inverse design problems of BCPs implemented using meta-heuristic algorithms (a) convergence of a multiblock blend formulation designed to stabilize coexistence of a line with spot features using the PSO algorithm. The fitness of the best agent in the swarm is plotted for each iteration with four solutions highlighted as red circles to illustrate evolutionary milestones compared to the target pattern.17 (b) Evolution of the objective function of a target letter “I” pattern using the CMA-ES optimization combined with CH model. The optimal morphology and spot positions are shown on the lower left corner.13 (c) The magnitude of the objective function corresponding to the best offspring as a function of CMA-ES iterations combined with coarse-grained many-body model of BCP for 3× density multiplication of a lamellar structure on a chemical pattern. Adaptation of the search step size is shown in the inset.14 | ||
Evolutionary algorithms widely known as genetic algorithms,12,90 genetic programming,91,92 evolution strategies,93 and evolutionary programming,94,95 have proven successful across various fields for problems with high dimensional combinatorial or continuous search spaces.96 Qin et al.13 utilized a combination of the CH equation and the CMA-ES for the determination of equilibrium BCP morphologies under chemical templating conditions.97 With this BCP model, it was possible to identify the optimal chemical pattern to assemble the BCP into non-regular morphologies. Polymer volume fraction and polymer interaction parameter are initially set to generate a lamellar structure for reference. A predetermined set of chemical anchoring spots are then allowed to move in order to determine their optimum locations within a population of parameter sets. The optimization algorithm iteratively minimizes an objective function that relates the generated topography to the target one. The solution converges when the objective function is minimized. During each generation, the chemical templating points are repositioned through the CMA-ES, and the equilibrium morphology of the polymer is determined using the CH equation as shown in Fig. 2b. The objective function is calculated for the population to allow the CMA-ES to propose a new population of locations of the chemical templating spots. The algorithm converged irrespective of the initial spot arrangements. The optimization technique was later combined with a more sophisticated model that includes molecular details and thermal fluctuations in full 3D simulations.14 In this system, a triblock copolymer system that assembles into lamellar structures was simulated on a periodic chemical pattern to give an approximately 3 to 4 density multiplied pattern (see Fig. 2c). The results were experimentally verified for a P2VP-b-PS-b-P2VP (polystyrene-b-poly-2-vinylpyridine) BCP on a silicon substrate. Even for such level of complexity, the CMA-ES is able to find the optimal set of parameters to produce a given target structure within only NGen ≈ 50 generations using a population of size NPop = 31 and NParam = 3 optimized parameters. Fig. 2c shows a plot of the objective function as a function of the number of generations taken from their study demonstrating this rapid convergence. This corresponds to NGenNPop = 1550 independent simulations. For a traditional forward approach, these parameters would have been divided into a search vector of length NBin that would require (NBin)NParam independent forward simulations to be performed. A typical search vector of NBin = 16 searching NParam = 3 parameters would require 163 = 4096 simulations. The number of forward simulations will rapidly increase when exploring a larger parameter space NParam, compared to the CMA-ES algorithm, assuming NGen stays roughly constant.
Inverse design of topographical templating has also proven to be successful in predicting considerably complex patterns with bends, terminations, and junctions, for open and closed domains.10 The topographical templates consist of posts with specific surface wetting condition that can be placed at different locations to control the BCP pattern that forms. Hannon et al.11 introduced the combination of a Monte-Carlo-like optimization search algorithm with an SCFT simulation to determine the optimum post locations. A schematic comparing the forward design methods used in prior work77,98 with these inverse methods in shown in Fig. 3. In this formalism, the target density profile is synthesized using a tiling technique of simple segments. The target density is held constant, while a fixed number of posts are allowed to be relocated. For every step, a single post is moved in a series of random walks to a new position and the potential fields are allowed to evolve to a steady state. The energy of the system is calculated and the post move is accepted if it results in an overall reduction to the system energy, otherwise after failing a certain number of steps, the post is returned to its original location. The formalism was further developed to include the polymer volume fraction and the number of posts as variables.10 A fidelity factor relating the density distribution in the generated and the target polymer densities is defined to gauge the optimum selected parameters. This fidelity factor is essentially the reciprocal inverse of an objective function which is maximized rather than minimized. The optimized post number and locations were verified experimentally for a PS-b-PDMS (polystyrene-b-polydimethylsiloxane) system where electron-beam lithography was employed to generate posts from HSQ (hydrogen silsesquioxane, an electron-beam resist) that were further functionalized to preferentially attract PDMS. It was interesting to note that the 2D SCFT simulations were sufficient to predict experimental results since the interactions are primarily constrained by the in-plane topography. Such work can be extended to find optimum interaction parameters χ and degree of polymerization N to further explore the possibility of different chemistries and chain architectures to produce a given target structure.
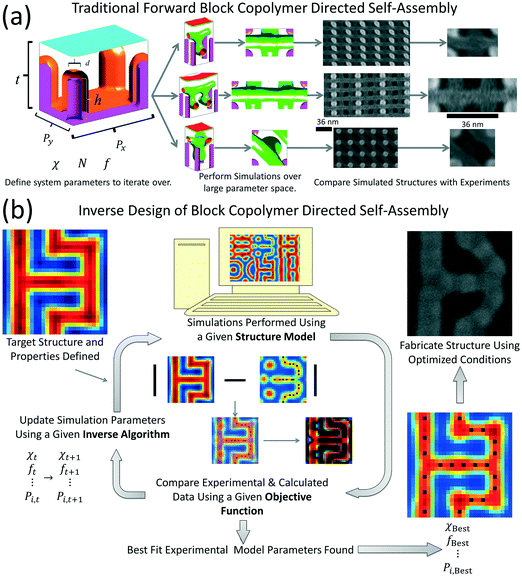 | ||
| Fig. 3 (a) Schematic showing from left to right how the general forward design process occurred in modeling the directed self-assembly of BCPs.76,98 (b) Schematic showing how the inverse design methodology works for the directed self-assembly of BCPs.10,77 | ||
The BCPs discussed in the context of inverse DSA design so far have generally been simple diblocks modeled using Gaussian chain statistics (i.e., coil–coil BCPs). The formalism provided can easily be expanded to more complicated systems where the chains are more rod or wormlike99,100 in behavior including rod–coil, rod–rod, and bottlebrush copolymers (where the backbone chain will likely exhibit rod/wormlike behavior). Using such models simply changes the structure model used as diagramed in Fig. 3b, and changes the total number of parameters optimized by the inverse search algorithm. As an example, rod–coil systems have been studied using SCFT models101–109 with the rod block modeled as a wormlike chain. These models add the additional degrees of freedom in the rod persistence length λ, the relative length of the rod segments to the Gaussian coil radius of gyration β, and Maier–Saupe interaction parameter μ to model the dipole–dipole interactions between neighboring rods.99,100 In principle, these parameters can all be optimized just as χN, f, and the DSA feature positions by algorithms such as the CMA-ES. Additionally, more complicated objective functions may be necessary to target not only the local density field profile desired for the constituent species, but also include a target orientation field for the rod/wormlike segments. To our knowledge, no study using such models has been published.
In order to implement the inverse design process with ever more increasingly complex physics-based models, more advanced inverse search algorithms need to be developed. Of the approaches discussed in this review, the CMA-ES algorithm appears to be one of the most efficient algorithms based on the prior studies as well as our own examination of it relative to other algorithms due to its speed of convergence and self-tuning nature.54 The algorithm does have an inherent disadvantage in not necessarily converging initially to the global objective function minima with the propensity for this to occur increasing with a larger parameter search space. Methods such as the PSO method17 may be able to overcome these limitations, but there are still inherent biases in the search in getting trapped in local minima, especially when there is high density of metastable states around the true energy minimum as in the case of large 3D simulations of bulk BCPs.12,16 Stochastic based methods such as Markov chain Monte Carlo will eventually always find the global minima by randomly walking through the search space with an optimized step size, but this requires very long calculations that do not gain much search speed over just doing a complete forward search parameter sweep. A possible approach to alleviate the inherent issues with the CMA-ES and PSO approaches in getting trapped in local minima solutions is to have a wrapper algorithm around the inverse search algorithm that resets the algorithm when the objective function saturates for an extended number of generations but keeps the knowledge of the best solution found, thus being able to search other parameter combinations that may have been missed due to a rapid convergence into a local minimum.
Conclusion and outlook
We have illustrated several research areas within the self-assembling materials community where inverse design strategies have been successful in finding the simulation and/or experimental conditions to produce a variety of designed structures or target properties, with particular emphasis on BCP DSA. These methods all share similar aspects in having to first define a set of target structures or material properties, creating an objective function based on those properties, selecting an appropriate simulation methodology that probes those structures or properties under a given parameter space, and ultimately through an inverse optimization routine finds the best set of parameters to yield the desired structure and/or properties. Of the inverse algorithms examined, self-tuning evolutionary based approaches such as the CMA-ES and PSO appear to be some of the best ways to reach optimal solutions in a timely manner, but these methods still have an inherent issue in getting trapped in local minima. Future development of algorithms that address these issues would be a great benefit in the inverse design process, especially as the physics-based models that the algorithms optimize become more complex with more degrees of freedom. In this respect, it is likely that recent advances in other fields will bear fruit on accelerating the inverse design paradigm in self-assembly materials. Of particular interest are neural networks (NN) and artificial intelligence (AI) which have shown immense promise in the discovery of organic molecules.110 Such methods seem to thrive when optimizing properties in high dimensional systems lacking a particular structure.Some interesting new areas of exploration in terms of inverse design would be a hybrid experimental–computational framework in which one could have direct in situ experimental input into the computation to adjust parameters on the fly during the optimization processes. While ambitious, this would provide a complete inverse design platform where features from the physical system as well as those from simulations are captured simultaneously.8,54,55,111 Both macroscopic physical features and computational molecular features are complementary, so it is foreseeable that we will learn much of the physics of these assembly processes by understanding their underlying correlations. Such correlations will become clearly apparent as one optimizes the building blocks to obtain a target system. In particular, the time coordinate does not seem to enter such protocols, but experimentally it is a very important variable. By controlling processing pathways, it is possible to frustrate the materials assembly and force the system to arrange into a particular metastable structure.112 This might be a new avenue in inverse design that could be quite useful and could also provide us with controlled “synthesis” routes and robust assembly pathways.
The inverse design paradigm has been successful for BCPs and for colloid assembly, but the methodology is general enough to be applied to other soft material systems where models are well developed for the given system of interest. Some examples are DNA nanotechnology and de novo protein design which have gathered much recent interest. It is without a doubt that optimization in these areas will yield also optimized sequences for given DNA and protein folding structures.113,114 Overall, it is foreseeable that the future of materials science research, and in particular self-assembling materials, will rely more extensively on inverse design methods to obtain tangible solutions because the parameter search spaces for new systems become more complex and practically unsearchable under traditional methods.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Support of NSF award 1246740 (Alexander-Katz, Ross) and 1606911 (Ross) is gratefully acknowledged. Adam Hannon acknowledges financial support in the form of a Cooperative Agreement Grant (award number 70NANB16H005) through Georgetown University in the Professional Research Experience Program.References
- G. B. Olson, Computational design of hierarchically structured materials, Science, 1997, 277(5330), 1237–1242 CrossRef CAS.
- G. J. Snyder and E. S. Toberer, Complex thermoelectric materials, Nat. Mater., 2008, 7(2), 105–114 CrossRef CAS PubMed.
- P. T. Mather, X. F. Luo and I. A. Rousseau, Shape Memory Polymer Research, Annu. Rev. Mater. Res., 2009, 39, 445–471 CrossRef CAS.
- E. H. Sargent, Colloidal quantum dot solar cells, Nat. Photonics, 2012, 6(3), 133–135 CrossRef CAS.
- A.-V. Ruzette and L. Leibler, Block copolymers in tomorrow's plastics, Nat. Mater., 2005, 4(1), 19–31 CrossRef CAS PubMed.
- A. Jain, J. A. Bollinger and T. M. Truskett, Inverse Methods for Material Design, AIChE J., 2014, 60(8), 2732–2740 CrossRef.
- S. Torquato, Optimal Design of Heterogeneous Materials, Annu. Rev. Mater. Res., 2010, 40, 101–129 CrossRef CAS.
- S. Paradiso, et al., Field-theoretic simulations of block copolymers: design and solvent annealing, Sandia National Laboratories, 2012 Search PubMed.
- M. Z. Miskin, et al., Turning statistical physics models into materials design engines, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(1), 34–39 CrossRef CAS PubMed.
- A. F. Hannon, et al., Optimizing topographical templates for directed self-assembly of block copolymers via inverse design simulations, Nano Lett., 2013, 14(1), 318–325 CrossRef PubMed.
- A. F. Hannon, et al., Inverse design of topographical templates for directed self-assembly of block copolymers, ACS Macro Lett., 2013, 2(3), 251–255 CrossRef CAS.
- C. L. Tsai, K. T. Delaney and G. H. Fredrickson, Genetic Algorithm for Discovery of Globally Stable Phases in Block Copolymers, Macromolecules, 2016, 49(17), 6558–6567 CrossRef CAS.
- J. Qin, et al., Evolutionary pattern design for copolymer directed self-assembly, Soft Matter, 2013, 9(48), 11467–11472 RSC.
- G. S. Khaira, et al., Evolutionary optimization of directed self-assembly of triblock copolymers on chemically patterned substrates, ACS Macro Lett., 2014, 3(8), 747–752 CrossRef CAS.
- H. M. Jaeger and J. J. de Pablo, Perspective: Evolutionary design of granular media and block copolymer patterns, APL Mater., 2016, 4(5), 053209 CrossRef.
- M. R. Khadilkar, S. Paradiso, K. T. Delaney and G. H. Fredrickson, Inverse Design of Bulk Morphologies in Multiblock Polymers Using Particle Swarm Optimization, Macromolecules, 2017, 50(17), 6702–6709 CrossRef CAS.
- S. P. Paradiso, K. T. Delaney and G. H. Fredrickson, Swarm intelligence platform for multiblock polymer inverse formulation design, ACS Macro Lett., 2016, 5(8), 972–976 CrossRef CAS.
- E. Edlund, O. Lindgren and M. N. Jacobi, Designing isotropic interactions for self-assembly of complex lattices, Phys. Rev. Lett., 2011, 107(8), 085503 CrossRef CAS PubMed.
- G. M. Whitesides and B. Grzybowski, Self-assembly at all scales, Science, 2002, 295(5564), 2418–2421 CrossRef CAS PubMed.
- S. Torquato, Inverse optimization techniques for targeted self-assembly, Soft Matter, 2009, 5(6), 1157–1173 RSC.
- E. Edlund, O. Lindgren and M. N. Jacobi, Designing isotropic interactions for self-assembly of complex lattices, Phys. Rev. Lett., 2011, 107(8), 085503 CrossRef CAS PubMed.
- R. Ruiz, et al., Density multiplication and improved lithography by directed block copolymer assembly, Science, 2008, 321(5891), 936–939 CrossRef CAS PubMed.
- J. Y. Cheng, et al., Dense Self-Assembly on Sparse Chemical Patterns: Rectifying and Multiplying Lithographic Patterns Using Block Copolymers, Adv. Mater., 2008, 20(16), 3155–3158 CrossRef CAS.
- C.-C. Liu, et al., Chemical patterns for directed self-assembly of Lamellae-forming block copolymers with density multiplication of features, Macromolecules, 2013, 46(4), 1415–1424 CrossRef CAS.
- I. Bita, et al., Graphoepitaxy of self-assembled block copolymers on two-dimensional periodic patterned templates, Science, 2008, 321(5891), 939–943 CrossRef CAS PubMed.
- F. A. Detcheverry, et al., Interpolation in the directed assembly of block copolymers on nanopatterned substrates: simulation and experiments, Macromolecules, 2010, 43(7), 3446–3454 CrossRef CAS.
- Q.-y. Tang and Y.-q. Ma, High density multiplication of graphoepitaxy directed block copolymer assembly on two-dimensional lattice template, Soft Matter, 2010, 6(18), 4460–4465 RSC.
- M. P. Stoykovich, et al., Directed self-assembly of block copolymers for nanolithography: Fabrication of isolated features and essential integrated circuit geometries, ACS Nano, 2007, 1(3), 168–175 CrossRef CAS PubMed.
- J. B. Chang, H. K. Choi, A. F. Hannon, A. Alexander-Katz, C. A. Ross and K. K. Berggren, Design rules for self-assembled block copolymer patterns using tiled templates, Nat. Commun., 2014, 5, 3305 Search PubMed.
- R. Bouchet, et al., Single-ion BAB triblock copolymers as highly efficient electrolytes for lithium-metal batteries, Nat. Mater., 2013, 12(5), 452–457 CrossRef CAS PubMed.
- E. Kim, et al., Directed Assembly of High Molecular Weight Block Copolymers: Highly Ordered Line Patterns of Perpendicularly Oriented Lamellae with Large Periods, ACS Nano, 2013, 7(3), 1952–1960 CrossRef CAS PubMed.
- A. Urbas, et al., Tunable block copolymer/homopolymer photonic crystals, Adv. Mater., 2000, 12(11), 812–814 CrossRef CAS.
- A. M. Urbas, et al., Bicontinuous cubic block copolymer photonic crystals, Adv. Mater., 2002, 14(24), 1850–1853 CrossRef CAS.
- I. Botiz and S. B. Darling, Optoelectronics using block copolymers, Mater. Today, 2010, 13(5), 42–51 CrossRef CAS.
- P. W. K. Rothemund, N. Papadakis and E. Winfree, Algorithmic self-assembly of DNA Sierpinski triangles, PLoS Biol., 2004, 2(12), 2041–2053 CAS.
- P. W. K. Rothemund, Folding DNA to create nanoscale shapes and patterns, Nature, 2006, 440(7082), 297–302 CrossRef CAS PubMed.
- B. Wei, M. J. Dai and P. Yin, Complex shapes self-assembled from single-stranded DNA tiles, Nature, 2012, 485(7400), 623 CrossRef CAS PubMed.
- E. Winfree, et al., Design and self-assembly of two-dimensional DNA crystals, Nature, 1998, 394(6693), 539–544 CrossRef CAS PubMed.
- D. Nykypanchuk, et al., DNA-guided crystallization of colloidal nanoparticles, Nature, 2008, 451(7178), 549–552 CrossRef CAS PubMed.
- C. Zhang, et al., A general approach to DNA-programmable atom equivalents, Nat. Mater., 2013, 12(8), 741–746 CrossRef CAS PubMed.
- C. A. Mirkin, et al., A DNA-based method for rationally assembling nanoparticles into macroscopic materials, Nature, 1996, 382(6592), 607–609 CrossRef CAS PubMed.
- É. Marcotte, F. H. Stillinger and S. Torquato, Communication: Designed diamond ground state via optimized isotropic monotonic pair potentials, J. Chem. Phys., 2013, 138, 061101 CrossRef PubMed.
- A. Jain, J. R. Errington and T. M. Truskett, Inverse design of simple pairwise interactions with low-coordinated 3D lattice ground states, Soft Matter, 2013, 9(14), 3866–3870 RSC.
- M. Watzlawek, C. N. Likos and H. Lowen, Phase diagram of star polymer solutions, Phys. Rev. Lett., 1999, 82(26), 5289–5292 CrossRef CAS.
- M. C. Rechtsman, F. H. Stillinger and S. Torquato, Optimized interactions for targeted self-assembly: application to a honeycomb lattice, Phys. Rev. Lett., 2005, 95(22), 228301 CrossRef PubMed.
- M. C. Rechtsman, F. H. Stillinger and S. Torquato, Self-assembly of the simple cubic lattice with an isotropic potential, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74(2), 021404 CrossRef PubMed.
- M. C. Rechtsman, F. H. Stillinger and S. Torquato, Synthetic diamond and wurtzite structures self-assemble with isotropic pair interactions, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75(3), 031403 CrossRef PubMed.
- G. Zhang, F. H. Stillinger and S. Torquato, Probing the limitations of isotropic pair potentials to produce ground-state structural extremes via inverse statistical mechanics, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88(4), 042309 CrossRef CAS PubMed.
- C. L. Phillips and G. A. Voth, Discovering crystals using shape matching and machine learning, Soft Matter, 2013, 9(35), 8552–8568 RSC.
- D. F. Sunday, et al., Template–polymer commensurability and directed self-assembly block copolymer lithography, J. Polym. Sci., Part B: Polym. Phys., 2015, 53(8), 595–603 CrossRef CAS.
- M. Wormington, et al., Characterization of structures from X-ray scattering data using genetic algorithms, Philos. Trans. R. Soc., A, 1999, 357(1761), 2827–2848 CrossRef CAS.
- A. Ulyanenkov, K. Omote and J. Harada, The genetic algorithm: refinement of X-ray reflectivity data from multilayers and thin films, Phys. B, 2000, 283(1), 237–241 CrossRef CAS.
- A. Kudla, Application of the genetic algorithms in spectroscopic ellipsometry, Thin Solid Films, 2004, 455, 804–808 CrossRef.
- A. F. Hannon, et al., Advancing x-ray scattering metrology using inverse genetic algorithms, J. Micro/Nanolithogr., MEMS, MOEMS, 2016, 15(3), 034001 CrossRef PubMed.
- G. Khaira, M. Doxastakis, A. Bowen, J. Ren, H. S. Suh, T. Segal-Peretz, X. Chen, C. Zhou, A. F. Hannon, N. J. Ferrier, V. Vishwanath, D. F. Sunday, R. Gronheid, R. J. Kline, J. J. de Pablo and P. F. Nealey, Derivation of Multiple Covarying Material and Process Parameters Using Physics-Based Modeling of X-ray Data, Macromolecules, 2017, 50(19), 7783–7793 CrossRef CAS.
- S. Santos, et al., The Mendeleev–Meyer force project, Nanoscale, 2016, 8(40), 17400–17406 RSC.
- F. S. Bates and G. H. Fredrickson, Block copolymers—designer soft materials, Phys. Today, 2008, 52(2), 32–38 CrossRef.
- C. T. Black, et al., Polymer self assembly in semiconductor microelectronics, IBM J. Res. Dev., 2007, 51(5), 605–633 CrossRef CAS.
- H. Yi, et al., Flexible Control of Block Copolymer Directed Self-Assembly using Small, Topographical Templates: Potential Lithography Solution for Integrated Circuit Contact Hole Patterning, Adv. Mater., 2012, 24(23), 3107–3114 CrossRef CAS PubMed.
- G. S. Doerk, et al., Enabling complex nanoscale pattern customization using directed self-assembly, Nat. Commun., 2014, 5, 5805 CrossRef PubMed.
- Y. Du, et al., Block copolymer directed self-assembly (DSA) aware contact layer optimization for 10 nm 1D standard cell library, in 2013 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), IEEE, 2013 Search PubMed.
- H. Yi, et al., A general design strategy for block copolymer directed self-assembly patterning of integrated circuits contact holes using an alphabet approach, Nano Lett., 2015, 15(2), 805–812 CrossRef CAS PubMed.
- M. Park, et al., Block copolymer lithography: periodic arrays of∼ 1011 holes in 1 square centimeter, Science, 1997, 276(5317), 1401–1404 CrossRef CAS.
- R. Li, et al., Dense arrays of ordered GaAs nanostructures by selective area growth on substrates patterned by block copolymer lithography, Appl. Phys. Lett., 2000, 76(13), 1689–1691 CrossRef CAS.
- H. Tsai, et al., Two-dimensional pattern formation using graphoepitaxy of PS-b-PMMA block copolymers for advanced FinFET device and circuit fabrication, ACS Nano, 2014, 8(5), 5227–5232 CrossRef CAS PubMed.
- K. Guarini, et al., Low voltage, scalable nanocrystal FLASH memory fabricated by templated self assembly, in Electron Devices Meeting, 2003. IEDM'03 Technical Digest. IEEE International, IEEE, 2003 Search PubMed.
- J. Y. Cheng, et al., Formation of a cobalt magnetic dot array via block copolymer lithography, Adv. Mater., 2001, 13(15), 1174–1178 CrossRef CAS.
- K. Naito, et al., 2.5-inch disk patterned media prepared by an artificially assisted self-assembling method, IEEE Trans. Magn., 2002, 38(5), 1949–1951 CrossRef CAS.
- C. Black, et al., Integration of self-assembled diblock copolymers for semiconductor capacitor fabrication, Appl. Phys. Lett., 2001, 79(3), 409–411 CrossRef CAS.
- C. T. Black, et al., High-capacity, self-assembled metal-oxide-semiconductor decoupling capacitors, IEEE Electron Device Lett., 2004, 25(9), 622–624 CrossRef CAS.
- X. D. Gu, et al., High Aspect Ratio Sub-15 nm Silicon Trenches From Block Copolymer Templates, Adv. Mater., 2012, 24(42), 5688–5694 CrossRef CAS PubMed.
- J. Y. Cheng, et al., Templated self-assembly of block copolymers: Top-down helps bottom-up, Adv. Mater., 2006, 18(19), 2505–2521 CrossRef CAS.
- S. O. Kim, et al., Epitaxial self-assembly of block copolymers on lithographically defined nanopatterned substrates, Nature, 2003, 424(6947), 411 CrossRef CAS PubMed.
- S. Darling, Directing the self-assembly of block copolymers, Prog. Polym. Sci., 2007, 32(10), 1152–1204 CrossRef CAS.
- A. Tavakkoli K. G., S. M. Nicaise, K. R. Gadelrab, A. Alexander-Katz, C. A. Ross and K. K. Berggren, Multilayer block copolymer meshes by orthogonal self-assembly, Nat. Commun., 2016, 7, 10518 CrossRef PubMed.
- K. G. A. Tavakkoli, et al., Sacrificial-Post Templating Method for Block Copolymer Self-Assembly, Small, 2014, 10(3), 493–499 CrossRef PubMed.
- K. G. A. Tavakkoli, et al., Rectangular Symmetry Morphologies in a Topographically Templated Block Copolymer, Adv. Mater., 2012, 24(31), 4249 CrossRef PubMed.
- G. Ouaknin, et al., Shape optimization for DSA, in Proc. SPIE, 2016 Search PubMed.
- C.-C. Liu, et al., Progress towards the integration of optical proximity correction and directed self-assembly of block copolymers with graphoepitaxy, in SPIE Advanced Lithography, International Society for Optics and Photonics, 2012 Search PubMed.
- K. Lai, et al., Computational lithography platform for 193i-guided directed self-assembly, in SPIE Advanced Lithography, International Society for Optics and Photonics, 2014 Search PubMed.
- F. A. Detcheverry, et al., Monte Carlo simulation of coarse grain polymeric systems, Phys. Rev. Lett., 2009, 102(19), 197801 CrossRef PubMed.
- R. D. Groot and P. B. Warren, Dissipative particle dynamics: bridging the gap between atomistic and mesoscopic simulation, J. Chem. Phys., 1997, 107(11), 4423 CrossRef CAS.
- G. H. Fredrickson, The equilibrium theory of inhomogeneous polymers, Clarendon, 2006 Search PubMed.
- K. Lai, et al., Design technology co-optimization assessment for directed self-assembly-based lithography: design for directed self-assembly or directed self-assembly for design?, J. Micro/Nanolithogr., MEMS, MOEMS, 2017, 16(1), 013502 CrossRef.
- S. Abrams and L. Pang, Fast inverse lithography technology, in Proc. SPIE, 2006 Search PubMed.
- I. Fister Jr, et al., A brief review of nature-inspired algorithms for optimization, 2013, arXiv preprint arXiv:1307.4186.
- A. Kaveh, Particle swarm optimization, in Advances in Metaheuristic Algorithms for Optimal Design of Structures, Springer, 2014, pp. 9–40 Search PubMed.
- K. S. Lee and Z. W. Geem, A new meta-heuristic algorithm for continuous engineering optimization: harmony search theory and practice, Comput. Methods Appl. Mech. Eng., 2005, 194(36), 3902–3933 CrossRef.
- R. Hassan, et al., A comparison of particle swarm optimization and the genetic algorithm, American Institute of Aeronautics and Astronautics, 2004 Search PubMed.
- D. E. Goldberg and J. H. Holland, Genetic algorithms and machine learning, Machine learning, 1988, vol. 32, pp. 95–99 Search PubMed.
- J. R. Koza, Genetic programming: on the programming of computers by means of natural selection, MIT press, 1992, vol. 1 Search PubMed.
- M. A. Keane, et al., Genetic programming IV: Routine human-competitive machine intelligence, Springer, 2006, vol. 5 Search PubMed.
- H.-P. P. Schwefel, Evolution and optimum seeking: the sixth generation, John Wiley & Sons, Inc., 1993 Search PubMed.
- D. B. Fogel, Evolutionary computation: toward a new philosophy of machine intelligence, John Wiley & Sons, 2006, vol. 1 Search PubMed.
- L. J. Fogel, A. J. Owens and M. J. Walsh, Artificial intelligence through simulated evolution, 1966 Search PubMed.
- T. Bäck, R. Breukelaar and L. Willmes, Inverse design of cellular automata by genetic algorithms: an unconventional programming paradigm, in Unconventional Programming Paradigms, Springer, 2005, pp. 161–172 Search PubMed.
- A. E. Eiben and J. E. Smith, Introduction to evolutionary computing, Springer, 2003 Search PubMed.
- A. Tavakkoli K. G., K. W. Gotrik, A. F. Hannon, A. Alexander-Katz, C. A. Ross and K. K. Berggren, Templating three-dimensional self-assembled structures in bilayer block copolymer films, Science, 2012, 336(6086), 1294–1298 CrossRef CAS PubMed.
- V. Pryamitsyn and V. Ganesan, Self-assembly of rod–coil block copolymers, J. Chem. Phys., 2004, 120(12), 5824–5838 CrossRef CAS PubMed.
- B. D. Olsen and R. A. Segalman, Self-assembly of rod–coil block copolymers, Mater. Sci. Eng., R, 2008, 62(2), 37–66 CrossRef.
- W. Song, et al., Phase behavior of semiflexible-coil diblock copolymers: a hybrid numerical SCFT approach, Soft Matter, 2011, 7(3), 929–938 RSC.
- W. Song, et al., New numerical implementation of self-consistent field theory for semiflexible polymers, Macromolecules, 2009, 42(16), 6300–6309 CrossRef CAS.
- Y. Jiang, W.-Y. Zhang and J. Z. Chen, Dependence of the disorder-lamellar stability boundary of a melt of asymmetric wormlike A B diblock copolymers on the chain rigidity, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84(4), 041803 CrossRef PubMed.
- J. Gao, et al., Self-assembly of semiflexible block copolymers: 2D numerical implementation of self-consistent field theory, Soft Matter, 2011, 7(11), 5208–5216 RSC.
- J. Gao, P. Tang and Y. Yang, Non-lamellae structures of coil–semiflexible diblock copolymers, Soft Matter, 2013, 9(1), 69–81 RSC.
- Y. Jiang and J. Z. Chen, Influence of Chain Rigidity on the Phase Behavior of Wormlike Diblock Copolymers, Phys. Rev. Lett., 2013, 110(13), 138305 CrossRef PubMed.
- Y. Jiang and J. Z. Chen, Self-consistent field theory and numerical scheme for calculating the phase diagram of wormlike diblock copolymers, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88(4), 042603 CrossRef PubMed.
- S. Li, Y. Jiang and J. Z. Chen, Phase transitions in semiflexible–rod diblock copolymers: a self-consistent field theory, Soft Matter, 2014, 10(44), 8932–8944 RSC.
- J. Tang, et al., Phase Diagram of Rod–Coil Diblock Copolymer Melts, Macromolecules, 2015, 48(24), 9060–9070 CrossRef CAS.
- D. K. Duvenaud, et al., Convolutional networks on graphs for learning molecular fingerprints, in Advances in neural information processing systems, 2015 Search PubMed.
- K.-H. Tu, Block Copolymer Self-Assembly: Lithography, Magnetic Nanofabrication, and Optimization, Ph.D. thesis, Massachusetts Institute of Technology, 2017 Search PubMed.
- D.-W. Sun and M. Müller, Process-accessible states of block copolymers, Phys. Rev. Lett., 2017, 118(6), 067801 CrossRef PubMed.
- P. Bradley, K. M. Misura and D. Baker, Toward high-resolution de novo structure prediction for small proteins, Science, 2005, 309(5742), 1868–1871 CrossRef CAS PubMed.
- L. Jiang, et al., De novo computational design of retro-aldol enzymes, Science, 2008, 319(5868), 1387–1391 CrossRef CAS PubMed.
Footnote |
| † Guest researcher. |
| This journal is © The Royal Society of Chemistry 2017 |